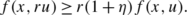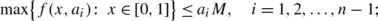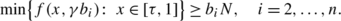Successive iteration and positive solutions for boundary value problem of nonlinear fractional q-difference equation

Abstract

In this paper, we investigate the positive solutions for a class of nonlinear q-fractional boundary value problem. We not only obtain the existence and uniqueness of positive solutions, but also establish the iterative schemes for approximating the solutions, which is benefit for computation and application.

1 Introduction

Consider the following boundary value problem of nonlinear fractional q-difference equation:

where f is a nonnegative continuous function and $D_{q}^{\alpha}$ is the fractional q-derivative of the Riemann-Liouville type.

Fractional differential calculus is a discipline to which many researchers are dedicating their time, perhaps because of its demonstrated applications in various fields of science and engineering [1]. Recently, there are many papers dealing with the boundary value problem of fractional differential equations, see [2–5] and references therein.

More recently, an attempt is being made to develop a discrete fractional calculus, and some results are already available in the literature [6–14].

The q-difference calculus or quantum calculus is an old subject that was initially developed by Jackson [15, 16]. Its basic definitions and properties can be found in [17]. The fractional q-difference calculus had its origin in the works by Al-Salam [18] and Agarwal [19]. More recently, Maybe due to the explosion in research within the fractional differential calculus setting, new developments in this theory of fractional q-difference calculus were made, see [20, 21].

The question of the existence of positive solutions for fractional q-difference boundary value problems is in its infancy, see [22–25]. In particular, the following problem was studied by Ferreira [24],

Although problem (P) is particular case of problem (P′), our results are new and interesting. In fact, the case that boundary conditions are equal to 0 was also studied extensively, see [3, 5, 12, 14]. In addition, as far as we know, there is few paper concerning the uniqueness of positive solutions for fractional q-difference boundary value problems. Main results in [22–25] were all concerned with the existence of at lest one positive solutions. But in this paper, we study uniqueness and multiplicity of positive solutions. Moreover, our methods are different from those in [22–25]. Our results can not only guarantee the existence of positive solution, but also be applied to construct an iterative scheme for approximating it, which can help us to find the solution and is important for evaluation and application.

This paper is organized as follows. In Sect. 2, some preliminaries are presented. In Sect. 3, discuss the existence and uniqueness of positive solutions for problem (P). By means of fixed point theory of u ₀ concave operator, we first obtain the uniqueness of solution for problem (P). Then, by using the monotone iterative technique and the cone expansion and compression fixed point theorem of norm type, we establish the multiplicity and uniqueness of positive solutions for problem (P). Some examples are also given to illustrate our main results.

2 Preliminaries

Let q∈(0,1) and define

$$ [a]_{q}=\frac{1-q^{a}}{1-q}, \quad a\in\mathbb{R}. $$

(2.1)

The q-analogue of the power function (a−b)ⁿ with n∈ℕ₀ is

$$ (a-b)^{0}=1,\qquad(a-b)^{n}=\prod _{k=0}^{n-1}\bigl(a-bq^{k}\bigr), \quad n\in \mathbb{ N},\ a,b\in\mathbb{R}. $$

(2.2)

More generally, if a∈ℝ, then

$$ (a-b)^{(\alpha)}=a^{\alpha}\prod _{n=0}^{\infty} \frac {a-bq^{n}}{a-bq^{\alpha+n}}. $$

(2.3)

Note that, if b=0 then a ^(α)=a ^α. The q-gamma function is defined by

$$ \varGamma_{q}(x) =\frac{(1-q)^{(x-1)}}{(1-q)^{x-1}},\quad x\in\mathbb {R}\setminus \{0,-1,-2,\dots\} $$

(2.4)

and satisfies Γ _q (x+1)=[x] _q Γ _q (x). The q-derivative of a function f is here defined by

$$ (D_{q}f) (x)=\frac{f(x)-f(qx)}{(1-q)x},\qquad(D_{q}f) (0)=\lim _{x\rightarrow0}(D_{q}f) (x) $$

(2.5)

and q-derivative of higher order by

$$ \bigl(D_{q}^{0}f\bigr) (x)=f(x),\qquad\bigl(D_{q}^{n}f \bigr) (x)=D_{q}\bigl(D_{q}^{n-1}f\bigr) (x),\quad n\in \mathbb{N}. $$

(2.6)

The q-integral of a function f defined in the interval [0,b] is given by

$$ (I_{q}f) (x)=\int_{0}^{x}f(t)d_{q}t=x(1-q) \sum_{n=0}^{\infty }f \bigl(xq^{n}\bigr)q^{n},\quad x\in[0,b]. $$

(2.7)

If a∈[0,b] and f defined in the interval [0,b], its integral from a to b is defined by

$$ \int_{a}^{b}f(t)d_{q}t=\int _{0}^{b}f(t)d_{q}t-\int _{0}^{a}f(t)d_{q}t. $$

(2.8)

Remark 2.1

([26])

If a=bq ⁿ,n∈ℕ and f(t)≥g(t) on [a,b], then

$$\int_{a}^{b}f(t)d_{q}t\geq\int _{a}^{b}g(t)d_{q}t. $$

Similarly as done for derivatives, an operator $I_{q}^{n}$ can be defined, namely,

$$ \bigl(I_{q}^{0}f\bigr) (x)=f(x),\qquad\bigl(I_{q}^{n}f \bigr) (x)=I_{q}\bigl(I_{q}^{n-1}f\bigr) (x),\quad n\in \mathbb{N}. $$

(2.9)

The fundamental theorem of calculus applies to these operators I _q and D _q , i.e.,

$$ (D_{q}I_{q}f) (x)=f(x) $$

(2.10)

and if f is continuous at x=0, then

$$ (I_{q}D_{q}f) (x)=f(x)-f(0). $$

(2.11)

Basic properties of the two operators can be found in [23]. We now point out three formulas that will be used later ( _i D _q denotes the derivative with respect to variable i)

Remark 2.2

([23])

We note that if α>0 and a≤b≤t, then

$$ (t-a)^{(\alpha)}\geq(t-b)^{(\alpha)}. $$

(2.12)

Definition 2.3

([19])

Let α≥0 and f be a function defined on [0,1]. The fractional q-integral of the Riemann-Liouville type is $(I_{q}^{0}f)(x)=f(x)$ and

$$ \bigl(I_{q}^{\alpha}f\bigr) (x)=\frac{1}{\varGamma_{q}(\alpha)}\int _{0}^{x}(x-qt)^{(\alpha-1)}f(t)d_{q}t, \quad\alpha>0,\ x\in[0,1]. $$

(2.13)

Definition 2.4

([23–25])

The fractional q-derivative of the Riemann-Liouville type of order α≥0 is defined by $(D_{q}^{0}f)(x)=f(x)$ and

$$ \bigl(D_{q}^{\alpha}f\bigr) (x)=\bigl(D_{q}^{m}I_{q}^{m-\alpha}f \bigr) (x),\quad\alpha >0, $$

(2.14)

where m is the smallest integer greater than or equal to α.

Next, we list some properties that are already known in the literature.

Lemma 2.5

([23–25])

Let α,β≥0 and f be a function defined on [0,1]. Then, the next formulas hold:

• 1. $(I_{q}^{\beta}I_{q}^{\alpha}f)(x)=(I_{q}^{\alpha+\beta}f)(x)$,

• 2. $(D_{q}^{\alpha}I_{q}^{\alpha}f)(x)=f(x)$.

Lemma 2.6

([23–25])

Let α>0 and p be a positive integer. Then, the following equality holds:

$$ \bigl(I_{q}^{\alpha}D_{q}^{p}f\bigr) (x)= \bigl(D_{q}^{p}I_{q}^{\alpha}f\bigr) (x)- \sum _{k=0}^{p-1} \frac{x^{\alpha-p+k}}{\varGamma_{q}(\alpha +k-p+1)}\bigl(D_{q}^{k}f\bigr) (0). $$

(2.15)

Lemma 2.7

([24])

Let u∈C[0,1], then the boundary value problem

$$ \begin{cases} (D_{q}^{\alpha}y)(x)=- u(x), \quad0<x<1,\ 2<\alpha\leq 3,\\ \noalign{\vspace*{1pt}} y(0)=(D_{q}y)(0)=0,\quad (D_{q}y)(1)=0,\end{cases} $$

(2.16)

has a unique solution

$$ y(x)=\int_{0}^{1}G(x,qt)u(t)d_{q}t, $$

(2.17)

where

$$ G(x,t)=\frac{1}{\varGamma_{q}(\alpha)} \left \{ \begin{array}{l@{\quad }l} (1-t)^{(\alpha-2)}x^{\alpha-1}-(x-t)^{(\alpha-1)},&0\leq t\leq x\leq1,\\[5pt] (1-t)^{(\alpha-2)}x^{\alpha-1},&0\leq x\leq t\leq1. \end{array} \right . $$

(2.18)

Lemma 2.8

([24])

Function G defined above satisfies the following conditions:

(2.19)

(2.20)

Remark 2.9

If we let 0<τ<1, then 0<τ ^α−1<1 and

(2.21)

Moreover,

(2.22)

Let E=C[0,1] be endowed with the ordering u≤v if u(t)≤v(t) for all t∈[0,1], and the maximum norm, ∥u∥=max_0≤t≤1|u(t)|. Define the cone P⊂E by

Assume that u ₀∈P, u ₀>0, i.e., u ₀(t) is not identically vanishing. Let $P_{u_{0}}= \{u\colon\allowbreak u\in E,\ \exists \lambda(u)>0,\ \mu(u)>0\ \mbox{s.t.}\ \lambda(u)u_{0}\leq u\leq \mu(u)u_{0} \}$.

Definition 2.10

([27])

Assume that A:P→P, u ₀>0. A is said to be u ₀ concave operator if A satisfies:

• (i) $\forall u>0,\ Au\in P_{u_{0}}$;

• (ii) There exists η(r,u)>0 such that $A(ru)\geq r(1+\eta(r,u))Au,\ \forall u\in P_{u_{0}},\allowbreak 0<\nobreak r<\nobreak1$.

Lemma 2.11

([27])

Assume that P is a normal cone of $E,\ u_{0}>0,\ A:P_{u_{0}}\rightarrow P_{u_{0}}$ is increasing and there exists η(r)>0 such that

Then A has a unique fixed point $u^{*}\in P_{u_{0}}$ if and only if there exist $w_{0}, v_{0}\in P_{u_{0}}$ such that w ₀≤Aw ₀≤Av ₀≤v ₀.

Remark 2.12

([27])

The above fixed point of A can be approximated by the following iterative schemes: for any x ₀∈[w ₀,v ₀], let x _n =Ax _n−1,n=1,2,… , one always obtain x _n →u ^∗.

3 Main results

Here we make the following hypotheses:

(A):

f∈C([0,1]×[0,∞)→[0,∞)),f(x,y) is increasing for y and f is not identically vanishing;

(B):

For any x∈[0,1], y∈[0,∞), there exist constant m,n, m≤0≤n<1 such that

• (i) c ⁿ f(x,y)≤f(x,cy)≤c ^m f(x,y), ∀0<c≤1.

Remark 3.1

Assume that (B) holds, we can deduce (ii) c ^m f(x,y)≤f(x,cy)≤c ⁿ f(x,y), ∀c≥1.

Theorem 3.1

Assume that (A), (B) are satisfied, then the problem (P) has unique one positive solution when $n<\frac{2m+1}{3}$.

Proof

Let $e(x)=x^{\alpha-1},A(y)=\int_{0}^{1}G(x,qt)f(t,y(t))d_{q}t$. By Lemma 2.8 and Remark 2.9, for any y∈P _e ,x∈[0,1], we have

(3.1)

and

(3.2)

Choosing $\lambda(y)=\int_{0}^{1}G(1,qt)f(t,y(t))d_{q}t,\mu(y)=\int_{0}^{1}\frac {(1-qt)^{(\alpha-2)}}{\varGamma_{q}(\alpha)}f(t,y(t))d_{q}t$, we have λ(y)e≤Ay≤μ(y)e, i.e. A:P _e →P _e . From (A), A is increasing operator. From (B), we obtain

By 0<n<1,0<c≤1, we have η(c)=c ⁿ⁻¹−1>0.

Let $h(x)=\int_{0}^{1}G(x,qt)f(t,t^{\alpha-1})d_{q}t$, $I_{1}=\min \{ 1,\int_{0}^{1}G(1,qt)f(t,t^{\alpha-1})d_{q}t \}$, $I_{2}=\max \{1,\int_{0}^{1}\frac{(1-qt)^{(\alpha-2)}}{\varGamma_{q}(\alpha)}f(t,t^{\alpha-1})d_{q}t \}$. Similar to (3.1) and (3.2), we can easily prove that I ₁ e(x)≤h(x)≤I ₂ e(x).

Let d>0 be a constant such that

From $n<\frac{2m+1}{3}$, we have $1-\frac{2(n-m)}{1-n}>0$. Since $4I_{2}^{\frac{(n-m)}{1-n}}\geq1$, we get d≥1.

Let

then $k_{1}\leq\frac{1}{2},k_{2}\geq2$. We can deduce dI ₁≥1,dk ₂ I ₂≥1.

Let w ₀(x)=k ₁ h(x),v ₀(x)=k ₂ h(x), then w ₀,v ₀∈P _e , and w ₀<v ₀. Hence Aw ₀<Av ₀. Moreover, from (A),(B), we have

and

Hence, for ∀x∈[0,1], we have

Similarly, we can obtain v ₀≥Av ₀. Hence, by means of Lemma 2.11, the problem (P) has unique one positive solution. □

Remark 3.2

The unique positive solution y ^∗ in Theorem 3.1 can be approximated by the following iterative schemes: for any x ₀∈[w ₀,v ₀], let x _n =Ax _n−1,n=1,2,… , one always obtain x _n →y ^∗.

Example 3.3

For (P), let f(x,y)=y ^(t+ε)/7,0<ε<1, ε is a constant. Let $m=0,\allowbreak n=\frac{2}{7}$, we have

• (i) c ⁿ f(x,y)≤f(x,cy)≤c ^m f(x,y), ∀0<c≤1;

• (ii) c ^m f(x,y)≤f(x,cy)≤c ⁿ f(x,y), ∀c≥1.

Then (A), (B) hold true and $n<\frac{2m+1}{3}$, so the problem (P) has unique one positive solution.

Let

Due to M,N being not easy to compute, we can replace them by M′,N′, respectively.

Obviously, 0<M′≤M≤N≤N′.

Theorem 3.4

Assume that the following conditions hold:

(H1):

there exist two constants a,b and b<a such that max{f(x,a):x∈[0,1]}≤aM, min{f(x,τ ^α−1 b):x∈[τ,1]}≥bN;

(H2):

for any u∈[0,a] and r∈(0,1), there exists η=η(u,r)>0 such that

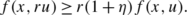
(H3):

f(x,u):[0,1]×[0,+∞)→[0,+∞) is increasing about u for any x∈[0,1].

Then boundary value problem (P) has a unique positive solution y ^∗ such that b≤∥y ^∗∥≤a and $\lim_{n\rightarrow\infty}A^{n}\tilde{y}=y^{\ast}$, i.e., $A^{n}\tilde{y}$ converges uniformly to y ^∗ in [0,1], where  $\tilde{y}\equiv a$.

Remark 3.5

The iterative scheme in Theorem 3.4 is $y_{1}=A\tilde{y},y_{n+1}=Ay_{n},\ n=1,\allowbreak 2,\dots$ . It starts off with constant function $\tilde{y}\equiv a$.

Proof

Set

Define the operator

(3.3)

By Lemma 2.8, we get

(3.4)

For any x∈[τ,1], we obtain

Similarly we have A(y)≥x ^α−1∥Ay∥, i.e., A(Q)⊂Q. From [24], we have that A is completely continuous. Let

(3.5)

If y∈Q[b,a], then

$$ \max_{x\in[0,1]}y(x)\leq a, \qquad \min_{x\in[\tau,1]}y(x)\geq\tau^{\alpha-1}\| y \|\geq\tau^{\alpha-1} b. $$

(3.6)

By (H1) and (H3), we have

$$ f\bigl(x,y(x)\bigr)\leq f(x,a)\leq aM,\quad x\in[0,1]; $$

(3.7)

$$ f\bigl(x,y(x)\bigr)\geq f\bigl(x,\tau^{\alpha-1} b\bigr)\geq bN,\quad x\in[ \tau,1]. $$

(3.8)

It follows that

Therefore, one has

(3.9)

Let $\tilde{y}= a$. Since 0<τ ^α−1<1, then $\tilde{y}\in Q[b,a]$. Let $y_{1}=A\tilde{y}$, then y ₁∈Q[b,a]. Let y _n+1=Ay _n ,n=1,2,… . It is easy to obtain that y _n ∈Q[b,a],n=1,2,… . Combining with the complete continuity of A, we have that $\{y_{n}\}_{n=1}^{\infty}$ possesses a convergent subsequence $\{y_{n_{k}}\}_{k=1}^{\infty}$ and a point y ^∗∈Q[b,a] such that $y_{n_{k}}\rightarrow y^{\ast}$.

Now, from y ₁∈Q[b,a], we can obtain

By induction, we have

$$ y_{n+1}(x)\leq y_{n}(x), \quad x\in[0,1],\ n=1,2,\dots. $$

(3.10)

Hence, $\lim_{n\rightarrow\infty}A^{n}\tilde{x}=x^{\ast}$. By the continuity of A and y _n+1=Ay _n , we can obtain Ay ^∗=y ^∗.

In the following, we show that the fixed point of A is unique. Suppose that y ^∗∗ is another fixed point of A, we can know that there exists λ>0 such that y ^∗∗≥λy ^∗. Let

Obviously, 0<c ₁<∞. Furthermore, we can prove that c ₁≥1. In fact, if 0<c ₁<1, by (H2), there exists η ₀>0 such that

$$f\bigl(x,c_{1}y^{\ast}\bigr)\geq(1+\eta_{0})c_{1}f \bigl(x,y^{\ast}\bigr). $$

It follows that

Hence, we have (1+η ₀)c ₁>c ₁. This contradicts with the definition of c ₁. So c ₁≥1. We have y ^∗∗≥c ₁ y ^∗≥y ^∗. Similarly, we can prove that y ^∗≥y ^∗∗. Thus, y ^∗=y ^∗∗. Therefore, problem (P) has unique solution y ^∗. By the definition of the cone Q, we know that the solution is positive in (0,1]. □

Corollary 3.6

Assume that (H3) and the following conditions hold:

(H1′):

$\limsup_{l\rightarrow0}\min_{x\in[\tau,1]}\frac {f(x,l)}{l}>\frac{N}{\tau^{\alpha-1}},\liminf_{l\rightarrow+\infty}\max_{x\in[0,1]}\frac{f(x,l)}{l}<M$;

(H2′):

for any y∈[0,a] and r∈(0,1), there exists η=η(y,r)>0 such that

$$f(x,ry)\geq r(1+\eta)f(x,y). $$

Then boundary value problem (P) possesses unique positive solution y ^∗ such that y ^∗∈Q and  $\lim_{n\rightarrow \infty}A^{n}\tilde{y}=y^{\ast}$, i.e. $A^{n}\tilde{u}$ converges uniformly to y ^∗ in [0,1], where  $\tilde{y}\equiv a$.

Theorem 3.7

Assume that the following conditions hold:

(H1″):

there exists a>0 such that max{f(x,a):x∈[0,1]}≤aM and f(x,u) is nondecreasing about u;

(H2″):

for any x∈[0,1], f(x,0)>0.

Then boundary value problem (P) has one positive solution y ^∗ such that 0<∥y ^∗∥≤a and lim _n→∞ A ⁿ0=u ^∗, i.e. A ⁿ0 converges uniformly to y ^∗ in [0,1].

Furthermore, if there exists k∈(0,1) such that

$$ \bigl|f(x,y_{1})-f(x,y_{2})\bigr|\leq kM|y_{1}-y_{2}|, \quad x\in[0,1],\ 0\leq y_{1}, y_{2}\leq1. $$

(3.11)

Then

$$\bigl\|A^{n+1}0-y^{\ast}\bigr\|\leq\frac{k^{n}}{1-k}\|A0\|. $$

Proof

Let

Similar to the proof of Theorem 3.1, we have

$$ A:Q[0,a]\rightarrow Q[0,a]. $$

Let $\tilde{y}= 0$, then $\tilde{y}\in Q[0,a]$. Let $y_{1}=A\tilde{y}$, Then y ₁∈Q[0,a]. Let y _n+1=Ay _n , n=1,2,… . then y _n ∈Q[0,a], n=1,2,… .

Combining with the complete continuity of A, we have that $\{y_{n}\}_{n=1}^{\infty}$ possesses a convergent subsequence $\{y_{n_{k}}\}_{k=1}^{\infty}$ and a point y ^∗∈Q[0,a] such that $y_{n_{k}}\rightarrow y^{\ast}$.

Now, from y ₁∈Q[0,a], we have

By induction, we have

(3.12)

Thus, $\lim_{n\rightarrow\infty}A^{n}\tilde{y}=y^{\ast}$. By the complete continuity of A and y _n+1=Ay _n , we have Ay ^∗=y ^∗.

By (H2″), we have that 0 is not a solution for boundary value problem. Therefore, by the definition of the cone Q, y ^∗ is a positive solution.

Since

$$ \bigl|f(x,y_{1})-f(x,y_{2})\bigr|\leq kM|y_{1}-y_{2}|,\quad x \in[0,1],\ 0\leq y_{1}, y_{2}\leq1, $$

(3.13)

we have

Thus, we can obtain

(3.14)

and

(3.15)

Therefore, let m→∞, then we have

(3.16)

Similarly, we can obtain the multiplicity of solutions. □

Theorem 3.8

Assume that (H3) holds and there exist 2n positive numbers a ₁,…,a _n ,b ₁,b ₂,…,b _n with b ₁<a ₁<b ₂<a ₂<⋯<b _n <a _n such that

(J′):

max{f(x,a _i ):x∈[0,1]}≤a _i M, min{f(x,γb _i ):x∈[τ,1]}≥b _i N.

Then boundary value problem (P) possesses n positive solutions  $y_{i}^{\ast},i=1,2,\dots,n$ such that b _i ≤∥y ^∗∥≤a _i and  $\lim_{n\rightarrow\infty}A^{n}\tilde{y_{i}} =y_{i}^{\ast}$, i.e., $A^{n}\tilde{y_{i}}$ converges uniformly to  $y_{i}^{\ast}$ in [0,1], where  $\tilde{y_{i}}\equiv a_{i}$.

Corollary 3.9

Assume that (H3) and the following conditions hold:

(H1′):

$\limsup_{l\rightarrow0}\min_{x\in[\tau,1]}\frac {f(x,l)}{l}>\frac{N}{\tau^{\alpha-1}},\liminf_{l\rightarrow+\infty}\max_{x\in[0,1]}\frac{f(x,l)}{l}<M$;

(J″):

There exist 2n−2 positive numbers a ₁<b ₂<a ₂<⋯<b _n such that

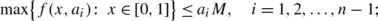
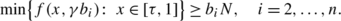
Then boundary value problem (P) possesses n positive solutions  $y_{i}^{\ast},i=1,2,\dots,n$ such that  $\lim_{n\rightarrow \infty}A^{n}\tilde{y_{i}}=y_{i}^{\ast}$, where  $\tilde{y_{i}}\equiv a_{i}$.

Example 3.10

Consider the following problem:

Let τ=0.5, then from Example 3.0.11 of [24], we have

By computation through Matlab, we can choose a=0.2366,b=0.1469 such that the condition (H1) of Theorem 3.4 is satisfied. In addition, $f(t,u)=\sqrt[3]{u}$ satisfies (H2) and (H3). Therefore, the above problem has a unique positive solution.

Example 3.11

Consider the following problem:

Let τ=0.5, then

By computation through Matlab, we can choose a=1.2662,k=0.98 such that the condition (H1″) of Theorem 3.4 are satisfied. In addition, f(t,u)=u ²+1 satisfies (H2″) and (3.11). Therefore, by Theorem 3.7 the above problem has a unique positive solution.