Introduction

There are two primary ways for measuring gravity value in surveying and mapping. The first is absolute gravity measurement, which directly determines the gravity value of a point. Another approach is called relative gravity measurement, which measures the difference in gravity between two sites and then computes the gravity values for each. In general, a large amount of relative gravity measurement is performed for gravity measurement, so there must be a beginning point inside the same system that its gravity value is known. The gravity datum refers to a gravity point with a known absolute gravity value with high-precision, which serves as the starting point for relative gravity measurement. On the other hand, the gravity datum is the basis for conducting gravity measurements (Torge 1998), providing a reference standard for.

determining the gravity values of other points. To get a more precise gravity datum, a gravity network with larger-scale relative gravity measurement must be constructed. For different countries, they have their own gravity datum by adjustment of gravity network (Boedecker et al. 1994; Csapo and Volgyesi 2001; Csapo and Szatmari 1994; Grgic et al. 2007; Volgyesi et al. 2007; Jiang et al. 2009; Stagpoole et al. 2021).

Even if absolute gravimeters like the FG-5 and A10 are the best alternative approach for terrestrial gravity measurement, they are still much more expensive and time-consuming to use in this field compared with relative gravimeters, although their accuracy is much higher. The relative gravimeter has to be extensively used in terrestrial gravity surveys.

A continental-scale gravity network has been established on the Chinese mainland, which is used for national basic surveying and economic development. In particular, the 2000 national basic gravity network (Guo et al. 2005) has been derived in 2000 years. In recent years, the Chinese government has been willing to renew the gravity network for the purpose of providing more accurate and the latest gravity datum to surveying, petroleum, and urban construction. And to provide timely and effective surveying services in areas such as economic construction, space technology, geological exploration, and earthquake prediction in China (Li and Li 2009). In order to derive the results of the high-precision gravity datum, the paper applies advanced data processing methods to conduct the gravity data, and robust estimation is used to perform the adjustment computation (Hwang et al. 2002). At presents, there are some existing software for processing data in gravity field like GrafLaB (Bucha and Janak 2013), GRAVSOFT (Forsberg and Tscherning 2008), GRAVNET (Hwang et al. 2002) and pyGABEUR-ITB (Wijaya et al. 2019), but the main focus of GrafLaB and GRAVSOFT are the spherical harmonic computation and gravity field modeling. As a matter of fact, it can not be used to process the observations of relative measurements. The GRAVNET can adjust relative gravity measurements and solve for gravimeter parameters using the weighted constraint and datum-free constrain models based on FORTRAN 90. Its insufficient is without graphical user interface so that the user is not easier to analysis data. To be excited, pyGABEUR-ITB has made a correction about above shortcoming. But the outlier detection method like \(\tau\)-criterion method may be not reliable for multiple outliers in observation compared to the robust estimation. At the same time, many mathematic error correction may be not considered in above discucced software and without the function of observation data analysis, particular much more manual intervention like outlier processing.Therefore, in this paper, a scientific software package called “GravNetAdj” is developed in the MATLAB programming language (Paliszek and Thomas 2020) by using a robust estimation method. By this way, the GravNetAdj is fast, simple, and user-friendly, which makes it easy to carry out the gravity network adjustment when the technicians are not familiar with the gravity data processing without much more manual intervention by load the standardized data.

In the next section, we will present the fundamental concepts and some mathematical formulas of basic data processing for relative gravity and adjustment computation. In Section “Design and module”, the detailed description of the GravNetAdj software is shown. In Section “Numerical experiments”, a case study about the local gravity reference network of China is conducted. The precision estimation of gravity points is given, and some statistical results are performed. In the last Section “Concluding remarks”, the conclusions are presented.

Theoretical fundamentals

Absolute gravity measurement is the best alternative approach for terrestrial gravity measurement. However, they are much more expensive and time-consuming to use in the field compared with relative gravity measurement. Therefore, relatively gravity measurements are widely applied for observing the gravity network (Hector & Hinderer 2016). Figure 1 show s commonly used field survey schemes with each letter denoting a station which is a double-time survey scheme (Chen et al. 2019). These redundant measurements help us reduce uncertainty. During the survey campaign, an average of one or two gravity observations can be made each hour. To improve efficiency, the double-time gravity survey is carried out using two gravimeters.

Fig. 1
figure 1

The field survey scheme for the relative gravity observation

Full size image

The manufacturer of the absolute gravimeter will provide the professional data processing software, which isn’t necessary to process once again because it may be less reliable than the commerce software. Therefore, the gravity network adjustment computation in this paper doesn’t consider the process of absolute gravity observations. And then we just deal with the relative gravity observations and the ending adjustment computation. Figure 2 displays the detailed procedure for processing relative gravity observations, including the error correction term and precision estimation.

Fig. 2
figure 2

The flowchart of processing relative gravity data

Full size image

According to the Fig. 2, if we want to get the last accurate gravity segment difference, the following computation step must be conducted.

  1. ((1))

    Conversion the readings to mGal

Firstly, the instrument value needs to be converted the mGal value according to the table of grid value provided by each instrument manufacturer. The Eq. (1) is designed by

$${g}_{R}={F}_{1}+\left(R-{R}_{1}\right)\cdot d{f}_{1}$$
(1)

where \(R\) is the actual instrument value,\({g}_{R}\) is the instrument value that the unit is expressed as mGal,\({R}_{1}\) is the corresponding parameter of table of grid value,\({F}_{1}\) is the parameter of table of grid value that the unit is treated as mGal,\(d{f}_{1}\) is the interval factor.

  1. (2)

    Atmospheric pressure correction

The next step is to compute the atmospheric pressure correction. The correction term can be computed in Eq. 2.

$$d{g}_{a}=0.3\left(P-{P}_{n}\right)$$
(2)

where \(d{g}_{a}\) is the value of atmospheric pressure correction(unit:\(\mu Gal\)), \(P\) is the real atmospheric pressure value at measuring point (unit: hPa),\({P}_{n}\) is standard atmospheric pressure value which can be computed as following equation.

$${P}_{n}=1.01325\times {10}^{3}\times {\left(1-0.0065H/288.152\right)}^{5.2559}$$
(3)

where H is the altitude (unit: m).

  1. (3)

    Height correction

The height correction can be simply calculated by

$$d{g}_{V}={V}_{g}\cdot h$$
(4)

where \(d{g}_{V}\) is the value of height correction (unit:\(mGal\)),\({V}_{g}\) is the vertical gradient of gravity at measurement point (it is denoted as 0.3086 mGal/m), h is the instrument height (unit: m).

  1. (4)

    Earth tide correction (Xu 1984)

The earth tide correction can be derived by

$$d{g}_{t}=-\left({\delta }_{th}\cdot G\left(t\right)-{\delta }_{fc}\right)$$
(5)

where \(G\left(t\right)\), \({\delta }_{th}\) and \({\delta }_{fc}\) can be computed by Eqs. (6) to (8) respectively.

$$\begin{array}{c}G\left(t\right)=-165.17F\left(\phi \right) {(c/r)}^{3}(Co{s}^{2}Z-1/3)-1.37{F}^{2}(\phi ){(c/r)}^{4} CosZ(5Co{s}^{2}Z-3)\\ -76.08F(\phi ){({C}_{s}/{r}_{s})}^{3}(Co{s}^{2}{Z}_{s}-1/3)\end{array}$$
(6)
$${\delta }_{fc}=-4.83+15.73Si{n}^{2}\Phi -1.59Si{n}^{4}\Phi$$
(7)
$$F(\varphi )=0.998327+0.00167Cos2\varphi$$
(8)

where \(\varphi\) is latitude of measuring station, \(\Phi\) is the geocentric latidude, \(G(t)\) is the theory earth tide, \(F(\varphi )\) is the \({\delta }_{th}\) is treated as tide factor that is set as 1.16, generally,\({\delta }_{fc}\) is the direct effects of permanent tides on gravity, c is average distance from earth’s center to moon’s center, r The distance from the center of the moon to the center of the earth, Cs is the average distance from the earth's center to the sun's center, rs is the distance from heliocentric to geocentric, Z is the geocentric zenith distance of the moon to the observation point, Zs is the geocentric zenith distance of the sun to the observation point.

  1. (5)

    Ocean tide correction

The computation term of ocean tide correction can be written as:

$$\delta {g}_{l}=\sum_{i}^{8}{\delta }_{i}{A}_{i}\text{cos}\left({\varphi }_{i}+{\omega }_{i}t+{k}_{i}\right)$$
(9)

where i is the index of tidal wave, A is the theoretical amplitude, \(\varphi\) is the theoretical phase, ω is the angular velocity, \(\delta\) is the deformation coefficient, k is the phase delay and t is the universal time (UT). It can be computed by the SPOTL software (Agnew 2012). If the user want to compute the ocean tide correction, they need to add the SPOTL software to the same path of the presented software GravNetAdj.

  1. (6)

    The computation of preliminary observations

Through adding the atmospheric pressure correction, height correction, earth tide correction, and ocean tide correction into gR, we can get \({g}_{RC}\).

$${g}_{RC}={g}_{R}+d{g}_{a}+d{g}_{V}+d{g}_{t}+\delta {g}_{l}$$
(10)
  1. (7)

    Drift calculation

In order to get the drift correction, we need to compute the drift rate in Eq. (11).

$$k=-\left({g}_{RC}^{2}-{g}_{RC}^{1}\right)/-\left({t}^{2}-{t}^{1}\right)$$
(11)

where \({g}_{RC}^{1}\) and \({g}_{RC}^{2}\) are preliminary observations for both forward and backward measurements at the starting point of the survey line, respectively. t1 and t2 are the corresponding observing time.

Then, the drift correction can be get by Eq. (12).

$$d{g}_{Z}=k\cdot \Delta t$$
(12)

where k is the drift rate, ∆t is the time difference between the observing time of measuring point and the observing time of the starting point.

  1. (8)

    Computation of last observations

The last observations of the measurement points can be derived by adding the above mentioned correction term. We can get \({g}_{RZ}\) as follows.

$${g}_{RZ}={g}_{RC}+d{g}_{Z}={g}_{R}+d{g}_{a}+d{g}_{V}+d{g}_{t}+d{g}_{Z}$$
(13)
  1. (9)

    Computation of the gravity segment difference

Firstly, we need to compute the forward segment difference \(\Delta {g}_{ij}^{1}\) by

$$\Delta {g}_{ij}^{1}=\left(\Delta {g}_{RZj}^{1}-\Delta {g}_{RZi}^{1}\right)\cdot C$$
(14)

Similarly, the backward measurements \(\Delta {g}_{ij}^{2}\) can be get as

$$\Delta {g}_{ij}^{2}=\left(\Delta {g}_{RZj}^{2}-\Delta {g}_{RZi}^{2}\right)\cdot C$$
(15)

Then, the computation Eq. (16) of the last segment difference can be written as

$$\Delta {g}_{ij}=\left(\Delta {g}_{ij}^{1}+\Delta {g}_{ij}^{2}\right)/2$$
(16)

where \(\Delta {g}_{ij}\) represent as the last observations of the segment difference,\(\Delta {g}_{RZi}^{1}\) and \(\Delta {g}_{RZi}^{2}\) are the last observations of the segment difference with ith measuring point for the forward measurement and backward measurement, respectively,\(\Delta {g}_{RZj}^{1}\) and \(\Delta {g}_{RZj}^{2}\) are the last observations of the segment difference with jth measuring point for the forward measurement and backward measurement, respectively, C is the scale factor of the used instrument.

  1. (10)

     Precision evaluation

The error estimation of the gravity segment difference can be presented as:

$$m=\pm \sqrt{\frac{\left[vv\right]}{n\left(n-1\right)}}$$
(17)

where v is the difference between the mean of segment difference and each segment difference, n is the number of the segment difference.

If a closed loop consists of n edges, closed error can be computed by:

$$w=\sum_{k=1}^{n}\Delta {g}_{k}$$
(18)

where \(\Delta {g}_{k}\) is the mean of the segemetn difference after Multiplied by scale factor. We set the critical point of close difference as \({W}_{0}\) which is derived as:

$${W}_{0}=2{m}_{0}\sqrt{n}$$
(19)

In generally,\({m}_{0}\) is set as \(\pm 10\mu Gal\).

  1. (11)

    Adjustment model and its realization

The adjustment model is similar to the one employed for the national German gravity base network DSGN76 (Boedecker 1987).

Absolute observations enter by observation equations of the type

$${v}_{i}={g}_{i}-{\overline{g} }_{i}$$
(20)

where \({v}_{i}\) is residual of the ith observation,\({g}_{i}\) is station gravity value to be estimated, \({\overline{g} }_{i}\) is observed gravity value.

After all correction term is added to the relative gravity observations, we can get the error equation for relative gravity observations. It is represented as

$$\begin{array}{c}{V}_{ij}={g}_{j}-{g}_{i}+\sum_{K=1}^{M}\left({g}_{RZi}^{K}-{g}_{RZj}^{K}\right)\cdot {C}_{K}+\sum_{n=1}^{P}{X}_{n}\left(\text{cos}\frac{{R}_{i}\cdot 2\pi }{{T}_{n}}-\text{cos}\frac{{R}_{j}\cdot 2\pi }{{T}_{n}}\right)\\ +\sum_{n=1}^{P}{Y}_{n}\left(\text{sin}\frac{{R}_{i}\cdot 2\pi }{{T}_{n}}-\text{sin}\frac{{R}_{j}\cdot 2\pi }{{T}_{n}}\right)\end{array}$$
(21)

where \({g}_{i}\) and \({g}_{j}\) are gravity value after adjustment for the ith and jth station, \({g}_{RZi}\) and \({g}_{RZi}\) are the last relative gravity observations for the ith and jth station,\({R}_{i}\) and \({R}_{j}\) are the observations for the ith and jth station, CK is the grid value correction factor which is related to the instrument when K = 1 or K = 2, Pij is the weight of observations, Xn and Yn are the periodic error parameter, Tn is the period of periodic error.

Based on Eqs. (20) and (21), the error equation including all observations can be set as follows:

$${\varvec{v}}={\varvec{A}}{\varvec{x}}-{\varvec{l}},\text{cov}\left({\varvec{l}}\right)={\sigma }_{0}^{2}{{\varvec{P}}}^{-1}$$
(22)

where v is the vector of residual, A is the design matrix, x is vector of unknown parameter vector to be estimated, l is vector of the observations, P is a weight matrix.

If the least square estimation is applied to the Eq. (22), the normal equations are

$${{\varvec{A}}}^{T}{\varvec{P}}{\varvec{A}}\widehat{{\varvec{x}}}={{\varvec{A}}}^{T}{\varvec{P}}{\varvec{l}}$$
(23)

The variance of \(\widehat{{\varvec{x}}}\) is computed by

$${\sum }_{\widehat{x}}={\widehat{\sigma }}_{0}^{2}{\left({{\varvec{A}}}^{T}{\varvec{P}}{\varvec{A}}\right)}^{-1}$$
(24)

If we consider that there are outliers in observations, the robust estimation should be used (Yang et al. 2002). Furthermore, we can get

$${{\varvec{A}}}^{T}\overline{{\varvec{P}}}{\varvec{A}}\widehat{{\varvec{x}} }={{\varvec{A}}}^{T}\overline{{\varvec{P}}}{\varvec{l} }$$
(25)

where \(\overline{P }\) is the so-called equivalent weight matrix, which can be derived by IGGIII scheme as follows. The IGGIII (Institute of Geodesy and Geophysics (IGG)III weight function) is a weight function for determine a equivalent weight when the robust estimation is adopted, and it is also named as a weight function method (Yang et al. 2002). For more detail, we can refer to the reference Yang et al. 2002.

$${\overline{p} }_{i}=\left\{\begin{array}{cc}{p}_{i}& \left|{v}_{i}{\prime}\right|=\left|\frac{{v}_{i}}{{\sigma }_{{v}_{i}}}\right|\le {k}_{0}\\ {p}_{i}\cdot \frac{{k}_{0}}{\left|{v}_{i}{\prime}\right|}{\left(\frac{{k}_{1}-\left|{v}_{i}{\prime}\right|}{{k}_{1}-{k}_{0}}\right)}^{2}& {p}_{i}\cdot {k}_{0}<\left|{v}_{i}{\prime}\right|\le {k}_{1}\\ 0& \left|{v}_{i}{\prime}\right|>{k}_{1}\end{array}\right.$$
(26)

where \({\overline{p} }_{i}\) and pi are the diagonal elements of \(\overline{{\varvec{P}} }\) and P, respectively. k0 and k1 are two experienced constants; k0 may be chosen as 1.5–2.0 from experience; and k1 may be chosen as 3–8.5. In theory or in practice, the constants k0 and k1 can be determined on the basis of the objective requirement of the problem. vi is the residual of the ith observations and the corresponding variance is \({\sigma }_{{v}_{i}}\). Therefore, \({v}_{i}{\prime}\) is the standard residual.

The detail computation step of the gravity network adjustment can be found in Fig. 3.

Fig. 3
figure 3

The flowchart of gravity network adjustment computation

Full size image

Design and module

The software is designed based on MATLAB software version 2018a. There are four main modules, such as the relative gravity data processing module, the data input module for gravity network adjustment computation, the data analysis module, and the adjustment computation module. The main interface of the GravNetAdj software is shown in Fig. 4.

Fig. 4
figure 4

The main interface of the GravNetAdj software

Full size image

The first module named relative gravity data processing module includes four sub contents. The parameter setting is used to choose the error correction, like the ocean tide for different requirements. At the same time, for specific data types, we provide the parameter selection so that it is more convenient to deal with the observations. And we can also load the original observation data by interface of input data. Here, the input data is not a raw files from CG5. We must adjust the data to a fixed format, which can be find in Fig.5.

Fig. 5
figure 5

An example of relative gravity data with two observing point for different instruments

Full size image

If we want to conduct the data processing of relative gravity observations, the interface of relative gravity computation must be opened. The last function of this module is to find the outlier for the processing results so that the relative gravity observations are credible (Fig. 6).

Fig. 6
figure 6

The interface of relative gravity data processing module

Full size image

The second module is named as the data inputting module for loading the absolute gravity and relative gravity data after processing, which can be used to adjustment computations directly (Fig. 7).

Fig. 7
figure 7

The interface of loading data module for adjustment computation

Full size image

The function of the observation analysis module is to analyze the gravity network, including the number of different data, instrument parameters, connectivity analysis, and closed loop analysis. The purpose is that the computation can use reliable adjustment data so that we can realize the high-precision gravity datum (Fig. 8).

Fig. 8
figure 8

The interface of data analysis module for observing network

Full size image

The last module is the adjustment computation module. It contains the function of loading data with instrument parameters. By setting the critical parameter, the method of parameter estimation like robust method can be accurately applied (Fig. 9).

Fig. 9
figure 9

The interface of adjustment computation module

Full size image

Numerical experiments

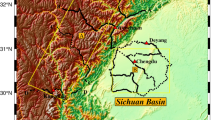
In this section, an example of the local gravity reference network in China is used to test the reliability of the GravNetAdj software. Firstly, we display the distribution of gravity data in Fig. 10 and the connected graph of the data is shown in Fig. 11. Then, quality analyses are performed for the above observations. At last, through the data of relative and absolute gravity, the adjustment results and precision estimation are given.

Fig. 10
figure 10

The distribution of the data in gravity network

Full size image
Fig. 11
figure 11

The connected graph of the data

Full size image

The measurement of the gravity network has been conducted in northeastern of China. There are 131 observing stations. Through connecting the two points of the network, 175 survey sections are formed. In order to get more accurate observations and increased redundancy of observations, we must measure six times for each surveying section so that 1050 relative gravity observations need to be conducted for error corrections. In this measurement, fourteen relative gravimeters are adopted for the measurement task. As usual, to avoid the rank deficiency of the adjustment computation, the absolute gravity observation must be employed. Therefore, we use the 217 absolute gravity observations as a datum control.

In fact, there are forty closed loops in the gravity network. By calculating the closure error of each loop, we have obtained the maximum and minimum values. They are 79.629 μGal and 0.973 μGal, respectively. To be surprised, it doesn’t exceed the tolerance 82.43 μGal, which shows that the basic relative gravity measurement is reliable. At the same time, we also know that there are thirteen relative gravimeters by analyzing the relative gravity observations. And the precision is determined as 18.86 μGal and 1.18 μGal for corresponding maximum and minimum values.

The ending normal equation is composed of 1380 observations, and there are 311 unknown parameters to be estimated. To compare the results of different adjustment methods, the least-square (LS) method and robust estimation strategy are adopted to resolve the error matrix. The statistical results can be found in Table 1.

Table 1 The adjustment results of LS method and robust estimation (unit: μGal)
Full size table

In Table 1, the precision of the gravity point is derived by the LS method and robust estimation, respectively. Apparently, the robust estimation is more reliable than the LS method through error estimation. The possible reason is that there may be some outliers in observation. The LS estimation is conducted without detection for the outliers, and the robust estimation which can resist the influence of outliers for the parameter estimation have detected the outliers successful. Similarly, these results can also be confirmed in Figs. 12 and 13. The ratio that absolute value residual is greater than the 3 times sigma is three percent for LS estimation in Fig. 12. However, from Fig. 13, we can derive that the ratio is only one percent for robust estimation. Therefore, robust estimation can resist the outlier in gravity network adjustment. Thus, it is concluded that the GravNetAdj software is fairly successful in the gravity network adjustment computation.

Fig. 12
figure 12

The statistical map of symbol for residual by LS method

Full size image
Fig. 13
figure 13

The statistical map of symbol for residual by Robust method

Full size image

Concluding remarks

In this paper, we first reviewed the computation formula for relative gravity data processing and adjustment computation for relative gravity and absolute gravity with robust estimation. Then GravNetAdj software based on MATLAB app designer is presented. The software can obtain reliable relative gravity adjustment data through the original observations, including the data quality analysis module and the data processing module. A local gravity network in China has been used to test the software so that its effectiveness can be evaluated. Therefore, when the form of the input original observations is identical to the format introduced in this paper, the software can be applied to derive the desired results. Furthermore, the software can be easily used in different target areas.