Introduction

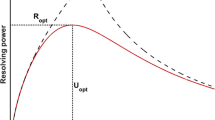
Drift tube ion mobility spectrometers separate different ion species based on the drift time they require to pass through a drift region with defined length, across which a drift voltage is applied. From this drift time, the ion mobility K can be determined. While a variety of experimental parameters, such as the length of the drift region, the width of the initial ion packet or the temperature and pressure of the drift gas, influence the analytical performance of this separation, the drift voltage by far influences the most processes occurring inside the drift tube. Thus, understanding these influences correctly and using this understanding to tune the drift voltage accordingly can allow for significant improvement of the analytical performance. The way the drift voltage influences the resolving power, being defined as the ratio of the drift time to the full width at half maximum (FWHM) of the peak, has been known for a long time [1] and has been extensively studied [2–4]. Briefly, a higher drift voltage decreases the peak width caused by diffusion as it shortens the drift time, leaving less time for diffusion, and increases the drift velocity, reducing the impact of the diffusion length on the temporal width. This increases the resolving power, as the peak width reduces faster than the drift time. However, when other broadening mechanism, such as the initial ion packet width or distortion by the transimpedance amplifier, begin to gain influence, the peak width cannot be reduced further. Therefore, an even higher drift voltage will only result in a slight increase and finally in a decrease in resolving power due to the continuous reduction of the drift time.

The influence of the drift voltage on the signal-to-noise-ratio and therefore the limits of detection is considerably less well-described, although it has also been studied in the past [5]. While many researchers have observed positive effects on these quantities when higher drift voltages where used [3], for example visible in voltage sweep ion mobility spectrometry [6], these effects were to our knowledge never thoroughly analyzed. The model used in [4] to predict the signal-to-noise-ratio at the resolving power optimal drift voltage considers the influence of the drift voltage caused by the different peak widths, the different amount of charge lost during the injection and the higher amount of possible averages during the same measurement time. Modelling these relationships, the equations achieve an excellent agreement with experimental signal-to-noise-ratios at the resolving power optimal drift voltage for different setups. However, they do not include a calculation for the signal-to-noise-ratio at arbitrary drift voltages. Extending this model as needed is the goal of the presented work.

Basics of the analytical model

In order to obtain the basic well-known model for the resolving power as used in [4], it is assumed that, upon a certain point in time, an ion packet with Gaussian shape and an initial temporal width w inj is injected into the drift region. The distance to the detector is defined as the drift length L d and the voltage applied across is the drift voltage U d . The ions travel with a drift velocity proportional to their ion mobility K and undergo broadening by diffusion, which is described using the absolute temperature T, Boltzmann’s constant kB and the elementary charge e. Upon arrival at the detector, the ions are discharged, generating an ion current which is amplified by a non-ideal transimpedance amplifier, adding the additional width w amp . From these assumptions, Eq. (1) can be derived, which describes the resolving power as the ratio of the drift time t d and the full peak width at half maximum (FWHM) or simply peak width w 0,5 .

$$ R=\frac{t_d}{w_{0,5}}=\frac{\frac{{L_d}^2}{K\ {U}_d}}{\sqrt{{w_{inj}}^2+{w_{amp}}^2+\frac{16\ {\mathrm{k}}_{\mathrm{B}\ }T \ln 2}{\mathrm{e}\ {U}_d}{\left(\frac{{L_d}^2}{K\ {U}_d}\right)}^2}} $$
(1)

As mentioned in the introduction, Eq. (1) possesses a maximum at the drift voltage at which the additional widths created by the ion injection and ion current amplification gain significant influence on the peak width. The voltage at which this maximum occurs, the resolving power optimal drift voltage U opt , can be found by calculating the derivative of Eq. (1) with respect to U d and is given by Eq. (2).

$$ {U}_{opt}=\sqrt[3]{\frac{8\ {\mathrm{k}}_{\mathrm{B}}\ T \ln 2}{\mathrm{e}\ {K}^2}\ \frac{{L_d}^4}{{w_{inj}}^2+{w_{amp}}^2}} $$
(2)

It is noteworthy that when the resolving power optimal drift voltage is applied, the term representing diffusive broadening under the square root in Eq. (1) becomes exactly twice as large as the sum of the terms representing injection and amplification as defined by Eq. (3).

$$ \frac{16\ {\mathrm{k}}_{\mathrm{B}\ }T \ln 2}{\mathrm{e}\ {U}_{opt}}{\left(\frac{{L_d}^2}{K\ {U}_{opt}}\right)}^2=2\left({w_{inj}}^2+{w_{amp}}^2\right) $$
(3)

Substituting Eq. (2) for the drift voltage in Eq. (1) leads to Eq. (4), which describes the maximum possible or optimal resolving power R opt for a given drift tube ion mobility spectrometer.

$$ {R}_{opt}=\sqrt[3]{\frac{\mathrm{e}}{24\ \sqrt{3} \ln 2\ {\mathrm{k}}_{\mathrm{B}}\ T\ K\ }\frac{{L_d}^2}{\sqrt{{w_{inj}}^2+{w_{amp}}^2}}} $$
(4)

Furthermore, it can be shown that the signal-to-noise-ratio of a drift tube ion mobility spectrometer operated at its resolving power optimal drift voltage is constant as long as the injection width w inj and the amplifier width w amp remain identical, regardless of their absolute values [4]. Thus, the resolving power optimal drift voltage is a well-known and easy to characterize operating point and therefore an excellent starting point for any model trying to predict the behavior of an ion mobility spectrometer at arbitrary drift voltages. Three steps are extremely helpful in building an applicable model. First, both the resolving power and the signal-to-noise ratio can be broken down into several other quantities, which can be modeled more easily. For the resolving power, the drift time t d and peak width w 0,5 can be used as given by Eq. (1). For the signal-to-noise-ratio (SNR), the peak width w 0,5 , the total charge at the detector Q and the standard deviation of the noise σ noise are needed as given by Eq. (5). The constant factor arises from the conversion between the area and the height of a Gaussian peak.

$$ SNR=2\sqrt{\frac{ \ln 2}{\uppi}}\ \frac{Q}{w_{0,5}\ {\sigma}_{noise}} $$
(5)

Furthermore, the noise can be related to the drift time, as it determines the amount of possible averages in a fixed time frame. Thus, we only need to model three quantities with respect to the drift voltage in order to obtain a complete model for the resolving power and the signal-to-noise-ratio of an ion mobility spectrometer – the drift time t d , the peak width w 0,5 and the transmitted charge Q. Second, the applied drift voltage can be described as a percentage of the resolving power optimal drift voltage by a dimensionless factor we named the β-factor. It represents the key component of the model presented in this work, as all further equations can be reduced to be solely functions of the β-factor.

$$ {U}_d=\beta {U}_{opt} $$
(6)

Third, instead of calculating absolute values, it is more convenient to simply calculate the relative change with respect to the well-known resolving power optimal operating point. Thus, all calculated quantities will be normalized to the quantities at the optimum drift voltage, which greatly simplifies the resulting equations.

Experimental setup

In order to validate a universal analytical model, a sufficient amount of test data from different setups is required. Here, we made measurements using two different ion mobility spectrometers designed at our institute – the ultra-high resolution drift cell [7] and a standard high resolution drift cell as for example used in our GC-IMS system [8]. The experimental parameters of the two ion mobility spectrometers are summarized in Table 1.

Table 1 Operational parameters of the two drift tubes
Full size table

In total, nine different measurement setups were tested: Three different injections widths for the ultra-high resolution drift tube, each in combination with two different amplifiers, and three different injection widths for the standard high resolution drift tube. Each of these measurements were repeated in triplicate, resulting in a total number of 27 full drift voltage sweeps. Spectra were measured at 200 different voltages within the voltage range given by Table 1 for the respective setup. For each drift voltage, the drift time, peak width, total charge, resolving power and signal-to-noise-ratio of the positive reactant ion peak (RIP) were measured. These measurements were smoothed across the drift voltage using a three-point, linear, unweighted Savitzky-Golay filter. From the resolving power measurements, the drift voltage at which the maximum resolving power occurred was determined and used to convert the drift voltage of each measurement into the corresponding β-factor. Then, the measured drift time, peak width, total charge, resolving power and signal-to-noise-ratio were normalized to their value at β = 1 in order to obtain the relative change.

All figures in the manuscript use the same symbols for the same measurements, however, they are mostly undiscernible from each other as they follow the model so closely. For the ultra-high resolution drift tube, dark grey symbols are used. Empty symbols represent the measurements using the amplifier with a width of 2.5 μs, filled symbols the ones using the amplifier with a width of 17 μs. The triangles represent an injection width of 5 μs, the squares 10 μs and the circles 15 μs. Light grey symbols represent the measurements from the standard high resolution drift tube, with the triangles being an injection width of 20 μs, the squares 40 μs and the circles 60 μs.

Results for the analytical model

It is now possible to calculate the expected change of every parameter with varying β-factor and compare the results against the obtained measurements. As it can be expected to show a near ideal behavior, the drift time will be analyzed first. The drift time can be easily calculated from the drift length, the ion mobility and the applied voltage. The ratio of the two drift times for an arbitrary drift voltage, which is expressed through the β-factor, and the optimum drift voltage is given by Eq. (7).

$$ \frac{t_d}{t_{d, opt}}=\frac{{L_d}^2}{K\ {U}_d}/\frac{{L_d}^2}{K\ {U}_{opt}}=\frac{{L_d}^2}{K{\ \beta U}_{opt}}/\frac{{L_d}^2}{K\ {U}_{opt}}=\frac{1}{\beta } $$
(7)

This relationship was then validated against the nine measurements as shown in Fig. 1. As expected, the agreement is excellent. The slight deviations, which are visible as not all measurement points vanish beneath the calculated line, can be attributed to two effects. First, we did not correct the drift time for start and end effects, as it would be necessary for ultra-high resolution mobility measurements. For an analytical model for identifying trends however, the accuracy is more than sufficient and the reduced effort more convenient. Second, as the β-factor was determined experimentally from the resolving power measurement, it may also contain an error, leading to the less than perfect agreement.

Fig. 1
figure 1

Relationship between relative drift time and β-factor. The solid black line represents the theoretical model and the grey markers nine different measurement setups (see “Experimental setup”). All measurements follow the calculations excellently

Full size image

From the relationship between the β-factor and the drift time, the relationship between the β-factor and the number of possible averages within a certain timeframe follows directly. Thus, if we can calculate the amount of noise present in an ion mobility spectrum from the number of collected averages, the noise can also be easily modelled. As shown in Fig. 2, the noise of the used amplifier perfectly follows the theoretical relationship expected for averaged white noise, as it is inversely proportional to the square root of the averaging time or respectively number of averages.

Fig. 2
figure 2

Transimpedance amplifier current noise as a function of averaging time. The solid black line represents the theoretical relationship, the grey circles the measurement, showing that the averaged noise follows a square root law

Full size image

Therefore, the relative noise can be easily described by Eq. (8).

$$ \frac{\sigma_{noise}}{\sigma_{noise, opt}}=\frac{1}{\sqrt{\beta }} $$
(8)

The second parameter to be modelled is the peak width, w 0,5 . Here, the knowledge that the diffusion term will be exactly twice as large as the sum of the other terms when the optimum drift voltage is applied, as shown by Eq. (3), will help immensely. Since the diffusion term scales proportionally to U d −3, as can be seen from Eq. (1), Eq. (9) can be directly derived without any further calculations. As in Eq. (7), every term but the β-factor cancels out.

$$ \frac{w_{0,5}}{w_{0,5, opt}}=\frac{\sqrt{1+2{\beta}^{-3}}}{\sqrt{1+2}}=\sqrt{\frac{1+2{\beta}^{-3}}{3}} $$
(9)

Again, the measurements were used to test the predicted relationship as shown in Fig. 3 and again the agreement between the predicted curve and the measured values is excellent. Thus, the width of the peak can also be considered to be sufficiently accurately modelled.

Fig. 3
figure 3

Relationship between relative peak width and β-factor. The solid black line represents the theoretical model and the grey markers nine different measurement setups (see “Experimental setup”). All measurements follow the calculations excellently

Full size image

The final missing quantity is the charge arriving at the detector. In [4], it was predicted to be proportional to the ratio of the electric field strengths at the shutter, as the shutter is the main location of ion loss in a short drift tube. This assumption produced an excellent agreement for the ion mobility spectrometer in use. Thus, if higher drift field strengths cause proportionally more charge to be transmitted into the drift tube, the relationship for the charge is given by Eq. (10).

$$ \frac{Q}{Q_{opt}}=\beta $$
(10)

It is however intuitively clear that this relationship can only hold as long as the ion transmission is low, as the amount of charge must saturate as the ion transmission approaches losslessness. The simplest function for decreasing growth to be used in an analytical model is the square root. Thus, for more advanced drift cells, one could expect the relationship between charge and β-factor to follow Eq. (11).

$$ \frac{Q}{Q_{opt}}=\sqrt{\beta } $$
(11)

Again, the theoretical expectations are compared to measurements as shown in Fig. 4. For both drift cells, the measured charge lies between the two models, but follows more closely to the square root relationship than the linear one. Thus, the square root model will be used for further investigations. It should be noted that if a further improvement of the model is desired, gaining a deeper understanding of the ion loss process would be the best starting point, as the model for the charge shows the largest total deviation.

Fig. 4
figure 4

Relationship between relative charge and β-factor. The solid black line represents the square root theoretical model, the dashed black line the linear model and the grey markers nine different measurement setups (see “Experimental setup”). While neither model is perfectly accurate, the square root model exhibits superior performance

Full size image

All three needed parameters have been modelled and can now be combined to obtain equations for the resolving power and the signal-to-noise-ratio. Most importantly, it should be noted that all three parameters depend only on the β-factor and therefore the complete equations will also contain no other terms. This means that these equations are completely unrelated to the actual drift tube being used and should possess universal validity. Considering how many parameters influence the performance of the drift tube, possessing a guideline on how this performance will change when the drift voltage is varied regardless of how all other parameters are chosen can be an invaluable tool for drift tube design.

First, we will consider the complete model for the resolving power, as given by Eq. (12) and based on Eqs. (7) and (9). Unsurprisingly, it has the same general shape as Eq. (1), as they both describe the resolving power with respect to the applied drift voltage. However, the interesting point of Eq. (12) is that the same change of the drift voltage, meaning the same β-factor, will always result in the same change of the resolving power, for any ion mobility spectrometer.

$$ \frac{R}{R_{opt}}=\frac{t_d}{t_{d, opt}}\ \frac{w_{0,5,\mathrm{opt}}}{w_{0,5}}=\sqrt{\frac{3}{\beta^2+2{\beta}^{-1}}} $$
(12)

Figure 5 compares the theoretical results from Eq. (12) with the measured resolving power values. All nine measurements follow the predicted trend well, however, the deviation of single points is much larger than for the single measurements of drift time and peak width. This can be attributed to the fact that both values decrease with increasing drift voltages. Individually, they both change by a factor of about ten, but the resolving power only changes by a factor of two. Thus, the added errors lead to a seemingly larger deviation from the expected value due to the smaller overall scale.

Fig. 5
figure 5

Relationship between relative resolving power and β-factor. The solid black line represents the theoretical model and the grey markers nine different measurement setups (see “Experimental setup”). The measurements follow the calculations well, as the visible spread is mainly caused by the small scale

Full size image

The much more interesting quantity is however the signal-to-noise-ratio, as its behavior has not been studied yet. Again, the complete model is built from the single quantities as shown by Eq. (13). Again, all other parameters cancel each other out from the final equation, showing that the signal-to-noise-ratio will, like the resolving power, always change by the same amount when the drift voltage is varied, regardless of the ion mobility spectrometer or the measurement parameters used.

$$ \frac{SNR}{SNR_{opt}}=\frac{Q}{Q_{opt}}\ \frac{w_{0,5,\mathrm{opt}}}{w_{0,5}}\ \frac{\sigma_{noise, opt}}{\sigma_{noise}}=\sqrt{\frac{3{\beta}^5}{\beta^3+2}} $$
(13)

The square root relationship between drift voltage and transmitted charge was used, as the measurements in Fig. 4 followed this theoretical model more closely. However, the linear model is shown additionally in Fig. 6 for comparison. All measured points fall between the two models and lie extremely close to the square root one. Thus, it can be considered sufficiently accurate to be used for predicting changes in the signal-to-noise-ratio.

Fig. 6
figure 6

Relationship between relative signal-to-noise-ratio and β-factor. The solid black line represents the square root theoretical model, the dashed black line the linear black model and the grey markers nine different measurement setups (see “Experimental setup”). Again, the square root model shows superior performance, agreeing with the results for the charge

Full size image

Using the developed model, it is now possible to predict for any drift tube ion mobility spectrometer how resolving power and signal-to-noise-ratio will change when the drift voltage is varied from its resolving power optimal value. In Fig. 7, both the resolving power and the square root model for the signal-to-noise-ratio are shown in order to illustrate the difference of their sensitivity to the drift voltage. While the resolving power has a relatively broad maximum and barely drops below 60 % of its maximum value within a β-factor range between 0.2 and 2, the signal-to-noise-ratio changes by more than an order of magnitude. For example, a β-factor of 1.475, which represents a 47.5 % higher than resolving power optimal drift voltage, would be sufficient to double the signal-to-noise-ratio and therefore halve the limits of detection. At the same time, the loss of resolving power would only be a little less than 8 %.

Fig. 7
figure 7

Theoretical curves for the resolving power (dashed grey line) and the signal-to-noise-ratio (solid black line). The latter shows a significantly higher sensitivity to β-factor variations

Full size image

A practical example

As a practical example to illustrate the application of the above findings, let us consider our standard high resolution drift tube, which achieves a resolving power of 100 at its optimal drift voltage with a drift length of 75 mm. It would now be interesting to know, whether we might reduce the drift length to 60 mm or increase it to 90 mm while keeping all other parameters constant in order to modify its performance.

According to Eq. (4), changing the drift length L d changes the optimal resolving power proportionally to L d 2/3. Thus, the 60 mm long drift tube would possess an optimal resolving power of 86.2, while the 90 mm long drift tube possesses an optimal resolving power of 112.9. The signal-to-noise-ratio and therefore the limits of detection should remain constant at the resolving power optimal operating point as given by [4]. However, we additionally need to consider that by changing the drift length at a constant drift voltage, the ion mobility spectrometer has now moved out of the resolving power optimal operating point. Equation (2) can be used to calculate how much the optimum drift voltage has changed due to its proportionality to L d 4/3. The values of the resulting β-factor are 1.347 for the 60 mm drift tube and 0.784 for the 90 mm drift tube. As a β-factor different from 1 leads to a loss of resolving power, the resulting resolving powers during operation are expected to be 82 and 110 respectively according to Eq. (12). However, the signal-to-noise-ratio has also changed according to Eq. (13) and, in fact, quite significantly. It has increased by 73 % for the 60 mm drift tube and decreased by 40 % for the 90 mm drift tube. Thus, the shorter drift tube would offer 25 % less resolving power than the longer one, but 65 % lower limits of detection. Which one of the two is the better choice depends on the measurement task at hand, but using the knowledge gained from a thorough analytical analysis, a quick yet extremely helpful estimation is possible.

Conclusion

In this paper, we presented a theoretical model for the influence of the drift voltage on the resolving power and signal-to-noise-ratio of a drift tube ion mobility spectrometer. It could be shown that the relative change of these quantities can be modeled using only one dimensionless factor we named β. Furthermore, the sensitivity of the resolving power to drift voltage changes is much lower than the sensitivity of the signal-to-noise-ratio, thus allowing the use of higher than resolving power optimal drift voltages to achieve increased signal-to-noise-ratios at only a slight loss of resolving power. Possessing an analytical model which is able to predict these changes can be an invaluable tool for the design or modification of a drift tube ion mobility spectrometer, as it allows for extremely useful estimates with only a minimum of effort. Thus, such a model can help identifying underlying trends and making the correct design decisions without requiring the complexity of a full finite element simulation. However, a simulation will still be required if greater accuracy in the analysis of non-idealities is desired, as they cannot be represented well by simple analytical equations.