Dynamic peer buffer adjustment to improve service availability on peer-to-peer on-demand streaming networks

Abstract

In general, on-demand video services enable clients to watch videos from beginning to end. As long as clients are able to buffer the initial part of the video they are watching, on-demand service can provide access to the video to the next clients who request to watch it. Therefore, the key challenge is how to keep the initial part of a video in a peer’s buffer for as long as possible, and thus maximize the service availability of a video for stream relay. In our previous research work, we proposed a novel caching scheme for peer-to-peer on-demand streaming, called Dynamic Buffering. The dynamic buffering relies on the feature of Multiple Description Coding to gradually reduce the number of cached descriptions held in a peer’s buffers, once the buffer is full. In this paper, we proposed three description dropping policies for dynamic buffering, called sequence dropping, m-dropping, and binary dropping. In addition, mathematical formulas of the reduced number of buffer adjustments of descriptions and the reduction of the average number of selectable descriptions for m-dropping and binary dropping by factors of the number of receiving descriptions (n) and the number of discarded descriptions (m) are established. Experimental results showed that the m-dropping, $\emph{m}=\left\lceil {\frac{n} {2}} \right\rceil$ generally outperformed m-dropping, $\emph{m}=2$ and binary dropping in terms of service availability. Even though the accumulated reduction of buffer adjustments for m-dropping policies was less than that for binary dropping, the average number of selectable descriptions for m-dropping was much greater than that for binary dropping. Furthermore, Compared with the sequence dropping, the m-dropping, $\emph{m}=\left\lceil {\frac{n} {2}}\right\rceil$, would have much less number of buffer adjustments with little difference of the number of selectable descriptions.

1 Introduction

With the rapid advances in Internet and networking technologies, there has been a dramatic increase in user demand for various multimedia applications, especially for media streaming services. In general, streaming services can be categorized into live streaming and on-demand streaming. In on-demand streaming systems, the streamed content (such as movies) is pre-recorded and available from the streaming server in the full version. Users require not only continuous but also complete playback of the requested streaming contents, regardless of when a request is made for service. In on-demand streaming systems, peers can relay current video blocks as well as initial blocks to subsequent peers, only the initial blocks remain cached in the buffer. Assuming peers’ forwarding bandwidth is sufficient, the ability of peers to relay blocks of a video to other peers depends mainly on whether the initial blocks of the video are held in the cache. In contrast, live streaming content is typically captured from live events, such as ball games and news. For peers logging on late, the missing initial part of the video is irrelevant to the Quality-of-Service (QoS) they perceive, and is ignored. Users watch the streaming content from the point where they first joined the broadcast, instead of from the beginning, and therefore, any peer with sufficient forwarding bandwidth can provide services to later peers. In this study, we only focus on on-demand video services.

In on-demand media streaming systems [1, 2], a streaming server is equipped with a limited amount of outbound bandwidth as well as a number of videos. Users issue requests to watch any one of the provided videos. Upon receiving a user’s request, on-demand streaming systems must ensure the user to receive a continuous and complete playback of the requested video. On-demand media streaming services generally require streaming servers to dedicate a substantial amount of forwarding bandwidth to each user, for a long period of time. Such resource consumption of media streaming has driven most service providers to shift system design from traditional Client-Server architecture to Peer-to-Peer (P2P) architecture [1–4]. In P2P systems, a user, also called as a peer, consumes resources from the system, and contributes resources to the system [5]. With the aid of users, the scalability of on-demand streaming systems can be increased and more users can be served.

In the past, there was a great deal of work done on providing on-demand streaming services in a P2P manner [6–10]. Most of these systems employed the cache-and-relay schemes [11, 12], that require each peer to cache the most recent video stream it receives. As long as the initial part of the video stream remains in its buffer, the peer can then relay the cached stream to late-arriving peers in a pipelining fashion. Figure 1 shows a snapshot of peers’ buffers at time 7 for the cache-and-relay scheme. To clarify the sequence of a video stream, the video is equally divided into a series of n blocks, denoted as b ₁, b ₂, ..., and b _n . Note that the data cached in the buffer is video blocks that have already been watched. In this example a peer’s buffer is capable of caching 4 video blocks at one time; loaded from the left to right in a pipeline fashion. There are three peers p ₁, p ₂, and p ₃, requesting the same video, and arriving at time 0, 2, and 5. Peer p ₁ is the first peer to request and receive the video stream from the server. At time 2, p ₂ arrives. Since p ₁ still holds the initial video block b ₁ in its cache, it forwards the cached video blocks to p ₂ sequentially. Similarly, when p ₃ arrives at time 5, p ₂ still holds b ₁, and forwards the cached video blocks to p ₃. Peers p ₂ and p ₃ arrive before the preceding peers have filled up the buffers, and are still holding the initial part of the video. Therefore, each peer can receive the entire requested video from its preceding peer(s) in a pipelining fashion. With the cache-and-relay scheme, much of the workload can effectively be shifted from the server to other capable peers, and the server can avoid wasting its limited outbound bandwidth on delivering duplicate video streams to peers with the same request.

Fig. 1

A snapshot of peers’ buffers at time 7

In Video-on-Demand (VoD) systems [13–15] based on the cache-and-relay scheme described above, the ability of a peer to contribute to the system for serving new peers depends both on the amount of available forwarding bandwidth and the existence of the initial part of a video stream in its buffers. For example, consider peer p arriving at time t and equipped with a buffer capable of caching s time units of the requested video stream. The peer cannot serve (relay blocks to) any peer arriving later than time (t + s) even though it has adequate available forwarding bandwidth. Because the initial segment of the video stream is not held in its buffer beyond time t + s, it cannot provide subsequent peers with the entire video. In other words, the service capability of p is restricted to [t + 1, t + s]. Most existing systems based on the conventional cache-and-relay scheme are vulnerable to asynchronous arrival of peers. If the time between peers’ arriving is long (in comparison to the buffer size), peers will not be able to cache or relay the video stream efficiently. Thus, the majority of peers have to rely on the streaming server to provide the requested video, leaving the forwarding bandwidth of most peers unused. In such cases, the intention of a P2P streaming system to take advantage of the peer resources (especially forwarding bandwidth) cannot be realized.

In general, on-demand video services enable clients to watch videos from beginning to end. As long as clients are able to buffer the initial part of the video they are watching, on-demand service can provide access to the video to the next clients who request to watch it. Therefore, the key challenge is how to keep the initial part of a video in a peer’s buffer for as long as possible, and thus maximize the service availability of a video for stream relay. In addition, to address the issues of delivering data on lossy network and providing scalable quality of services for clients, the adoption of multiple description coding has been proven as a feasible resolution by much research work [16–20]. In our previous research work, we proposed a novel caching scheme for peer-to-peer on-demand streaming, called Dynamic Buffering [21, 22]. The dynamic buffering relies on the feature of multiple description coding to gradually reduce the number of cached descriptions held in a peer’s buffers, once the buffer is full. Preserving as many initial parts of descriptions in the buffer as possible, instead of losing them all at one time, effectively extends peers’ service time.

In dynamic buffering, buffered descriptions in a peer are sequentially selected to discard, and their buffer space is reallocated to prolong the availability of initial blocks of other descriptions. What will be the impact on service availability in terms of the number of selectable descriptions if applying multiple descriptions dropping? Should the number of discarded descriptions be constant each time buffer adjustment is occurred? Or can it be an adaptive value based on the number of selectable descriptions in a peer’s buffer? In this paper, we proposed three description dropping policies for dynamic buffering, called sequence dropping, m-dropping, and binary dropping. With sequence dropping, each time a peer’s buffer gets filled up, it would sequentially discard descriptions one by one and then reallocate the released buffer space to other description in order to prolong their initial blocks. Furthermore, a peer needs to report its buffer status to the server for bookkeeping purposes at each buffer adjustment, which inevitably causes computation and communication overheads. Such overheads can be avoided by m-dropping and binary description dropping policies which generally discard multiple descriptions at each buffer adjustment. In addition, we discuss two cases of m-dropping which are $\emph{m}=2$ and $m=\left\lceil {\frac{n} {2}} \right\rceil$. Mathematical formulas of the reduced number of buffer adjustments of descriptions and the reduction of the average number of selectable descriptions for m-dropping and binary dropping by factors of n and m are established. It is noted that different from our previous work [21, 22] which studied the characteristics of dynamic buffering based on the assumption of releasing the buffer space of one description at a time, in this paper we not only formally established a solid mathematical model of service availability for dynamic buffering but also further studied the impact of dropping multiple descriptions at a time on the issues of the service availability of a source peer. Based on our experimental results, we observed that compared with the sequence dropping, the m-dropping, $m=\left\lceil {\frac{n} {2}} \right\rceil$ would have much less number of buffer adjustments with little difference of the number of selectable descriptions.

The remainder of the paper is organized as follows. In Section 2 we introduce the concepts of multiple description coding (MDC), CoopNet, and dynamic buffering. In Section 3 we present the analysis of service availability of three description dropping policies for dynamic buffering. The experimental results and analysis are presented in Section 4, and finally conclusions are drawn in Section 5.

2 Literature review

2.1 Multiple description coding

To address the issue of delivering video over lossy networks, many Multiple Description Coding (MDC) schemes have been proposed in the last few years. These MDC schemes aim to reduce the effects of transmission errors by coding video signals in two or more correlated sub-streams, call descriptions. Normally, descriptions are independently transmitted over separate channels by exploiting path diversity of the multicast tree on P2P networks. Whenever all descriptions arrive without error, the fidelity of a video is maintained. In cases of transmission error due to broken links or a substantial data loss, the lost information can partially be recovered from the received descriptions. In addition, MDC can be used to provide scalable Quality of Service (QoS) for clients with various levels of downloading/forwarding bandwidth. In extreme cases, clients with limited network bandwidth, such as mobile devices, could still enjoy low quality videos by receiving only one description. The perceived QoS of watching videos depends on the number of descriptions a client receives.

Multiple Description Coding (MDC) [16–20] is a flexible encoding technique capable of encoding a video into multiple sub-streams, called descriptions. Any subset of descriptions can be received and decoded by a peer to reconstruct the original video content with fidelity commensurate to the number of descriptions they receive. The more descriptions are received, the higher the quality the reconstructed video content is. The flexibility of MDC enables peers with heterogeneous downloading capacity to receive a limited number of descriptions, but still enjoy a limited level of viewing quality according to the individual downloading capacity [20]. There has been a lot of research into the realization of MDC with existing coding standards. In particular, a great deal of effort has gone into developing an H.264/AVC standard-compliant multiple description (MD) encoder. Such MDC schemes can generally be divided into two categories:

• 1. Schemes that exploit the spatial correlation between each frame of the sequence, such as Polyphase Spatial Subsampling Multiple Description Coding (PSSMDC) [23] and Multiple Description Motion Coding (MDMC) [24]

• 2. Schemes that take advantage of the temporal correlation between each frame of the sequence, such as Multiple State Video Coder (MSVC) [25] and the Motion-Compensated Multiple Description (MCMD) [26] video coding.

2.2 CoopNet

CoopNet is a typical P2P media streaming approach based on conventional cache-and-relay schemes. The primary characteristic distinguishing CoopNet from previous systems lies in its attempt to enhance the robustness of streaming services by means of MDC. In CoopNet, the streaming server encodes the streaming content into multiple descriptions using MDC, and distributes these descriptions among peers. Each peer is expected to receive descriptions from as many different parents as possible. With such a multi-parent transmission paradigm, peers are able to continue receiving parts of the streaming content and watch them at a lower quality level, even if some of the parents stop forwarding the streaming data due to accidental failure or intentional departure. However, like most conventional cache-and-relay schemes, CoopNet suffers from asynchronous arrival of peers and inefficient peer resource utilization. For example, suppose that the provided video is encoded into multiple descriptions of the same bit rate r, and peer p receives descriptions n with a buffer size b. In CoopNet, p will cache all received descriptions and its buffer will be saturated with the streaming content b/(n ×r) time units after arriving. The initial parts of all the received descriptions are then squeezed out of the buffer by incoming data, and p is no longer able to forward the complete video to any newly arrived peer in a pipelining manner. Therefore, when peers subsequent to p arrive too late, such as during off-peak time or requesting unpopular videos, the outbound bandwidth of p tends to be unused, and the server is burdened with a greater workload.

To address the aforementioned problems inherent in conventional cache-and-relay schemes, in our previous work we seek to take advantage of the flexible encoding potential of MDC like CoopNet and proposed a novel caching scheme, called Dynamic Buffering [21]. In conventional cache-and-relay schemes, the service capability of peers will suddenly disappears after the peers’ buffer fills up with streaming data. In this proposed dynamic buffering scheme, the service capability of peer degrades more gradually. We expected the dynamic buffering scheme to deal with asynchronous requests more effectively, and thus to achieve a more efficient utilization of peer resources, further alleviating the workload imposed on the server. To the best of our knowledge, this was the first paper to propose the application of dynamic buffering schemes to on-demand MDC streaming for P2P networks. Simulation results showed that the proposed dynamic buffering scheme significantly outperformed conventional cache-and-relay schemes such as CoopNet.

2.3 Dynamic buffering

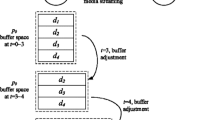
When the buffer of a peer is saturated, in our previous work we proposed Dynamic Buffering [21] which drops the descriptions that have not been forwarded to any peer one by one. Then it evenly distributes the released buffer to other descriptions to prolong the service time of the initial part of the video. In other words, with the concept of dynamic buffering the number of buffered descriptions gradually decreased once the buffer of a peer gets full. With dynamic buffering, the buffer is released on description basis. That is, only a buffer for a non-forwarded description is released at a time. If there is more than one non-forwarded, the description with the most aggregate forwarding bandwidth is selected to drop. Note that such an adjustment does not cause the degradation of viewing quality but does limit the selection of forwarded descriptions. As an example shown in Fig. 2, the 12-minute video is encoded into 4 even-rated descriptions d ₁, d ₂, d ₃, and d ₄. The first peer, p ₀, arrives at the 0th min and receives 4 descriptions from the server with each buffering length equals 3 min. At time 3rd minute, p ₀’s buffer is filled up with 4 descriptions. Instead of losing the initial parts of all 4 descriptions at one time as the conventional cache-and-relay scheme does, p ₀ chooses one description, says d ₁, to discard and then evenly distributes the released buffer to other descriptions. In this way, now the buffer length of the remaining descriptions is 4 min, providing one-extra minute for servicing new peers. p ₀ will repeat the above process every time its buffer is filled up until there is only one description left in its buffer. As shown in Fig. 2 during the time 3 and 4, time 4 to 6, and time 6–12, p ₀ would only have 3, 2, and 1 description to forward, respectively. If peer p ₁ arrives after time 12, since p ₀ has no the initial part of any description to offer, p ₁ will requests the desired descriptions the server.

Fig. 2

An example of dynamic buffering with 12 min buffer

In the design of a P2P on-demand streaming systems based on conventional cache-and-relay schemes, a key issue is how to maintain peer service capability for as long as possible. “Service capability,” refers to the ability of peers to serve subsequent peers with the entire video stream they request. More specifically, a peer p _i is considered to have service capacity for another peer p _j only if:

• 1. p _i keeps the initial part of the video stream it receives in its buffer so that it can provide p _j with the entire video stream in a pipelining manner,

• 2. p _i has enough forwarding bandwidth to deliver the video stream, and

• 3. the video stream p _i is able to provide is required by p _j .

Despite the assumptions made here, the dynamic buffering scheme presented in this study can be easily adapted to situations where more than one video is provided and encoded into multiple descriptions of different bit rates. For simplicity sake, however, let us assume that there is only one video provided for users to select and watch. The video is encoded into m descriptions of equal bit rate r, denoted as d ₁, d ₂, ..., d _m . Similar to conventional cache-and-relay schemes, the dynamic buffering scheme requires each peer to cache all the descriptions it receives until its buffer is filled up. Once the buffer of a peer is saturated with the streaming data, the peer must stop caching one of the descriptions it receives and discard the cached streaming data of the selected description to make room for subsequent streaming data of other descriptions. To avoid disrupting the video playback of a peer’s children, a peer may stop caching and discard only those descriptions that have not been forwarded to any peers. Each peer is required to repeat the above process every time its buffer is filled up until there are no descriptions left that the peer may discard or only one description is left in its buffer.

Figure 3 shows a general example to illustrate the dynamic buffering scheme. In Fig. 3, a peer p arrives at time t and receives n descriptions from other peers and/or the server. Suppose p is equipped with a buffer of size b. The buffer will be filled up with the streaming data of the n descriptions at time t + b/(n×r) as shown in Fig. 3a. Instead of trying to keep but eventually losing the initial parts of all the n descriptions as in the conventional cache-and-relay scheme, p will choose one description to discard so as to preserve the integrity of the other (n − 1) descriptions. Note that ceasing to keep and discarding one description will not degrade p’s viewing quality. Peer p still enjoys n-description viewing quality since it merely chooses not to cache one of the n descriptions it receives after playback. As shown in Fig. 3b, after sacrificing one description, p is able to continue keeping the initial parts of the other (n − 1) descriptions until time t + b/(n×r) + (b/(n×r))×r/((n − 1)×r) = t + b/((n − 1)×r), where (b/(n×r))×r indicates the room made by discarding one description and (b/(n×r))×r/((n − 1)×r) the additional time period for which the other (n − 1) descriptions can be preserved. If no peer arrives and requests descriptions from p all the while, ultimately there will be only one description left in p’s buffer, and p will not be able to preserve the initial part of the description that it has ever received and thus will lose its service capability after time t + b/r, as shown in Fig. 3c.

Fig. 3

An illustration of the dynamic buffering scheme. a p’s buffer map at time t + b/(n×r), which indicates which descriptions and blocks p has cached. b p’s buffer map at time t + b/((n − 1)×r). c p’s buffer map at time t + b/r

From Fig. 3a–c, it can be observed that the dynamic buffering scheme allows a peer to gracefully degrade rather than completely losing its service capability after its buffer is filled up with the descriptions it keeps. More specifically, the conventional cache-and-relay scheme prohibits p from supplying any description in its entirety to subsequent peers after time t + b/(n×r), whereas the dynamic buffering scheme enables p to supply (n − k) descriptions in time period [t + b/((n − k + 1)×r), t + b/((n − k)×r)], where 1 ≤ k ≤ n − 1. Since the expiration time of p’s service capability is largely extended from t + b/(n×r) to t + b/r, p has a greater opportunity to fully utilize its forwarding bandwidth, thereby effectively alleviating the workload of the streaming server. The dynamic buffering scheme is expected to outperform the conventional cache-and-relay scheme especially when peers are equipped with a small buffer or their inter-arrival times are large, such as in the case of unpopular videos or off-peak times.

It is worthwhile to note that the concept of dynamic buffering is different from the buffer management scheme proposed in [27], in which the authors proposed a P2P VoD system that utilizes SVC for the minimization of startup and recovery delay, and to deal with heterogeneous user capability. Starting from the SVC base layer only, the startup delay for a peer can be reduced. Furthermore, by dynamically adding or dropping SVC enhancement layers, the occurrences of frame freezing due to network congestion and insufficient peer bandwidth can be minimized. The assumptions made in [27] and its goals of system design were intrinsically different from ours. First, in [27] they assumed unlimited buffer space of a peer so that they did not address the issue of losing service availability of a peer due to missing initial block of the cached video caused by limited buffer space as the assumption made in this paper. Second, the SVC assumed in the paper is so called layer coding which consists of a base layer and multiple enhancement layers. Layers have strong dependency for decoding and must be decoded in order. On the contrary, the SVC we applied is so called multiple description coding where descriptions do not exist any coding dependency. Any number of descriptions can be combined to provide fractional quality of a video. Third, the buffer management in [27] aims at balancing startup delay and playback quality, while our dynamic buffering focusing on prolonging the service availability of a peer in order to alleviate server loading.

3 Service availability for dynamic buffering

3.1 Sequence dropping

Assume that a peer with the buffer space of b receives n descriptions of equal bit rate r at time T = 0. Therefore, b/n buffer space is allocated to each description. For simplicity of analysis, assume that r is equal to the bit rate of one description, and r = 1. Figure 4 shows the diagram of service availability for dynamic buffering. As discussed previously in dynamic buffering, the available number of descriptions in $\emph{n}, \emph{n}-1, \emph{n}-2, \ldots , 2, 1$ will be expired at time $\emph{b}/\emph{n}$, $\emph{b}/(\emph{n}-1)$, $\emph{b}/(\emph{n}-2), \ldots , \emph{b}/2, \emph{b}$, respectively. It is interesting to observe that the available service durations, indicated by solid line in the figure, for $\emph{n}, \emph{n}-1, \ldots , 2$, and 1 description are not equal. The available service duration for servicing n descriptions can be computed by subtraction of its expiration and available service times. For example, the available service duration for servicing $\emph{n}-1$ descriptions is $\emph{b}/(\emph{n}-1) - \emph{b}/\emph{n} = \emph{b}/\emph{n}(\emph{n}-1)$. The ratios of available service durations for providing $\emph{n}, \emph{n}-1, \emph{n}-2, \ldots , 2$, and 1 are $1/\emph{n}$, $1/\emph{n}(\emph{n}-1)$, $1/(\emph{n}-1)(\emph{n}-2), \ldots ,1/(3\times2)$, and 1/2, respectively. It is worthy to note that the service time for providing one description is one half of the whole service time of a peer. In contrast, the ratio of the service available duration of providing the most number of descriptions is always $1/\emph{n}$, and its significance depends on the value of n. Figure 5 shows the ratios of available duration for 2, 4, 8, and 16 available descriptions. As an example of a new peer receiving $\emph{n}=4$ descriptions, there is 1/4 chance that there is four descriptions (the most number) can be selected to forward, and there is 1/2 chance that there is only one description (the least number) can be selected to forward, when a relay request comes in. Note that the duration of providing the most number of descriptions is the time spending on initial buffer filling up. The larger the value of n, the less significance of duration of proving the most number of descriptions to subsequent peers.

Fig. 4

Diagram of service availability for dynamic buffering

Fig. 5

Ratios of available duration for 2, 4, 8, and 16 descriptions. a n = 2, b n = 4, c n = 8, d n = 16

When a peer receiving n descriptions first provides stream relay service to a subsequent peers, within the available service duration, b, in the best cases there are n descriptions which can be selected; on the other hand, in the worst case there is only one description that can be forwarded. It is important to estimate the average number of descriptions which can be selected for stream relay. And the average number of descriptions can be computed by the summation of the product of each possible number of available descriptions and its ratio of available service duration as,

$$\begin{array}{lll} &&{\kern-5pt} n \times \frac{1} {n} + (n - 1) \times \frac{1} {{n(n - 1)}} + (n - 2) \times \frac{1} {{(n - 1)(n - 2)}} \\ &&{\kern6pt} +\, \cdots + 2 \times \frac{1} {{2 \times 3}} + 1 \times \frac{1} {{1 \times 2}} \\ &&{\kern6pt} = 1 + \frac{1} {n} + \frac{1} {{n - 1}} + \frac{1} {{n - 2}} + \cdots + \frac{1} {3} + \frac{1} {2} \\ &&{\kern6pt} = \sum\limits_{i = 1}^n {\frac{1} {i}} = \ln n + \gamma . \end{array}$$

It is interesting to note that the average number of selectable descriptions for relay in a new join peer receiving n descriptions is n-th harmonic number, and its approximate value is well-known as ln n + γ where γ is Euler’s constant (~ 0.57721). For the examples in Fig. 5, the average number of selectable descriptions $\emph{n}=2$, 4, 8, and 16 are 1.27, 1.96, 2.66, and 3.35. When the number of buffered descriptions in a peer is increased by a factor of two, the average number of selectable descriptions is also increased by a constant of 0.7 . It indicates that coding a description in a larger number of n does not effectively increase the number of selectable descriptions. Intuitively, n equal to 4, 8, or 16 is a rational choice in our case.

3.2 M-dropping

In dynamic buffering, a peer needs to evenly allocate the released buffer space to other descriptions once the buffer is filled up. In addition, a peer needs to regularly report its buffer status to the server at each buffer adjustment for bookkeeping purposes. Such computation and communication overheads can be avoided by m-dropping which selects m descriptions to drop, when buffer allocation adjustment is necessary. In the aspect of system implementation, a server could establish two socket connections with a peer for control messaging and data delivery. After each buffer adjustment, a peer would report its buffer status including, the available descriptions to forward, the buffer lengths of cached descriptions, the available buffer space of each description, and etc., to a server for the scheduling of peer joining and failure recovery. Discussing detailed communication protocols of dynamic buffering are beyond the scope of this paper. It is noted that when the number of selectable descriptions, c, is less than or equal to m, the sequence dropping is applied for the rest of descriptions. By dropping buffer space of multiple descriptions at a time, we may alleviate overheads of buffer adjustment of descriptions but inevitably reduce the service availability of a peer since a peer can no longer relay discarded descriptions to subsequent peers. Take example of m equal to 2. When n is equal to 8, as shown in Fig. 6a, with sequence dropping policy, the average service availability is 2.718. In Fig. 6b, with m-dropping policy, the average service availability becomes 2.583, which is 0.135 less than sequence dropping, and 7 + 5 + 3 = 15 times buffer adjustments of descriptions.

Fig. 6

The time line of service availability for n equal to 8 with sequence dropping and m-dropping, $\emph{m}=2$. a Sequence dropping. b M-dropping, m = 2

From above examples, we observe that the duration where a peer that can originally relay $\emph{n}-1$ descriptions with sequence dropping now can provide only $\emph{n}-2$ descriptions with m-dropping by m equal to 2. That is, the average numbers of buffered descriptions in a peer with sequence dropping and m-dropping are $(\emph{n}-1)/(\emph{n}\times(\emph{n}-1))$ and $(\emph{n}-2)/(\emph{n}\times(\emph{n}-1))$, respectively. Comparing to sequence dropping, the reduction of service availability is $1/(\emph{n}\times(\emph{n}-1))$ but saving $\emph{n}-1$ times of buffer adjustments of descriptions. Based on the analysis of the previous example, we may establish the mathematical relationships between the value of m in m-dropping policy and service availability.

Lemma 1

Compared to sequence dropping, the reduced number of buffer adjustments of descriptions for a peer with m-dropping is,

$$ \mathop \sum \limits_{i = 0}^{\left\lfloor {\frac{{n - 1}} {m}} \right\rfloor - 1} \mathop \sum \limits_{j = 1}^{m - 1} (n - j - mi){\text{}}, 0<m<n. $$

In Lemma 1, $\left\lfloor {\frac{{n - 1}} {m}} \right\rfloor$ represents the number of discarding m descriptions in a peer, and $\mathop \sum \limits_{j = 1}^{m - 1} (n - j - mi)$ represents the reduced number of buffer adjustments of descriptions each time m descriptions is discarded. Table 1 shows the reduced number of buffer adjustments of descriptions for various n (1 to 12) and m (1 to 6). When m equals to 1, the sequence dropping policy is applied, and therefore the reduced number of buffer adjustments of descriptions is zero. the reduced number of buffer adjustments of descriptions for various n, m.

Table 1 The reduced number of buffer adjustments of descriptions for various n, m

Given a duration that a peer with sequence dropping can relay $\emph{n}-1$ descriptions, now with m-dropping a peer can only relay $\emph{n}-\emph{m}$ descriptions in the same duration, resulting in the reduction of the average number of selectable descriptions $(\emph{m}-1)/(\emph{n}\times(\emph{n}-1))$, from $(\emph{n}-1)/(\emph{n}\times(\emph{n}-1))$ to $(\emph{n}-\emph{m})/(\emph{n}\times(\emph{n}-1))$.

Lemma 2

Compared to sequence dropping, the reduction of the average number of selectable descriptions for m-dropping is,

$$ \mathop \sum \limits_{i = 0}^{\left\lfloor {\frac{{n - 1}} {m}} \right\rfloor - 1} \mathop \sum \limits_{j = 0}^{m - 2} \frac{{m - j - 1}} {{\left( {n - mi - j} \right)(n - mi - j - 1)}}, 0<m<n. $$

In Lemma 2, $\left\lfloor {\frac{{n - 1}} {m}} \right\rfloor$ represents the number of discarding m descriptions, and $\mathop \sum \limits_{j = 0}^{m - 2} \frac{{m - j - 1}} {{\left( {n - mi - j} \right)(n - mi - j - 1)}}$ represents the reduction of service availability each time a peer discards m descriptions. Table 2 shows the reduction of the average number of selectable descriptions for various n (1 to 12) and m (1 to 6).

Table 2 The reduced number of the average number selectable descriptions for various n, m

Lemma 3

For all the number of receiving descriptions, n, is equal to 2k, where $k \in {{\text{N}}^ + }$ and k > 2, the values of the reduction of service availability for 2-dropping (m = 2) and k-dropping $(m=k=\frac{n}{2})$ are the same. That is,

$$\mathop \sum \limits_{i = 0}^{\left\lfloor {\frac{{n - 1}} {2}} \right\rfloor - 1} \frac{1} {{\left( {n - 2i} \right)(n - 2i - 1)}} = \mathop \sum \limits_{j = 0}^{\frac{n} {2} - 2} \frac{{\frac{n} {2} - j - 1}} {{\left( {n - j} \right)(n - j - 1)}}.$$

Proof

Since n is an even number, we may write

$$ \mathop \sum \limits_{i = 0}^{\left\lfloor {\frac{{n - 1}} {2}} \right\rfloor - 1} \frac{1} {{\left( {n - 2i} \right)(n - 2i - 1)}} = \mathop \sum \limits_{i = 0}^{\frac{n} {2} - 2} \frac{1} {{\left( {n - 2i} \right)(n - 2i - 1)}}. $$

Here we are dealing with the open statement

$$ \emph{S}(\emph{n})\!:\! \mathop \sum \limits_{i = 0}^{\frac{n} {2} - 2}\frac{1} {{\left( {n - 2i} \right)(n - 2i - 1)}} \!=\! \mathop \sum \limits_{j = 0}^{\frac{n} {2} - 2}\! \frac{{\frac{n} {2} - j - 1}} {{\left( {n - j} \right)(n -j - 1)}}. $$

We start with the statement S(6) and find that

$$\begin{array}{lll} \emph{S}(6): \mathop \sum \limits_{i = 0}^1 \frac{1} {{\left( {6 - 2i} \right)\left( {5 - 2i} \right)}} &=& \frac{1}{{6 \times 5}} + \frac{1} {{4 \times 3}} \\ &=& \frac{2} {{6 \times 5}} + \frac{1} {{5 \times 4}} \\ &=& \mathop \sum \limits_{j = 0}^1 \frac{{2 - j}} {{\left( {6 - j} \right)(5 - j)}}. \end{array}$$

So S(6) is true. Now we assume the truth of S(a), for some (particular) $\emph{a}=2\emph{k}$, where $k \in {{\text{N}}^ + }$ and k > 3. That is,

$$ \mathop \sum \limits_{i = 0}^{\frac{a} {2} - 2} \frac{1} {{\left( {a - 2i} \right)(a - 2i - 1)}} = \mathop \sum \limits_{j = 0}^{\frac{a} {2} - 2} \frac{{\frac{a} {2} - j - 1}} {{\left( {a - j} \right)(a - j - 1)}} $$

is a true statement (when n is replaced by a). From this assumption we want to deduce the truth of

$$\begin{array}{lll} &&{\kern-6pt} \emph{S}(\emph{a}+2):\mathop \sum \limits_{i = 0}^{\frac{a} {2} -1} \frac{1} {{\left( {a - 2i + 2} \right)(a - 2i + 1)}} \\ &&{\kern6pt} = \mathop \sum \limits_{j = 0}^{\frac{a} {2} - 1} \frac{{\frac{a} {2} - j}}{{\left( {a - j + 2} \right)\left( {a - j + 1} \right)}}. \end{array}$$

Using the induction hypothesis S(a), we find that

$$\begin{array}{lll} &&{\kern-6pt} \mathop \sum \limits_{i = 0}^{\frac{a} {2} - 1} \frac{1} {{\left( {a - 2i + 2} \right)\left( {a - 2i + 1} \right)}}\\ &&{\kern6pt}= \mathop \sum \limits_{i = - 1}^{\frac{a} {2} - 2} \frac{1} {{\left( {a - 2i} \right)\left( {a - 2i - 1}\right)}}\\ &&{\kern6pt}=\mathop \sum \limits_{i = 0}^{\frac{a} {2} - 2} \frac{1} {{\left( {a - 2i} \right)\left( {a - 2i - 1} \right)}} + \frac{1} {{\left( {a + 2} \right)\left( {a + 1} \right)}} \\ &&{\kern6pt}= \mathop \sum \limits_{j = 0}^{\frac{a} {2} - 2} \frac{{\frac{a} {2} - j - 1}} {{\left( {a - j} \right)\left( {a - j - 1} \right)}} \\ &&{\kern18pt}+ \left( \frac{{\frac{a} {2}}} {{\left( {a + 1} \right)\left( a \right)}} + \frac{{\frac{a} {2} + 1}} {{\left( {a + 2} \right)\left( {a + 1} \right)}}\right.\\ &&{\kern36pt} \left.-\, \frac{1} {{\left( {\frac{a} {2} + 2} \right)\left( {\frac{a} {2} + 1} \right)}} - \frac{1} {{\left( {\frac{a} {2} + 2} \right)}} + \frac{1} {{\left( {a + 2} \right)}} \right) \\ &&{\kern6pt}= \mathop \sum \limits_{j = 0}^{\frac{a} {2} - 2} \frac{{\frac{a} {2} - j - 1}} {{\left( {a - j} \right)\left( {a - j - 1} \right)}}\\ &&{\kern18pt} - \left( \frac{1} {{\left( {\frac{a} {2} + 2} \right)\left( {\frac{a} {2} + 1} \right)}} - \frac{{\frac{a} {2}}} {{\left( {a + 1} \right)\left( a \right)}} \right.\\ &&{\kern36pt}\left.-\, \frac{{\frac{a} {2} + 1}} {{\left( {a + 2} \right)\left( {a + 1} \right)}} + \frac{1} {{\left( {a + 2} \right)}} - \frac{1} {{\left( {\frac{a} {2} + 2} \right)}} \right)\\ &&{\kern6pt}= \mathop \sum \limits_{j = - 2}^{\frac{a} {2} - 3} \frac{{\frac{a} {2} - j - 1}} {{\left( {a - j} \right)\left( {a - j - 1} \right)}} - \left( {\frac{1} {{\left( {\frac{a} {2} + 2} \right)}} - \frac{1} {{\left( {a + 2} \right)}}} \right)\\ &&{\kern6pt}= \mathop \sum \limits_{j = - 2}^{\frac{a} {2} - 3} \frac{{\frac{a} {2} - j - 1}} {{\left( {a - j} \right)\left( {a - j - 1} \right)}} \\ &&{\kern18pt}- \left( {\mathop \sum \limits_{j = - 2}^{\frac{a} {2} - 3} \frac{1} {{\left( {a - j - 1} \right)}} - \mathop \sum \limits_{j = - 2}^{\frac{a} {2} - 3} \frac{1} {{\left( {a - j} \right)}}} \right) \\ &&{\kern6pt}= \mathop \sum \limits_{j = - 2}^{\frac{a} {2} - 3} \frac{{\frac{a} {2} - j - 1}} {{\left( {a - j} \right)\left( {a - j - 1} \right)}} - \mathop \sum \limits_{j = - 2}^{\frac{a} {2} - 3} \frac{1} {{\left( {a - j} \right)\left( {a - j - 1} \right)}}\\ &&{\kern6pt}= \mathop \sum \limits_{j = - 2}^{\frac{a} {2} - 3} \frac{{\frac{a} {2} - j - 2}} {{\left( {a - j} \right)\left( {a - j - 1} \right)}}\\ &&{\kern6pt}= \mathop \sum \limits_{j = 0}^{\frac{a} {2} - 1} \frac{{\frac{a} {2} - j}} {{\left( {a - j + 2} \right)\left( {a - j + 1} \right)}} \end{array}$$

and the general result follows by the Principle of Mathematical Induction.□

Lemma 4

For all the number of receiving descriptions, n , is equal to 2k, where $k \in {{\text{N}}^ + }$ and k > 0, as n increases, the ratio of accumulated service time of first half of selectable description becomes smaller. That is,

$$1 - \mathop \sum \limits_{i = 1}^{\frac{n} {2}} \frac{1} {{i\left( {i + 1} \right)}} > 1 - \mathop \sum \limits_{i = 1}^{\frac{{n + 2}} {2}} \frac{1} {{i(i + 1)}}.$$

Proof

Since n is equal to 2k, we may write S(n) as S(2k).

$$\emph{S}(2\emph{k}): \mathop \sum \limits_{i = 1}^k \frac{1} {{i\left( {i + 1} \right)}} < \mathop \sum \limits_{i = 1}^{k + 1} \frac{1} {{i\left( {i + 1} \right)}}.$$

Then $\mathop \sum \limits_{i = 1}^k \frac{1} {{i\left( {i + 1} \right)}} = \mathop \sum \limits_{i = 1}^{k + 1} \frac{1} {{i\left( {i + 1} \right)}} - \frac{1} {{\left( {k + 1} \right)\left( {k + 2} \right)}}$.

Since $\frac{1} {{\left( {k + 1} \right)\left( {k + 2} \right)}}{\text{}} \in {{\text{N}}^ + }$, we find that the open statement $\emph{S}(\emph{n})$ is true.□

For example in Table 2, for $\emph{n}=8$, the reduction of average number of selectable descriptions for 4-dropping and 2-dropping is the same, 0.135, but as shown in Table 1, a peer with 4-dropping has a greater reduced number of buffer adjustments of descriptions than a peer with 2-dropping. Because the ratio of service time is inversely proportional to the number of selectable descriptions, first dropping one half of the number of receiving description may have little influence on average number of selectable descriptions. In conclusion, when receiving $\emph{n}=2\emph{k}$ descriptions, a peer applying k-dropping would get better performance in reducing number of buffer adjustments of descriptions as applying 2-dropping.

3.3 Binary dropping

Inspired from the conclusion of last section, it is interesting to discuss another dropping description policy, called binary dropping, where each time a peer would discard one half of number of buffered descriptions once its buffer gets full. That is, each time $\left\lceil {\frac{c} {2}} \right\rceil$ number of buffered descriptions is dropped, where c represents the number of buffered descriptions, and initially c equals to n. At i-th dropping, the number of buffered descriptions in a peer, $\emph{c}=\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor$, $\emph{i}=0, 1, 2, \ldots$. The descriptions in buffer would be dropped in this fashion until there is only one description left.

Lemma 5

Compared to sequence dropping, the reduced number of buffer adjustments of descriptions for a peer with binary dropping is,

$$\mathop \sum \limits_{i = 0}^{\left\lfloor {{\text{lo}}{{\text{g}}_2}\frac{n} {3}} \right\rfloor {\text{}}} \mathop \sum \limits_{j = 1}^{\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - \left\lfloor {\frac{n} {{{2^{(i + 1)}}}}} \right\rfloor - 1} \left(\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - j\right), 0<m<n.$$

When c equals to 2, the number of discarded descriptions for sequence dropping and binary dropping is the same, and when c equals to 3, the number of discarded descriptions for binary dropping is 2. Therefore, when a peer buffers ${\text{3}} \times {{\text{2}}^k}$ descriptions, $\left\lceil {\frac{c} {2}} \right\rceil$ descriptions are discarded totally $\emph{k}+1$ times, and k is equal to $\left\lfloor {{\text{lo}}{{\text{g}}_2}\frac{n} {3}} \right\rfloor$. With binary dropping, a peer would totally make ($\left\lfloor {{\text{lo}}{{\text{g}}_2}\frac{n} {3}} \right\rfloor +1$) times buffer adjustment, and each time a peer discards one half of the number of buffer descriptions. Each discarding can save the number of buffer adjustment of descriptions by $\mathop \sum \limits_{j = 1}^{\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - \left\lfloor {\frac{n} {{{2^{(i + 1)}}}}} \right\rfloor - 1} (\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - j)$

Lemma 6

Compared to sequence dropping, the reduction of the average number of selectable descriptions for binary dropping is,

$$\mathop \sum \limits_{i = 0}^{\left\lfloor {{\text{lo}}{{\text{g}}_2}\frac{n} {3}} \right\rfloor {\text{}}} \mathop \sum \limits_{j = 1}^{\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - \left\lfloor {\frac{n} {{{2^{(i + 1)}}}}} \right\rfloor - 1} \frac{{\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - \left\lfloor {\frac{n} {{{2^{(i + 1)}}}}} \right\rfloor - j}} {{(\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - j + 1)\left( {\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - j} \right)}}, 0<m<n.$$

Given duration that a peer can serve $\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - 1$ descriptions with sequence dropping, with binary dropping now a peer can serve ${\left\lfloor {\frac{n} {{{2^{(i + 1)}}}}} \right\rfloor }$ descriptions. The average number of selectable descriptions is changed from $(\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - 1)/(\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor (\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - 1))$ sequence dropping to $\left\lfloor {\frac{n} {{{2^{\left( {i + 1} \right)}}}}} \right\rfloor /(\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor (\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - 1))$ with binary dropping, a reduction of service availability of $(\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - \left\lfloor {\frac{n} {{{2^{(i + 1)}}}}} \right\rfloor - 1)/(\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor (\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - 1))$. Because a peer discards $\left\lceil {\frac{c} {2}} \right\rceil$ descriptions when c equals to 3, $\left\lfloor {{\text{lo}}{{\text{g}}_2}\frac{n} {3}} \right\rfloor + 1$ represents the number of $\left\lceil {\frac{c} {2}} \right\rceil$ descriptions discarded, and for each discarding the reduction of service availability is $\mathop \sum \limits_{j = 1}^{\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - \left\lfloor {\frac{n} {{{2^{(i + 1)}}}}} \right\rfloor - 1} \frac{{\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - \left\lfloor {\frac{n} {{{2^{(i + 1)}}}}} \right\rfloor - j}} {{(\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - j + 1)\left( {\left\lfloor {\frac{n} {{{2^i}}}} \right\rfloor - j} \right)}}$, as shown in Lemma 6.

4 Experimental results and analysis

In this section, we present the experimental results of sequence dropping, m-dropping, and binary dropping policies and provide insightful analysis on the accumulated reduction of buffer adjustment of descriptions, service availability, and the reduction of service availability. It is noted that these experimental results were derived from MATLAB without real system implementation. Lemmas of 1 to 6 were input into MATLAB to observe the performance of proposed dropping policies of dynamic buffering. Only the service availability of a peer was studied and there was no simulation topology involved.

Figure 7 shows the accumulated reduction of buffer adjustment of descriptions for m-dropping and binary dropping policies for various number of receiving descriptions, compared to sequence dropping. The sequence dropping serves as the baseline for comparison, and therefore has a reduction of zero. As shown in figure, the accumulated reduction of buffer adjustment of descriptions for m-dropping and binary dropping increases along with the increase of the number of receiving descriptions. The binary dropping has the most accumulated reduction of buffer adjustment of descriptions, followed by the m-dropping, $\emph{m}=\left\lceil {\frac{n} {2}} \right\rceil$ and m-dropping, $\emph{m}=2$. With the number of receiving descriptions $\emph{n}=32$, it is notable that the binary dropping has 28% and 84% more on accumulated reduction of buffer adjustment of descriptions, respectively. Binary dropping and m-dropping, $\emph{m}=\left\lceil {\frac{n} {2}} \right\rceil$ discard one half of the number of receiving descriptions at first time of buffer adjustment and intuitively have greater accumulated reduction of buffer adjustment of descriptions than m-dropping, $\emph{m}=2$.

Fig. 7

The accumulated reduction of buffer adjustments for various number of receiving descriptions with description dropping policies

Figure 8 shows the average number of selectable descriptions for various number of receiving descriptions with description dropping policies. The average number of selectable descriptions for the three description dropping policies increases along with the number of receiving descriptions. As expected, the sequence dropping and the binary dropping have the most and the least average number of selectable descriptions. The average number of selectable descriptions for m-dropping is between that for sequence dropping and binary dropping, but the average number of selectable descriptions m-dropping, $m=\left\lceil {\frac{n} {2}} \right\rceil$ is closer to that of sequence dropping. With m-dropping, $\emph{m}=2$, when the number of receiving descriptions is not the factor of 2, the average number of selectable descriptions is smaller. On the other hand, with binary dropping there is a significant increase on the average number of selectable descriptions when the number of receiving description is ${{\text{2}}^k}$. As shown in figure, the average number of selectable descriptions for those description dropping policies increases sharply when the number of receiving descriptions is eight or less. Beyond that, the increase becomes slower. The number of receiving descriptions is 8 or 16 would be a good choice in our experiments.

Fig. 8

The average number of selectable descriptions for various number of receiving descriptions with description dropping policies

Figure 9 shows the reduction of average number of selectable descriptions for various number of receiving descriptions with description dropping policies. As shown in figure, the m-dropping, $m=\left\lceil {\frac{n} {2}} \right\rceil$ has the lowest reduction of average number of selectable descriptions, and after n equals to 8, its values does not increase significantly along with the increase of the number of receiving descriptions. This is because as n increases, the ratio of accumulated service time of first half of selectable description becomes smaller. The significance of dropping one half of receiving descriptions becomes lesser when the n gets greater. Furthermore, when n is even, the reduction of average number of selectable descriptions for m-dropping, $m=\left\lceil {\frac{n} {2}} \right\rceil$ and $\emph{m}=2$, is the same, which be easily proved by the Principle of Mathematical Induction in Lemma 3. In addition, the binary dropping has the greatest reduction of average number of selectable descriptions among those description dropping policies. After n is greater 8, the reduction of average number of selectable descriptions for binary dropping is significantly more than that for m-dropping, even at $\emph{n}={{\text{2}}^k}$. It is notable that when n equals to 8, 16, and 32, the reduction of average number of selectable descriptions for binary dropping is 57%, 117%, and 195% more than that of m-dropping, respectively.

Fig. 9

The reduction of average number of selectable descriptions for various number of receiving descriptions with description dropping policies

5 Conclusion and future work

In this paper, we proposed three description dropping policies for dynamic buffering, called sequence dropping, m-dropping, and binary dropping. With sequence dropping, each time a peer’s buffer gets filled up, it would sequentially discard descriptions one by one and reallocate the released buffer space to other description in order to prolong their initial blocks. Furthermore, a peer needs to report its buffer status to the server for bookkeeping purposes at each buffer adjustment, which inevitably causes computation and communication overheads. Such overheads can be avoided by m-dropping and binary description dropping policies which generally discard multiple descriptions at each buffer adjustment of descriptions. In addition, we discuss two cases of m-dropping which are $\emph{m}=2$ and $\emph{m}=\left\lceil {\frac{n} {2}} \right\rceil$. Mathematical formulas of the reduced number of buffer adjustments of descriptions and the reduction of the average number of selectable descriptions for m-dropping and binary dropping by factors of n and m are established. Experimental results showed that the m-dropping, $\emph{m}=\left\lceil {\frac{n} {2}} \right\rceil$ generally outperformed m-dropping, $\emph{m}=2$ and binary dropping in terms of service availability. Note that even though the accumulated reduction of buffer adjustment of descriptions for m-dropping was less than that for binary dropping, the average number of selectable descriptions for m-dropping was much greater than that for binary dropping.

In our previous work [22], we already presented the idea of how to select a description to drop based on balancing group-wise aggregate forwarding bandwidths of descriptions in order to maximize the service throughput. With this balancing policy, dropped descriptions would be well distributed among peers. To determine m descriptions to drop as argued in this paper, we could apply m times of such a description selecting policy. For detailed information of how to select a description to drop in dynamic buffering scheme, please refer to [22]. It is noted that this process requires the involvement of P2P system statistics kept in a streaming server. Such a centralized scheme for global maximization of system throughput has been proven in much research work as a feasible solution on P2P streaming networks, such as [22, 28, 29].

In the future, we plan to extend our model to cope with the dynamic join of peers for other extended versions of dynamic buffering, such as balanced dynamic buffering [22]. Performance measures on a more practical experimental platform will be reported in our future publication.