Introduction

When a population is introduced into a region where it is initially absent, it may spread across the landscape with a characteristic speed. In the idealized case of a homogenous, time-invariant, and infinite landscape, the invasion proceeds as a wave of fixed shape moving at a constant speed (given some assumptions described below). The speed of this invasion wave depends on both demography (i.e., on the rates of survival, development, reproduction, etc.) and on dispersal (i.e., on the probability distribution of distances dispersed by individuals at each stage of their life cycle), and can be calculated from an integrodifference equation model. Because the invasion speed, c *, integrates demography and dispersal into a single index of population spread, it plays a role analogous to that played by the population growth rate (λ or r = logλ) in demographic analysis (Neubert and Caswell 2000). Sensitivity and elasticity analyses of c * provide insight into how demographic and dispersal parameters influence invasion speed, and permit LTRE decomposition of observed differences in invasion speed into contributions from both kinds of parameters (Caswell et al. 2003).

Environments fluctuate, but such fluctuations do not appear in these idealized calculations. In this paper, we derive the invasion speed, and its sensitivity and elasticity, from models for periodically and stochastically varying environments. Periodic models can be used to describe seasonal variation within a year. Seasonality has obvious effects on both demography and dispersal, because in many species breeding biology and dispersal behavior exhibit strong seasonal variation. Periodic models can also be used on interannual time scales to study the effects of the frequency of occurrence of some environmental event (e.g., fire, flood, etc.). Stochastic models extend such calculations to include random components (variance, covariance, and temporal autocorrelation) of environmental fluctuations. Schreiber and Ryan (2010), in an accompanying paper, rightly emphasize the importance of stochastic models to address predictions of increased interannual stochastic variability as a result of climate change.

Neubert et al. (2000) derived expressions for invasion speed in variable environments in the special case of unstructured, scalar populations. Those results, however, do not apply to invasions by age- or stage-structured populations, because of the interaction between the fluctuating environment and the changing population structure. Our approach here, which includes any demographic stage structure, extends the approach of Neubert and Caswell (2000). In that paper, we derived the invasion speed from the dominant eigenvalue of a matrix that includes, in a very particular way, both demography and dispersal. In this paper, we derive invasion speeds in periodic and stochastic environments from periodic and stochastic products of such matrices.

Time-invariant invasion models have by now been applied to many species, in order to explore the properties responsible for invasion speed or to identify targets for potential management strategies (e.g., Miller and Tenhumberg 2010; Smith et al. 2009; Tinker et al. 2008; Jongejans et al. 2008; Bullock et al. 2008; Skarpaas and Shea 2007; Garnier and Lecomte 2006; Vellend et al. 2006; Jacquemyn et al. 2005; Buckley et al. 2005; Le Corff and Horvitz 2005; Bullock and Pywell 2005; Powell et al. 2005; Shea 2004; Neubert and Parker 2004; Caswell et al. 2003; Fagan et al. 2002). Our results will extend these applications to variable environments.

This paper presents four results: the invasion speed in periodic environments, the invasion speed in stochastic environments, the sensitivity analysis in periodic environments, and the sensitivity analysis in stochastic environments. We state these results in “Periodic environments”, “Stochastic environments”, and “Sensitivity and elasticity analysis”. The derivations of these results are an essential part of the paper; for clarity, we have collected these in an Appendix A. We present a simple example in “An example” and conclude with a discussion.

Invasion speed in constant environments

We suppose that the life cycle has been divided into a set of demographically relevant stages. The state of the population is given by a vector n(x, t), whose entries are the densities of the stages at location x and time t. We assume that the landscape is one dimensional.

The demographic rates are incorporated into a density-dependent projection matrix B [n(x, t)]. In the absence of dispersal, the population at location x would grow according to

$${\bf n}(x,t+1) = {\bf B}[{\bf n}(x,t)] \; {\bf n}(x,t). $$
(1)

This system has an equilibrium at n = 0; the matrix of the linear approximation near this equilibrium is \({\bf B}[{\boldsymbol{0}}] \equiv {\bf A}\). This low-density approximation describes population dynamics near the front of the invasion wave, and will be used in calculating the wave speed.

Movement is described by a matrix K(x, y) of dispersal kernels, where k ij (x, y) is the probability density function of the location x of an individual at time t + 1 given that it was at location y at time t, and that it moved from stage j to stage i during the interval. If the environment is spatially homogeneous (as we will assume here), K(x, y) depends only on the distance between x and y, and can be written K(x − y).

Dispersal and demography are combined into the integrodifference equation

$$ {\bf n}(x,t+1) = \int_{-\infty}^{\infty} \left({\bf K}(x-y) \circ {\bf B}[{\bf n}(y,t)] \right) {\bf n}(y,t)\, {\rm d}y,$$
(2)

where ∘ is the Hadamard, or element-by-element product. The model (2) says that the population at every location x at time t + 1 derives from the growth of the population at all other locations and on the arrival of individuals from those locations, integrated over the entire landscape.

We make the usual biological assumptions that B[n] is non-negative and primitive for all n ≥ 0. We also assume that the density-dependence includes no Allee effects, satisfies

$${\bf B} [{\bf n} ] {\bf n} \le {\bf A} {\bf n} {\label{eq:dd_assumption}} $$
(3)

Lui (1989), Neubert and Caswell (2000), and is cooperative; i.e.,

$${\bf n} \ge {\bf m } \Longrightarrow {\bf B} [{\bf n} ] {\bf n} \ge {\bf B} [{\bf m} ] {\bf m} $$
(4)

(e.g., Weinberger et al. 2002). Under these conditions, the invasion speed is governed by the low-density leading edge of the invasion wave, where the demography is described by the linearization A , and the invasion is described by the linear integrodifference equation

$${\bf n} (x,t+1) = \int_{-\infty}^{\infty} \left( {\bf K} (x-y) \circ {\bf A} \right) {\bf n}(y,t)\, {\rm d}y . $$
(5)

The wavespeed is calculated from the moment-generating function of the dispersal kernel matrix

$${\bf M}(s) = \int_{-\infty}^{\infty} {\bf K}(x) e^{sx} {\rm d}x. $$
(6)

In these calculations, we make frequent use of the matrix

$$ {\bf H}(s) = {\bf M}(s) \circ {\bf A}. {H(s)} $$
(7)

This matrix projects, from one time to the next, a wave with an exponential shape proportional to e  − sx; hence we call it the wave projection matrix (see Eq. 57).

In terms of the wave projection matrix, the asymptotic invasion speed is given by

$$c^* = \min_{s > 0} \left( \frac{1}{s} \log \rho(s) \right) $$
(8)

where ρ(s) is the dominant eigenvalue of H(s) (Neubert and Caswell 2000). We denote by s * the value of s associated with c *.

Periodic environments

Suppose now that the environment cycles, with a period p, through a set of distinct phases (e.g., seasons). Associated with each phase i is a density-dependent matrix B i [n], a low-density linearization A i , a dispersal kernel matrix K i (x − y), a moment-generating function matrix M i (s), and a wave projection matrix H i (s). The wave projection matrix over a complete environmental cycle, from t to t + p, is the product of the H i ,

$${\bf H}(s) = {\bf H}_p(s) {\bf H}_{p-1}(s) \cdots {\bf H}_1(s) $$
(9)

(note the order of the matrices, from right to left, in the product). Let ρ per(s) be the dominant eigenvalue of H(s). The invasion speed measured as distance per environmental cycle length (i.e., from t to t + p) is

$$c^* = \min_s \left( \frac{1}{s} \log \rho_{{\rm{per}}} (s) \right) $$
(10)

The average invasion speed, measured as distance per unit time, is

$$\bar{c}^* = \frac{1}{p} \min_s \left( \frac{1}{s} \log \rho_{{\rm{per}}} (s) \right). $$
(11)

For the derivation of Eq. 10, see “Invasion speed in periodic environments: derivation”.

Stochastic environments

Suppose now that A and/or K are generated by a stochastic environmental process, producing sequences A t , K t , H t , and H t . We assume that the environmental process is stationary and ergodic. A stationary process is one in which, roughly speaking, the statistical properties of the environment do not change over time. More exactly, the joint distribution of the states at any set of times {t, t + δ 1,...,t + δ n } is constant, independent of the starting time t, the intervals δ i , and the number of intervals n. An ergodic process is one that eventually “forgets” the effects of its starting state. This class is wide enough to include some of the most commonly used stochastic ecological models, including independent and identically distributed (iid) environments, finite state Markov chains, and ARIMA processes (Tuljapurkar 1990). We will describe assumptions on A t and K t below.

Let logρ stoch be the stochastic growth rate (more generally, the dominant Lyapunov exponent) of the random matrix product of the H t (s); that is,

$$\log \rho_{\rm stoch} = \lim_{T \rightarrow \infty} \frac{1}{T} \log \left\| \left( \prod\limits_{i=0}^{T-1} {\bf H}_i(s) \right) {\bf w} \right\| $$
(12)

where w is an arbitrary non-negative vector. This is the time-averaged growth rate over the distribution generated in a single long realization of the environmental process. The long-term average invasion speed in this stochastic environment is, with probability 1,

$$\bar{c}^* = \min_{s>0} \left( \frac{1}{s} \; \log \rho_{\rm stoch} \right) . $$
(13)

For the derivation of the stochastic invasion speed, see “Invasion speed in stochastic environments: derivation”.

Conditions sufficient for the convergence of Eq. 12 are well known in demography (e.g., Cohen 1976; Tuljapurkar and Orzack 1980; Tuljapurkar 1990). In general, it is sufficient that the stochastic process defining the environment be ergodic and that the matrices be non-negative and sufficiently well behaved that any sufficiently long sequence of them forgets the initial state of the population. Since the A t are non-negative and the M t are positive, the H t (s) have the same pattern of zero and positive entries as do the A t . Thus, a sufficient condition for ergodicity of the H t is that the A t are drawn from an ergodic set of matrices; i.e., a set with the property that a product of any large enough number of members of the set will be positive with probability 1. An example of an ergodic set is a set of primitive matrices that share a common incidence matrix.

Sensitivity and elasticity analysis

Invasion speed depends on a set of stage-specific parameters, some related to demography, some to dispersal, and some possibly to both. One of the advantages of calculating invasion speed from a model is that it permits perturbation analysis, which gives the sensitivity and elasticity of c * to changes in the parameters (Neubert and Caswell 2000). The results may suggest targets for management interventions designed to slow the spread of invasive pests, or hasten the recovery of reintroduced species. They also permit LTRE analyses to explain differences in invasion speed in terms of contributions from the vital rates and the dispersal parameters (Caswell et al. 2003).

The invasion speeds in constant environments (Eq. 8), periodic environments (Eq. 10) and stochastic environments (Eq. 13) each depend on a growth rate measure ρ. Sensitivity analysis in the time-invariant case was presented by Neubert and Caswell (2000). Here, we present a new, general, formulation for sensitivity that encompasses the constant, periodic, and stochastic cases, using the matrix calculus developed by Magnus and Neudecker (1985, 1988); see Caswell (2006, 2007, 2008, 2009a, b), Verdy and Caswell (2008), Jenouvrier et al. (2010), Klepac and Caswell (2010) for other ecological applications. In what follows, the derivative of a m×1 vector z with respect to a n×1 vector u is the m×n Jacobian matrix

$${\frac{d{\bf z}}{d{\bf u}^{\mbox{\tiny \sf T}}}} = \left({\frac{dy_{i}}{dx_{j}}}\right) $$
(14)

Derivatives of matrices are calculated by transforming the matrix into a vector using the vec operator, which stacks the columns of the matrix one above the other.

The elasticity of a z with respect to u isFootnote 1

$${\frac{\varepsilon {\bf z}}{\varepsilon {\bf u}^{\mbox{\tiny \sf T}}}} = \mathfrak{D}({\bf z})^{-1} \; {\frac{d {\bf z}}{d {\bf u}^{\mbox{\tiny \sf T}}}} \; \mathfrak{D}({\bf u}) $$
(15)

where \(\mathfrak{D}({\bf u})\) is a diagonal matrix with the vector u on the diagonal and zeros elsewhere (produced in Matlab by the command diag(x)).

Suppose that demography, dispersal, or both depend on a vector \({\boldsymbol{\theta}}\) (dimension q ×1) of parameters. These parameters might include matrix elements, lower-level vital rates, or parameters appearing in the dispersal kernel. The vector \({\boldsymbol{\theta}}\) might also include parameters that define the response of demography or dispersal to the state of the environment. The sensitivities of c * to \({\boldsymbol{\theta}}\) are given by the (1 ×q) derivative vector

$${\frac{dc^{*}}{d\boldsymbol{\theta}^{\mbox{\tiny \sf T}}}} = \frac{1}{s^{*}} {\frac{d\log \rho}{d \boldsymbol{\theta}^{\mbox{\tiny \sf T}}}}. \label{eq:general_sens} $$
(16)

The details of the calculation depend on the nature of ρ, which in turn depends on whether the environment is constant, periodic, or stochastic. For the derivation of Eq. 16, see “Perturbation analysis: derivations”.

Sensitivity in constant environments

In a constant environment, ρ is the dominant eigenvalue of H(s *) = A ∘ M (s *). Let w and v be the right and left eigenvectors of H(s *), scaled so that \({\bf v}^{\mbox{\tiny \sf T}} {\bf w} =1 \).

The invasion speed c * is given by Eq. 8. Its sensitivity is

$${\frac{dc^{*}}{d \boldsymbol{\theta}^{\mbox{\tiny \sf T}}}} = \frac{1}{s^{*}} {\frac{d\log \rho}{d\boldsymbol{\theta}^{\mbox{\tiny \sf T}}}} $$
(17)

where the matrix calculus version (Caswell 2010) of the well-known eigenvalue sensitivity equation (Caswell 2001) is

$${\frac{d \log \rho}{d\boldsymbol{\theta}^{\mbox{\tiny \sf T}}}} =\left( {\frac{{\bf w}^{\mbox{\tiny \sf T}} {\otimes} {\bf v}^{\mbox{\tiny \sf T}}}{\rho}} \right){\frac{d\mbox{vec}{\bf H}(s^*)}{d\boldsymbol{\theta}^{\mbox{\tiny \sf T}}}} $$
(18)

and

$${\label{eq:dvecH}} \begin{array}{rll} {\frac{d {{\mbox{vec} \,} {\bf H}(s^*)}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} &=& {\mathfrak{D} \,}({\mbox{vec} \,} {\bf A}) {\frac{d {{\mbox{vec} \,} {\bf M}(s^*)}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} \\ && +\; {\mathfrak{D} \,} \big({\mbox{vec} \,} {\bf M}(s^*)\big) {\frac{d {{\mbox{vec} \,} {\bf A}}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} . \end{array} $$
(19)

Here, ⊗ denotes the Kronecker product and \({\mathfrak{D} \,}({\bf u})\) is a matrix with u on the diagonal and zeros elsewhere. The elasticities of c * are given by

$${\frac{\varepsilon {c^*}}{ \varepsilon {{\boldsymbol{\theta}}}}} = \frac{1}{c^*} {\frac{d {c^*}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} \; {\mathfrak{D}} ({\boldsymbol{\theta}})$$
(20)

Sensitivity in periodic environments

The invasion speed c * is given by Eq. 10, where ρ per is the dominant eigenvalue of the periodic product

$$ {\bf H}(s^*) = {\bf H}_p(s^*) \cdots {\bf H}_1(s^*). $$

Again, let w and v be the eigenvectors of H(s *). The parameter vector will generally vary with time; let the value at phase i of the cycle be \({\boldsymbol{\theta}}_i\). Then

$${\frac{d {c^*}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} = \frac{1}{s^*} {\frac{d {\log \rho_{{\rm{per}}}}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} $$
(21)

where

$${\frac{d {\log \rho_{{\rm{per}}}}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} = \left( \frac{{\bf w}^{{\mbox{\tiny \sf T}}} {\otimes} {\bf v}^{{\mbox{\tiny \sf T}}}}{\rho_{{\rm{per}}}} \right) \sum\limits_{i=1}^p {\frac{\partial {{\mbox{vec} \,} {\bf H}}}{\partial {{\mbox{vec} \,}^{{\mbox{\tiny \sf T}}} {\bf H}_i}}} \left. {\frac{d {{\mbox{vec} \,} {\bf H}_i}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} \right|_{{\boldsymbol{\theta}} = {\boldsymbol{\theta}}_i}, $$
(22)

with

$${\frac{d {{\mbox{vec} \,} {\bf H}_i}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} = {\mathfrak{D} \,}({\mbox{vec} \,} {\bf A}_i) {\frac{d {{\mbox{vec} \,} {\bf M}_i}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} \; + \; {\mathfrak{D} \,}({\mbox{vec} \,} {\bf M}_i) {\frac{d {{\mbox{vec} \,} {\bf A}_i}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} {\label{eq:dvecHi}} $$
(23)

and

$${\frac{\partial {{\mbox{vec} \,} {\bf H}}}{\partial {{\mbox{vec} \,}^{{\mbox{\tiny \sf T}}} {\bf H}_i}}} \!=\! \left\{ \begin{array}{ll} {\bf I} {\otimes} \left( {\bf H}_p \cdots {\bf H}_2 \right) & i=1 \\[1ex] \left({\bf H}_{i-1}\cdots {\bf H}_1 \right)^{{\mbox{\tiny \sf T}}} {\otimes} \left( {\bf H}_p \cdots {\bf H}_{i+1} \right) & 1 < i < p \\[1ex] \left( {\bf H}_{p-1} \cdots {\bf H}_1 \right)^{{\mbox{\tiny \sf T}}} {\otimes} {\bf I} & i=p \end{array} \right. $$
(24)

The matrices H i and M i and all derivatives are evaluated at s = s * and \({\boldsymbol{\theta}} ={\boldsymbol{\theta}}_i\).

The elasticities of c * are

$$ \begin{array}{rll} {\frac{\varepsilon {c^*}}{ \varepsilon {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} &=& \frac{1}{c^*}\frac{1}{ s^*} \left( \frac{{\bf w}^{{\mbox{\tiny \sf T}}} {\otimes} {\bf v}^{{\mbox{\tiny \sf T}}}}{\rho_{{\rm{per}}}} \right) \\ && \times \sum\limits_{i=1}^p {\frac{\partial {{\mbox{vec} \,} {\bf H}}}{\partial {{\mbox{vec} \,}^{{\mbox{\tiny \sf T}}} {\bf H}_i}}} \left. {\frac{d {{\mbox{vec} \,} {\bf H}_i}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} \right|_{{\boldsymbol{\theta}} = {\boldsymbol{\theta}}_i} \; {\mathfrak{D} \,}({\boldsymbol{\theta}}_i) \end{array} $$
(25)

The sensitivity of the average speed over one cycle of the environment, \(\bar{c}^*\), is

$${\frac{d {\bar{c}^*}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} = \frac{1}{p} {\frac{d {c^*}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}}. $$
(26)

The elasticities of \(\bar{c}^*\) are the same as the elasticities of c *. For derivations, see “Perturbation analysis: derivations”.

Note that environment-specific sensitivities, giving the effect of perturbations applied only in certain phases of the cycle, can be obtained by defining a set \(\mathfrak E\) of environmental states in which the perturbation is applied, and then setting

$${\frac{d {{\mbox{vec} \,} {\bf H}_i}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} = {\boldsymbol{0}} \qquad \mbox{for $i \notin \mathfrak E$} {\label{eq:envspecific}} $$
(27)

(Caswell 2005; Aberg et al. 2009).

Sensitivity in stochastic environments

In a stochastic environment, the long-term average invasion speed is given by Eq. 13, where logρ stoch is the familiar stochastic growth rate generated by the random matrix product

$$ {\bf H}_t(s^*) \cdots {\bf H}_0(s^*). $$

The sensitivity of \(\bar{c}^*\) is

$${\frac{d {\bar{c}^*}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} = \frac{1}{s^*} {\frac{d {\log \rho_{{\rm{stoch}}}}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} $$
(28)

The derivative of logρ stoch is calculated using the algorithm of Tuljapurkar (1990), extended to lower-level vital rates (Caswell 2005) and rewritten in terms of matrix calculus (Caswell 2010). For some large T, generate a sequence of matrices \({\bf H}_i(s^*)\) for i = 0,...,T − 1. Pick an arbitrary w(0) with || w(0) || = 1 and generate forward sequences of structure vectors

$${\bf w}(t+1) = \frac{{\bf H}_t {\bf w}(t)}{\| {\bf H}_t {\bf w}(t) \|} $$
(29)

and 1-step growth rates

$$R_t = \| {\bf H}_t {\bf w}(t) \| . $$
(30)

Pick an arbitrary v(T), with || v(T)|| = 1 and generate the backward sequence of stochastic reproductive value vectors

$${\bf v}^{{\mbox{\tiny \sf T}}} (t-1) = \frac{{\bf v}^{{\mbox{\tiny \sf T}}} (t) {\bf H}_t}{\| {\bf v}^{{\mbox{\tiny \sf T}}} (t) {\bf H}_t \|} $$
(31)

Then the derivative of logρ stoch is

$${\frac{d {\log \rho_{{\rm{stoch}}}}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} = \frac{1}{T} \sum\limits_{i=0}^{T-1} \frac{\left[ {\bf w}^{{\mbox{\tiny \sf T}}} (i) {\otimes} {\bf v}^{{\mbox{\tiny \sf T}}} (i+1) \right]}{R_i {\bf v}^{{\mbox{\tiny \sf T}}}(i+1) {\bf w}(i+1)} {\frac{d {{\mbox{vec} \,} {\bf H}_i}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} {\label{eq:dc_stoch}} $$
(32)

where \(d {\mbox{vec} \,} {\bf H}_i/ d{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}\) is given by Eq. 23 and H i and the derivatives are evaluated at s = s * and \({\boldsymbol{\theta}}={\boldsymbol{\theta}}_i\). The elasticity of \(\bar{c}^*\) is

$${\frac{\varepsilon {\bar{c}^*}}{ \varepsilon {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} = \frac{1}{\bar{c}^*} \frac{1}{ s^*} \; \frac{1}{T} \sum\limits_{i=0}^{T-1} \frac{\left[ {\bf w}^{{\mbox{\tiny \sf T}}} (i) {\otimes} {\bf v}^{{\mbox{\tiny \sf T}}} (i+1) \right]}{R_i {\bf v}^{{\mbox{\tiny \sf T}}}(i+1) {\bf w}(i+1)} {\frac{d {{\mbox{vec} \,} {\bf H}_i}}{d {{\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}}}} \; {\mathfrak{D} \,}({\boldsymbol{\theta}}_i) $$
(33)

Environment-specific sensitivities can be calculated as in Eq. 27. Note that, regardless of whether the environment is constant, periodic, or stochastic, if the parameters in \({\boldsymbol{\theta}}\) affect only demography, or only dispersal, then terms involving \(d {\mbox{vec} \,} {\bf M}_i/d {\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}\) or \(d {\mbox{vec} \,} {\bf A}_i/ d {\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}\), respectively, will be zero. The present formulation, however, permits calculating all the sensitivities and elasticities at once, as well as including parameters that affect both demography and dispersal.

An example

Here we present an example, and use it to compare the calculated invasion speeds with the speeds measured in simulation. We also carry out perform sensitivity and elasticity analysis on the invasion speed. We purposely make both demography and dispersal simple.

Model construction

The demographic model is a modified version of the two-stage (juvenile and adult) model of Neubert and Caswell (2000). Adult fertility (ϕ) is a decreasing function of the local density of adults. The other vital rates—juvenile survival (σ 1), maturation (γ), and adult survival (σ 2)—are density-independent. We suppose that environmental variability affects only fertility, so that ϕ is a function of time and the remaining vital rates are constant. The resulting density-dependent projection matrix is

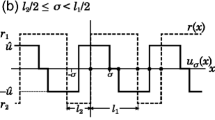
$${\bf B}[{\bf n}] = {\left(\begin{array}{cc} \sigma_1(1-\gamma) & \frac{\phi(t)}{1 + n_2} \\ \sigma_1 \gamma & \sigma_2 \end{array}\right)} {\label{eq:B_example}} $$
(34)

We suppose that dispersal occurs only when juveniles become adults; i.e., in the (2,1) position in K. As a dispersal kernel we use the generalized beta distribution

$$ k_{21}(x; b, \nu) = \frac{ \left[ (b+x)(b-x) \right]^{\nu-1}}{(2 \nu)^{2 \nu - 1} B(\nu,\nu) }, \label{eq:beta_kernel} $$
(35)

with |x| ≤ b, b > 0, ν > 0, and where B(a, b) is Euler’s beta function (Whittaker and Watson 1935).

This kernel has a flexible shape (Fig. 1) and has the satisfying property that infinite distance dispersal is impossible. It is symmetric around the origin, and vanishes beyond a finite maximum dispersal distance b. When the shape parameter ν < 1 the kernel is bimodal, with peaks near the maximum dispersal distance, reminiscent of ballistic kernels (Neubert and Parker 2004). When ν > 1 the mode is at the origin; as ν grows the kernel becomes more peaked. The moment-generating function of k 21(x) is the confluent hypergeometric functionFootnote 2

$$ m_{21}(s) =\, _{0}\!F_{1} \left( \frac{1}{2} + \nu, \frac{b^2 s^2}{4} \right). {\label{eq:beta_kernel_mgf}} $$
(36)
Fig. 1
figure 1

The generalized beta dispersal kernel (Eq. 35) with scale parameter (maximum dispersal distance) b = 1

Full size image

We suppose that all the dispersal parameters are constant except for the scale parameter (the maximum dispersal distance) b, which varies with time as b(t). The dispersal kernel and moment-generating function matrices are then

$$ \mathbf{K}_{t}(x) = {\left(\begin{array}{cc} \delta(x) & \delta(x) \\ k_{21}(x,t) & \delta(x) \end{array}\right)} \label{eq:Kmat} $$
(37)
$$ \mathbf{M}_{t}(s) = {\left(\begin{array}{cc} 1 & 1 \\ m_{21}(s,t) & 1 \end{array}\right)} $$
(38)

where δ(x) is the Dirac delta function.

Invasion speed

As a simple example, we consider an environment that switches between two states, “good” and “bad”, with fertility, ϕ(t), and dispersal distance, b(t), both reduced in a bad year. We set parameters in the two types of years to:

$$\begin{array}{@{\kern-.5pt}lll} & \mbox{good} & \mbox{bad}\\ \phi & {\boldsymbol{3.0}} & {\boldsymbol{1.8}} \\ \gamma & 0.5 & 0.5 \\ \sigma_1 & 0.4 & 0.4 \\ \sigma_2 & 0.5 & 0.5 \\ b & {\boldsymbol{0.5}} & {\boldsymbol{0.2}} \\ \nu & 2 & 2 \end{array} {\label{eq:parameters}} $$
(39)

We suppose that, in the periodic environment, good and bad years alternate, and a stochastic environment in which good and bad years occur independently with a probability of 0.5. The invasion speeds, calculated from Eq. 11 in the periodic environment and from Eq. 13 in the stochastic environment, are

$$\bar{c}^* = \left\{\begin{array}{ll} 0.0347 & \mbox{periodic} \\ 0.0333 & \mbox{stochastic} \end{array} \right. $$
(40)

where logρ stoch is calculated from Eq. 12 with \(T=\mbox{10,000}\).

As a comparison with these calculated invasion speeds, we simulated both periodic and stochastic environments. In the periodic simulation, the oscillation of the shape of the invasion wave front is apparent in Fig. 2. Fig. 3 shows the location of the wave front as a function of time; the front advances during good years, and retreats during bad years, but regardless of whether it is measured in good years or bad years, it advances at a constant speed. That speed should be \(\bar{c}^*\) as calculated from Eq. 11, and Fig. 4 shows the convergence of the average speed to time t of the simulation to the calculated value of \(\bar{c}^* = 0.0347\). Similarly, Fig. 5 shows the convergence of the stochastic simulation to the calculated value of \(\bar{c}^*=0.0333\).

Fig. 2
figure 2

A structured two-cycle invasion wave generated by the nonlinear integrodifference model Eq. 42, with B[n] given by Eq. 34 and K defined by Eq. 35, in a periodic environment with period 2. Parameter values are given in Eq. 39. Inset: the leading edges of the waves

Full size image
Fig. 3
figure 3

The location of the juvenile and adult wave fronts in the simulation shown in Fig. 2, in a periodic environment

Full size image
Fig. 4
figure 4

The average speed from time 0 to time t of an invasion generated by the model in Fig. 2 in a periodic environment. The average speed (solid line) converges to the prediction (dashed line) based on the linearization given by formula (11) Parameter values given in Eq. 39

Full size image
Fig. 5
figure 5

a The location of the invasion front in 20 realizations of a stochastic environment. b The average speed of the wave to time t for 20 realizations. The model is the stochastic version of that shown in Fig. 2, but with good and bad years occurring independently with a probability of 0.5. The average speed (solid lines) converges to the prediction (dashed line) based on the linearization given by formula (13) Parameter values are given in Eq. 39

Full size image

Sensitivity analysis

We define the parameter vector as

$${\boldsymbol{\theta}} = {\left(\begin{array}{cccccc} \phi & \gamma & \sigma_1 & \sigma_2 & b & \nu \end{array}\right)}^{\mbox{\tiny \sf T}} $$
(41)

where the first four parameters affect only demography (in A) and the last two affect only dispersal [in M(s)]. The derivatives \(d {\mbox{vec} \,} {\bf A} / d {\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}\) and \(d {\mbox{vec} \,} {\bf M}/d {\boldsymbol{\theta}}^{{\mbox{\tiny \sf T}}}\) required in Eqs. 19 and 23 are given in Appendix B.

The sensitivities and elasticities of \(\bar{c}^*\) are shown in Fig. 6. In this case (and it need not be so in general), the patterns for the periodic environment and the stochastic environment are qualitatively similar. The sensitivities and elasticities to all the demographic parameters and to the scale of dispersal (b) are all positive, while the sensitivity to the shape parameter (ν) is negative.

Fig. 6
figure 6

Sensitivity and elasticity of the invasion wave speed \(\bar{c}^*\) to changes in each of the demographic and dispersal parameters; parameter values given in Eq. 39. In the periodic case, the environment alternates between the two states. In the stochastic case, the two environmental states occur independently with probability 1/2

Full size image

In this hypothetical example, management tactics that reduce juvenile survival (σ 1) would be an attractive option, although proportional reductions in ϕ would have almost as great an effect.

Discussion

The invasion speed of a structured population is obtained from a product (periodic or stochastic, as the case may be) of demography-dispersal matrices. Because matrix multiplication is not commutative, this implies that the order in which the environmental states appear must be taken into account. Just as in demographic models, one cannot apply results for scalar populations (Neubert et al. 2000) to the eigenvalues of the matrices \({\bf H}_i(s^*)\). Situations exist where invasion is impossible in every environmental state (i.e., \(\rho \left[ {\bf H}_i(s^*) \right] <1\) for all i) and yet it is possible in a periodic environment that varies among the states (i.e., \(\rho \left[ {\bf H}_p(s^*) \cdots {\bf H}_1(s^*) \right]>1\)). Or vice-versa (e.g., Caswell 2001, Example 13.2).

Matrix integrodifference equation models are easily parameterized from commonly collected kinds of demographic and dispersal data (Neubert and Caswell 2000). This extends to the periodic and stochastic versions, which require only population projection matrices and/or dispersal kernels expressed as functions of the environmental state. As in the example in “An example”, this may require as few as two projection matrices and/or dispersal kernels. Stochastic analyses have become common in demographic studies; we expect that they will also do so in studies of invasion. For example, studies of how the statistics of the environment (e.g., the frequency of good or bad years) affects invasion speeds are only beginning (Schreiber and Ryan 2010).

Our findings complete a set of results on invasion speed and its perturbation analysis for scalar and structured populations in constant, periodic, and stochastic environments (Kot et al. 1996; Neubert and Caswell 2000; Neubert et al. 2000). Table 1 summarizes the calculation of invasion speed in each of these six cases. In each case, the invasion speed is the minimum, over the shape parameter s, of a growth rate calculated from a demographic model and the moment-generating function of a dispersal kernel.

Table 1 Calculation of invasion speeds for scalar and structured populations in constant, periodic, and stochastic environments
Full size table

These calculations share a related set of assumptions. They assume that the environment is spatially homogeneous and infinite in extent. They assume that the linear conjecture (van den Bosch et al. 1990; Weinberger et al. 2002) holds, so that the invasion speed is determined by the linearization of the demographic model around zero. This requires the assumption that no Allee effects operate (for an analysis of such effects, see Wang et al. 2002). The calculations in Table 1 also assume that an asymptotic wave speed exists, which requires that the dispersal kernels are exponentially bounded, so that the moment-generating functions exist. If this assumption is violated, the invasion may result in a continually accelerating invasion wave. Such accelerating invasions, however, cannot occur if there is a finite maximum dispersal distance, no matter how large.

Convergence and transients

Like the population growth rate, the invasion wave speed is an asymptotic property. There is every reason to expect short-term transients to be important in the early stages of an invasion. Comparing time-invariant, periodic, and stochastic models (Table 1), we see that convergence to the asymptotic invasion speed requires as many as three distinct kinds of convergence, each of which requires the system to “forget” one kind of initial condition:

  1. 1.

    Convergence of the environment to its stationary distribution of states. The rate of this convergence is a property of the stochastic model for the environment. A constant environment is always in its stationary state.

  2. 2.

    Convergence of the stage structure to its stable form, or, in a stochastic environment, convergence of the probability distribution of the stage structure to an invariant distribution. The rate of this convergence depends on the structure of the life cycle underlying the demographic matrices B i . A scalar population is always at its stable structure.

  3. 3.

    Convergence of the spatial distribution of the population to its travelling wave form. The rate of this convergence depends on the dispersal kernel causing the population to forget its initial form.

Each “dimension” introduces another rate of convergence. A scalar population in a constant environment has only a single dimension of convergence (convergence of the spatial structure to the travelling wave shape). A structured population in a constant environment must converge in stage structure and spatial structure. A scalar population in a variable environment, must converge in a spatial structure, and the environment must converge to its stationary form. A structured population in a stochastic environment must converge in all three dimensions. To our knowledge, the operation of the factors that determine these rates of convergence, and the transient dynamics during convergence, have not yet been studied.