Introduction

Dengue is an infectious disease caused by an arbovirus of Flaviviridae family (Westaway et al. 1985). Dengue fever can be caused by any of the four types of dengue viruses: DEN-1, DEN-2, DEN-3 and DEN-4. Each of them can cause diseases varying from mild to deadly (Gubler 2002). Currently, there is a great interest in studying the dengue epidemic. This disease is recognized in more than 100 countries around the world (Bricks 2004), and it is considered the most significant in terms of mortality and economic cost, since it is responsible for more deaths and infections in humans than any other arthropod-borne viruses (Gubler 2002). This scenario can be even worse, considering that the disease exact number of cases is not known. Several cases are not reported because they may clinically manifest with few or no symptoms (Kurane and Takasaki 2001).

Due to the large number of exposed people, and the absence of medicines able to cure the infected ones, the expansion of dengue epidemics has motivated an intensive study of mechanical and chemical control mechanisms aiming to eliminate the mosquito Aedes aegypti. The mechanical control, relying on educational campaigns for the removal of containers that accumulate water, results in a significant decrease in the population size of the vector when performed on any of the seasons (Toro-Zapata et al. 2010; Arduino 2014; Parks and Lloyd 2004; Dumont and Chiroleu 2010). Moreover, the mechanical control is effective only considering the awareness of the human population to identify and eliminate outbreaks of dengue in their own houses (Luz et al. 2009). The chemical control, based on the use of insecticide and larvicide, was tested for the reduction in vector population (Parks and Lloyd 2004; Dumont and Chiroleu 2010; Luz et al. 2009; Burattini et al. 2008). More recently, in parallel, dengue vaccines were developed and they are still under clinical tests (Johnson and Roehring 1999; Johansson et al. 2011; Julander et al. 2011). Consequently, the efficacy evaluation of distinct vaccination strategies becomes imperative.

In recent years, the field of public health has been benefited from the use of mathematical models for the study of infectious disease epidemic spreading. Mathematical epidemiology studies about interaction models between host–vector and human populations for dengue disease transmission were proposed in (Yang et al. 2016; Abboubakar et al. 2015; Andraud et al. 2012; Aldila et al. 2013; Coutinho et al. 2006; Derouich and Boutayeb 2006; Yang and Ferreira 2008; Esteva and Vargas 1998). The focus was on the study of the basic reproductive rate from the stability analysis of equilibrium points using systems of ordinary differential equations (ODEs).

There are a large number of studies using mathematical models and computer simulation that discuss the vector control methods (Aldila et al. 2013; Antonio and Yoneyama 2001; Dumont and Chiroleu 2010; Blayneh et al. 2010; Moulay et al. 2011, 2012) and inefficient vaccines (Garba et al. 2008; Rodrigues et al. 2014) as human protection tools. Models that use optimal vaccine to immunize the human population against the dengue virus were presented by Dumont and Chiroleu (2010), Rodrigues et al. (2014) and Moulay et al. (2011). The papers (Aldila et al. 2013; Blayneh et al. 2010; Moulay et al. 2012; Rodrigues et al. 2014; Dias et al. 2015) focus on models that combine the use of larvicide, adulticide and vaccination strategies to combat the host–vector and the virus in humans. They use two control strategies: one for mosquito-reduction functions and the other for human immunization. Dumont and Chiroleu (2010), Rodrigues et al. (2014 and Moulay et al. (2011) discuss optimal prevention (individual protection), vector control (Larvae reduction) and treatment strategies. The papers (Bartley et al. 2002 and Knerer et al. 2015) present strategies of modeling using vector control and vaccination. The results highlight magnitude of outbreaks using a combined environmental and biological approach considering characteristics of vector population and seasonality (Bartley et al. 2002). A four-serotype model was considered in this work (Knerer et al. 2015).

Other papers can be used to study the modeling of spread dengue epidemic from partial differential equations (PDEs) associated with mosquitoes and humans population mobility (Maidana and Yang 2007; Cummings and Huang 2004; Maidana and Yang 2009). The dispersion of dengue virus can be attributed to the mosquitoes and humans populations. Over the years, public health authorities have directed attention to the spread of the dengue virus in infected mosquitoes through the implementation of adulticide spraying programs in international airports for mosquito reduction (Wilder-Smith and Gubler 2008). These efforts aim to prevent the introduction of dengue through infected mosquitoes, but this fact considers outbreaks in association with the mosquito movement which are not supported by evidence (Getis et al. 2003). Infected humans are the most likely source of the import dengue virus worldwide (Stoddard et al. 2009).

So, in this paper, we evaluate three strategies—mechanical and chemical control, and vaccination strategies—in order to find the best way to eradicate dengue. In relation to previous Yang and Ferreira (2008) work, the present model analysis was extended in order to describe the dengue impact in the following factors: chemical control (insecticide and larvicide) described by exponential functions, mechanical control by drawing random variable and proposed vaccination strategies while evaluating their efficacies (infection by all four serotypes). As minor changes, seasonality (favorable, unfavorable and intermediate periods), growth exponentially for human population and disease mortality rate are used in the present analysis.

The paper is organized as follows. Section 2 introduces the ordinary differential equations of the model. Section 3 describes mechanical and chemical control strategies, as well as the factors that justify the use of information based on climate strategies and rainfall modeling. The vaccination campaign effects and the efficiency of these mechanisms are also highlighted. Section 4 presents the model solutions obtained by numerical integration and evaluates the efficiency of each strategy. Section 5 draws some conclusions.

Mathematical model for dengue

In some epidemic models, it is useful to separate the vector and host populations in classes according to their stage in the infection cycle. In the case of dengue, for instance, it is useful to consider the existence of three classes for the vector and four for the host. Such stratification is suggested because both the vector and the host contract the virus go through a period of latency in which the individual has the virus but is not capable of transmitting it. So, they become infective, but only humans recover from the disease (Newton and Reiter 1992).

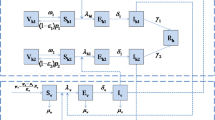
The dengue mosquito, female Aedes aegypti, can be infected with the virus when it feeds from infected human blood. Once it has acquired the virus, the mosquito remains infected throughout its life. So, it is feasible to divide the population of adult midges into susceptible, exposed and infected (SEI). In turn, the human population can recover from the illness, and for this reason, in addition to the existing classes for the vector, there is the recovered human class (Chan and Johansson 2012). These classes define a SEIR (susceptible–exposed–infectious–recovered) model (Korobeinicov 2009). In this approach, a population is represented by state variables associated with the different compartment models, which evolve in time according to the interaction rules (see Fig. 1).

Fig. 1
figure 1

Compartmental model SEI-SEIR, where the mosquito population is represented by six compartments: eggs (E), larvae (L), pupae (P), susceptible (\(M_{\mathrm{s}}\)), exposed (\(M_{\mathrm{e}}\)) and infectious (\(M_{\mathrm{i}}\)) mosquito; and the human population by four compartments: susceptible (s), exposed (e), infectious (i) and removed (r)

Full size image

Our mathematical model, based on the one which was developed by Yang and Ferreira (2008), comprises 10 nonlinear first-order ordinary differential equations. These equations include variables describing two classes of individuals: humans and mosquitoes. The phases in the mosquito life cycle are represented as follows: egg (E), larvae (L), pupa (P) and adult (M). The last one is composed of three subpopulations that differ from each other in their stages of infection, namely susceptible (\(M_{\mathrm{s}}\)), exposed (\(M_{\mathrm{e}}\)) and infected (\(M_{\mathrm{i}}\)).

The parameters of the model are related to biotic and abiotic factors: effective rates of natural mortality and contact rates between human and mosquito populations at distinct stages of infection.

The oviposition (\(\phi\)), mortality of eggs, larvae, pupae, adult midges \(\mu _{j}\) (\(j = e, l, p, w\)) and the transition between the phases of egg, larvae, pupa, adult midges \(\sigma _{j}\), are functions of temperature, humidity and rainfall. In system (1), two parameters correspond to biotic factors, which are subjected to the direct interference of the human activity. They are the carrying capacity, which is represented by the letter \(C'\) (available amount of breeding sites) regarding the aquatic form, and the chemical control, which are represented by the functions \(\mu '_{i}\), (\(i = l, p, w\)). The carrying capacity can be modulated through the elimination of breeding grounds as a result of educational campaigns that were tested to eliminate the aquatic vector population reservoirs. The chemical control is another parameter which takes into account the work of health agents that are responsible for preventing vector proliferation in every stage of its life cycle, from the aquatic to the adulthood phase.

Regarding the population of eggs, we have considered the per capita oviposition rate as \(\phi \,\left( 1-\frac{E}{C'}\right) M\) which describes the rate of deposited eggs (\(\phi\)) by the total mosquito population (M) on carrying capacity (\(C'\)). In the model, the total population of adult mosquitoes is composed only by blood feeding females. The term \(\sigma _{e}\,E\) means per capita rate of eclosion eggs which become larvae, and \(\mu _{e}E\) refers to mortality of eggs. In addition, the model contains exposure rate of infected mosquitoes (\(\gamma _{w}\)), natural death (\(\mu _{w}\)) and insecticide (\(\mu _{w}'\)) rates. The larvicide, in order to eliminate the larvae and pupae, has the rates \(\mu '_{l}L\) and \(\mu '_{p}P\), respectively. The terms \(\sigma _{l}\,L\) and \(\sigma _{p}\,P\) are, respectively, the per capita transformation from larvae to pupa and from pupa to mosquito. We have considered the per capita natural death of the larvae (\(\mu _{l}L\)) and pupa (\(\mu _{p}P\)).

The evolution equations that describe the dengue vector populations in each stage of epidemics are:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}E(t)= & {} \phi \, \left[ 1-\frac{E(t)}{C'} \right] \,M(t)-(\sigma _{e}+\mu _{e})\,E(t) \nonumber \\ \frac{\mathrm{d}}{\mathrm{d}t}L(t)= & {} \sigma _{e}\,E(t)-(\sigma _{l}+\mu _{l}+\mu '_{l})\,L(t) \nonumber \\ \frac{\mathrm{d}}{\mathrm{d}t}P(t)= & {} \sigma _{l}\,L(t)-(\sigma _{p}+\mu _{p}+\mu '_{p})\,P(t) \nonumber \\ \frac{d}{dt}M_{\mathrm{s}}(t)= & {} \sigma _{p}\,P(t)-\left[ \beta _{w}\frac{i(t)}{N}+\mu _{w}+ \mu '_{w}\right] \,M_{\mathrm{s}}(t) \nonumber \\ \frac{\mathrm{d}}{\mathrm{d}t}M_{\mathrm{e}}(t)= & {} \beta _{w}\,\frac{i(t)}{N}\,M_{\mathrm{s}}(t)-(\gamma _{w}+\mu _{w}+ \mu '_{w})\,M_{\mathrm{e}}(t) \nonumber \\ \frac{\mathrm{d}}{\mathrm{d}t}M_{\mathrm{i}}(t)= & {} \gamma _{w}\,M_{\mathrm{e}}(t)-(\mu _{w}+\mu '_{w})\,M_{\mathrm{i}}(t) \end{aligned}$$
(1)

Here, the total mosquito population is written as: \(M(t)=M_{\mathrm{s}}(t)+M_{\mathrm{e}}(t)+M_{\mathrm{i}}(t)\).

The equations for the human populations are coupled and separated in susceptible (s), exposed (e), infected (i) and recovered (r) compartments. In our model, we take into account the presence of only one virus serotype. System (2) introduces the nonlinear ordinary differential equations for the time evolution of human population.

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}s(t)= & {} \mu _{n}\,N(t)-\left[ \beta _{h}\,\frac{M_{\mathrm{i}}(t)}{M(t)} + \mu _{h}\right] \,s(t) \nonumber \\ \frac{\mathrm{d}}{\mathrm{d}t}e(t)= & {} \beta _{h}\,\frac{M_{\mathrm{i}}(t)}{M(t)}\,s(t)-(\gamma _{h}+\mu _{h})\,e(t)\nonumber \\ \frac{\mathrm{d}}{\mathrm{d}t}i(t)= & {} \gamma _{h}\,e(t)-(\sigma _{h} + \mu _{h})\,i(t)\nonumber \\ \frac{\mathrm{d}}{\mathrm{d}t}r(t)= & {} \sigma _{h}\,i(t) - \mu _{h}\,r(t) \end{aligned}$$
(2)

By adding the four equations from system (2), we obtain the total human population \(N(t)=s(t)+e(t)+i(t)+r(t)\), represented by

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}N(t) = \frac{\mathrm{d}}{\mathrm{d}t}s(t)+\frac{\mathrm{d}}{\mathrm{d}t}e(t)+\frac{\mathrm{d}}{\mathrm{d}t}i(t)+\frac{\mathrm{d}}{\mathrm{d}t}r(t) \end{aligned}$$

which yields a constant population if we assume that the overall input (considering natality and immigrations) is balanced by overall mortality (encompassing mortality and emigration) \(\mu _{h}=\mu _{n}\). We are not taking into account the disease-induced mortality; therefore, \(N=N_{0}\) is constant. In this case, the total human population has “zero growth.” If \(\mu _{n}>\mu _{h}\), the total human population grows exponentially.

The rate from exposed to infected human is \(\gamma _{h}\). The infected humans are transferred with the rate \(\sigma _{h}\) to the recovered class (or immune).

We assumed the law of mass action (De Jong et al. 1995; Wilson and Woecester 1945) to describe the transmission of dengue infection among humans and mosquitoes. The transmission coefficient \(\beta _{w}\), which measures the rate of effective contact between susceptible mosquitoes and infected humans, is the rate at which susceptible mosquitoes are infected during blood meal \(\left( \beta _{w}\,\frac{i(t)}{N}\,M_{\mathrm{s}}(t)\right)\). This transmission coefficient depends on the number of bites per mosquito per day, also on the bite probability on an infectious human \(\left( \frac{i(t)}{N(t)}\right)\) and on the transmission probability, which occurs through the bite. We assume that mosquitoes always have a constant number of bites on humans per day.

Similarly, \(\beta _{h}\) measures the rate of effective contact between uninfected humans and infected mosquitoes. The infection rate \(\beta _{h}\) is the product of the average number of bites per human per day times the probability that a mosquito bite will successfully transmit the virus to the human times the probability \(\left( \frac{M_{\mathrm{i}}}{M}\right)\) of the mosquito being infectious. The per capita incidence rate or the force of infection is expressed by \(\beta _{h}\,\frac{M_{\mathrm{i}}(t)}{M(t)}s(t)\).

Control strategies

The influence of climate and temperature

The climate is one of the factors that affect the environment where Aedes aegypti is present (Nakhapakorn and Tripathi 2005). The Aedes is found primarily in tropical and subtropical areas, where the constant temperatures are around \(24\,^{\circ }\)C (Setzer 1966). The temperature has direct and indirect influences on the insect development and feeding (Gubler 1997). Consequently, the effects of temperature on the life cycle of insects can be considered relevant to the population dynamics of dengue vectors and can be exploited to develop appropriate vector control strategies.

However, there are examples in which two communities have very different epidemiological behaviors, but the same climate (Ramos et al. 2008). There are other settings with semiarid climate with endemic transmission (Rodrigues et al. 2016), but in general, the dengue epidemic is strongly correlated with the climate and their variables.

In Brazil, the fall begins in March, winter in June, spring in September and summer in December. But these four seasons are neatly marked only in the southern region, São Paulo, Mato Grosso do Sul, as well as in the mountain regions of Minas Gerais and Rio de Janeiro, occupying approximately \(15\%\) of the Brazilian territory. In other regions, there are only two regimes: the rainy and the dry seasons.

Taking into consideration the climatic variability in Brazil, we have divided a year into three periods, namely favorable, unfavorable and intermediate. These periods were defined in terms of the maximum and minimum rainfall, which is a major determinant of the mosquito population. Indeed, the Aedes aegypti has a weak resistance at low temperatures. Temperatures between 22 and \(30\,^{\circ }\)C are favorable to its life cycle, and the extremes, below \(18\,^{\circ }\)C and above \(34\,^{\circ }\)C, have negative effects on its development (Koppen 1948).

The most favorable period for the vector development is from December to March, due to high temperatures and rainfall. The colder months (June, July, August and September) are unfavorable for the development of Aedes aegypti. The intermediate period is from April to May or from October to November (Beserra et al. 2006). According to the model values, parameters corresponding to the dynamics of the mosquito vary seasonally as listed in Table 1. The values in this table were assumed taking into account the typical characteristics of the weather in terms of temperature, humidity and precipitation. Each of the different coefficients is evaluated using the results of other models referenced in the third column of the table. For instance, the Otero et al 2006 work presents a thermodynamic model for poikilothermal development where the maturation process is controlled by one enzyme which is active in a given temperature range. According to this model, different coefficients involved in the events, egg hatching, pupation, adult emergence and gonotrophic cycle, were obtained for our case. In general, all parameter values present in Table 1 describe the climatic and epidemiological conditions of Brazil.

Table 1 Parameters and their values used in the model. The transformation rates in the aquatic phase as well as the mosquito mortality rates are subdivided into periods: Favorable (F), unfavorable (U) and intermediate (I)
Full size table

Mechanical control

It is widely known that a population cannot grow indefinitely because the environment has a limited capacity of resources to sustain their individuals (Gotelli 2009). The population size of the dengue mosquito increases considerably in rainy seasons due to the increasing number of containers with standing water, which are ideal places for the mosquito oviposition and also for the nourishment of the immature stages of the vector (WHO 2012). Thus, the environmental support capacity of the dengue vector is primarily related to the amount of available sites for laying eggs, since the necessary resources for the maintenance of adult vectors, such as food and shelter, are virtually unlimited. Consequently, if breeding grounds are eliminated, a decrease in the population size of the vector, in cases of dengue fever, will be expected.

In Eq. (1), the environmental support capacity \(C'\) for the population of eggs is interpreted as the physical space available for the mosquito oviposition. A method to control the population growth of the mosquitoes is to decrease \(C'\) through the elimination of breeding grounds. This is usually done mechanically, at different times of the year, according to the climatic conditions.

In order to take into account this control strategy, our model assumes that the support capacity \(C'\) is a function of a random variable \(C_{i}=C_{i}(t)\), which raffles one number in each simulation time step, following a uniform distribution. Specifically,

$$\begin{aligned} C'= & {} C_{i}C_{0} \end{aligned}$$
(3)

in which \(C_{0}\) is the supportability of the containers in the absence of control measures and

$$\begin{aligned} 0 < C_{i} \le 1 \end{aligned}$$
(4)

varies seasonally.

When \(C_{i}\) assumes values close to 0, leading to a very small \(C'\), there are few locations for oviposition. In contrast, when \(C_{i}\sim 1\), the support capacity remains virtually unchanged and there is no reduction in mosquito breeding sites. We assume that efforts for mechanical control should be daily. Due to this, the control would represent efforts for remove, for instance, from a cap bottles that can accumulate rainwater (small support capacity) until tanks opened (big support capacity). In turn, the value of \(C_{0}\) varies with the annual seasons.

In the favorable period, characterized by high temperatures and humidity (Câmara et al. 2007), a value \(C_{0} = 700\) was fixed. During the unfavorable period (cold and arid) (Koopman et al. 1999), we set \(C_{0} = 300\). For the months that comprise the mild period, a supportability of \(C_{0} = 500\) is assumed.

Chemical control

There are two types of chemicals that kill the dengue vector: insecticides, which affect adult mosquitoes, and larvicides, which kill vector larvae. We have assumed that the chemical control does not act on the pupae population (\(\mu '_{p}=0\)). The insecticides are the most used agent for the vector control, and larvicides are complementarily employed to perform this control. In our model, those chemical methods are represented by the variables \(\mu '_{w}\) and \(\mu '_{l}\) that affect winged mosquitoes and larvae, respectively.

The mortality rates decay exponentially with time from the chemicals release (see Table 2). We have built these functions considering the terms of withdrawal which are present in larvae (\(\sigma _{l}+\mu _{l}+\mu '_{l}\)) and susceptible mosquitoes (\(\mu _{w}+\mu '_{w}\)) in the absence of humans \(\left( \frac{i}{N}\rightarrow 0\right)\). These expressions have maximum value equal to 1. We used this one to estimate \(\mu '^{0}_{l,w}\) in Eq. (5).

$$\begin{aligned} \mu '_{l,w}= \mu '^{0}_{l,w}\,e^{-k\,t} \end{aligned}$$
(5)

We estimate k’s assuming that the chemicals are released during the first weeks of every month, and that they persist for 15 days in the environment. On the first day, the chemical release is maximum (\(t=0, \mu '_{l,w}=\mu '^{0}_{l,w}\)), and at most \(10\%\) of the total amount of released chemicals remains in the environment. They also change with the period of the year as it is shown in Table 2.

Table 2 Continuous functions representing the chemical control by insecticide and larvicidal, at the favorable, unfavorable and intermediate periods
Full size table

Vaccination campaign

It has been a long time that the fight against dengue is restricted to eradication methods of its vector. The development of new tools to combat dengue, for instance a vaccine, requires further knowledge about the biological characteristics of the virus and its interaction with the hosts. Currently, the development of a tetravalent vaccine against the dengue virus is a reality (WHO 2016). After Mexico, the Philippines is the second country to license the vaccine and the first one to have anti-dengue vaccine in the world. Brazil, El Salvador and Paraguay have also approved the use of the vaccine (Carvalho et al. 2016). The World Health Organization (WHO) recommends the use of the dengue vaccine Dengvaxia (WHO 2016).

Our model, which is described by Eqs. (1) and (2), does not take into account people who die by the disease and by the vaccine that makes humans immune to the dengue virus. Considering these two features of the epidemics, we extended our model as follows. The death of infected humans is introduced through the addition of a mortality rate \(\mu _{d}\) in the infected compartment:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}i(t) = \gamma _{h}\,e(t)-(\sigma _{h} + \mu _{h} + \mu _{d})\,i(t) \end{aligned}$$
(6)

In order to represent a possible vaccination campaign, a proportional fraction to a vaccination rate \(\nu\) of susceptible individuals is removed and added directly to the recovered compartment. Also, the efficiency of the vaccine is taken into account through the variable \(\xi\). If \(\xi =0\), the vaccine is not effective and does not change the system, whereas if \(\xi =1\), the vaccine is fully effective, and all the vaccinated individuals become immunized. So, the effect of a vaccination campaign on the susceptible and recovered populations is given by:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}s(t)= & {} \mu _{h}\,N(t) - \left[ \beta _{h}\,\frac{M_{i}(t)}{M(t)} + \mu _{h} \right] s(t) - \xi \,\nu \,s(t) \end{aligned}$$
(7)
$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}r(t)= & {} \sigma _{h}\,i(t) - \mu _{h}\,r(t) + \nu \,\xi \,s(t) \end{aligned}$$
(8)

The period that a campaign lasts is varied in order to find out the time demanded to eliminate the virus.

Effectiveness

For each control method, its effectiveness percentual \(\Sigma\) can be defined as

$$\begin{aligned} \Sigma = \left( 1-\frac{A_{c}}{A_{o}} \right) 100\% \end{aligned}$$
(9)

in which \(A_{c}=\int _{0}^{T}M(t)\,\mathrm{d}t\) represents the area under the curve of the total mosquito population in the time interval [0, T] when the control methods are used. And \(A_{o}=\int _{0}^{T}M(t)\,\mathrm{d}t\) is the area under the curve of the total mosquito population during the period of time 0 to T, without any control method.

Results

The results refer to the numerical analysis of the system of equations (1) and (2) for a time period of approximately 20–50 years, corresponding to, respectively, 730,000–1,825,000 simulation time steps. The parameter values listed in Table 1 were adopted in order to describe the coexistence between populations of humans and mosquitoes (aquatic and adult) taking into account the favorable, intermediate and unfavorable periods.

Dengue fever, especially in its most severe form, is hemorrhagic and may have a lethality rate greater than \(20\%\) (Bricks 2004). In order to increase the realism of the model, we added to the human infected compartment, Eq. (6), the rate of death by illness \(\mu _{d}\). As shown in Fig. 2, this new factor has a quantitative impact on disease epidemics, leading to delays of outbreaks at short or long term.

Since the Epidemiological Bulletin of the Brazilian Ministry of health in 2005 reported a \(4\%\) lethality level for dengue (MDS 2005), we used \(\mu _{d} = 0.006\)/day for the numerical solutions performed in the following sections. To get to the achieved rate \(\mu _{d}\), we solved the equation \(\dfrac{\mu _d}{\sigma _h + \mu _h + \mu _d} = 0.04\) for \(\mu _d\), whose the other parameters (\(\sigma _h\), \(\mu _h\)) was obtained from Table 1. The term \(\dfrac{\mu _d}{\sigma _h + \mu _h + \mu _d}\) is the probability of someone leaving the infectious class by death.

Fig. 2
figure 2

Evolution in time of the infected human population with and without the disease mortality rate parameter \(\mu _{d}\). We used the natality rate a\(\mu _{n}=0.00042\)/day and b\(\mu _{n}=0.000042\)/day

Full size image

In Sect. 4.1, we assumed that the human population grows exponentially (\(\mu _{n}=0.00042\)/day), as suggested by the United Nations (UN) (UN 2014). Finally, a simulation for a stationary human population (\(\mu _{n}=0.000042\)/day) is performed in Sect. 4.2.

Total human population with exponential growth

Mechanical control

The female Aedes aegypti lays its eggs in places containing stagnant water. In order to test the impact of the mechanical control on the population of adult vectors, a periodical decrease has been made in the carrying capacity, following the rule described in Sect. 3.2.

Figure 3 compares the results of when the mechanical control was applied daily at distinct annual periods (dashed line), namely favorable, unfavorable, intermediate and throughout the year, with those in which no control was performed (full line). The greatest efficiency was obtained when the mechanical control was carried out throughout the year (Fig. 3d). In all cases, the frames show 600 days of the simulation, since the behavior repeats over the 20 years in which the simulation was performed.

Figure 4 describes the evolution in time of the infected mosquito and human populations, when no control is performed (full line), and when the mechanical control is executed daily only in the intermediate period (dashed line). In the time interval between 240 and 360 days, there was an increase in the number of disease cases in comparison with simulations without mechanical control. However, in the following interval (between 360 and 480 days) this number was smaller. This delay in decreasing the number of dengue cases is due to the fact that the mechanical control only eliminates the aquatic stages of the mosquito.

Fig. 3
figure 3

Comparison between the population sizes of the dengue vector with and without mechanical control. The control is held daily in: a favorable period; b unfavorable period; c intermediate period; d throughout the year. The case in which the mechanical control is performed (dashed line) is compared to the one that no control type was executed (full line)

Full size image

When the control is performed in only one of the annual periods, an increase in the number of infected humans in that period is observed despite the decrease in the number of infected vectors, as shown in Fig. 4.

The use of mechanical control throughout the year can lead to a greater efficiency in dengue control. However, the Aedes aegypti mosquito is not eradicated by only using the mechanical control, and consequently, the virus remains in the human population. Thus, the use of insecticide and larvicide was tested and the corresponding results are discussed below.

Fig. 4
figure 4

a Mosquitoes and b humans infected when no control is performed and when the mechanical control is performed daily in the intermediate period

Full size image

Chemical control

We used the functions in Table 2 in order to evaluate the impact of insecticides and larvicides on the control of dengue epidemic. In addition, to discriminate the impact of different types of chemical control, simulations were performed considering only one type of control at a time.

Figure 5 presents the evolution in time of the Aedes aegypti population when an insecticide was applied. As it can be seen, the use of insecticide was unable to eradicate the mosquito, even when the application was made throughout the year (Fig. 5d). The protocol generates the greatest impact on the total population. Indeed, this control had only \(21\%\) of efficiency, as calculated according to Eq. (9).

Fig. 5
figure 5

Mosquito population sizes after applying the insecticide, assuming that the chemicals are released during the first day of every month of the: a favorable period, b unfavorable period, c intermediate period and d throughout the all months of year

Full size image

In Figure 6, the results for the larvicide application are shown. The efficiency is very low, around \(5\%\), and the population evolves, practically, as if no control mechanism was used. This indicates that such control is not feasible to eradicate the Aedes aegypti mosquito.

Fig. 6
figure 6

Mosquito population sizes after applying the larvicide, assuming that the chemicals are released during the first day of every month of the: a favorable period, b unfavorable period, c intermediate period and d throughout the all months of year

Full size image

The long-term control done by chemicals, such as those considered here, should be analyzed carefully because its continued use can generate resistant vector populations (Braga and Valle 2007). In addition, according to the technical note no 109/2010 (MDS 2010), it is important to consider that there are no insecticides suitable for use in public health. Considering this, all these products are used, specifically, for agriculture.

Mechanical and chemical control

Since the use of insecticide and larvicide, separately, was inefficient to eliminate the population of dengue adult vectors, we considered a scenario in which the two chemicals were applied simultaneously combined with the mechanical control throughout the year.

The results are shown in Fig. 7 for different control strategies. The mechanical control is performed daily considering all the months of the year, while the chemical control is done applying insecticide and larvicide together on the first day of the month, considering all the months of the year. When the chemical control was combined with the mechanical control, the efficiency was \(86\%\) (dotted curve). In comparison, if only the mechanical control (dashed curve) is carried out, the efficiency falls to \(26\%\). However, even if both types of control are applied, it is still not possible to eliminate dengue from the system, leaving the human population at risk of contracting the disease. These results are corroborated with empirical data available in (Andersson et al. 2015).

Fig. 7
figure 7

Evolution in time of dengue vector population under different applications of chemical (insecticide and larvicide) and mechanical controls. The combined use of chemical and mechanical controls resulted in an 86% efficiency (dotted curve). In turn, the efficiency falls to 26% if only the mechanical control (dashed curve) is used

Full size image

Figure 8 shows the impact of mechanical and chemical controls on the population of infected humans. The result is independent of the control methods. Despite a decrease in the number of individuals at a given time, this number increases again, leading to a control efficiency of less than \(1\%\). This indicates that the density of infected mosquitoes does not interfere with the virus remains into the system, unless there is a critical population size that guarantees virus support. Accordingly, in countries in an endemic state, most of their districts present a vector index below the value required for the risk of dengue fever epidemics (Câmara et al. 2007). The incidence of infection was high even in areas with low numbers of dengue mosquito breeding sites (Teixeira et al. 2002). Furthermore, small mosquito breedings with outbreaks in those areas’ neighborhoods can ensure the presence of dengue virus in all other districts of a city (Braga and Valle 2007).

Fig. 8
figure 8

Comparison of the population size of infected humans when no control is carried out and when the chemical and mechanical controls are performed together throughout the year

Full size image

Vaccination campaign

Since the chemical and mechanical controls were unable to eliminate the dengue virus circulation in the human population, we tested the effects of an eventual vaccine against dengue fever on its spreading dynamics. In order to simulate a vaccination, a fraction, proportional to the vaccination rate, \(\nu\), is withdrawn from the compartment of susceptible humans—Eq. (8)—and directly added into the recovered compartment, Eq. (7).

It is widely known that vaccines licensed by health agencies are not \(100\%\) effective. Due to this fact, the efficiency \(\xi\) of the vaccine was also considered. \(\xi = 0\) corresponds to an absolutely ineffective vaccine that does not develop immunity, whereas \(\xi = 1\) means that the vaccine is completely effective, immunizing all the vaccinated individuals.

With an efficiency fixed at \(\xi =1\), the time during which the campaign should be maintained in order to eliminate the virus was estimated. Figure 9a shows that a campaign kept on for four consecutive months eradicated the virus from the population when we assumed a vaccination rate \(\nu =0.13\)/day. However, if we reduced the vaccination rate in one order of magnitude (\(\nu =0.013\)/day), it would require 12 months to eradicate the virus (see Fig. 9b).

Fig. 9
figure 9

Time evolution of dengue epidemic for different time spans of the vaccination campaign. We assumed an efficiency vaccine \(\xi =1\) in the scenarios: a\(\nu =0.13\)/day and b\(\nu =0.013\)/day

Full size image

Furthermore, Fig. 10 shows the time evolution of the infected human population for different values of \(\xi\) for a 4-month campaign. A vaccine that is \(60\%\) or \(70\%\) efficient does not eliminate the virus. For a vaccine with \(80\%\) efficiency, there is a significant decrease in the number of cases over time. In order to eliminate the dengue fever from the human population, at least \(90\%\) efficiency is required. Larger \(\xi\) values (\(>90\%\)) only differ from each other in the time spent to eradicate the virus.

Fig. 10
figure 10

Comparison of different rates of efficiency for the vaccine against the dengue virus: a 90%, b 80%, c 70% and d 60% efficiencies

Full size image

Total human population without exponential growth

As previously mentioned, dengue is present in many places, including Brazil and other South American countries, where the population growth rate is not enough to reach levels as high as those of the African ones. According to a study by the Brazilian Institute of Geography and Statistics (IBGEFootnote 1), the Brazilian population has been decreasing its growth rate since the \(60's\), when it was \(3.04\%\). The IBGE estimates that this reduction should still last for many years until it reaches the so-called zero growth in 2039 (IBGE 2011). We also adjusted the birth rate of the human population to a value closer to the mortality one. So, in this simulation the birth rate (\(\mu _{n}\)) is now fixed in 0.000042/day.

Considering this new birth rate for the human population and the use of mechanical control throughout the year, an efficiency of \(80\%\) was reached. However, as shown in Fig. 11, the reduction in the mosquito population does not imply a decrease in the infected humans. The latter remains the same as when the control was not used. We noticed that, even with a low number of infected mosquitoes, the dengue virus still remains in the human population. This is possible because the dengue mosquito feeds itself several times during a single life cycle, as it was revealed by histological studies. Consequently, a single female can contaminate several humans in the same cycle (Morrison et al. 1997).

Fig. 11
figure 11

Mosquitoes (total and infected) and infected human population when no control is in effect and when it is done mechanically throughout the year with birth rate \(\mu _{n} = 0.000042\)/day: a total mosquito population; b population of infected mosquitoes; c population of infected humans

Full size image

Since only the mechanical control was unable to eliminate the dengue fever epidemic, a chemical control was applied in order to check its efficiency taking into account that new birth rate. Figure 12 shows the response of the system to the use of mechanical control (throughout the year), as well as the insecticide and larvicide applied in different periods of the year.

Fig. 12
figure 12

Evolution in time of mosquito and human population with the use of mechanical (throughout the year), birth rate \(\mu _{n}= 0.000042\)/day and chemical control for the favorable, unfavorable and intermediate periods: a total population of mosquitoes; b population of infected mosquitoes; c population of infected humans

Full size image

We can notice that the chemical control is efficient to eradicate the dengue viruses regardless of the period in which it is applied. Even eliminating all the infected mosquitoes in the system, the control does not reduce significantly the susceptible population of the vector. In the paper written by Burattini et. al, it was possible to evaluate the use of chemical control, which had a considerable impact to prevent the spread of dengue fever epidemic (Burattini et al. 2008).

The persistence of Aedes aegypti, even uninfected, in the system permits dengue fever to reappear at any time if any infected person is introduced into it. Therefore, the dengue epidemic can reemerge in the human population, since the vector of the virus is still present.

It is known that vector elimination campaigns, by means of chemical agents, often occur in the favorable period of the year. Accordingly, we performed the chemical control in this period to see how the system would respond to the emergence of infected people.

Figure 13 shows the simulation of the results in which 10 individuals infected with the dengue virus appear on May, 1st (10th year, indicated by an arrow), when the disease was already extinguished (see Fig. 12). If these infected individuals come into the system when chemical control is applied in the unfavorable period (dashed line), dengue will reappear, but this system remains free of the disease. On the other hand, if they are introduced when there is chemical control in the favorable period (continuous line), we observe periodic outbreaks of the disease. This suggests that a control campaign performed only in a period of the year may not be effective to eliminate dengue completely, since the virus can reappear through the emergence of infected people.

Fig. 13
figure 13

Evolution in time of a populations of infected mosquitoes and b humans for a scenario in which 10 infected humans appear in a system free of viruses. The analyses were carried out when chemical control is used in the favorable and unfavorable periods. The mechanical control is applied throughout the year

Full size image

With the rate \(\mu _{n}=0.000042\)/day the human population does not grow exponentially, and the use of chemical control makes possible the absence of infected people. However, even with the complete elimination of the population of infected vectors, it is still not possible to eliminate all the susceptible mosquito population in the system, as shown in Fig. 13. The dengue fever may reappear at any time, unless there is a vaccine to protect the population from the virus.

Vaccination campaign

Figure 14 shows different scenarios of a vaccination campaign (Eqs. 8 and 7) when \(\mu _ {n}=0.000042\)/day. In all of them, the vaccines were applied during the first 3 months of summer for 4 years. The results show that if we increase the rate of vaccination (\(\nu\)) and efficiency (\(\xi\)), it generates a delay in recurrence of the disease. In Fig. 14d, when \(\nu =0.13\)/day was used, the disease reappears \(\approx 33\) years after the end of the vaccination campaign.

Fig. 14
figure 14

Vaccination campaign with different rates \(\nu\) and efficiencies \(\xi\)

Full size image

In the next simulations, the vaccination campaign is represented by the withdrawal of a fixed number of susceptible individuals (\(\psi\)) that is added into the recovered population. Thus, the vaccination rate is no longer proportional to the number of susceptible individuals, and it is described by Eqs. (10) and (11). In this case, the efficiencies \(\xi\) for the vaccine are considered for each serotype DEN-1, DEN-2, DEN-3 and DEN-4.

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}s(t)= & {} \mu _{h}\,N(t) - \left[ \beta _{h}\,\frac{M_{\mathrm{i}}(t)}{M(t)} + \mu _{h} \right] s(t) - \xi \,\psi \end{aligned}$$
(10)
$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}r(t)= & {} \sigma _{h}\,i(t) - \mu _{h}\,r(t) + \xi \,\psi \end{aligned}$$
(11)
Fig. 15
figure 15

Vaccination campaign with different rates \((\psi ;\xi )\): a (130; 0.5), b (200; 0.42), c (90; 0.74) and d (90; 0.777)

Full size image

Figure 15 shows the system behavior under immunization of \(\psi\) people per day for 3 months, with different time spans of the campaigns. We used the efficiencies a) \(\xi =50.3\%\), b) \(\xi =42.3\%\), c) \(\xi =74\%\) and d) \(\xi =77.7\%\), respectively, for the emergence of the virus types DEN-1, DEN-2, DEN-3 and DEN-4 (Villar et al. 2015), taking into account different quantities of people that were vaccinated. These quantities were used in the threshold of the disease disappearance (full line). The greater the effectiveness of the vaccine is, the fewer the people have to be vaccinated for a more effective vaccination campaign. It can be observed that, if the campaign lasts for only 5 consecutive years, the dengue virus reemerges in populations of mosquitoes and humans and the epidemic reappears. However, if the duration of the campaign is 10 years, it is possible to eradicate the dengue virus from the human population for at least 60 years, the total simulation time. To find out the time required for the permanent eradication of the virus from the system, further simulations, considering longer time intervals, should be performed.

The vaccine is essential for the elimination of dengue viruses in human populations. Several studies indicate vaccines protecting the human population from the dengue virus. A tetravalent vaccine, using attenuated viruses, has been tested in order to characterize the interactions between the different serotypes of dengue virus. This test indicates that it is possible to create an effective vaccine against all four serotypes of the dengue virus (Anderson et al. 2011). However, an important point to be considered is that whether a live vaccine, which is made of attenuated viruses, does not offer risks to human health, since it is not clear that the presence of the four strains into a single vaccine might increase the risk of developing severe forms of the disease (Silva and Richtmann 2006). Recent studies about immunization are satisfactory and show a positive result about the vaccine (Hadinegoro et al. 2015; Villar et al. 2015).

Conclusions

Mathematical models are valuable tools to understand the dynamics of infectious diseases such as the dengue fever. Here, the compartmental model proposed by Yang and Ferreira (2008) was adapted in order to test new control strategies of dengue epidemics. Specifically, the mechanical and chemical controls, as well as vaccination strategies for the human population, were investigated.

For human populations growing exponentially, we found that the use of the mechanical and chemical controls, individually, was not effective in reducing the population of Aedes aegypti. Furthermore, the control based only on larvicides had a very low contribution to that reduction, probably because the time interval between its application and its impact on the population of adult vectors is very long (Andersson et al. 2015). But regarding the mechanical control, it must be applied throughout the year. Indeed, since this control is effective only for a short time, after its application, there is an increase in the number of cases in those periods. The use of mechanical and chemical controls together was much more efficient than each of them individually, but they were unable to eliminate the disease.

One of the consequences of the chemical control is that it affects ecosystem killing another insects, besides the development of mosquito resistance to it. The larvicide there is not residual effect and the efficacy is very low, contrarily to the insecticide which has longer residual effect and higher efficacy. On the other side, the mechanical control is a clean ecological control, but to be effective, a higher proportion of carrying capacity needs be removed (Thomé et al. 2010). However, aquatic places are breeding sites such as lakes and swimming pool. Additionally, there are others control mechanism dengue as, for instance, release a higher proportion of sterile mosquitoes relative to the natural mosquitoes (Pio et al. 2008; Esteva and Yang 2005).

The variable \(\mu _{d}=0.006\)/day was introduced to represent the portion of infected people who died due to complications related to dengue fever. The addition of this new factor did not alter significantly the appearance of new outbreaks of the disease. It was possible to notice the existence of annual cycles and a strong seasonality of epidemic cycles (Nakhapakorn and Tripathi 2005). A major concern about the safety of live vaccines is the genetic stability. The use of molecular tools is required to ensure quality, safety and authenticity of the genetic vaccine (Rodrigues et al. 2014).

When the birth rate was changed to 0.000042/day, it was no longer possible to observe an exponential growth of the human population. In this case, the efficiency of the mechanical control remained at \(80\%\). In the same way for the previous simulations, there was no significant decrease on the infected human population. The chemical control can eliminate the infected population, but the outbreaks do not end. With 10 infected individuals introduced after elimination of the dengue virus, periodic outbreaks of the disease occurred.

The only way to stop the dengue epidemic, regardless of the form of population growth, is to create a vaccine to immunize the population against the virus. When the population grows exponentially, a fraction, proportional to the vaccination rate of individuals \(\nu = 0.13\)/day, is required. For this campaign to be effective, it is necessary to have duration of 4 months and a vaccine efficiency rate of at least \(90\%\). When it comes to the “zero growth,” the campaign is based on daily immunization \(\psi\), with different efficiencies. In the case of serotype DEN-4, which has an efficiency of \(77\%\), it is necessary to maintain the campaign (\(\psi =90\)) for 4 months, for at least 10 years, to ensure 60 years of a population free from the disease. Lower vaccine efficiencies are admitted since be used together form of vector control to decrease significant number of infectious (Hendron and Bonsall 2016; Kim et al. 2017; Christofferson and Mores 2015).

However, field researches are still necessary in order to promote a better understanding of the mechanisms that are responsible for generating these dynamics. In addition, more simulations must be carried out in order to consider a longer time of observation, while considering the possibility of the emergence of other serotypes of the disease and biological ways of eliminating its vector. Another possibility of study is to expand the model presented here to include the secondary dengue infection, incorporating the dependent antibody enhancement.