1 Introduction

The study of the physical behaviour in superdense astronomical objects is an important subject for investigation in physics in a general relativistic setting. It is believed that higher values of the central densities at the core create appropriate conditions for the relativistic nucleons to convert to hyperons or to produce condensate structures. The modelling of the stellar interior in a quark phase was first performed by Witten [1] and Farhi and Jaffe [2]. The exact constitution of the matter distribution in the core of the star requires deeper investigation. In most of the treatments of highly dense bodies, the core region is surrounded by an envelope or nuclear crust made up of baryonic matter. A relevant description with this matter distribution is provided in Sharma and Mukherjee [3] consisting of neighbouring distributions of different phases, an inner layer comprising a deconfined quark phase and an outer layer of baryonic matter which is less compact. In the model, comprising a core and an envelope, in a dense stellar configuration the matter distributions in the two neighbouring layers have distinct physical properties.

Precise details of the behaviour of matter in superdense compact stars are not fully understood. Nauenberg and Chapline [4], Rhoades and Ruffini [5] and Hartle [6] pointed out that when the matter density of a spherical stellar compact object is much higher than the nuclear density, it is difficult to have an exact description of stellar matter distributions. As pointed out by Gangopadhyay et al [7], recent observations of the pulsar PSRJ1614-2230 with an accurate mass measured around \(1.97 \pm 0.08M_\odot \), and the results on the pulsar J0348+0432 with mass \(2.01 \pm 0.04M_\odot \), generate strong constraints on the composition of highly dense matter beyond the saturation nuclear density. The uncertainty about the type of the equation of state for stellar matter beyond the nuclear regime led some researchers to consider a different approach in the modelling of highly dense stars, called hybrid model or core envelope model. It is also worth mentioning that in studies in nuclear physics or studies in particle physics, it is a challenge to choose an appropriate equation of state for the matter distribution that connects the inner quark matter core to the neighbouring nuclear matter. Therefore, in an attempt to address this issue, various studies have been carried out in core–envelope models with changes in the type of equation of state, in previous years. Previous investigations have showed that a hybrid star composed of nuclear and quark matter can produce a mass–radius relationship consistent with that predicted for a star composed of purely nucleonic matter. Such physical features of the model can be affected by the presence of electromagnetic field. Hansraj et al [8] generated regular core–envelope models by analysing the Einstein–Maxwell system and solved the resulting nonlinear Riccati equation. Alternative gravity theories, with higher-order curvature corrections, impact on the central densities and the mass–radius relation. For a recent study in Einstein–Gauss–Bonnet gravity, see the results of Bhar et al [9] which establish the impact of additional curvature terms on the gross physical behaviour of a compact star. Also, note that gravastars, describing a new endpoint of gravitational collapse with a Bose–Einstein condensate, require neighbouring space–time regions with different equations of state. A core–envelope description is well suited to describe the relevant physics in such situations as pointed out in several papers including [10,11,12,13,14].

Particular stellar models, with a core and an envelope, for dense relativistic spheres have been obtained previously in general relativity. Durgapal and Gehlot [15, 16] found exact interior models in the core and envelope with distinct energy densities. Fuloria et al [17, 18] found non-terminating series for neutron stars, displaying isothermal behaviour, which have the properties of being bound and gravitationally stable. Stellar models displaying a parabolic energy density in the core regions had been considered by Negi et al [19, 20]. Sharma and Mukherjee [3, 21] related their model, with a core and an envelope, to the X-ray pulsar Her X-1, a compact and binary object, for a quark–diquark distribution in an equilibrium state. Paul and Tikekar [22], Tikekar and Thomas [23], Thomas et al [24] and Tikekar and Jotania [25] found exact core–envelope models with the inner region having both isotropic pressures and anisotropic pressures in the core. They also specified the manifold to have parabolic geometry, spheroidal geometry or pseudospheroidal geometry to solve the field equations. More recently, Mafa Takisa and Maharaj [26] generated a core–envelope model with both anisotropy and electric field.

In this paper, we seek to model a highly compact relativistic gravitating object using a core–envelope description. We characterise our model with two features. Firstly, the matter distribution is anisotropic. Various results of Tikekar and Jotania [25], and others, show that anisotropy is an important feature for a superdense star in hydrostatic equilibrium which satisfies all physical conditions for the core and the envelope. Secondly, the matter configuration obeys an equation of state which is barotropic in all regions of the star. An equation of state is a desirable feature for the matter distribution on physical grounds. The equation of state in this model is taken to be linear in the core layer. Close to the central region, the radial pressure is higher. An appropriate linear equation of state, describing stellar models, has been investigated by Mafa Takisa and Maharaj [27], Thirukkanesh and Ragel [28] and Mafa Takisa et al [29]. The equation of state in this model is taken to be quadratic in the envelope layer. This has the advantage of ensuring that the radially directed pressure in the envelope is lower than pressure in the core. Structures with quadratic equations of state, describing stellar models, have been analysed by Feroze and Siddiqui [30], Maharaj and Mafa Takisa [31] and Mafa Takisa et al [32]. In most of the previous studies of stars with a core and an envelope, the matter distribution is arbitrary; our approach ensures that there is an equation of state throughout the interior of the star.

We establish, in this paper, a new structure for compact objects by connecting two inner space–time regions satisfying distinct equations of state. The outer region is described by the Schwarzschild line element. We review the Einstein field equations in §2. In §3, we give the exact solution describing the core and the exact solution describing the envelope. In §4, the matching conditions at the interfaces describing the three space–time regions are explored. Masses, radii and physical quantities for some stellar objects are presented in tables 1 and 2. In §5, the matter variables are graphically studied, and we analyse the physical features of our solution in relation with the particular pulsar PSR J1614-2230. Our calculations with changing core and envelope radii are shown in tables 3 and 4. We briefly comment on the results derived in this work in §6.

Table 1 Values of model parameters that generate masses and radii for five pulsars.
Full size table
Table 2 Values of radii, densities and pressures for five pulsars.
Full size table
Table 3 PRS J1416-2230: Changing core radial values.
Full size table
Table 4 PRS J1416-2230: Changing envelope radial values.
Full size table

2 The model

The interior of the body with neutral matter and anisotropic pressures is described by the physically relevant energy momentum tensor

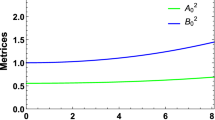
$$\begin{aligned} T^{\mu \nu }=\text {diag}(-\rho , p_{\mathrm{r}}, p_{\mathrm{t}}, p_{\mathrm{t}}) \end{aligned}$$
(1)

with \(\rho \), \(p_{\mathrm{r}}\) and \(p_{\mathrm{t}}\) being the energy density, radial pressure and tangential pressure, respectively (see figures 1–3). It is convenient to introduce the degree of anisotropy \(\Delta =p_{\mathrm{t}}-p_{\mathrm{r}}\) which vanishes for isotropic pressures (see figure 4). In our analysis, we choose a static geometry for which the interior space–time is given as

$$\begin{aligned} \mathrm{d}s^{2} = -\mathrm{e}^{2\nu } \mathrm{d}t^{2} + \mathrm{e}^{2\lambda } \mathrm{d}r^{2} + r^{2}(\mathrm{d}\theta ^{2} + \sin ^{2}{\theta }\, \mathrm{d}\phi ^{2}) \end{aligned}$$
(2)

with \(\nu =\nu (r)\) and \(\lambda =\lambda (r)\) being the metric potentials. Equation (2) is a reasonable approximation for a highly compact gravitating body such as a neutron star.

With regard to the above considerations, the Einstein field equations governing the physical behaviour of an uncharged anisotropic sphere have the form

$$\begin{aligned} 8\pi \rho= & {} \frac{1}{r^{2}} \left[ r(1-\mathrm{e}^{-2\lambda }) \right] ', \end{aligned}$$
(3)
$$\begin{aligned} 8\pi p_{\mathrm{r}}= & {} - \frac{1}{r^{2}} ( 1-\mathrm{e}^{-2\lambda }) + \frac{2\nu '}{r}\mathrm{e}^{-2\lambda } , \end{aligned}$$
(4)
$$\begin{aligned} 8\pi p_{\mathrm{t}}= & {} \mathrm{e}^{-2\lambda }\left( \nu '' + \nu '^{2}+ \frac{\nu '}{r} -\frac{\lambda '}{r} -\lambda '\nu '\right) , \end{aligned}$$
(5)

with the primes representing the derivatives with respect to r. The nonlinear character of the Einstein system of equations creates difficulties when solving analytically. To find a solution we have to restrict the behaviour of the potentials, specify the matter distribution or select a specific equation of state.

Fig. 1
figure 1

Energy density \(\rho \).

Full size image
Fig. 2
figure 2

Radial pressure \(p_{\mathrm{r}}\).

Full size image
Fig. 3
figure 3

Tangential pressure \(p_{\mathrm{t}}\).

Full size image
Fig. 4
figure 4

Anisotropy \(\Delta \).

Full size image
Fig. 5
figure 5

Radial speed of sound \({\mathrm {d}p_{\mathrm{r}}}/{\mathrm {d}\rho }\).

Full size image
Fig. 6
figure 6

Adiabatic index \(\Gamma _{\mathrm {ad}}\).

Full size image

In many relativistic stellar structures, the inside matter distribution is composed of two regions: a core (inner) layer and an envelope (outer) layer both having different pressures. To model such a star, with a core and an envelope, it is necessary to separate space–time into a number of distinct regions. These three regions consist of the core (\(0\le r\le R_{\mathrm{I}}\), Region \(\mathrm{I}\)), the envelope (\(R_{\mathrm{I}}\le r\le R_{\mathrm{II}}\), Region \(\mathrm{II}\)) and the exterior (\(R_{\mathrm{II}}\le r\), Region \(\mathrm{III}\)). The line elements for the three regions are given by

$$\begin{aligned} \mathrm{d}s^{2}|_{\mathrm{I}}=&-\mathrm{e}^{2\nu _{\mathrm{I}}} \mathrm{d}t^{2} + \mathrm{e}^{2\lambda _{\mathrm{I}}} \mathrm{d}r^{2}\nonumber \\&+ r^{2}(\mathrm{d}\theta ^{2} + \sin ^{2}{\theta }\, \mathrm{d}\phi ^{2}), \end{aligned}$$
(6)
$$\begin{aligned} \mathrm{d}s^{2}|_{\mathrm{II}} =&-\mathrm{e}^{2\nu _{\mathrm{II}}} \mathrm{d}t^{2} + \mathrm{e}^{2\lambda _{\mathrm{II}}}\, \mathrm{d}r^{2}\nonumber \\&+ r^{2}(\mathrm{d}\theta ^{2} + \sin ^{2}{\theta }\, \mathrm{d}\phi ^{2}), \end{aligned}$$
(7)
$$\begin{aligned} \mathrm{d}s^{2}|_{\mathrm{III}} =&-\left( 1- \frac{2M}{r} \right) \mathrm{d}t^{2} + \left( 1- \frac{2M}{r} \right) ^{-1} \mathrm{d}r^{2}\nonumber \\&+ r^{2}(\mathrm{d}\theta ^{2} + \sin ^{2}{\theta }\, \mathrm{d}\phi ^{2}). \end{aligned}$$
(8)

Equation (8) is the Schwarzschild exterior solution which is related to the Region \(\mathrm{III}\) which is the exterior of the gravitating star.

Physical viability requires that the model should satisfy the following conditions in all three regions (core, envelope and exterior):

  1. (i)

    The metric functions and matter variables should be defined at the centre and should be well behaved throughout the inside of the star.

  2. (ii)

    We must have \(\rho > 0\) and the gradient of density \(\rho ^{\prime } < 0\) both in the core and the envelope.

  3. (iii)

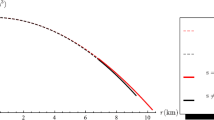
    Also \(p_{\mathrm{r}}> 0\), \(p_{\mathrm{t}}> 0\), the speed \({\mathrm {d}p_{\mathrm{r}}}/{\mathrm {d}\rho }\le 1\) for sound and \({\mathrm {d}p_{\mathrm{r}}}/{\mathrm {d}r}<0\) for the gradient in the core and the envelope (figure 5).

  4. (iv)

    At the stellar boundary \(p_{\mathrm{r}}(R_{\mathrm{II}})=0\).

  5. (v)

    The metric potentials of the core layer should match smoothly with the gravitational potentials of the envelope region.

  6. (vi)

    The gravitational potentials of the envelope layer should match smoothly with the Schwarzschild exterior metric.

3 Core and envelope

We choose neutral solution of the exact models of Maharaj and Mafa Takisa [31] satisfying a linear equation of state for the core. This class of solutions is helpful for describing anisotropic stars, quark stars and distributions with strange matter. Mafa Takisa et al [29], in a comprehensive treatment, showed that the model with a linear equation of state generates mass and radius values in agreement with recent updated values for relativistic compact stars. This is the motivation for selecting the results of Maharaj and Mafa Takisa [31] for Region \(\mathrm{I}\). In the range \(0\le r\le { R_{\mathrm{I}}}\) we choose

$$\begin{aligned}&\mathrm{e}^{2\lambda _{\mathrm{I}}}=\frac{1+ar^2}{1+br^2}, \end{aligned}$$
(9)
$$\begin{aligned}&p_{\mathrm{r}}=\alpha \rho - \beta , \end{aligned}$$
(10)

with a, b, \(\alpha \), \(\beta \) being constants. Then, the field equations (3)–(5) yield the metric function

$$\begin{aligned} \mathrm{e}^{2\nu _{\mathrm{I}}} = B(1+ar^2 )^{2m_{\mathrm{I}}}[1+br^2]^{2n_{\mathrm{I}}}\exp [2F_{\mathrm{I}}(r)], \end{aligned}$$
(11)

where B is a constant. The function \(F_{\mathrm{I}}(r)\) is given explicitly by

$$\begin{aligned} F_{\mathrm{I}}(r) = -\frac{a\beta r^2}{4b}. \end{aligned}$$
(12)

The constants \(m_{\mathrm{I}}\) and \(n_{\mathrm{I}}\) have the form

$$\begin{aligned}&m_{\mathrm{I}}= \frac{\alpha }{2}, \end{aligned}$$
(13)
$$\begin{aligned}&n_{\mathrm{I}}=\frac{1}{8b(a-b)^{2}}\left[ b^{2}(-4\alpha a^{3} b)(1+5\alpha )\right. \nonumber \\&\qquad \left. -\,b^{2}(1+3\alpha )+2\beta b)\right] \!. \end{aligned}$$
(14)

Consequently, the matter variables have the form

$$\begin{aligned}&8\pi \rho = \dfrac{(a-b)(3+ar^2)}{(1+ar^2)^{2}}, \end{aligned}$$
(15)
$$\begin{aligned}&p_{\mathrm{r}} = \alpha \rho -\beta , \end{aligned}$$
(16)
$$\begin{aligned}&8\pi \! p_{\mathrm{t}} = p_{\mathrm{r}}+\Delta , \end{aligned}$$
(17)
$$\begin{aligned}&8\pi \Delta = \frac{4r^2(1+br^2)}{1+ar^2}\nonumber \\&\qquad \quad \times \left[ \frac{m_{\mathrm{I}}(m_{\mathrm{I}}-1)a^{2}}{(1+ar^2)^{2}}+\frac{2m_{\mathrm{I}}n_{\mathrm{I}}ab}{(1+ar^2)(1+br^2)}\right. \nonumber \\&\qquad \quad \left. + \frac{2m_{\mathrm{I}}a{F}_{\mathrm{I}}^{\prime }(r)}{1+ar^2}+\frac{b^{2}n_{\mathrm{I}}(n_{\mathrm{I}}-1)}{(1+br^2)^{2}} \right. \nonumber \\&\qquad \quad \left. + \frac{2n_{\mathrm{I}}b F_{\mathrm{I}}^{\prime }(r)}{1+br^2}+ F_{\mathrm{I}}^{\prime \prime }(r)+ F_{\mathrm{I}}^{\prime }(r)^{2}\right] \nonumber \\&\qquad \quad \times \left[ \frac{am_{\mathrm{I}}}{1+ar^2}+ \frac{bn_{\mathrm{I}}}{1+br^2} + F_{\mathrm{I}}^{\prime }(r) \right] \nonumber \\&\qquad \quad +\left[ -\frac{2(a-b)r^2}{(1+ar^2)^{2}}+\dfrac{4(1+br^2)}{(1+ar^2)}\right] \nonumber \\&\qquad \quad -\frac{1}{(1+ar^2)^{2}}[(a-b)-\beta (1+ar^2)^{2}]\nonumber \\&\qquad \quad -\alpha \left[ \frac{((a-b))(3+ar^2)}{(1+ar^2)^{2}}\right] \!. \end{aligned}$$
(18)

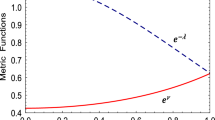
The metric functions and matter variables are continuous and well behaved in the core.

We select the neutral subcase of the exact solution of Maharaj and Mafa Takisa [31] satisfying a modified quadratic equation of state for the envelope region. Incorporating a nonlinear term in the equation of state leads to a consistent model and generates expressions for the mass, radius and central density consistent with observed stellar objects (see Mafa Takisa et al [32]). This is the motivation for selecting the results of Maharaj and Mafa Takisa [31] with a modified quadratic equation of state for Region \(\mathrm{II}\). In the range \(R_{\mathrm{I}}\le r\le { R_{\mathrm{II}}}\) we make the choice

$$\begin{aligned}&\mathrm{e}^{2\lambda _{\mathrm{II}}}=\frac{1+ar^2}{1+br^2}, \end{aligned}$$
(19)
$$\begin{aligned}&\quad p_{\mathrm{r}}=\gamma \rho ^{2}-\eta , \end{aligned}$$
(20)

where a, b, \(\gamma \) and \(\eta \) are constants. Then the field equations (3)–(5) give the potential

$$\begin{aligned} \mathrm{e}^{2\nu _{\mathrm{II}}} = D\!\left( 1+ar^2 \right) ^{2m_{\mathrm{II}}}[1+br^2]^{2n_{\mathrm{II}}}\exp [2F_{\mathrm{II}}(r)],\nonumber \\ \end{aligned}$$
(21)

where the constant B is the result of integration. The quantity \(F_{\mathrm{II}}(r)\) is defined by

$$\begin{aligned} F_{\mathrm{II}}(r)&= \gamma \!\left[ \frac{2(2b-a)(1+ar^2)+(b-a)}{2(1+ar^2)^{2}}\right] \nonumber \\&\qquad -\frac{4\eta a r^2}{4b}. \end{aligned}$$
(22)

The constants \(m_{\mathrm{II}}\) and \(n_{\mathrm{II}}\) have the form

$$\begin{aligned}&m_{\mathrm{II}} = \gamma [2(a-b)]^{2}\\&\qquad \times \left[ \frac{b^{2}}{(b-a)^{3}}+\frac{b}{(b-a)^{2}}+\frac{1}{4}\right] \!,\\&n_{\mathrm{II}} = \frac{(a-b)}{4b}+\gamma [2(a-b)]^{2} \\&\qquad \times \left[ \frac{b^{2}}{(b-a)^{3}}+\frac{b}{(b-a)^{2}}+ \frac{1}{4}\right] \\&\qquad +\frac{\eta (a-b)}{4 b^2}. \end{aligned}$$

Then the matter variables are given by

$$\begin{aligned}&8\pi \rho = \dfrac{(a-b)(3+ar^2)}{(1+ar^2)^{2}}, \end{aligned}$$
(23)
$$\begin{aligned}&p_{\mathrm{r}} = \gamma \rho ^{2}-\eta , \end{aligned}$$
(24)
$$\begin{aligned}&8\pi p_{\mathrm{t}} = p_{\mathrm{r}}+\Delta , \end{aligned}$$
(25)
$$\begin{aligned}&8\pi \Delta = \frac{4r^2(1+br^2)}{1+ax}\nonumber \\&\qquad \quad \quad \times \left[ \frac{m_{\mathrm{II}}(m_{\mathrm{II}}-1)a^{2}}{(1+ar^2)^{2}}+\frac{2m_{\mathrm{II}}n_{\mathrm{II}}ab}{(1+ar^2)(1+br^2)}\right. \nonumber \\&\qquad \quad \quad \left. + \frac{2m_{\mathrm{II}}a{F}_{\mathrm{II}}^{\prime }(r)}{1+ar^2}+\frac{b^{2}n_{\mathrm{II}}(n_{\mathrm{II}}-1)}{(1+br^2)^{2}} \right. \nonumber \\&\qquad \quad \quad \left. + \frac{2n_{\mathrm{II}}b F_{\mathrm{II}}^{\prime }(r)}{1+br^2}+ F_{\mathrm{II}}^{\prime \prime }(r)+ F_{\mathrm{II}}^{\prime }(r)^{2}\right] \nonumber \\&\qquad \quad \quad \times \left[ \frac{am_{\mathrm{II}}}{1+ar^2}+ \frac{bn_{\mathrm{II}}}{1+br^2} + F_{\mathrm{II}}^{\prime }(r) \right] \nonumber \\&\qquad \quad \quad +\left[ -\frac{2(a-b)r^2}{(1+ar^2)^{2}}+\dfrac{4(1+br^2)}{(1+ar^2)}\right] \nonumber \\&\qquad \quad \quad +\gamma \left[ \frac{2(2b-a)(1+ar^2)+(b-a)}{2(1+ar^2)^{2}}\right] \nonumber \\&\qquad \quad \quad -\frac{1}{(1+ar^2)^{2}}[(a-b)-\eta (1+ar^2)^{2}]. \end{aligned}$$
(26)

We note that the metric functions and matter variables are defined and well behaved in the envelope (figure 6).

4 Matching conditions

Metrics (6) and (7) must match smoothly at \(r=R_{\mathrm{I}}\). This gives the restrictions

$$\begin{aligned} \mathrm{e}^{2\lambda _{\mathrm{I}}({R_{\mathrm{I}}})}= & {} \mathrm{e}^{2\lambda _{\mathrm{II}}({R_{\mathrm{I}}})}, \end{aligned}$$
(27)
$$\begin{aligned} \mathrm{e}^{2\nu _{\mathrm{I}}({ R_{\mathrm{I}}})}= & {} \mathrm{e}^{2\nu _{\mathrm{II}}({R_{\mathrm{I}}})}. \end{aligned}$$
(28)

Metrics (7) and (8) have to connect smoothly at \(r=R_{\mathrm{II}}\). This gives the restrictions

$$\begin{aligned} \mathrm{e}^{2\lambda _{\mathrm{II}}(R_{\mathrm{II}})}= & {} \left( 1-\frac{2M}{R_{\mathrm{II}}}\right) ^{\!-1}, \end{aligned}$$
(29)
$$\begin{aligned} \mathrm{e}^{2\nu _{\mathrm{II}}(R_{\mathrm{II}})}= & {} 1-\frac{2M}{R_{\mathrm{II}}}. \end{aligned}$$
(30)

The radial pressure should be continuous at \(r=R_{\mathrm{I}}\) so that

$$\begin{aligned} \alpha \rho ({R_{\mathrm{I}}}) - \beta = \gamma \rho ^{2}(R_{\mathrm{I}}) - \eta \end{aligned}$$
(31)

is satisfied. The radial pressure has to be zero at the external boundary of the star \(r=R_{\mathrm{II}}\) which gives

$$\begin{aligned} \gamma \rho ^{2}(R_{\mathrm{II}}) - \eta = 0. \end{aligned}$$
(32)

In eqs (27)–(32) the constants that arise, namely a, b, B, D, \(R_{\mathrm{I}}\), \(R_{\mathrm{II}}\), M, \(\alpha \), \(\beta \), \(\eta \) and \(\gamma \), are unknowns. Equations (27)–(32) are an undetermined system of six equations in 11 unknowns. Note that it is possible to write certain parameters in terms of other parameters.

The physical quantities that are relevant are the mass M and the radius \(R_{\mathrm{II}}\) of the star. From systems (27)–(32), we obtain

$$\begin{aligned} M = \frac{(a-b)R_{\mathrm{II}}^{3}}{2(1+a R_{\mathrm{II}}^2)}, \end{aligned}$$
(33)

which is the mass of the composite. In addition, the quantity

$$\begin{aligned} R_{\mathrm{II}}= & {} \frac{1}{\sqrt{2}} \!\left( \sqrt{\frac{\sqrt{\gamma } (a-b) (a \sqrt{\gamma }-b \sqrt{\gamma }+8 \sqrt{\eta })}{a^2 \eta }} \right. \nonumber \\&-\frac{b \sqrt{\gamma }}{a \sqrt{\eta }}\left. -\frac{2}{a}+\frac{\sqrt{\gamma }}{\sqrt{\eta }} \right) ^{\!1/2} \end{aligned}$$
(34)

defines the radius of the star. It follows that the constants \(\beta \), D, B are given in terms of M, \(R_{\mathrm{II}}\). The constants \(\beta \), D, B have the form

$$\begin{aligned} \beta= & {} \frac{\alpha (a-b) (3 + a R_{\mathrm{I}}^2)}{\left( 1 + a R_{\mathrm{I}}^2\right) ^2}\nonumber \\&-\frac{\gamma (a-b)^2 (3+a R_{\mathrm{I}}^2)^2}{\left( 1+ a R_{\mathrm{I}}^2\right) ^4}+\eta , \end{aligned}$$
(35)
$$\begin{aligned} D= & {} \frac{(R_{\mathrm{II}}-2 M) (1 + a R_{\mathrm{II}}^2)^{-\frac{\gamma (a-3 b)^2}{4 (a-b)}}}{R_{\mathrm{II}}}\nonumber \\&\times (1+ b R_{\mathrm{II}}^2)^{-\frac{\eta (a-b)}{4 b^2}+\frac{\gamma (a-3 b)^2}{4 (a-b)}-\frac{a}{4 b}+\frac{1}{4}}\nonumber \\&\times \exp \left( -\frac{\gamma (a (-2 a R_{\mathrm{II}}^2+4 b R_{\mathrm{II}}^2-3)+5 b)}{2 (1+ a R_{\mathrm{II}}^2)^2}\right. \nonumber \\&+\left. \frac{a \eta R_{\mathrm{II}}^2}{4 b} \right) , \end{aligned}$$
(36)
$$\begin{aligned} B= & {} D \exp \left( \frac{\gamma (a (-2 a R_{\mathrm{I}}^2 + 4 b R_{\mathrm{I}}^2-3)+5 b)}{2 (a R_{\mathrm{I}}^2+1)^2}\right. \nonumber \\&+\left. \frac{a \beta R_{\mathrm{I}}^2}{4 b} -\frac{a \eta R_{\mathrm{I}}^2}{4 b}\right) \nonumber \\&\times \, (1+ a R_{\mathrm{I}}^2)^{\frac{\gamma (a-3 b)^2}{4 (a-b)}-\frac{\alpha }{2}}\nonumber \\&\times (1+b R_{\mathrm{I}}^2)^{-\frac{a (\alpha b+b+\beta )}{4 b^2}+\frac{\eta (a-b)}{4 b^2}}\nonumber \\&\times \, (1+b R_{\mathrm{I}}^2)^{-\frac{\gamma (a-3 b)^2}{4 (a-b)}+\frac{a}{4 b}+\frac{3 \alpha }{4}+\frac{\beta }{4 b}}. \end{aligned}$$
(37)

In (33)–(37) the remaining constants a, b, \(\alpha \), \(\eta \), \(\gamma \) and \(R_{\mathrm{I}}\) are free parameters.

5 Physical analysis

We can show that the core–envelope model generated in this paper is consistent with the observed astronomical objects. With the choice of \(a=2.03\times 10^{-4} ~\hbox {km}^{-2}\), the parameter b in the range \(-0.00489\le b \le -0.00523~\hbox {km}^{-2}\), we can generate specific numerical values for the physical quantities, such as the core radius \(R_{\mathrm{I}}\), central density \(\rho _{\mathrm{c}}\), radial central pressure \({p_{\mathrm{r}}}_\mathrm {c}\), surface density \(\rho _\mathrm {s}\), the envelope radius \(R_{\mathrm{II}}\) and the stellar mass M for the objects Vela X-1, PSR J1416-2230, Cen X-3, PSR J1903\(+\)327 and also SMC X-1. The numerical values of the envelope radius \(R_{\mathrm{II}}\), the mass \(M (M_{\odot })\), the model parameters \(\beta \), B and D for different pulsars are given in table 1. Some physical quantities, including the surface red-shift, are listed in table 2.

We find that the values for the stellar radius \(R_{\mathrm{II}}\) and the mass M are in agreement with our previous investigation in [26] for the model with a core and an envelope. We also note the consistency of these results with the analysis of Mafa Takisa et al [29] in which exact solutions were generated with linear equation of state with no electromagnetic field. We observe that similar values for the masses of the stars were given by Gangopadhyay et al [7], Mafa Takisa et al [29] and Mafa Takisa et al [32]. Surface red-shifts \(Z_{\mathrm{s}}\) and compactifications \(M(M_\odot )/R_{\mathrm{II}}\) for the five compact objects have also been presented in table 2. We find that the Buchdahl [33] limit (also see Sharma and Maharaj [34]) of (\({2M}/{R_{\mathrm{II}}})<\frac{8}{9}\) is satisfied.

6 Discussion

In our treatment we have applied the core and the envelope description to study an uncharged star with anisotropic pressures. We chose two distinct equations of state for the two inner regions. The linear equation of state, in the first layer (core), and the quadratic equation of state, in the second layer (envelope), were utilised. Therefore, the core matter configuration is of quark matter. The pressure in the first layer has higher values than the pressure in the envelope. We showed explicitly that the inner layer, envelope and the Schwarzschild exterior connect smoothly at their interfaces. The radii, masses and red-shifts of five stellar compact objects PSR J1614-2230, PSR J1903\(+\)327, Vela X-1, SMC X-1, Cen X-3 were found. These results are consistent with the works of Mafa Takisa et al [29], Mafa Takisa et al [32] and the investigation of Mafa Takisa and Maharaj [26]. We plotted some physical quantities connected to the particular dense star PSR J1614-2230. Expressions for the matter quantities and metric functions are regular throughout the star, and there is smooth matching between the various interfaces. We showed that the radius of the core and the radius of the envelope can change by selecting different parameter values. This enables us to consider a hybrid model, comprising two inner regions, with different compactness parameters in both regions. In summary, we have generated a core–envelope stellar model containing distinct equations of state for the core layer and the envelope layer. The core has a quark matter distribution. In future work, it will be interesting to see how other equations of state affect the physics.