1 Introduction

Fractional delay differential equations (FDDE) are dynamical systems involving non-integer order derivatives as well as time delays. These equations have found many applications in control theory [1, 2], agriculture [3, 4], chaos [5–9], bioengineering [10, 11] and so on.

Due to its non-local nature, fractional derivative [12–15] is capable of modelling memory and hereditary properties. The time-delay [16] in the model also has similar properties. Hence, the models containing fractional derivative as well as time delay are crucial.

The stability of linear time invariant fractional delay systems (LTIFDS) has been studied by many researchers. Hotzel [17] gave stability conditions for LTIFDS with characteristic equation (as α + b) + (cs α + d)e − ρs = 0. Chen and Moore [18] used Lambert function to study the stability of LTIFDS \(\dot{y}(t)=ay(t-1)\). This equation is generalized by Deng et al [19]. They have used Laplace transform to find characteristic equation for n-dimensional LTIFDS. Lazarevic and Debeljkovic [20] discussed finite time stability of LTIFDS. A numerical algorithm was proposed by Hwang and Cheng [21] to study the bounded input and bounded output (BIBO) stability of LTIFDS. Analysis of robust BIBO stability of LTIFDS in the presence of real parametric uncertainties is discussed by Moorani and Haeri in [22]. Graphical test is used by Yu and Wang [23] to study BIBO interval stability tests of such systems. Hamamci [24] used fractional order PI λ D μ controller to stabilize LTIFDS.

The stability of nonlinear delay differential equations of fractional order have not been reported much. In this article, we use the method of critical curves [16, 25] to study the stability of a class of nonlinear FDDEs: \(D^{\alpha} y(t) = a f\left(y(t-\tau)\right) - b y(t)\), where D α is a Caputo fractional derivative of order 0 < α ≤ 1. We discuss the chaos in fractional order logistic equation using the developed theory.

2 Preliminaries

Let us start with some definitions [12, 13, 26].

Definition 2.1

A real function f(t), t > 0 is said to be in space \(C_\alpha,\, \alpha \in \Re\) if there exists a real number p (> α), such that \(f(t)= t^pf_1(t)\) where f 1(t) ∈ C[0, ∞ ).

Definition 2.2

A real function f(t), t > 0 is said to be in space \(C_{\alpha}^{m}, \, m\in {\rm I}\!{\rm N} \bigcup \left\{0\right\}\) if \(f^{(m)} \in C_\alpha.\)

Definition 2.3

Let f ∈ C α and α ≥ − 1, then the (left-sided) Riemann–Liouville integral of order μ, μ > 0 is given by

$$ I^\mu f(t)=\frac{1}{\Gamma(\mu)}\int_0^t(t-\tau)^{\mu-1}f(\tau)\,\mathrm{d}\tau, \quad t>0. $$
(1)

Definition 2.4

The (left-sided) Caputo fractional derivative of f, \(f\in C_{-1}^{m}, m\in {\rm I}\!{\rm N} \bigcup \left\{0\right\},\) is defined as

$$ \begin{array}{rll} D^\mu f(t) && = \frac{\mathrm{d}^m}{\mathrm{d} t^m} f(t) ,\quad \mu=m \\ && = I^{m-\mu} \frac{\mathrm{d}^m f(t)}{\mathrm{d} t^m}, \quad m-1<\mu<m,\quad m\in {\rm I}\!{\rm N}. \end{array} $$
(2)

Note that for m − 1 < μ ≤ m, m ∈ IN,

$$ I^\mu D^\mu f(t)= f(t)-\sum^{m-1}_{k=0} \frac{\mathrm{d}^k f}{\mathrm{d} t^k}(0)\frac{t^k}{k!}, $$
(3)
$$ I^\mu t^\nu = \frac{\Gamma (\nu + 1)}{\Gamma (\mu + \nu + 1)} t^{\mu + \nu}. $$
(4)

3 Main results

Consider the fractional order delay differential equation (FDDE) of the form

$$ \begin{array}{rll} &&{\kern-8pt}D^{\alpha} y(t) = a f\left(y(t-\tau)\right) - b y(t),\quad b>0,\quad 0<\alpha\leq 1,\\ &&{\kern-8pt}y(t) = y_0(t), \quad -\tau \leq t \leq 0. \end{array} $$
(5)

An equilibrium point y * of eq. (5) satisfies the equation

$$ a f(y^*) - b y^*=0. $$
(6)

Let ξ = y − y * be a small perturbation from an equilibrium point and y τ  = y(t − τ), ξ τ  = ξ(t − τ). Then using Taylor’s expansion of f about y * and eq. (6), we get

$$ \begin{array}{rll} D^{\alpha} \xi &=& D^{\alpha}y\\ &=& a f\left(y_{\tau}\right) - b y\\ &=& a f(\xi_{\tau}+y^*) - b (\xi+y^*)\\ &=& a f(y^*) +af'(y^*)\xi_{\tau} -by^* -b\xi\\ &=& a f'(y^*)\xi_{\tau} - b \xi. \end{array} $$
(7)

Equation (7) is called as a linearized equation for system (5) [25, 27]. The trajectories of the nonlinear system in the neighbourhood of an equilibrium point have the same form as the trajectories of linearized system.

Using Laplace transform [19], eq. (7) yields a characteristic equation

$$ \lambda^{\alpha} + b - a f'(y^*)\thinspace\mathrm{exp}(-\lambda \tau) = 0. $$
(8)

An equilibrium point y * is asymptotically stable if all the roots λ i of characteristic equation (8) satisfy

$$ \mathrm{Re}(\lambda_i)<0,\, \forall i. $$
(9)

Let \(\lambda= u+\imath v\), \(u, v\in \Re\). A change in stability can occur only when the value of λ crosses the imaginary axis at \(\lambda= \imath v\) and the characteristic equation becomes

$$ \left(\imath v\right)^\alpha + b = a f'(y^*)\thinspace\mathrm{exp}(-\imath v \tau). $$
(10)

Using \(\imath v=v\,\mathrm{exp}(\imath \pi/2)\), \( v\in \Re\) and separating real and imaginary parts in (10) we get

$$ b + v^\alpha \cos\!\left(\frac{\alpha \pi}{2}\right) = a f'(y^*) \cos(v\tau) $$
(11)
$$ v^\alpha \sin\!\left(\frac{\alpha \pi}{2}\right) = -a f'(y^*) \sin(v\tau). $$
(12)

Squaring and adding

$$ v^{2\alpha} + 2b v^\alpha \cos\!\left(\frac{\alpha \pi}{2}\right) + b^2 = a^2f'(y^*)^2. $$
(13)

This gives

$$ v^\alpha = -b \cos\!\left(\frac{\alpha \pi}{2}\right)\pm \sqrt{-b^2 \sin^2\!\left({\alpha \pi}/{2}\right)+a^2f'\left(y^*\right)^2}. $$
(14)

Also, from (11)

$$ \tau = \frac{1}{v}\left(2n\pi \pm \arccos\left(\frac{b+v^\alpha \cos ({\alpha \pi}/{2}) }{a f'\left(y^*\right)}\right)\right),\quad n=0,1,\ldots. $$
(15)

Thus, we get critical surfaces

$$ \begin{array}{rll} \tau_1(n) &=& \dfrac{2n \pi +\arccos\!\left(\dfrac{b+\left(-b \cos\!\left({\alpha \pi}/{2}\right)+\sqrt{-b^2 \sin^2\left({\alpha \pi}/{2}\right)+a^2f'\left(y^*\right)^2} \right)\cos({\alpha \pi}/{2})}{af'\left(y^*\right)}\right)}{\left( -b \cos\!\left({\alpha \pi}/{2}\right)+\sqrt{-b^2 \sin^2\left({\alpha \pi}/{2}\right)+a^2f'\left(y^*\right)^2}\right)^{1/\alpha}}, \\ && \qquad\qquad\qquad n=0,1,\ldots \end{array} $$
(16)
$$ \begin{array}{rll} \tau_2(n) &=& \dfrac{2n \pi -\arccos\!\left(\dfrac{b+\left(-b \cos\!\left({\alpha \pi}/{2}\right)+\sqrt{-b^2 \sin^2\left({\alpha \pi}/{2}\right)+a^2f'\left(y^*\right)^2} \right)\cos({\alpha\pi}/{2})}{af'\left(y^*\right)}\right)}{\left( -b \cos\!\left({\alpha \pi}/{2}\right)+\sqrt{-b^2 \sin^2\left({\alpha \pi}/{2}\right)+a^2f'\left(y^*\right)^2}\right)^{1/\alpha}}, \\ && \qquad\qquad\qquad n=1,2,\ldots. \end{array} $$
(17)

In eq. (14) we can take minus sign as well, but we get the same surfaces as in eqs (16) and (17) because the delay τ in our analysis is always positive. There are similar critical curves below the a = 0 axis corresponding to the negative values of τ, which are not of our interest.

Theorem 3.1

There is only one stability region for y * between the plane τ = 0 in the (a,b) parameter space and the closest critical surface τ(0) in the (τ,a,b) parameter space.

Proof

For \(|af'\left(y^*\right)|>b\) and for a fixed v > 0, the stability regions are confined between a set of two surfaces τ 1(n) and τ 2(n) in the (τ, a, b) parameter space if du/dτ on any of these surfaces is negative and on other it is positive.

Differentiating characteristic eq. (8) with respect to τ, we get

$$ \frac{\mathrm{d}\lambda}{\mathrm{d}\tau}=\frac{-af'\left(y^*\right)\lambda \,\mathrm{exp}(-\lambda \tau)}{\alpha \lambda^{\alpha-1}+af'\left(y^*\right)\tau \,\mathrm{exp}(-\lambda \tau)}=\frac{-\lambda \left(\lambda^{\alpha}+b\right)}{\alpha \lambda^{\alpha-1}+\tau\!\left(\lambda^{\alpha}+b\right)}. $$
(18)
$$ \begin{array}{rll} && \therefore \frac{\mathrm{d}\lambda}{\mathrm{d}\tau} \bigg|_{u=0}=\frac{-(\imath v) \left((\imath v)^{\alpha}+b\right)}{\alpha (\imath v)^{\alpha-1}+\tau\!\!\left((\imath v)^{\alpha}+b\right)}\\ &&=\frac{-v^{\alpha+1}\cos({(\alpha+1)\pi}/{2})-\imath\!(v^{\alpha+1}\sin({(\alpha+1)\pi}/{2})+bv)}{\tau b +\alpha v^{\alpha-1}\cos({(\alpha-1)\pi}/{2})+\tau v^\alpha \cos\frac{\alpha\pi}{2} +\imath\!(\alpha v^{\alpha-1}\sin({(\alpha-1)\pi}/{2})+\tau v^\alpha \sin({\alpha\pi}/{2})}\\ &&= -\frac{z_1+\imath z_2}{z_3+\imath z_4} \mbox{(say)}. \end{array} $$
(19)

On critical surfaces (16) and (17),

$$ \frac{\mathrm{d}u}{\mathrm{d}\tau} = \mbox{Re}\!\left(\frac{\mathrm{d}\lambda}{\mathrm{d}\tau}\right)\bigg|_{u=0}=-\frac{z_1z_3+z_2z_4}{z_3^2+z_4^2}. $$
(20)

Since 0 < α < 1, v > 0 and b > 0, we have

$$ -(z_1z_3+z_2z_4)=\alpha v^{\alpha} \left(v^{\alpha}+b\cos(\alpha\pi/2)\right) >0. $$
(21)

Hence, from eq. (20) (du/dτ) > 0 on each of the critical surfaces τ 1(n) and τ 2(n). This implies that there does not exist any eigenvalue with negative real part across the critical surfaces (16) and (17). Also, the equilibrium point is stable for τ = 0 when af′(y *) − b < 0. Thus, there is only one stability region enclosed by τ = 0 and the critical surface τ(0), closest to it.

4 Illustrative example

We illustrate the proposed results using fractional order logistic equation with delay [5]

$$ \begin{array}{rll} &&{\kern-8pt}D^{\alpha} y(t) = a y(t-\tau)\left(1-y(t-\tau)\right) - b y(t),\quad b>0\\ &&{\kern-8pt}y(t) = 0.5, -\tau \leq t \leq 0,\, 0<\alpha\leq 1. \end{array} $$
(22)

The system (22) shows chaotic behaviour for certain parameters τ, a and b. As the instability of equilibrium points is a necessary condition of chaos, we discuss these conditions using our theory. We use a predictor–corrector scheme developed in [28] for simulations.

Equilibrium points of the system (22) are given by \(y_1^*=(a-b)/a\) and \(y_2^*=0\).

  • Stability of \(y_1^*\):

    Substituting f(y) = y(1 − y) in eqs (16) and (17) we get critical surfaces

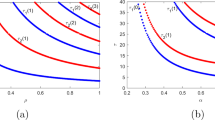
    $$ \begin{array}{rll} && \tau_1(n) = \dfrac{2n \pi +\arccos\!\left(\dfrac{b+\left(-b \cos\!\left({\alpha \pi}/{2}\right)+\sqrt{-b^2 \sin^2\left({\alpha \pi}/{2}\right)+(2b-a)^2} \right)\cos({\alpha \pi}/{2})}{a}\right)}{\left( -b \cos\!\left({\alpha \pi}/{2}\right)+\sqrt{-b^2 \sin^2\left({\alpha \pi}/{2}\right)+(2b-a)^2}\right)^{1/\alpha}},\\ &&\qquad\qquad\qquad n=0,1,\ldots \end{array} $$
    (23)
    $$ \begin{array}{rll} &&\tau_2(n) = \dfrac{2n \pi -\arccos\!\left(\dfrac{b+\left(-b \cos\!\left({\alpha \pi}/{2}\right)+\sqrt{-b^2 \sin^2\left({\alpha \pi}/{2}\right)+(2b-a)^2} \right)\cos({\alpha \pi}/{2})}{a}\right)}{\left( -b \cos\!\left({\alpha \pi}/{2}\right)+\sqrt{-b^2 \sin^2\left({\alpha \pi}/{2}\right)+(2b-a)^2}\right)^{1/\alpha}},\nonumber\\[28pt] &&\qquad\qquad\qquad n=1,2,\ldots . \end{array} $$
    (24)

    Figure 1 shows critical curves τ 1(0), τ 1(1), τ 1(2) (solid lines) and τ 2(1), τ 2(2), τ 2(3)(dashed lines) respectively for α = 0.9 and b = 26.

  • Stability of \(y_2^*\):

    Critical surfaces, in this case are given

    $$ \begin{array}{rll} &&\tau_1(n)=\dfrac{2n \pi +\arccos\!\left(\dfrac{b+\left(-b \cos\!\left({\alpha \pi}/{2}\right)+\sqrt{-b^2 \sin^2\!\left({\alpha \pi}/{2}\right)+a^2} \right)\cos({\alpha \pi}/{2})}{a}\right)}{\left( -b \cos\!\left({\alpha \pi}/{2}\right)+\sqrt{-b^2 \sin^2\!\left({\alpha \pi}/{2}\right)+a^2}\right)^{1/\alpha}}, \\ &&\qquad\qquad\qquad n=0,1,\ldots \end{array} $$
    (25)
    $$ \begin{array}{rll} &&\tau_2(n) = \dfrac{2n \pi -\arccos\!\left(\dfrac{b+\left(-b \cos\!\left({\alpha \pi}/{2}\right)+\sqrt{-b^2 \sin^2\!\left({\alpha \pi}/{2}\right)+a^2} \right)\cos({\alpha \pi}/{2})}{a}\right)}{\left( -b \cos\!\left({\alpha \pi}/{2}\right)+\sqrt{-b^2 \sin^2\!\left({\alpha \pi}/{2}\right)+a^2}\right)^{1/\alpha}},\\ &&\qquad\qquad\qquad n=1,2,\ldots. \end{array} $$
    (26)

    The critical curves τ 1(0), τ 1(1), τ 1(2) and τ 2(1), τ 2(2), τ 2(3) are plotted in figure 2 for α = 0.9.

  • Chaos in system (22):

    Chaos exists in system (22) only when the equilibrium points are unstable. Figure 3 shows stable behaviour of the system for parameters τ = 0.5, a = 70, b = 26, α = 0.9 which are in the stable region. If we consider the parameters (τ, a, b, α) = (0.5, 79.3, 26, 0.9) which are on the boundary of the stable region for \(y_1^*\) then system shows periodic oscillations as shown in figure 4. Now consider the point (τ, a, b, α) = (0.5, 104, 26, 0.9) in unstable region. It can be observed from figure 5 that the system is chaotic in this case.

Figure 1
figure 1

Critical curves for \(y_1^*=(a-b)/a\), b = 26.

Full size image
Figure 2
figure 2

Critical curves for \(y_2^*=0\), b = 26.

Full size image
Figure 3
figure 3

(a) Stable phase portrait and (b) converging time series.

Full size image
Figure 4
figure 4

(a) Periodic limit cycle and (b) periodic time series.

Full size image
Figure 5
figure 5

(a) Chaotic attractor and (b) chaotic time series.

Full size image

5 Conclusion

We have studied the stability of a class of nonlinear FDDEs of the form \(D^{\alpha} y(t) = a f\left(y(t-\tau)\right) - b y(t)\), where D α is a Caputo fractional derivative of order 0 < α ≤ 1. Explicit expressions for determining stability of critical surfaces are given. The theory developed is applied for studying chaos in fractional order logistic equation. It is observed that the system is chaotic only if the parameters are in the unstable region.