1 Introduction

Three phase flows are important in several industrial contexts. Flow forms in three phase flows are intricate and differ considerably from system to system. A multiphase flow system is one in which distinct phases exist at the same time, with a two-phase system being the simplest form. Even though the oil industry is the primary driver of research in this area, multiphase flow in porous media continues to attract a lot of attention because it occurs in a wide range of engineering disciplines. It is also dominant in many natural phenomena, for example, sediment transport in rivers is subject to multiphase flow. When compared to single-phase flow, characterizing, and quantifying the nature of the flow is significantly more difficult due to the presence of many phases. Due to a lack of understanding about the velocities of each phase at a single site and varied mechanisms regulating them, the velocity distribution is difficult to compute. As a result, it's critical to comprehend the nature and behavior of flow in multiphase systems.

Multiphase flows are not limited to three phases, direct-contact freeze crystallization is an example of a four-phase flow system. Practically all processing technologies, from cavitating pumps and turbines to electro photographic processes, papermaking, and the pellet form of almost all raw polymers, must cope with the multiphase flow. The majority of problems in the geophysics, petroleum industry, plasma physics, and other related fields involve multi fluid flow scenarios. Three-phase flows appear in a wide range of industrial processes, from the production stages of oil and gas Bello et al. [1], in the transport of biomass Miao et al. [2] or some chemical reactors Scott and Rao [3], nuclear waste decommissioning Mao et al. [4], pulp and paper production, and in various applications of air injections Orell [5]. Thus, it's critical to optimize three-phase flows, which is a process with plenty of space for improvement Ghasemi [6].

Vafai and Kim [7] offered the first accurate solution for fluid flow in the interface region. The fluid flow and heat-transfer interfacial conditions between a porous medium and a fluid layer were studied by Alzami and Vafai [8]. Porosity formation in solidifying castings of the mushy zone for three phase model was studied by Kuznetsov and Vafai [9]. Comparison of various formulations of three phase flow in porous media was established by Zhangxim and Richord [10]. Authors have discussed various formulations of the governing equations which describe three phase flow in porous media which includes phase, global and pseudo-global pressure saturation formulations, and have presented theoretically and numerically.

Malashetty et al. [11, 12] analyzed one and two fluid flow models for permeable fluid in horizontal and inclined channels. Frontiers and progress in multiphase flow and heat transfer was presented by Cheng and Ghajar. [13]. Multiphase modeling techniques and their challenges can be understood from multiphase-flows in biomedical applications by Jingliang Dong et al. [14]. Umavathi et al. [15,16,17] analyzed fluid flow models sandwiched between viscous fluids in horizontal and vertical channels. Umavathi and Hemvathi [18] examined convective flow in a vertical porous channel saturated with nanofluid packed between viscous fluid layers recently. The results showed that silver as a nanoparticle had the optimum velocity while titanium oxide had the least velocity. Recently Patra and Nayak [19], Satish and Kishan [20] are study the effects of nonfluids. Hoseinzadeh [21] examined the effect of varied channel cross-sectional geometries on pulsating flow in a three-dimensional channel employing alumina nanofluid with varying volume percentages as a working fluid. It is observed that when the volume proportion of nanoparticles increases, the fluid temperature decreases.

Only sluggish flows in porous media with low permeability are suitable for the Darcy model, Nakayama et al. [22]. Many advanced applications of porous media have high flow velocities. Inertial effects become important at greater flow rates or in hyper porous media Bear [23]. The momentum equation for porous medium must account for divergence from linearity in such cases. This divergence is caused by Forchheimer’s term, which reflects quadratic drag. From a physical aspect, quadratic drag emerges in the momentum equation for porous media because the form of drag owing to solid barriers becomes comparable to surface drag due to friction at high filtration velocities Nield and Bejan [24].

Internal heat generation inside both the solid and fluid phases has recently been highlighted as having an impact on the temperature field inside the porous medium [25,26,27,28,29,30,31]. Internal heat generation and absorption can occur from a variety of causes, including viscous heating in both the solid and fluid phases of a porous material. Heat generation/absorptions occur as source/sink terms in the energy conversation equations of a porous material's solid and fluid phases, making these equations non-homogeneous. As a result, getting an analytical solution to such issues becomes more challenging. Yang and Vafai [27] examined the influence of constant internal heat generation on the temperature field in the porous medium under LTNE in the fully developed region of a porous channel. It is established that the internal heat generation in the solid phase is important for characteristics of heat transfer.

Because of many practical applications, porous-media with high flow velocities and the possibility of occurrence of internal heat generation due to viscous heating is involved, the work of Umavathi and Hemavathi [18] was extended to study the effect of internal heat generation on the flow and heat transfer of a nanofluid (water as base fluid and copper as nanoparticle) saturated composite porous medium sandwiched between two fluid layers, which has not been previously addressed. In this paper we have investigated a numerical analysis of heat transfer characteristics of nano fluids on different models which are related to industrial system applications such as heat exchangers, heat storage, geothermal systems, and drying techniques. This paper is related to designing of industrial systems and studying of its heat transfer characteristics. Further, in this study, local thermal non-equilibrium (LTNE) conditions were adopted in the middle region of the system, because when high flow velocities are involved, fluid and solid phases of the porous material are at different temperatures. The flow and heat transfer characteristics depend on Grashof number Gr, Brinkman number Br, solid volume fraction ϕ, porous parameter \(\sigma \), interphase heat transfer H, internal heat generation ws, Forchheimer parameter F, nanofluid to solid porous-matrix thermal conductivity ratio parameter kr, porosity \(\varepsilon \) of the medium. The momentum and energy equations are coupled and nonlinear in respective regions. Galerkin finite element method is used to solve these equations to obtain Nusselt number profiles. For the current study, an ANN model is suggested to forecast heat transfer for various parameters included in the investigation Hoseinzadeh et al. [32].

2 Mathematical formulation

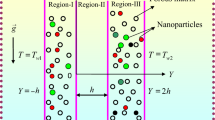
Figure 1 depicts the physical configuration. The flow of three immiscible fluids in a vertical channel has been studied as a continuous, laminar mixed convective flow. The X-axis is taken parallel to the channel, while the Y-axis is taken perpendicular to it. The region 0 ≤ y ≤ L is occupied by the Nanofluid and the regions − L ≤ y ≤ 0, L ≤ y ≤ 2L are occupied by the viscous fluid. The flow in all three regions is assumed to be incompressible and fully developed. The thermo physical properties are assumed to be constant except for the density in the buoyancy term in the momentum equation. The fluid rises in the channel driven by buoyancy forces.

Fig. 1
figure 1

Physical model

Full size image

Both regular and nanofluid transport characteristics are considered to be constant. The channel's boundary walls are kept at distinct constant temperatures, i.e., Tw1 at the left wall and Tw2 at the right wall with Tw1 ≥ Tw2. We have assumed the Boussinesq approximation. Further, it is presumed that at the two interphases there is continuity of velocity, temperature, and heat fluxes. With these assumptions and also employing the nanofluid model recommended by Tiwari and Das [33], the momentum and energy equations are adopted from Ghasemi and Aminossadati [34], Muthtamilselvan et al. [35], Vajravelu et al. [36], Yasser Mahmoudi [25].

To solve problems involving nanofluids mathematically, two types of models are used. One is a single-phase model, while the other is a two-phase one. The Tiwari and Das model is an example of a single-phase model. In a single phase model, the fluid, velocity, and temperature are all considered to be the same. In the two-phase model, the fluid velocity and the temperature of the nanoparticles are assumed to be different. The single-phase model has the advantage of being simpler and easier to solve numerically because the slip processes are ignored. In the Tiwari and Das model volume concentration of nanoparticles ranges between 3 and 20%.

2.1 Physical domain

2.2 Governing equations

Region-I

$$\frac{d{v}_{1}}{dy}=0$$
(1)
$${\mu }_{f}\frac{{d}^{2}{u}_{1}}{{dy}^{2}}+{\rho }_{f}g{\beta }_{f}\left({T}_{1}-{T}_{w2}\right)-\frac{\partial p}{\partial x}=0$$
(2)
$${K}_{f}\frac{{d}^{2}{T}_{1}}{{dy}^{2}}+{\mu }_{f}{\left(\frac{d{u}_{1}}{dy}\right)}^{2}=0$$
(3)

Region-II

$$\frac{d{v}_{2}}{dy}=0$$
(4)
$$-\frac{\partial p}{\partial x}+{\mu }_{nf}\frac{{d}^{2}{u}_{2}}{{dy}^{2}}+{\rho }_{nf}g{\beta }_{nf}\left({T}_{2}-{T}_{w2}\right)-\frac{{\mu }_{nf}}{k}{u}_{2}-\frac{{\rho }_{nf}{C}_{I}}{\sqrt{k}}{u}_{2}^{2}=0$$
(5)
$$ {K}_{nf}\frac{{d}^{2}{T}_{2f}}{{dy}^{2}}+{\mu }_{nf}{\left(\frac{d{u}_{2}}{dy}\right)}^{2}+\frac{{\mu }_{nf}}{k}{{u}^{2}}_{2} +\frac{{h}_{nfs}}{\varepsilon {(\rho c)}_{nf}}\left({T}_{s}-{T}_{nf}\right)+{s}_{f}=0 $$
(6)
$${K}_{s}\frac{{d}^{2}{T}_{2s}}{{dy}^{2}}+\frac{{h}_{nfs}}{(1-\varepsilon ){(\rho c)}_{s}}\left({T}_{nf}-{T}_{s}\right)+{s}_{s}=0$$
(7)

Region-III

$$\frac{d{v}_{3}}{dy}=0$$
(8)
$${\mu }_{f}\frac{{d}^{2}{u}_{3}}{{dy}^{2}}+{\rho }_{f}g{\beta }_{f}\left({T}_{3}-{T}_{w2}\right)-\frac{\partial p}{\partial x}=0$$
(9)
$${K}_{f}\frac{{d}^{2}{T}_{3}}{{dy}^{2}}+{\mu }_{f}{\left(\frac{d{u}_{3}}{dy}\right)}^{2}=0$$
(10)

Following are the boundary and interface conditions for the velocity and temperature as in [37]

2.3 Boundary conditions

$${u}_{1}\left(-L\right)=0, { u}_{1}\left(0\right)={u}_{2}\left(0\right), {\mu }_{f}\frac{d{u}_{1}\left(0\right)}{dy}{=\mu }_{nf}\frac{d{u}_{2}\left(0\right)}{dy} , { u}_{2}\left(L\right)={u}_{3}\left(L\right), {\mu }_{nf}\frac{d{u}_{2}(L)}{dy}{=\mu }_{f}\frac{d{u}_{3}(L)}{dy}, {u}_{3}\left(2L\right)=0$$
(11)
$${T}_{1}\left(-L\right)={T}_{w2}, { T}_{1}\left(0\right)={T}_{2}\left(0\right), {K}_{f}\frac{d{T}_{1}\left(0\right)}{dy}{=K}_{nf}\frac{d{T}_{2}\left(0\right)}{dy} , { T}_{2}\left(L\right)={T}_{3}\left(L\right),{K}_{nf}\frac{d{T}_{2}(L)}{dy}{=K}_{f}\frac{d{T}_{3}(L)}{dy}, {T}_{3}\left(2L\right)={T}_{w1}$$
(12)

The effective density of nanofluid is given by

$${\rho }_{nf}=\left(1-\phi \right){\rho }_{f}+\phi {\rho }_{s}$$
(13)

The thermal diffusivity, heat capacitance and thermal expansion coefficients of the nanofluid are given by

$${\alpha }_{nf}=\frac{{k}_{nf}}{{(\rho {C}_{p})}_{nf}}$$
(14)
$${(\rho {C}_{p})}_{nf}=\left(1-\phi \right){\left(\rho {C}_{p}\right)}_{f}+\phi {(\rho {C}_{p})}_{s}$$
(15)
$${(\rho \beta )}_{nf}=\left(1-\phi \right){\left(\rho \beta \right)}_{f}+\phi {(\rho \beta )}_{s}$$
(16)

The effective dynamic viscosity of the nanofluid is given by [38]

$${\mu }_{nf}=\frac{{\mu }_{f}}{{(1-\phi )}^{2.5}}$$
(17)

For spherical nanoparticles, according to Max- well [39], this can be written as

$${K}_{nf}={K}_{f}\frac{{K}_{s}+2{K}_{f}-2\phi ({K}_{f}-{K}_{s})}{{K}_{s}+2{K}_{f}+\phi ({K}_{f}-{K}_{s})}$$
(18)

To transform the Eqs. (1)–(12) in to dimensionless form, we introduce the following dimensionless parameters

$${y}^{*}=\frac{y}{L}, {u}_{i}^{*}={u}_{i}\left(\frac{{\rho }_{f}}{{\mu }_{f}}\right)L,$$
(19a)
$${\theta }_{i}=\frac{{T}_{i}-{T}_{w2}}{{T}_{w1}-{T}_{w2}}, { \theta }_{nf2}=\frac{{T}_{nf2}-{T}_{w2}}{{T}_{w1}-{T}_{w2}}, {\begin{array}{c} \\ \theta \end{array}}_{s2}=\frac{{T}_{s2}-{T}_{w2}}{{T}_{w1}-{T}_{w2}},$$
(19b)
$$Gr=\frac{g{\beta }_{f}\left({T}_{w1}-{T}_{w2}\right){L}^{3}}{{v}_{f}^{2}}, Br=\frac{{\mu }_{f}^{3}}{{\rho }_{f}^{2}{L}^{2}\left({T}_{w1}-{T}_{w2}\right){k}_{f}}, P=-\frac{{{\rho }_{f}L}^{3}}{{\mu }_{f}^{2}}\frac{\partial P}{\partial x},$$
(19c)
$$\sigma =\frac{L}{\sqrt{k}}, F=\frac{{\rho }_{nf}{C}_{I}{{u}_{i}L}^{2}}{{\mu }_{nf}\sqrt{K}}, H=\frac{{h}_{nfs}{L}^{2}}{{K}_{nf}}, { k}_{r}=\frac{{K}_{nf}}{\left(1-\varepsilon \right){K}_{s}},$$
(19d)
$${w}_{f}=b{s}_{f}, {w}_{s}=H {k}_{r}{s}_{s}$$
(19e)

Substituting the above quantities in to Eqs. (1)–(12), after dropping asterisks we get the following non-dimensionalized equations.

Region-I

$$\frac{{d}^{2}{u}_{1}}{{dy}^{2}}+Gr{\theta }_{1}+P=0$$
(20)
$$\frac{{d}^{2}{\theta }_{1}}{{dy}^{2}}+Br{\left(\frac{d{u}_{1}}{dy}\right)}^{2}=0$$
(21)

Region-II

$$\frac{{d}^{2}{u}_{2}}{{dy}^{2}}+Gr{\theta }_{2nf}-{\sigma }^{2}{u}_{2}+P{\left(1-\phi \right)}^{2.5}-F{u}_{2}^{2}=0$$
(22)
$$\frac{{d}^{2}{\theta }_{2nf}}{{dy}^{2}}+Br b\left[{\left(\frac{d{u}_{2}}{dy}\right)}^{2}+{\sigma }^{2}{{u}^{2}}_{2}\right]+\frac{H}{\varepsilon }\left({\theta }_{2s}-{\theta }_{2nf}\right)+{w}_{f}=0$$
(23)
$$\frac{{d}^{2}{\theta }_{2s}}{{dy}^{2}}+H{k}_{r}\left({\theta }_{2nf}-{\theta }_{2s}\right)+{w}_{s}=0$$
(24)

Region-III

$$\frac{{d}^{2}{u}_{3}}{{dy}^{2}}+Gr{\theta }_{3}+P=0$$
(25)
$$\frac{{d}^{2}{\theta }_{3}}{{dy}^{2}}+Br{\left(\frac{d{u}_{3}}{dy}\right)}^{2}=0$$
(26)

where

$$a={\left(1-\phi \right)}^{2.5}\left[\left(1-\phi \right)+\frac{\phi {\left(\rho \beta \right)}_{s}}{{\left(\rho \beta \right)}_{f}}\right], bb=\frac{1}{{\left(1-\phi \right)}^{2.5}}\left(\frac{{K}_{s}+2{K}_{f}+\phi \left({K}_{f}-{K}_{s}\right)}{{K}_{s}+2{K}_{f}-2\phi \left({K}_{f}-{K}_{s}\right)}\right),$$
(27)

In the non-dimensional form, the boundary and interface conditions become

$${u}_{1}\left(-1\right)=0, { u}_{1}\left(0\right)={u}_{2}\left(0\right), \frac{d{u}_{1}\left(0\right)}{dy}=\frac{{\mu }_{nf}}{{\mu }_{f}}\frac{d{u}_{2}\left(0\right)}{dy} , { u}_{2}\left(1\right)={u}_{3}\left(1\right), \frac{d{u}_{2}\left(1\right)}{dy}=\frac{{\mu }_{f}}{{\mu }_{nf}}\frac{d{u}_{3}\left(1\right)}{dy}, {u}_{3}\left(2\right)=0$$
(28)
$${\theta }_{1}\left(-1\right)={\theta }_{w2}, { \theta }_{1}\left(0\right)={\theta }_{2}\left(0\right), \frac{d{\theta }_{1}\left(0\right)}{dy}=\frac{{K}_{nf}}{{K}_{f}}\frac{d{\theta }_{2}\left(0\right)}{dy} , { \theta }_{2}\left(1\right)={\theta }_{3}\left(1\right),\frac{d{\theta }_{2}\left(1\right)}{dy}=\frac{{K}_{f}}{{K}_{nf}}\frac{d{\theta }_{3}\left(1\right)}{dy}, {\theta }_{3}\left(2\right)={\theta }_{w1}, {\theta }_{wr}=\frac{{\theta }_{w1}}{{\theta }_{w2}}.$$
(29)

The Nusselt number, which is given in [37, 40], can be used to predict the heat transfer rate at the microporous channel.

$${Nu}_{1}=\frac{{q}_{w1}\left(2L\right)}{{k}_{1}\left({T}_{w1}-{T}_{1,m}\right)}=\frac{2}{{\theta }_{1, m}},{Nu}_{2 nf}=\frac{{q}_{w2}\left(2L\right)}{{k}_{2f}\left({T}_{w2}-{T}_{2f,m}\right)}=\frac{2}{{\theta }_{2nf, m}},{Nu}_{3}=\frac{{q}_{w2}(2L)}{{k}_{3}({T}_{w2}-{T}_{3,m})}=\frac{2}{{\theta }_{3, m}}$$
(30)

where \({\theta }_{1, m}=\frac{{\int }_{-1}^{0}{u}_{1}{\theta }_{1}dy}{{\int }_{-1}^{0}{u}_{1}dy}\), \({\theta }_{2nf, m}=\frac{{\int }_{0}^{1}{u}_{2}{\theta }_{2nf}dy}{{\int }_{0}^{1}{u}_{2}dy}\), \({\theta }_{3, m}=\frac{{\int }_{1}^{2}{u}_{3}{\theta }_{3}dy}{{\int }_{1}^{2}{u}_{3}dy}\) is the dimensionless mean temperature difference.

$${Nu}_{avg}=\frac{{q}_{wi}(3L)}{{k}_{fi}({T}_{wi}-{T}_{if,m})}=\frac{3}{{\theta }_{avg, m}}$$
(31)

where\({\theta }_{avg, m}=\frac{{\int }_{-1}^{0}{u}_{1}{\theta }_{1}dy+{\int }_{0}^{1}{u}_{2}{\theta }_{2nf}dy+{\int }_{1}^{2}{u}_{3}{\theta }_{3}dy}{{\int }_{-1}^{0}{u}_{1}dy+{\int }_{0}^{1}{u}_{2}dy+{\int }_{1}^{2}{u}_{3}dy}\) is the dimensionless mean temperature.

3 Numerical scheme

To predict the heat transfer behavior in the porous medium, Eqs. (20)–(26) are solved using the Finite element method (FEM). The Galerkin method is used to obtain matrix form equations from governing equations. A simple linear element with two nodes is used within the element to represent variations in the velocity and temperature functions. The values of u, θf and θs that vary within the element are written as [37, 41].

$$ u \, = \, u_{i} N_{i} + \, u_{j} N_{j} , \theta_{f} = \, \theta_{fi} N_{i} + \, \theta_{fj} N._{j,} \theta_{s} = \, \theta_{si} N_{i} + \, \theta_{sj} N_{j} $$
(32)

where \({N}_{i}=\frac{{y}_{j}-y}{{y}_{j}-{y}_{i}},{N}_{j}=\frac{y-{y}_{i}}{{y}_{j}-{y}_{i}}\).

Using the FEM formulation, Eqs. (20)–(26) are converted into matrix form equations for the elements, as in [41]. The coupled matrix equations for the elements are combined to obtain the global matrix for the entire domain, which is solved iteratively to obtain u, θf and θs in the porous medium. To obtain converged results, the error level of solution for u, θf and θs are set to 10−4. When the above-mentioned error level, which is the difference between previous and current iterations for a variable at all nodes, is reached, the iterative process is terminated.

3.1 Validation

As observed in Table 1 the obtained Nu values in the present study at the channel walls y = − 1 and y = 2 for different values of Gr are compared with Umavathi and Hemvathi [18] and also Ansys simulations and found in good agreement.

Table 1 Values of Nu for the values of P = 1, Br = 0.01, ϕ = 0.02, σ = 4, H = F = kr = ws = wf = 0
Full size table

4 Results and discussions

The model is numerically solved for velocity and temperature profiles using the Galerkin finite element method, and all computations are performed in Matlab. The range for the parameters H, ws, F, kr and ε in this study are \(0\le H\le 150, -5\le {w}_{s}\le 5, 0\le F\le 1{0}^{5}, 0.1\le {k}_{r}\le 1, 0.1\le \varepsilon \le 0.9.\)

4.1 Nusselt number profiles

The influence of wall temperature ratio \({\theta }_{wr}\) on Nusselt number Nu is observed in the following figures for the Regions-I, II and III. Region-I \(\left(-L\le y\le 0\right)\) and Region-III \(\left(0\le y\le L\right)\) are occupied by the clear viscous fluid and Region-II \(\left(L\le y\le 2L\right)\) is nano fluid saturated porous medium. The combined effect of Grash ofnnumber Gr and wall temperature ratio \({\theta }_{wr}\) on Nusselt number is observed in Fig. 2 for all the three regions. As seen, in all three regions, increasing Gr causes an increase in the Nusselt number which is due to an increase in the wall temperature. However, heat transfer is found to be more in the nano fluid saturated porous channel when compared to the channels saturated with clear viscous fluids. Also, it is seen that Nusseltnnumber is independent of \({\theta }_{wr}\) in all the three regions for different values of Gr.

Fig. 2
figure 2

Nusselt number profiles for different values of Grashof number Gr

Full size image

Figure 3 shows the effect of wall temperature ratio and Brinkman number on Nu using copper–water based nanofluid in the middle region. It is observed that an increase in the Brinkman number leads to decrease in the Nusselt number. This may be due to an increase in the temperature of the bulk fluid near the wall with the increase in the Br. However, heat transfer is found to be more in the nano fluid saturated porous channel when compared to the channels saturated with clear viscous fluids. For all different values of Br, it is found that there is no variation of Nu with the wall temperature ratio.

Fig. 3
figure 3

Nusselt number profiles for differentt values of Brinkman number Br

Full size image

Figures 4 and 5 show the effect of solid volume fraction ϕ, and porous parameter \(\sigma \) respectively on Nusselt number as the wall temperature ratio \({\theta }_{wr}\) increases. A slight rise in the value of Nu is noticed with an increase in the values of ϕ and \(\sigma \). Increasing \(\sigma \) means decrease in the permeability of the porous medium. The velocity distribution appears to be more uniform with lower permeability, which contributes to an improvement in Nu. For various values of ϕ and \(\sigma \), Nu values are found to be greater in the middle region compared to the other two end regions. The velocity reduces as the ϕ increases. This finding can be explained by the fact that as nanoparticles are applied to a pure fluid, the concentration of the fluid increases and the fluid becomes denser, resulting in a reduction in the fluids velocity in the channel and an increase in Nu. For various values of ϕ and \(\sigma ,\) an increase in \({\theta }_{wr}\) has no visible impact on Nu in any of the three regions.

Fig. 4
figure 4

Nusselt number profiles for various values of solid volume fraction ϕ

Full size image
Fig. 5
figure 5

Nusselt number profiles for different values of porous parameter \(\sigma \)

Full size image

Figure 6 depicts the effect of H on Nu as the increasing wall temperature ratio \({\theta }_{wr}\). It demonstrates that in a channel occupied with clear viscous fluid, the interphase heat transfer coefficient H does not influence Nu. In the middle region, Nu drops as H increases. Increasing the interface heat transfer coefficient, in other words, enhances thermal communications between the two phases of a porous material. As the temperature of the solid porous matrix falls, the temperature of the nanofluid rises. As a consequence, the temperature difference between the nanofluid and the hot wall reduces, and the average Nusselt number of the nanofluid drops.

Fig. 6
figure 6

Nusselt number profiles for various values of interphase heat transfer coefficient H

Full size image

The effects of internal heat generation and wall temperature ratio on the Nu are displayed in Fig. 7 for all three regions, respectively. It has been noticed that increasing the internal-heat-generation values raises the Nusselt number in all three regions. When compared to the right and left walls of the channel, the effect of enhancement on the Nu is dominant in the middle region of the channel (saturated nanofluid-with porous media).

Fig. 7
figure 7

Nusselt number profiles for various solid internal-heat-generation ws values

Full size image

The influence of the Forchheimer number F on the Nusselt number inside the enclosure is shown in Fig. 8a–c. It can be seen that when the F increases, the Nu decreases in all three regions. The influence of Forchheimer number is stronger in the middle region saturated with copper water-based nanofluid than on the right and left walls of the channels. A higher Forchheimer number indicates increased flow resistance, which leads to slower filtration and a lower Nusselt number.

Fig. 8
figure 8

Profiles of Nusselt number for various values of Forchheimer numbers F

Full size image

The effect of the parameters nanofluid to solid porous matrix thermal conductivity ratio kr and the porosity ε of the medium on Nusselt number are shown in Fig. 9a, b with the variable wall temperature ratio \({\theta }_{wr}\). Increase in kr and ε leads to enhancement of Nusselt number. Hence it can be stated that porosity has a beneficial impact on the overall heat transfer rate. For various values of kr and ε, it is discovered that the variable wall temperature ratio has no visible effect on the Nusselt number.

Fig. 9
figure 9

Profiles of Nusselt numbers for various values of a Nanofluid to solid porous matrix thermal conductivity ratio parameter kr b Porosity of the medium \(\varepsilon \), Region-II

Full size image

Figure 10a, b depict the influence of Grashof number Gr and Brinkman number Br respectively on Average Nusselt Number with the varying wall temperature ratio \({\theta }_{wr}\). Negative \({\theta }_{wr}\) values indicate that one of the channel's walls is hot and the other is cold, whereas positive values imply that both walls are either hot or cold. As expected, increasing Gr induces an increase in wall temperature, which raises Nu and increasing Br causes the decrease in Nu which can be seen from the Fig. 10a, b respectively. These figures reveal that Nu decreases asymptotically to a common minimum value with varying \({\theta }_{wr}\) from the negative values to positive values.

Fig. 10
figure 10

Profiles of average Nusselt numbers for various values of a Grashof number Gr b Brinkman number Br

Full size image

Figure 11a, b display the variation in Nu with the variation in the values of solid-volume-fraction ϕ and the porous parameter \(\sigma \) respectively. According to these results, Nu appears to be less sensitive to changes in the values of ϕ and \(\sigma \) which could be due to its effect on the small cross-sectional area of the porous region. Nu, on the other hand, increases in a negligible way as the values of ϕ and \(\sigma \) increase.

Fig. 11
figure 11

Average Nusselt number profiles for differentvvalues of a solid volume fraction ϕ, b porous parameter \(\sigma \)

Full size image

The influence of the interphase heat transfer coefficient H and the Forchheimer number F on Nu is shown in Fig. 12a, b. Nu decreases when the heat transfer coefficient H rises, possibly due to rising fluid temperature profiles in the channel. It's also worth noting that Nu decreases as the Forchheimer number rises. With varying \({\theta }_{wr}\) from negative to positive values, figures show that Nu decreases asymptotically to a common minimum value.

Fig. 12
figure 12

Average Nusselt number profiles for different values of a Interphase heat transfer coefficient H, b Forchheimer number F

Full size image

Figure 13a depicts the variations in Nu caused by simultaneous changes in the solid internal heat generation parameter and the wall temperature ratio. The heat absorption case of the solid corresponds to negative values of ws, while the heat generation case corresponds to positive values of ws. As ws rises, the fluid warms, resulting in an increase in Nu. The effect of the nanofluid to solid porous matrix thermal conductivity ratio parameter kr on Nu as the wall temperature ratio increases is shown in Fig. 13b. The consequence of the parameter kr is that Nu increases as kr rises, owing to an increase in the fluid's thermal conductivity.

Fig. 13
figure 13

Average Nusselt number profiles for-various values of a solid internal heat-generation ws b nanofluid to solid porous matrix thermal conductivity ratio parameter kr

Full size image

4.2 ANN model

Figure 14 depicts the ANN configuration model. The input parameters are Gr, Br, ϕ, \(\sigma \), H, F, ws, kr and \({\theta }_{wr}\) and the output parameter is the Nusselt number. During the construction of an artificial neural network model, the available data set is divided into two datasets. The first dataset 20% is used to train the ANN model, and the second dataset 80% is used to validate it. The predicted outcomes of the ANN model are compared to the remaining data. The proposed scheme employs four different types of back propagation algorithms: LMB, SCGB, BRB, and RB. Figure 14 shows how to reduce the error between expected output outcomes and input data by adjusting weights and biases. The numerical investigation's dataset is used to create an optimal ANN model for forecasting heat transfer. The procedure for determining the best framework in the ANN is based on changing the number of neurons in a hidden layer and planning the ANN execution for each neuron number [42,43,44,45,46]. The optimal ANN’s results are more consistent with the theoretical dataset, and it can predict heat transfer better than the correlation, as shown in Fig. 14.

Fig. 14
figure 14

Comparison between the theoretical data and the ANN outputs

Full size image

Table 2 demonstrates that the values for the Nu for all the governing parameters at three regions. The Nusselt number is maximum for silver nanoparticle in the left and middle regions and minimum for SiO2 and titanium oxide nanoparticle, whereas it is extreme for diamond nanoparticle and least for SiO2 nanoparticle in the right region respectively [47,48,49,50].

Table 2 Values of Nusseltnnumber fixing the values as \(Gr=5, P=1, Br=0.01, \phi =0.02, \sigma = 4, F=10, H=10, {w}_{s}=5 and \varepsilon =0.5\)
Full size table

4.3 Velocity and temperature profiles

Table 3 demonstrates that the variations of velocity and temperature profiles for all the governing parameters at three regions. The amplitude of the increase in velocity is lower in region II when compared to region I and in region III when compared to region II because the fluid is saturated with porous media in the middle of the channel. The temperature profiles initially rise at the left wall (clear viscous fluid), then change to a parabolic shape in the middle of the channel (saturated nanofluid with porous media), then fall at the right wall (clear viscous fluid), and eventually reach one.

Table 3 Variations of velocity and temperature for the values of P = 5.0, Br = 0.1, ϕ = 0.02, σ = 4, Gr = 5, H = F = 10, kr = 1, ws = 1, wf = 0
Full size table

There are numerous methods and procedures used in the process of finding solutions to the numerous issues encountered in the manufacturing business [51,52,53,54]. Initially, the experimental method was used to handle a broad variety of issues in the industrial sector [55,56,57,58]. Because of technological developments, testing methods can now be assessed and the outcomes of those tests can be predicted before the techniques are implemented [59,60,61,62,63,64].

5 Conclusions

Under local thermal nonequilibrium conditions, the effect of internal heat on heat transfer in a nanofluid saturated vertical channel with a porous matrix layer sandwiched between two fluid layers is investigated in this study. The Darcy–Forchheimer equation is used to simulate flow in a porous material. To characterize the nanofluid, the Tiwari and Das model is used. Using the Finite element Galerkin technique, the governing equations are transformed into matrix form. This equation system is solved for velocity and temperature profiles. The Nusselt number is calculated using these profiles. From this study, the following conclusions were drawn:

  • Increasing the Grashof number and internal heat generation parameters improves heat transfer in all three regions.

  • Heat transfer in the middle porous region, which is saturated with nanofluid, is observed to be higher than in regions one and three. Because the improvement in the thermal properties, including higher thermal conductivity and higher convective heat transfer coefficients than pure fluids.

  • The heat transfer in all three regions was reduced as the Forchheimer number and Brinkman number were increased.

  • Heat transfer in the middle region is reduced when interphase heat transfer is increased.

  • Heat transfer was optimal when silver was employed as a nanoparticle. However, heat transfer was poor when titanium oxide was used.