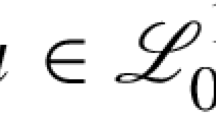Extended Sobolev scale on $\mathbb {Z}^n$

Abstract

In analogy with the definition of “extended Sobolev scale" on $\mathbb {R}^n$ by Mikhailets and Murach, working in the setting of the lattice $\mathbb {Z}^n$, we define the “extended Sobolev scale" $H^{\varphi }(\mathbb {Z}^n)$, where $\varphi$ is a function which is RO-varying at infinity. Using the scale $H^{\varphi }(\mathbb {Z}^n)$, we describe all Hilbert function-spaces that serve as interpolation spaces with respect to a pair of discrete Sobolev spaces $[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]$, with $s_0<s_1$. We use this interpolation result to obtain the mapping property and the Fredholmness property of (discrete) pseudo-differential operators (PDOs) in the context of the scale $H^{\varphi }(\mathbb {Z}^n)$. Furthermore, starting from a first-order positive-definite (discrete) PDO A of elliptic type, we define the “extended discrete A-scale" $H^{\varphi }_{A}(\mathbb {Z}^n)$ and show that it coincides, up to norm equivalence, with the scale $H^{\varphi }(\mathbb {Z}^n)$. Additionally, we establish the $\mathbb {Z}^n$-analogues of several other properties of the scale $H^{\varphi }(\mathbb {R}^n)$.

1 Introduction

Owing to their role in the discretization of continuous problems, difference equations and the corresponding pseudo-differential operators (PDO) on the lattice $\mathbb {Z}^n$ have attracted quite a bit of attention in the last decade; see, for instance the papers [8, 9, 14, 17, 29, 31,32,33], keeping in mind that in some articles $n=1$. Another milestone in this field of study was marked by the article [6], in which the authors developed the corresponding global symbol calculus. In this setting, $\mathbb {Z}^n\times \mathbb {T}^n$ (here, $\mathbb {T}^n:=\mathbb {R}^n/\mathbb {Z}^n$) plays the role of the phase space, whereby the frequency component belongs to the n-torus $\mathbb {T}^n$. It turns out that the symbol class $S^{m}_{\rho ,\delta }(\mathbb {Z}^n\times \mathbb {T}^n)$, with $m,\rho ,\delta \in \mathbb {R}$, introduced in [6] (see definition 2.1 below for the special case $S^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$ with $\rho =1$ and $\delta =0$), bears some resemblance to that of the so-called SG-operators discussed in [10, 13]. With the symbol calculus at their disposal, the authors of [6] proved a number of fundamental results concerning, among other things, $\ell ^2(\mathbb {Z}^n)$-boundedness (here, $\ell ^2(\mathbb {Z}^n)$ denotes the space of square summable complex-valued functions on $\mathbb {Z}^n$), compactness, and $H^{(s)}(\mathbb {Z}^n)$-boundedness of the corresponding operators, where, $H^{(s)}(\mathbb {Z}^n)$, $s\in \mathbb {R}$, indicates (see Sect 2.5 below for details) the Sobolev scale on $\mathbb {Z}^n$. Subsequently, the authors of [11] studied further properties of PDO on $\mathbb {Z}^n$, including the relationship between the maximal and minimal realizations of a pseudo-differential operator in $\ell ^2(\mathbb {Z}^n)$. More recently, the authors of [19] considered weighted $M^{m}_{\rho ,\Lambda }(\mathbb {Z}^n\times \mathbb {T}^n)$-type symbols (discrete counterparts of $M^{m}_{\rho ,\Lambda }$-type symbols on $\mathbb {R}^n$ discussed in [12, 15, 16, 35]), and after developing the corresponding calculus and defining the corresponding weighted Sobolev scale on $\mathbb {Z}^n$, investigated various questions concerning the corresponding PDOs on $\mathbb {Z}^n$.

In parallel with the developments described in the preceding paragraph, starting with the seminal papers [24, 25] (see also Sect. 2.4 of the monograph [26]), Mikhailets and Murach proposed the so-called extended Sobolev scale $H^{\varphi }(\mathbb {R}^n)$, defined similar to $H^{(s)}(\mathbb {R}^n)$, $s\in \mathbb {R}$, but with $\varphi (\langle \xi \rangle )$ in place of $\langle \xi \rangle ^{s}$, where $\varphi$ is a function RO-varying at $\infty$ and satisfies some additional properties; see Sect. 2.6 below for precise description of the function class RO. It turns out that the scale $H^{\varphi }(\mathbb {R}^n)$ is a more general version of the so-called refined Sobolev scale, introduced by Mikhailets and Murach earlier in [23] (see also Sect. 1.3 in [26]). What makes the scale $H^{\varphi }(\mathbb {R}^n)$ particularly interesting is the following interpolation property (established in [25]; see also [27] for bounded domains $\Omega \subset \mathbb {R}^n$ with Lipschitz boundary): a Hilbert space $\mathscr {S}$ is an interpolation space with respect to a pair (see Sect. 2.8 below for this concept) of the form

$$\begin{aligned}{}[H^{(s_0)}(\mathbb {R}^n),H^{(s_1)}(\mathbb {R}^n)], \qquad -\infty<s_0<s_1<\infty , \end{aligned}$$

if and only if $\mathscr {S}=H^{\varphi }(\mathbb {R}^n)$, for some $\varphi \in RO$.

The aforementioned interpolation property (and other useful attributes studied in [23, 25, 27]) of the refined (and extended) Sobolev spaces, sets a convenient stage for elaborating the theory of elliptic boundary-value problems on $\mathbb {R}^n$ (and closed manifolds) and for establishing various results from spectral theory of differential operators on $\mathbb {R}^n$ (and closed manifolds) in analogy with those that hold in the setting of the usual Sobolev spaces. To get a taste of the degree of activity in this area during the last fifteen years, besides the papers mentioned so far, we refer the reader to the monograph [26], papers [2, 3, 28, 36], and numerous references therein. For a study of $H^{\varphi }$-scale on compact manifolds with boundary see [18]. For theory of parabolic boundary-value problems on $\mathbb {R}^n$ in the so-called anisotropic generalized Sobolev spaces, see the recent paper [21], the monograph [22], and references therein.

The present article lies at the intersection of the two research tracks described in the preceding three paragraphs. After defining the (extended) Sobolev scale $H^{\varphi }(\mathbb {Z}^n)$, $\varphi \in RO$ (see Sect. 2.7 for the definition), we show that the aforementioned interpolation property (and its variants) hold in the setting of (extended) Sobolev spaces on $\mathbb {Z}^n$; see theorems 2.1 and 2.2 below. Furthermore, in analogy with a “quadratic interpolation" result of [27] for bounded domains $\Omega \subset \mathbb {R}^n$ with Lipschitz boundary, we show that (see theorem 2.3 below) the class $H^{\varphi }(\mathbb {Z}^n)$ is closed under interpolation with a function parameter. In theorem 2.4 we establish additional properties of the scale $H^{\varphi }(\mathbb {Z}^n)$, including the density of the Schwartz space $S(\mathbb {Z}^n)$ in $H^{\varphi }(\mathbb {Z}^n)$ and an embedding result $H^{\varphi }(\mathbb {Z}^n)\hookrightarrow \ell ^{\infty }(\mathbb {Z}^n)$, where $\ell ^{\infty }(\mathbb {Z}^n)$ stands for bounded functions on $\mathbb {Z}^n$.

A property from [6] says that a PDO A of order $m\in \mathbb {R}$ on $\mathbb {Z}^n$ (see Sect. 2.16 below for the definition of such PDOs) extends to a bounded linear operator $A:H^{(s)}(\mathbb {Z}^n)\rightarrow H^{(s-m)}(\mathbb {Z}^n)$. If, in addition, A is an elliptic operator of order m, then $A:H^{(s)}(\mathbb {Z}^n)\rightarrow H^{(s-m)}(\mathbb {Z}^n)$ is a Fredholm operator whose index does not depend on s (see theorem 4.2 in [11] for the case $s=m=0$ and proposition 10.2 below for general s and m). With this in mind, we use the interpolation result of theorem 2.2 to prove the corresponding mapping property and the Fredholmness property for PDOs in the scale $H^{\varphi }(\mathbb {Z}^n)$, $\varphi \in RO$; see theorems 2.5 and 2.6 below.

As in the corresponding definition in [28] for closed manifolds, working in the setting of $\mathbb {Z}^n$, for $\varphi \in RO$ and for a first-order PDO A of elliptic type (see definition 2.2 below) satisfying $(Au,u)\ge \Vert u\Vert ^2$ for all $u\in S(\mathbb {Z}^n)$, we define the so-called extended A-scale $H_{A}^{\varphi }(\mathbb {Z}^n)$. Under these hypotheses, in theorem 2.7 we show that, up to norm equivalence, we have $H_{A}^{\varphi }(\mathbb {Z}^n)=H^{\varphi }(\mathbb {Z}^n)$.

Lastly, we remark that the analogues of interpolation results of our article hold for the Sobolev scale $H^{(s)}(\hbar \mathbb {Z}^n)$ on the lattices $\hbar \mathbb {Z}^n$, $\hbar \in (0,1]$, and the corresponding mapping and Fredholmness properties hold for PDOs with $S^{m}_{\rho ,\delta }(\hbar \mathbb {Z}^n\times \mathbb {T}^n)$-type symbols from [7] (here $0\le \delta <\rho \le 1$). Furthermore, the results of our article also carry over to the weighted Sobolev spaces $H^{(s)}_{\Lambda }(\mathbb {Z}^n)$ and operators with $M^{m}_{\rho ,\Lambda }(\mathbb {Z}^n\times \mathbb {T}^n)$-type symbols from [19]. To keep our presentation simpler, we chose to work in the setting of $S^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$-type symbols from [6, 11].

The article consists of eleven sections and an appendix. In Sect. 2 we summarize the basic notations, define the usual Sobolev scale on $\mathbb {Z}^n$, RO-varying functions, the extended Sobolev scale on $\mathbb {Z}^n$, and PDOs on $\mathbb {Z}^n$, and we recall basic concepts concerning the interpolation with a function parameter. Additionally, in Sect. 2 (more specifically Sects. 2.10–2.13, 2.17, 2.18, and 2.20) we state the main results (seven theorems and one corollary) of the article. For reader’s convenience, in Sect. 3 we recalled the statements of a few auxiliary results on interpolation with a function parameter. Sects. 4–11 contain the proofs of the main results. In the appendix we discuss the anti-duality of the spaces $H^{(s)}(\mathbb {Z}^n)$ and $H^{(-s)}(\mathbb {Z}^n)$.

2 Notations and results

2.1 Basic notations

In this paper, the notations $\mathbb {Z}$, $\mathbb {N}$, and $\mathbb {N}_0$ indicate the sets of integers, positive integers, and non-negative integers respectively. For $n\in \mathbb {N}$, we denote the n-dimensional integer lattice by $\mathbb {Z}^n$. For an n-dimensional multiindex $\alpha =(\alpha _1, \alpha _2, \dots , \alpha _n)$ with $\alpha _j\in \mathbb {N}_0$, we define $|\alpha |:=\alpha _1+ \alpha _2+ \dots + \alpha _n$, and $\alpha !:=\alpha _1\alpha _2\dots \alpha _n$. For $k=(k_1,k_2,\dots ,k_n)\in \mathbb {Z}^n$ and $\alpha \in \mathbb {N}_0^{n}$, we define

$$\begin{aligned} k^{\alpha }:=k_1^{\alpha _1}k_2^{\alpha _2}\dots k_n^{\alpha _n} \end{aligned}$$

and

$$\begin{aligned} |k|:=\sqrt{k_1^2+k_2^2+\cdots +k_n^2}. \end{aligned}$$

2.2 Basic operators

Let $\{e_j\}_{j=1}^{n}$ be a collection of elements such that

$$\begin{aligned} e_j:=(0,0,\dots , 1,0, \dots , 0), \end{aligned}$$

with 1 occupying the j-th slot and 0 occupying the remaining slots.

For a function $u(k_1,k_2,\dots ,k_n)$ of the input variable $k=(k_1,k_2,\dots , k_n)\in \mathbb {Z}^n$, the first partial difference operator $\Delta _{k_j}$ is defined as

$$\begin{aligned} \Delta _{k_j}u(k):=u(k+e_j)-u(k), \end{aligned}$$

where $k+e_j$ is the usual addition of the n-tuplets k and $e_j$. For a multiindex $\alpha \in \mathbb {N}_0^{n}$, we set

$$\begin{aligned} \Delta ^{\alpha }_k:=\Delta ^{\alpha _1}_{k_1}\Delta ^{\alpha _2}_{k_2}\dots \Delta ^{\alpha _n}_{k_n}. \end{aligned}$$

We now recall basic differential operators on the n-dimensional torus $\mathbb {T}^n:=\mathbb {R}^n/\mathbb {Z}^n$. For $x\in \mathbb {T}^n$ and $\alpha \in \mathbb {N}^n$, we define

$$\begin{aligned} D_{x_j}:=\frac{1}{2\pi i}\frac{\partial }{\partial {x_j}},\qquad D^{\alpha }_x:=D^{\alpha _1}_{x_1}D^{\alpha _2}_{x_2}\dots D^{\alpha _n}_{x_n}, \end{aligned}$$

where i is the imaginary unit. Additionally, for $l\in \mathbb {N}_0$ we define,

$$\begin{aligned} D^{(l)}_{x_j}:=\prod _{r=0}^{l-1}\left( \frac{1}{2\pi i}\frac{\partial }{\partial {x_j}}-r\right) ,\qquad D^{(0)}_{x_j}:=1, \end{aligned}$$

where “1" refers to the identity operator. For $\alpha \in \mathbb {N}_0^{n}$, we define

$$\begin{aligned} D^{(\alpha )}_{x}:=D^{(\alpha _1)}_{x_1}D^{(\alpha _2)}_{x_2}\dots D^{(\alpha _n)}_{x_n}. \end{aligned}$$

2.3 Schwartz space

As specified in [6] and [11], the Schwartz space $\mathcal {S}(\mathbb {Z}^n)$ consists of the functions $u:\mathbb {Z}^n\rightarrow \mathbb {C}$ such that for all $\alpha ,\beta \in \mathbb {N}_0^n$ we have

$$\begin{aligned} \displaystyle \sup _{k\in \mathbb {Z}^n}|k^{\alpha }(\Delta _{k}^{\beta }u)(k)|<\infty . \end{aligned}$$

The symbol $S'(\mathbb {Z}^n)$ indicates the space of tempered distributions, that is, continuous linear functionals on $\mathcal {S}(\mathbb {Z}^n)$.

2.4 Discrete $L^p$-space

For $1\le p<\infty$ we define $\ell ^p(\mathbb {Z}^n)$ as the space of functions $u:\mathbb {Z}\rightarrow \mathbb {C}$ such that $\Vert u\Vert _{p}<\infty$, where

$$\begin{aligned} \Vert u\Vert _{p}^{p}:=\sum _{k\in \mathbb {Z}^n}|u(k)|^p. \end{aligned}$$

In particular for $p=2$ we get a Hilbert space $\ell ^2(\mathbb {Z}^n)$ with the inner product

$$\begin{aligned} (u,v):=\sum _{k\in \mathbb {Z}^n}u(k)\overline{v(k)}. \end{aligned}$$

(2.1)

To simplify the notation we will denote the corresponding norm in $\ell ^2(\mathbb {Z}^n)$ by $\Vert \cdot \Vert$.

We define $\ell ^{\infty }(\mathbb {Z}^n)$ as the space of functions $u:\mathbb {Z}\rightarrow \mathbb {C}$ such that $\Vert u\Vert _{\infty }<\infty$, where

$$\begin{aligned} \Vert u\Vert _{\infty }:=\sup _{k\in \mathbb {Z}^n}|u(k)|. \end{aligned}$$

2.5 Sobolev scale on $\mathbb {Z}^n$

To formulate our results we will need discrete Sobolev spaces as described in Sect. 2 of [11].

For $s\in \mathbb {R}$, we define

$$\begin{aligned} \langle k\rangle :=(1+|k|^2)^{\frac{1}{2}}, \qquad k\in \mathbb {Z}^n. \end{aligned}$$

(2.2)

Next, for $s\in \mathbb {R}$ we define

$$\begin{aligned} H^{(s)}(\mathbb {Z}^n):=\{u\in \mathcal {S}'(\mathbb {Z}^n):\langle k\rangle ^{s} u\in \ell ^2(\mathbb {Z}^n)\} \end{aligned}$$

(2.3)

with the norm $\Vert u\Vert _{H^{(s)}}:=\Vert \langle k\rangle ^{s}u\Vert$, where $\Vert \cdot \Vert$ is the norm corresponding to the inner product (2.1) in $\ell ^2(\mathbb {Z}^n)$.

Remark 2.1

We can view the space $H^{(s)}(\mathbb {Z}^n)$ as a weighted space $\ell _{\langle k\rangle ^{2s}}^2(\mathbb {Z}^n)$, that is, the $\ell ^2$-space with weight $\langle k\rangle ^{2s}$.

Remark 2.2

An important property, established in lemma 3.16 of [11], is the density of the space $\mathcal {S}(\mathbb {Z}^n)$ in $H^{(s)}(\mathbb {Z}^n)$ for all $s\in \mathbb {R}$.

The definition of “extended Sobolev scale,” as specified in Sect. 2.4 of [26], relies on the so-called RO-varying functions.

2.6 RO-varying functions

Throughout this section we follow the terminology of Sect. 2.4.1 in [26].

We say that a function $\varphi :[1,\infty )\rightarrow (0,\infty )$ is RO-varying at infinity if

• (i) $\varphi$ is Borel measurable

• (ii) there exist numbers $a>1$ and $c\ge 1$ (depending on $\varphi$) such that

  $$\begin{aligned} c^{-1}\le \frac{\varphi (\lambda t)}{\varphi (t)}\le c, \qquad \text {for all }t\ge 1,\,\,\lambda \in [1,a]. \end{aligned}$$

  (2.4)

In the sequel, the inclusion $\varphi \in RO$ means that a function $\varphi :[1,\infty )\rightarrow (0,\infty )$ is RO-varying at infinity.

By proposition 1 of [25], if $\varphi \in RO$, then $\varphi$ is bounded and separated from zero on every interval of the form [1, b] with $b>1$. Furthermore, according to the same proposition, the condition (2.4) has the following equivalent formulation: there exist numbers $s_0\le s_1$ and $c\ge 1$ such that

$$\begin{aligned} t^{-s_0}\varphi (t)\le c\tau ^{-s_0}\varphi (\tau ),\qquad \tau ^{-s_1}\varphi (\tau )\le ct^{-s_1}\varphi (t) \qquad \text {for all }1\le t\le \tau . \end{aligned}$$

(2.5)

To conclude this section, we review the concept of lower/upper Matuszewska indices of $\varphi \in RO$. Let $\varphi \in RO$. Setting $\lambda :=\frac{\tau }{t}$, we can rewrite (2.5) as

$$\begin{aligned} c^{-1}\lambda ^{s_0}\le \frac{\varphi (\lambda t)}{\varphi (t)}\le c\lambda ^{s_1}, \qquad \text {for all }t\ge 1,\,\,\lambda \ge 1. \end{aligned}$$

(2.6)

We define the lower Matuszewska index $\sigma _0(\varphi )$ as the supremum of all $s_0\in \mathbb {R}$ such that the leftmost inequality in (2.6) is satisfied. Likewise, we define the upper Matuszewska index $\sigma _1(\varphi )$ as the infimum of all $s_1\in \mathbb {R}$ such that the rightmost inequality in (2.6) is satisfied. Note that $-\infty<\sigma _0(\varphi )\le \sigma _1(\varphi )<\infty$.

2.7 Extended Sobolev scale on $\mathbb {Z}^n$

For $\varphi \in RO$ we define $H^{\varphi }(\mathbb {Z}^n)$ as

$$\begin{aligned} H^{\varphi }(\mathbb {Z}^n):=\{u\in S'(\mathbb {Z}^n):\varphi (\langle k \rangle )u\in \ell ^2(\mathbb {Z}^n)\}. \end{aligned}$$

(2.7)

As in the case of the spaces $H^{(s)}(\mathbb {Z}^n)$, it turns out that $H^{\varphi }(\mathbb {Z}^n)$ is a Hilbert space with the inner product

$$\begin{aligned} (u,v)_{H^{\varphi }(\mathbb {Z}^n)}:=\sum _{k\in \mathbb {Z}} [\varphi (\langle k \rangle )]^2 u(k)\overline{v(k)} \end{aligned}$$

(2.8)

and the norm corresponding to (2.8) will be denoted by $\Vert \cdot \Vert _{H^{\varphi }(\mathbb {Z}^n)}$.

Note that if $\varphi (t)=t^{s}$, $s\in \mathbb {R}$, the space $H^{\varphi }(\mathbb {Z}^n)$ leads to the Sobolev space $H^{(s)}(\mathbb {Z}^n)$. In this article, by extended Sobolev scale on $\mathbb {Z}^n$ we mean the class of spaces $\{H^{\varphi }(\mathbb {Z}^n):\varphi \in \mathbb {R}\}$.

In the next section we review some terminology from Sects. 1.1.1 and 1.1.2 of [26] concerning interpolation of a pair of Hilbert spaces with a function parameter.

2.8 Interpolation between Hilbert spaces

By an admissible pair of separable complex Hilbert spaces we mean an ordered pair $[\mathscr {H}_{0},\mathscr {H}_{1}]$ such that $\mathscr {H}_{1}\hookrightarrow \mathscr {H}_{0}$, with the embedding being continuous and dense. As indicated in Sect. 1.2.1 of [20], every admissible pair $[\mathscr {H}_{0},\mathscr {H}_{1}]$ is equipped with a so-called generating operator J, such that

• (i) J is a positive self-adjoint operator in $\mathscr {H}_{0}$ with ${\text {Dom}}(J)=\mathscr {H}_{1}$;

• (ii) $\Vert Ju\Vert _{\mathscr {H}_{0}}=\Vert u\Vert _{\mathscr {H}_{1}}$, for all $u\in {\text {Dom}}(J)=\mathscr {H}_{1}$.

According to Sect. 1.1.1 in [26], the operator J is uniquely determined by the admissible pair $[\mathscr {H}_{0},\mathscr {H}_{1}]$.

Let $\mathcal {B}$ be the set of all Borel measurable functions $\psi :(0,\infty )\rightarrow (0,\infty )$ satisfying the following two properties: $\psi$ is bounded that on every interval [a, b] with $0<a<b<\infty$, and $\frac{1}{\psi }$ is bounded on every interval $(c,\infty )$ with $c > 0$. For an admissible pair $\mathscr {H}:=[\mathscr {H}_{0},\mathscr {H}_{1}]$ with generating operator J and for a function $\psi \in \mathcal {B}$, spectral calculus gives rise to a (positive self-adjoint) operator $\psi (J)$ in $\mathscr {H}_{0}$. We define a (separable, Hilbert) space $[\mathscr {H}_{0},\mathscr {H}_{1}]_{\psi }$ (or, in abbreviated form, $\mathscr {H}_{\psi }$) as follows: $[\mathscr {H}_{0},\mathscr {H}_{1}]_{\psi }:={\text {Dom}}(\psi (J))$ with the inner product

$$\begin{aligned} (u,v)_{\mathscr {H}_{\psi }}:=(\psi (J)u,\psi (J)v)_{\mathscr {H}_{0}}, \end{aligned}$$

(2.9)

and the corresponding norm $\Vert u\Vert _{\mathscr {H}_{\psi }}:=\Vert \psi (J)u\Vert _{\mathscr {H}_{0}}$, where $(\cdot ,\cdot )_{\mathscr {H}_{0}}$ and $\Vert \cdot \Vert _{\mathscr {H}_{0}}$ are the inner product and the norm in ${\mathscr {H}_{0}}$.

Having defined the space $[\mathscr {H}_{0},\mathscr {H}_{1}]_{\psi }$, we proceed to describe the notion of interpolation parameter $\psi \in \mathcal {B}$. We say that a function $\psi \in \mathcal {B}$ is an interpolation parameter if the following condition is satisfied for all admissible pairs $\mathscr {H}:={[}\mathscr {H}_{0},\mathscr {H}_{1}]$ and $\mathscr {K}:={[}\mathscr {K}_{0},\mathscr {K}_{1}]$ and for all linear operators T with $\mathscr {H}_{0}\subseteq {\text {Dom}}(T)$: if the restrictions $T|_{\mathscr {H}_{0}}$ and $T|_{\mathscr {H}_{1}}$ act as bounded linear operators $T:\mathscr {H}_{0}\rightarrow \mathscr {K}_{0}$ and $T:\mathscr {H}_{1}\rightarrow \mathscr {K}_{1}$, then the restriction $T|_{\mathscr {H}_{\psi }}$ acts as a bounded linear operator $T:\mathscr {H}_{\psi }\rightarrow \mathscr {K}_{\psi }$.

In this case, we say that the space $\mathscr {H}_{\psi }$ is obtained by interpolation of the pair $\mathscr {H}={[}\mathscr {H}_{0},\mathscr {H}_{1}]$ with a function parameter $\psi \in \mathcal {B}$. Moreover, we have the following continuous dense embeddings: $\mathscr {H}_{1}\hookrightarrow \mathscr {H}_{\psi }\hookrightarrow \mathscr {H}_{0}$.

2.9 Interpolation space

Let $[\mathscr {H}_{0},\mathscr {H}_{1}]$ be an ordered pair of separable complex Hilbert spaces such that $\mathscr {H}_{1}\hookrightarrow \mathscr {H}_{0}$, where the arrow stands for continuous embedding. We say that a Hilbert space $\mathscr {S}$ is an interpolation space with respect to a pair $[\mathscr {H}_{0},\mathscr {H}_{1}]$ if the following conditions are satisfied:

• (i) we have continuous embeddings $\mathscr {H}_{1}\hookrightarrow \mathscr {S}\hookrightarrow \mathscr {H}_{0}$;

• (ii) any linear operator T in $\mathscr {H}_{0}$ which acts as a bounded linear operator $T:\mathscr {H}_{0}\rightarrow \mathscr {H}_{0}$ and $T:\mathscr {H}_{1}\rightarrow \mathscr {H}_{1}$, has the property that $T:\mathscr {S}\rightarrow \mathscr {S}$ is also a bounded linear operator.

Remark 2.3

Part (ii) of the above definition leads to the following property (see theorem 1.8 in [26] or theorem 2.4.2 in [5]):

$$\begin{aligned} \Vert T\Vert _{\mathscr {S}\rightarrow \mathscr {S}}\le C \max \{\Vert T\Vert _{\mathscr {H}_0\rightarrow \mathscr {H}_0},\Vert T\Vert _{\mathscr {H}_1\rightarrow \mathscr {H}_1}\}, \end{aligned}$$

where $C>0$ is a constant independent of T.

2.10 First interpolation result

Our first result concerns interpolation of a pair of (usual) Sobolev spaces $[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]$, where $s_0<s_1$ are real numbers. This result is an analogue of theorem 1 of [25] concerning the pair $[H^{(s_0)}(\mathbb {R}^n), H^{(s_1)}(\mathbb {R}^n)]$, $s_0<s_1$.

Before stating the result, we recall (see proposition 3.4 in [11]) that there is a continuous (and dense) embedding $H^{(s_1)}(\mathbb {Z}^n)\hookrightarrow H^{(s_0)}(\mathbb {Z}^n)$, $s_0<s_1$.

Theorem 2.1

The following are equivalent:

• (i) A Hilbert space $\mathscr {S}$ is an interpolation space with respect to a pair $[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]$, where $s_0<s_1$ are some real numbers.

• (ii) Up to norm equivalence, we have $\mathscr {S}=H^{\varphi }(\mathbb {Z}^n)$, for some function $\varphi \in RO$ satisfying the condition (2.6).

For future reference, we recall the definition of an interpolation space with respect to a scale of Hilbert spaces. Let $\{\mathscr {H}_{s}:s\in \mathbb {R}\}$ be a scale of Hilbert spaces such that there is continuous embedding $\mathscr {H}_{s_1}\hookrightarrow \mathscr {H}_{s_0}$ for all $s_0<s_1$. We say that a Hilbert space $\mathscr {S}$ is an interpolation space with respect to the scale $\{\mathscr {H}_{s}:s\in \mathbb {R}\}$ if there exist numbers $s_0<s_1$ such that $\mathscr {S}$ is an interpolation space with respect to the pair $[\mathscr {H}_{s_0},\mathscr {H}_{s_1}]$.

Corollary 2.1

The following are equivalent:

• (i) A Hilbert space $\mathscr {S}$ is an interpolation space with respect to the scale $\{H^{(s)}(\mathbb {Z}^n):s\in \mathbb {R}\}$.

• (ii) Up to norm equivalence, we have $\mathscr {S}=H^{\varphi }(\mathbb {Z}^n)$, for some function $\varphi \in RO$.

2.11 Second interpolation result

The result below captures the implication (ii)$\implies$(i) of theorem 2.1 in a more explicit form. For an analogous result in the context of a bounded domain $\Omega \subset \mathbb {R}^n$ with Lipschitz boundary, see theorem 5.1 of [27].

Theorem 2.2

Let $\varphi \in RO$, $s_0<\sigma _0(\varphi )$, and $s_1>\sigma _1(\varphi )$. Define $\psi$ as follows:

$$\begin{aligned} \psi (t):=\left\{ \begin{array}{cc} \tau ^{-s_0/(s_1-s_0)}\varphi (\tau ^{1/(s_1-s_0)}), &{} \tau \ge 1, \\ \varphi (1), &{} 0<\tau <1, \end{array}\right. \end{aligned}$$

(2.10)

Then, $\psi \in \mathcal {B}$ and $\psi$ is an interpolation parameter. Furthermore, with equality of norms, we have

$$\begin{aligned} {[}H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]_{\psi }=H^{\varphi }(\mathbb {Z}^n). \end{aligned}$$

2.12 Quadratic interpolation

Our next result shows that $\{H^{\varphi }(\mathbb {Z}^n):\varphi \in RO\}$ is closed with respect to interpolation with a function parameter. This result is an analogue of theorem 5.2 of [27] for the class $\{H^{\varphi }(\Omega ):\varphi \in RO\}$ where $\Omega \subset \mathbb {R}^n$ is a bounded domain with Lipschitz boundary.

Theorem 2.3

Assume that $\varphi _0,\,\varphi _1\in RO$ and $\frac{\varphi _0}{\varphi _1}$ is bounded in a neighborhood of $\infty$. Let $\psi \in \mathcal {B}$ be an interpolation parameter. Then, the following hold:

• (i) $[H^{\varphi _0}(\mathbb {Z}^n), H^{\varphi _1}(\mathbb {Z}^n)]$ is an admissible pair;

• (ii) up to the norm equivalence we have

  $$\begin{aligned}{}[H^{\varphi _0}(\mathbb {Z}^n), H^{\varphi _1}(\mathbb {Z}^n)]_{\psi }=H^{\varphi }(\mathbb {Z}^n), \end{aligned}$$

  (2.11)

where

$$\begin{aligned} \varphi (t):=\varphi _0(t)\psi \left( \frac{\varphi _1(t)}{\varphi _0(t)}\right) . \end{aligned}$$

(2.12)

2.13 Further properties of $H^{\varphi }(\mathbb {Z}^n)$

The next theorem summarizes additional properties of the class $\{H^{\varphi }(\mathbb {Z}^n):\varphi \in RO\}$. In the setting of $\mathbb {R}^n$, analogous properties were demonstrated in proposition 2 of [25].

Theorem 2.4

We have the following properties:

• (i) Assume that $\varphi \in RO$. Then $\mathcal {S}(\mathbb {Z}^n)$ is dense in $H^{\varphi }(\mathbb {Z}^n)$.

• (ii) Assume that $\varphi _0,\,\varphi _1\in RO$ and $\frac{\varphi _0}{\varphi _1}$ is bounded in a neighborhood of $\infty$. Then we have a continuous embedding $H^{\varphi _1}(\mathbb {Z}^n)\hookrightarrow H^{\varphi _0}(\mathbb {Z}^n)$.

• (iii) Assume that $\varphi \in RO$. Then, the sesquilinear form (2.1) extends to a sesquilinear duality (separately continuous sesquilinear form)

  $$\begin{aligned} (\cdot ,\cdot ):H^{\varphi }(\mathbb {Z}^n)\times H^{\frac{1}{\varphi }}(\mathbb {Z}^n)\rightarrow \mathbb {C}. \end{aligned}$$

  (2.13)

  The spaces $H^{\varphi }(\mathbb {Z}^n)$ and $H^{\frac{1}{\varphi }}(\mathbb {Z}^n)$ are mutually dual relative to (2.13).

• (iv) Assume that $\varphi \in RO$ satisfies

  $$\begin{aligned} \sum _{k\in \mathbb {Z}^n}\frac{1}{[\varphi (\langle k\rangle )]^2}<\infty , \end{aligned}$$

  (2.14)

  where $\langle k\rangle$ is as in (2.2). Then, we have a continuous embedding $H^{\varphi }(\mathbb {Z}^n)\hookrightarrow \ell ^{\infty }(\mathbb {Z}^n)$.

In our next result we establish a mapping property of pseudo-differential operators (PDO) acting on $H^{\varphi }(\mathbb {Z}^n)$. Before stating this result, we recall some elements of PDO calculus on $\mathbb {Z}^n$, as developed by the authors of [6].

2.14 Symbol classes

We begin with the definition of the symbol class $S^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$, as introduced in [6].

Definition 2.1

For $m\in \mathbb {R}$, the notation $S^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$ indicates the set of functions $a:\mathbb {Z}^n\times \mathbb {T}^n\rightarrow \mathbb {C}$ satisfying the following properties:

• (i) for all $k\in \mathbb {Z}^n$, we have $a(k,\cdot )\in C^{\infty }(\mathbb {T}^n)$;

• (ii) for all $\alpha ,\,\beta \in \mathbb {N}_0^{n}$, there exists a constant $C_{\alpha ,\beta }>0$ such that

  $$\begin{aligned} |D_{x}^{(\beta )}\Delta ^{\alpha }_{k}a(k,x)|\le C_{\alpha ,\beta }(1+|k|)^{m-|\alpha |}, \end{aligned}$$

  for all $(k,x)\in \mathbb {Z}^n\times \mathbb {T}^n$.

We new recall the definition of an elliptic symbol from [6].

Definition 2.2

For $m\in \mathbb {R}$, the elliptic symbol class $ES^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$ refers to the set of functions $a\in S^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$ satisfying the following property: there exist constants $C>0$ and $R>0$ such that

$$\begin{aligned} |a(k,x)|\ge C(1+|k|)^m, \end{aligned}$$

for all $x\in \mathbb {T}^n$ and all $k\in \mathbb {Z}^n$ such that $|k|>R$.

An important ingredient in the definition of a PDO on $\mathbb {Z}^n$ is the discrete Fourier transform, which we describe next.

2.15 Discrete Fourier transform

For $u\in \ell ^1(\mathbb {Z}^n)$, its discrete Fourier transform $\widehat{u}(x)$ is a function of $x\in \mathbb {T}^n$ defined as

$$\begin{aligned} \widehat{u}(x):=\sum _{k\in \mathbb {Z}^n}e^{-2\pi i k\cdot x}u(k), \end{aligned}$$

where $k\cdot x:=k_1x_1+k_2x_2+\dots +k_nx_n$. It turns out that the discrete Fourier transform can be extended to $\ell ^2(\mathbb {Z}^n)$, and by normalizing the Haar measure on $\mathbb {Z}^n$ and $\mathbb {T}^n$, the Plancherel formula takes the following form:

$$\begin{aligned} \sum _{k\in \mathbb {Z}^n}|u(k)|^2=\int _{\mathbb {T}^n}|\widehat{u}(x)|^2\,dx. \end{aligned}$$

The corresponding inversion formula looks as follows:

$$\begin{aligned} u(k)=\int _{\mathbb {T}^n}e^{2\pi i k\cdot x}\widehat{u}(x)\,dx,\qquad k\in \mathbb {Z}^n. \end{aligned}$$

(2.15)

2.16 Pseudo-differential operator

The pseudo-differential operator $T_{a}$ corresponding to $a\in S^m(\mathbb {Z}^n\times \mathbb {T}^n)$, also denoted as $\text {Op}[a]$, is defined as

$$\begin{aligned} (T_{a}u)(k):= \int _{\mathbb {T}^n} e^{2\pi i k\cdot x}a(k,x)\widehat{u}(x)\,dx,\quad u\in \mathcal {S}(\mathbb {Z}^n). \end{aligned}$$

(2.16)

In proposition 3.15 of [11], the authors showed that the operator $T_{a}$ maps $\mathcal {S}(\mathbb {Z}^n)$ into $\mathcal {S}(\mathbb {Z}^n)$. For a linear operator $P:\mathcal {S}(\mathbb {Z}^n)\rightarrow \mathcal {S}(\mathbb {Z}^n)$, its formal adjoint $P^{\dagger }$ is defined using the following relation:

$$\begin{aligned} (Pu,v)=(u, P^{\dagger } v), \end{aligned}$$

(2.17)

for all $u,\,v\in \mathcal {S}(\mathbb {Z}^n)$, where $(\cdot ,\cdot )$ is as in (2.1).

Finally, we note that the (linear) operator $T_{a}:\mathcal {S}(\mathbb {Z}^n)\rightarrow \mathcal {S}(\mathbb {Z}^n)$ extends to a (linear) operator

$$\begin{aligned} T_{a}:S'(\mathbb {Z}^n)\rightarrow S'(\mathbb {Z}^n) \end{aligned}$$

defined as follows:

$$\begin{aligned} (T_{a}F)(\overline{u}):=F\left( \overline{T_{a}^{\dagger }u}\right) , \qquad F\in \mathcal {S}'(\mathbb {Z}^n),\,\,u\in \mathcal {S}(\mathbb {Z}^n). \end{aligned}$$

(Here, $T_{a}^{\dagger }$ is the formal adjoint of $T_{a}$ and $\overline{z}$ is the conjugate of $z\in \mathbb {C}$.)

2.17 Mapping property of PDO on $\mathbb {Z}^n$

Our mapping property is an analogue of the property stated in Sect. 4 of [25] for the $\mathbb {R}^n$-setting.

Theorem 2.5

Assume that $a\in S^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$, where $m\in \mathbb {R}$. Let $\varphi \in RO$. Then $T_{a}$ extends to a bounded linear operator

$$\begin{aligned} T_{a}:H^{\varphi }(\mathbb {Z}^n)\rightarrow H^{t^{-m}\varphi }(\mathbb {Z}^n), \end{aligned}$$

where $t^{-m}\varphi$ denotes the product of the functions $t^{-m}$ and $\varphi$.

2.18 Fredholmness of PDO on $\mathbb {Z}^n$

Let $\mathscr {B}_{1}$ and $\mathscr {B}_{2}$ be Banach spaces and let $T:\mathscr {B}_{1}\rightarrow \mathscr {B}_{2}$ be a bounded linear operator. As in defintion 8.1 of [34], T is said to be a Fredhlom operator if the following conditions are satisfied: (i) $\dim (\text {Ker }T)<\infty$, (ii) $\text {Ran }T$ is closed, and (iii) $\dim (\text {Coker }T)<\infty$, where $\text {Coker}T:=\mathscr {B}_{2}/(\text {Ran } T)$.

Remark 2.4

Actually, for a bounded linear operator $T:\mathscr {B}_{1}\rightarrow \mathscr {B}_{2}$, the condition $\dim (\text {Coker }T)<\infty$ implies that $\text {Ran }T$ is closed; see lemma 8.1 in [34].

For a Fredholm operator $T:\mathscr {B}_{1}\rightarrow \mathscr {B}_{2}$, we define the index $\kappa (T)$ as

$$\begin{aligned} \kappa (T):=\dim (\text {Ker } T)-\dim (\text {Coker }T). \end{aligned}$$

Let $a\in S^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$ with $m\in \mathbb {R}$, and let $T_{a}$ and $T_{a}^{\dagger }$ be as in Sect. 2.16. In the formulation of the theorem we will use the following sets:

$$\begin{aligned} \mathscr {K}:=\{u\in H^{\infty }(\mathbb {Z}^n):T_{a}u=0\},\qquad \mathscr {K}^{\dagger }:=\{u\in H^{\infty }(\mathbb {Z}^n):(T_{a})^{\dagger }u=0\},\nonumber \\ \end{aligned}$$

(2.18)

where $H^{\infty }(\mathbb {Z}^n):=\cap _{r\in \mathbb {R}}H^{(r)}(\mathbb {Z}^n)$.

The following theorem is a discrete analogue of theorem 2.28 in [26] (or theorem 3 in [24]), which was situated in the setting of compact manifolds:

Theorem 2.6

Assume that $a\in ES^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$, where $m\in \mathbb {R}$ and $ES^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$ is as in Definition 2.2. Let $\varphi \in RO$ and let $t^{-m}\varphi$ denote the product of the functions $t^{-m}$ and $\varphi$. Then

$$\begin{aligned} T_{a}:H^{\varphi }(\mathbb {Z}^n)\rightarrow H^{t^{-m}\varphi }(\mathbb {Z}^n), \end{aligned}$$

is a (bounded) Fredholm operator. Furthermore, keeping in mind the notations (2.18), the following properties hold:

• (i) $\text {Ker } T_{a}=\mathscr {K}$;

• (ii) $\text {Ran } T_{a}=\{v\in H^{t^{-m}\varphi }(\mathbb {Z}^n):(v,w)=0,\,\,\text {for all }w\in \mathscr {K}^{\dagger }\}$, where $(\cdot ,\cdot )$ is the sesquilinear duality between $H^{t^{-m}\varphi }(\mathbb {Z}^n)$ and $H^{\frac{t^{m}}{\varphi }}(\mathbb {Z}^n)$, as described in (2.13);

• (iii) the index of $T_{a}$ is $\kappa (T_{a})=\dim (\mathscr {K})-\dim (\mathscr {K}^{\dagger })$. (Hence, $\kappa (T_{a})$ is independent of $\varphi$.)

In our last result we use the concept of “extended Hilbert scale” from [28].

2.19 Extended Hilbert Scale

In this section we follows the terminology from Sect. 2 of [28]. Let $\mathscr {H}$ be a separable complex Hilbert space with inner product $(\cdot ,\cdot )_{\mathscr {H}}$ and norm $\Vert \cdot \Vert _{\mathscr {H}}$. Let A be a self-adjoint operator in $\mathscr {H}$ such that $(Au,u)_{\mathscr {H}}\ge \Vert u\Vert ^2_{\mathscr {H}}$ for all $u\in {\text {Dom}}(A)$.

Using spectral calculus we define the operator $A^{s}$ for each $s\in \mathbb {R}$. Note that ${\text {Dom}}(A^s)$ is dense in $\mathscr {H}$; in particular, if $s\le 0$ we have ${\text {Dom}}(A^s)=\mathscr {H}$. The space $H_{A}^{(s)}$ is defined as the completion of ${\text {Dom}}(A^s)$ with respect to the inner product

$$\begin{aligned} (u,v)_{s}:=(A^su,A^sv)_{\mathscr {H}}, \qquad u,v\in {\text {Dom}}(A^s). \end{aligned}$$

It turns out that $H_{A}^{(s)}$ is a separable Hilbert space whose inner product and norm will be denoted by $(\cdot ,\cdot )_{s}$ and $\Vert \cdot \Vert _{s}$. We call $\{H_{A}^{(s)}:s\in \mathbb {R}\}$ Hilbert scale generated by A or, in shorter form, A-scale. As mentioned in Sect. 2 of [28], for $s\ge 0$ we have $H_{A}^{(s)}={\text {Dom}}(A^s)$, while for $s<0$ we have $H_{A}^{(s)}\supset \mathscr {H}$.

According to Sect. 2 of [28], for all $s_0<s_1$, $[H_{A}^{(s_0)},H_{A}^{(s_1)}]$ is an admissible pair (in the sense of Sect. 2.8 above). Recalling the definition of interpolation space (see Sect. 2.9 above), the term extended Hilbert scale generated by A or extended A-scale refers to the set of all Hilbert spaces that serve as interpolation spaces with respect to pairs of the form $[H_{A}^{(s_0)},H_{A}^{(s_1)}]$, $s_0<s_1$.

Remembering the hypotheses on A and using spectral calculus, for a Borel measurable function $\varphi :[1,\infty )\rightarrow (0,\infty )$, we can define a (positive self-adjoint) operator $\varphi (A)$ in $\mathscr {H}$. Furthermore, we define $H_{A}^{\varphi }$ as the completion of ${\text {Dom}}(\varphi (A))$ with respect to the inner product

$$\begin{aligned} (u,v)_{\varphi }:=(\varphi (A)u,\varphi (A)v)_{\mathscr {H}}, \qquad u,v\in {\text {Dom}}(\varphi (A)). \end{aligned}$$

According to Sect. 2 of [28], $H_{A}^{\varphi }$ is a separable Hilbert space, and its inner product and norm will be denoted by $(\cdot ,\cdot )_{\varphi }$ and $\Vert \cdot \Vert _{\varphi }$. Furthermore (see Sect. 2 of [28]), we have $H_{A}^{\varphi }={\text {Dom}}(\varphi (A))$ if and only if $0\notin \text {Spec}(\varphi (A))$.

2.20 Extended Hilbert scale on $\mathbb {Z}^n$

We make the following assumptions on our operator $A:=\text {Op}[a]$:

• (H1) $a\in ES^{1}(\mathbb {Z}^n\times \mathbb {T}^n)$, where $ES^{1}(\mathbb {Z}^n\times \mathbb {T}^n)$ is as in definition 2.2;

• (H2) $(Au,u)\ge \Vert u\Vert ^2$, for all $u\in \mathcal {S}(\mathbb {Z}^n)$, where $(\cdot ,\cdot )$ is as in (2.1) and $\Vert \cdot \Vert$ is the corresponding norm in $\ell ^2(\mathbb {Z}^n)$.

Remark 2.5

Under the assumptions (H1)–(H2), $A|_{\mathcal {S}(\mathbb {Z}^n)}$ is a formally self-adjoint operator whose symbol a belongs to the class $ES^{1}(\mathbb {Z}^n\times \mathbb {T}^n)$. Therefore (as a consequence of theorem 3.19 in [11]), the operator $A|_{\mathcal {S}(\mathbb {Z}^n)}$ is essentially self-adjoint in $\ell ^2(\mathbb {Z}^n)$. Furthermore, by proposition 3.18 from [11], the domain of the self-adjoint closure of A is the space $H^{(1)}(\mathbb {Z}^n)$. To keep our notations simpler, we denote the self-adjoint closure of $A|_{\mathcal {S}(\mathbb {Z}^n)}$ again by A. With this clarification, as in Sect. 2.19 above (now in the setting $\mathscr {H}=\ell ^2(\mathbb {Z}^n)$), for a Borel function $\varphi :[1,\infty )\rightarrow (0,\infty )$ we define the space $H_{A}^{\varphi }$ corresponding to an operator A satisfying (H1)–(H2).

The theorem below is an analogue of theorem 5.1 in [28] for the $\mathbb {R}^n$-setting.

Theorem 2.7

Let $\varphi \in RO$. Assume that $A:=\text {Op}[a]$ is an operator satisfying (H1)–(H2). Then, up to norm equivalence, we have

$$\begin{aligned} H^{\varphi }_{A}(\mathbb {Z}^n)=H^{\varphi }(\mathbb {Z}^n), \end{aligned}$$

(2.19)

where $H^{\varphi }_{A}(\mathbb {Z}^n)$ is as in Remark 2.5 and $H^{\varphi }(\mathbb {Z}^n)$ is as in Sect. 2.7.

Remark 2.6

The condition $a\in ES^{1}(\mathbb {Z}^n\times \mathbb {T}^n)$ in (H1) can be replaced by $a\in ES^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$, with $m>0$. In this case, the following variant of (2.19) holds: $H^{\varphi }_{A}(\mathbb {Z}^n)=H^{\varphi _{m}}(\mathbb {Z}^n)$, where $\varphi _{m}(t):=\varphi (t^m)$, $t\ge 1$.

3 Auxiliary results

In this section we collect various results from literature that are used in proofs of main results of this paper.

For future reference, we say that a Borel measurable function $\psi :(0,\infty )\rightarrow (0,\infty )$ is pseudoconcave in a neighborhood of $\infty$ if there exists a concave function $\psi _1 :(c,\infty )\rightarrow (0,\infty )$, where $c>1$ is a large number, such that $\frac{\psi }{\psi _1}$ and $\frac{\psi _1}{\psi }$ are bounded on $(c,\infty )$.

We begin with a proposition for which we refer to theorem 1.9 in [26].

Proposition 3.1

A function $\psi \in \mathcal {B}$ is an interpolation parameter if and only if $\psi$ is pseudoconcave in a neighborhood of $\infty$.

The next proposition, for which we refer to theorem 11.4.1 in [30], plays an important role in showing the implication (i)$\implies$(ii) of theorem 2.1.

Proposition 3.2

Let $\mathscr {H}=[\mathscr {H}_{0},\mathscr {H}_{1}]$ be an admissible pair of Hilbert spaces. Assume that a space $\mathscr {S}$ is an interpolation space for the pair $\mathscr {H}$. Then, up to the norm equivalence, we have $\mathscr {S}=\mathscr {H}_{\psi }$, for some function $\psi \in \mathcal {B}$ such that $\psi$ is pseudoconcave in a neighborhood of $\infty$.

For the proof of the following proposition, see theorem 4.2 in [27]:

Proposition 3.3

Let $s_0<s_1$ be two real numbers and let $\psi \in \mathcal {B}$. Define

$$\begin{aligned} \varphi (t):=t^{s_0}\psi (t^{s_1-s_0}),\quad t\ge 1. \end{aligned}$$

(3.1)

Then, the following are equivalent:

• (i) $\psi$ is an interpolation parameter;

• (ii) $\varphi$ satisfies (2.6) with some constant $c\ge 1$ independent of t and $\lambda$.

The key instrument for justifying the implication (ii)$\implies$(i) of Theorem 2.1 will be the next proposition (see the proof of the sufficiency part of theorem 2.4 in [27]):

Proposition 3.4

Assume that $\varphi \in RO$ satisfies the condition (2.6). Define $\psi$ as follows:

$$\begin{aligned} \psi (t):=\left\{ \begin{array}{cc} \tau ^{-s_0/(s_1-s_0)}\varphi (\tau ^{1/(s_1-s_0)}), &{} \tau \ge 1, \\ \varphi (1), &{} 0<\tau <1, \end{array}\right. , \end{aligned}$$

(3.2)

where $s_0<s_1$ are as in (2.6). Then the following properties hold:

• (i) $\psi \in \mathcal {B}$ and $\psi$ satisfies (3.1);

• (ii) $\psi$ is an interpolation parameter.

4 Proof of Theorem 2.1

We first prove a key proposition:

Proposition 4.1

Let $s_0<s_1$ be two real numbers and let $\psi \in \mathcal {B}$ be an interpolation parameter. Let $\varphi$ be as in (3.1).

Then the following properties hold:

• (i) $\varphi \in RO$;

• (ii) we have (with equality of norms)

  $$\begin{aligned}{}[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]_{\psi }=H^{\varphi }(\mathbb {Z}^n). \end{aligned}$$

  (4.1)

Proof

Part (i) was proved in lemma 1 of [25]. To prove part (ii), we use the definition of the space $[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]_{\psi }$ from Sect. 2.8. First, we recall (see Proposition 3.4 in [11] and Remark 2.2) that there is a continuous (and dense) embedding $H^{(s_1)}(\mathbb {Z}^n)\hookrightarrow H^{(s_0)}(\mathbb {Z}^n)$. Thus, $[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]$ is an admissible pair.

Remembering the definitions of the norms in $H^{(s_0)}(\mathbb {Z}^n)$ and $H^{(s_1)}(\mathbb {Z}^n)$ and taking into account remark 2.1, we see that the multiplication operator $Ju:=\langle k\rangle ^{s_1-s_0}u$ by the function $\langle k\rangle ^{s_1-s_0}$ constitutes a generating operator for the pair $[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]$.

As J is a multiplication operator by the function $\langle k\rangle ^{s_1-s_0}$, it follows that $\psi (J)$ is a multiplication operator by the function $\psi (\langle k\rangle ^{s_1-s_0})$. Denoting

$$\begin{aligned} \mathscr {H}:=[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)] \end{aligned}$$

and referring to the definitions (2.9), (2.3) and (2.8), for all $u\in S(\mathbb {Z}^n)$ we have

$$\begin{aligned}&\Vert u\Vert ^2_{\mathscr {H}_{\psi }}=\Vert \psi (J)u\Vert ^2_{H^{(s_0)}}=\Vert \psi (\langle k\rangle ^{s_1-s_0})u\Vert ^2_{H^{(s_0)}}\nonumber \\&=\Vert \langle k\rangle ^{s_0}\psi (\langle k\rangle ^{s_1-s_0})u\Vert ^2=\Vert \varphi (\langle k\rangle )u\Vert ^2=\Vert u\Vert ^2_{H^{\varphi }}, \end{aligned}$$

(4.2)

where the fourth equality follows from (3.1). Thus, we obtain (4.1) with equality of norms. (By remark 2.2, Schwartz space $S(\mathbb {Z}^n)$ is dense in the spaces $H^{(s_j)}(\mathbb {Z}^n)$, $j=0,1$, and, hence, in the interpolation space $[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]_{\psi }$.) This concludes the proof of the proposition. $\square$

Continuation of the Proof of Theorem 2.1

We first prove that (i) implies (ii). Since $\mathscr {S}$ is an interpolation space with respect to the pair $[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]$, for some $s_0<s_1$, we may apply proposition 3.2 to infer $\mathscr {S}=\mathscr {H}_{\psi }$, up to norm equivalence, where $\psi \in \mathcal {B}$ is pseudoconcave in a neighborhood of $\infty$. (By proposition 3.1, this means that $\psi$ is an interpolation parameter.) With $\psi \in \mathcal {B}$ at our disposal, define $\varphi$ by the formula (3.1). Next we apply proposition 3.3 to infer that the function $\varphi$ satisfies the condition (2.6), and, hence, $\varphi \in RO$. To conclude the proof of the implication, it remains to use proposition 4.1.

We now prove that (ii) implies (i). Let $\varphi \in RO$ be a function satisfying the condition (2.6), and define $\psi$ as in (3.2), with $s_0<s_1$ as in (2.6). By proposition 3.4 it follows that $\psi \in \mathcal {B}$ and $\psi$ is an interpolation parameter, and, moreover, $\psi$ satisfies the condition (3.1). To conclude the proof of the implication, it remains to apply proposition 4.1. $\square$

5 Proof of Corollary 2.1

The implication (i)$\implies$(ii) follows directly from theorem 2.1. We now prove the implication (ii)$\implies$(i). Let $\varphi \in RO$ and let $s_0<\sigma _0(\varphi )$ and $s_1>\sigma _1(\varphi )$. Then $\varphi$ satisfies the condition (2.6). Thus, by theorem 2.1, we have (up to norm equivalence) that $H^{\varphi }(\mathbb {Z}^n)$ is an interpolation space with respect to the pair $[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]$. Hence, up to norm equivalence, $H^{\varphi }(\mathbb {Z}^n)$ is an interpolation space with respect to the scale $\{H^{(s)}(\mathbb {Z}^n):s\in \mathbb {R}\}$. $\square$

6 Proof of Theorem 2.2

By proposition 3.4 we have $\psi \in \mathcal {B}$ and $\psi$ is an interpolation parameter. Furthermore, by the same proposition, $\psi$ satisfies (3.1). Therefore, theorem 2.2 follows from proposition 4.1. $\square$

7 Proof of Theorem 2.3

With theorem 2.2 at our disposal, the proof of theorem 2.3 we follows the scheme of [27] (see theorem 5.2 there) for the case $\Omega \subset \mathbb {R}^n$, where $\Omega$ is a bounded domain with Lipschitz boundary.

The following proposition can be found in [26] (see theorem 1.3 there):

Proposition 7.1

Assume that $\lambda ,\eta ,\psi \in \mathcal {B}$ and that $\frac{\lambda }{\eta }$ is bounded in a neighbourhood of $\infty$. Let $\mathscr {H}$ be an admissible pair of Hilbert spaces. Then, with the notations of Sect. 2.8, we have

• (i) $[\mathscr {H}_{\lambda }, \mathscr {H}_{\eta }]$ is an admissible pair;

• (ii) we have $[\mathscr {H}_{\lambda }, \mathscr {H}_{\eta }]_{\psi }= \mathscr {H}_{\omega }$, with norm equality, where

  $$\begin{aligned} \omega (t):= \lambda (t) \psi \left( \frac{\eta (t)}{\lambda (t)}\right) ,\qquad t>0. \end{aligned}$$

  (7.1)

• (iii) If $\lambda ,\eta ,\psi \in \mathcal {B}$ are interpolation parameters, then so is $\omega$.

The first step in the proof of theorem 2.3 is to choose numbers $s_0,\,s_1$ such that $s_0<\sigma _0(\varphi _j)$ and $s_1>\sigma _1(\varphi _j)$, $j=0,1$. With these $s_0$ and $s_1$, we define $\lambda _j$, $j=0,1$, as

$$\begin{aligned} \lambda _j(t):=\left\{ \begin{array}{cc} \tau ^{-s_0/(s_1-s_0)}\varphi _j(\tau ^{1/(s_1-s_0)}), &{} \tau \ge 1, \\ \varphi _j(1), &{} 0<\tau <1. \end{array}\right. \end{aligned}$$

(7.2)

Notice that $\frac{\lambda _0}{\lambda _1}$ is bounded in a neighborhood of $\infty$.

By theorem 2.2 we have

$$\begin{aligned}{}[[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]_{\lambda _0},[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]_{\lambda _1}]=[H^{\varphi _0}(\mathbb {Z}^n),H^{\varphi _1}(\mathbb {Z}^n)]. \end{aligned}$$

(7.3)

As the left hand side displays an admissible pair (see part (i) of proposition 7.1), the pair on the right hand side is also admissible. This proves part (i) of theorem 2.3.

Let $\psi$ be as in the hypothesis of theorem 2.3. Returning to (7.3) and interpolating with a function parameter $\psi$, we get (after appealing to part (ii) of proposition 7.1 with $\mathscr {H}=[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]$)

$$\begin{aligned} {[}H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]_{\omega }=[H^{\varphi _0}(\mathbb {Z}^n),H^{\varphi _1}(\mathbb {Z}^n)]_{\psi }, \end{aligned}$$

(7.4)

where (the interpolation parameter) $\omega$ is given by

$$\begin{aligned} \omega (t):=\varphi _0(t) \psi \left( \frac{\varphi _1(t)}{\varphi _0(t)}\right) ,\qquad t\ge 1. \end{aligned}$$

(7.5)

The same way as it was done in the proof of theorem 5.2 of [27], one can check that the function $\varphi$ from (2.12) satisfies the condition

$$\begin{aligned} \varphi (t)=t^{s_0}\omega (t^{s_1-s_0}),\quad t\ge 1. \end{aligned}$$

Therefore, by proposition 3.3 we have $\varphi \in RO$. Consequently, by proposition 4.1 we obtain

$$\begin{aligned}. [H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]_{\omega }=H^{\varphi }(\mathbb {Z}^n), \end{aligned}$$

which, upon taking into account (7.4), leads to (2.11). $\square$

8 Proof of Theorem 2.4

With theorem 2.2 and remark 2.2 at our disposal, the proofs of properties (i)–(iv) are relatively straightforward. We give the details below:

To prove part (i), start with $\varphi \in RO$ and select numbers $s_0,\,s_1$ such that $s_0<\sigma _0(\varphi )$ and $s_1>\sigma _1(\varphi )$. Defining $\psi$ as in (3.2), we have by theorem 2.2 that $\psi \in \mathcal {B}$ is an interpolation parameter and have $[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]_{\psi }=H^{\varphi }(\mathbb {Z}^n)$, with equality of norms. Referring to part (i) of the definition of the interpolation space (see Sect. 2.9), we have a continuous embedding

$$\begin{aligned} H^{(s_1)}(\mathbb {Z}^n)\hookrightarrow H^{\varphi }(\mathbb {Z}^n)\hookrightarrow H^{(s_0)}(\mathbb {Z}^n). \end{aligned}$$

Now the density of $S(\mathbb {Z}^n)$ in $H^{\varphi }(\mathbb {Z}^n)$ follows from remark 2.2 above.

To prove part (ii), first note that hypotheses of theorem 2.3 are satisfied. Thus, $[H^{\varphi _0}(\mathbb {Z}^n),H^{\varphi _1}(\mathbb {Z}^n)]$ is an admissible pair, and we have a continuous embedding $H^{\varphi _1}(\mathbb {Z}^n)\hookrightarrow H^{\varphi _0}(\mathbb {Z}^n)$.

For part (iii), we proceed similarly as in the proof of theorem 4.4 in [36] for the “refined Sobolev scale" on a compact manifold. First, according to lemma A.1 below, for all $s\in \mathbb {R}$ the sesquilinear form (2.1) extends to a sesquilinear duality (separately continuous sesquilinear form)

$$\begin{aligned} (\cdot ,\cdot ):H^{(s)}(\mathbb {Z}^n)\times H^{(-s)}(\mathbb {Z}^n)\rightarrow \mathbb {C}. \end{aligned}$$

(8.1)

The spaces $H^{(s)}(\mathbb {Z}^n)$ and $H^{(-s)}(\mathbb {Z}^n)$ are dual relative to the duality (A.1): for each $s\in \mathbb {R}$, the map $f(u):=(u,\cdot )$, with $u\in H^{(s)}(\mathbb {Z}^n)$, is an isomorphism $f:H^{(s)}(\mathbb {Z}^n)\rightarrow (\overline{H^{(-s)}(\mathbb {Z}^n)})'$, where $(\overline{H^{(-s)}(\mathbb {Z}^n)})'$ is the anti-dual space of $H^{(-s)}(\mathbb {Z}^n)$.

Let $\varphi \in RO$, let $s_0<\sigma _0(\varphi )$, $s_1>\sigma _1(\varphi )$, and let $\psi$ be as in (3.2). Thus, we have an isomorphism

$$\begin{aligned} f:[H^{(s_0)}(\mathbb {Z}^n),H^{(s_1)}(\mathbb {Z}^n)]_{\psi }=[(\overline{H^{(-s_0)}(\mathbb {Z}^n)})',(\overline{H^{(-s_1)}(\mathbb {Z}^n)})']_{\psi }. \end{aligned}$$

(8.2)

Moreover, by (abstract) theorem 1.4 in [26], we have

$$\begin{aligned} {[}(\overline{H^{(-s_0)}(\mathbb {Z}^n)})',(\overline{H^{(-s_1)}(\mathbb {Z}^n)})']_{\psi } =\left( \overline{[(H^{(-s_1)}(\mathbb {Z}^n)),(H^{(-s_0)}(\mathbb {Z}^n))]_{\widetilde{\psi }}}\right) ', \end{aligned}$$

(8.3)

where $\widetilde{\psi }:=\frac{t}{\psi (t)}$. Appealing again to theorem 1.4 from [26], $\widetilde{\psi }\in \mathcal {B}$ is an interpolation parameter.

Since $\psi$ satisfies (3.1) (as guaranteed by proposition 3.4), a quick check shows that $\widetilde{\varphi }:=\frac{1}{\varphi }$ satisfies

$$\begin{aligned} \widetilde{\varphi }(t)=t^{-s_1}\widetilde{\psi }(t^{-s_0-(-s_1)}). \end{aligned}$$

Therefore, by proposition 4.1, we have (with equality of norms)

$$\begin{aligned}{}[H^{(-s_1)}(\mathbb {Z}^n),H^{(-s_0)}(\mathbb {Z}^n)]_{\widetilde{\psi }}=H^{\frac{1}{\varphi }}(\mathbb {Z}^n). \end{aligned}$$

(8.4)

Combining (8.2), (8.3), (8.4) and recalling (see theorem 2.2) that

$$\begin{aligned} H^{\varphi }(\mathbb {Z}^n)=[H^{(s_0)}(\mathbb {Z}^n),H^{(s_1)}(\mathbb {Z}^n)]_{\psi }, \end{aligned}$$

we get an isomorphism

$$\begin{aligned} f:H^{\varphi }(\mathbb {Z}^n)\rightarrow \left( \overline{H^{\frac{1}{\varphi }}(\mathbb {Z}^n)}\right) '. \end{aligned}$$

Thus, up to norm equivalence, the spaces $H^{\varphi }(\mathbb {Z}^n)$ and $H^{\frac{1}{\varphi }}(\mathbb {Z}^n)$ are mutually dual with respect to the sesquilinear form (2.13).

Recall that lemma A.1 tells us that (A.1) is an extension by continuity of the form (2.1). Additionally, recall that we have continuous embeddings $H^{(s_1)}(\mathbb {Z}^n)\hookrightarrow H^{\varphi }(\mathbb {Z}^n)$ and $H^{(-s_0)}(\mathbb {Z}^n) \hookrightarrow H^{\frac{1}{\varphi }}(\mathbb {Z}^n)$. Therefore, the form (2.13) is an extension by continuity of the form (2.1).

To prove part (iv), note that

$$\begin{aligned} |u(k)|&\le \sum _{k\in \mathbb {Z}^n} |u(k)|=\sum _{k\in \mathbb {Z}^n}|u(k)|\varphi (\langle k \rangle )[\varphi (\langle k \rangle )]^{-1}\\&\le \left( \sum _{k\in \mathbb {Z}^n}[\varphi (\langle k \rangle )]^{-2}\right) ^{1/2}\left( \sum _{k\in \mathbb {Z}^n}|u(k)|^2[\varphi (\langle k \rangle )]^2\right) ^{1/2}\\&=C\Vert u\Vert _{H^{\varphi }}, \end{aligned}$$

where $0<C<\infty$ is a constant. Here, in the second estimate we used Cauchy–Schwarz inequality, and in the last equality we used the assumption (2.14) and the definition (2.8).

Therefore, we get $\Vert u\Vert _{\infty }\le C\Vert u\Vert _{H^{\varphi }}$, and this concludes the proof of part (iv). $\square$

9 Proof of Theorem 2.5

Let $\varphi \in RO$ and let $s_0<\sigma _0(\varphi )$ and $s_1>\sigma _1(\varphi )$. Let $T_{a}=\text {Op}[a]$ with $a\in S^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$, where $m\in \mathbb {R}$. Then, according to corollary 3.3 in [11] (or corollary 5.6 in [6]),

$$\begin{aligned} T_{a}:H^{(s_0)}(\mathbb {Z}^n)\rightarrow H^{(s_0-m)}(\mathbb {Z}^n),\qquad T_{a}:H^{(s_1)}(\mathbb {Z}^n)\rightarrow H^{(s_1-m)}(\mathbb {Z}^n) \end{aligned}$$

(9.1)

are bounded linear operators.

Defining $\psi$ as in (3.2) and referring to proposition 3.4 we see that $\psi \in \mathcal {B}$ is an interpolation parameter satisfying (3.1). Furthermore, by proposition 4.1 we have (with equality of norms)

$$\begin{aligned}{}[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]_{\psi }=H^{\varphi }(\mathbb {Z}^n). \end{aligned}$$

(9.2)

Setting $\widetilde{\varphi }:=t^{-m}\varphi$, we see that (3.1) can be written as

$$\begin{aligned} \varphi (t)=t^{s_0-m}t^{m}\psi (t^{(s_1-m)-(s_0-m)}), \end{aligned}$$

that is,

$$\begin{aligned} \widetilde{\varphi }(t)=t^{s_0-m}\psi (t^{(s_1-m)-(s_0-m)}). \end{aligned}$$

Thus, we may use proposition 4.1 with $s_0-m$ and $s_1-m$ in place of $s_0$ and $s_1$ respectively and with $\widetilde{\varphi }=t^{-m}\varphi$ in place of $\varphi$. Therefore, we get (with equality of norms)

$$\begin{aligned}{}[H^{(s_0-m)}(\mathbb {Z}^n), H^{(s_1-m)}(\mathbb {Z}^n)]_{\psi }=H^{t^{-m}\varphi }(\mathbb {Z}^n). \end{aligned}$$

(9.3)

Looking at (10.3), keeping in mind the Properties (9.2)–(9.3), and remembering the definition of interpolation space (see Sect. 2.9), we get a bounded linear operator

$$\begin{aligned} T_{a}:H^{\varphi }(\mathbb {Z}^n)\rightarrow H^{t^{-m}\varphi }(\mathbb {Z}^n), \end{aligned}$$

and this concludes the proof of the theorem. $\square$

10 Proof of Theorem 2.6

Let $\mathscr {B}_{1}$ and $\mathscr {B}_{2}$ be Banach spaces and let $T:\mathscr {B}_{1}\rightarrow \mathscr {B}_{2}$ be a bounded linear operator. The notation $(\mathscr {B}_{j})^{*}$ indicates the dual space of $\mathscr {B}_{j}$, $j=1,2$, and the notation $(v,f)_{j}$ describes the action of a functional $f\in (\mathscr {B}_{j})^{*}$ on a vector $v\in \mathscr {B}_{j}$ (Here, the form $(\cdot ,\cdot )_{j}$ is linear in the first variable and conjugate linear in the second variable.)

By the adjoint of T we mean a (bounded linear) operator $T^*:(\mathscr {B}_{2})^{*}\rightarrow (\mathscr {B}_{1})^{*}$ defined as follows:

$$\begin{aligned} (Tu,f)_{2}=(u, T^*f)_{1}, \qquad f\in (\mathscr {B}_{2})^{*},\,\, u\in \mathscr {B}_{1}. \end{aligned}$$

(10.1)

We now recall an abstract fact (see theorem 2.3.11 in [1]) regarding Fredholm operators (as defined in Sect. 2.18 above).

Proposition 10.1

Let $\mathscr {B}_{1}$ and $\mathscr {B}_{2}$ be Banach spaces and let $T:\mathscr {B}_{1}\rightarrow \mathscr {B}_{2}$ be a Fredholm operator. Then, $T^*$ is a Fredholm operator.

Furthermore, the following properties hold:

• (i) $\text {Ran } T=\{v\in \mathscr {B}_{2}:(v,g)_{2}=0,\,\,\text {for all }g\in \text {Ker }T^*\}$, where $(\cdot ,\cdot )_{2}$ is as in (10.1);

• (ii) $\text {Ker } T^{*}=\{g\in (\mathscr {B}_{2})^{*}:(v,g)_{2}=0,\,\,\text {for all }v\in \text {Ran }T\}$, where $(\cdot ,\cdot )_{2}$ is as in (10.1);

• (iii) the index of T is $\kappa (T)=\dim (\text {Ker }T)-\dim (\text {Ker }T^*)$.

The first step in proving theorem 2.6 is to establish the Fredholmness of an elliptic operator of order m in the Sobolev scale $H^{(s)}(\mathbb {Z}^n)$:

Proposition 10.2

Assume that $a\in ES^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$, where $m\in \mathbb {R}$ and $ES^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$ is as in Definition 2.2. Then, for all $s\in \mathbb {R}$,

$$\begin{aligned} T_{a}:H^{(s)}(\mathbb {Z}^n)\rightarrow H^{(s-m)}(\mathbb {Z}^n) \end{aligned}$$

is a (bounded) Fredholm operator. Furthermore, taking into account the notations (2.18), the following properties hold:

• (i) $\text {Ker } T_{a}=\mathscr {K}$;

• (ii) $\text {Ran } T_{a}=\{v\in H^{(s-m)}(\mathbb {Z}^n):(v,w)=0,\,\,\text {for all }w\in \mathscr {K}^{\dagger }\}$, where $(\cdot ,\cdot )$ is the sesquilinear duality between $H^{(s-m)}(\mathbb {Z}^n)$ and $H^{(-s+m)}(\mathbb {Z}^n)$, as described in (A.1).

• (iii) the index of $T_{a}$ is $\kappa (T_{a})=\dim (\mathscr {K})-\dim (\mathscr {K}^{\dagger })$. (Hence, $\kappa (T_{a})$ is independent of s.)

Proof

The Fredholmness assertion is justified by using the same argument as in theorem 4.2 of [11] for the case of $m=s=0$. For completeness, we outline the proof based on an abstract fact due to Atkinson (see propsition 8.2 in [34]), according to which it is enough to show that we can find a bounded linear operator $B:H^{(s-m)}(\mathbb {Z}^n)\rightarrow H^{(s)}(\mathbb {Z}^n)$ and compact operators $K_1:H^{(s)}(\mathbb {Z}^n)\rightarrow H^{(s)}(\mathbb {Z}^n)$ and $K_2:H^{(s-m)}(\mathbb {Z}^n)\rightarrow H^{(s-m)}(\mathbb {Z}^n)$ such that

$$\begin{aligned} BT_{a}=I+K_{1},\qquad T_{a}B=I+K_{2}, \end{aligned}$$

(10.2)

where I indicates (by slight abuse of notation) the identity operators on $H^{(s)}(\mathbb {Z}^n)$ and $H^{(s-m)}(\mathbb {Z}^n)$.

Since $T_{a}$ is an elliptic operator of order m, theorem 3.6 in [6] grants us a parametrix $T_{b}$ with $b\in S^{-m}(\mathbb {Z}^n\times \mathbb {T}^n)$ such that

$$\begin{aligned} T_{b}T_{a}=I+K_{1},\qquad T_{a}T_{b}=I+K_{2}, \end{aligned}$$

where $K_1$ and $K_2$ are operators whose symbols belong to $\cap _{r\in \mathbb {R}}S^{r}(\mathbb {Z}^n\times \mathbb {T}^n)$.

Thus, $T_{b}$ plays the role of the operator B in (10.2). It remains to show that $K_1:H^{(s)}(\mathbb {Z}^n)\rightarrow H^{(s)}(\mathbb {Z}^n)$ and $K_2:H^{(s-m)}(\mathbb {Z}^n)\rightarrow H^{(s-m)}(\mathbb {Z}^n)$ are compact operators, which will do just for $K_1$ (as $K_2$ can be handled in the same way).

First, note that for all $t>s$, $K_1:H^{(s)}(\mathbb {Z}^n)\rightarrow H^{(t)}(\mathbb {Z}^n)$ is a bounded linear operator (because the symbol of $K_1$ belongs to $\cap _{r\in \mathbb {R}}S^{r}(\mathbb {Z}^n\times \mathbb {T}^n)$). Furthermore, by theorem 3.5 in [11], for all $t>s$ the inclusion

$$\begin{aligned} \iota :H^{(t)}(\mathbb {Z}^n)\rightarrow H^{(s)}(\mathbb {Z}^n) \end{aligned}$$

is a compact operator.

Therefore, writing $K_1=\iota K_1$, we infer that $K_1:H^{(s)}(\mathbb {Z}^n)\rightarrow H^{(s)}(\mathbb {Z}^n)$ is a compact operator, which concludes the proof of the Fredholmness property for $T_{a}$.

To prove the property (i), it is enough to observe that for $a\in ES^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$ we can use elliptic regularity to show that $T_{a}u=0$ implies $u\in \cap _{r\in \mathbb {R}}H^{(r)}(\mathbb {Z}^n)=H^{\infty }(\mathbb {Z}^n)$. The property (ii) follows from part (i) of proposition 10.1, lemma A.1, and the fact that $(T_{a})^{\dagger }u=0$ implies $u\in \cap _{r\in \mathbb {R}}H^{(r)}(\mathbb {Z}^n)=H^{\infty }(\mathbb {Z}^n)$ (because $(T_{a})^{\dagger }$ is also an elliptic operator of order m). With this information, the property (iii) follows from part (iii) of proposition 10.1. $\square$

Before proving theorem 2.6, we recall the following interpolation property (see Theorem 1.7 in [26]), with the terminology as in Sects. 2.8 and 2.9.

Proposition 10.3

Let $\mathscr {H}:=[\mathscr {H}_{0},\mathscr {H}_{1}]$ and $\mathscr {G}:=[\mathscr {G}_{0},\mathscr {G}_{1}]$ be two admissible pairs of Hilbert spaces, and let $\psi \in \mathcal {B}$ be an interpolation parameter, where the class $\mathcal {B}$ is as in Sect. 2.8. Assume that T is a linear operator acting on $\mathscr {H}_{0}$ and satisfying the following properties:

• (i) the restrictions of T to the spaces $\mathscr {H}_{j}$, with $j=0,1$, are bounded Fredholm operators $T:\mathscr {H}_{j}\rightarrow \mathscr {G}_{j}$, $j=0,1$;

• (ii) the operators $T:\mathscr {H}_{j}\rightarrow \mathscr {G}_{j}$, $j=0,1$, have a common kernel;

• (iii) the operators $T:\mathscr {H}_{j}\rightarrow \mathscr {G}_{j}$, $j=0,1$, have the same index.

Then, the restriction of T to the interpolation space $\mathscr {H}_{\psi }$ is a bounded Fredholm operator $T:\mathscr {H}_{\psi }\rightarrow \mathscr {G}_{\psi }$ whose kernel and the index are the same as those of the operators $T:\mathscr {H}_{j}\rightarrow \mathscr {G}_{j}$, $j=0,1$.

Furthermore, we have $T(\mathscr {H}_{\psi })=\mathscr {G}_{\psi }\cap T(\mathscr {H}_{0})$.

Continuation of the Proof of Theorem 2.6

Let $\varphi \in RO$ and let $s_0<\sigma _0(\varphi )$ and $s_1>\sigma _1(\varphi )$. Since $a\in ES^{m}(\mathbb {Z}^n\times \mathbb {T}^n)$, $m\in \mathbb {R}$, we can use proposition 10.2 to infer that

$$\begin{aligned} T_{a}:H^{(s_0)}(\mathbb {Z}^n)\rightarrow H^{(s_0-m)}(\mathbb {Z}^n),\qquad T_{a}:H^{(s_1)}(\mathbb {Z}^n)\rightarrow H^{(s_1-m)}(\mathbb {Z}^n) \end{aligned}$$

(10.3)

are bounded Fredholm operators, with a common kernel and index (as described in items (i) and (iii) of proposition 10.2).

Defining $\psi$ as in (3.2) and referring to proposition 3.4 we see that $\psi \in \mathcal {B}$ is an interpolation parameter satisfying (3.1). Thus, according to (9.2) and (9.3) we have

$$\begin{aligned}{}[H^{(s_0)}(\mathbb {Z}^n), H^{(s_1)}(\mathbb {Z}^n)]_{\psi }=H^{\varphi }(\mathbb {Z}^n) \end{aligned}$$

and

$$\begin{aligned}{}[H^{(s_0-m)}(\mathbb {Z}^n), H^{(s_1-m)}(\mathbb {Z}^n)]_{\psi }=H^{t^{-m}\varphi }(\mathbb {Z}^n). \end{aligned}$$

Thus, we can apply proposition 10.3 to infer that

$$\begin{aligned} T_{a}:H^{\varphi }(\mathbb {Z}^n)\rightarrow H^{t^{-m}\varphi }(\mathbb {Z}^n) \end{aligned}$$

is a bounded Fredholm operator whose kernel and index are described in items (i) and (iii) of proposition 10.2. This proves the Fredholmness property and the assertions (i) and (iii) of the theorem.

We now justify assertion (ii) of the theorem. By the last sentence in proposition 10.3, we have

$$\begin{aligned} T_{a}(H^{\varphi }(\mathbb {Z}^n))= H^{t^{-m}\varphi }(\mathbb {Z}^n)\cap T(H^{(s_0)}(\mathbb {Z}^n)). \end{aligned}$$

Combining this equality with item (ii) of proposition 10.2 (with $s_0$ in place of s) and using the fact that $H^{t^{-m}\varphi }(\mathbb {Z}^n)\subset H^{(s_0-m)}(\mathbb {Z}^n)$, we obtain

$$\begin{aligned} \text {Ran } T_{a}=\{v\in H^{t^{-m}\varphi }(\mathbb {Z}^n):(v,w)=0,\,\,\text {for all }w\in \mathscr {K}^{\dagger }\}, \end{aligned}$$

where $\mathscr {K}^{\dagger }$ is as in (2.18). This concludes the proof of the theorem $\square$

11 Proof of Theorem 2.7

The following abstract result was established in theorem 2.5 of [28]:

Proposition 11.1

Let $\varphi \in RO$, $s_0<\sigma _0(\varphi )$, and $s_1>\sigma _1(\varphi )$. Let $\psi$ be as in (3.2). Let $H^{(s_j)}_{A}$, $j=0,1$, and $H^{\varphi }_{A}$ be as in Sect. 2.19.

Then, $\psi \in \mathcal {B}$ and $\psi$ is an interpolation parameter. Furthermore, we have (with equality of norms)

$$\begin{aligned}{}[H^{(s_0)}_{A}, H^{(s_1)}_{A}]_{\psi }=H^{\varphi }_{A}. \end{aligned}$$

Let us go back to the setting of theorem 2.7, as described in Sect. 2.20.

Lemma 11.1

Assume that $A:=\text {Op}[a]$ satisfies the hypotheses (H1)–(H2). Then, up to norm equivalence, we have

$$\begin{aligned} H_{A}^{(k)}(\mathbb {Z}^n)=H^{(k)}(\mathbb {Z}^n),\quad \text {for all }k\in \mathbb {Z}. \end{aligned}$$

Proof

It is enough to show the result for $k\in \mathbb {N}_{0}$, as the case $k=-1,-2,\dots$ follows by duality from the case $k\in \mathbb {N}$. The case $k=0$ is obviously true. Therefore, we need to consider the case $k\in \mathbb {N}$ only.

Remembering the hypotheses (H1)–(H2) and Remark 2.5, we see that A is a positive self-adjoint operator in $\ell ^2(\mathbb {Z}^n)$ such that ${\text {Dom}}(A)=H^{(1)}(\mathbb {Z}^n)$. Therefore A establishes an isomorphism $A:H^{(1)}(\mathbb {Z}^n)\rightarrow \ell ^2(\mathbb {Z}^n)$. Taking into account the definition of $H^{(1)}_{A}(\mathbb {Z}^n)$, we infer that $H^{(1)}_{A}(\mathbb {Z}^n)=H^{(1)}(\mathbb {Z}^n)$, up to norm equivalence.

As in the case of pseudo-differential operators on $\mathbb {R}^n$ (with symbols in the uniform Hörmander class), we have the following “elliptic regularity" property for $A=\text {Op}[a]$ with $a\in ES^{1}(\mathbb {Z}^n\times \mathbb {T}^n)$: If $s>1$ and if $u\in H^{(1)}(\mathbb {Z}^n)$ satisfies $Au\in H^{(s-1)}(\mathbb {Z}^n)$, then $u\in H^{(s)}(\mathbb {Z}^n)$. (Theorem 3.6 in [6] guarantees the existence of (a unique) parametrix $B=\text {Op}[b]$ with $b\in S^{-1}(\mathbb {Z}^n\times \mathbb {T}^n)$. Then, the mentioned “elliptic regularity" property follows by using the usual parametrix-type argument.)

Using the “elliptic regularity" property and the mentioned isomorphism

$$\begin{aligned} A:H^{(1)}(\mathbb {Z}^n)\rightarrow \ell ^2(\mathbb {Z}^n), \end{aligned}$$

we infer that $A^k$ gives rise to an isomorphism

$$\begin{aligned} A^k:H^{(k)}(\mathbb {Z}^n)\rightarrow \ell ^2(\mathbb {Z}^n). \end{aligned}$$

(11.1)

Using the isomorphism (11.1) and the definition of $H^{(k)}_{A}(\mathbb {Z}^n)$, we arrive at $H^{(k)}_{A}(\mathbb {Z}^n)=H^{(k)}(\mathbb {Z}^n)$, up to norm equivalence. $\square$

Continuation of the Proof of Theorem 2.7

Let $\varphi \in RO$, let $k\in \mathbb {N}$ be a number such that $-k<\sigma _0(\varphi )$ and $k>\sigma _1(\varphi )$. Define $\psi$ as in (3.2) with $s_0=-k$ and $s_1=k$. Proposition 11.1 tells us that (up to norm equivalence)

$$\begin{aligned}{}[H^{(-k)}_{A}, H^{(k)}_{A}(\mathbb {Z}^n)]_{\psi }=H^{\varphi }_{A}(\mathbb {Z}^n). \end{aligned}$$

(11.2)

Taking into account (11.2) and lemma 11.1 we obtain, up to norm equivalence,

$$\begin{aligned} {[}H^{(-k)}(\mathbb {Z}^n), H^{(k)}(\mathbb {Z}^n)]_{\psi }=H^{\varphi }_{A}(\mathbb {Z}^n). \end{aligned}$$

On the other hand, theorem 2.2 tells us that

$$\begin{aligned} H^{\varphi }(\mathbb {Z}^n)=[H^{(-k)}(\mathbb {Z}^n), H^{(k)}(\mathbb {Z}^n)]_{\psi }. \end{aligned}$$

Therefore, we have (up to norm equivalence), $H^{\varphi }_{A}(\mathbb {Z}^n)=H^{\varphi }(\mathbb {Z}^n)$. $\square$

Anti-duality between discrete Sobolev spaces

In this section we adapt the proof of lemma 4.4.4 in [4] to discrete Sobolev spaces.

We begin with a brief review of terminology. Denote by $\overline{V}$ the conjugate of a (complex) vector space V. Viewed as real vector spaces, $\overline{V}$ and V are the same. The only difference is that the multiplication of a vector $v\in \overline{V}$ by a scalar $z\in \mathbb {C}$ is defined as $\overline{z}v$, where $\overline{z}$ is the conjugate of z. The space of linear (respectively, anti-linear) functionals on V will be denoted by $V^{'}$ (respectively, $(\overline{V})^{'}$).

Let $V_1$ and $V_2$ be two topological (complex) vector spaces. By a pairing of $V_1$ and $V_2$ we mean a continuous sesquilinear map $B:V_1\times V_2\rightarrow \mathbb {C}$. (Here, “sesquilinear" means linear in the first and anti-linear in the second slot.) The pairing B gives rise to continuous linear maps $\tau :V_1\rightarrow (\overline{V_2})^{'}$ and $\kappa :\overline{V_2}\rightarrow V_{1}^{'}$ as follows:

$$\begin{aligned} \tau (u):=B(u,\cdot )\,\qquad \kappa (v):=B(\cdot , v). \end{aligned}$$

The pairing B is said to be perfect if $\tau$ and $\kappa$ are (linear) isomorphisms.

Lemma A.1

Let $s\in \mathbb {R}$. Then the $\ell ^2$-inner product (2.1), initially considered on $\mathcal {S}(\mathbb {Z}^n)\times \mathcal {S}(\mathbb {Z}^n)$, extends to a (continuous sesquilinear) pairing

$$\begin{aligned} (\cdot ,\cdot ):H^{(s)}(\mathbb {Z}^n)\times H^{(-s)}(\mathbb {Z}^n)\rightarrow \mathbb {C}. \end{aligned}$$

(A.1)

The pairing $(\cdot ,\cdot )$ is perfect and induces isometric (linear) isomorphisms $\overline{H^{(-s)}(\mathbb {Z}^n)}\cong (H^{(s)}(\mathbb {Z}^n))^{'}$ and $H^{(s)}(\mathbb {Z}^n)\cong (\overline{H^{(-s)}(\mathbb {Z}^n)})^{'}$.

Proof

Let $(\cdot ,\cdot )$ be as in (2.1) and let $\langle k\rangle$ be as in (2.2). For all $u,v\in \mathcal {S}(\mathbb {Z}^n)$ we have

$$\begin{aligned} |(u,v)|=|(\langle k\rangle ^s u,\langle k\rangle ^{-s} v)|\le \Vert \langle k\rangle ^s u\Vert \Vert \langle k\rangle ^{-s}v\Vert =\Vert u\Vert _{H^{(s)}}\Vert v\Vert _{H^{(-s)}}, \end{aligned}$$

(A.2)

where we used Cauchy–Schwarz inequality in $\ell ^2(\mathbb {Z}^n)$.

As $\mathcal {S}(\mathbb {Z}^n)$ is dense in the spaces $H^{\pm s}(\mathbb {Z}^n)$ (see lemma 3.16 in [11]), from (A.2) we infer that the $\ell ^2$-inner product extends to a (continuous sesquilinear) pairing $(\cdot ,\cdot ):H^{(s)}(\mathbb {Z}^n)\times H^{(-s)}(\mathbb {Z}^n)\rightarrow \mathbb {C}$.

Additionally, from (A.2) we obtain

$$\begin{aligned} \Vert u\Vert _{H^{(s)}}=\sup \{|(u,v)|:v\in \mathcal {S}(\mathbb {Z}^n) \text { and } \Vert v\Vert _{H^{(-s)}}=1\}. \end{aligned}$$

(A.3)

Using the density of $\mathcal {S}(\mathbb {Z}^n)$ in the space $H^{(-s)}(\mathbb {Z}^n)$, observe that the right hand side of (A.3) is equal to the norm of the functional $\tau (u)\in (\overline{H^{(-s)}(\mathbb {Z}^n)})^{'}$ corresponding to $u\in H^{(s)}(\mathbb {Z}^n)$ via $\tau (u):=(u,\cdot )$. Therefore, $\tau :H^{(s)}(\mathbb {Z}^n)\rightarrow (\overline{H^{(-s)}(\mathbb {Z}^n)})^{'}$ is an isometry.

In the same way, using (A.2) we can show that the map $\kappa :\overline{H^{(-s)}(\mathbb {Z}^n)}\rightarrow (H^{(s)}(\mathbb {Z}^n))^{'}$ defined as $\kappa (v):=(\cdot ,v)$ is an isometry.

In particular, the maps $\tau$ and $\kappa$ are injective. From the injectivity of $\kappa$ we infer that the range of $\tau$ is dense in $(\overline{H^{(-s)}(\mathbb {Z}^n)})^{'}$. As $\tau$ is an isometry, it follows that $\tau$ is surjective. Therefore, $\tau$ is an isometric isomorphism. In the same way, we can show that $\kappa$ is an isometric isomorphism. $\square$