1 Introduction

Algebraic reasoning is a cognitive activity organised around noticing and expressing generality (Kaput, 2008). In the functional thinking approach to early algebra, children generalise with the idea of function and express generality with representations such as tables, natural language, and symbolic notation. There are illuminating accounts of how elementary students can develop generalisation skills and algebraic conceptions (Blanton et al., 2015a, 2015b; Pinto & Cañadas, 2019; Stephens et al., 2017). However, there are open issues regarding the learning mechanisms that support such development. In particular, the conceptual changes in the transition from arithmetic to functional thinking are still unclear.

Consider that the concepts required for noticing and expressing generalisation have no precedent in students’ knowledge of number and arithmetic (Martinez & Brizuela, 2006; Tanışlı, 2011). Therefore, functional thinking not only extends the current mathematical knowledge of elementary students. It is a radical reorganisation of their mathematical cognition. How can children build upon arithmetic knowledge to construct the abstract algebraic concepts involved in functional thinking?

Fischbein (1975) defines intuitions as “a kind of knowledge which is not based on scientific empirical evidence or on rigorous logical arguments and, despite all this, one tends to accept it as certain and evident” (p. 26). In this paper we explore the pre-instructional intuitions that ground the transition from arithmetic to functional thinking. Our work is based upon the Framework Theory Approach to Conceptual Change (Vosniadou, 2017). We use a mixed-methods design to examine how students without early algebra instruction respond to generalisation tasks that tap into different levels of functional thinking (McEldoon & Rittle-Johnson, 2010).

2 Literature review

2.1 The transition from arithmetic to algebra

The transition from arithmetic to working with algebraic representations, objects, and operations has attracted much attention since the 1980s. Kieran (1981) uncovered two notions of equality in the thinking of secondary students. In the arithmetic notion, students interpreted the equal sign as an operator that indicates executing the chain of operations on the left side and writing the numerical result on the right side, as in \(5+4-1=8\). In the algebraic conception, the equal sign denotes equivalence, as in \(3 (x+2) = 3x+6\). Filloy and Rojano (1989) pointed to conceptual, symbolic, and operational changes related to working with unknown quantities, which are crucial for learning algebraic methods of solving equations.

Booth (1984) and Küchemann (1981) identified that students aged 11–16 read algebraic expressions and symbols with numerical views or using either algebraic or idiosyncratic interpretations of variables. Küchemann (1981) categorised students’ interpretations of the letters as follows: letters evaluated, letters not used, letters as objects, letters as specific unknowns, letters as generalised numbers, and letters as variables. Sfard and Linchevski (1994) proposed that the transition to algebra is a reification process. Rojano and Sutherland (2001) analysed the nature of symbolic algebraic methods in contrast to arithmetic methods.

This literature suggests that arithmetic knowledge obstructs the assimilation of algebraic concepts and methods. How does arithmetic knowledge interfere with early algebra learning?

In line with the idea of ‘extracting the algebraic from the arithmetic’, current early algebra views emphasise the relevance of explicitly teaching the properties of numbers and their operations. Numerous studies have confirmed the feasibility of this approach. These investigations have focused on nurturing functional thinking (e.g., Blanton et al., 2015a, 2015b; Cañadas et al., 2016; Carraher et al., 2008). However, there is space for more studies directed at explaining how students mobilise their numerical knowledge during the transition from arithmetic to functional thinking.

2.2 The transition from arithmetic to functional thinking

Blanton and Kaput (2011) conceptualise functional thinking as “… building and generalising patterns and relationships, using diverse linguistic and representational tools and treating generalised relationships, or functions, that result as mathematical objects useful in their own right” (p. 8). Below, we review literature about the initial understandings of generalisation and symbolic notation.

2.2.1 Initial understandings of generality

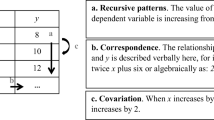
Different accounts of how children begin generalising are available. The literature establishes three approaches to generalisation, namely, recursive patterning, covariation, and correspondence. Carraher et al., (2008) defined recursive patterning as a process that “runs again and again”, as in number sequences like \({a}_{n}\to {a}_{n+1}\). According to Confrey and Smith (1991), covariation is noticing how quantities change together, for example \({a}_{n} \to {a}_{n +1}\) and \(f({a}_{n})\) \(\to\) \(f({a}_{n + 1})\); and correspondence is linking quantities by forming pairs, e.g., \({a}_{n} \to f({a}_{n})\).

Students can learn about generalisation approaches with various visual representations (Carraher et al., 2008; Rivera & Becker, 2011). However, tables are prominent in the literature. If children attend to the spatial organisation of numbers, they can focus on noticing functional patterns and expressing generalisation (Carraher et al., 2008; Pinto et al., 2021; Wilkie, 2016).

However, generalising around function tables is not trivial. Some studies suggest that children begin generalising with recursive patterning before adopting covariational and correspondence approaches. For example, in teaching experiments such as those conducted by Brizuela et al. (2015) and Tanışlı (2011), children started working with recursive patterns or numerical relationships between specific quantities. Children needed much guidance to discover covariation and correspondence approaches.

In contrast, other studies suggested that recursive patterning is not necessarily the beginning. Blanton et al. (2015a, 2015b) and Pinto and Cañadas (2019) observed how students could begin generalising with covariation and correspondence approaches.

Students can also begin to generalise with hybrid forms of reasoning (Carraher et al., 2008; Tanışlı, 2011). For example, Martinez and Brizuela (2006) examined a child using a table to define the number of people that can seat in a restaurant depending on the number of tables. The child introduced a sequence between the number of tables and the number of people seated. This strategy is recursive because it involves a number sequence. It is also functional because it works for defining output numbers.

Covariation and correspondence approaches to generalisation are counterintuitive. Children’s initial attempts to generalise with these approaches involve forms of reasoning and misconceptions that remain unexplained.

2.2.2 Initial understandings of symbolic notation

Symbolic notation is the highest level of functional thinking, located above skills such as defining missing numbers with a function rule, or expressing function rules with words (McEldoon & Rittle-Johnson, 2010). Children can express generalisation with non-symbolic representations (Radford, 2011). There is, however, much interest in introducing symbolic expressions in the elementary grades (e.g., Cooper & Warren, 2008; Kaput et al., 2008a, 2008b).

The literature about symbol sense in functional thinking focuses on acquiring two notions. First, students must shift from focusing on specific quantities to generalising relations between number sets. Then they can form a placeholder for any number in a set; that is, they form the notion of variable as an indeterminate quantity (Molina et al., 2018). Second, students need a way of representing indeterminate quantities in a unitary form (Kaput et al., 2008a, 2008b).

Symbolic skills do not emerge spontaneously without instruction. However, illuminating interventions like those introduced by Blanton et al., (2015a, 2015b) and Carraher et al. (2006) show that students acquire symbolisation skills with proper teaching and materials. However, symbolic notation is a concept hard to acquire.

Brizuela et al. (2015) guided students to organise functional data with tables and then asked them to formulate a function rule. Some students rejected the use of letters and numbers in the same expression. Others used letters diversely, as labels, objects, or representing quantitative relations using the ordinal relations between letters. Molina et al. (2018) also found that many students rejected symbols when asked to express symbolic rules for the first time. Some assigned to the letter a fixed quantity based on its position in the alphabet; others used letters to represent a fixed quantity with an arbitrary value. Some ‘early adopters’ represented indeterminate quantities with symbols.

These studies illustrate that symbolic notation is counterintuitive for most elementary students. There is, however, much uncertainty regarding the cognitive shifts involved in constructing concepts that lie at the core of symbol sense, such as variable and variable notation.

2.3 A conceptual change perspective on the arithmetic to functional thinking transition

Combining existing knowledge is not the only way to construct new concepts. We can construct new conceptual systems incommensurable with the ones we already possess (Carey, 2009). In cognitive development, conceptual change happens when children re-assign a concept to a different ontological category or construct a new one (Carey & Spelke, 1994). This kind of conceptual change happens without instruction, for example, during the formation of a naïve theory of biology (Inagaki & Hatano, 2008). In instruction-based learning, conceptual change involves radical cognitive shifts experienced after exposure to counterintuitive science and mathematics concepts (Vosniadou, 2017). This kind of conceptual change produces concepts that cannot emerge spontaneously. Such is the case for algebra concepts.

2.3.1 The framework theory approach to conceptual change

In this paper we investigate the conceptual changes in the transition from arithmetic to functional thinking, focusing on noticing and expressing generalisation. Our theoretical framework is the Framework Theory Approach to Conceptual Change. This approach is suitable for our study because it was developed to describe and explain conceptual changes required for learning counterintuitive concepts in science and mathematics (Vamvakoussi et al., 2018).

The Framework Theory Approach to Conceptual Change predicts that, when exposed to counterintuitive concepts, students use constructive learning mechanisms to connect new information with their prior knowledge, organising “… their intuitive understandings in loose and narrow but nevertheless relatively cohesive framework theories” (Vosniadou, 2019, p. 3).

Framework theories support explanations and predictions. However, these theories lack formal consistency and explanatory power; and are expected to include misconceptions. These misconceptions are not accidental, but the product of hybrid conceptions children construct to connect new scientific or mathematical information with their prior knowledge (Vosniadou, 2017).

Learners change some parts of their framework theory to assimilate counterintuitive information. These changes result in hybrid conceptions characterised as fragmented or synthetic. Fragmented conceptions lack coherence or explanatory power. Synthetic conceptions are erroneous hybridisations of initial and scientific understandings that possess explanatory power and internal consistency. These are, in a way, the seeds of learning.

2.3.2 A framework theory view of functional thinking

The Framework Theory Approach to Conceptual Change proposes a perspective on learning mathematics that can help us to gain insights into why noticing and expressing generalisation are counterintuitive. Vosniadou (2017) argued that learning mathematics is partly a conceptual change process. Children’s mathematical knowledge begins and develops around the concept of natural number. The capacity for processing magnitudes emerges very early. Children use it to perform approximate estimation, addition, and subtraction before mathematics instruction (Spelke, 2011). In preschool, children master the counting principles that support arithmetic inference (Leslie et al., 2008).

Then, the first years of elementary instruction focus on arithmetic, reinforcing coherent explanatory frameworks based on natural number properties (Vosniadou et al., 2008). These frameworks can inhibit the acquisition of more abstract mathematical concepts, like rational numbers (Vamvakoussi et al., 2018) and variables (Christou & Vosniadou, 2012).

We argue that functional thinking requires the learning of counterintuitive concepts incommensurable with children’s arithmetic knowledge. For example, the concept of variable is absent in traditional elementary mathematics curricula, which focus on natural number arithmetic. In the arithmetic domain, numbers are the product of counting, patterning, or computing. Therefore, students must construct a new ontological category for numbers as indeterminate quantities. This conceptual change is necessary for the process of constructing a placeholder for the notion of variable.

3 Overview

Previously we observed how, before instruction, children displayed effortful intuitive attempts to solve functional tasks (Xolocotzin & Rojano, 2015). In the research reported in this paper we studied the pre-instructional intuitions of children solving generalisation tasks. We aim to contribute to explaining how children transition from arithmetic to functional thinking.

In line with the Framework Theory Approach to Conceptual Change, we hypothesised that children would experience more conflicts in the areas where operating with natural numbers differs from operating with variables. We addressed two research questions, as follows:

  • RQ1 What is the relation between children’s prior arithmetic knowledge and their pre-instructional performance in functional thinking tasks?

  • RQ2 What characterises children’s pre-instructional intuitive conceptions of functional thinking content?

4 Method

4.1 Context and participants

The research was conducted in urban government-funded schools located in central Mexico. Here, the elementary curriculum lacks early algebra content and emphasises arithmetic concepts and skills, focusing on computational fluency (SEP, 2011). Therefore, this was an adequate context for studying pre-instructional algebraic intuitions. We worked with children in two Grade 3 classrooms (n = 43) and two Grade 5 classrooms (n = 49). Teachers and school administrators approved the study protocol. Parents or carers received a consent form clarifying that partaking was free, voluntary, anonymous, and unrelated to school results. Children received the same information in their classrooms and agreed to participate.

4.2 Instruments

4.2.1 Arithmetic

To assess children’s current arithmetic knowledge, we used the Evaluación Neuropsicológica Infantil [Children’s neuropsychological assessment] (ENI, Matute et al., 2007). This instrument was suitable for our study because it matched the national mathematics curriculum. The ENI arithmetic scale includes the following four subscales:

Counting. Includes items that require numbering objects with and without interference, e.g., “How many stars and bells are in this card?”.

Number knowledge. Includes four tasks that assess decimal system knowledge, involving reading numbers, writing numbers, comparing numbers, and ordering numbers.

Calculation. Includes forwards numerical sequences, backward numerical sequences, mental calculations, and written calculations.

Problem-solving. Involves word problems, e.g., “A second-hand motorcycle was sold for $ 8,700, which is three-fourths of its original price. What is its original price?”.

4.2.2 Functional thinking assessment

We used the Functional Thinking Assessment (FTA) instrument by McEldoon and Rittle-Johnson (2010) to investigate children’s pre-instructional intuitions. The FTA assesses functional thinking skills with tabular tasks drawn from the literature. The tasks assess skills of different levels, ranging from lower-level skills such as following a rule to complete a table, to higher-level skills such as representing a function rule with symbolic notation. The tasks are in order of increasing difficulty. This design allowed us to assess students’ intuitions about noticing and expressing generalisation.

The reported reliability of the FTA is high (0.99). A pilot study with Mexican children revealed floor effects. Therefore, we added easier items involving additive relations across the levels of the FTA. Table 1 shows the FTA contents used in the current study.

Table 1 Structure and contents of the functional thinking assessment (McEldoon & Rittle-Johnson, 2010)
Full size table

4.3 Analysis

We used a mixed approach for analysing our data, including quantitative and qualitative components that complement each other.

4.3.1 Quantitative analysis

The quantitative component included descriptive and correlational analyses of students’ performances in the ENI Arithmetic subscale and each FTA level. This analysis gives an overview of how students might connect their prior knowledge with functional thinking content.

4.3.2 Qualitative analysis

Rationale. Developing functional thinking requires the construction of counterintuitive algebraic concepts that have no precedent in the arithmetic experience of elementary students. However, according to the Framework Theory of conceptual change, students can construct framework theories for working with functional tasks even without instruction. These framework theories are the initial state in the construction of algebraic concepts.

We analysed students’ intuitive answers to the FTA to explore students’ framework theories. This instrument was fit for our purpose because it assesses skills of increasing difficulty related to understanding function tables, ranging from following an explicit rule to expressing a function rule with symbols. Therefore, it can indicate the degree to which students without instruction can form intuitive notions of crucial concepts and skills. We employed a sequential qualitative analysis with two stages to characterise such intuitions as framework theories.

Data source. We focused on students’ written answers to the FTA’s Sects. 3 and 4. These items focus on skills such as finding missing values, expressing verbal rules, and expressing symbolic rules. Figure 1 shows examples of items in each section. Section 3 included the functions A + 7 = B, A × 3 – 2 = B; and Sect. 4 included the functions A + 4 = B, A × 3 = B, and A × 3 + 2 = B. These items offer a global view of students’ intuitive reasoning.

Fig. 1
figure 1

Examples of items from FTA Sects. 3 and 4

Full size image

Coding intuitive answers. In the first analysis we categorised students’ answers to the following tasks: finding missing values and expressing verbal and symbolic rules. Answers to each item were the unit of analysis. The dataset had 572 answers. Following Saldaña (2015), we went through the data with an interpretive approach, coding the answers with Transana V.4.00 (Woods, 2021). We wrote analytic memos detailing children’s answers, which helped refine the coding scheme. Then we coded answers in several iterations, discussing and resolving discrepancies. We compared our coding to the coding of a research assistant who analysed a random sample of 172 answers (about 30% of the data). We obtained high reliabilities across tasks (\(\upkappa \ge .79)\)

Characterisation of students’ conceptions. In the second qualitative analysis we characterised how students reorganised their prior arithmetic knowledge and formed framework theories. We mapped the intuitive answers coded in the first qualitative analyses on to the constructs of the Framework theory. This theory predicts two kinds of hybrid conceptions students can construct when introduced to counterintuitive mathematical information, namely, fragmented and synthetic. Both conceptions can involve misconceptions, but synthetic conceptions possess explanatory power and internal consistency, unlike fragmented conceptions. In the results section, we present examples of students’ intuitive conceptions. We defined fragmented and synthetic conceptions as follows.

Fragmented conception: This is an erroneous hybrid of arithmetic and algebra that does not have task-solving power, produces ad-hoc answers, and lacks internal consistency. An ad-hoc answer works for only one aspect of a task. For example, an operation that transforms a number in column A to get a missing number in B that applies only to one row is ad-hoc. This answer is consistent with a correspondence approach but denotes misconceptions about generality. Therefore, it cannot support verbal and symbolic function rules.

Synthetic conception: This is an erroneous hybrid of arithmetic and algebra, characterised by some task-solving power and internal consistency. Internal consistency implies that students’ answers share underlying conceptions. Because synthetic conceptions are not specific or unitary, children might have different synthetic conceptions, internally coherent and powerful in their own way.

We made profiles for each participant, listing their answers as coded in the first analysis and including notes produced during the coding. These profiles became the unit of analysis. We considered that a conception had internal coherence if the student used similar answer types across items. The conception had explanatory power if the answers were approximate to the expected answers. While assessing students’ conceptions, we discovered conceptions heavily constrained by prior arithmetic knowledge. We defined these conceptions as Arithmetic. Also, we characterised some conceptions as Unclear, including those in which students did not answer most items or used answers that were not interpretable.

4.4 Procedure

The students answered the FTA in group sessions, but worked individually. The first author gave a five-minute introduction, asking students to imagine a dog shelter and how many eyes they would see depending on a given number of dogs. Then, with guidance, students completed a table with missing instances of the number of eyes depending on specific numbers of dogs, including non-consecutive and far numbers. More than instructional purposes, this introduction helped students to understand how function tables work so they could make meaningful answers to the FTA tasks.

We administered the ENI arithmetic scale in individual sessions in a quiet room within the school. Our final sample included 20 Grade 3 students, 12 girls, \({M}_{years}=9.24, { SD}_{years}=0.89\), and 24 Grade 5 students, 12 girls, \({M}_{years}=11.16, { SD}_{years}=0.48\). The sample did not include students with more than 70% unanswered FTA items or who did not complete the ENI test.

5 Results

5.1 Performance in arithmetic

Table 2 presents students’ arithmetic scores. We computed an aggregated score by averaging the proportion of accurate responses across subscales. As expected, Grade 5 students scored more highly (Med = 0.65) than Grade 3 students (Med = 0.55), Mann–Whitney \(U=117.00, p=0.004\).

Table 2 Performance in arithmetic by subscale (top score) and grade
Full size table

5.2 Accuracy in the functional thinking assessment

We defined accuracy in the FTA as the number of correct answers in Sects. 1 and 2. In Sects. 3 and 4, we used the rubric attached as supplementary material. Table 3 presents students’ accuracies by level and grade. Accuracies indicate how easy or difficult were the tasks in the FTA for our participants.

Table 3 Performance in the functional thinking assessment by level and grade
Full size table

Most students responded correctly in Level 1, which suggests that children did not experience difficulties applying a given function rule to define missing numbers. In Level 2, less than half of Grade 3 students, and a majority of Grade 5 students, gave correct answers. This indicates that a sizeable portion of students successfully solved tasks such as extracting a function rule from a complete table and determining a near instance of a dependent variable. However, some students could not keep up with their peers.

In Level 3, the rates of correct responses decreased to less than a quarter in Grade 3 and less than half in Grade 5. That is, most students struggled with tasks such as defining far missing instances of a dependent variable and expressing function rules with words. We observed lower levels of accuracy in Level 4, which suggests that the production of symbolic expressions was extremely difficult.

5.3 Linking performances in functional thinking and arithmetic

We assessed the correlation between arithmetic performance and FTA performance using Spearman’s Rho, controlling for the effects of grade level. The analyses revealed large correlations between students’ arithmetic scores and their accuracies in the pre-symbolic levels of the FTA. Those with more developed arithmetic skills also performed better in tabular functional tasks such as following a rule for defining missing dependent variable numbers \({(\mathrm{FTA Level }1, r}_{s} = .45, p= .002)\), identifying and selecting the underlying rule of a table with complete data \({(\mathrm{FTA Level }2, r}_{s} = .34, p= .024)\), and identifying a consecutive instance of a dependent variable and expressing the correspondence rule in words (FTA Level 3, \({r}_{s} = .40, p= .007)\). In contrast, the development of students’ arithmetic skills was unrelated to the capacity to express a functional rule with symbols \(\left(\mathrm{FTA Level }4, {r}_{s} = .24, p= .12\right)\).

5.4 Intuitive answers to the FTA items

5.4.1 Finding missing values

Table 4 shows students’ strategies for finding missing instances of a dependent variable. Not all students wrote the calculations performed to answer the tasks. In these cases, we sought strategies consistent with the numbers the children wrote in the table and considered the function rule’s expressions. In Grade 3, about half of the answers were not interpretable, and only about a third of answers involved correspondence. In Grade 5, correspondence approaches were the most frequent. There were other generalisation forms, including recursive patterning and hybrid patterns combining recursive and correspondence approaches. Other strategies without generality involved the fragmentation of the table.

Table 4 Categories of students’ intuitive responses to missing numbers tasks (f = frequency)
Full size table

5.4.2 Expressing verbal rules

Table 5 shows categories of answers to the tasks requesting a function rule with words. That is, expressions made with natural language, including words, numbers, operators or even letters, but not symbolic algebraic expressions like equations. In Grade 3, about half of the answers were not interpretable. In Grade 5, these answers were less prominent. In both grades, the most frequent interpretable answers involved operations without letters. The operations were mostly accurate, but students did not use variable notation. Albeit infrequently, some answers described operations with letters. These answers can be considered approximate function rules because they combined letters with operators and numbers.

Table 5 Categories of students’ intuitive verbal expressions (f = frequency)
Full size table

In both grades, only 10% of answers were accurate function rules, which attest to the challenging nature of the task. Other answers reflected some structural aspects. For example, answers that linked A numbers and B with equalities or answers that described an iterative use of the same operation across rows. Few answers suggested disengagement with the task, such as writing letters or saying things like “to get a result”. These were very rare, the same as reversal errors.

5.4.3 Expressing symbolic rules

Table 6 shows students’ answers when asked for a symbolic function rule. Most answers were not interpretable, which reflects the lack of instruction. Accurate symbolic expressions were rare in Grade 3 and represented 20% in Grade 5. Remarkably, some students managed to produce symbolic function rules without instruction. There were reversal errors like those observed in secondary students. Especially in Grade 5, students attempted to use letters without representing variable notation, for example, writing character strings or using letters as numbers. Some other answers could be considered approximate function expressions, for example, answers that established equalities between letters. Answers involving letters as labels indicate that students accepted the use of letters but used them without any discernible meaning. Sometimes students extended the table, suggesting they noticed generality but did not map it onto symbols.

Table 6 Categories of students’ intuitive symbolic expressions (f = frequency)
Full size table

5.5 Intuitive conceptions

Table 7 shows the frequencies of each kind of conception that emerged from the second qualitative analysis. We found six students whose conceptions could not be classified. We defined them as unclear because they had many unanswered items or the answers were not interpretable. We do not discuss these cases further. Students tended to produce more fragmented and synthetic conceptions than arithmetic ones. Arithmetic conceptions were more likely in Grade 3. Fragmented conceptions were similarly frequent in both grades, and synthetic conceptions were more likely in Grade 5.

Table 7 Students’ conceptions by grade
Full size table

Below we describe arithmetic, fragmented and synthetic conceptions with illustrative cases. The descriptions include details about students’ answers across items 13–17, but the figures include only items 15–17. We focus on these items because they include answers to the three types of tasks, namely, finding missing values, expressing verbal rules, and expressing symbolic rules.

5.5.1 Arithmetic conceptions

These conceptions reflected how some students reacted to function tables by applying their knowledge of natural number arithmetic without adjusting their beliefs. For example, student 5ID001 enacted the belief that numbers are the product of operations and not part of sets. Figure 2 shows how this student defined missing B values using a correspondence strategy on item 16 (A + 4 = B), applying the transformation + 4 across rows. Then he applied fragmentation strategies. On item 16 (A × 3 = B) he used the transformation + 4, but this applies only to the first complete row. Similarly, on item 17 (A × 3 + 2 = B), the student used a + 6 transformation across rows, but this applies only to the first row.

Fig. 2
figure 2

Answers to items 15 (A + 4 = B), 16 (A × 3 = B), and 17 (A × 3 + 2 = B) that illustrate the arithmetic conception of student 5ID001

Full size image

We considered that this way of finding missing values indicates an arithmetic conception because the student applies a strategy that works only for the first row in the table without generalising. He did not notice that A and B numbers are part of the same set and share the same relation.

The student’s verbal rules show further evidence of an arithmetic conception. He did not produce a verbal rule in item 14 (A × 3 – 2 = B), referring to equality/inequality in the other items, that is, focusing on equalising quantities without describing a function rule. He emphasised what is needed (“four are missing” or “six are missing”) for producing a result (“the quantity”). Moreover, the student described only transformations without mentioning variables. We believe that for him, the task was about making operations to get a specific number, just as in any arithmetic situation.

We argue that the arithmetic conception of this student constrained his symbolisation. He did not produce a symbolic expression on item 13 (A + 7 = B), but in the other items, he made strings, neglecting letters and linking the numbers in column B (items 15 and 16) or column A (items 14 and 17) with operation symbols.

Arithmetic conceptions possess internal consistency but lack explanatory power. They cannot produce answers that could be considered intuitive algebraic conceptions. This example illustrates how, before instruction, prior arithmetic knowledge can determine how students reason about functional content.

5.5.2 Fragmented conceptions

These conceptions reflected how some students produced ad-hoc responses, reorganising their arithmetic beliefs but lacking a framework for producing intuitive algebraic notions. For example, student 3ID044 reacted to the tasks with different approaches, depending on the specific demands of each item. Her verbal responses suggest that the central belief of her conception is that numbers are the product of operations. Her framework theory had sufficient explanatory power to support the finding of missing values. However, it was not enough to support the noticing and expression of generality.

Figure 3 shows a correspondence strategy on item 15 (A + 4 = B) and recursive strategies on items 16 (A × 3 = B) and 17 (A × 3 + 2 = B). The framework of this student supported an approximation to generality that was not constrained by arithmetic approaches, e.g., focusing on specific numbers. She generalised in both items, but differently. However, her verbal expressions reflect her belief that numbers are the product of operations and not instances of sets. She did not answer item 14 (A × 3 – 2 = B). In the other items, her verbal expressions described the operation involved in the transformation as means to get ‘the result’. On item 13 (A + 7 = B) she wrote “B is a result”. These answers suggest that she did not construct a notion of variable, which could explain why she did not produce symbolic expressions.

Fig. 3
figure 3

Answers to items 15 (A + 4 = B), 16 (A × 3 = B), and 17 (A × 3 + 2 = B) that illustrate the fragmented conception of student 3ID044

Full size image

5.5.3 Synthetic conceptions

These conceptions show that some students reorganised their prior arithmetic knowledge to construct frameworks incorporating intuitive notions of algebraic ideas such as generality and generalisation expressions. As expected, these initial frameworks involved misconceptions but supported meaningful approximations of the learning outcomes of functional thinking instruction.

For example, student 5ID080 defined the missing instances of all items, including those with two-operation functions. She could even produce verbal function rules that involved correct transformations. However, she did not use letters when representing two-operation functions and did not produce symbolic expressions.

Figure 4 shows illustrative answers by 5ID080. Note that this student had misconceptions and limitations in her arithmetic knowledge. In item 17 (A × 3 + 2 = B) she used repeated addition to get the multiplicative part of the transformation, suggesting limited computation skills. She also denoted an operational understanding of the equal sign. Expressions like 15 × 3 = 45 + 2 = 47 are incorrect equalities. Therefore, we believe the student used the equal sign to indicate the results of making operations. For example, 45 is the result of multiplying 15 × 3, and 47 is the result of adding 45 + 2. However, the arithmetic knowledge of 5ID080 did not constrain her answers completely. She made some calculation mistakes but defined the missing values of all items with correspondence strategies, applying consistent transformations across rows. She constructed notions of correspondence and generality.

Fig. 4
figure 4

Answers to items 15 (A + 4 = B) and 17 (A × 3 + 2 = B) that illustrate the synthetic conception of student 5ID080

Full size image

She did not produce verbal expressions in item 14. In other items, she described iterative procedures (item 13) or transformations without variables (item 17). However, in items 15 and 16, she produced correct verbal function rules. This inconsistency suggests that she is beginning to construct a placeholder for the indeterminate quantity concept. However, because this concept is under construction, she could not produce symbolic expressions.

We considered that the conception of this student was synthetic because she was consistent in using correspondence approaches to define missing values across items, denoting internal consistency. Moreover, this conception has much explanatory power, considering that she approached the task as making correspondence relations and even managed to produce verbal expressions of the rule.

6 Discussion

Previous studies suggest that generality and symbolic notation are counterintuitive. Many children begin to generalise with recursive or hybrid approaches before adopting correspondence and covariation approaches. Also, many misconceptions emerge in the first attempts with symbolic notation. In the research reported in this paper we analysed the nature of these conflicts with the Framework Theory Approach to Conceptual Change (Vamvakoussi et al., 2018; Vosniadou et al., 2008).

We found that students struggle to connect their prior arithmetic knowledge with the content of functional thinking tasks in areas where operating with natural numbers differs from operating with variables. These conflicts stem from the intuitive conceptions children construct in the initial stages of the transition from arithmetic to functional thinking. Below we discuss the possible implications of these findings.

6.1 Prior arithmetic knowledge and functional thinking performance

Our data show that current views about the assessment and progressions of functional thinking apply in pre-instructional contexts. First, we confirmed the validity of the FTA (McEldoon & Rittle-Johnson, 2010). Second, we found that students’ performance decreased as the FTA tasks departed from arithmetic to become more algebraic. This result corroborates findings that describe different progressions across functional thinking levels (McEldoon & Rittle-Johnson, 2010; Stephens et al., 2017).

Following function rules and identifying function rules with complete tables were easy tasks. Tasks such as defining far dependent variable instances and expressing function rules with words were harder. Symbolic tasks were extremely difficult. Joining these differences in performance across FTA levels and the correlations with arithmetic skills reveal areas of conflict in the transition from arithmetic to functional thinking. These results respond to the interest in extracting the algebraic from the arithmetic (Blanton et al., 2015a, 2015b; Pinto & Cañadas, 2019; Stephens et al., 2017).

We found that arithmetic skills correlated more with the performance in tasks that require incipient skills for noticing generalisation, for example, following a given rule, identifying a function rule from a complete table, and defining the next consecutive instance of a dependent variable. Students would be expected to experience little conflict connecting their arithmetic knowledge with the content of these tasks. Therefore, they can scaffold the initial encounters with functional thinking.

However, misconceptions are likely to emerge. Students could use computation or patterning skills to identify regularities in a table and map them onto given function rules. Finding regularities does not entail noticing generalisation (Martinez & Brizuela, 2006; Tanışlı, 2011).

Arithmetic skills also correlated with performance in tasks requiring noticing and expressing generalisation, such as defining far instances of a dependent variable and producing verbal function rules. With teaching support, tasks of this kind could help students connect their arithmetic knowledge and the idea of a generalised function rule. However, this result implies some uncertainty.

Students might use patterning and calculation skills to figure out how to transform A to get B, without grasping the concept of functional relations. When asked to express function rules with words, we know that students often focus on operations without mentioning variables (Molina et al., 2018; Stephens et al., 2017).

Arithmetic skills did not correlate with performance in higher-level tasks involving symbolic notation. Before instruction, children could not connect their arithmetic knowledge with algebraic ideas like using letters for representing sets or combining letters with numbers and operators. This result supports the hypothesis that the conflicts between arithmetic knowledge and functional thinking concentrate on areas where arithmetic and algebra differ. In the following section we discuss how students’ arithmetic knowledge constrained their intuitions about algebraic ideas.

6.2 Intuitive conceptions of functional thinking content

Our data revealed that students’ framework theories generated arithmetic, fragmented, and hybrid conceptions. Only seven students could not be mapped on to any conception because they produced very few written answers. This result attests to the potential of the Framework Theory Approach to Conceptual Change to theorise about the construction of algebraic concepts. This contribution is relevant because cognitive factors like conceptual change have received little attention in the early algebra literature.

The arithmetic conceptions we found might explain prior findings that attribute the difficulties in noticing generalisation to the interference of prior arithmetic knowledge (e.g., Pinto & Cañadas, 2019). The Framework Theory Approach to Conceptual Change assumes that the presuppositions that constrain the learning of new ideas are not under the conscious control of the learner (Vosniadou et al., 2008). Therefore, without teaching, it seems natural that some students are firmly attached to their current beliefs for solving novel functional tasks.

As expected, most students constructed hybrid conceptions. These conceptions illustrate how students reorganised their prior knowledge differently. The conflicts emerged in areas where arithmetic and algebra differ, such as generality, indeterminate quantities, and symbolic notation.

Fragmented conceptions seemed to emerge from the belief that missing B numbers resulted from sequences or operations with specific quantities. This belief did not constrain children’s intuitions about generality. However, it obstructed the construction of placeholders for concepts like variable and variable notation. For example, student 5ID001 used recursive patterning and correspondence approaches to find missing numbers. She had generality intuitions. However, her verbal and symbolic expressions emphasised the obtaining of a result, or a quantity, without mentioning variables.

Synthetic conceptions show that, even before instruction, some students can reconcile prior arithmetic beliefs with functional content. Many students used the same transformation of A to get B numbers in iterative ways across rows (e.g., student 5ID080). This reasoning is a strong starting point in understanding correspondence forms of generalisation. However, it does not necessarily mean that students understand the numbers as instances of sets A and B. Without this notion, students cannot begin to construct the notion of variable.

In describing students’ intuitive conceptions, we found two aspects that differentiate our results from the findings of previous studies. First, instructional studies such as the one by Molina et al. (2018), report that the first instructed attempts at symbolic notation tend to focus on using letters. In our study, students’ intuitions about symbolic notation were diverse and did not necessarily focus on using letters.

Second, the role of the equal sign in developing functional thinking has received little attention. Our study shows that beliefs about the equal sign can play a critical role in the generation of conceptual conflicts between arithmetic knowledge and functional thinking. Many students invoked equalities to represent function rules and displayed an operational notion of the equal sign (e.g., student 5ID080).

6.3 Limitations

Developmental differences in functional thinking deserve attention in future studies. One limitation of our study is that our small samples do not let us make precise comparisons between Grade 3 and Grade 5 students. Another limitation is the use of written answers. Future studies can benefit from triangulating different data sources, complementing written answers with interviews or verbal protocols. Also, our study relied on tabular tasks. It is unclear whether our results can be generalised to other visual representations, e.g., figural patterns (Rivera & Becker, 2011).

7 Conclusions

Our study extends the current understanding of algebraic reasoning to include conceptual change processes. This contribution offers a new approach to analysing how children reorganise their arithmetic knowledge to construct counterintuitive algebraic concepts. We found a core development in the transition from arithmetic to functional thinking. That is, shifting from the conception that numbers are the result of operations or sequences to the conception that numbers are instances of an indeterminate quantity, i.e., variables. One instructional implication that deserves further exploration is the necessity of introducing the mathematics of change in the elementary classroom.