1 Introduction

1.1 Making knowledge connections in task design

The fragmentation of mathematics curriculum and teaching in the US is put forward as a major explanation for unsatisfactory mathematics learning in the United States (Schmidt et al. 1997; Stevenson and Stigler 1992).Encouraging connection-building is an important goal of mathematics education, rather than treating mathematics as a body of isolated concepts and procedures (e.g., Elementary Mathematics Department 2005; Cockcroft 1982); building connections represents a major shift in some states in the United States curriculum from traditional practice in mathematics instruction (Common Core State Standards Initiative 2010). From a learning perspective, Duckworth (1979) proposed the notion of “learning with depth and breadth” and argued that intellectual breadth and depth “is a matter of making connections.” She continued:

What is the intellectual equivalent of building in breadth and depth? I think it is a matter of making connections: breadth could be thought of as the widely different spheres of experience that can be related to one another; depth can be thought of as the many different kinds of connections that can be made amongst different facets of our experience. I am not sure whether or not intellectual breadth and depth can be separated from each other, except in talking about them (p. 7).

From the perspective of teachers’ knowledge, Ma (1999) further clarified that a teacher with profound understanding of fundamental mathematics has a general intention to make connections amongst mathematical concepts and procedures and amongst individual pieces of knowledge, in order to reveal the underlying connections amongst different mathematical operations and subdomains. Depth and breadth depend on both the connectedness of different concepts, and thoroughness—the capability of ‘passing through’ all parts of the field—to weave them together. This thoroughness means to ‘glue’ knowledge of mathematics into a coherent whole. From a task design perspective, how to make connections has been considered important (e.g., ICMI Study 22; Sun 2016). Sun (2011a) illustrates a Chinese approach to organizing a curriculum with an emphasis on connectedness, by discerning relationships through the use of a variation approach from local pedagogical traditions and philosophies, ‛no clarification, no comparison’ (沒有比較就沒有鑒別), rather than ‘to consolidate one topic or skill, before moving on to another’, a notion broadly used in most textbook development (Rowland 2008) in Europe and throughout the world. The ‘one-thing-at-a-time’ design, which reflects a hidden conception that making a connection could happen naturally, might miss the chance of discerning critical aspects between two or more topics. Obviously, it would clearly provide fewer opportunities for ‘making connections’ compared to those of contemporaneous variation approaches. More importantly, the variation approach provides a platform to discern and compare the invariant feature of the relationship amongst concepts and solutions that may lead to ‘the general relationship or mathematical abstraction in the topic of fraction division’ (e.g., Sun 2007, 2011a). This paper further clarifies the Chinese approach and its framework for making connections between whole numbers and fractions using problem variations. The purpose of the framework is to characterise task designs with or without connections, and to clarify how knowledge can be connected within the Chinese tradition in the definition of fractions and fraction operations.

1.2 Learning and teaching studies of whole number arithmetic

Current learning and teaching studies of whole number algorithms (WNAs) lack the perspective of historical tradition. For example, few recent reviews of concepts and trends for teaching WNAs have considered the historical traditions of different cultures (e.g., Nunes et al. 2016), which suggests an underlying assumption that all school mathematics derives from the same tradition. It possibly supposes that all students experience the same psychological development of number concepts. Clearly, this kind of research has neglected the historical perspective of traditions and their impact on teaching and learning. The recent studies of whole number generally lack the perspective of connections with fractions (e.g., Venkat et al. 2018). Mainstream studies of WNAs also lack the perspective of the Chinese tradition. Nunes et al. (2016) identify three categories in the literature of the Western theoretical mathematics tradition, namely, arithmetic, quantity relationships, and problem solving. These three categories have been integrated in the Chinese applied mathematics tradition. Within this tradition, the approach of presenting both arithmetic procedures and quantity relationships using problem solving seems unique. In this paper, I explain how knowledge connections for teaching and learning development can be made using problem variations from the Chinese tradition, which have rarely been examined in the recent international mathematics education community.

1.3 The legacy of ancient China’s arithmetic and pedagogy: problem variations

Sun (2018) argued that most international research studies are conducted in the Western deductive tradition, which is strongly influenced by a geometric perspective. For example, the classic mathematical literature edited by Kline (1972) and the history of algebra’s development (Sfard 1995) lack Chinese history. As Wu (1995) pointed out: “there are two core thoughts/paths through the mathematical history of the world. One is axiomatic thought from the Greek Euclidean system. Another is mechanistic thought which originated in China and influenced India and the whole world” (cited in Gu 2010, p. IX). The missing paradigm from an algebraic tradition has rarely been examined.

Given the Chinese algebraic tradition, it is not surprising that the Chinese also developed local pedagogical tools for algebra development (Sun 2018). The two most repeated terms in Chinese mathematical pedagogy—the ‘Two Basics’ and ‘variant teaching’—originally indicated a local notion of teaching practice, stressing the ‘invariant’ and ‘variant’ elements, which may be traced back to Taoism’s profound influence on Chinese culture. The central Taoist idea of the evolution of events as a process of change and the acceptance of the inevitability of change reveals the ideologies of ‘grasping ways beyond categories’ and ‘categorising to unite categories’ (以法通類, 以類相從) (Sun 2011a). In China, for more than 5,000 years, mathematics knowledge was elicited by word problems, which stems from the ‘Shu’ (术) spirit (similar to ‘general methods’) in the problem-oriented tradition of Oriental mathematics: “… to produce new methods from word problems, promote them up to the level of general method, generalise them into ‘Shu,’ and deploy these ‘Shu’ to solve various similar problems which are more complicated, more important, and more abstruse” (Wu 1995, p. IX). Under the influence of this idea, problems in ancient China used to be organised into different categories in terms of situations or algorithms. For example, The Nine Chapters on the Mathematical Art (九章算术), the major classical document of Chinese mathematics, used 246 word problems in nine categories to spread mathematical knowledge, which also reflects Chinese pedagogical thought: the ‘Categorisation Approach’ (Sun 2016, 2018). The ‘Categorisation Approach’ meant ‘categorising to unite categories’. One distinctive instructional feature of these problems is that they aim to develop the ability to identify the category of problems (识类) and discern different categories (归类)—namely, to distinguish between invariant and variant elements of problems and recognise the ‘class’ every problem belongs to. This design approach is generally called biànshì (变式), where ‘biàn’ stands for ‘changing’ and ‘shì’ means ‘form’; it can be translated loosely as ‘variation’ in English (Sun 2011a, b). Biànshì strategy concretely refers to habitual, routinely spoken teaching terms: ‘One Problem, Multiple Solution Methods’ (OPMSM—題多解, varying solutions), ‘One Problem, Multiple Changes’ (OPMC一題多變, varying conditions and conclusions), ‘Multiple Problems, One Solution Method’ (MPOSM 多題一解, varying presentations/contexts). These terms are mentioned infrequently in other places (Sun 2011b). It indicates that some teachers immersed in other traditions might find it harder to extend one example into a category of similar problems, for instance in a routine warm-up skill: using sub-problems at the beginning of lessons before the main problem. The distinction is between a Pudian problem (‘laying the foundations’, 铺垫 in Chinese) and extended problems (拓展問題).

In contrast, the strategy using variation problems, which is valued by Chinese teachers, experts and educators, can be easily found in teaching material (such as textbooks and teaching plans) at school and learning material (such as student exercises and worksheets) done after school in China. Cai and Nie (2007) have argued that the use of this type of variation problem is widespread in China. In their survey, teachers were asked to point out how often they use these problem-solving activities in the classroom. The results showed that all the teachers used these problem-solving activities. Over half of the teachers surveyed used OPMS, MPOS and OPMC very often in their instruction. The studies above indicate that this practice seems rather popular in China. This approach is also closely related to the features of the Chinese language, a tonal and logographic language, where each character has multiple meanings (一詞多義) and each word plays multiple roles in its context (一词多性), where local unspoken meta-rules should be developed in the process of teaching and learning the Chinese language at the same time. To learn to write Chinese and increase their orthographic awareness, students have to develop sensitivity concerning variation as their tacit epistemology, by distinguishing characters that are often very hard to tell apart (Marton et al. 2010; Sun and Bartolini Bussi 2018). In seeking a basic algorithm as a demonstration tool, problem variations aim to avoid numerical heuristic trial and error by eliciting relationship reasoning, using variation as a scaffold for discerning the invariant, in a kind of pre-algebraic thinking (Kieran 2011). In using variation problems as an ‘indigenous’ Chinese practice, the aim is to discern and compare the invariant features of the relationships amongst concepts and solutions (e.g., Sun 2018). This practice shows how to set a relationship space to clarify the invariant elements using problem variation, which is a valuable tool for quantitative reasoning development, not from deductive, but from inductive algebraic traditions (Sun 2018). This practice also aims to provide opportunities for making connections, since comparison is considered the pre-condition for perceiving structures, dependencies and relationships, or for quantitative reasoning, as advised by researchers (e.g., Nunes et al. 2016). Inspired by this direction, the goal of this study is to examine variation problems in textbooks, a basic channel for teaching and learning.

1.4 Textbook comparisons

Although there is a robust literature on textbook comparison in the field of mathematics education, there are few textbook studies that show how to make connections in task design with invisible problem variation. One possible reason is that the main direction of textbook comparisons focuses on visible, surface features of textbooks (contents and problems). For example, Fuson et al. (1988) concentrated on the grade placement of topics, topics covered and page space devoted to each topic. Research from the ‘problem’ perspective (e.g., Li 2000) has stressed (1) the number of steps required (single vs. multiple computational procedures); (2) context (purely mathematical vs. illustrative context); (3) response type (numerical answer, numerical expression or explanation); (4) cognitive expectation (conceptual understanding, procedural fluency, problem solving or special requirement) (Charalambous et al. 2010); (5) types of problems (Stigler et al. 1986); (6) repetition or novelty; (7) reasoning or non-reasoning (Stylianides 2009); and (8) worked-out examples (Mayer et al. 1995). Rowland (2008) pointed out that the use of variation in structured exercises varies considerably from country to country and from text to text. In this paper, I illustrate how to make connections in textbook task design, beyond superficial variations (e.g., context or digit variation).

1.5 The teaching and learning difficulty of fraction

Many studies have indicated a difference between how students learn fractions and whole numbers (e.g., Mack 1998). Stafylidou and Vosniadou (2004) argue that the reason why the mathematical notion of fractions is systematically misinterpreted is that fractions are not consistent with the counting principles that apply to the natural numbers to which children often relate. The difference is the tendency in children to use the single-unit counting scheme applied to whole numbers to interpret data on fractions, called ‘whole number bias’ (Ni and Zhou 2005). Tirosh (2000) refers to these as intuitively-based mistakes. For example, in the addition and subtraction of fractions, many students would add and subtract both fractional numerators and denominators when they learned the algorithm for fraction addition and subtraction (e.g., Vinner et al. 1981).

For fraction multiplication, the misconception that multiplication makes fractions larger is a major learning difficulty when a student learns fraction multiplication, as is the misconception that division makes fractions smaller when a student learns fraction division (e.g., Graeber et al. 1989; De Castro 2008). Luo (2009) pointed out that a significant proportion of pre-service teachers cannot successfully transfer their knowledge of ‘fraction by whole number’ multiplication to that of ‘fraction by fraction’ multiplication. Many researchers argue that the old model of repeated addition to explain the multiplication of whole numbers cannot be used for the topic of fraction multiplication. One reason is that repeated addition cannot extend the fraction (e.g., Fischbein et al. 1985). But the variation approach makes full use of varying the size of equal groups (equal to 1, more than 1, less than 1) to make the connection between whole numbers and fractions. For example, 3 × 5 means 5 + 5 + 5, i.e., 3 rods of 5 m length in a row; ½ × 5 means half of 5, i.e. 1/2 rods of 5 m length in a row. In this way, repeated addition (3 × 5 means 5 + 5 + 5, i.e., 3 rods of 5 m length in a row) can be continued for 2/3 * 1/4 = 2/12. 2/3 of 1/4 means 2/3 rods of 1/4 m length in a row. The approach used in the Chinese community to bridge whole number multiplication and fraction multiplication by changing the size of the multiplier might be broadly unknown in the international community. Therefore readers may wish to know more about this Chinese approach to link ‘fraction by whole number’ multiplication to that of ‘fraction by fraction’ multiplication. It is worth noting that fraction multiplication is a much more central concept than is fraction division because it is a core piece in both the topic of fraction division in the previous studies (Ma 1999; Sun 2011a) and the topic of fraction multiplication. The topic of fraction multiplication is the main focus in this previous study.

For fraction division, the approach consists of remembering a particular rule, separate from whole number division (e.g., Ball 1990). Both the invert-and-multiply procedure and the idea that the quotient may be either larger or smaller than the dividend are different from the whole number rule that the quotient of whole number division must be smaller than the dividend. Sun (2011a) depicted how a Chinese textbook example develops its underlying rationale using problem variation in the topic of fraction division. This study will focus on how to clarify the idea that the quotient may be either larger or smaller than the dividend, not reported previously.

Concerning the meaning of fractions, Levin (1998) pointed out that half of the sample students were unable to explain how fractions and division were related, after learning about these topics for at least 2 years. She argued that the skills of writing quotients from whole number division problems as mixed numbers or identifying the fraction bar as a division symbol are missing from the American elementary, middle-school, and algebra textbook curriculum. Could fractions be defined as division? Naturally, the dividend may be either larger or smaller than the divisor if a fraction is defined as division, which is different from the division of whole numbers, in which the dividend may only be larger than the divisor.

These differences or similarities could be related to the fact that the algorithms of whole numbers can be activated again in the student’s mind. The initial algorithms seem to become so rooted in the learner’s mind that they continue to exert control over mental behaviour for a long time. This consideration is critical, because many students find that the same algorithms do not hold true for performing fundamental operations on fractions as they do for whole numbers (e.g., De Castro 2008). Without intervention, the development of operational reasoning will not resolve by itself. Here we collect the misconceptions when they learn fraction algorithms (see Table 1). Thus, readers may ask how concepts first introduced in the fraction section can remain coherent after assimilation into their existing conceptual structures of whole numbers.

Table 1 Learning difficulties between fundamental algorithms of whole numbers and fractions
Full size table

These questions inspire us to examine the fraction section of the Chinese curriculum, which is linear and non-repetitive in design, rather than spiral in form (Ma 2013; Sun 2016). The approach could enable connections in the other fraction operations, which could help curriculum developers, teachers and educators to know how to make connections between fractions and whole numbers to overcome such difficulties. For the first time (to the best of my knowledge), I systematically discuss the connectedness of the four fraction operations with whole number arithmetic to overcome such whole number bias.

The research questions may be further clarified as follows:

How do the problem sets for the addition and subtraction concepts of fractions connect with the concepts for whole numbers, to avoid the addition and subtraction of denominators according to the whole number rule? How do the problem sets for the multiplication concept of fractions connect to the concept for whole numbers to avoid the idea that the product is larger than the factors, based on the whole number rule? How do the problem sets for the division concept of fractions connect to the concept for whole number division, to show why the inversion-and-multiplication procedure is valid and the quotient may be either larger or smaller than the dividend, which is different from the whole number rule? How do the problem sets for the definition of fractions connect to the division concept for whole numbers, to avoid the idea that the dividend is always larger than the divisor, following the whole number rule?

2 A conceptual framework

To use indigenous variation practices, we translate them into codes: in Chinese mathematics curricula, these practices are ‘One Problem, Multiple Solution Methods’ (OPMSM一題多解, varying solutions), ‘Multiple Problems, One Solution method’ (MPOS 多題一解, varying presentations). In a project, we found that a closer analysis of the distinctness and connectedness of mathematical concepts and solutions is useful in the field of text comparisons. A framework is thus developed in what follows (Sun 2011a).

  1. a.

    Problem variations with and without concept connection

Concept connection means there is a change from the concept of whole number to the concept of fractions underlying the original problem and variation problems in the paper. Problem variations with concept connection reflect the mathematical structure underlying the problems, and thus stress generalisation of the invariant concept system behind multiple concepts. In contrast, problem variations without concept connection illustrate objects in the problems, but do not reflect the mathematical structure of problem design.

  1. b.

    Problem variations with and without solution connection

Problem variations with solution connection (i.e., multiple solution connection features) provide a setting in which learners are required to compare and possibly expand the solution structure and generalise the invariant solution system behind multiple solutions. Problem variations without solution connection (i.e., one solution feature) illustrate the surface solution structure of the problems that the curriculum designers intend the student to learn.

Significantly, the framework stresses not only conception and solution connection, but also ‘invariance’ beyond mathematical connections, which play an important role in making coherent, consistent design. From practice to its re-constructed rational explanation, this ‘indigenous’ framework is different from Western models, as it takes variation into account as abstracting and generalising conditions in mathematical task design (Sun 2011a, 2016, 2018). Clearly, because problem design is often carried out in mathematical curriculum centres, this framework can demonstrate how to design a connected curriculum and more deeply uncover Chinese ‘indigenous’ daily practice in mathematical textbook practice (i.e., ‘mathematics-specific knowledge’).

3 Research questions and methods

  1. 1.

    How do problem variations for the addition and subtraction concepts of fractions connect to those of whole numbers, to avoid adding and subtracting numerators and denominators according to whole number rules?

  2. 2.

    How do problem variations for the multiplication concept of fractions connect to those of whole numbers, to avoid the idea (from whole number rules) that a product is larger than its factors?

  3. 3.

    How do problem variations for the division concept of fractions connect to the concept for whole number division? The invert-and-multiply result and quotient may be either larger or smaller than the dividend, which is different from whole number rules.

  4. 4.

    How do problem variations have a definition of fraction that connects to the division concept of whole numbers but avoids the idea that the dividend is larger than the divisor?

For this purpose, we selected a widely used textbook, namely, Mathematics Textbook Developer Group for Elementary School (2014), which has been used for many years by the majority of students from many backgrounds. This textbook is considered representative of the Chinese national curriculum in comparison with most other textbooks (e.g., Sun 2011a).

To address these questions, I identify the first group of examples in a textbook that introduces the concept of fractions and operations on fractions. This group includes the core concepts and procedures of fractions, explicitly or implicitly, as first presented in a Chinese textbook and the accompanying teacher’s manual. The distinctness and connectedness of mathematical concepts and solutions within problem sets in the examples were the focus Since the connections between fraction and whole number are backgrounded and foregrounded across fraction operations, we also examined the explanations that have been addressed in the teachers’ manual in order to explicitly or implicitly understand the examples fully without misunderstanding. The author and one doctoral student examined the textbook series separately and created individual observation notes. Each lesson was read several times, and the teachers’ manuals were also consulted. During the first reading, we introduced codes, focused on the research questions above. After each reading, the two coders discussed their notes. Whenever a problem variation emerged, we attempted to determine together whether the pattern was unique. Across all four research questions, the percentage agreement ranged between 90% and 99%. Problem variation with or without concept connection and Problem variation with or without solution connection (the framework above) guided our analysis.

4 Results and discussion

4.1 How do the problem variations for the addition and subtraction of fractions connection to the concept for whole numbers?

Here is a representative prototypical example of adding two proper fractions using problem variations with solution connection in the Chinese textbook. (The most common procedures demonstrated in the examples were adding two proper fractions. There are not examples adding two mixed numbers or improper fractions, subtracting two proper fractions, and subtracting two mixed numbers or improper fractions in the textbook.). Within the ‘problem set’, two solutions are made available. The first uses the ‘counting’ solution with 1/8 as its new unit. The second solution uses fraction addition. Clearly, OPMS aims to identify and compare the invariant concept of addition between whole numbers and fractions (i.e., addition is equal to counting in both the whole number and fraction systems), which is important for developing a coherent, consistent curriculum. OPMS, which includes both the addition method and the alternative approach of counting, promotes rational thinking and explains how the reasoning and procedure are interrelated. Accordingly, students are expected to draw attention to connections and contrasts between fraction counting with unit fractions, rather than counting with ones as unit and adding fractions; the result is new knowledge, and a deeper understanding of the ‘invariant addition concept’ beyond similar features, because the text excerpt itself does not point to the patterns of invariance amidst variation. Given children’s inclination to distort new information (about fractions) to fit their counting based whole number theory (Stafylidou and Vosniadou 2004), the approach is important in order to clarify the continuity or invariance of counting while drawing attention to the variation in what counts as the unit (Fig. 1).

Fig. 1
figure 1

An example from the Chinese textbook introducing the fraction multiplication concept, using problem variation with concept connection (Mathematics textbook developer group for elementary school 2014, Vol. 11, p. 89)

Full size image

In the ‘counting’ solution, three units (in Chinese unit ge) of 1/8 highlight that the ‘invariant counting unit’ is 1/8. The fraction addition solution is the same as the ‘counting’ approach with whole numbers. The difference in approaches, called by Marton and Pang (2006) critical features, is in counting with a unit, and with unit fractions, respectively. It could be helpful to students in their understanding of why the principle is that addition and subtraction of fractions involves only the numerators, not the denominators, which is different from whole number rules (e.g., Vinner et al. 1981).

4.2 How do the problem variations for the multiplication concept of fractions connect to the concept for whole numbers?

There are four examples of fraction multiplication that connect with multiplication of whole numbers. We illustrate them as follows (Fig. 2):

Fig. 2
figure 2

An example from the Chinese textbook introducing the fraction multiplication concept using problem variation with concept connection (Mathematics textbook developer group for elementary school 2014, Vol. 11, p. 22)

Full size image

4.2.1 The first example: using problem variation to make a connection between the repeated addition model and the counting model, with an emphasis on continuity between whole number multiplication and fraction multiplication

Here is a prototypical example of problem variations with solution connection in the Chinese textbook. In the variation problems above, 2/9 × 3 = 6/9 = 2/3 is designed to naturally introduce a solution system for fraction multiplication (Fig. 3). Within the ‘problem set’, there are three solutions made available. The first uses the ‘count’ solution involving addition. The second solution uses fraction addition, and the third uses fraction multiplication. Clearly, OPMS aims to identify and compare the invariant concept of multiplication between multiplication of whole numbers and of fractions (i.e., multiplication is equal to repeated addition), which is important for developing the curriculum in a consistent way. OPMS, which includes explaining the multiplication method and the alternative approach of addition and counting at the same time, promotes ‘rational thinking’ and explains how the three kinds of reasoning and procedure are interrelated. Accordingly, students are expected to make connections and contrasts between counting, fraction addition and fraction multiplication; the result is new knowledge, which deepens their understanding of the ‘invariant multiplication concept of repeated addition’ beyond its similar features. The ‘counting’ solution of three (Ge) units of 2/9 highlights that the ‘invariant unit’ is 2/9, and shows the simplified relationship leading from counting to addition/multiplication.

Fig. 3
figure 3

An example from the Chinese textbook introducing the fraction multiplication concept using problem variation with concept connection (Mathematics textbook developer group for elementary school 2014, Vol. 11, p. 3)

Full size image

An (2008) found that 64% of the U.S. teachers in her sample would prefer to use one representational area to illustrate fraction multiplication, while 67% of Chinese teachers in the sample use two representations, namely, area and repeated addition. This finding indicates that the area model of fractions could be regarded as an isolated concept, which could not be combined with the repeated addition model of fraction multiplication in some instances. Mack (1998) pointed out that many situations with fractions involve taking a part of a part of a whole, e.g., 1/3 × 2/5, which means ‘take one-third of two-fifths.’ In such a situation, students’ additive reasoning has no meaningful interpretation. He further concluded such additive reasoning in the multiplication of fractions interfered with their efforts to make sense of fractions. Then the statement in the repeated addition model can no longer be applied to the multiplication of fractions (e.g., Fischbein et al. 1985), which indicates that the repeated addition model and the multiplication of fractions model could not be integrated as a whole from those researchers` perspectives. Thus the design above clearly sheds light on an approach that aims to make connections.

In contrast, withouting using additive reasoning in the multiplication of fractions, a typical design transform ‘fraction multiplication by whole numbers’ into ‘fraction multiplication by the fraction of the denominator as one unit’, which emphasises the procedure alone: ‘the first step is to multiply the numerators and the second step is to multiply the denominators’, and the sequence of operations (i.e., the algorithm) is repeated (see the example in Rose et al. 1996, Vol. 8, p. 128).

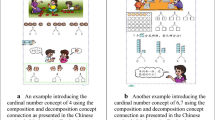
4.2.2 The second example: bridging whole number multiplication and fraction multiplication using problem variation, with an emphasis on the invariant concept of fractions and multiplication

Here is a second illustrative prototypical example of problem variations with concept connection in the Chinese textbook. In the variation problems cited, there is a change from the concept of whole number multiplication to the concept of fractions underlying the original problem and variation problems (Fig. 3), which may impart the concept clarification and connection between familiar whole number multiplication concepts and unfamiliar fraction multiplication concepts. There is a ‘multiplier conversion’ from the whole number 3 to the fraction 1/4, which switches the multiplication of whole numbers to the multiplication of fractions (Fig. 3). The design adapts existing whole number multiplication knowledge to fractions, which is a new type of multiplication. This design explains why products of fractions do not become larger, rather than following the principle of whole number multiplication. It is also noteworthy that there are three figures, 3, 1/2, and 1/4, amongst the three problems (called “critical features” by Marton and Pang 2006), which may help students to focus on the concept variation of the multiplier, rather than the multiplicand variation. The task draws students into a ‘space of relations between the multipliers and their products’ as opposed to directing attention to the object itself, with the multiplicand 12 as its invariant unit.

This design aims to clarify how the meaning of fraction multiplication is connected with the meaning of multiplication and meaning of fraction as a whole, not isolated. The connectedness tends to be neglected. For example, Son and Senk (2010) point out the most widely used of the standards-based textbooks for elementary grades in the USA introduces fraction multiplication as “part of a fractional part” and avoids the word “times”. The South Korean national textbook, determined by its national Ministry of Education, addresses the meaning of multiplication of fractions using the meaning of “times”, which is an expansion to fractions meaning “part of a fractional part”. The idea of ‘the first step is to multiply the numerators, and the second step is to multiply the denominators’ as an algorithm for fraction multiplication, assisted by verbal explanations, is directly provided, but does not connect with the meaning of multiplication and meaning of fraction, which could not explain why products do not become larger.

4.2.3 The third example: bridging unit fraction multiplication and non-unit fraction multiplication using problem variation, with an emphasis on the invariant concept of multiplication

Here is a third typical example of problem variations with concept connection in the Chinese textbook. In the Chinese textbook, there is a change from the concept of whole numbers and the multiplier ½ × 1 to the concept of unit fractions and proper fractions underlying the original problem and variation problems (Fig. 4), which may impart the concept clarification and connection amongst familiar fraction concepts, unit fractions and unfamiliar fraction multiplication concepts. There is a ‘multiplier conversion’ from unit-fraction 1/5 to non-unit fraction 3/5. The design adapts existing fraction knowledge to unit fraction multiplication and proper fraction multiplication, which is a new type of multiplication. It is also noteworthy that there are three figures, 1/2, 1/5, and 3/5, amongst the three problems, which may help students to focus on the concept variation of the multiplier, rather than the multiplicand. This approach aims to clarify the different roles of the multiplier in numerator and denominator, elucidate why the procedure works, and also explain why the product of two fractions does not become larger.

Fig. 4
figure 4

An example from the Chinese textbook introducing the fraction multiplication concept, using problem variation with concept connection (Mathematics textbook developer group for elementary school 2014, vol. 11, p. 4)

Full size image

The example is same as the conception of an iterative fraction scheme (Steffe and Olive 1990). It is hypothesised that children can use their number knowledge in conjunction with an equipartitioning scheme to reorganise their fraction knowledge through iterating unit fractions to produce non-unit fractions (e.g., 3/5, 7/5).

4.2.4 The fourth example: bridging multiplying fractions and whole numbers using problem variation, with an emphasis on the invariant concept of multiplication

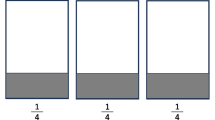
Here is the fourth ‘prototype’ example of problem variations with concept connection in the Chinese textbook. In the example, there is a change from the concept of fractions (the multiplier 4/45) to the whole number concept (30) underlying the original problem and variation problems (Fig. 5), which may impart concept clarification and connection amongst unfamiliar fraction multiplier concepts and familiar whole number multiplier concepts. There is a ‘multiplier conversion’ from 4/45 to 30, the critical aspects (Marton and Pang 2006), while the multiplicand remains invariant. The design may help students to focus on concept variation of the multiplier, rather than variation of the digit.

Fig. 5
figure 5

An example from the Chinese textbook introducing the fraction multiplication concept using problem variation with concept connection (Mathematics textbook developer group for elementary school 2014, vol. 11, p. 5)

Full size image

The design above could be helpful to transfer their knowledge of ‘fraction multiplied by whole number’ to that of ‘fraction multiplied by fraction’, the important learning gap of fraction multiplication mentioned above (Luo 2009). Comparatively, the approach above would be helpful for many curricula, in which the unit role of the multiplicand is not made clear and the relationship between the product and multiplier, which involves a part of a part of a whole (e.g. 3/4 of 4/5), is not made clear using problem variation. The following incorrect diagram for 3/4 × 4/5 also presents the unit of the multiplier 4/5 as one, not 3/4, which fails to present the relationship of multiplier and multiplicand (Fig. 6). This error is found in many studies (e.g., Brookie et al. 2008).

Fig. 6
figure 6

The incorrect diagram for 3/4 × 4/5

Full size image

Figure 6 fails to express the unit meaning of the multiplicand as a whole; the multiplier denoting part of the multiplicand. The Chinese approach (Based on Fig. 4 above) advises that the multiplier (4/5) denotes part of the ‘whole’. multiplicand (3/4), part of part, not an isolated fraction (Fig. 6). It is worth mentioning that the overlapping approach is broadly used in many countries (The multiplicand must be represented vertically in the figure and the multiplier horizontally, alone or in reverse. The product is the overlapping area.). But it is rarely mentioned in the literature that the other fraction models, such as the cake figure, number line, set model, are unable to express the overlapping approach to fraction multiplication.

Besides the above, problem variation between sets also compares and contrasts fraction ‘count’, fraction addition, and fraction multiplication (example 1), multiplication of whole numbers and multiplication of fractions (example 2), multiplication of unit fractions by fraction and multiplication of proper fractions by fraction (example 3); multiplication of fraction by fraction and multiplication of fractions by whole number (example 4). The four examples aim to combine all types of fraction multiplications into a whole. This approach tries to draw the different concepts underlying the examples into a ‘space of relations’ by eliciting the different concepts underlying the examples, including fraction, multiplier, multiplicand, counting, multiplication, division, addition of fractions, multiplication of fractions, and equations, which are bundled together into a knowledge package. In this way, all nine concepts shape the Chinese text, and its intended curriculum features a knowledge package (Fig. 7) consistent with the previous studies (Ma 1999; Sun 2011a) by using problem solving in the textbook examples. Obviously, problem solving in Chinese textbook examples plays an important role in eliciting, not an isolated piece of knowledge, but a knowledge package using problem variation. This finding is important for studies of problem solving, textbook development, and task design, which are rarely discussed in the research literature. The knowledge package is critical for fraction multiplication development too.

Fig. 7
figure 7

A knowledge package of fraction multiplication elicited in the Chinese textbook

Full size image

What could we learn of the mathematical affordances and constraints, by examining these Chinese textbook examples of fraction multiplication above?

Clearly, the sizes, roles, and relationships between the multiplicand, multiplier, and product are emphasized heavily in the Chinese textbook above. However, the unit role of the multiplicand is not made clear, nor is the relationship between product and multiplier, which brings learning constraints. For example, Sutherland et al. (2001) stated that the notion of multiplication was first introduced as repeated addition of equal groups (the array model), and in English, French and Hungarian texts, this model evolved into representing multiplication as an m × n array. These texts also use the notion of function, in the form of ‘jumps on a number line’, to introduce multiplication. Clearly, the multiplication unit can be confusing when a student learns an array model or area model of the expression 3 × 4 + 2. The result can be confusion. Bass (2015) argued: “The difficulty of the area model, from a measure perspective, is that numbers and their products then have different units of measure (for example, length and area) so that it is problematic to assign meaning to an expression like a·b + c” (p. 11). Although an advantage of the area model is that it is visible, and it is easier to us as a tool to present the multiplication property, and it is used as the main model of multiplication in textbooks of many countries, it rarely used to present multiplication in the Chinese tradition. Discussing the use of visual aids when teaching division of fractions, Wu (1996) pointed out the limitations of such explanations. He claimed that these aids suffice only when dividing simple fractions, and yet students need also to understand problems that cannot be visualized.

4.3 How do problem variations for the concept of fraction connect to the concept of whole number division?

The fraction division algorithm in Fig. 8 is as follows: four-fifths of a sheet of paper is separated into two parts. What fraction is each part of the sheet of paper? The example tries to explain the algorithm of division by whole numbers through OPMS. One solution begins from the fact that four-fifths of the sheet of paper is separated into two parts. Thus 1/5 + 1/5 + 1/5 + 1/5 is separated into two parts. One part is 1/5 + 1/5. Thus, one part can be computed by the sum divided by 2 (i.e., \(\frac{4}{5}\)\(\div\) 2 = \(\frac{{4 \div 2}}{5}=\frac{2}{5}\)). The other solution is as follows: four-fifths of a sheet paper is separated into two parts; each part is one-half of the sum (i.e., \(\frac{4}{5}\)\(\div\) 2 = \(\frac{4}{5} \times \frac{1}{2}=\frac{2}{5}\)).

Fig. 8
figure 8

An example from the Chinese textbook explaining the algorithm of division by whole numbers, using problem variation with connection to multiplication and division methods (Mathematics Textbook Developer Group for Elementary School 2014, p. 30)

Full size image

This OPMS aims to explain the rationale of the ‘invert-and-multiply’ algorithm (i.e., why division by a divisor is equal to multiplying by the reciprocal), which is important for understanding the concept of the fraction division algorithm. This problem set justifies the procedure of fraction division as equivalent to multiplication by the reciprocal. The new concept, fraction division, turns into the familiar concepts of division of a whole number and fraction multiplication. OPMS plays an important role in bridging fraction division and whole number multiplication. Although whether students will recognise the relationship between the two solutions is not certain, OPMS provides a setting for enforcing the comparison of two solutions and explaining why the algorithm works. It also explains why in the fraction algorithm products do not become larger, even though they become larger in the whole number algorithm. Thus the whole number division algorithm will not work for fraction division.

4.4 How do problem variations connect the definition of fractions to the concept of the division of whole numbers?

Here is a prototypical example of problem variations with concept connection in the Chinese textbook. In the example, there is a change from the concept of division (a÷b) to the definition of a fraction (a/b) underlying the original problem and variation problems (Fig. 9). It may impart concept clarification and connections amongst familiar division concepts and unfamiliar fraction concepts. There is a ‘symbol conversion’ from the division symbol ‘÷’ to the fraction symbol ‘/’, while the digit remains invariant. The design may help students to focus on concept variation, rather than the digital variation. It explains how fractions and division are related (Levin 1998) and why the fraction algorithm works like the whole number algorithm of division, but there is a new principle: the dividend can be smaller than the divisor (Tirosh 2000). The connection can help overcome the conflict with the implicit model’s rule of division for whole numbers, in which the dividend must be larger than the divisor, and similar intuitively-based mistakes.

Fig. 9
figure 9

An example from the Chinese textbook introducing the fraction multiplication concept, using problem variation with concept connection (Mathematics textbook developer group for elementary school 2014, vol. 10, p. 80)

Full size image

These findings indicate that the conceptualisations of fractions and division are incomplete in many teaching and learning resources around the world. With respect to fractions, these conceptualisations focus heavily on the part-vs-whole pictorial representations of fractions (the area model) from a geometrical perspective alone. Many students believe there is something inherently wrong with fractions greater than one (improper fractions or mixed numbers). Although the part-vs-whole, continuous-to-discrete model is an excellent start, it should not be the only model (even though it is in many countries). In addition to the part-vs-whole model, the widely used number-line model is difficult for students to apply and interpret when fractions are improper (‘How is it possible to take nine-eighths? There are eight bits and then take one more?’). If there is little emphasis on the connection between fractions and division, a student cannot understand that division can also be used for the mathematical definition of a fraction. Hence, a student may not recognise that the numerator of a fraction has the same function as the dividend in division.

In Chinese mathematics history, a fraction is defined as a part of the result of a division, the remainder being taken as the numerator and the divisor as the denominator; this definition is used in the Book on Numbers and Computation and The Nine Chapters on the Mathematical Art from the Chinese algebra tradition (Guo 2010). It is not surprising that it has appeared in almost all current Chinese textbooks. Clearly some practices from the Chinese tradition need to be systematically investigated (Sun and Sun 2012).

5 Conclusion

A central issue in the mathematics curriculum is that we want students to make connections; this issue has been analysed in a series of textbook design and analysis studies. Moving towards mathematics connections—and away from treating mathematics as a body of isolated concepts and procedures—is an important goal of mathematics education. Although many studies identify whole number bias in the learning of fractions, few studies have examined how to overcome this obstacle. The paper aims to clarify how problem variation in Chinese textbooks helps to make concept connections between fractions and whole numbers. To the best of our knowledge, this study systematically addresses the central issue of the unity of four fraction operations and whole number arithmetic to overcome long-standing whole number bias for the first time, which represents a significant curriculum practice gap. This study’s framework for understanding variation practice, in order to make connections, with an emphasis on the invariant concepts, also is helpful for textbook or instructional design and analysis, thus overcoming a significant curriculum development theory gap.

Clearly, OPMC and OPMS play key roles by weaving all concepts into a complete knowledge tree. In the cited examples, they introduce a new concept from an old concept (Sun 2016), and then extend the relationship between counting, addition, multiplication and division of fractions into the idea of counting with unit fractions in the examples. These concepts form the rudimentary yet the powerful basis for the algebra curriculum students will learn later. The approach also makes connections with the central concept of counting, which the students have already learned in whole number arithmetic. This paper further indicates how to develop a coherent curriculum on the topic of fraction addition and subtraction, fraction multiplication and fraction division, with an emphasis on the invariant concepts of units, using the problem variation approach.

This paper addresses the gap in the current literature and clarifies the following misconceptions about learning fraction concepts.

  1. 1.

    It shows how a problem variation approach can explain why addition and subtraction of numerators must be changed using the common denominator algorithm, and why denominators are not added as with whole numbers.

  2. 2.

    It also shows why multiplication makes products larger if the multiplier is greater than one. Multiplication makes the product smaller if the multiplier is a proper fraction (less than one). Multiplication does not make a product larger or smaller if the multiplier is one. In all these cases, the multiplicand plays the role of the unit. The product is determined by the multiplier, rather than following the old rules of whole number multiplication (making the product larger or division making the number smaller). Problem variations can address the gap between whole number multiplication and fraction multiplication by focussing on the size of the multiplier.

  3. 3.

    Problem variation also explains why the algorithm of fraction division works, and why the fraction algorithm means that the result is not necessarily smaller as in the whole number algorithm.

  4. 4.

    Problem variations use a definition of fractions connected to the concept of whole number division, which explains why the fraction algorithm works like the whole number division algorithm. However, the dividend could be smaller than the divisor. This connection could be helpful in overcoming the conflict between the implicit rules of the model for whole number division, in which the dividend must be larger than the divisor.