1 Rational numbers: a stumbling block in mathematics education

Research has amply shown that a good understanding of rational numbers is an essential part of mathematical literacy, which is important both in daily life and in a student’s school career. Particularly, students’ understanding of fractions has been studied intensively. For example, Siegler et al. (2012) found that fifth graders’ fraction knowledge predicted algebra and overall mathematics scores in high school, even after controlling for reading achievement, IQ, working memory, whole number knowledge, family income, and family education. Still, research in cognitive psychology and mathematics education has repeatedly shown that children and even adults struggle with different aspects of rational numbers (Cramer et al. 2002; Li et al. 2009; Mazzocco and Devlin 2008; Vamvakoussi et al. 2012). In the present study, we will briefly discuss the natural number bias, which is known to explain—at least in part—the difficulties learners have with understanding rational numbers. Next, conceptual change theory is discussed, which is a theoretical framework that can explain the origin and persistence of the natural number bias.

2 The natural number bias

The phenomenon that children and even adults have a lot of difficulties dealing with various aspects of rational numbers is often—at least in part—attributed to the “natural number bias” (Vamvakoussi et al. 2012). This term refers to the tendency to inappropriately use natural number knowledge in tasks with rational numbers (Ni and Zhou 2005).

Before primary education, children encounter natural numbers quite often in their daily experiences. Building on these experiences with natural numbers, they construct natural-number based ideas of what numbers are (Vamvakoussi and Vosniadou 2004). A systemization of this idea of numbers takes place in the first years of primary education. Indeed, both in daily life and in the beginning of their school career, children come across rational numbers far less frequently than natural numbers (Greer 2004). This can result in problems and misconceptions when rational numbers are introduced, because the characteristics and rules accounting for rational numbers do not always correspond with those for natural numbers (Gelman 2000; Saxe et al. 2013; Smith et al. 2005; Vamvakoussi and Vosniadou 2004). These problems and misconceptions become clear in the systematic errors learners make in rational number tasks where natural number reasoning leads to an incorrect answer (hereafter these tasks will be called incongruent items; an example of an incongruent item is the comparison of 0.12 and 0.5: to come to the right answer that 0.5 is larger than 0.12, learners have to inhibit their natural number knowledge that 12 is larger than 5) (Moss 2005; Ni and Zhou 2005; Smith et al. 2005; Vamvakoussi and Vosniadou 2004). At the same time, learners perform accurately on tasks where the correct reasoning is in line with natural number reasoning (hereafter these tasks will be called congruent items; an example of a congruent item is the comparison of 0.37 and 0.2: the right answer that 0.37 is larger than 0.2 is in line with learners’ natural number knowledge that 37 is larger than 2) (Nunes and Bryant 2008). Recent studies further show that it is easier for learners when new information about rational numbers is presented in a context that still allows for reasoning along the principles of natural numbers (Mamede et al. 2005; Moss 2005).

While some other authors refer to this phenomenon as the whole number bias (e.g., Ni and Zhou 2005), we prefer the term natural number bias for the following reason. Our study does not solely focus on the non-whole character of rational numbers, but also on the fact that, unlike natural numbers, rational numbers can also be negative, and this positive character of natural numbers may be inappropriately assumed when dealing with rational number tasks too (Van Dooren et al. 2012; Van Hoof et al. 2014).

From the research literature on this topic, it becomes clear that systematic errors may be caused by three main aspects wherein natural numbers differ from rational numbers. The first aspect is density: whereas natural numbers are characterized by discreteness (one can always say which number follows a given number; e.g., after 17 comes 18), rational numbers are dense (one cannot say which number follows a given number, because there are always infinitely many numbers between any two given rational numbers). This difference between natural and rational numbers leads to several misconceptions. For example, many learners have difficulties understanding that between two pseudo-successive numbers such as 5.31 and 5.32 there are still (infinitely) many other numbers (Merenluoto and Lehtinen 2004; Vamvakoussi et al. 2011).

The second aspect is size. In the research literature it is known that learners make systematic mistakes in size comparison tasks involving rational numbers because of their incorrect assumption that “longer decimals are larger” and “shorter decimals are smaller” (Resnick et al. 1989). A second systematic mistake with respect to size is to assume that when a fraction’s denominator, numerator, or both increase, the numerical value of the total fraction increases (Gómez et al. 2014; Mamede et al. 2005; Meert et al. 2010).

The third aspect relates to the arithmetic operations on rational numbers. Given that during the first years of elementary education learners do arithmetic with natural numbers only, they may rely on these experiences and implicitly assume that multiplication and addition will always ‘make larger’ while division and subtraction will always ‘make smaller’ (Christou 2014). These assumptions correspond with those implied in Fischbein’s primitive models of arithmetical operations (Fischbein et al. 1985). The primitive model of addition is putting together, that of subtraction is taking away, multiplication is repeated addition, and division is equal sharing. As a result, a common mistake is, for example, stating that 0.71 * 3 will result in an outcome larger than 3 (Hasemann 1981; Vamvakoussi et al. 2012).

An additional difficulty, which intersects with the three aforementioned aspects, is that rational numbers can be represented by fractions and decimals, and within each of these two representational types even by an infinite number of possible representations. For example, ‘one half’ can be represented as 0.5, but also as 0.50, 0.500, 1/2, 8/16, … Research has shown that students often do not see fractions and decimals as representations of the same number (Vamvakoussi et al. 2012) and moreover consider a fraction as two (natural) numbers instead of as a number in its own right (e.g., Smith et al. 2005).

3 Theoretical framework: conceptual change theory

Several researchers claim that conceptual change is needed in order to develop a complete understanding of rational numbers (Merenluoto and Lehtinen 2004; Smith et al. 2005; Vamvakoussi and Vosniadou 2004). Indeed, the conceptual change theory, and more specifically the framework theory approach towards conceptual change as described by Vosniadou (1994), Vosniadou et al. (2008), provides a valuable theoretical framework to understand the origin and persistence of the natural number bias. The framework theory approach towards conceptual change assumes that people interpret their experiences in everyday life and organize them in a coherent framework theory (Vamvakoussi and Vosniadou 2010). When new information is introduced, it will be more difficult and take more time to understand and master it when this new information is incompatible with this initial framework theory, as compared with the situation when the new information affirms and enriches that theory (Vosniadou et al. 2008). In the former situation, conceptual change is needed, given that the initial framework theory needs to be accommodated to the incompatible new information. This is a gradual and time-consuming process that can lead to misconceptions, such as synthetic models, which are the consequence of students’ attempts to make sense of new incompatible information without entirely revising the presuppositions underlying their initial framework theories. An example of such a synthetic model is that learners apply the density principle for decimals, but not for fractions (Vosniadou et al. 2008). Thus, conceptual change is not an all-or-nothing issue: It is possible that learners undergo a partial conceptual change, but still make mistakes or show inconsistencies in their answers depending on certain task characteristics (Vosniadou et al. 2008).

The inappropriate reasoning in terms of natural numbers in tasks with rational numbers can also—at least in part—be considered as an inhibition problem. Indeed, while a congruent rational number task can be answered (purely) based on prior natural number knowledge, this is not true for incongruent items. For the latter items, an answer based on prior natural number knowledge may come to mind, but it needs to be inhibited as further reasoning is required to respond correctly.

4 Research goals

Although a lot of research has been done about each of the three aforementioned aspects of the natural number bias (density, size, and operations) in elementary school children, so far no study has investigated them in an integrated manner. We acknowledge that Vamvakoussi et al. (2012) study did include items from every aspect, but the number of items was quite limited and the data from the different aspects were not included in one overall analysis. So, nothing could be concluded about the co-occurrence of the natural number bias in all these aspects. Using a comprehensive paper-and-pencil-test that includes a sufficiently large number of both congruent and incongruent items about density, size, and operations, we tried to characterize the natural number bias in fourth graders in a more systematic and comprehensive way. Fourth graders are a relatively young age group in which to investigate rational number understanding, as many, if not most, aspects of rational number knowledge will be extensively dealt with in later years. Still, fourth graders have already been confronted—at least to some extent—with all aspects of rational numbers, allowing them, in principle, to solve the rational number tasks that are provided to them. Thus, it was interesting to investigate the influence of the natural number bias in their reasoning about these three different aspects of rational numbers.

4.1 Using the same comprehensive test instrument in both parts, the present study had two major research goals

Our first research goal was to characterize the natural number bias as it occurs across different item types in fourth graders. If fourth graders were to exhibit a natural number bias—and according to the literature we had every reason to think so—pupils should make more mistakes on incongruent items than on congruent items throughout the test. Moreover, we investigated whether the natural number bias would be present in all three aspects. Besides an overall indication of a bias, we predicted a bias and thus a better performance on congruent than on incongruent items for all three aspects separately as well. Still we wondered if the natural number bias would be equally strong in all three aspects. To answer these questions, we used a repeated measures—because we did several observations within single students—logistic regression analysis, in which we modelled the probability of answering an item correctly by the task characteristics congruency and aspect.

With our second research goal, we wanted to focus more deeply on the phenomenon of inhibiting natural number knowledge in rational number tasks as such. Because we were interested in the children’s ability to inhibit inappropriate use of natural number knowledge, only the data from the incongruent items were used for this part (because correct answers to congruent items are not informative for children’s ability to inhibit their natural number knowledge). Specifically, our second goal was to answer the question whether rational number reasoning—and more specifically the inhibition of the inappropriate use of natural number knowledge in rational number tasks—can be considered as a one-dimensional construct. To meet this goal, we applied a specific type of analysis, namely item response theory (IRT) modeling. While most research about the natural number bias uses methods of the classical test theory (CTT), we extended this research by also using IRT, which is becoming more and more standard in test development (e.g., Embretson and Reise 2000). In CTT, conclusions are based on sum scores of subjects’ answers to items, which is based on the—most often problematic—assumption that all items have an equal difficulty level. IRT, however, does not make this assumption. Indeed, IRT is a latent trait theory that is characterized by conjoint measurement: IRT decomposes the answers of persons on items in two determinants: both the subjects’ ability and the items’ difficulty (Embretson and Reise 2000).

So far, several studies have pointed at pupils’ difficulties in solving a variety of rational number tasks, and all these difficulties could be explained by the inappropriate reliance on natural number knowledge and the incapability to inhibit this natural number knowledge (e.g., Vamvakoussi et al. 2012). So, rationally speaking, these studies assume that there is a single explanatory factor behind learners’ errors. Consequently, individual differences in this factor would then explain all individual differences between students in the performance on different sets of items. Still, there is no empirical evidence that all these phenomena go back to the same root, that is, a bias in pupils’ thinking to rely on natural number knowledge and their incapability to inhibit this natural number knowledge. If the latter were to be true, this would imply that rational number reasoning can be considered a one-dimensional construct. If the data indicate that rational number understanding is indeed a one-dimensional construct, a further question is whether there are systematical differences in the difficulty levels of the different aspects. However, if the test results could not be captured by a one-dimensional model so that a multidimensional model is needed, this would imply that the individual differences in test performance refer to individual differences in different aspects, making it less likely that there is one common cause—namely the incapability to inhibit natural number knowledge—for the weak performance on items covering the different aspects of rational numbers. This would mean that students develop an understanding of the different aspects relatively independently of each other. While we could have investigated the one-dimensionality of learners’ ability to inhibit the inappropriate use of natural number knowledge in rational number tasks by conducting an exploratory factor analysis, we want to argue that IRT modeling is beneficial for several reasons. IRT modeling not only provides an answer to our research question (can the inhibition of the inappropriate use of natural number knowledge in rational number tasks be considered as a one-dimensional construct), but it has some extra advantages. Since the persons and items are placed on a common scale, this has the advantage that ability levels can be directly compared to items. When the item difficulty equals the person’s ability, this person has a 50 % likelihood of answering this item correctly. Further, IRT modeling has the advantage that, once a fitting model for the data is obtained, it is possible to construct a shorter version of the test instrument that still has a good diagnostic value. This shortened test provides a score that is still situated on the same scale as the original, longer test, and can be used in new studies. Finally, exploratory factor analysis is part of the CTT, which makes the problematic assumption, as described above, that all items have an equal difficulty level, while IRT modeling does not make this assumption.

5 Method

5.1 Data collection

The current study fits into a larger research project aimed at mapping the development of rational number understanding throughout the elementary and secondary school curriculum. Based on an extensive literature review and on an analysis of the Flemish mathematics curriculum, a comprehensive paper-and-pencil test was created to be administered in the fourth to the 12th grade. The test included items of the three aforementioned aspects of size, density, and operations. Every type of item was presented in its fraction and decimal form or a combination of both. The test further included both positive and negative numbers, open and multiple-choice questions, and the items were characterized by varying degrees of difficulty. A common set of core items was given to all students (which were the items for the fourth graders), but we also administered additional items that were adapted to each particular grade. In its complete form, the test consisted of 179 items, 88 of which were incongruent (thus requiring the inhibition of natural number knowledge-based answers), while 42 were congruent (thus where natural number reasoning leads to the correct answer) and 49 items were neutral in terms of the helpfulness of natural number knowledge.Footnote 1 In total 21 schools (9 primary schools and 12 secondary schools) from the different parts of Flanders participated in the study, which resulted in a total sample of 1,343 learners.

The results reported in this study are the ones from the fourth graders; in total 213 learners from nine different schools in Flanders participated. The test of the fourth graders consisted of 53 items, 34 of which (3 density items, 18 size items, and 13 operations items) were incongruent, while 19 (1 density item, 15 size items, and 3 operations items) were congruent. Examples are given in Table 1. Only a limited number of density items was provided in the test of the fourth graders, because the density principle is only briefly introduced in elementary school in Flanders. The internal consistency of the test for the fourth graders was high (Cronbach’s alpha = 0.87).

Table 1 Examples of congruent and incongruent test items about density, size, and operations
Full size table

The data were collected during the spring of 2012. In a whole-class test setting, pupils were asked to solve the paper-and-pencil test. No time limit was used and all pupils solved the test in 25–40 min.

5.2 Analysis

The data analyses for the first goal about the characterization of the natural number bias in fourth graders were done by means of a repeated measures logistic regression analysis modelling the probability that an answer to a specific item was correct. This was done using the generalized estimation of equations (GEE) module in SPSS 22, in order to correct for repeated (and therefore probably correlated) measures within subjects (Liang and Zeger 1986). To search for an overall natural number bias, the main effect of congruency was analyzed. By looking at the interaction effect between congruency and aspect and the pairwise comparisons underlying this interaction, we investigated whether a natural number bias could be found within each aspect as well. Based on the odds ratios (OR) and their confidence intervals (CI) per aspect, we could moreover investigate whether the natural number bias was relatively stronger for some aspects than for others.

With regard to our second goal—related to the question whether the inhibition of the inappropriate use of natural number knowledge in rational number tasks can be considered as a one-dimensional construct—we analyzed the data using item response theory (IRT) modeling. To find out whether fourth graders’ rational number understanding can be considered as a one-dimensional construct or as a multidimensional construct, we looked at whether the Rasch model fitted our data well. The Rasch model is the most simple IRT model and models the probability of answering an item correctly as a function of the difference between the person’s ability parameter and the item’s difficulty parameter (Rasch 1960/1980). Further, the Rasch model is characterized by the one-dimensionality assumption, which is important for this study. This assumption means that only one underlying variable or skill is measured by the items in the test instrument. This would mean that if the Rasch model fits the data well, we can deduce the fact that inhibiting natural number knowledge in rational number tasks in fourth graders is indeed a one-dimensional construct. Using the GOF.rasch function in the ltm package in R studio, a parametric Bootstrap Goodness-of-fit test was conducted using the Pearson’s χ 2 statistic to test the null hypothesis that the observed data have been generated under the Rasch model. Of course, because we were interested in pupils’ ability to inhibit their natural number knowledge only the data from the incongruent items were used for this analysis.

6 Results

6.1 The natural number bias as it occurs across different item types in fourth graders

A significant main effect of congruency, χ 2(1, N = 11,289) = 531.65, p < .001 was found. Fourth graders’ accuracy level was significantly higher on congruent (78.7 %) than on incongruent items (41.7 %), which confirms that an overall natural number bias was present in fourth graders. A significant interaction effect between congruency and aspect was also found χ 2(3, N = 11,289) = 96.681, p < .001. Figure 1 shows an overview of the percentages of correct responses grouped by congruency and aspect.

Fig. 1
figure 1

Accuracy levels (in %) per congruency and per aspect

Full size image

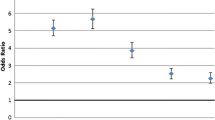
Pairwise comparisons of the mean accuracies were conducted for the congruent and incongruent items within each aspect. These revealed significantly higher accuracies on congruent than on incongruent items—and thus evidence for the natural number bias—for every aspect: density items (91.5 vs. 15.3 %, p < .001), size items (79.8 vs. 52.6 %, p < .001), and operations items (68.5 vs. 32.6 %, p < .001). The odds ratios per aspect of correctly answering congruent versus incongruent items gave an indication of the relative strength of the bias for each aspect. These odds ratios showed that the strength of the natural number bias was by far largest in density items (OR = 59.80, 95 % CI [35.25, 101.46]), but still clearly present in size items (OR = 3.56, 95 % CI [3.20, 3.96]) and operations items (OR = 4.50, 95 % CI [3.74, 5.41]), with no significant difference in the strength of the bias between the latter two.

6.2 Rational number understanding as a one-dimensional or multidimensional construct

Based on 200 data-sets, the non-significant p value (p = 0.57) suggests an acceptable fit of the model (with all items included) and confirms the null hypothesis that the observed data have been generated under the Rasch model. This result leads to the conclusion that the inhibition of natural number knowledge in fourth graders can be considered as a one-dimensional construct. To determine whether there are systematical differences in the difficulty levels of the different aspects, we looked more closely at the distribution of the items on the IRT-scale, which can be found in Fig. 2. The items are ranked according to their difficulty level (β) and the Rasch scale was identified by fixing the mean ability at zero. The obtained Rasch model showed that the density items were located at the very top of the IRT scale, meaning that they had the highest difficulty levels. Most size items were located at the bottom of the scale, having the lowest difficulty levels (although some of them are also located more towards the top of the scale). The operations items were distributed all over the scale, implying that they have varying difficulty levels. So, for fourth graders a good understanding of the size of rational numbers is a prerequisite for gaining understanding in operations with rational numbers. Further, both understanding in the size of rational numbers and in operations with rational numbers form a prerequisite for gaining understanding of density of rational numbers.

Fig. 2
figure 2

IRT scale with items ranged according to their difficulty level (β)

Full size image

Examples of items with a low versus high difficulty level per aspect can be found in Table 2. As already shown in Fig. 2, there were no density items with a low difficulty level.

Table 2 Examples of items with a low versus high difficulty level (β) per aspect
Full size table

7 Conclusions and discussion

Research has amply shown that a good understanding of rational numbers is an essential part of mathematical literacy. However, studies have repeatedly shown that children and even adults have a lot of difficulties with various aspects of rational numbers. This phenomenon is often—at least in part—attributed to the natural number bias. The results of this study extend previous research on the natural number bias in two ways. First, while there have already been studies about the three aforementioned aspects (density, size, and operations), no single study has addressed all of them in an integrated manner. Using a paper-and-pencil-test that included both congruent and incongruent items from every aspect (density, size, and operations) we tried to characterize the natural number bias as it occurs across different item types in fourth graders. Second, while several researchers found evidence for the natural number bias in the three different aspects separately, it remained unclear whether all these phenomena go back to the same root, that is, a bias in pupils’ thinking to rely on natural number principles. In this study we answered the question whether rational number reasoning can be considered as a one-dimensional construct, which would then refer to the more general capacity to inhibit natural number knowledge in rational number tasks.

First, the data from the paper-and-pencil test confirmed that students were hampered by the natural number bias. Evidence for an overall natural number bias was found in the higher accuracy levels on congruent items in comparison with incongruent items. This difference in accuracy was found in all three aspects, but not to the same extent. Pupils were most strongly biased on density items, while pupils showed a weaker, but still significant, bias on size and operations items. Second, using the data of the incongruent items of the same paper-and-pencil test, the IRT analyses showed that we succeeded in creating an instrument that measures one underlying skill, namely fourth graders’ ability to inhibit natural number knowledge in tasks with rational numbers, covering the various aspects which are reported in the research literature. Indeed, the Rasch model fitted for our data well, which implies that we can conclude that differences among fourth graders’ rational number reasoning—and more specifically their ability to inhibit the inappropriate use of natural number knowledge—can be considered a one-dimensional construct. One could argue that by not including an explicit test that measures individual differences in inhibition skills, we can not conclude that the underlying construct was indeed inhibition. However, conceptually speaking, one can argue that a specific type of reasoning (i.e., reasoning based on natural numbers) that is already acquired at an early age and that is well automatized needs to be inhibited in order to give an answer that is based on a type of reasoning that is achieved at a later age, and that is less automatized. Moreover, numerous studies that use reaction time data to investigate the natural number bias suggest that inhibition needs to take place in order to respond correctly to incongruent items (e.g., Obersteiner et al. 2013). These studies rely on the dual process theory, which distinguishes between intuitive reasoning (fast, automatic, and undemanding of working memory) and analytical reasoning (slow, controlled, and demanding of work memory) to investigate reasoning processes where interference takes place, such as the natural number.

While multidimensionality would have meant that students may develop an understanding of one aspect relatively independently of developing understanding of another aspect, the results of this study showed that this was not the case. More specifically, we found that a good understanding of size is a prerequisite for gaining understanding in operations and both understanding in both size and operations form a prerequisite for gaining understanding of density. Indeed, the results showed that the density items were located at the very top of the IRT scale with the highest difficulty levels, while most size items were located at the bottom of the scale, having the lowest difficulty levels. The operations items were found to be located throughout the scale, implying that they have varying difficulty levels. However, because there was only a limited number of density items included in the test, some caution is needed with the conclusion that a good understanding of size and operations forms a prerequisite for gaining understanding of density. While this is a possibly interesting finding, further research is required. A drawback of our method relying merely on a paper-and-pencil test is that the interference of natural number reasoning can only be demonstrated by participants’ erroneous answers. Future research would benefit from also including reaction time data to complement these accuracy data. Relying on the dual process theory, reaction time data are more and more used in order to show interference of intuitive reasoning processes in mathematical tasks, even in cases where correct answers are provided (Gillard et al. 2009; Obersteiner et al. 2013). Typically, the reaction times for congruent items and incongruent items are compared with each other. The main prediction is then that it takes more time to respond correctly to incongruent items than to congruent items. So, reaction time studies have the advantage that they can reveal the interference of natural number reasoning in rational number tasks even when answered correctly, by demonstrating that more time is needed to solve incongruent items correctly (Van Hoof et al. 2013).

A second drawback of the study, as already mentioned above, was the limited number of density items included in the test instrument of the fourth graders. Because the density principle is only briefly introduced in elementary school in Flanders, we chose to limit the number of items of this type. The data from the older age groups are needed to confirm the result of this study that density items are characterized by having consistently high difficulty levels as compared with items of other aspects. In line with this, we also do not know whether the one-dimensionality of rational number understanding is also applicable in the older age groups; and if this were to be the case, a closer look is also needed as to whether the same systematical differences could be found in the difficulty levels of the different aspects.

Nevertheless, the results of this study lead to several educational implications. First of all, the finding that a good understanding of size is a prerequisite for gaining understanding in operations (and probably also in density; however, more research is needed to confirm this claim) implies that initially more attention should go in the classroom to enhancing pupils’ understanding of the size of rational numbers. Further, continued instructional efforts seem to be needed to suppress the natural number bias more generally, by systematically pointing out the differences between natural numbers and rational numbers to the pupils.

Secondly, the results of this study have also some implications for further research. We have created an instrument that measures fourth graders’ ability to inhibit their natural number knowledge in tasks with rational numbers, and in our further work instruments for sixth to 12th graders may follow. These instruments create several possibilities for further research. The fact that a Rasch scale has been obtained implies that it is possible to construct a shorter version of the test that still has good diagnostic value. Such a shortened test version provides a score that is still situated on the same scale as the original, longer test, and can be used in new studies. These can, for instance, be investigations on the effectiveness of specific interventions to improve students’ rational number knowledge, or to conduct (internationally) comparative research, or studies relating the scores on this test to other aspects of students’ number sense and/or other student characteristics. The instrument can, for example, be used to further investigate the relation between natural and rational number sense. Only a few researchers have already investigated this relationship. Based on a longitudinal design, Bailey et al. (2014) found for example that first graders’ whole number magnitude knowledge predicted their knowledge of fraction magnitudes in middle school, after they had controlled for whole number arithmetic proficiency, domain-general cognitive abilities, parental income and education, race, and gender. These authors further found that, after controlling for the same variables, first graders’ knowledge of whole number arithmetic predicted their knowledge of fractions arithmetic in middle school. However, our test instrument can provide more fine-grained conclusions, given several limitations of this study. First of all, Bailey et al. measured rational number understanding in a rather general sense; they did not focus on rational number tasks where natural number knowledge may interfere in obtaining the correct response. Second, their test instrument only contained items from the aspects size and operations; and within both of the aspects, only a limited number of items was provided. Finally, only fractions were used in their study, so no conclusions could be made about decimal numbers. Using our instrument, a more complete view on rational number understanding in all its aspects can be obtained.