1 Introduction

Young children learn about and develop concepts, including geometrical concepts, before they begin first grade (Clements et al. 1999). At this age, young children begin to perceive attributes but may not realize which attributes are critical for identifying a figure and which are not (van Hiele and van Hiele 1958). For example, studies have found that when a triangle is not oriented with a horizontal side, children may not identify it as a triangle (e.g., Burger and Shaughnessy 1986). Children may also accept curved sides, either concave or convex, when identifying triangles (Tsamir et al. 2008). Fischbein (1993) considered the figural concepts as an interesting situation where intuitive and formal aspects interact. The image of the figure promotes an immediate intuitive response, yet geometrical concepts are abstract ideas derived from formal definitions. Concept images are not always in line with the formal concept definitions and thus conflicts may arise (Vinner 2011). One of our aims as educators is to promote, as early as possible, a concept image which is in line with the concept definition. Another aim is to promote the habit of consulting the concept definition when a conflict does arise. Taking into consideration that children are exposed to geometrical shapes from an early age, it is essential that proper intervention and guidance are given before intuitions become rooted and habits become set and difficult to amend. Towards these aims, early education can make a difference. Studies have found that the quality of preschool care is linked to adolescent functioning including cognitive-academic achievement (Vandell et al. 2010). Regarding mathematics, “focused early mathematical interventions help young children develop a foundation of informal mathematics knowledge, especially for children at risk for later school failure” (Clements and Sarama 2007, p. 136).

Recognizing the importance of learning geometry during the early years, several countries have developed guidelines for teaching geometrical concepts to young children. This paper will refer to education for children aged 4–6 years as early-years education. In Israel, by the time children enter first grade they are expected to differentiate between different polygons by considering the number of sides and vertices of each shape, as well as identify and name various two and three-dimensional figures (INMPC 2008). Developing children’s mathematical language and reasoning is also an important aim of early-years education (e.g., NCTM 2006).

The early-years teacher has an important role in fostering children’s mathematical knowledge, including their geometrical knowledge. Studies have shown that teachers’ subject-matter knowledge (SMK) is an important factor in their instruction (Ball et al. 2008; Blömeke and Delaney 2012; Shulman 1986). In mathematics, SMK includes knowledge of mathematical definitions (Delaney 2012), of which mathematical language is an inherent element. The early-years teacher “should use correct mathematical language in order to prevent, or at least minimize, the developments of misconceptions later on (INMPC 2008, p. 12). Yet, early-years teachers may not always be prepared to teach geometry (Ginsburg et al. 2006) and may require additional professional development for this purpose (Clements and Sarama 2011). In this ZDM issue, Moss et al. (2015) describe their professional development model, designed to support teachers in developing content knowledge and new approaches for teaching geometry and spatial reasoning.

Our study investigates early-years teachers’ concept images and concept definitions for some two- and three-dimensional figures. It also investigates teachers’ use of correct and precise mathematical language, and reference to critical and non-critical attributes.

2 Theoretical framework

Geometrical concepts, images, and definitions are at the heart of this paper. This section begins with a general discussion of theories related to concept formation and then reviews Vinner and colleagues’ (Tall and Vinner 1981; Vinner 1991; Vinner and Hershkowitz 1980) concept image/concept definition theory. The notions of critical and non-critical attributes, as they specifically relate to geometry, are discussed. Finally, we review some studies related to early-years teachers’ knowledge of geometry and mathematical language.

Concept formation within the domain of geometry, as in other domains, is a complex process. Some cognitive psychologists take the classical view that categories are represented by a set of defining features which are shared by all examples (Klausmeier and Sipple 1980; Smith et al. 1974). The features of a new stimulus would then be judged against the features of a known category in order to determine if it is or is not an example of that category. A second view is the prototypical view. This view suggests the existence of ideal examples, called prototypes, which are often acquired first and serve as a basis for comparison when categorizing additional examples and non-examples (Attneave 1957; Rosch 1973).

Within mathematics education, both views are reflected in the formation of geometrical concepts. Initially, the mental construct of a concept contains mostly images based on perceived visual similarities of examples, also known as “characteristic features” (e.g., Smith et al. 1974). This initial discrimination may lead to only partial concept acquisition. Later on, examples serve as a basis for both perceptible and non-perceptible attributes, ultimately leading to a concept based on its characterizing features. Such a process was described by Vinner and Hershkowitz (1980) who introduced the terms “concept image” and “concept definition” in reference to geometrical concepts. The term concept image is used to describe “the total cognitive structure that is associated with the concept, which includes all the mental pictures and associated properties and processes” (Tall and Vinner 1981, p. 152). A concept image includes all associations with the concept, including verbal, visual, vocal, and possibly other sensory associations as well (Vinner 2011). Concept images vary from person to person and from one culture to another. The concept definition refers to “a form of words used to specify that concept” (Tall and Vinner 1981, p. 152). A formal concept definition is a definition accepted by the mathematical community, whereas a personal concept definition may be formed by the individual and change with time and circumstance.

When teaching subjects other than mathematics, teachers often introduce new concepts by giving some general explanation, followed by a few examples (Vinner 2011). The role these general explanations have in concept formation is often inconsequential; in many cases, the collection of examples form a class in the student’s mind and the explanation is merely a matter of adding language to the image already formed.

As opposed to the general explanations often given for everyday concepts, definitions in mathematics are apt to contain only necessary and sufficient conditions required to identify an example of the concept. Other critical attributes may be reasoned out from the definition. Hence, if we define a parallelogram as a “quadrilateral with two pairs of opposite sides parallel,” we may then reason that the parallelogram is a quadrilateral that also has opposite sides of equal length, opposite angles of equal measure, and diagonals which intersect each other. The critical attributes then include (a) quadrilateral, (b) two pairs of parallel sides, (c) two pairs of sides with equal length, (d) two pairs of opposite angles of equal measure, (e) diagonals which bisect each other, and (f) other attributes of a quadrilateral. Non-critical attributes include, for instance, the overall size of the figure (large or small) and orientation (horizontal sides). It is often the non-critical attributes which contribute to the makings of a prototypical example. Hershkowitz (1989) reported that in addition to the necessary and sufficient (critical) attributes that all examples share, prototypical examples have special (non-critical) attributes “which are dominant and draw our attention” (p. 73). The prototypical examples often have the longest list of attributes. For example, the isosceles triangle with a horizontal base on the “bottom” may be considered prototypical of triangles. This often leads to a narrow concept image of triangles which in turn limits the examples students include in their example space. It may also cause students to incorrectly include non-examples which are visually similar to the prototype in the example space of that concept.

Within the domain of mathematics, having precise definitions for concepts provides the foundation for building mathematical theories and ensures mathematical coherence. However, these same mathematical concepts may have been encountered by the individual in other forms prior to being formally defined. Even after they are defined, mathematical concepts often invoke personal images. For example, in school mathematics, a function is usually defined as a correspondence between two sets which assigns to each element in the first set exactly one element in the second set. However, even after being introduced to this definition, some students will claim that a function is a rule of correspondence (Vinner 1991). This image does not contradict the definition. However, it eliminates the possibility of an arbitrary correspondence. In other words, the concept image contains a conglomerate of ideas, some of which may coincide with the definition while others may not. Accordingly, one of our major aims, as educators, is to bring our students to use only definitions as the deciding factor in identifying examples and forming geometrical concepts. Using precise mathematical language may contribute towards this aim. Thus, it is important that teachers, including early-years teachers, be knowledgeable of mathematical definitions and the critical attributes of each geometrical figure, and be fluent in mathematical language, knowing how to use language that is accessible to young children and yet precise (Ball et al. 2005).

In their review of research related to primary teachers’ geometry knowledge, Clements and Sarama (2011) noted that many teachers categorize shapes only on the basis of their overall physical similarity to prototypes, and at best recognize and characterize shapes by their properties. Few reach a level of relational thinking in geometry. Fujita and Jones (2006) found that many prospective primary teachers could draw a square but few could provide a sufficient definition of a square. Clements and Sarama (2011) also noted similar results in their research with early-years teachers. While few studies focused on early-years teachers’ knowledge of mathematical language, several educators (e.g., Ginsburg et al. 2008) pointed out the role of language in learning mathematics and, specifically, the importance of mathematical language. For example, the amount of teachers’ mathematics-related talk was found to be significantly associated with the growth of children’s conventional mathematical knowledge over the school year (Klibanoff et al. 2006).

Taking all of the above into consideration, and focusing on triangles, circles and cylinders (shapes introduced to children aged 4–6 years according to the mandatory early-years curriculum in Israel), the following questions guide this study: (1) Are early-years teachers familiar with definitions for triangles, circles, and cylinders and do they use correct and precise mathematical language when defining these shapes? (2) Are teachers able to identify various examples and non-examples for triangles, circles, and cylinders? (3) Is there a relationship between the definitions given by early-years teachers for triangles, circles, and cylinders and their success in identifying examples and non-examples of these figures?

3 Methodology

3.1 Participants and tools

In Israel, mandatory school begins at age three. For the past several years, we have been providing professional development for early-years teachers aimed at promoting their knowledge for teaching mathematics to young children (e.g., Tirosh et al. 2011). All teachers who participated in our programs had a first degree in education and were teaching 4–6-year-old children in municipal programs. Furthermore, the programs these teachers attended were all located in the same professional development center, serving the needs of the local community of teachers. Thus, the teachers had similar educational backgrounds and similar practical experiences.

At the beginning of each program, teachers were asked to fill out a questionnaire with two parts. One part focused on two-dimensional figures and a separate part focused on three-dimensional figures. This study focuses on triangles, circles, and cylinders, figures explicitly mentioned in the mandatory curriculum. We did not include rectangles and squares, also mentioned in the curriculum, because we did not want to involve the complexity of hierarchy. For a three-dimensional figure we included cylinders because they were considered to be recognizable from everyday situations and were often found in the early-years classrooms we visited.

The first part of the questionnaire requested participants to define a triangle (or a circle or a cylinder). They were explicitly told to write a definition that would be mathematically acceptable and not necessarily one they would use when talking to children. After teachers completed the first part, they submitted it to the didactician who then gave them the second part of the questionnaire. The second part of the questionnaire consisted of a series of figures (see Figs. 1, 2, and 3). Each figure was accompanied by a question: Is this a triangle (or circle or cylinder)? Yes/No.

Fig. 1
figure 1

Is this a triangle?

Full size image
Fig. 2
figure 2

Is this a circle?

Full size image
Fig. 3
figure 3

Is this a cylinder?

Full size image

The data for this study was gathered from different groups of teachers who participated in the various programs. Thus, the same number of teachers did not fill out each part of the questionnaires or even both parts of the questionnaire. However, all teachers who were requested to identify examples and non-examples of a figure were first requested to define that figure (see Table 1).

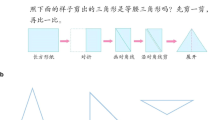
Table 1 Number of participants requested to fill out each part of each questionnaire
Full size table

In choosing the figures, we considered both mathematical and psycho-didactical dimensions. That is, we not only consider whether the figure is an example or a non-example of the target geometrical shape but also what developmental and cognitive issues might arise when identifying geometrical figures. Specifically, we consider whether or not the figure, be it an example or non-example, would intuitively be recognized as such. When considering triangles, for example, the equilateral triangle may be considered a prototypical triangle and thus intuitively recognized as a triangle, accepted immediately without the feeling that justification is required (Hershkowitz 1990; Tsamir et al. 2008). The scalene triangle may be considered a non-intuitive example because of its “skinniness.” The non-examples of each shape were also chosen in order to negate different critical attributes. For example, the open “triangle” contradicts the critical attribute of a triangle being a closed shape; the rounded “triangle” contradicts the necessity for the vertices to be sharp and pointy; the pizza has a side which is not straight; and the elongated pentagon is visually similar to a triangle but it has five, and not three, sides. Whereas a circle may be considered an intuitive non-example of a triangle, the pizza-like “triangle” may be considered a non-intuitive non-example because of visual similarity to a prototypical triangle (Tsamir et al. 2008).

While triangles may vary in the degree of their angles providing a wide variety of examples, the circle’s symmetry limits the variability of its characteristic features. In essence, only the size (i.e., the length of the radius) may be varied. Thus, only one example of a circle was given. With regard to cylinders, from our experience with children (Tirosh and Tsamir 2008) the long upright cylinder was considered to be an intuitive example. The “cone” with its top cut off negates the critical attribute of cylinders having two congruent circular bases and the “cylinder” cut on a slant negates the critical attribute that the bases must be on parallel bases. Because these figures are difficult to draw and difficult to visualize, we photographed solids that were available and constructed for the purpose of this research the “cylinder” cut on a slant and the “cone” with its top cut off.

3.2 Analyzing the data

Geometrical concepts may have several equivalent definitions. When analyzing teachers’ definitions, we referred to the definitions of triangles, circles, and cylinders found on the Ministry of Education’s official “Geometrical Definitions” website (http://www.education.gov.il/tochniyot_Limudim/math/geometria.htm#ge15). This site contains formal definitions for the various figures which are part of the curriculum from kindergarten through Grade 12. Teachers’ personal concept definitions were analyzed in terms of which critical attributes were mentioned, were those attributes sufficient to define the targeted concept, was the definition minimal or did it consist of extra critical attributes, and were extra non-critical attributes mentioned that constricted the targeted concept. In addition, the use of precise mathematical language versus everyday terminology was assessed. Two experts in the field of early-years mathematics education validated the analysis of teachers’ definitions. At times, the teachers did not use complete or precise mathematical language, and thus validation included a discussion among the researchers regarding whether or not a term used by the teacher referred to a critical attribute of the concept. Examples of such instances, as they pertain to the different figures, are given in the results section.

Teachers’ concept images were analyzed by investigating their identification of various examples and non-examples of the figures as well as by analyzing their written definitions in terms of the use of everyday notions that might point to the images teachers had in mind when referencing the figure. Regarding identifications, a mean score was configured for each participant per figure. For example, when investigating identification of a triangle, six illustrations were presented. Thus, a participant who correctly identified (either as an example or as a non-example) three out of the six figures received a score of 50 %. Finally, the mean score of the group was configured per figure.

4 Results

In this section we report on the findings for each figure separately. We begin with the results of teachers’ identification of the various examples and non-examples (see Figs. 1, 2, and 3). We then analyze teachers’ written definitions, first in terms of correctness and mention of critical attributes, assessing also the teachers’ use of mathematical language, and then in terms of what we can further learn about teachers’ concept images from their written definitions. (The terms “teachers’ written definitions” and “teachers’ definitions” refer to what teachers wrote when requested to write a definition, even if what they wrote would not be considered a definition by the mathematical community.) Finally, we compare teachers’ identifications with their written definitions and compare the results for the different figures.

4.1 Triangle identifications and definitions

Eighteen teachers were requested to identify examples and non-examples of triangles. Results indicated that most teachers succeeded in identifying the examples and non-examples presented (M = .96, SD = .14). All incorrect identifications related to claiming that a non-example is an example of a triangle (see Fig. 1). Three teachers did not identify the rounded-corner “triangle” as a non-example. One teacher did not identify correctly the open “triangle” and one teacher did not identify correctly the elongated pentagon as non-examples.

According to the Ministry of Education’s website, a triangle is defined as “a polygon with three sides.” This is a minimal definition. Out of 31 definitions, 29 were considered correct (see Table 2). One incorrect definition, “A triangle is a geometrical shape which has 3 straight lines,” was missing the critical attribute of the shape being closed. The second incorrect definition, “A triangle is equal sided—it has 3 equal sides,” narrows down the concept and excludes all triangles that are not equilateral triangles. Out of 29 correct definitions, five were correct and minimal. (Two teachers wrote that a triangle is “a polygon with 3 sides” and three teachers wrote that a triangle is “a polygon with three vertices.”) Twenty-four definitions were correct but not minimal. One teacher wrote that a triangle is a “closed polygon with three sides.” It is not necessary to write that the polygon is closed as closure is implied in the term polygon. One teacher added that the lengths of the sides do not have to be equal. Two teachers wrote that a triangle is “a three-sided polygon whose angle sum is 180°.” The rest (20 teachers) wrote that a triangle is “a polygon with three sides and three vertices (or three angles).” While in all of the above examples minimal definitions were not given, the nature of the additions varied. The teacher who added that the sides of a triangle do not have to be equal may have been addressing a common misconception among young children that triangles must be equilateral. The teachers who wrote that a triangle must have three sides and three vertices may have been relating to children’s fragmented knowledge of polygons (although they were told to write mathematical definitions that would not necessarily be used in the early-years classroom). Some children only check the sides of a polygon, without noting if the corners are pointy or round, while some children only check vertices, not noticing if the sides are straight or curved. In other words, it may be that the reasons that so many teachers offered definitions that were not minimal was due to their experience addressing young children’s geometrical conceptions.

Table 2 Correct and incorrect triangle definitions
Full size table

Three definitions were questionable, but ultimately considered correct. One teacher wrote that a triangle is “a geometrical shape having 3 straight lines which are closed.” According to the exact wording, the lines are closed. However, we took this to mean that the shape was closed and if a closed shape consists of 3 straight lines, it must be a triangle. Another teacher wrote as her definition, “3 sides, 3 angles, 3 lines.” Because the term “sides” implies a polygon, we considered it a correct definition, although there was no explicit reference to a polygon or a closed geometric shape. Another unclear definition was the following: “having 3 straight sides where all of the sides meet at one point.” It was deemed that the term “meet at one point” refers to the shape being closed. Notice that the last two definitions did not begin with placing a triangle in a larger class of items such as polygons or shapes. Definitions that begin by identifying a larger class within which the defined object falls, and then distinguishing that item from the rest of the class, are called genus–differentia definitions (Ouvrier-Buffet 2006). Except for the last two examples of definitions, all of the teachers’ definitions were of this form.

A triangle has several critical attributes, including: polygon, closed, three sides, three vertices, three angles, the sum of every two sides is greater than the third, and the sum of the interior angles is 180°. As can be seen from Table 3 all of the teachers wrote the critical attribute of “three.” Few teachers mentioned angles and even fewer referred to the sum of the angles. This may not be surprising as the notion of an angle and the sum of the angles of a triangle is a property usually derived from other geometrical properties during upper primary or lower secondary school.

Table 3 Frequency (%) of terminology used in triangle definitions (N = 31)
Full size table

Regarding the use of mathematical language, almost all teachers used correct and precise mathematical language. One teacher used the term “corner” instead of “vertex.” The term “shape,” used by 16 teachers, is rather general, and by itself may be considered less precise than using the term “polygon.” Is the shape closed or open? Is it two-dimensional or three-dimensional? However, a closer look reveals that the term “shape” was not used alone. Two of the teachers who used the term “shape” also used the term “polygon,” which infers a two-dimensional closed figure. Eight teachers used the combination of “closed shape,” indicating that their concept image of a triangle included closed shapes. In other words, only six teachers used the term “shape” alone. However, those teachers added that the shape had three sides or three vertices and having sides infers that the shape is two-dimensional and closed.

Finally, we compare teachers’ identifications with their definitions. All of the teachers correctly identified all of the examples of triangles, and only three teachers incorrectly identified some of the non-examples. Nearly all teachers who were requested to write a definition for a triangle wrote mathematically correct definitions using precise mathematical language. Regarding the incorrect identifications, two teachers incorrectly identified the rounded-corner “triangle” and one teacher incorrectly identified the rounded-corner “triangle,” the elongated pentagon, and the open “triangle.” Yet, these three teachers gave correct definitions. The first two teachers specifically related to the term “vertices” in their definitions. For example, one teacher wrote that a triangle is “a shape with 3 sides and 3 vertices and 3 angles.” Perhaps the teacher is not aware that a vertex must be a point and that angles are formed by 2 line segments (or rays) meeting at a point. In other words, the misunderstanding here may be twofold; the teachers may have an image of a rounded triangle which they consider to be an example of a triangle (like the yield sign seen on a road, often called a triangle in everyday language) and/or they may not comprehend the mathematical meaning of the term vertex. The third teacher, who incorrectly identified three non-examples, wrote that a triangle is “a polygon with 3 sides.” This is a minimal definition. The teacher did not specifically mention vertices or that the polygon must be closed. We are left wondering if the teacher merely recited a known definition without comprehending the term “polygon” or if her concept image of triangles includes those non-examples which are often called triangles in everyday usage. In other words, being able to correctly cite a geometrical definition does not guarantee correct identification and it is sometimes necessary to investigate concept images of the individual terms which make up the definition.

4.2 Circle identifications and definitions

In general, teachers (N = 18) were able to identify the examples and non-examples presented (M = .98, SD = .07). One teacher incorrectly identified the ellipse as a circle and one teacher incorrectly identified the spiral as a circle.

Out of 28 teachers who were requested to write a definition for a circle, 23 responded. One of the issues with defining a circle is that in Hebrew, there is a word, “igul,” which refers to the perimeter of the circle, and a different word, “ma’agal,” which refers to the interior area of the circle. This anomaly of the language does not appear for any other geometrical figure. Out of the 23 teachers who attempted to write a definition, five statements related to this issue without relating to any attributes associated with circles. These were excluded from the sample.

According to the Ministry of Education’s website, a circle is defined as “the set of all points in a plane that are equidistant from a given point. That point is called the center of the circle.” None of the teachers gave this definition or what may be considered an equivalent definition. In addition, unlike the definitions given for a triangle, teachers’ definitions for a circle were less clear, included a wide variety of terms, and required interpretation. For example, one teacher wrote, “A closed shape, from the middle point go out equal rays.” Thus, instead of categorizing the definitions into correct and incorrect definitions, we itemized the terms used, discussed our interpretations, and categorized these terms according to their possible reference to the critical attributes of a circle. The circle definition above leads to the following critical attributes of a circle: closed, planar figure (the set of all points), equidistant, given point. In the above definition, for example, the teacher does not explicitly write “all points in a plane” but she does write that a circle is a closed shape. We classified “middle point” as referring to some “given point,” and “equal rays” as referring to “equidistant.” Of course, rays may not be measured. However, the teacher’s mention of the rays being equal allows us to focus first on what critical attributes were alluded to by the teacher and then discuss the problem of language. Similarly, the term “middle point” may not be precise, but it does show that this teacher acknowledges that there is such a point from which the distance to other points must be measured. Our reason for analyzing the definitions in the above manner also arose from several definitions which contained fewer referrals to critical attributes. For example, one teacher wrote that a circle is “a closed shape with no vertices.” This teacher did not refer to the attributes of having points equidistant from some given point. Table 4 displays the number of teachers who wrote terms which may be associated with critical attributes of the circle, including examples of the terms we linked with those attributes.

Table 4 Frequency (%) of terminology used in circle definitions (N = 18)
Full size table

None of the teachers referred to the notion of a set of points. In addition, while none of the teachers specifically used the terms “planar figure” or “two-dimensional shape,” from our experience with teachers we concluded that the use of the term “shape,” for most teachers, refers to two-dimensional shapes. All of the teachers except one referred to the circles as a closed shape or curve, placing circles in the class of two-dimensional figures. This is the beginning of a genus–differentia definition. The difficulty for the teachers was mainly with the differentiating attributes. Approximately half of the teachers referred to the notions of equidistance and having a given point from which this distance is measured.

Teachers’ language also provided a window into their concept images for circles. Two teachers, besides writing that the circle is a closed curve, added that the curve has no beginning and no end. This added description relates to those teachers’ concept image of a circle. A different teacher described the closed shape as being “round.” While other shapes, such as ellipses, may be considered round, in Hebrew the term for round has the same root as the term for circle, so that the two concepts are linguistically linked. Recall that Vinner (2011) claimed that concept images include verbal associations. Similarly, the teacher who used “middle point” to refer to the center of the circle may not know that the term midpoint is used in relation to line segments and, for the circle, the given point is called the center. The teachers who used the terms rays, instead of line segments, may not know the difference between rays and line segments. Or perhaps, for those teachers, a circle invokes an image of a point from where rays go forth in the sense that they have a beginning and go on from there, till they hit the circle itself. In other words, the teacher is attempting to define the circle by describing how to construct it, and not by mentioning differentiating critical attributes. We term this type of definition a “construction-based definition,” a definition based on ideas of how to construct different shapes. This type of definition may be considered a product of one’s concept image. Note, however, that although the terms were not always precise, in general the teachers used mathematical terms and did not revert to everyday language to define the circle.

Four teachers wrote in their definitions that a circle does not have certain attributes. Two of those teachers referred to a circle as a closed shape and then wrote attributes which the circle does not have. For example, one wrote, a circle is “a closed shape without any vertices.” Certainly, a shape that has vertices cannot be a circle. However, not all shapes that are without vertices are circles. Two teachers wrote that a circle has certain attributes and does not have others. For example, one wrote that a circle is “a shape without vertices where all of the parts are distanced equally from the center.” It seems that for these teachers, their image of a circle includes not only what it is, but what it is not, or what attributes it cannot have.

Finally, we compare teachers’ identifications with their definitions. Only two teachers incorrectly identified one non-example each and both of those teachers did not write any definition for the circle. In fact, when requested to write a definition for a circle, the teacher who misidentified the spiral wrote, “problematic definition!” In contrast to their ability to correctly identify the examples and non-examples presented, teachers had difficulties writing a correct definition and referencing a circle’s critical attributes. We do note, however, that the teachers did attempt to use mostly mathematical language. In addition, while all of the teachers’ definitions were of the genus–differentia form, placing circles in the class of closed curves or closed shapes, we see a hint of another form of definition, a construction-based definition which describes how to construct the figure.

4.3 Cylinder identifications and definitions

In general, teachers were able to identify examples and non-examples of cylinders (M = 86, SD = .14). Taking a closer look, when considering identification of examples versus non-examples, 87 % of the identifications of examples were correct whereas 78 % of the identifications of non-examples were correct. The two figures most difficult to identify were the cylinder cut on a slant and the “coin-like” cylinder (see Table 5).

Table 5 Frequency (%) of correct identification of cylinders (N = 45)
Full size table

Out of 45 teachers who were requested to write a definition for a cylinder, 23 responded. According to the Ministry of Education’s website, “A cylinder is a solid figure composed of two congruent circles lying on parallel planes and all of the line segments connecting these two circles.” The website also offers an informal definition for a cylinder: “A cylinder has two congruent circle bases which are parallel and a ‘stretched’ casing which enwraps them.” None of the teachers wrote either of the above definitions. Thus, as with the circle definitions, we searched each teacher’s definition for references to a cylinder’s critical attributes. The above definitions were broken up in the following way, leading to six critical attributes of a cylinder: a cylinder is (1) a solid figure composed of (2) two (3) congruent (4) circles on (5) parallel planes and (6) a casing (all of the line segments connecting the two circles). We then asked two questions: Did the teacher refer to the critical attributes in some manner and did the teacher use precise mathematical language? For example, one teacher wrote, “a cylinder is a solid figure which has volume, whose base is circular and whose head is circular.” We concluded that this teacher referred to three critical attributes: solid, two, and circles. Although the teacher did not write that there were exactly two circles, reference was made to the “head” and to the “base,” and so the critical attribute of “two” was inferred. For each critical attribute a bank of associated words was created (see Table 6). Some of the terms refer to a critical attribute and make use of correct and precise mathematical language (e.g., writing “three-dimensional figure” instead of the word “solid”) while other terms we took as a reference to a critical attribute but did not make use of precise mathematical language (e.g., writing “a rolled-up shape” instead of the word “solid”).

Table 6 Frequency (%) of terminology used in cylinder definitions (N = 23)
Full size table

Nearly all teachers wrote that the cylinder has two bases and most wrote that the bases must be circles. Most teachers referred to the cylinder as a solid figure. One teacher incorrectly wrote that the cylinder is a polygon. One referred to the cylinder as a geometrical shape, without specifying that it was a three-dimensional shape. Five teachers listed attributes without first placing the cylinder in a larger class. For example, one teacher wrote, “two circle bases and a casing which opens to a quadrilateral.”

One teacher mentioned that the circles formed by the bases must be congruent. None mentioned that the bases must be in parallel planes. These results raise the question of whether the teachers did not realize that these attributes are critical or perhaps they did not have the language to express these ideas. Looking back at the results from the teachers’ identification, we arrive at a clearer picture. Nearly a quarter of the teachers claimed that the “cone” with its top cut off is a cylinder. However, this figure has two circular bases which are not congruent. Nearly half of the teachers claimed that the “cylinder” cut on a slant is an example of a cylinder. However, the bases are not on parallel planes. The teacher who did mention that the bases must form congruent circles incorrectly identified the “cylinder cut on a slant” as a cylinder. In other words, for some teachers, the absence of mentioning a critical attribute went along with their incorrect identifications of related non-examples. In general, non-indication of critical attributes in a definition may lead to misidentifying examples and non-examples.

Three teachers attempted to define the cylinder by describing how to construct this figure. One teacher wrote that a cylinder is “a rectangle whose parallel edges are connected forming two circles at the ends.” One can almost envision a rectangular paper being rolled so that the two parallel edges meet. This teacher correctly identified all of the examples and non-examples presented. However, two other teachers who gave similar construction-based definitions did not identify the coin-like cylinder as a cylinder.

In the case of the cylinder, as opposed to both the triangle and circle definitions, what stood out was the teachers’ use of everyday language. At times, as shown above, the everyday terms were used to reference, and perhaps reinforce, the presence of critical attributes. One teacher wrote that a cylinder is “a solid with two circular bases that are far away from each other, and a piece which connects, which enwraps, both.” The terminology of “a piece which connects, which enwraps” uses everyday language to express the attribute of having connecting line segments. This term was present in the informal definition of cylinders given on the Ministry of Education website, and thus may be deemed acceptable. However, the above definition also presents the teacher’s concept image in that the circular bases must be “far away from each other.” Essentially, this teacher added an attribute which is not critical. Recall that many teachers did not identify the “coin-like” cylinder as a cylinder. Perhaps the reason for this is expressed in the above definition. In the coin-like cylinder, the bases are quite near to each other. Similarly, one teacher included in her definition that the cylinder is “a long object.” Much of this everyday language used in the cylinder definitions (e.g., far away, long) offers a glimpse into the teachers’ concept images. For example, three teachers mentioned that the cylinder rolls. This sense of motion is part of the teachers’ concept image. Four teachers said that the cylinder is similar to a toilet-paper roll or a pipe. Five wrote that the cylinder was “hollow” or that it had “two openings.”

To summarize, we learned from the teachers’ written definitions, that their concept image of a cylinder is of a long, tubular object that has a circular base on both ends, but not necessarily on parallel planes, and rolls. Recall that 23 out of 45 teachers attempted to write a definition for a cylinder. Of those teachers, nine (40 %) misidentified at least one example or non-example of a cylinder. On the other hand, 20 out of 22 teachers (91 %) who did not write anything for the definition made at least one error. While we cannot know for sure why those teachers erred, it could be that their concept image of a cylinder was similar to the image mentioned above.

5 Summary and discussion

This study set out to investigate early-years teachers’ concept images and concept definitions for triangles, circles, and cylinders and the relationship between the definitions and images. When comparing the results for each figure (see Table 7) we see that, in general, teachers were able to identify examples and non-examples of triangles and define triangles; they were able to identify examples and non-examples of circles but had difficulties defining circles; and they had some difficulties in both identifying examples and non-examples of cylinders and defining cylinders. In addition, for each figure, teachers were slightly more successful in identifying examples than non-examples. This is in contrast to other studies which found that children are sometimes more successful in identifying non-examples of a figure than examples of that figure (e.g., Tsamir et al. 2008). Of course, results of such studies are dependent on the specific examples and non-examples presented to participants, as well as the age and educational background of the participants.

Table 7 Summarizing identifications and definitions
Full size table

When it came to defining triangles, teachers not only used correct mathematical language, but also exhibited an extended knowledge of critical attributes associated with the triangle. When defining the circle, several teachers neglected some of the critical attributes and others had difficulty finding precise mathematical terminology. One reason for these difficulties could be attributed to the teachers’ educational background. Although both these two-dimensional figures are introduced to children before first grade, polygons, and triangles in particular, are discussed and defined in primary schools and their attributes are studied extensively in secondary schools; while circles are introduced in the primary schools only in the sixth grade, and the formal definition and attributes of circles are only introduced during secondary school and are mostly emphasized in the high-level mathematical classes.

The fact that teachers did not recall the definition for a circle nor all of the critical attributes of a circle did not hinder their ability to identify the figures presented to them. As mentioned previously, unlike other geometrical shapes, there is less variability among examples of circles. That is, among triangles, one can vary, within bounds, the angles of the triangle and the lengths of the sides. One can also vary the orientation of a triangle. In a circle, one can only vary the distance of the points from the center, essentially varying its size, but nothing else. Thus, another possible reason for the teachers’ difficulties in writing a definition for a circle may have been that, considering the ease of identifying examples of circles, it may seem unnecessary to know the definition of a circle, and, as with other “unnecessary” facts learned in school, the definition was quickly forgotten. This is reminiscent of the teaching experience described by van Dormolen and Arcavi (2000) when students were introduced to the concept of a circle by citing its definition and hardly anyone could satisfactorily reproduce the definition at a later time. The authors concluded that the definition was meaningless until the students had first learned about the concept, investigating and experiencing the different elements that make up a circle. Similarly, a separate study found that many kindergarten teachers begin teaching geometry with the circle because it is round, has no corners, and is easy to draw with only one stroke of the pencil (Inan and Dogan-Temur 2010). In other words, the circle is viewed as a less complicated figure than the rectangle or triangle, seemingly disregarding its critical attributes.

Another interesting point is that some teachers felt the need to include in their circle definitions that a circle does not have vertices. Yet, none of the teachers wrote in their triangle definitions that a triangle is not round. This might stem from the teachers’ experience teaching shapes in kindergarten. Most of the two-dimensional shapes introduced in kindergarten are polygons. The one non-polygon shape introduced in kindergarten is the circle. Thus, teachers may define the circle in a way which differentiates it from polygons, not quite feeling the necessity to differentiate it from other non-polygon shapes. This is in line with the early-years curriculum which states, “children at this stage should recognize basic attributes such as, the number of sides, the number of vertices or a shape without any vertices, …” (INMPC 2008, p. 55).

While it may be that teachers relied on their concept image of circles, rather than their concept definitions, to identify examples and non-examples of circles, this reliance led to mostly correct identifications. This was not the case with cylinders. Teachers’ reliance on their concept images did not always lead to correct identifications. Studies have pointed out young children’s tendency to identify shapes based on the whole image and how this may lead to misconceptions (Tsamir et al. 2008; van Hiele and van Hiele 1958). Children may say that a figure is a triangle because it looks like the roof of a house, or that a figure is a rectangle because it looks like a door, and thus not identify triangles and rectangles which are not prototypes. As mathematics educators, our aim is to move students and teachers away from this type of reasoning, encouraging them to rely on the critical attributes of figures when solving geometry tasks. In this study, when defining cylinders, we found that teachers reverted back to whole-image reasoning, writing that the cylinder looks like a pipe or a toilet paper roll. This type of reasoning arose when teachers did not refer to certain attributes. We note that teachers’ responses to the questionnaires helped us to plan appropriate professional development for the different participants.

It might be argued that children in kindergarten do not need to know formal geometrical definitions. If this is the case, then it also might be argued that it is not necessary for their teachers to know these definitions. In addition, one may be knowledgeable of a concept definition, yet act in accordance with their concept image (Vinner 1991). We feel, however, that there are reasons for promoting teachers’ knowledge of definitions and use of appropriate mathematical language. In general, teachers’ knowledge impacts on the design of instruction and may mediate task selection and implementation. Specifically, knowledge of the critical attributes of a figure may help teachers plan activities which demonstrate these attributes. For example, one can demonstrate the critical attributes of a circle by having children attach a pencil to one end of a length of string and a pin or tack to the other end of the string, and thus draw a circle. Such an activity can demonstrate the importance of having one set central point and a determined length to create a circle. Being aware of critical, as well as non-critical, attributes of a triangle may help teachers choose various examples and non-examples to include in geometric activities and plan ways to help children differentiate and focus on each critical attribute. Levenson et al. (2011) described how one early-years teacher who participated in their program put up a sign board in her class with icons representing each of the critical attributes of a triangle. Other teachers developed, along with the teacher educators, a non-minimal working definition, one that children could use, that points to all the critical attributes, and that children could refer to and check back with when examining a geometrical figure. Finally, language is an element of culture. Using correct mathematical language, even at a young age, introduces children to the culture of doing mathematics.

We end with a few additional questions. Other studies investigating teachers’ knowledge of definitions presented teachers with various definitions and requested the teachers to evaluate those definitions (e.g., Zazkis and Leikin 2008). If the early-years teachers had been asked to evaluate definitions of circles, would they have recognized a correct definition for a circle, realizing that their own definitions were deficient? Another question regards the order of the questions on the questionnaires. Might the results have been different if the order of the requests was reversed? For example, if the teachers had first seen the various non-examples of the circles, would this have triggered them to add to their definitions that all of the points on the circle must be equidistant from some given point? If teachers had first seen the coin-like example of a cylinder, might at least those who correctly identified this figure as a cylinder not felt the need to use everyday terminology when describing the cylinder? Another possible methodology might have been to keep the present order and then request the teachers again to write a definition for each figure, allowing us to compare the definition given before seeing the figures with the definition given after presenting the figures. Future studies of kindergarten teachers’ geometric knowledge may take into consideration these possibilities.