1 In search of a participatory framework

There are three main emphases in research on and with mathematics teachers: their knowledge, beliefs, and identity. These lines of research use somewhat different theoretical or conceptual frameworks. Most research on teachers’ knowledge and beliefs is inspired by constructivism, although references to socio-cultural theory are increasing in number. In contrast, studies of teacher identity generally adopt a more social approach.

The relationships between individual and social aspects of human functioning have been subject to debate in mathematics education, but primarily in relation to the students. Some call for theoretical consistency and argue for the use of one family of theoretical frameworks. Currently, the emphasis is on the social character of human meaning-making and on the related metaphor of participation for learning (Lerman 2006; Sfard 2008). In contrast, others argue for the necessity of coordinating perspectives in spite of their theoretical incompatibility. In particular, it has been argued that social practice theory, socio-cultural theory, and radical constructivism all provide valuable insights and that a complementary use of participation and acquisition as guiding metaphors is needed for the pragmatic purposes of understanding and further contributing to classroom practice (Cobb 2007; Cobb and Yackel 1996; Sfard 1998).

There has been less discussion about the relationships between the underlying theoretical perspectives in research on and with mathematics teachers. More specifically, it is less explicit how to deal with the contrasts between the primarily acquisitionist underpinnings of research on teachers’ knowledge and beliefs and the participationist ones of research on identity.

In the present paper I present a framework for understanding the role of the teacher for emerging classroom practices. The notion of emergence is also important in the studies of student learning mentioned above that use multiple perspectives. However, the framework proposed here does not combine analyses of what is traditionally phrased in terms of knowledge, beliefs, and identity by coordinating theoretical perspectives across the acquisition–participation divide. Instead it uses a participatory approach and searches for patterns in individual teachers’ participation in different social practices, some of which are mathematical, while others are meta-mathematical or relate to broader aspects of the social situation at the school or in the classroom. The framework is in line with other recent attempts to theorise classroom practices from the perspective that human meaning-making and action are dynamic and ever-evolving rather than an enactment of relatively stable characteristics of the mental make-up of the individual (e.g. Wagner and Herbel-Eisenmann 2009).

From this perspective, the teacher contributes to classroom interaction by re-engaging in other past and present practices, possibly reinterpreting and transforming them in the process. For instance, the ways of substantiating a mathematical claim may change, if the teacher simultaneously seeks to be in line with a reform, to negotiate the school management’s position on how to take care of students with social problems, and to position herself within a team of cooperating teachers. The teacher’s contribution to the interaction, then, is influenced by and pieced together by her re-engagement in other, significant discourses and practices on the basis of the meaning she makes of the interaction itself. Highly malleable, the size, shape, and colour of these other ‘pieces’, e.g. the character and influence of the reform, are not given in advance, but emerge in the process. In each interaction, then, the ‘pieces’ form a fluctuating pattern that indicates the shifting significance of different, prior discourses and practices as well as the dynamic relationships between them. The proposed patterns-of-participation framework (PoP) intends at one level of analysis to piece together the pattern in the teacher’s contribution to individual classroom episodes; at another, it looks across individual episodes and builds on longitudinal studies to discern patterns of patterns, i.e. to point to trends and developments in the recurrent and possibly routinised ways in which the teacher engages with the students and the contents.

The main intention of this paper is to present PoP as a coherent, participatory framework, i.e. one that is able to address issues normally dealt with in the distinct fields of teachers’ knowledge, beliefs, and identity. PoP grew out of attempts to meet the conceptual and methodological challenges of belief research, i.e. to suggest an alternative to the elusive notion of beliefs as a key construct in mathematics education (Skott et al. 2011). In the first two sections below I outline the promises and problems of the field of beliefs and introduce PoP as developed in relation and opposition to this field. This includes discussions of two main theoretical sources of inspiration, social practice theory and symbolic interactionism. In the following sections I extend the framework to what is traditionally phrased in terms of knowledge and identity. This is the backdrop of an analysis of two short classroom episodes from an on-going study of a novice teacher, Anna. The analysis illustrates the use of PoP for the first of the two purposes mentioned above, i.e. of piecing together Anna’s contribution to specific interactions from her participation in significant prior practices and discourses. In turn this serves as the basis for a further specification of the concepts and methods of PoP.

2 The promises and problems of belief research

Since the 1980s much research has been done on teachers’ beliefs about mathematics and its teaching and learning as well as on the role beliefs play as teachers make sense of and contribute to classroom practice (Leder et al. 2002; Maasz and Schlöglmann 2009; Rösken et al. 2011; Thompson 1984). This line of research was and still is based on the assumption that teachers’ beliefs are a main obstacle to educational change, and that belief research may remedy what is generally referred to as the problems of implementation (cf. Skott 2008, 2009b).

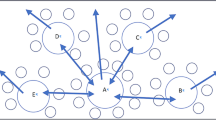
However, belief research is notorious for its conceptual and methodological problems. Beliefs are generally characterised as relatively stable, value-laden, mental constructs, which carry a subjective truth value. They are described as the result of comprehensive, prior social experiences, which are interpreted and filtered by pre-existing beliefs. It is the premise of the larger part of the field that teachers’ beliefs significantly influence teaching–learning processes, even to the extent that they are used as explanatory principles for practice (cf. Skott 2009a). Beliefs, then, are conceived as what Sfard calls objectifications, i.e. reified social experiences that gradually come to take on a life of their own independently of the processes that gave rise to them (Sfard 2008) (see Fig. 1).

Fig. 1
figure 1

Beliefs in mainstream belief research: a link between experience and practice

Full size image

The notion of beliefs, however, is still somewhat underspecified, and the discussion continues on how to distinguish it from knowledge, conceptions, emotions, and values. There is, then, as yet no consensus about an explicit definition of the term, in spite of the characteristics outlined above.

Further, beliefs pose methodological problems. As they reside entirely within the individual, they are difficult to access, and the best one can hope for are approximate inferences based on the teacher’s own accounts or instructional decisions. The problem is similar to inferring knowledge, but the situation is further aggravated as espoused versions are not necessarily a window on what people “really believe” (Wilson and Cooney 2002).

The conceptual–methodological impasse in belief research is particularly apparent when investigating belief–practice relationships. As Lester (2002) points out, there is a circular argument involved in attempts to infer beliefs from practice while explaining practice with reference to beliefs. Further, the premise that beliefs impact practice implies that there is little more to explain if a teacher’s beliefs, as inferred on the basis of questionnaires and interviews, are deemed compatible with the practices of the classroom. If there appear to be discrepancies between the two, attempts to come to the rescue of the premise include suggesting that the teacher is inconsistent (Raymond 1997); that the discrepancies are an artefact of the methods used and may be overcome by doing more fine-grained analyses (Speer 2008); that in the particular situation belief impact is overruled by the school culture (Ernest 1991); that there is more to the task of teaching than facilitating student learning and that instructional activity depends also on beliefs not related to mathematics (Skott 2001; Sztajn 2003); and that beliefs are situated and that the ones a teacher holds in the classroom differ from those of the research interview (Hoyles 1992; Lerman 2001).

The last three of these attempts adopt a more social perspective than most. They address the belief–practice quandary by viewing the role of teachers’ beliefs as a relational propensity in which (different understandings of) ‘context’ influences, respectively, the degree of belief impact, the selection of which beliefs are important at the instant, and the character of the beliefs themselves. None of them, however, question that beliefs are the default explanation for classroom practice.

3 From beliefs to patterns of participation

There are, then, few exceptions in belief research to the expectation that individuals’ acts and meaning-making are based on objectified mental constructs, beliefs. PoP is an outcome of previous studies that also focused on beliefs (Skott 2001, 2004, 2009a; Wedege and Skott 2006). Using recent developments of grounded theory (Charmaz 2000, 2006), these studies came to question the core assumptions of belief research and to call for more processual understandings of the role of the teacher for classroom practice.

PoP adopts a dynamic perspective on classroom practices as well as on the teacher’s contributions to them. As far as the former is concerned, the practices of the mathematics classroom are viewed as an ever-evolving outcome of individual and communal acts of meaning-making on the part of the teacher and the students. With regard to the latter, i.e. to the role the teacher, PoP does not focus on beliefs as objectified mental constructs, but on the role of the pre-reified processes that are said to give rise to them. It is assumed neither that teachers’ meaning-making is based on stable and objectified mental entities, nor that the acts of teaching should be seen as the release of such entities in a given context. Inspired by social interpretations of human functioning, especially symbolic interactionism (Blumer 1969) and social practice theory (Lave 1988, 1996; Lave and Wenger 1991; Wenger 1998), PoP seeks to understand how a teacher’s interpretations of and contributions to immediate social interaction relate dynamically to her prior engagement in a range of other social practices.

The inspiration from social practice theory is apparent when comparing what has been said already to Wenger’s understanding of practice and participation (Wenger 1998). Wenger sees practice as embedded in a community, which is further characterised by a joint enterprise, mutual engagement, and a shared repertoire. A practice is the collective pursuit of enterprises, during which “we interact with each other and with the world and tune our relations with each other and the world accordingly” (p. 45). This tuning of relations constitutes individual and communal learning.

To participate is in Wenger’s terms to engage in the negotiation of the meaning of a practice by employing a position of mutual recognition vis-à-vis other members of the community, even when the relationship is one of conflict. Further, the social character of participation is implied also when we are physically or temporally at a distance from the community in which the practice unfolds. Both these characteristics of participation are in line with my use of the term. However, for my present purposes I need to further specify how a teacher’s participation relates to her engagement in other past and present practices. Like Bauersfeld (1994) and Voigt (1996), I find Chicago school symbolic interactionism helpful for this purpose.

Symbolic interactionism is based on Mead’s challenge to psychological behaviourism, in which he showed that “mind and self are, without remainder, generated in a social process” (Morris 1962, p. xv). In his account of symbolic interactionism, Blumer lists three premises of the approach (Blumer 1969). First, a person acts towards an object, whether physical or not, based on the meanings it has for her. Second, meaning emanates from symbolic interaction and is neither embedded in the object itself nor a result of an entirely individual process of construction. And third, meaning is in any situation handled and modified in an interpretive process in which the person by means of internalised communication indicates to herself what (aspects of the) objects to act on and negotiates the different meanings they may have.

The notion of symbolic interaction is based on the ability of humans to take the attitude of individual and generalised others. It consists of the dual process of interpreting others’ actions symbolically, including their (possible) reactions to one’s own physical and verbal gestures, and making indications to them about what to do (Blumer 1969). As part of this, the acting individual becomes an object to herself. This implies a processual view of self as consisting of two aspects or phases, an ‘I’ and a ‘me’ (Mead 1934). The ‘I’ contributes to immediate human interaction, while the ‘me’ is the essence and outcome of the individual becoming an object to herself. Taking the attitude of the other, then, implies that as the ‘I’ acts (says, does, thinks), we interpret the act as we think significant others do and tend to modify the indications we make in the process.

Viewed from this perspective, the teacher negotiates classroom practices by interpreting the students’ and her own possible contributions to the interactions symbolically. Some of these practices relate to mathematics, while others do not, and the teacher may simultaneously try to initiate an investigative activity, solve a (non-mathematical) dispute between groups of students, manifest her own professional authority, ensure a student’s position in the classroom, and prepare the class for the next test. Doing so, she takes the attitude of individual and generalised others and draws on practices stemming from her own schooling, from exchanges or less explicit interactions with her colleagues, from meetings with the parents or the school management, from theoretical discussions in her teacher education programme, and many more.

As my colleagues and I argue elsewhere, aspects of teachers’ participation in these prior social practices are enacted and re-enacted, moulded, fused, and sometimes changed beyond recognition as they confront, merge with, transform, substitute, subsume, are absorbed by, and further develop those that are related to the more immediate situation (Skott et al. 2011). PoP intends to disentangle the continuous shifts of participation in different social practices, and by doing so shed light on the role of the teacher in the practices that emerge in the classroom.

4 Extending the framework to knowledge

PoP initially focused on the roles of the teacher as they relate to norms, for instance: why a specific task raises a good mathematical question; why it may lead to valuable mathematical activity; what an acceptable mathematical solution is; and how a solution may be justified in the particular context. This is similar to belief research, as the emerging objects for which meaning is developed include the ones of mathematics, mathematical significance, mathematical proficiency, and mathematical learning. It should be reiterated, however, that in contrast to mainstream belief research these objects, as well as the practices that give rise to them, are seen as fluctuating, always in the making, and continuously renegotiated in classroom interaction.

In this and the following section PoP is extended from what is traditionally phrased in terms of teachers’ beliefs to knowledge and identity.

Over the last few decades much progress has been made in understanding the character of mathematics teachers’ content preparation (Ball et al. 2008; L. Ma 1999; Rowland et al. 2009). Building on Shulman (1986, 1987), these studies suggest that there are mathematical types of knowledge and ways of knowing that are special to the profession. It is, then, not only teachers’ pedagogical content knowledge, but parts of their knowledge of the content itself that must be related to instruction. This, however, does not in and of itself challenge acquisitionism, as one may argue that the teacher needs to acquire and possess a different kind of mathematics than what is taught in a standard university course, not that a more processual and participatory understanding is needed of what it means to know.

Sfard (2008) adopts a more participatory approach. Building on Vygotsky and Wittgenstein, she coins the term commognition to suggest that cognition and communication are but different manifestations of the same process. From this perspective mathematical proficiency is a matter of engaging in a discourse characterised by its own vocabulary, by certain visual mediators, by a set of routines (for instance for substantiating claims), and by endorsed narratives, i.e. the results of such substantiations.

Sfard focuses on mathematics as a generic socio-cultural practice. She does discuss examples of how students engage in mathematical discourse, including some in which they interact with more proficient ‘mathematists’. However, her discussion does not concern other aspects of the situations in question, and in this sense her approach differs from PoP. In spite of that, it may be combined with more locally social accounts. Transformations in ways of endorsing mathematical narratives may for instance be interpreted as an outcome of taking the attitude of different significant others. It is this understanding of knowing-in-action that we use in PoP.

5 Extending the framework to identity

In contrast to research on knowledge and beliefs, the more recent interest in identity is social at its core (Boaler and Greeno 2000; Brown and McNamara 2010; Sfard and Prusak 2005; Wagner and Herbel-Eisenmann 2009). This is the case also in studies on and with teachers (e.g. Hodgen and Askew 2007; Horn et al. 2008; J. Y. Ma and Singer-Gabella 2011).

These studies build on theoretical imports to mathematics education such as Wenger (1998) and Holland et al. (1998). They do so to develop understandings of the reflexive relationships between teachers’ identities and their participation in different social practices at and beyond their schools and teacher education or development programmes. This is much in line with the intentions of PoP. However, while some of these studies seem to coordinate acquisitionist and participationist analyses of teacher development, somewhat in line with the studies referred to previously on student learning, my intention here is to explore the potential of a more purely participationist analysis. I do so using some of same sources of inspiration as the studies mentioned above.

To Wenger (1998), identity is a continuous process of interpreting and reconciling negotiated experiences of membership of multiple communities of practice. It relates to the coordination of different trajectories of participation within and across the boundaries between communities. To any newcomer, “paradigmatic trajectories” indicate the possible and privileged modes of moving from peripheral to fuller types of participation. For a novice teacher, for instance, there are more or less clearly delineated ways of negotiating one’s position at the school and of developing professional identities in the process.

Somewhat similarly, Holland et al. (1998) view identity as “the imaginings of self in worlds of action” (p. 5). They link self-in-practice to figured worlds, i.e. to collective as-if worlds that shape and are shaped by the social practices through which they unfold. Their examples of figured worlds include academia, environmental activism, games of Dungeons and Dragons, and Alcoholics Anonymous. In each of these, “particular characters and actors are recognised, significance is assigned to certain acts, and particular outcomes are valued over others” (p. 52). Holland and colleagues use self and identity interchangeably as the dynamic relationship between the symbolic meaning systems of figured worlds and individuals’ positionings in their everyday social encounters. They mention Mead as an early inspiration for their work, and their notion of self-in-practice resembles the I–me dynamic in Mead’s (1934) view of self (cf. Sect. 3). Both emphasise the significance of immediate social interaction, and as Blumer (1969) points out, Mead’s notion of ‘self’ is more a matter of process than of structure. It allows for, or even insists on, the possibility of multiple, situated selves.

As a novice teacher positions herself in relation to her colleagues and the students she draws on multiple, often conflicting, figured worlds. She does so not merely by the contents of her verbal actions, but also by how she moves in the classroom, how she—possibly unreflectively—reacts to disruptive behaviour, and the assertion with which she addresses her colleagues in staff meetings. These acts may relate to her narratives about herself as being a good mathematician, an important role model for the students, a good colleague, or a mother of three and a brilliant tennis player, for that matter. It is, however, an empirical question how the significance, meanings, and mutual relationships of these narratives relate to her contributions to the practices that emerge in the classroom. To address this question I adopt a situated perspective on identity, one that sees it not as equivalent to self, but one that emphasises the shifting versions of the me that emerge in interaction.

I need also to clarify my use of the notion of participation. As mentioned before, it is to Wenger linked to a community of practice, which is further characterised by mutual engagement, a joint enterprise, and a shared repertoire. Some of these characteristics may be relevant also for one’s relation to a figured world. However, the notions of mutual engagement and joint enterprise need to be stretched to account for instance for the relationship between a novice teacher and the figured world of the reform, even though they may characterise the one between the teacher and her peers in a development programme that introduces the reform discourse. In spite of that I use participation also to account for the former situation. Participation is then a matter of negotiating meaning and of positioning oneself in an internalised discourse about the teaching and learning of mathematics. The teacher may, for instance, engage with the figured world of ‘the reform’, which enters the specific situation as a generalised other to inform the I–me dynamic and modify the indications and interpretations the teacher makes to herself and the way she contributes to on-going interaction.

6 PoP and empirical study: the case of Anna at Northgate

PoP conducts analyses that cut across what is traditionally phrased in terms of teachers’ knowledge, beliefs, and identity. As any other framework, it orients the questions asked, informs the research design, and influences what and how data are generated and analysed. Exemplary questions for PoP include: What roles, if any, do a teacher’s tales of herself as a professional play in how she engages the students in endorsing mathematical narratives? How, if at all, does her relation to educational discourses such as the reform modulate how she and her students negotiate the meaning of mathematical proficiency? What is the connection, if any, between how she engages with mathematics in and outside classroom contexts? And how, if at all, does collaboration with her colleagues play a part in how she positions herself in relation to the students in the classroom?

These questions are reflexively related to the unit of analysis and have implications for the research design. Person-in-practice, often suggested as the unit of analysis in studies with a social perspective on human functioning, is a possibility also in PoP, the practice in question being the one that evolves in the classroom. The design, however, must as far as possible allow access to practices, and figured worlds beyond the classroom, for instance as represented in the teacher’s narratives about her own schooling; about formal and informal collaborative activities with her colleagues; and about discursive manifestations such as the reform. The unit of analysis may then be described as the teacher-in-multiple-practices-and-figured worlds as they relate to classroom interaction.

I refer to a study of Anna, a young Danish lower secondary teacher, to exemplify the use of PoP. The general question of the study is what roles she plays in emerging classroom practices. In the course of the study it became apparent that this includes the more specific questions mentioned above.

6.1 Methods

The study of Anna is part of an on-going multiple case study of teachers’ professional identities prior to and in the first few years after their graduation. Anna works at Northgate Primary and Lower Secondary School, a school of approximately 750 students in a well-to-do area a few miles from the centre of a city in Denmark.

There are three methodological challenges in the study. First, we need an approach that views instruction as continuous transformations of teachers’ modes of participation in the classroom in view of broader social practices and figured worlds at the institution in question and beyond. Second, an interpretive stance is needed that views these practices as well as shifts in the teachers’ engagement in them from the perspective of the teachers themselves. Finally, it is not apparent at the outset what practices and figured worlds are significant for the teacher in question, and the design needs to be so flexible as to allow for new and unexpected ones to turn up.

To meet these challenges we use a qualitative approach inspired by grounded theory (Charmaz 2006). We have previously used grounded theory without the objectivist connotations often associated with it, and we by no means consider ourselves free from theoretical prerequisites in the present study. However, we still use the coding schemes, constant comparisons, and memo writing of grounded theory as means to theorise classroom processes. These methods have proved helpful when addressing the challenges mentioned above.

The criteria for the selection of the research participants include their commitment to the profession and their mathematical and pedagogical self-confidence as evidenced in a questionnaire and in the first interview. If possible these criteria are supplemented with whether the schools have clear educational and/or school mathematical priorities. These criteria are not based on the expectation that the participants’ verbal accounts are a window on contextually stable understandings of themselves as teachers or teachers-to-be. Their accounts may, though, indicate practices and figured worlds, for instance the one of the reform, that are discursively significant for the participants themselves, and that may turn out to inform their contribution to school and classroom practice. Between them the criteria are to ensure that the cases are critical (Flyvbjerg 2006), and may bring to the fore elements of conflict and congruence between the participants and the dominant practices at their schools that are less likely to be apparent if other criteria are used. In turn, this may allow novel interpretations and analytic generalisations about relationships between teachers’ participation in mathematics classrooms on the one hand and in educational practices and discourses beyond it on the other.

Anna certainly meets these criteria. It should also be mentioned that we did not know Anna beforehand, and that she had no prior relationship with the universities involved in the study.

At present the data on Anna include: a questionnaire; 4 interviews, including 2 using stimulated recall; observations of 30 lessons organised as 15 sessions of 90 min; observations of 2 meetings in Anna’s team at Northgate, i.e. between Anna and her 3 closest colleagues; short, informal interviews made after almost every observation; and informal observations of staff-room communication. Examples of students’ work and of Anna’s interpretations of it have also been collected.

I conducted semi-structured interviews with Anna after her graduation and again towards the end of her first year of full-time teaching. In the first, she was asked to reflect on good and bad experiences with mathematics teaching and learning in school, at college, or during her practicum; the second focused on her experiences with teaching mathematics at Northgate and on her relationships with the school, her colleagues, and the students. Two stimulated recall interviews were conducted in the middle of her second year and the beginning of her third year of teaching, i.e. after observations of 8 and 24 lessons of teaching, respectively.

The classroom observations are from three periods of 2 weeks in three consecutive terms, beginning in the autumn of the second year after Anna’s graduation, when she teaches grade 7. One class, 7A, is observed in all three periods for 8, 8, and 6 lessons, respectively. In the present context I focus on the first two periods of observations in 7A, i.e. on the ones from Anna’s second year as a full-time teacher.

Observations and interviews are audio and video recorded, respectively, and transcribed in order to allow for analyses of verbal and gestural communication. Anna’s colleagues are opposed to recording team meetings, and the data are texts written immediately after each meeting based on comprehensive observation notes.

6.2 Becoming a teacher

Anna is 25 years old when she finishes her teacher education programme at a prestigious college, having studied mathematics as one of four school subjects. Eighteen months before her graduation she gets a part-time position at Northgate, teaching mathematics and science in grade 8. In retrospect she considers the combination of this teaching experience and the theoretical part of her teacher education programme important, as she has used her experiences to prioritise and inform her interpretations of the theoretical contents of her college education. Upon her graduation Anna accepts the offer of a permanent position at Northgate.

In the interviews Anna signals being highly committed to her new profession and confident to take on the responsibilities involved. She always wanted to teach, and she was always good in mathematics, her favourite subject in school (int. 1).

Anna’s college education is important. She is “in no way the same person as […] 4 years ago”, and being a teacher “has become like a part of oneself”. Further, Anna is

not just someone who teaches mathematics, I am a mathematics teacher […] someone who guards the profession and who burns [with enthusiasm] for it. […] You have to want something for the students, otherwise there is no reason. (int. 1)

She refers to real-world applications, a reduced role for standard algorithms, “landscapes of investigation”, and in particular to student communication to specify what she finds important (several interviews). Commenting on the second episode below, Anna elaborates on why she finds communication important:

[The students] simply find it so difficult to put it into words. […] ‘Then you just do like this.’ Yes, but why? […] I think that the communication part is so important, ’cause if they don’t know […] why they can change between percentages and fractions the way they do, if they don’t know why, I don’t think they remember in six months. (int. 3)

Anna’s enthusiasm for mathematics is more than matched by her insistence on building trusting relationships with the students and being an important role model for them (int. 1). She finds this easier with 13–16 year olds than with younger children, because she is not much older than the students. Comparing her present position with experiences from primary school in her practicum, she says: “This is where I belong. I’m completely different […] much more myself and much more alive […] than with young children” (int. 1).

To summarise, Anna’s tales of herself as a confident and committed professional relate to her experiences with school mathematics, with aspects of a reform discourse, and with student–teacher relations. These experiences are different in substance as well as in the amount of time she was involved and the extent to which they are based on non-verbal exchanges or are discursive in an explicit verbal sense. Also, they differ in their degree of specificity of the imagined actions and social relations. In spite of that, they qualify as figured worlds, i.e. as significant ‘as if’ worlds in which Anna re-engages at Northgate. I refer to them as ‘mathematics’, ‘the reform’, and ‘relationing’.

6.3 Anna at Northgate

Anna enjoys working at Northgate, not least as the teachers are organised in teams that teach (almost) all subjects to a year group. In the first year after her graduation Anna is in a team of four, who teach grade 9, the last year of lower secondary school. In her second year the same team teaches grade 7, Anna teaching mathematics in all three classes. In her third year the team follows the same group into grade 8, but Anna only teaches mathematics in one class, 8A. In both years she is the ‘class teacher’ for 7A/8A. This means that she is responsible for the overall progress of the class, for how it functions socially, and for collaboration with the parents.

Anna’s team meets approximately every 3 weeks for 1½–2 h. They discuss individual students’ problems and social problems in the year-group as well as PTA-meetings, the school’s sports day, and changes in the timetable. They do not, however, plan instruction or teach together. As a consequence, Anna in her second year is trusted with all responsibilities related to mathematics in the year group. The other side to this is that she is very much on her own. In that year she once asks an older colleague for suggestions, and she sometimes shares ideas with another novice “in the corridor” (int. 2). These two teachers are not in Anna’s team.

In the interviews, Anna does not consider the lack of cooperation about instruction a problem. She is confident professionally as well as mathematically, and she is backed by good relations with the students and frequent praise from the parents (int. 3). Also, she is explicit that the practices she wants to promote are not widely shared by the mathematics teachers at Northgate. This is evident for instance as the students never discussed mathematics before she came: to them “words do not belong in mathematics, […] only numbers” (int. 3). In contrast, her instructional approach is never questioned by members of her team.

While Anna is content with her professional isolation as it relates to the teaching of mathematics, she highly appreciates her collaboration with Ian and Jenny, the two other class teachers in her team. Anna tries to capitalise on Ian’s 25 years of experience and “maybe copy a little of what [he] does”, as it relates to communicating with the parents, keeping one’s teaching–learning materials organised, and maintaining a high level of commitment to the job. Ian has “this way of being with the students”, which Anna admires and finds helpful in her own attempts to build trusting relationships with them (int. 2). Jenny shares Anna’s interest in such relationships, and they both use the term “class mom” about their relationship to “their own classes”, i.e. the ones for which they are the class teacher.

In summary, there are two tasks to professionalism in Anna’s team. One is to assume individual responsibility for all content-related issues. The joint enterprise of the team, then, does not encompass the facilitation of students’ subject-matter learning, and Anna is not only entitled, but expected or even required, to manifest her own professional authority as it relates to mathematics. The other task is to address individual and social problems in the year-group. This is more collaborative and requires Anna to notice individual students’ home problems, changes in their reactions to the school, and problematic relations between students in the class or the year-group as well as to raise and address these issues in team meetings.

Anna’s mathematical self-confidence allows her to fill the void embedded in the former task, while her commitment to the students is fully compatible with the latter. Engaging in both, Anna gradually positions herself in her team and moves towards full participation in it, renegotiating the meaning of ‘teaming’ in the process. As she does so, ‘teaming’ becomes yet another small, but important, figured world for Anna, and a source of inspiration for her tales of herself as a professional. This is so both when she interacts directly with other team members and when ‘teaming’ functions as what Lave (1988) calls a structuring resource for the practices of the mathematics classroom.

The data generated so far suggest that there are four significant practices or figured worlds to Anna’s sense of her professionalism at the beginning of her teaching career: ‘relationing’, ‘the reform’, ‘mathematics’, and ‘teaming’. Their mutual roles differ across classes and across episodes within classes, also in 7A.

6.4 Anna in 7A

There are 8 girls and 13 boys in 7A. Anna is fond of the class and vice versa. A few students have social and domestic problems, but not to such an extent that Anna finds it difficult to cope. The main challenge is that the students’ mathematical proficiency varies a lot.

Anna is often engaged in ‘relationing’. She continuously interprets individual students’ emotional state as it relates to mathematical activity; she jokingly disarms what may otherwise turn into disciplinary conflicts; she invites the students to talk about their plans for the week-end and shares her own plans; and she helps them with individual problems as well as problems related to the social functioning of the class. It is indicative that a girl in 7A calls Anna during an interview to ask for help, because of a conflict with girls in Jenny’s class. After the call Anna comments:

I am happy that I am not 14 years old. […] Some of the girls can really make trouble. […] I have to call Jenny tonight and have a class-mom talk with her. (int. 4)

Although Anna values being an important adult to the students, ‘relationing’ is not easy, and she needs to balance what she half-jokingly describes as being “somewhere between a mother and a friend” against facilitating student learning (int. 4).

Also, Anna often draws on ‘mathematics’ and ‘the reform’ in the classroom. She endorses students’ mathematical narratives and introduces meta-discursive practices, for instance as they relate to mathematical communication. She insists that the students share their understandings and discuss how the content relates to everyday life and jointly make sense of concepts, procedures, and solutions, both in whole-class settings and when working at their desks.

The two episodes below are selected to show different ways in which the four figured worlds mentioned previously may support and constrain one another as Anna contributes to classroom interaction.

6.4.1 Episode 1: integrating ‘mathematics’, ‘relationing’ and ‘the reform’

Re-introducing statistics in 7A, Anna asks the students what they have done on it before, and why it may be useful. The students suggest a range of data sets they may collect, among them their own sports activities, their heights, and what people pay in taxes. They use frequencies and relative frequencies, without using the terms, and discuss ways of representing the results graphically. At all times Anna invites the students to make and question suggestions, explain procedures, and evaluate results. Sometimes she explicitly rejects the students’ proposals or makes her own suggestions for improvement. For instance, Annika suggests using “a curve” to show that nine out of the 16 students do sports. She is invited to the board to explain her thinking, but after a discussion in the class Anna comments that “I don’t think Annika’s suggestion was a good one. Curves may be used for all kinds of things, but not right here.”

They continue to discuss different descriptors, Anna asking them to explain in their own words what the descriptors may tell about the data set. The last descriptor is the mean, and the example suggested is the students’ shoe size:

1:

Anna: Can anybody explain in their own words what a mean is? Anton.

2:

Anton: It is like, […] we take [the shoe sizes] that have been mentioned and then divide by the ones who answered, and then we get the mean […].

3:

Anna: Yes, that is compl//that is a very good explanation of how you find the mean, but what is the mean? If you are going to say it in your own words, ’cause you’re completely//I can tell that you know how to find it, and that you also know what it means.

4:

Anton: It is like…I don’t know, it is sort of normal-like.

5:

Anna: Yes, I suppose that is one way of putting it. But then again, there is no shoe size that is normal, is there?

6:

Anton: No, no, but…

7:

Anna: Does anybody want to help, there are lots who want to help, JoAnn, do you want to help?

8:

JoAnn: You know for example, it is in a way the ones that there are the most of. The mean height for [people of] some age, the ones that there are the most of […] that is the height that is the mean.

9:

Anna: Yes, but what if we met two men who were 2 m tall, one who was one and a half, one that was one-sixty and one that was one-seventy, then there would have been the most who were 2 m. Is that the mean, then?

10:

JoAnn: No, but it is like of all of them.

11:

Anna: Nahh, Debra, you try.

The discussion continues for 4–5 min, seven students offering their suggestions. Towards the end Anna, pretending to be thinking aloud, says that the mean is what you get if you “mixed up all the feet and shared them so that everybody had the same”. She then asks if anybody calculated the mean, and when a student provides an answer she asks if it “makes sense”, i.e. whether the number is reasonable considering the data set. They agree that it does, and the students begin working at their desks.

Anna comments on the episode in an interview and says that the episode exemplifies that her “communication hobbyhorse […] can be pretty difficult at times” (int. 4), but communication is important as without it, the students will not understand.

In this episode Anna engages with individual students in turn, but takes the attitude of the class in general as she combines her mathematical authority with one of positioning herself almost as a more knowledgeable peer. She acknowledges the students’ attempts to explain what the mean is, but pushes them to move beyond procedural explanations (3; 5). None of the students produce what to Anna is a satisfactory explanation, and she suggests a wording herself. In this interpretation ‘relationing’ is combined seamlessly with the ‘mathematical’ activity of defining and with an implicit meta-discussion about defining as making conceptual sense of procedural explanations. In this episode, then, ‘mathematics’, ‘relationing’, and ‘the reform’ appear compatible or even integrable.

6.4.2 Episode 2: ‘relationing’ versus ‘mathematics’ and ‘the reform’

Interactions in 7A sometimes work out differently. Introducing an instructional sequence on fractions, decimals, and percentages, Anna asks the students what they did on it before, and the students say that they have discussed how it is used in everyday life. Anna asks what the proportion of girls is in the class, and the numbers are used to exemplify the conversions between the fractions, decimals, and percentages. Afterwards the students work on textbook tasks. In some they are to make conversions themselves, while in others the book suggests a conversion. In all cases, the students are to explain why or why not a conversion is correct, using oral and written language as well as drawings or diagrams. Introducing the tasks Anna says: “The most important […] is that you say the words, that you also talk [about this] in pairs. The more you talk mathematics, the better you get.”

Many students call for help. Anna walks around, and soon after she stays 3½ min with Debra and Annika, who are trying to explain why 20 % = 0.20 = \( \frac{1}{5} \), a result that is given in the book. Annika got stuck in her attempt to reduce \( \frac{20}{100} \). Debra has written “\( \frac{20}{100} = \frac{2}{10} \)” in her notebook:

1:

Anna: Try to look at what Debra has written.

[Annika looks in Debra’s notebook.]

2:

Debra: And then you divide by 2 and then it becomes 1 and 5 [writes; it now says “\( \frac{20}{100} = \frac{2}{10} = \frac{1}{5} \)”]. That is also what it says here [points in the book].

3:

Anna: But how did you go from here to here, Debra [points at the first equals sign]. Try to explain your steps so that Annika can see what you mean.

4:

Debra: Really, I am not very good//

5:

Anna: Yes, you are, come on now//

6:

Debra: So I just say that I take away the zero, and then I take half of that [points]. But I don’t really know if that is the easiest.

7:

Annika: But that depends on what kind of decimal number you have.

8:

Anna: [to Annika] Absolutely. […]

[…]

9:

Debra: But is it correct?

10:

Anna: Completely correct. It is really good. Now you two talk about this. Make a drawing and write some text that explains why what Debra did is right. [Leaves them.]

Asked to comment on Debra’s explanation, Anna says in the interview:

What immediately comes to mind, which I am sure it didn’t at the instant, is that ‘take away the zero’ (6), you know, why does she do that? There is no explanation […] she explains what she does, but not why she does it […] this is not a mathematical explanation. (int. 3)

Commenting on her own reaction in the episode, Anna says that “Debra […] thinks she is the weakest in mathematics in the whole world, which is not the case at all […], and she does actually put into words what she did, and that is probably why I accepted it”.

In this episode Anna asks Annika to look for help from Debra. Debra produces a procedural explanation, but Annika objects that the procedure does not always work (7). Anna supports her in this, but they do not follow up on it. Anna leaves them, confirming to Debra that her procedure is right.

Anna does not engage in ‘mathematical’ activity, neither about conversions between fractions, decimals, and percentages, nor about reducing fractions. When Debra begs for sympathy, approval, and support (4 and 9), Anna accepts her explanation in spite of Annika’s objection and of her own observation in the interview that the explanation does not qualify as a mathematical one. The situation changes for Anna from being one of mathematical substance to one of not jeopardising her relationship with Debra by acting judgementally. ‘Relationing’, then, becomes of prime importance and the substantiation rules of ‘mathematics’ are discarded, while the meaning of communication within ‘the reform’ loses its implicit prefix of ‘mathematical’ and is transformed into merely being a matter of verbal exchanges. It should be reiterated that Anna’s comments in the interview as well as her interactions with other students indicate that these transformations are neither due to lack of command of the relevant mathematics on her part, nor to an interpretation of Debra’s comment as a satisfactory mathematical explanation.

6.4.3 Comparing the episodes

In spite of the differences, the two episodes are similar in a number of ways. In both, the students use their own language, examples, and drawings or diagrams. They do so to reflect on what they have done before, to suggest how the contents may be linked to out-of-school experiences, and to discuss the contents between them. The use of colloquial vocabulary and self-made visual mediators is in line with the processual emphasis of ‘the reform’ as well as with ‘relationing’. Anna initiates, at least implicitly, a meta-level discourse that indicates that the value of ‘mathematics’ lies in its applications and that mathematical proficiency is communicative. At the same time she signals that what matters is the sense the students make of the subject and that she expects them to relate it to what is personally important for them.

Both episodes also seem to support Anna’s continued journey along the paradigmatic trajectory towards full participation in her team. The openness of the content-related part of ‘teaming’ allows her to build on ‘mathematics’ and ‘the reform’, but even as her participation in these figured worlds are challenged and changed, it does not question her professional self and self-confidence, as she connects to the other side of ‘teaming’, i.e. to ensuring the social functioning of the class, including the students’ well-being.

7 Concepts and methods revisited

PoP is an attempt to develop a processual and coherent framework for understanding the role of teachers in mathematics classrooms. Classroom practices are viewed as emerging, meaning as negotiated, and action as meaningful participation in current and other past and present practices, the character and significance of which are continually modulated as the I is informed by shifting interpretations of the me. The empirical question is what the patterns are in this participation. Addressing the question, PoP-research investigates for instance if and how certain modes of participation become dominant, transformed, or subsumed by others, and how their robustness or permeability and susceptibility to change influences the teacher’s contribution to the practices that evolve at the instant.

One part of the background to PoP is the methodological problems of more acquisitionist approaches. Participation in a distinct practice is more easily accessible than objectified, mental constructs such as beliefs, but there is more to practice than behaviour and there is no easy access to all the practices and figured worlds that are likely to be significant for classroom interaction. Difficulties arise for instance if they relate to the teacher’s own schooling, upbringing, or teacher education programmes. However, based on a previous study (Skott et al. 2011) as well as on the one on Anna, I suggest that the use of multiple open interviews and stimulated recall in combination with observations of classroom and staff-room interactions may allow some understanding of the meaning these practices may come to have for the teacher in classroom interaction.

These methods are also used in other approaches to research on and with teachers, and it is generally assumed that they shed light on the same underlying construct, whether it is beliefs, knowledge, or identity. In PoP the intention of methodical triangulation is different. Its strength is not that it enables one to ‘locate’ or specify one and the same construct, e.g. beliefs, with greater accuracy. Quite the opposite, different methods provide at least some access to different social practices and figured worlds, which may turn out to be significant for the interpretation of the teacher’s interaction with the students.

Another part of the background to PoP is the intention of developing a dynamic and contextual understanding of teaching. As mentioned previously, there are attempts to situate teachers’ knowledge and beliefs closer to instructional activity, and to challenge the de-contextualised understandings that used to dominate these fields. The intention of PoP is to take this one step further by limiting the emphasis on acquisition and include a perspective on the dynamics between the current practice and the individual teacher’s engagement in other past and present ones.

Finally, the acquisitionist underpinnings of knowledge and beliefs are at odds with the more processual approach generally taken to the study of identity. One may, of course, adopt a more dynamic perspective on knowledge and beliefs and define the former as the ability and propensity to engage in mathematical discourse in multiple situations and the latter as recurrent and value-laden participation in meta-discursive practices. However, the terms of beliefs and knowledge carry connotations of relative stability and expectations of impact that are at odds with the more processual emphasis. In PoP, it is an empirical question, not an a priori expectation, what the recurrent patterns are in a teacher’s contributions to classroom interaction, and how they are linked to the teacher’s shifting tales of herself as a professional. This makes it more in line with research on identity. Using a processual approach in relation to what is normally phrased as knowledge and beliefs may, then, have the potential to develop into a coherent approach to understanding the role of the teacher in mathematics classrooms.