Modeling Damage Growth in Oxidized High-Temperature Polymeric Composites

Thermal oxidation is a major degradation mechanism for polymers and composites operating at high temperatures. Controlling the damage progression in oxidative environments is critical for enhancing the long-term durability of these materials. The surface oxidation of the material and the damage evolution in high-temperature polymer matrix composite materials (HTPMCs) are highly coupled mechanisms. In this article, three-dimensional, finite-element methods are used to simulate both oxidation layer and damage growth in polymers subjected to bending loads and laminated composites subjected to uniaxial tension. An oxygen diffusion–reaction model determines the changes in properties due to oxidation and chemical strains induced by oxidation. The damage growth is simulated using mesh-free extended finite-element techniques and suitable damage initiation laws. The damage evolution observed with simulations is seen to be consistent with experimental observations reported in the literature.

Introduction

Patterns of oxidative damage growth in resin materials indicate that oxygen diffusion and surface cracking are highly coupled processes. Typically, surface cracks initiate in the oxidized resins and penetrate deeper through the thickness.1 The crack growth accelerates oxidation as crack faces adsorb oxygen and allow permeation of oxygen deeper into the material. The stress concentration at the crack tip also accelerates oxygen diffusion into the material and the oxides forming are weaker and brittle. The oxidation growth and surface cracking in a unidirectional composite are orthotropic with the fiber axis being the direction of preference.2 The oxide layers transverse to the fiber are thinner than those along the fiber axis due to diffusion anisotropy. Fibers also arrest the crack growth in the transverse direction. The oxidation front is highly heterogeneous in the fiber direction. Oxidation is seen to propagate deeper into the laminate in the regions where damage is evident. These highly coupled mechanisms make simulation-based life predictions extremely challenging for high-temperature polymer matrix composite materials (HTPMCs).

The chemical and microstructural changes in HTPMCS due to oxidation have been well studied. Evolution of crack and damage in polymer matrix composites under mechanical loading has received considerable attention as well. There are several methods for computational modeling of crack growth in composites. These include remeshing techniques to incorporate new crack boundaries3–7 in element-free Galerkin methods,8 embedded crack models for localized crack growth modeling,9–13 and extended finite-element methods (XFEM) or meshless methods.14–16 Methods enabling displacement discontinuity to propagate independently of the mesh are desirable. Although embedded crack models simulate localized crack growth without remeshing,17,18 the discontinuity must be confined to a single finite element. The XFEM is an extension of the conventional finite-element method based on the concept of partition of unity.16 It allows the presence of discontinuities in an element by enriching the interpolations for the Degree of Freedoms (DOFs) with special displacement functions. An XFEM approximation of a function is composed of a standard FE approximation and enrichment terms.19 These terms handle crack surface displacement discontinuities and specialized interpolations for the crack tip asymptotic stress fields.

In this article, we describe a framework for simulating oxidation and damage growth in resins and HTPMCs. Determining the oxidized structure after each aging time step and mapping appropriate stiffness and oxidization-induced strain fields into the mechanics model leads to a time-dependent simulation of oxidation and damage evolution in neat resins and composites. Fracture toughness and failure models are used to predict the extent of damage in the structure. We will describe the model and simulations performed in the two subsequent sections.

Oxidation and Damage Model

The adsorption, diffusion, and reaction interactions of oxygen with the matrix induce dimensional, modulus, and toughness changes leading to the development of damage and eventual failure of the structure. Damage evolution in HTPMCs is modeled with a sequential and decoupled method as shown in Fig. 1. A suitable time step is selected (typically 1–10 h) and the oxidation state is determined for the structure at the end of the time step. This entails identifying the stiffness and strength properties as a function of the oxidation state. An oxidation-induced chemical strain field is computed and mapped to the mechanics model. The stress and damage states are then computed for that time step. Boundary conditions in the oxidization are updated for newly created crack surfaces exposed to oxidizing environment. The process is then repeated for the next time step.

Fig. 1

Schematic of thermo-oxidation induced stress and fracture modeling

Oxidation State Model

The oxidation model for composites is based on simulating oxygen sorption, diffusion, reaction with the polymer, and conversion of polymer into oxides. HTPMCS reinforced by graphite or glass fibers operate at temperatures low enough to assume that the fibers are stable against oxidative degradation. The model has been described in detail in previous publications.20–22 Summarizing briefly, the oxidation state in the polymer is tracked throughout the aging process with a state variable ($\varphi$). The unoxidized polymer is denoted with $\varphi$ = 1 and the oxidized polymer has a limiting value of $\varphi = \varphi_{\text{ox}}$ that can be correlated to fully oxidized polymer.

$$ \frac{d\varphi }{dt} = - \alpha \left( t \right)R(C,T,\varphi ) $$

(1)

$$ R\left( {C,T,\varphi } \right) = R_{0} (T)\left\{ {\frac{{\varphi - \varphi_{\text{ox}} }}{{1 - \varphi_{\text{ox}} }}} \right\}\left[ {\frac{2\beta C}{1 + \beta C}\left( {1 - \frac{\beta C}{{2\left( {1 + \beta C} \right)}}} \right)} \right] $$

(2)

$$ \frac{\partial C}{\partial t} = \left[ {D\left( {\varphi ,T} \right)} \right]\nabla^{2} C - R(C,T,\varphi ) $$

(3)

$$ D\left( {\varphi ,T} \right) = D^{\text{un}} (T)\left\{ {\frac{{\varphi - \varphi_{\text{ox}} }}{{1 - \varphi_{\text{ox}} }}} \right\} + D^{\text{ox}} (T)\left\{ {\frac{{1 - \varphi_{\text{ox}} }}{{1 - \varphi_{\text{ox}} }}} \right\} $$

(4)

Assuming $C = C(\bar{x},t)$ denotes the dissolved oxygen concentration in a polymeric material at a material point $\bar{x}$ and time t, and R(C, T, $\varphi$) is the reaction rate that is temperature (T), concentration, and oxidation state ($\varphi )$ dependent. We consider the rate of polymer into oxide products as given in Eq. 1. The oxidation state of the polymer after complete oxidation is denoted by $\varphi_{\text{ox}}$. The reaction rate dependence in Eq. 2 shows the single parameter (β) that controls the concentration dependence. The functional form of the concentration dependence approaches unity when βC is greater than 3. The proportionality term $\alpha \left( t \right)$ is seen to be larger during the initial aging times and decrease after 200 h for several polymers.21 While the Arrhenius relation can characterize the temperature dependence of the reaction rate, the concentration dependence is shown in Eq. 2. The concentration dependence shows that the reaction will be oxygen starved when the soluble concentrations are low. The mass balance for the problem is shown in Eq. 3. The diffusivity is considered to be dependent on the oxidation state ($\varphi$) as described in Eq. 4, which reflects homogenized diffusivity from oxidized (superscript ox) and unoxidized (un)diffusivities of the polymer. Equation 3 is solved both on the spatial domain and over the aging times to determine the soluble concentrations with appropriate boundary conditions. Note that all the parameters are temperature dependent and the aging studies are typically isothermal; hence, no thermal diffusion is considered.

Stress and Damage Evolution

Conversion from unoxidized polymer to oxidized state leads to density and dimensional changes. Therefore, oxidation introduces mechanical strain that drives damage growth even when there are no applied mechanical loads. The oxidation state dependent stiffness model and the oxidation-induced strains have been discussed in a previous publication23 for the class of polyimides investigated in this article.

The XFEM, which was introduced by Belytschko and Black,16 uses the concept of partition of unity14 and allows local enrichment functions to be easily incorporated into the finite-element interpolation functions. Meshing to incorporate the discontinuities across the crack surfaces will no longer be necessary, making the XFEM methods suitable for damage propagation analyses. The enrichment functions typically consist of the asymptotic functions that capture the singularity around the crack tip and a discontinuous function that represents the jump in displacement across the crack surface as shown in Eq. 5.

$$ \mathbf{u} = \mathop \sum \limits_{I = 1}^{N} N_{I} \left( x \right)[ \mathbf{u}_{I} + H\left( x \right) \mathbf{a}_{I} + \mathop \sum \limits_{k = 1}^{4} F_{k} (r,\theta ) \mathbf{b}_{I}^{k} ] $$

(5)

In this interpolation function, $N_{I} \left( x \right)$ are the usual nodal shape functions and $\mathbf{u}_{I}$ is the usual nodal displacement vector associated with the continuous part of the finite element solution. Two damage-characterizing variables (a _I and b _I ) track the discontinuities passing through the element. The second term in Eq. 5 is the product of the nodal enriched degree of freedom vector $\mathbf{a}_{I}$ and the associated discontinuous jump function $H\left( x \right)$ across the crack surfaces, and it will enrich the element when a shape function support is cut by the crack interior. The third term enriches when a crack tip is detected by $\mathbf{b}_{I}^{k}$ and the associated elastic asymptotic crack-tip functions $F_{k} (r,\theta )$ are added for incorporating the asymptotically singular stress fields appropriate for that region. The asymptotic crack tip functions in an isotropic elastic material are written with respect to $\left( {r, \theta } \right)$, the polar coordinate system with its origin at the crack tip, and $\theta = 0$ is tangent to the crack tip. Accurately modeling the crack-tip singularity requires constantly keeping track of crack surfaces and propagation direction.

$$ F_{k} \left( {r,\theta } \right) = [\sqrt r \sin \frac{\theta }{2} \sqrt r \cos \frac{\theta }{2} \sqrt r \sin \theta \sin \frac{\theta }{2} \sqrt r \sin \theta \cos \frac{\theta }{2}] $$

(6)

We used Hashin–Rotem failure theory25,26 for composite lamina to detect damage initiation. The fiber tensile failure in the longitudinal (L-) direction is given by Eq. 7. Equations 8 through 10 denote the failure laws for the longitudinal direction under compression and transverse direction under tension and compression, respectively. $F_{\text{L}}^{t}$, $F_{\text{T}}^{t}$, and $F_{\text{Z}}^{t}$ are the tensile strengths of the composite in L- (along the fiber for a 0° ply.), T- (Transverse), and Z- (through the thickness) directions, respectively; $F_{\text{L}}^{c}$,$F_{\text{T}}^{c}$, and $F_{\text{Z}}^{c}$ are the compressive strengths of the composite in L-, T-, and Z-directions, respectively; and $F_{\text{LT}}^{s}$,$F_{\text{TZ}}^{s}$, and $F_{\text{ZL}}^{s}$ are the shear strengths in LT-, TZ-, and ZL-directions, respectively. $\xi$ is a contribution factor that determines the participation of the shear and z-axis stresses to the failure law. The driving stress state is denoted by {$\sigma_{{{\text{L}},}} \sigma_{{{\text{T}},}} \sigma_{{{\text{Z}},}} \sigma_{\text{TZ,}} \sigma_{\text{ZL,}} \sigma_{\text{LT}} \}$. As continuum solid elements are used, a three-dimensional extension to the classical plane–stress failure theory is used.

$$ \sigma_{\text{L}} > 0: \left( {\frac{{\sigma_{\text{L}} }}{{F_{\text{L}}^{t} }}} \right)^{2} + \xi \left[ {\left( {\frac{{\sigma_{\text{LT}} }}{{F_{\text{LT}}^{s} }}} \right)^{2} + \left( {\frac{{\sigma_{\text{ZL}} }}{{F_{\text{ZL}}^{s} }}} \right)^{2} } \right] \ge 1 $$

(7)

$$ \sigma_{\text{L}} < 0:\left( {\frac{{\sigma_{\text{L}} }}{{F_{\text{C}}^{t} }}} \right)^{2} \ge 1 $$

(8)

$$ \sigma_{\text{T}} > 0: \left( {\frac{{\sigma_{\text{T}} + \sigma_{\text{Z}} }}{{F_{\text{T}}^{t} }}} \right)^{2} + \left( {\frac{{\sigma_{\text{TZ}} }}{{F_{\text{TZ}}^{s} }}} \right)^{2} - \left( {\frac{{\sigma_{\text{T}} \sigma_{\text{Z}} }}{{\left( {F_{\text{TZ}}^{s} } \right)^{2} }}} \right) + \left( {\frac{{\sigma_{\text{LT}} }}{{F_{\text{LT}}^{s} }}} \right)^{2} + \left( {\frac{{\sigma_{\text{ZL}} }}{{F_{\text{ZL}}^{s} }}} \right)^{2} \ge 1 $$

(9)

$$ \begin{gathered} \sigma_{\text{T}} < 0: \hfill \\ \frac{1}{{F_{\text{T}}^{c} }}\left[ {\left( {\frac{{F_{\text{T}} }}{{2F_{\text{TZ}}^{s} }}} \right)^{2} - 1} \right]\left( {\sigma_{\text{T}} + \sigma_{\text{Z}} } \right) + \left( {\frac{{\sigma_{\text{T}} + \sigma_{\text{Z}} }}{{2F_{\text{TZ}}^{t} }}} \right)^{2} + \left( {\frac{{\sigma_{\text{TZ}} }}{{F_{\text{TZ}}^{s} }}} \right)^{2} - \left( {\frac{{\sigma_{\text{T}} \sigma_{\text{Z}} }}{{\left( {F_{\text{TZ}}^{s} } \right)^{2} }}} \right) + \left( {\frac{{\sigma_{\text{LT}} }}{{F_{\text{LT}}^{s} }}} \right)^{2} + \left( {\frac{{\sigma_{\text{ZL}} }}{{F_{\text{ZL}}^{s} }}} \right)^{2} \ge 1 \hfill \\ \end{gathered} $$

(10)

Simulations

Two specific cases representing damage growth in oxidative environments were studied. The first case entails bending an oxidized resin specimen to observe crack growth due to a combination of the oxidation-induced chemical strains and the mechanically applied loading. The second case simulated is the damage state near the open hole of a cross-ply laminated composite oxidized for 200 h under tensile loading. The heterogeneity in the oxidation layer23 growth due to orthotropy of the diffusivity in various plies is considered in the second case.

Case I: Damage Growth in an Oxidized Polymer Bending Specimen

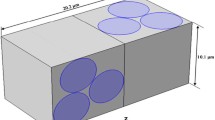
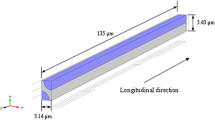
Consider a Bismaleimide (BMI) specimen subjected to a bending under displacement control as shown in Fig. 2. The specimen is subjected to isothermal aging at 177°C with one surface (bottom surface in the figure) assumed to be subjected to oxidative environment. The dimensions of the computational domain shown are 1 mm × 0.3 mm × 0.1 mm thick, which is embedded inside a larger bending specimen. A maximum displacement of 0.02 mm is applied to the center of the specimen as shown. A series of initial microcracks ($10 \, \mu {\text{m}}$ depth) is assumed are placed as shown in Fig. 3. Solving Eqs. 1 through 4 simulated the oxidation growth and the oxidation state for each material point is communicated to the mechanics analysis. Oxidation is simulated for every 50 h and the oxidation state was communicated to the mechanics model. The material properties utilized in the simulation are listed in Table I. Mechanical analysis is conducted with XFEM as implemented in the commercial finite-element software, Simulia (Dassault Systèmes, Vélizy-Villacoublay, France). After 200 h of oxidation, the crack growth is observed as shown in Fig. 4. The figure shows the crack propagation at the center of the specimen for various applied displacements. Figure 5 shows the contours of the damage state variable for various initial cracks. Multiple cracks start to propagate near the center of the specimen as the mechanical loading is increased. From the simulations, we can observe that the cracks are confined to the oxidized zone when the mechanical loading is under 4 μm, and further displacement loading is necessary for the cracks to penetrate into the unoxidized zones of the specimen. However, as the crack surfaces immediately adsorb oxygen to the saturation level, the dissolved oxygen concentration is higher near the crack surfaces.2 This leads to increase in oxidation reaction rate (Eq. 2) and further penetration of the cracks under the constant loading.

Fig. 2

Bending specimen and computational domain

Fig. 3

Meshing and XFEM model of a resin plate under bending load. The insert indicates the depth of an initial surface crack in the middle of the bottom surface

Table I Material Properties of BMI Used in Numerical Simulation

Fig. 4

Crack propagation in oxidized BMI resin plate. Oxidized zone is at the bottom on the specimen

Fig. 5

Damage state in oxidized BMI resin plate

Case #2: Damage Evolution Around an Open Hole in a Composite Laminate

Damage evolution of composites under oxidation depends on several factors including the fiber orientation of each layer, stacking sequence, oxidation layer thickness, and loading direction. In order to simulate damage pattern in the laminate composites, a homogenized stiffness24 and failure model for fiber-reinforced composites was adopted. The material behavior of the undamaged composite is assumed linearly elastic, and Hashin–Rotem failure laws25,26 govern the damage initiation. Postfailure behavior is modeled by stiffness degradation in the element to a specified but a small fraction of the original stiffness.

The oxidation-induced damage propagation near an open hole of a 16-ply composite plate is considered under tensile applied loading. The quarter symmetry model for the plate and through-thickness lay up of the composite is shown in Fig. 6. The dimensions of the computational domain shown are 25 mm × 10 mm × 2 mm. A 2-mm radius hole is located in the middle of the plate. The ply thickness is 0.125 mm and the plate thickness is 2 mm. The stacking sequence considered corresponds to a cross-ply composite [0/90]_4s. The materials chosen for the laminate composite are BMI resin with graphite fiber IM7. The corresponding parameters for the simulation are summarized in Table II. The material properties for the composite are determined from the rule of mixtures based on the properties of BMI matrix and IM7 fibers. The fiber volume fraction is assumed to be 50%. The material behavior of each fiber-reinforced polymer layer is assumed to be orthotropic. The elastic properties, including longitudinal modulus E ₁₁ and transverse modulus E ₂₂, shear moduli G ₁₂, and Poisson’s ratios ν ₁₂ and ν ₂₁ are listed in Table III. The damage initiation and evolution behavior is also assumed to be orthotropic as listed in Table IV, including the ultimate values of the longitudinal failure stresses $F_{\text{L}}^{t}$ and $F_{\text{L}}^{c}$, transverse failure stresses $F_{\text{T}}^{t}$ and $F_{\text{L}}^{c}$, and in-plane shear failure stress $F_{\text{LT}}^{s}$. The superscripts t and c refer to tension and compression, respectively. The subscript L and T refer to fiber direction and transverse direction, respectively. The interlaminar regions are lined with cohesive elements with zero thickness enabling simulation of delamination. A displacement with a magnitude of 0.016 mm is applied quasi-statically to the end of the plate along the 0° fiber direction. The plate is subjected to isothermal aging at 177°C with only the hole subjected to oxidative environment. The simulation, therefore, corresponds to a small diameter hole in a composite laminate subjected to oxidation around the hole. As indicated in the previous experiments and simulations,23 the oxidation layer growth is dependent on the fiber orientation as well as that in the adjacent layers. The oxidation layer sizes for each of the sixteen plies after 200 h aging was calculated using the oxidation model. Figure 6 also depicts the oxidized regions near the hole. The top view shows the oxidized region around the hole for the top (0°) lamina. The side view shows the heterogeneity associated with the fiber orientation angle. The 0° plies show deeper oxidation thickness compared to the 90° plies. The oxidation layer measurements for various 0° and 90° plies are shown in the figure. The 90° plies flanked by 0° have deeper oxidation zones than the center plies flanked by another 90° ply. The predicted oxidation zones for the 0° and 90° plies are 161 μm, 127 μm, and 119 μm after 200 h of aging time. Figure 7 shows the details of the finite-element mesh used in the analysis. Meshing in the oxidized and adjacent regions close to the hole is refined to capture the material property changes in the oxidized zone while it is relatively coarse away from the hole for optimum computation efficiency.

Fig. 6

Top and side views of the quarter symmetry laminated plate model

Table II Material properties of BMI matrix and IM7 fiber

Table III Homogenized properties of the lamina

Table IV Lamina strength properties

Fig. 7

Finite-element mesh of oxidative damage growth in a 16-ply HTPMC plate with a hole

A nominal mechanical load corresponding to a displacement (U _x  = 1 μm) is applied at the edge of the specimen along the fiber axis and the stress fields are determined with oxidation-induced strains. Figure 8 shows the normal stress contours near the open hole. The maximum normal stress in the 0° plies near the hole is observed to be about 66 MPa while the transverse stress of –12 MPa is observed near the symmetry face. Figure 9 shows the shear stress and first principal strain for this model. The maximum shear stress is 2.9 MPa and peak principal strain is observed to be 557 με. As simulated no damage will be initiated at 200 h without additional mechanical loading as the failure strengths of IM7/BMI composites far exceed these stress values.

Fig. 8

Normal stresses in the laminate without the damage. Stresses shown are in MPa

Fig. 9

Shear stresses in the laminate without the damage. Stress values are in MPa

Oxidative aging is carried out for an additional 200 h and additional displacement loading (u _x  = 10 μm) is applied to the model. Furthermore, the cohesive elements are added between the lamina to track delamination growth. Figure 10 shows the damage growth patterns in the 0° and 90° layers. The damage initiation is modeled the criteria proposed by Hashin25,26 as described in the previous section. Four different failure modes including fiber tension, fiber compression, matrix tension, and matrix compression are specified, respectively. In each failure mode, a corresponding damage variable evolves tracking the failure state. Figure 10a, b show the matrix tensile damage level (ϕ _T(z)t ) as given in Eq. 9 for the 0° and 90° plies, respectively. Figure 10c shows the damage level (ϕ _Lt) as given in Eq. 7 for the 0° ply. Figure 10b shows considerable transverse damage in the 90° plies and indicates the direction of crack propagation into the laminate.

Fig. 10

Damage patterns in the 16-ply HTPMC plate near an open-hole. (a) Matrix-tension damage level in the 0° layers, (b) matrix tension damage level in the 90° layers, and (c) fiber tension damage level in the 0° layer

A Note on Validation of the Simulations

Experimental observations27 of the damage and oxidation growth in high-temperature graphite/bismaleimide composites show that the damage growth is anisotropic and the discrete crack growth is in the range of 1–1.5 μm per hour. The damage growth patterns and the relative size of the damage zones as predicted for the two cases agree qualitatively with experimental observations. Two aspects of this problem make quantitative comparisons of experimental results with simulations results very challenging. First, the fracture toughness at elevated temperatures for both the matrix and the fiber–matrix interface are critical for accurate quantitative presentation and must be obtained with careful micromechanics experimentation. As the properties needed are for the oxidized matrix, there is a considerable need for additional experimentation. Then, the local microstructure characteristics (e.g., fiber spacing and undulations) influence the damage growth and drive the stochastic nature of damage as seen in experimental observations. The model must be refined to incorporate the characteristics that have the most influence on the damage growth. Therefore, the framework presented in this article is an essential first step toward a quantitative prediction of microcrack evolution in oxidizing structures, but it requires additional experimental characterizations for generating material behavior parameter values.

Concluding Remarks

This article presents a modeling framework for predicting damage growth after oxidation in polymer matrices and HTPMCs. Oxidation layer growth is simulated from a previously established thermochemomechanics model. Using XFEM techniques in combination with the oxidation growth models, we simulated damage growth in neat resins and HTPMCs. The simulations show that the crack initiation and propagation in the neat resins can predict cohesive elements with traction–separation laws along with both oxidation-induced strains and applied mechanical loads. The laminated composite simulation shows the complexity of interaction between the orthotropy of the oxidation growth and the orthotropy in mechanical properties and strengths. The damage mode, location, and extent can be predicted using the methodology described in this article.

One weakness in the described method is the segregation of the oxidation model and the mechanics model with the assumption that the stress state does not affect the oxygen diffusion or reaction rates. In reality, the diffusion is accelerated in the areas of high stress such as crack tips, and the oxidation model must consider the stress state in the model.