System-Based Approaches for Structural Optimization of Flexible Mechanisms

Abstract

This paper reviews the state-of-the-art methods to perform structural optimization of flexible mechanisms. These methods are based on a system-based approach, i.e. the formulation of the design problem incorporates the time response of the mechanism that is obtained from a dynamic simulation of the flexible multibody system. The system-based approach aims at considering as precisely as possible the effects of nonlinear dynamic loading under various operating conditions. Also, the optimization process enhances most existing studies which are limited to (quasi-) static or frequency domain loading conditions. This paper briefly introduces flexible multibody system dynamics and structural optimization techniques. Afterwards, the two main methods, named the weakly and the fully coupled methods, that couple both disciplines are presented in details and the influence of the multibody system formalism is analyzed. The advantages and drawbacks of both methods are discussed and future possible research areas are mentioned.

1 Introduction and Context

In the industry, engineers continuously face the challenge of providing high quality solutions that satisfy numerous requirements, often antagonistic. For instance, in many applications, the goal is to design the lightest component with the strongest mechanical resistance while achieving the lowest production cost. In the past, trial-and-error approaches were commonly used to design a satisfactory solution. However, these methods are expensive, time consuming and there is no guarantee to reach an optimized design. Concurrently to the development of numerical tools, analysis capabilities have been improved whereupon automatic design methods were developed to obtain the best solution in a rational way and to remove the arbitrary component of trial-and-error methods from the design process. Nowadays, in high technology industries such as aerospace and automotive sectors, structural optimization techniques are commonly employed to design the best solution resulting from a trade-off between various design criteria.

Traditionally, structural optimization of mechanical system components is performed using a component-based approach, i.e. interactions between the optimized component and its environment (system) are often disregarded. For instance, to minimize the mass of a vehicle suspension upper-arm, the arm is first isolated from the vehicle and then a set of representative static loads with appropriate boundary conditions are applied to the component, so that they mimic the complex loading to which it is subjected. Generally, these loads derive from the designer’s experience, from experiments or from standards. Dynamic amplification factors or safety factors are generally introduced to account for unmodeled phenomena. The resulting heuristic design processes can be justified in incremental design procedures, wherein the experience from the past is relevant for the new design. However, it becomes clearly questionable when addressing innovative designs and breakthroughs. Albeit the component-based approach stands when the overall system can be considered as stiff, the approach is arguable when flexibility effects become larger. Indeed, with the design of lighter and more flexible components, the interactions between the system components play a more important role on the system dynamics and they can no longer be neglected. The component-based approach should then be extended to account for the dynamic behavior of the entire system.

Analysis tools for mechanical systems must account for large relative displacements of the interconnected components. The earliest formulations were based on the assumptions that all system components behave as rigid bodies. However, under high static forces and/or high speed motion, this assumption leads to discrepancies in the response. Therein, the need of introducing flexibility within the analysis was rapidly motivated [50]. Later on, multibody system dynamic formulations have been developed to capture the compliant effects of the flexible bodies on the gross motion of the system in an integrated approach  [10, 28, 62, 116].

This review article is concerned with a system-based approach that supersedes and tends to replace the traditional component-based approach. This advanced approach takes advantage of the evolution of virtual prototyping. It combines the capabilities of modern multibody system (MBS) simulation tools with structural optimization techniques to perform an integrated optimization of flexible components. Figure 1 illustrates the system-based approach.

Fig. 1

System-based approach for the design of flexible mechanisms

2 Literature Review

2.1 From Mechanism Synthesis to Structural Optimization

The design of a mechanism able to accomplish a desired task can be performed by mechanism synthesis techniques which define the mechanism at a system level in the conceptual design phase, i.e. the design variables are “global” such as the dimensions of the system, the number and the nature of kinematics joints, etc. The precise design of each component is usually not addressed. The mechanism synthesis is generally performed using the static or kinematic response of the system considering rigid or flexible components, see for instance [36, 37, 40, 49, 50, 66–69, 72, 86, 87, 92, 99, 100, 107, 112, 119, 125]. Some of these studies also incorporate structural parameters such as the areas of cross section in the optimization process to achieve mechanical requirements.

Once the mechanism is defined at a system level, two more detailed design problems can be addressed. The first design problem concerns the optimal control of mechanisms, which aims at establishing the motor control laws, i.e. the actuator forces as a function of time, such that a certain optimality criterion is achieved, see for instance [9, 18, 19, 97, 142, 143]. The second design problem is the structural optimization of components that modifies some structural parameters to satisfy design requirements. For instance, a typical problem is to minimize the mass of a component by varying several structural parameters while respecting an upper bound on the stress maximum value. This latter problem is the main concern of the paper and a detailed literature review is hereafter conducted.

2.2 System-Based Approach for Structural Optimization of Flexible MBS

Taking advantage of the evolution of MBS simulation tools, Bruns and Tortorelli [26] initiated an approach combining rigid MBS analysis and optimization techniques to perform structural optimization of components with load cases evaluated during the MBS analysis. The method was illustrated on the design of a slider-crank mechanism loaded with the maximum tensile force calculated during the simulation. Almost at the same period, Oral and Kemal Ider [102] investigated the optimization problem that incorporates the dynamic response coming from the MBS simulation using a dynamic recursive formulation [84]. They incorporated a time-dependent constraint either by the most critical constraint or by agglomerating it using a Kresselmeier-Steinhauser function. To perform structural optimization of MBS, Etman et al. [53] applied the approximation concepts instead of considering a direct coupling between the MBS analysis and the optimizer. They used linear approximations of the responses with respect to intermediate variables, and a combination of a constraint screening strategy with pointwise constraints to treat the time-dependent constraints. They validated the approach and illustrated it on various mechanisms.

Nowadays, two main methods are identified to perform structural optimization of flexible mechanisms: the weakly and the fully coupled methods. The weakly coupled method deals with a static response optimization wherein the dynamic response is mimicked by a set of equivalent static scenarios derived from the MBS simulation. On the other hand, the fully coupled method concerns the optimization problem incorporating the time response coming directly from the MBS analysis.

2.2.1 Weakly Coupled Method

The weakly coupled method has been initiated by Saravanos and Lamancusa [109] to perform structural optimization of robotic arms. The authors selected several configurations of the mechanism whereupon the optimization was carried out based on representative static loading conditions coming from the designer’s experience for each posture. Even if the strategy tries to account for the entire system, this approach is approximate since a few configurations can hardly represent the overall motion as well as the various operating conditions. Moreover, the optimal design strongly depends on the designer’s choices in the load definition.

The transformation of the dynamic loading into a set of equivalent static scenarios can be properly defined with the incorporation of a MBS analysis in the optimization process. This transformation is realized in a two step approach. Firstly, a MBS simulation is performed whereby the loads applied to each component can be computed as a function of time. Secondly, each component is optimized independently using a quasi-static approach in which a series of static load cases evaluated at the first step are applied to the respective components. The equivalent static loads are fixed during the optimization whereas they are design-dependent. Hence, cycles between MBS analyses and the static response optimization processes are needed to account for this dependence. A series of studies were realized in which a couple of load cases associated to the reaction forces of the kinematic joints and boundary conditions were evaluated during the MBS analysis, and then considered for the static optimization process [3, 73, 74]. This approach has also been combined with lifetime prediction and durability analysis [2, 85].

An important breakthrough has been realized by Kang et al. [89] who proposed a method to define equivalent static loads (ESL) for the optimization of flexible mechanisms. For each time step and for each optimized component, it is possible to define an ESL producing the same displacement field as the one generated by the dynamic load at the considered time step in a body-attached frame. However, even if the concept seems totally general, it has been developed for MBS based on a floating frame of reference formulation. This formalism separates the elastic coordinates from the coordinates describing the global motion of the bodies which enables to define the ESL for each optimized component by simply isolating some terms of the equations of motion. The method has been extended to nonlinear finite element formalisms in [76, 129, 138, 140]. The ESL approach has been employed in numerous studies with conclusive results [79, 91, 118, 130, 148] and is implemented in commercial software tools.

The weakly coupled method sounds appealing as it circumvents solving a complex dynamic response optimization problem. However, the method focuses on the optimization of isolated components albeit the load cases stem from a system analysis.

2.2.2 Fully Coupled Method

In lieu of solving an equivalent static response optimization problem, the fully coupled method incorporates the time response coming directly from the MBS analysis in the optimization problem. Thereby, the optimization considers the system as a whole instead of isolated components as with the weakly coupled method. The fully coupled method leads to dynamic response optimization problems which are more challenging to solve than classical structural optimization problems chiefly due to the difficulties of evaluating the dynamic response and then incorporating it in the optimization [70]. In particular, the treatment of time-dependent constraints is an essential issue as well as the computation of the sensitivities of the displacements, velocities and accelerations, that can become costly [103]. Also, the local or global approximation of the original problem used in response surface methods or mathematical programming approaches is more complex as reported in [52, 80, 94, 95, 98]. The fully coupled problem can be solved using either the conventional nested approach or the Simultaneous ANalysis and Design (SAND) approach [65]. In the conventional nested formulation, only the design variables are treated as optimization variables whereas the state variables are solved by forward integration. With the SAND formulation, the design variables and the state variables are treated as optimization variables.

These issues were already encountered for structural optimization of structures considering transient loads and comprehensive studies were initiated in the seventies. The paradigm was to overcome the limitations of frequency response optimization. One of the earliest work consisted in minimizing the weight of frame structures subject to base motion and constraints on dynamic stresses and displacements [58]. Amongst the earliest studies, one can mention [1, 54, 147] as well as the literature survey [106]. Later on, the concepts of approximation were applied to incorporate the dynamic responses [31]. Interested readers may refer to the review article [90] for further details. Nowadays, dynamic response optimization is still a field of active research in structural mechanics.

Focusing on structural optimization of mechanical systems, the fully coupled method has been employed to solve optimization problems with crashworthiness and dynamic requirements [105]. Later on, topology optimization of flexible mechanism components has been carried out by taking advantage of the evolution of numerical tools [24]. The authors showed the feasibility and convenience of integrating the flexible MBS simulation directly in the optimization loop. Indeed, dynamic effects are naturally incorporated into the design problem. Amongst other recent works, the fully coupled approach has been adopted to design controlled flexible MBS [114] and also to solve problems incorporating durability-based constraints [133]. In the latter work, the authors avoid post-processing the MBS simulation results by evaluating the damage values during the MBS simulation to hasten their computations. The sensitivity analysis, a central step of the optimization loop, has been revisited for the direct method [139] and the adjoint method [77]. A method with iterative steps has been proposed to perform the sensitivity analysis efficiently [45]. Topology optimization of MBS has been investigated with an approximated sensitivity analysis [63]. By eliminating the terms that are assumed to have low order of magnitude while being numerically expensive to compute, convergence of the optimization process can be achieved in a reasonable computation time. This approximation leads to a sensitivity analysis comparable to the weakly coupled method. Contributions to the fully coupled method have also been realized by PhD thesis, see for instance [44, 75, 136, 144].

3 Assumptions and Layout of the Paper

The present paper reviews the state-of-the-art techniques to perform structural optimization of flexible MBS. The mechanism synthesis aspect is not considered by assuming that the mechanical system has a fixed configuration and topology (at the system level). Also, the optimal control is not directly discussed in this paper but future works may address the coupling between structural optimization and optimal control.

Graphically, this review paper navigates in the 3-dimensional space illustrated in Fig. 2. The three axes represent the MBS modeling accuracy, the type of optimization problem and the level of coupling between MBS analyses and optimization techniques. By moving away from the origin, the complexity of each branch increases and consequently leads to more challenging design problems.

Fig. 2

3-dimensional space of the design complexity in structural optimization of flexible MBS. The classification of the methods adopted in the figure aims to be general but exceptions may exist

Section 4 is dedicated to the problem formulation wherein the two fundamental tools to perform structural optimization of MBS are presented. Firstly, standard MBS formalisms are introduced. The design of lighter and more flexible mechanical systems requires advanced and accurate numerical tools for the analysis. The choice of a MBS formalism is important since it impacts the accuracy of the response as well as the computation time. The discussion is limited to a brief description of the formalisms since the justification of a particular formalism is out of the scope of this paper. Secondly, structural optimization techniques are presented. A special attention is devoted to the treatment of time-dependent constraints since this is an essential issue in dynamic system optimization.

Once the fundamental tools are presented, the fully coupled method is reviewed in Sect. 5. After a general description of the method, the discussion points out the consequences of the time-dependent constraint formulation over the optimization process convergence. Sensitivity analysis methods related to this method are also presented since the sensitivity analysis can drastically affect the computation time of the optimization process if not treated properly. A discussion on the choice of an optimization algorithm closes this section.

The weakly coupled method is reviewed in Sect. 6. After a general definition of the ESL method for MBS optimization, the formulation of an equivalent static response optimization problem and the framework of the solution process are presented. Afterwards, the ESL derivation adapted to the formalisms introduced in Sect. 4.1 is reviewed. The ESL derivation is an essential step of the weakly coupled method since the ESLs govern the optimized design.

In Sect. 7, the weakly and the fully coupled methods are compared and their advantages and bottlenecks are discussed. Also, this section highlights some future potential research areas. Section 8 concludes the paper.

4 Problem Formulation

4.1 Flexible Multibody System Dynamics

A flexible multibody system can be defined as a collection of rigid and flexible bodies interconnected by rigid and flexible kinematic joints (e.g. revolute, prismatic or universal joints) and by force elements (e.g. springs or dampers). A schematic MBS is depicted in Fig. 3. The analysis of such systems may involve strong couplings between the gross motion and deformations within the system.

Fig. 3

Multibody system diagram

Owing to the research conducted during the last decades and the growth of computational resources, flexible mechanisms are nowadays commonly analyzed using MBS simulation tools. The forward dynamics of MBS is the most usual approach and consists in understanding how the system moves under the influence of forces. Conversely, the inverse dynamics studies the forces that are needed to move the system in a desired manner.

Over the past years, several formulations have been developed to analyze flexible MBS. Hereafter, some standard formalisms are introduced.

4.1.1 General Form of the Equations of Motion

Let us consider that, after spatial semi-discretization, the configuration of a flexible multibody system is represented by a k-dimensional and time dependent coordinate vector $\mathbf {q}(t)$. The specific definition of these coordinates will depend on the selected formalism. Using fundamental principles of mechanics, the equations of motion of a MBS can be stated in a general way as

$$\begin{aligned} \begin{array}{lll} \dot{\mathbf {q}}(t) &{}=&{} \mathbf {Z}(\mathbf {q}(t))\,\mathbf {v}(t),\\ \mathbf {M}(\mathbf {q}(t))\,\dot{\mathbf {v}}(t) + \mathbf {B}^T(\mathbf {q}(t))\, \varvec{\lambda }(t) &{}=&{} \mathbf {g}\left( \mathbf {q}(t),\mathbf {v}(t),t\right) ,\\ \mathbf {\Phi }\left( \mathbf {q}(t)\right) &{}=&{} \mathbf {0}, \end{array} \end{aligned}$$

(1)

where $\mathbf {v}(t)$ is the velocity vector, $\mathbf {Z}$ is the velocity compatibility matrix, $\mathbf {M}$ is the mass matrix, $\mathbf {g}\left( \mathbf {q},\mathbf {v},t\right) =\mathbf {g}_{ext}\left( \mathbf {q},t\right) -\mathbf {g}_{gyr}(\mathbf {q},\mathbf {v})-\mathbf {g}_{int}(\mathbf {q})$ and $\mathbf {g}_{ext}$, $\mathbf {g}_{gyr}$ and $\mathbf {g}_{int}$ are respectively the external, gyroscopic and internal force vectors. The first equation in (1) is the velocity compatibility equation which takes several expressions depending on the adopted definition for the variables $\mathbf {q}$ and $\mathbf {v}$. In the simplest case, the compatibility equation boils down to $\dot{\mathbf {q}}(t) = \mathbf {v}(t)$. The vector $\mathbf {\Phi }$ stands for the kinematic constraints, $\mathbf {B}$ is the matrix of kinematic constraint gradients and $\varvec{\lambda }(t)$ is the Lagrange multipliers vector associated with the constraints. In this work, the presentation is limited to holonomic and scleronomic constraints but the extension to rheonomic or non-holonomic constraints can be included in the formalism without major difficulty.

4.1.2 Time Integration

The equations of motion (1) for a constrained mechanical system form a mixed set of second order differential and algebraic equations (DAEs). This results from the kinematic constraints that are represented by algebraic equations. The equations of motion are generally classified as “stiff” because the eigenfrequencies of the system are distributed over a broad frequency range. Numerical treatments of such DAEs are rather difficult compared to ordinary differential equations (ODEs).

A first solution strategy consists in removing the kinematic constraints by using some techniques such as the constraint regularization or the constraint reduction. As a result, the DAE system is transformed into an ODE system whereupon time integration can be performed with standard methods, e.g. linear multistep methods or implicit Runge–Kutta methods [48]. Also, the equations of motion can be directly expressed as a set of ODEs by formulating them in terms of minimal coordinates. This can be achieved either by performing a coordinate partitioning [146] or by employing the Maggi’s formulation [10]. Initial conditions, $\mathbf {q}(0)=\mathbf {q}^0$ and $\mathbf {v}(0)=\mathbf {v}^0$, must be associated to the equations of motion (1) in order to initiate the integration process.

Alternatively, time integration can be performed by applying algorithms directly to the DAE system. The choice of a particular algorithm is essential and, as detailed in [82], the following characteristics are usually desired: one-step implementation, unconditional stability and second-order accuracy. As a result, a popular family of algorithms in structural dynamics is the Newmark family. Indeed, with an optimal choice of parameters, the implicit Newmark algorithm exhibits an unconditional stability for linear problem, second-order accuracy and a one-step implementation. Modifications have been proposed to the classical Newmark time integrator scheme to introduce high frequency dissipation while preserving second-order accuracy. Numerical damping is especially valuable to eliminate spurious high frequency effects caused by higher-order modes of finite element models. Amongst others, one can cite the $\alpha$-method [78] or the generalized-$\alpha$ method [35]. When solving DAE system, the numerical dissipation of the integrator is of utmost importance [29].

Besides the implicit Newmark and generalized-$\alpha$ methods, alternative schemes have also been proposed in the literature for DAEs in flexible multibody dynamics such as explicit methods [83] or energy conserving schemes [12, 121–123].

4.1.3 Floating Frame of Reference Formulation

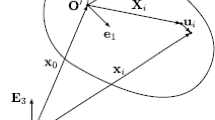
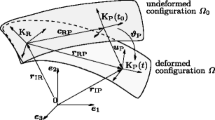
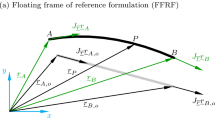
Currently, a widely used approach to model flexible MBS is the floating frame of reference formulation [59, 115, 116]. This formalism adopts two sets of coordinates to describe the motion of a flexible body in a MBS. On the one hand, a set of rigid body coordinates $\mathbf {q}_{r}$ represents the large displacement, i.e. translation and rotation, of a reference frame $K_R$ which follows the gross motion of the body. On the other hand, a set of elastic coordinates $\mathbf {q}_{e}^b$ describes the deformation of the body with respect to the reference frame (Fig. 4).

The absolute position vector $\mathbf {r}_{IP}$ of a point P lying in a flexible body can be expressed as

$$\begin{aligned} \mathbf {r}_{IP}(\mathbf {c}_{RP},t) = \mathbf {r}_{IR}(t) + \mathbf {A}(t) \left( \mathbf {c}_{RP} + \mathbf {u}_{P}(\mathbf {c}_{RP},t)\right) , \end{aligned}$$

(2)

where $\mathbf {r}_{IR}$ represents the motion of the reference frame, $\mathbf {c}_{RP}$ the position with respect to the undeformed configuration, $\mathbf {u}_{P}$ the elastic displacement and $\mathbf {A}$ the transformation matrix that defines the orientation of the reference frame with respect to the global coordinate system [115]. The elastic displacement $\mathbf {u}_{P}$ is often approximated by a Ritz-approach whereby it can be written as a product of the global shape functions $\mathbf {S}$ and the elastic coordinates $\mathbf {q}_e^b$ of body b used to introduce flexibility as

$$\begin{aligned} \mathbf {u}_{P}(\mathbf {c}_{RP}, t) = \mathbf {S}(\mathbf {c}_{RP})\mathbf {q}_{e}^b(t). \end{aligned}$$

(3)

The elastic velocity field is then represented by $\mathbf {v}_{e}^b=\dot{\mathbf {q}}_{e}^b$. The proper choice of global shape functions and of the reference frame belongs to the modeling process and has been addressed by many authors, see for instance [60, 111]. Regarding structural optimization, it is important to point out that regardless of these choices, the global shape functions $\mathbf {S}$ depend on the design variables.

Fig. 4

Kinematics of a flexible body using the floating frame of reference approach

The position and orientation of the floating frame is affected by the gross motion of the complete system. Some additional position and velocity coordinates, $\mathbf {q}_{r}$ and $\mathbf {v}_{r}$, have to be introduced to represent this gross motion. The two sets of coordinates for the system are gathered respectively at position and velocity levels as $\mathbf {q} = \left[ \mathbf {q}_{r}^{T}\, \mathbf {q}_{e}^{1 T}\,\ldots \, \mathbf {q}_{e}^{n_{b} T}\right] ^{T}$ and $\mathbf {v} = \left[ \mathbf {v}_{r}^{T}\, \mathbf {v}_{e}^{1 T}\,\ldots \, \mathbf {v}_{e}^{n_{b} T}\right] ^{T}$, where $n_{b}$ is the total number of bodies. The derivation of the equations of motion in a standard form can be found in [116].

In the special case of flexible MBS possessing a tree structure, it is possible to rely on a set of independent coordinates $\mathbf {q}$. This implies that the kinematic constraints disappear and that the equations of motion take the form of a set of ODEs.

4.1.4 Absolute Nodal Coordinate Formulation

Modeling flexible MBS is also commonly achieved by resorting to the absolute nodal coordinate formulation (ANCF) [117], that relies on a particular finite element discretization in terms of position and slope coordinates. In this approach, the position vector $\mathbf {r}^i_{IP}(\mathbf {c}_{RP},t)$ of a material point of a finite element i is approximated by the product of global shape functions $\mathbf {S}^i$ and nodal degrees of freedom $\mathbf {q}^i$. The latter gathers absolute positions and slopes. Formally, the position vector reads

$$\begin{aligned} \mathbf {r}^i_{IP}(\mathbf {c}_{RP},t)=\mathbf {S}^i(\mathbf {c}_{RP})\mathbf {q}^i(t). \end{aligned}$$

(4)

For a MBS composed of several flexible bodies, the generalized coordinate vector $\mathbf {q}$ includes the complete set of nodal position and slope coordinates of the different finite element meshes. The velocity variable is simply defined as $\mathbf {v}=\dot{\mathbf {q}}$. As previously mentioned, MBS modeling requires kinematic constraints, denoted by $\mathbf {\Phi }(\mathbf {q})=\mathbf {0}$, to ensure the connections between bodies due to hinges, spherical joints, etc.

The equations of motion are finally obtained by a standard finite element assembly procedure and it is worth noticing that the choice of absolute positions and slopes as nodal degrees of freedom leads to a constant mass matrix for each finite element formulated according to the ANCF.

4.1.5 Classical Nonlinear Finite Element Formalism

Flexible MBS can also be modeled using a geometrically exact nonlinear finite element formulation [62]. In this approach, absolute nodal coordinates corresponding to the nodal displacements and orientations are gathered in the generalized coordinate vector $\mathbf {q}$.

For example, considering a Timoshenko elastic beam with centerline coordinate $\alpha$, the position of arbitrary point on the beam element i can be represented as

$$\begin{aligned} \mathbf {r}^i_{IP}(\mathbf {c}_{RP},t)=\mathbf {r}_{IR}(\alpha ,t) + \mathbf {A}(\alpha ,t) \mathbf {c}_{RP}, \end{aligned}$$

(5)

where $\mathbf {r}_{IR}$ is the position of the reference point on the centerline, $\mathbf {A}$ is the cross-section orientation, and $\mathbf {c}_{RP}$ is the position of the point within the cross-section. According to the Timoshenko assumption, cross sections remain undeformed which implies that $\mathbf {c}_{RP}$ is constant in time. Then, the position and orientation fields $\mathbf {r}_{IR}(\alpha ,t)$ and $\mathbf {A}(\alpha ,t)$ have to be discretized along the centerline coordinate $\alpha$. For example, a two-node finite element i of length $L^i$ with $\alpha \in [0,L^i]$ relies on the 12-dimensional coordinate vector

$$\begin{aligned} \mathbf {q}^i(t)=\left[ \mathbf {r}_{IR}^T(0,t)\,\varvec{\uppsi }^T(0,t)\,\mathbf {r}_{IR}^T(L^i,t)\,\varvec{\uppsi }^T(L^i,t)\right] ^T, \end{aligned}$$

where $\varvec{\uppsi }(\alpha ,t)$ is a set of three parameters representing the rotation matrix $\mathbf {A}(\alpha ,t)$.

In this classical nonlinear finite element formalism, the position and orientation fields are interpolated independently, i.e. the interpolated value $\mathbf {r}_{IR}(\alpha ,t)$ is obtained by a linear interpolation between the two extreme values $\mathbf {r}_{IR}(0,t)$ and $\mathbf {r}_{IR}(L^i,t)$, while the interpolated value $\varvec{\uppsi }(\alpha ,t)$ is obtained by a specific interpolation between the two extreme values $\varvec{\uppsi }(0,t)$ and $\varvec{\uppsi }(L^i,t)$. It is important to remark that the rotation parameters are not interpolated linearly but that a nonlinear approach is implemented to guarantee the objectivity of the formulation [39].

4.1.6 Local Frame Formalism

In a classical nonlinear finite element approach [10, 62], the treatment of rotations is an important and non-trivial question. To illustrate the problem complexity, one can observe the non-commutative property of the rotation matrix product, i.e. reversing the order of two successive rotations around two different axes leads to different geometric configurations of the object to which they are applied. Also, a parameterization of the rotation variables is needed and may strongly affect the efficiency of the nonlinear computations as it depends on the adequacy of the set of parameters adopted [11]. Furthermore, singularities of the parameterization exist and require a careful consideration.

Recently, a particular Lie group formalism has been introduced which, among others, provides a more natural answer to the problem of rotation parameterization. While continuing with a nonlinear finite element approach as in [62], the dynamics of flexible MBS is alternatively described on a k-dimensional manifold G with a Lie group structure [25, 126, 127]. From a mathematical point of view, a Lie group G is a differentiable manifold for which the product (or composition) and inversion operations are smooth maps and on which differential geometry can be employed to perform operations. This mathematical framework leads to a new point of view on various problems related with the spatial interpolation and time integration of rotation variables.

The Lie group formalism is also at the core of the development of the so-called local frame formulation for MBS, which significantly attenuates the influence of geometric nonlinearities on the equations of motion. It relies on the representation of the motion based on $4\times 4$ transformation matrices evolving on SE(3), the Lie group of special Euclidean transformations.

Back to the example of an elastic beam, the position of an arbitrary point lying in a finite element i can be represented as

$$\begin{aligned} \begin{bmatrix}\mathbf {r}^i_{IP}(\mathbf {c}_{RP},t)\\ 1 \end{bmatrix}=\mathbf {H}(\alpha ,t) \begin{bmatrix}\mathbf {c}_{RP} \\ 1\end{bmatrix} \end{aligned}$$

(6)

with

$$\begin{aligned} \mathbf {H}(\alpha ,t)=\begin{bmatrix} \mathbf {A}(\alpha ,t)&\mathbf {r}_{IR}(\alpha ,t)\\ \mathbf {0}_{1\times 3}&1\end{bmatrix}. \end{aligned}$$

(7)

The Lie group formalism can then be exploited to formulate a consistent spatial interpolation for the $4\times 4$ matrix $\mathbf {H}(\alpha ,t)$. For instance, a two-node finite element i of length $L^i$ with $\alpha \in [0,L^i]$ relies on an interpolation of the matrix $\mathbf {H}(\alpha ,t)$ between the two extreme nodal values $\mathbf {H}(0,t)$ and $\mathbf {H}(L^i,t)$. Unlike in the classical finite element formulation discussed in the previous section, the interpolation formula couples the translation and rotation variables. For each node, a $4\times 4$ matrix is introduced and a 6-dimensional velocity vector $\mathbf {v}=[\mathbf {u}^T\varvec{\omega }^T]^T$ can be defined as

$$\begin{aligned} \dot{\mathbf {H}} = \mathbf {H}\widetilde{\mathbf {v}} \end{aligned}$$

(8)

with

$$\begin{aligned} \widetilde{\mathbf {v}}=\begin{bmatrix} 0&-\omega _3&\omega _2&u_1\\ \omega _3&0&-\omega _1&u_2\\ -\omega _2&\omega _1&0&u_3\\ 0&0&0&0 \end{bmatrix}. \end{aligned}$$

(9)

It turns out that $\mathbf {u}$ is the 3-dimensional linear velocity of the node and $\varvec{\omega }$ is the 3-dimensional angular velocity of the nodal frame. These two vectors are represented in the local frame attached to the node.

The Lie group formalism also offers a convenient framework to derive the equations of motion in terms of quasi-coordinates, i.e. without the need of introducing a parameterization of the matrix $\mathbf {H}(\alpha ,t)$. For a MBS including several interconnected bodies, the nodal matrices are collected in a block diagonal matrix

$$\begin{aligned} \mathbf {H}=\text {diag}(\mathbf {H}^1 \ldots \mathbf {H}^{n_{n}}), \end{aligned}$$

(10)

and the nodal velocities are collected in global vector

$$\begin{aligned} \mathbf {v}=[\mathbf {v}^{1T}\ldots \mathbf {v}^{n_{n}T}]^T, \end{aligned}$$

(11)

where $n_{n}$ is the number of nodes. Using classical principles of mechanics, the equations of motion have the following index-3 differential-algebraic (DAE) structure

$$\begin{aligned} \begin{array}{lll} \dot{\mathbf {H}}(t) &{} = &{} \mathbf {H}(t)\,\widetilde{\mathbf {v}}(t),\\ \mathbf {M}\,\dot{\mathbf {v}}(t)+ \mathbf {B}^T(\mathbf {H}(t))\,\varvec{\lambda }(t) &{}=&{} \mathbf {g}(\mathbf {H}(t),\mathbf {v}(t),t),\\ \mathbf {\Phi }(\mathbf {H}(t)) &{}=&{} \mathbf {0}_{m\times 1}, \end{array} \end{aligned}$$

(12)

where $\mathbf {g}(\mathbf {H},\mathbf {v},t)=\mathbf {g}_{ext}(\mathbf {H},t)-\mathbf {g}_{gyr}(\mathbf {H},\mathbf {v})-\mathbf {g}_{int}(\mathbf {H})$. The system configuration is represented by $\mathbf {H}\in G$ where G is a Lie group. Notice that the first equation is a matrix equation while the other two are vector equations. The equations of motion (12) represent the dynamics of a general class of conservative flexible multibody systems in a local frame approach. The formulation can be easily extended to account for non-conservative forces. It is also remarkable that, as for the velocities, the different forces appearing in (12) are also represented in the local frame and are thus much less sensitive to geometric nonlinearities.

These equations of motion can be directly integrated on the nonlinear manifold without introducing generalized coordinates, i.e. without introducing a parameterization of rotations. The adopted Lie group time integrator described in [22, 25] is an extension of the generalized-$\alpha$ time integration method. This Lie group time integrator exhibits second-order accuracy for all solution components, i.e. for nodal translations, rotations and Lagrange multipliers.

4.2 Structural Optimization Problem

4.2.1 Design Parameterization and Design Variable

Over years, optimization techniques have been developed to improve the design process and to lessen empirical or intuitive choices of the designer. The generality of optimization methods is somehow related to the number of inputs coming from the designer. Indeed, a smaller number of inputs usually leads to a broader design space since fewer restrictions are introduced. Nevertheless, a more general optimization problem typically requires a higher computational cost, which explains the concurrent evolution of optimization techniques and computational performance.

Optimal sizing of structures, also known as automatic sizing, is the simplest strategy in structural optimization. This method mainly concerns the modifications of transverse dimensions of structural components, such as the cross section of bars and beams or the thickness of plate and shell elements (Fig. 5), considering that the shape and the connectivity of the structure are known a priori and fixed during the optimization process. Since no geometrical modification of the structure arises, the same structural model, e.g. the finite element mesh, is kept along the optimization process.

Fig. 5

Structural optimization parameterizations

Zienkiewicz and Campbell [150] initiated the developments of shape optimization whereupon a rapid evolution occurred until reaching an industrial maturity. Shape optimization is a more ambitious method consisting in the design of internal and external boundaries of the structure without modifying the component topology. Two different approaches can be adopted. On the one hand, the optimization problem can be formulated at the CAD model level, independently of the finite element model, wherein the design variables are the parameters describing the geometrical entities such as a length, a radius, etc, or more generally, the control points of NURBS curves [13, 21]. On the other hand, the shape optimization problem can accommodate the nodal coordinates and nodal thicknesses as design variables whereby the optimizer directly works on the finite element mesh [17]. Shape optimization is suitable to improve the detailed design of structures considering simultaneously numerous criteria such as displacement, frequency, stress or buckling requirements.

Topology optimization has been developed to determine the optimal design of a component without a priori information of the component layout [14, 51]. The optimization method only requires the definitions of a spatial design domain, material properties, boundary conditions and load cases. Hence, regarding the reduction of the cost function, this method outperforms the two previous methods for which the designer’s initial choices strongly influence the outcome of the optimization process.

4.2.2 Design Problem Formulation

Engineering design problems can be cast into mathematical optimization problems upon which numerical methods can be applied. The optimization problem concerns the minimization of an objective function $f_0\left( \mathbf {p}\right)$ subjected to $n_c$ constraints $f_j\left( \mathbf {p}\right) \le \overline{f}_{j}$ which ensure the integrity of the structural design and its manufacturability [20, 65, 101]. The vector $\mathbf {p}$ gathers the $n_v$ independent design variables $p_i$ that are modified by the optimizer. Side-constraints $\underline{p}_{i} \le p_{i} \le \overline{p}_{i}$ limit the design space and reflect technological considerations. Mathematically, the optimization problem reads

$$\begin{aligned} \begin{array}{llllllll} &{} \underset{\mathbf {p}}{\text {minimize}} &{} &{} f_0 \left( \mathbf {p} \right) &{}\\ &{} \text {subject to} &{} &{} f_{j} \left( \mathbf {p} \right) \le \overline{f}_{j}, &{} j = 1,\ldots , n_c,\\ &{}&{}&{} \underline{p}_{i} \le p_{i} \le \overline{p}_{i}, &{} i = 1,\ldots , n_v. \end{array} \end{aligned}$$

(13)

The static response optimization of a structure modeled according to the finite element method can be formulated in this framework. Depending on the type of optimization, the design variables $\mathbf {p}$ can be geometrical parameters of CAD features, such as the radius of a circle, or the position of NURBS curve control points in shape optimization. In topology optimization, they can be related to the volume fraction of each element. The cost and constraint functions $f_0$ and $f_j$ are generally implicit nonlinear functions of the design variables. They represent the mass, the compliance, the displacements, the stresses, etc, and their evaluation requires an analysis of the structure, e.g. the solution of the equilibrium equation for a given static load.

A more explicit formulation of the optimization problem (13) involves the generalized displacements $\mathbf {q}$ of the finite element model. Consequently, the problem formulation yields

$$\begin{aligned} \begin{array}{llllllll} &{} \underset{\mathbf {p}}{\text {minimize}} &{} &{} f_0 \left( \mathbf {p},\mathbf {q}\right) &{} \\ &{} \text {subject to} &{} &{} \text {SEE}(\mathbf {p},\mathbf {q})=\mathbf {0}, \\ &{}&{}&{} f_j \left( \mathbf {p},\mathbf {q}\right) \le \overline{f}_{j}, &{} j = 1,\ldots , n_c,\\ &{}&{}&{} \underline{p}_{i} \le p_{i} \le \overline{p}_{i}, &{} i = 1,\ldots , n_v, \end{array} \end{aligned}$$

(14)

where $\text {SEE}(\mathbf {p},\mathbf {q})=\mathbf {0}$ represents the static equilibrium equation. For a linear problem, this equation takes the form

$$\begin{aligned} \text {SEE}(\mathbf {p},\mathbf {q}):=\mathbf {K}(\mathbf {p})\mathbf {q}-\mathbf {g}_{ext}(\mathbf {p}). \end{aligned}$$

(15)

Actually, this equilibrium equation is used to eliminate the dependent variables $\mathbf {q}$, that can then be expressed as a function of the design parameters $\mathbf {p}$. This approach is known as the “nested approach” [65].

With the general and robust design framework provided by this problem formulation, optimization problems can be solved using various types of optimization algorithms, ranging from heuristic to gradient-based algorithms.

4.2.3 Extension of the Design Problem Formulation for MBS Optimization

MBS optimization problems are formulated as an extension of the optimization problem formulation (13) in which the time parameter t steps in, leading to a dynamic response optimization problem. Extending the formulation (13) and incorporating explicitly the equations of motion (1), the design problem reads

$$\begin{aligned} \begin{array}{llllll} &{} \underset{\mathbf {p}}{\text {min}} &{} &{} f_0 \left( \mathbf {p},\mathbf {s}(\cdot )\right) &{}\\ &{} \text {s.t.} &{} &{} \text {EOM}(\mathbf {p},\mathbf {s}(t),t)=\mathbf {0}, &{} t \in \left[ t_0 , t_f\right] ,\\ &{} &{}&{} \mathbf {q}(t_0)=\mathbf {q}^0(\mathbf {p}),&{}\\ &{}&{}&{}\mathbf {v}(t_0)=\mathbf {v}^0(\mathbf {p}),&{}\\ &{}&{}&{} f_j \left( \mathbf {p},\mathbf {s}(t),t\right) \le \overline{f}_{j}, &{} j = 1,\ldots , n_{ct},\\ &{}&{}&{} f_j \left( \mathbf {p},\mathbf {s}(\cdot )\right) \le \overline{f}_{j}, &{} j = n_{ct}+1,\ldots , n_{c},\\ &{}&{}&{} \underline{p}_{i} \le p_{i} \le \overline{p}_{i}, &{} i = 1,\ldots , n_v, \end{array} \end{aligned}$$

(16)

where $t \in \left[ t_0 , t_f\right]$ is valid for all equations in (16). The vector $\mathbf {s}(t)$, defined as

$$\begin{aligned} \mathbf {s}(t) = \left[ \mathbf {q}(t), \dot{\mathbf {q}}(t), \mathbf {v}(t), \dot{\mathbf {v}}(t), \varvec{\lambda }(t)\right] , \quad t \in \left[ t_0 , t_f\right] , \end{aligned}$$

(17)

is denoted as a set of “dependent” variables since the MBS response depends implicitly on the design variable vector $\mathbf {p}$ that rules the optimization process. The equations of motion represented by $\text {EOM}(\mathbf {p},\mathbf {s}(t),t)=\mathbf {0}$ depends now on the design variables. The design problem includes $n_{ct}$ time-dependent constraints imposed at every time instant and $n_{cg}$ global constraints which involve aggregated quantities over the whole time interval. We have thus $n_{ct}+n_{cg}=n_c$. It is worth noting that the optimization problem (16) is totally general and can incorporate equality constraints as well.

The constraint functions $f_j$ involved in such design problems are spatio-temporal constraints. A typical example is the stress constraints for which the stress value depends on the material point and on time. So far, most of works related to MBS optimization have neglected the spatial dependency since this leads to a very complex design problem with a huge number of constraints.

The incorporation of time responses into the optimization problem is an arduous task because it can drastically impact the convergence of the optimization process (see Sect. 5.1). As early proposed in [70], the cost function can be expressed in a general way as

$$\begin{aligned} f_0(\mathbf {p},\mathbf {s}(\cdot )) = G^f(\mathbf {p}, \mathbf {s}(t_f), t_f) + \int _{t_{0}}^{t_{f}}F\left( \mathbf {p},\mathbf {s}(t),t\right) \mathrm{d}t. \end{aligned}$$

(18)

In optimal control, this formulation is known as a Bolza objective function [47]. The terminal cost $G^f$ is referred to as the Mayer term and the integral contribution as the Lagrange term. Global constraints can be formulated in a similar manner. Nonetheless, the treatment of time-dependent constraints is more complex. Several approaches have been proposed to incorporate them in the optimization problem and they are hereafter reviewed.

4.2.4 Treatment of Time-Dependent Constraints

The optimization problem (16) is stated in a continuous time domain. However, since numerical methods are used to solve the governing equations of the mechanical system, the functions involved in the optimization problem (16) can eventually be treated in a discrete time domain.

Let us consider a general time-dependent function

$$\begin{aligned} f_j \left( \mathbf {p} , \mathbf {s}(t) ,t\right) , \quad t \in \left[ t_0 , t_f\right] . \end{aligned}$$

(19)

After time discretization, (19) becomes

$$\begin{aligned} f_j \left( \mathbf {p}, \mathbf {s}_n, t_n\right) , \quad n = 1,\ldots ,n_{end}, \end{aligned}$$

(20)

where the subscript n numbers the time steps.

4.2.4.1 Pointwise constraints

To restrict the response of the system at selected integration time steps, pointwise constraints can be enforced. Incorporating in the optimization problem a constraint that accounts for all time steps, for instance (20), is referred to as a local formulation. Since $n_{end}$ can be large, incorporating directly the set of discrete functions can be costly. First, the high number of constraints complexifies the task of the optimizer. Second, using gradient-based algorithms, the gradient computation of the response is required at each time step. Thereby, particular treatments of the constraint (20) have been proposed to ease the optimization process. Four standard formulations are hereafter discussed (Fig. 6).

• All time steps combined with an active set strategy The time-dependent constraint can be treated by considering all time steps combined with an active constraint set strategy. Depending on the problem, this approach can reduce the number of constraints by neglecting non-active constraints (Fig. 6a).

• All local maxima A drastic treatment consists in considering all local maxima of the response as constraints (Fig. 6b). Additional effort is required to track the local maxima. In [64], an algorithm is proposed to identify the maxima.

• All local maxima and their neighborhood The previous treatment may suffer from convergence difficulties since the local maxima can vary in time as the design proceeds, i.e. a local maximum can move to a different time step at the next iterations. Including a couple of points around each maximum may help the convergence. The number of constraints is marginally increased but remains relatively moderate (Fig. 6c).

• Worst case approach A simplistic treatment is to restrict the constraint to the worst case approach, i.e. the maximum response (Fig. 6d). As a consequence, a single constraint is considered except if multiple points have the same maximum value. However, this treatment generally exhibits a slow convergence or divergence as the worst case time step generally changes in a discontinuous way as the optimization proceeds. While this treatment seems to be cumbersome, it has been used in several studies, see for instance [70, 102].

Fig. 6

Treatments of pointwise constraints, $f_j\le 0$

4.2.4.2 Functional constraints

Alternatively to the pointwise constraint formulations of (20), the continuous form of this equation can be replaced by a single equivalent functional. The equivalent functional is expressed as

$$\begin{aligned} F_j( \mathbf {p},\mathbf {s}(\cdot )) = \int _{t_0}^{t_f} \left\langle f_j \left( \mathbf {p} , \mathbf {s}(t),t\right) \right\rangle \mathrm {d}t, \end{aligned}$$

(21)

where

$$\begin{aligned} \left\langle f_j \left( \mathbf {p} ,\mathbf {s}(t),t\right) \right\rangle \equiv \left\{ \begin{matrix} 0 &{} \text {if} &{} f_j < \overline{f}_j\\ f_j-\overline{f}_j &{} \text {if} &{} f_j \ge \overline{f}_j \end{matrix}\right. . \end{aligned}$$

(22)

It follows that satisfying $F_j \le 0$ is equivalent to satisfying $f_j \le \overline{f}_j$. More details about this approach are given in [54, 90, 93].

The concept of using mathematical tools to transform many active or violated constraints into one or a few constraints, is denoted as a global formulation. Other mathematical tools can also be used to perform this aggregation.

Let us exemplify the use of a p-norm function in the particular case where the function $f_j^+$ has only positive values, i.e. $f_j^+ \ge 0$. Mathematically, the constraint reads

$$\begin{aligned} \Vert f_j^+ \left( \mathbf {p} ,\mathbf {s}(\cdot ),\cdot \right) \Vert _p = \left( \int _{t_0}^{t_f} \left( f_j^+ \right) ^p \mathrm {d}t\right) ^{1/p} \le \left\| \overline{f}_j^+\right\| _p, \end{aligned}$$

(23)

where $p \in \mathbb {R}$ and $p\ge 1$. If $p=2$, one resorts to the Euclidean norm and dividing the integral by the time duration yields

$$\begin{aligned} \sqrt{\frac{1}{t_f-t_0}\int _{t_0}^{t_f}\left( f_j^+ \right) ^2 \mathrm {d}t} \le \overline{f}_{j,RMS}^+, \end{aligned}$$

(24)

which can be interpreted as the root mean square value of the constraint. If the parameter $p\rightarrow \infty$, the p-norm reaches the infinity norm, also known as the maximum norm, i.e.

$$\begin{aligned} \Vert f_j^+ \left( \mathbf {p} ,\mathbf {s}(\cdot ),\cdot \right) \Vert _\infty = \max _{t} f_j^+. \end{aligned}$$

(25)

This formulation enables to identify the maximum value of the function, however, the infinity norm is a non-differentiable function. We note that the infinity norm leads to a similar formulation as the worst case approach.

When a global formulation is adopted to agglomerate the response function $f_j^+$, it must be noted that the constraint bound definition can become more difficult since it is no longer directly related to the physical response of the system but to the agglomerated response.

5 The Fully Coupled Method

The fully coupled method aims at solving the optimization problem (16) and it is thus by essence a natural extension of classical structural optimization. Instead of relying on the response of a static analysis, this method incorporates the time response coming directly from the MBS analysis into the optimization problem. That said, this extension is not so simple because the resulting dynamic response optimization problem is more challenging than classical structural optimization problems. The main difficulties arise chiefly due to the evaluation and the incorporation of the dynamic response into the optimization problem.

More precisely, the optimization problem (16) can be solved based on a nested approach [65]. In this approach, the equations of motion are exploited to eliminate the dependent variables $\mathbf {s}$ which are expressed as a function of $\mathbf {p}$. For any given value of $\mathbf {p}$, the dynamic response $\mathbf {s}(\mathbf {p},t)$ is evaluated based on a MBS dynamic analysis. As a consequence, the optimization problem is formulated only in terms of the independent design variables $\mathbf {p}$ and not in terms of the dependent variables $\mathbf {s}$. Indeed, the dependent variables become intermediate variables which only arise within the evaluation of the design functions.

The flowchart of the fully coupled method is given in Fig. 7. As depicted by the shaded box, the MBS simulation and the optimization process work in an integrated manner, i.e. at each iteration of the optimization process, a MBS simulation and a sensitivity analysis are performed to provide the time response and the associated sensitivities to the optimizer. The optimization process loops until a convergence criterion is achieved. The sensitivity analysis can be integrated in the time integration scheme of the equations of motion to be carried out efficiently. Indeed, the sensitivities are then obtained as a supplementary result of the analysis with a low computational cost.

In this section, the impact of the optimization problem formulation on the convergence is first discussed based on a design space analysis. The MBS sensitivity analysis is then reviewed since this step is the cornerstone of gradient-based methods. This section ends with a discussion on the algorithms that have been employed to perform the design process.

Fig. 7

Fully Coupled Method framework

5.1 Discussion on the MBS Optimization Problem Formulation

The design problem of MBS components is quite complex and poor convergence properties are encountered if the problem is not properly formulated. The existence of significant couplings between vibrations and large amplitude motion, the influence of the changes of component inertial property on the vibrations as well as the interactions between flexible components lead to a daunting task for the optimizer.

In order to tightly control the optimized design and to have a precise control of the design at each time step, a local formulation of the constraints can be used wherein constraints are enforced at each time step. This local formulation can be coupled with an active set strategy to ease the optimizer task. However, this formulation generally involves numerous constraints which hinder the optimization convergence. Moreover, as explained in [137], it turns out that each individual constraint resulting from such a formulation leads to a tortuous design space, i.e. it exhibits a lot of oscillations (Fig. 8a). Consequently, the design space is not suited for gradient-based algorithms which tend to get trapped in local minima. As introduced in Sect. 4.2.4, global formulations involve a smaller number of constraints and ease the convergence. Unfortunately, the precise control at each time step is lost due to their global nature. Nonetheless, global formulations create a smooth design space which is really convenient and well-suited for gradient-based algorithms (Fig. 8b).

As an illustrative example of the influence of the optimization problem formulation, Fig. 8 represents the design space of the mass minimization problem of a robot subject to a trajectory tracking constraint [137]. The 2-dof robot has six design variables (arm thickness) and the design space is plotted when varying the design parameters $p_5$ and $p_6$ while others are fixed. As previously explained, we observe that the global constraint exhibits a smoother design space than the local constraint. A deeper analysis of the influence of time-dependent constraint formulation is given in [137].

Fig. 8

Design space representation for a local formulation at time step $n=20$ (a) and for a global formulation (b), from [137]

5.2 Sensitivity Analysis

The sensitivity analysis is the essential link between the system analysis and the numerical optimization. The solution of the structural optimization problem can be actively supported and facilitated providing accurate sensitivity information. Sensitivities indicate the influence of parameters over the system response. They can also serve to establish structural approximations of the original problem [52]. Using the fully coupled method, the sensitivity analysis can be costly if not addressed with care as a nonlinear dynamic analysis is considered. Hence, this section reviews the sensitivity analysis for flexible MBS.

A simple and easy-to-implement way to compute gradients is by numerical differentiation. Employing this method, the flexible MBS simulation can be treated as black-box model and no further information about the system is required. However, finite difference methods suffer from several deficiencies [135]. For instance, the gradient is only an approximation and the optimal perturbation of the design variables is not known a priori. Also, finite difference schemes require at least one additional simulation per design variable at each optimization iteration whereby the CPU time grows by a factor $n_v+1$, where $n_v$ is the number of design variables. This is especially relevant with the fully coupled approach since the time of MBS simulations is much larger than for a static analysis. In particular, for large-scale topology optimization problems, the computational costs using numerical differentiation are prohibitively expensive because of the large value of $n_v$. Furthermore, for nonlinear systems, the derivatives can be wrong if a bifurcation of the response occurs.

Besides finite difference schemes, analytical methods such as the direct differentiation method and the adjoint method have been developed to perform accurately and efficiently the sensitivity analysis [135, 141]. Regarding kinematic systems, Sohoni and Haug [125] were amongst the first to propose a method generating the equations for both the primal analysis and the sensitivity analysis. The dynamics was afterwards included in the equations by the same authors [72]. Later on, several contributions to the development of sensitivity analysis methods for dynamic systems were proposed, see for instance [5, 7, 15, 16, 23, 30, 42, 43, 45, 81, 134, 145].

In the following, the basics of the direct differentiation and adjoint methods are presented and the main steps of the derivation are discussed. Thereby, it is assumed that the design variables $\mathbf {p}$ only describe geometrical and material properties of the flexible bodies and that the equations of motion of the flexible MBS are given as a set of ODEs in state-space representation as

$$\begin{aligned} & \dot{\mathbf {q}} = \mathbf {Z}(\mathbf {q})\mathbf {v},\\ &\mathbf {M}(\mathbf {p},\mathbf {q})\dot{\mathbf {v}}= \mathbf {g}\left( \mathbf {p},\mathbf {q},\mathbf {v},t\right) , \end{aligned}$$

(26)

where the variables $\mathbf {q}$, $\mathbf {v}$ and $\dot{\mathbf {v}}$ depend on $\mathbf {p}$ and t. The initial conditions $\mathbf {q}^0$ and $\mathbf {v}^0$ are considered as design independent. For the sensitivity analysis of MBS with kinematic constraints in DAE form, interested readers are referred to [16, 71, 139]. The more special case of applying analytical methods for MBS with kinematic constraints that are rewritten in minimal coordinates by a coordinate partitioning or employing Maggi’s formulation are discussed in [77] and [46], respectively. Finally, the sensitivity analysis in a Lie group formulation is discussed in [23, 127].

Also, for the sake of conciseness, the discussion is restricted to integral-type response functions such as

$$\begin{aligned} f(\mathbf {p}) = \int _{t_0}^{t_f} F\left( \mathbf {p},\mathbf {q}(\mathbf {p},t), \mathbf {v}(\mathbf {p},t), t\right) \mathrm {d}t. \end{aligned}$$

(27)

In contrast to the more general objective function (18), the Mayer term $G^f$ is omitted and the Lagrange term F depends on the position and velocity variables $\mathbf {q}$ and $\mathbf {v}$ respectively, and on the design variables $\mathbf {p}$.

5.2.1 Basics of Analytical Methods

The key idea of the direct differentiation method and the adjoint method is to employ variational calculus to unveil all explicit and implicit dependencies of the response function f with respect to the design variables $\mathbf {p}$.

Provided that the initial time $t_0$ and the final time $t_f$ are constant, the variation of the objective function (27) reads

$$\begin{aligned} \delta f = \int _{t_0}^{t_f}\left( \dfrac{\partial F}{\partial \mathbf {q}}\delta \mathbf {q} + \dfrac{\partial F}{\partial \mathbf {v}}\delta \mathbf {v} \right) \mathrm{d}t + \int _{t_0}^{t_f}\dfrac{\partial F}{\partial \mathbf {p}}\mathrm{d}t\, \delta \mathbf {p}. \end{aligned}$$

(28)

It can be observed that there are two types of variations in (28). On the one hand, there are the independent variations $\delta \mathbf {p}$ and, on the other hand, there are the dependent variations of the position and velocity coordinates $\delta \mathbf {q}$ and $\delta \mathbf {v}$.

In order to compute the gradient $\mathrm{d} f/\mathrm{d} \mathbf {p}$ from (28), the dependent variations $\delta \mathbf {q}$ and $\delta \mathbf {v}$ have to be eliminated. This is typically performed by employing either the direct differentiation or the adjoint methods. Both methods require additional information on the system that is provided by considering the variations of the equations of motion (26). The variation of the velocity compatibility equation leads to

$$\begin{aligned} \delta \dot{\mathbf {q}} - \dfrac{\partial \mathbf {u}}{\partial \mathbf {q}}\delta \mathbf {q} - \dfrac{\partial \mathbf {u}}{\partial \mathbf {v}}\delta \mathbf {v} = \mathbf {0}, \end{aligned}$$

(29)

with $\mathbf {u}(\mathbf {q},\mathbf {v}) := \mathbf {Z}(\mathbf {q})\mathbf {v}$ and the variation of the dynamic equilibrium equation gives

$$\begin{aligned} \mathbf {M}\delta \dot{\mathbf {v}} + \dfrac{\partial \mathbf {r}}{\partial \mathbf {q}}\delta \mathbf {q} + \dfrac{\partial \mathbf {r}}{\partial \mathbf {v}}\delta \mathbf {v} + \dfrac{\partial \mathbf {r}}{\partial \mathbf {p}}\delta \mathbf {p} = \mathbf {0}, \end{aligned}$$

(30)

with $\mathbf {r}:=\mathbf {M}(\mathbf {p},\mathbf {q})\dot{\mathbf {v}} - \mathbf {g}(\mathbf {p},\mathbf {q}, \mathbf {v},t)$ being introduced for the sake of readability.

5.2.2 Direct Differentiation Method

The direct differentiation method eliminates directly the dependent variations by expressing them in terms of the independent variations. In that goal, we first express the variations of the generalized position coordinates $\mathbf {q}(\mathbf {p},t)$ and of the velocity coordinates $\mathbf {v}(\mathbf {p},t)$ that read

$$\begin{aligned} \delta \mathbf {q} = \dfrac{\mathrm{d}\mathbf {q}}{\mathrm{d}\mathbf {p}}\delta \mathbf {p} \quad \text {and} \quad \delta \mathbf {v} = \dfrac{\mathrm{d}\mathbf {v}}{\mathrm{d}\mathbf {p}}\delta \mathbf {p}. \end{aligned}$$

(31)

The derivatives ${\mathrm{d}\mathbf {q}}/{\mathrm{d}\mathbf {p}}$ and ${\mathrm{d}\mathbf {v}}/{\mathrm{d}\mathbf {p}}$ are respectively denoted as sensitivity matrices $\mathbf {Q}_{\mathbf {p}}(\mathbf {p},t)$ and $\mathbf {V}_{\mathbf {p}}(\mathbf {p},t)$ in the literature. Accordingly, the variations of the time derivatives of the position and velocity coordinates give

$$\begin{aligned} \delta \dot{\mathbf {q}} = \dot{\mathbf {Q}}_{\mathbf {p}}\delta \mathbf {p}\quad \text {and} \quad \delta \dot{\mathbf {v}} = \dot{\mathbf {V}}_{\mathbf {p}}\delta \mathbf {p}. \end{aligned}$$

(32)

Then, inserting (31) and (32) in the varied response function (28) leads to

$$\begin{aligned} \delta f = \left\{ \int _{t_0}^{t_f}\left( \dfrac{\partial F}{\partial \mathbf {q}} \mathbf {Q}_{\mathbf {p}} + \dfrac{\partial F}{\partial \mathbf {v}} \mathbf {V}_{\mathbf {p}} + \dfrac{\partial F}{\partial \mathbf {p}}\right) \mathrm{d}t\right\} \delta \mathbf {p}, \end{aligned}$$

(33)

where the expression in curved brackets is the sought gradient $\mathrm{d} f/\mathrm{d} \mathbf {p}.$

In order to evaluate the gradient, the sensitivity matrices $\mathbf {Q}_{\mathbf {p}}$ and $\mathbf {V}_{\mathbf {p}}$ must be known. Thusly, inserting (31) and (32) in the varied equations of motion (29)-(30) yields

$$\begin{aligned}&\left[ \dot{\mathbf {Q}}_{\mathbf {p}} - \dfrac{\partial \mathbf {u}}{\partial \mathbf {q}}\mathbf {Q}_{\mathbf {p}} - \dfrac{\partial \mathbf {u}}{\partial \mathbf {v}}\mathbf {V}_{\mathbf {p}} \right] \delta \mathbf {p} = \mathbf {0}, \nonumber \\&\left[ \mathbf {M}\dot{\mathbf {V}}_{\mathbf {p}} + \dfrac{\partial \mathbf {r}}{\partial \mathbf {q}}\mathbf {Q}_{\mathbf {p}} + \dfrac{\partial \mathbf {r}}{\partial \mathbf {v}}\mathbf {V}_{\mathbf {p}} + \dfrac{\partial \mathbf {r}}{\partial \mathbf {p}}\right] \delta \mathbf {p} = \mathbf {0}. \end{aligned}$$

(34)

Since (34) must hold for all possible variations $\delta \mathbf {p}$, it follows that the expressions in square brackets have to be zero. Consequently, (34) provides the pseudo problem

$$\begin{aligned} \dot{\mathbf {Q}}_{\mathbf {p}}&= \dfrac{\partial \mathbf {u}}{\partial \mathbf {q}}\mathbf {Q}_{\mathbf {p}} + \dfrac{\partial \mathbf {u}}{\partial \mathbf {v}}\mathbf {V}_{\mathbf {p}}, \nonumber \\ \mathbf {M}\dot{\mathbf {V}}_{\mathbf {p}}&= -\dfrac{\partial \mathbf {r}}{\partial \mathbf {q}}\mathbf {Q}_{\mathbf {p}} - \dfrac{\partial \mathbf {r}}{\partial \mathbf {v}}\mathbf {V}_{\mathbf {p}} - \dfrac{\partial \mathbf {r}}{\partial \mathbf {p}}, \end{aligned}$$

(35)

to solve for the unknown sensitivity matrices $\mathbf {Q}_{\mathbf {p}}$ and $\mathbf {V}_{\mathbf {p}}$, also known as pseudo responses. It must be noted that the pseudo problem depends on the number of design variables and it must be solved as many times as the number of design variables.

The ODE system (35) can be integrated in time together with the equations of motion of the flexible MBS. The initial conditions $\mathbf {Q}^0_{\mathbf {p}}$ and $\mathbf {V}^0_{\mathbf {p}}$ follow from the variation of the initial conditions of the flexible MBS and are equal to zero under the assumption of design independent initial conditions.

5.2.3 Adjoint Method

The basic idea of the adjoint method is to augment the varied objective function (28) by two zero terms using a Lagrange multiplier method. The arbitrary Lagrange multipliers are denoted as the adjoint variables. In the adjoint method, the dependent variations $\delta \mathbf {q}$ and $\delta \mathbf {v}$ are eliminated by determining properly the adjoint variables.

The first zero term comes from the varied kinematic relation (29). Multiplying from the left by the vector of adjoint variables $\varvec{\upmu }(t)$ gives

$$\begin{aligned} \varvec{\upmu }^{T}\left[ \delta \dot{\mathbf {q}} - \dfrac{\partial \mathbf {u}}{\partial \mathbf {q}}\delta \mathbf {q} - \dfrac{\partial \mathbf {u}}{\partial \mathbf {v}}\delta \mathbf {v} \right] = 0. \end{aligned}$$

(36)

Since (36) is of different structure than (28), it has to be transformed. Hence, integrating (36) over the simulation time

$$\begin{aligned} \int _{t_0}^{t_f} \varvec{\upmu }^{T}\left[ \delta \dot{\mathbf {q}} - \dfrac{\partial \mathbf {u}}{\partial \mathbf {q}}\delta \mathbf {q} - \dfrac{\partial \mathbf {u}}{\partial \mathbf {v}}\delta \mathbf {v} \right] \mathrm{d}t = 0, \end{aligned}$$

(37)

and integrating by parts the first term to move the time derivative from $\delta \dot{\mathbf {q}}$ to $\varvec{\upmu }$, it yields

$$\begin{aligned}&\varvec{\upmu }^{f^{T}}\delta \mathbf {q}^f - \varvec{\upmu }^{0^{T}}\delta \mathbf {q}^0 \nonumber \\&-\int _{t_0}^{t_f} \left( \dot{\varvec{\upmu }}^{T}\delta \mathbf {q} + \varvec{\upmu }^{T}\dfrac{\partial \mathbf {u}}{\partial \mathbf {q}}\delta \mathbf {q} + \varvec{\upmu }^{T}\dfrac{\partial \mathbf {u}}{\partial \mathbf {v}}\delta \mathbf {v}\right) \mathrm{d}t = 0. \end{aligned}$$

(38)

Since the initial conditions of the position variables $\mathbf {q}^0$ are assumed to be design independent, the variation of the initial position coordinates $\delta \mathbf {q}^0$ vanishes.

Similarly, the second zero term is obtained. Multiplying the varied dynamic equation (30) from the left by the adjoint variables $\varvec{\upnu }\left( t\right)$, integrating over the simulation time and moving the time derivative from $\delta \dot{\mathbf {v}}$ to the term $\mathbf {M}\varvec{\upnu }$ using integration by parts leads to

$$\begin{aligned}&\varvec{\upnu }^{f^{T}}\mathbf {M}^f\delta \mathbf {v}^f - \varvec{\upnu }^{0^{T}}\mathbf {M}^0\delta \mathbf {v}^0 \nonumber \\&- \int _{t_0}^{t_f}\left( \dot{\varvec{\upnu }}^{T}\mathbf {M} + \varvec{\upnu }^{T}\dot{\mathbf {M}} - \varvec{\upnu }^{T}\dfrac{\partial \mathbf {r}}{\partial \mathbf {v}}\right) \delta \mathbf {v} \,\mathrm {d}t \nonumber \\&+ \int _{t_0}^{t_f} \varvec{\upnu }^{T} \dfrac{\partial \mathbf {r}}{\partial \mathbf {q}} \delta \mathbf {q}\mathrm{d}t + \int _{t_0}^{t_f}\varvec{\upnu }^{T} \dfrac{\partial \mathbf {r}}{\partial \mathbf {p}} \delta \mathbf {p} \,\mathrm {d}t = 0. \end{aligned}$$

(39)

Again, $\delta \mathbf {v}^0$ is zero since initial conditions for the velocity variables are assumed to be design independent.

Incorporating (38) and (39) in the varied response function (28) and rearranging the terms with respect to the different variations gives

$$\begin{aligned} \delta f =\, &\varvec{\upmu }^{f^{T}}\delta \mathbf {q}^f \nonumber \\&+ \int _{t_0}^{t_f} \left( -\dot{\varvec{\upmu }}^{T} - \varvec{\upmu }^{T}\dfrac{\partial \mathbf {u}}{\partial \mathbf {q}} + \varvec{\upnu }^{T}\dfrac{\partial \mathbf {r}}{\partial \mathbf {q}} + \,\dfrac{\partial F}{\partial \mathbf {q}}\right) \delta \mathbf {q} \,\mathrm {d}t \nonumber \\&+\quad\varvec{\upnu }^{f^{T}}\mathbf {M}^f\delta \mathbf {v}^f \nonumber \\&+ \int _{t_0}^{t_f} \left( -\varvec{\upmu }^{T}\dfrac{\partial \mathbf {u}}{\partial \mathbf {v}} - \dot{\varvec{\upnu }}^{T}\mathbf {M} - \varvec{\upnu }^{T}\dot{\mathbf {M}}\right. \\& \left. + \,\varvec{\upnu }^{T}\dfrac{\partial \mathbf {r}}{\partial \mathbf {v}} + \dfrac{\partial F}{\partial \mathbf {v}}\right) \delta \mathbf {v} \,\mathrm {d}t \nonumber \\&+ \left\{ \int _{t_0}^{t_f} \left( \varvec{\upnu }^{T}\dfrac{\partial \mathbf {r}}{\partial \mathbf {p}} + \,\dfrac{\partial F}{\partial \mathbf {p}} \right) \mathrm{d}t \right\} \delta \mathbf {p}. \end{aligned}$$

(40)

It can be seen that the term in curly brackets corresponds to the sought gradient $\mathrm{d} f/\mathrm{d} \mathbf {p}$, if the adjoint variables are chosen such that the dependent variations $\delta \mathbf {q}$ and $\delta \mathbf {v}$ vanish at all times, including the final time $t_f$. From this condition and provided that the mass matrix is symmetric, the system of adjoint differential equations for the variables $\varvec{\upmu }$ and $\varvec{\upnu }$ can be derived and expressed as

$$\begin{aligned} \dot{\varvec{\upmu }}&= - \left( \dfrac{\partial \mathbf {u}}{\partial \mathbf {q}}\right) ^{T}\varvec{\upmu } + \left( \dfrac{\partial \mathbf {r}}{\partial \mathbf {q}}\right) ^{T}\varvec{\upnu } + \dfrac{\partial F}{\partial \mathbf {q}}, \nonumber \\ \mathbf {M}\dot{\varvec{\upnu }}&= - \left( \dfrac{\partial \mathbf {u}}{\partial \mathbf {v}}\right) ^{T}\varvec{\upmu } - \dot{\mathbf {M}}\varvec{\upnu } + \left( \dfrac{\partial \mathbf {r}}{\partial \mathbf {v}}\right) ^{T}\varvec{\upnu } + \dfrac{\partial F}{\partial \mathbf {v}}. \end{aligned}$$

(41)

This system is solved by a backward time integration starting at the final time $t_f$ with $\varvec{\upmu }^f = \mathbf {0}$ and $\varvec{\upnu }^f = \mathbf {0}$.

It should be mentioned that the adjoint differential equations and, hence, the effort to solve them do not depend on the number of design variables $\mathbf {p}$. In contrast, the adjoint system of equations must be solved for each response function that is involved in the optimization problem.

With the computed adjoint variables, the gradient can thus be evaluated as

$$\begin{aligned} \frac{\mathrm{d} f}{\mathrm{d} \mathbf {p}} =&\int _{t_0}^{t_f}\left( \dfrac{\partial F}{\partial \mathbf {p}} + \left( \dfrac{\partial {\mathbf {r}}}{\partial \mathbf {p}}\right) ^{T}\varvec{\upnu }\right) \mathrm{d}t. \end{aligned}$$

(42)

5.2.4 Direct Differentiation Method Versus Adjoint Method

Both analytical methods allow the exact computation of gradients, i.e. without truncation errors. The choice of a method is chiefly guided by the optimization problem. Indeed, the adjoint method requires solving one adjoint problem for each response function, whereas the direct differentiation method requires solving one pseudo problem for each design parameter. As a consequence, the adjoint method is favored if the number of response functions is less than the number of design parameters. In the opposite case, the direct differentiation method is preferred.

5.3 Optimization Algorithms

Most studies adopted mathematical programming tools to solve the structural optimization problem (16) due to their success in solving large scale structural and multidisciplinary optimization problems [41, 120]. These methods have high convergence rates which limit the number of function evaluations, i.e. MBS simulations, required to obtain an optimal solution. This property renders these methods very attractive. Nonetheless, the drawback of gradient-based algorithms is that they require gradient computations of the cost and constraint functions. Also, as encountered for most methods, they are sensitive to local optima, i.e. the optimizer can converge towards different optimized designs depending on the starting point. Standard algorithms resulting from the mathematical programming approach are, for instance, the sequential quadratic programming (SQP) [110], the CONvex LINearization (ConLin) [55], the method of moving asymptotes (MMA) [131], MMA extensions, e.g. the globally convergent method of moving ssymptotes (GCMMA) [132] and the globally convergent method (GCM) [27], and interior-point methods [57, 149].

The MMA is a standard method to perform classical structural optimization. Hence, by extension it has been widely adopted to carry out MBS optimization. This algorithm stems from the sequential convex programming (SCP) approach which relies on two concepts. The original optimization problem is usually nonlinear and implicit with respect to the design variables whereas the number of function evaluations to solve the problem can be relatively large. Thereby, in the SCP approach, a local approximation of the original optimization is first built using the sensitivities and a variant of the Taylor series expansion of the design functions. Then, efficient mathematical programming algorithms such as a Lagrangian maximization (dual method) or interior point methods are used to solve the local convex sub-problems. The SCP approach is illustrated in Fig. 9.

Fig. 9

Sequential convex programming

In contrast to these gradient-based methods, meta-heuristic optimization methods have the advantage of exploring the entire design space and therefore should provide better performances in complex design space configurations. Only a few papers applied such algorithms to solve flexible MBS optimization problems. Studies would tend to indicate that meta-heuristic optimization methods do not necessarily perform better than gradient-based methods. Moreover, they generally require a lot of function evaluations, i.e. MBS analyses, and thus are rather slow to converge. Lastly, the optimized design is generally not significantly better than the one provided by gradient-based methods [137].

6 The Weakly Coupled Method

The weakly coupled method reformulates the optimization problem (16) such that the dynamic response of the system is replaced by a series of static responses, i.e. at each time step $t_n$, the component deformation under the dynamic loading is mimicked by an Equivalent Static Load (ESL). Hence, all the standard techniques of static response optimization can be applied to solve the reformulated optimization problem.

This section introduces the ESL method fundamentals. Then, the formulation of an equivalent static optimization problem is detailed and the framework of the optimization process is explained. The ESL derivation for the MBS formalisms introduced in Sect. 4.1 is afterwards discussed.

6.1 The ESL Method for an Isolated Structure

Safety factors, dynamic amplification factors, designer’s experience, etc, were traditionally used to convert a dynamic loading into static loads and to account for unmodeled phenomena. However, this approach may increase the weight of the structure and decrease its reliability, i.e. the design is not optimal with respect to the actual loading cases. The concept of converting a dynamic loading into static loads has been clarified with the ESL method that was introduced for the structural optimization of an isolated structure subjected to a dynamic loading [32, 33]. The authors proposed to define the ESL based on the displacement field resulting from the dynamic loading as follows:

When a dynamic load is applied to a structure, the equivalent static load is defined as the static load that makes the same displacement field as that by the dynamic load at an arbitrary time.

Hence, the dynamic loading is mimicked by a series of static loads, namely the ESLs, that give at each time step the same displacement field as the one given by the dynamic loading. Regarding the analysis, this transformation is useless. However, the utility lies in the optimization procedure where the ESL method allows transforming the dynamic response optimization into a static response optimization problem by regenerating the displacement field from only static loads.

6.2 The ESL Method for MBS Optimization

The ESL definition of an isolated structure has been extended for the optimization of flexible MBS, firstly for MBS dynamics described via a floating frame of reference formulation [89] and later on for other MBS formalisms.

The ESL method aims at solving a simplified version of the problem (16) in which the design functions only depend on the local displacements $\mathbf {q}_{e}=\left[ \mathbf {q}_{e}^{1 T} \ldots \mathbf {q}_{e}^{n_{b} T}\right] ^{T}$ of the individual flexible bodies of the system. The problem takes the form

$$\begin{aligned} \begin{array}{llllll} &{} \underset{\mathbf {p}}{\text {min}} &{} &{} f_0 \left( \mathbf {p},\mathbf {q}_{e}(\cdot )\right) \\ &{} \text {s.t.} &{} &{} \text {EOM}(\mathbf {p},\mathbf {s}(t),t)=\mathbf {0}, &{} t \in \left[ t_0 , t_f\right] ,\\ &{} &{}&{} \mathbf {q}(t_0)=\mathbf {q}^0(\mathbf {p}),\\ &{}&{}&{}\mathbf {v}(t_0)=\mathbf {v}^0(\mathbf {p}),\\ &{}&{}&{} f_j \left( \mathbf {p},\mathbf {q}_{e}(t),t\right) \le \overline{f}_{j}, &{} j = 1,\ldots , n_{ct},\\ &{}&{}&{} f_j \left( \mathbf {p},\mathbf {q}_{e}(\cdot )\right) \le \overline{f}_{j}, &{} j = n_{ct}+1,\ldots , n_{c},\\ &{}&{}&{} \underline{p}_{i} \le p_{i} \le \overline{p}_{i}, &{} i = 1,\ldots , n_v, \end{array} \end{aligned}$$

(43)

where $t \in \left[ t_0 , t_f\right]$ is valid for all equations in (43) and the vector $\mathbf {s}(t)$ is defined by (17). The local displacements $\mathbf {q}_{e}$ are extracted from the position coordinates $\mathbf {q}$ based on a formula that depends on the selected MBS formalism, as will be shown in Sect. 6.3.

The method relies on the definition of a well-posed static problem for each body $b=1,\ldots ,n_{b}$ represented by the static equilibrium equation

$$\begin{aligned} \text {SEE}^b(\mathbf {p},\mathbf {q}_{e}^b,\mathbf {g}_{eq}^b):=\mathbf {g}_{int}^b(\mathbf {p},\mathbf {q}_{e}^b)-\mathbf {g}_{eq}^b=\mathbf {0}, \end{aligned}$$

(44)

where $\mathbf {g}_{int}^b$ and $\mathbf {g}_{eq}^b$ represent respectively the inner force vector and the equivalent static load vector acting on body b. As the body is isolated from the rest of the system, boundary conditions have to be included in this static problem in order to prevent rigid body modes.

The initial problem (43) is then reformulated as

$$\begin{aligned} \begin{array}{llllll} &{} \underset{\mathbf {p}}{\text {min}} &{} &{} f_0 \left( \mathbf {p},\hat{\mathbf {q}}_{e}(\cdot )\right) \\ &{} \text {s.t.} &{} &{} \text {EOM}(\mathbf {p},\mathbf {s}(t),t)=\mathbf {0}, &{} t \in \left[ t_0 , t_f\right] ,\\ &{} &{}&{} \mathbf {q}(t_0)=\mathbf {q}^0(\mathbf {p}),\\ &{}&{}&{}\mathbf {v}(t_0)=\mathbf {v}^0(\mathbf {p}),\\ &{}&{} &{} \text {SEE}^b(\mathbf {p},\hat{\mathbf {q}}_{e}^b(t),\mathbf {g}_{eq}^b(t))=\mathbf {0}, &{} b=1,\ldots ,n_{b},\\ &{}&{} &{} \text {SEE}^b(\mathbf {p},\mathbf {q}_{e}^b(t),\mathbf {g}_{eq}^b(t))=\mathbf {0}, &{} b=1,\ldots ,n_{b},\\ &{}&{}&{} f_j \left( \mathbf {p},\hat{\mathbf {q}}_{e}(t),t\right) \le \overline{f}_{j}, &{} j = 1,\ldots , n_{ct},\\ &{}&{}&{} f_j \left( \mathbf {p},\hat{\mathbf {q}}_{e}(\cdot )\right) \le \overline{f}_{j}, &{} j = n_{ct}+1,\ldots , n_{c}, \end{array} \end{aligned}$$

(45)

with $t \in \left[ t_0 , t_f\right]$ valid for all equations in (45). The optimization problem formulation (45) is formally equivalent to (43). Indeed, since the static equilibrium equation is well-posed, it admits a unique solution. Thus, the solution of the optimization problem is such that $\hat{\mathbf {q}}_{e}(t)=\mathbf {q}_{e}(t)$. As the load $\mathbf {g}_{eq}^b(t)$ leads to the same static displacement as in the dynamic response, it is interpreted as the equivalent static load for body b. It is clear from this definition that the equivalent static loads are design dependent.

Nevertheless, the weakly coupled method assumes that the ESLs are fixed in an inner static response optimization procedure. Hence, to account for the effects of design modifications over the ESLs, cycles are needed between the MBS analysis and the static response optimization. Following the initial idea proposed in [34] for elastic component optimization and later on extended to MBS optimization in [89], the problem (45) is solved by iterations over simpler subproblems according to the following sequence:

• 1. Initialization: initialize the design variables $\mathbf {p}$ and set the cycle counter it to 0.

• 2. Flexible MBS analysis: evaluate the trajectory $\mathbf {q}(t)$ by forward time integration of the DAE

  $$\begin{aligned} \begin{array}{l} \text {EOM}(\mathbf {p},\mathbf {s}(t),t)=\mathbf {0}, \quad t \in \left[ t_0 , t_f\right] ,\\ \mathbf {q}(t_0)=\mathbf {q}^0(\mathbf {p}),\\ \mathbf {v}(t_0)=\mathbf {v}^0(\mathbf {p}). \end{array} \end{aligned}$$

  (46)

• 3. ESL process: for each flexible body b, extract the local displacements $\mathbf {q}_{e}^b(t)$ from the trajectory $\mathbf {q}(t)$ obtained in step 2 and evaluate the ESLs $\mathbf {g}_{eq}^b(t)$ from the algebraic equation

  $$\begin{aligned} \text {SEE}^b(\mathbf {p},\mathbf {q}_{e}^b(t),\mathbf {g}_{eq}^b(t))=\mathbf {0}, \quad b=1,\ldots ,n_{b}, \end{aligned}$$

  (47)

  with $t \in \left[ t_0 , t_f\right]$.

• 4. Convergence criterion: If $it=0$, go to step 5. If $it>0$ and if

  $$\begin{aligned} \dfrac{\displaystyle \int _{t_0}^{t_f} \Vert \mathbf {g}_{it,eq}^{b}(t)-\mathbf {g}_{it-1,eq}^{b}(t)\Vert \mathrm{d} t}{\displaystyle \int _{t_0}^{t_f} \Vert \mathbf {g}_{it-1,eq}^{b}(t)\Vert \mathrm{d} t} < \varepsilon , \end{aligned}$$

  (48)

  then stop. Otherwise go to step 5.

  The tolerance value $\varepsilon$ of the stopping criterion is typically set to 0.001.

• 5. Static response optimization: update the design variable $\mathbf {p}$ by solving an approximate optimization problem which is based on the assumption that the ESLs computed in step 3 are design independent:

  $$\begin{aligned} \begin{array}{llllll} &{} \underset{\mathbf {p}}{\text {min}} &{} &{} f_0 \left( \mathbf {p},\hat{\mathbf {q}}_{e}(\cdot )\right) \\ &{} \text {s.t.} &{} &{} \text {SEE}^b(\mathbf {p},\hat{\mathbf {q}}_{e}^b(t),\mathbf {g}_{eq}^b(t))=\mathbf {0}, &{} b=1,\ldots ,n_{b},\\ &{}&{}&{} f_j \left( \mathbf {p},\hat{\mathbf {q}}_{e}(t),t\right) \le \overline{f}_{j}, &{} j = 1,\ldots , n_{ct},\\ &{}&{}&{} f_j \left( \mathbf {p},\hat{\mathbf {q}}_{e}(\cdot )\right) \le \overline{f}_{j}, &{} j = n_{ct}+1,\ldots , n_{c},\\ &{}&{}&{} \underline{p}_{i} \le p_{i} \le \overline{p}_{i}, &{} i = 1,\ldots , n_v, \end{array} \end{aligned}$$

  (49)

  with $t \in \left[ t_0 , t_f\right]$ valid for all equations in (49).

  The iterations to solve this optimization problem are usually denoted as inner iterations.

• 6. Set $it= it+1$ and go to step 2.

The solution procedure is based on the iterative process of solving a static response optimization problem with multiple load cases for each optimized component b. For each component, the number of load cases depends on the optimization problem formulation and is equal to the number of time steps if all time steps are taken into account. Thereby, although the dynamic response optimization problem is transformed into a static response optimization problem, the treatment of time-dependent constraints is still present and the discussion of Sect. 4.2.4 is also valid. Solving static response optimization problems under multiple load cases is standard in structural optimization and its solution can rely on efficient numerical procedures, especially if the static equilibrium equation can be linearized, which is often possible.

The proposed sequence is valid for all MBS formalisms and generalizes the sequence proposed in [89]. A stopping criterion based on the relative change of the ESLs is used to terminate the cycles while a criterion based on the absolute change of the ESLs is used in [89]. Recent studies also employ classical stopping criteria, such as those based on the change of the design variable values to stop the optimization process [88, 96]. The convergence of the solution obtained using the weakly coupled method towards the optimal solution of the original dynamic response optimization problem has been discussed in [128]. The author criticized the proof establishing that if the ESL algorithm terminates then the KKT conditions of the original problem and the final sub-problem are identical [104]. As a result, a modified version of the algorithm has been proposed for which the claimed result is proven [128].

The optimization process framework for the weakly coupled method is illustrated in Fig. 10. One can observe that it strongly differs from the fully coupled method framework depicted in Fig. 7. Indeed, the MBS analysis and the optimization process are no longer fully coupled but weakly coupled via an intermediate step related to the ESL process.

Fig. 10

Weakly Coupled Method framework

6.3 ESL Derivation for Standard MBS Formalisms

The following subsections discuss how the local displacements and the equivalent static problems are derived for the MBS formalisms introduced in Sect. 4.1.

6.3.1 ESL Combined with a Floating Frame of Reference Formulation

The ESL method is easily implemented with the floating frame of reference formulation. This is due to the fact that two sets of coordinates are used to describe the overall motion of the body. On the one hand, rigid body degrees of freedom $\mathbf {q}_{r}$ describe the large overall translations and rotations of the floating reference frames, and, on the other hand, a set of elastic coordinates $\mathbf {q}^b_{e}$ is used to describe the elastic deformations for each body b. The extraction of the elastic coordinates $\mathbf {q}^b_{e}$ from the system coordinates $\mathbf {q}$ is thus trivial.

Thereby, it is possible to partition the force vector into contributions to the rigid and elastic equilibrium as $\mathbf {g} = \left[ \mathbf {g}_{r}^{T}\, \mathbf {g}_{e}^{1 T}\,\ldots \, \mathbf {g}_{e}^{n_{b} T}\right] ^{T}$. If the elastic displacements with respect to the floating frame remain small, a linear elastic model can be used and the internal force vector takes the form

$${\mathbf{g}}_{{int}} = \left[ {\begin{array}{*{20}l} {\mathbf{0}} \\ {{\mathbf{K}}_{e}^{1} {\mathbf{q}}_{e}^{1} + {\mathbf{D}}_{e}^{1} \mathop {{\mathbf{q}}_{e}^{1} }\limits^{.} } \\ \vdots \\ {{\mathbf{K}}_{e}^{{n_{b} }} {\mathbf{q}}_{e}^{{n_{b} }} + {\mathbf{D}}_{e}^{{n_{b} }} \mathop {{\mathbf{q}}_{e}^{{n_{b} }} }\limits^{.} } \\ \end{array} } \right],$$

(50)

where the expression of the elastic forces involves the stiffness matrix $\mathbf {K}_{e}^b$ and the expression of the damping forces involves the damping matrices $\mathbf {D}_{e}^b$.

Subsequently, the equivalent static problem is simply formulated as

$$\begin{aligned} \text {SEE}^b(\mathbf {p},\mathbf {q}_{e}^b,\mathbf {g}_{eq}^b):=\mathbf {K}_{e}^b(\mathbf {p})\mathbf {q}^b_{e}-\mathbf {g}_{eq}^b. \end{aligned}$$

(51)

The problem of boundary conditions is handily circumvented since the floating frame of reference formulation already includes boundary conditions to connect the floating frame to the moving body. For instance, the Component Mode Synthesis method can be employed to introduce flexibility, wherein boundary conditions are defined to perform the modal analysis [116]. Hence, the necessary boundary conditions are automatically included in (51) which fix all rigid body modes. It is also worth observing that the static subproblem is naturally obtained in a linear form since the linear elasticity assumption is usual in the floating frame of reference formulation.

6.3.2 ESL Combined with the ANCF

The optimization of flexible MBS described with the ANCF can also be achieved by using the ESL method. However, the definition of an equivalent static problem is more arduous since the ANCF stems from a nonlinear finite element approach.

Considering the dynamic equilibrium equation of a flexible MBS (1), the equivalent static subproblem for body b can be written as

$$\begin{aligned} \text {SEE}^b(\mathbf {p},\mathbf {q}^b,\mathbf {g}_{eq}^b) = \mathbf {g}_{int}(\mathbf {p}, \mathbf {q}^b) - \mathbf {g}^b_{eq}, \end{aligned}$$

(52)

where the inertia and applied forces are gathered in the equivalent load vector $\mathbf {g}^b_{eq}$. As mentioned in Sect. 4.1.4, the ANCF leads to a constant mass matrix $\mathbf {M}$ but to a highly nonlinear elastic force vector $\mathbf {g}_{int}$. As a consequence, the subproblem (52) depends in a nonlinear way on the generalized nodal coordinates $\mathbf {q}^b$. Hence, the solution of the equivalent static subproblem and, in particular, the sensitivity analysis become more complex.

A first approach consists in linearizing the original nonlinear subproblem (52) around the undeformed configuration [129]. As a result, the inner forces $\mathbf {g}^b_{int}$ can be expressed as

$$\begin{aligned} \mathbf {g}^b_{int} = \mathbf {K}_{lin}^b\left( \mathbf {p}, t\right) \mathbf {q}_e^b, \end{aligned}$$

(53)

where $\mathbf {K}_{lin}^b$ is a linear stiffness matrix of body b and $\mathbf {q}_e^b$ is the local displacement vector, determined by removing the rigid body motion $\mathbf {q}_{r}^b$ from the overall motion $\mathbf {q}^b$. Hence, a linearized version of the equivalent static subproblem (52) reads

$$\begin{aligned} \text {SEE}^b(\mathbf {p},\mathbf {q}^b_e,\mathbf {g}_{eq}^b) := \mathbf {K}_{lin}^b\left( \mathbf {p}, t\right) \mathbf {q}_{e}^b - \mathbf {g}^b_{eq}. \end{aligned}$$

(54)

Kinematic constraints lead to a singular stiffness matrix $\mathbf {K}_{lin}^b$ since the component is isolated from the system. Consequently, rigid body motions must be properly prevented. While this approach seems to be similar to the ESL method combined with the floating frame of reference, it is worth noticing that the linear stiffness matrix is valid at a given time step. Thereby, for each subproblem, a different linearized stiffness matrix must be computed since the original stiffness matrix depends on the system configuration and evolves with respect to time.

Alternatively, a solution process directly based on the nonlinear dynamic equilibrium equations has been proposed [76]. In this approach, ESLs are not explicitly defined but the simplification process occurs in the sensitivity analysis. Adopting the idea of the ESL method, the loads are considered independent of the design variables whereupon the sensitivity analysis is greatly simplified in the dynamic response. In other words, compared to the full sensitivity analysis of the equations of motion, some terms are dropped out. Also, in order to evaluate the sensitivity of the inner forces in an efficient way, an analytic approach based on the adjoint method has been proposed. The inner forces $\mathbf {g}_{int}$ are first reformulated as

$$\begin{aligned} \mathbf {g}^b_{int} = \left( \mathbf {K}_1(\mathbf {p}) + \mathbf {K}_2(\mathbf {p}, \mathbf {q}^b) \right) \mathbf {q}^b, \end{aligned}$$

(55)

where $\mathbf {K}_1(\mathbf {p})$ is an invariant matrix and $\mathbf {K}_2(\mathbf {p}, \mathbf {q}^b)$ is an auxiliary matrix, see [61] for details. The derivatives $\mathrm{{d}} \mathbf {g}^b_{int}/\mathrm {d}\mathbf {p}$ are then computed efficiently using (55). Compared to the ESL method associated with the floating frame of reference, this approach is more general in the sense that large deformations are naturally accounted for. However, since ESLs are not explicitly defined, inner iterations are limited to a single iteration whereupon a new MBS simulation is needed. Consequently, more dynamic analyses may be required which will thus lengthen the computation time.

To the knowledge of the authors there is currently no comparison between the two different approaches. However, both formulations have proven their worth in diverse application examples.

6.3.3 ESL Combined with a Classical Nonlinear Finite Element Formalism

As already seen with the ANCF, the formulation of an equivalent static problem adapted to a classical nonlinear finite element formalism [62] is not as easy as it is for the floating frame of reference formulation. Indeed, the equations of motion are developed in an inertial frame, i.e. the elastic forces are not expressed in a body-attached frame. Moreover, rigid body motions and elastic deformations exhibit no decoupling, in addition to the fact that the tangent stiffness matrix is not constant and evolves with the system configuration.

The method proposed in [138] evaluates the ESLs in a post-processing step of the MBS analysis, without modifying the analysis. The approach relies on the definition of a corotational frame which follows the gross motion of each flexible body. Then, it is possible to extract the local displacements and rotations of the nodes of the body $\mathbf {q}_{e}^b$ with respect to the corotational frame from the vector of absolute positions and orientations $\mathbf {q}$. In that sense, the procedure is similar to the one developed for the floating frame of reference formulation since the quantities of interest are extracted from a local frame. Figure 4 can thusly illustrate the proposed approach if the local frame is interpreted as a corotational frame. The rigid body modes are simply prevented using the boundary conditions associated with the definition of the corotational frame. The reference configuration is defined such that the body is undeformed and that the corotational frame coincides with the inertial frame. As the local displacements are defined in the corotational frame, a constant tangent stiffness matrix $\mathbf {K}_{t, ref}^b$ evaluated in the reference configuration can be considered for the static analysis. It follows that the static problem is defined in the corotational frame for the component b as

$$\begin{aligned} \text {SEE}^b(\mathbf {p},\mathbf {q}_{e}^b,\mathbf {g}_{eq}^b):= \mathbf {K}_{t,ref}^b (\mathbf {p}) \mathbf {q}_{e}^b - \mathbf {g}_{eq}^b. \end{aligned}$$

(56)

This linearized model is valid if the local displacements with respect to the corotational frame $\mathbf {q}_{e}^b$ are sufficiently small.

6.3.4 ESL Combined with a Local Frame Formalism

While still describing the MBS dynamics via a nonlinear finite element formalism, the formulation on the special Euclidean group SE(3) exhibits several attractive properties for the weakly coupled approach [140]. In particular, combining the special Euclidean group SE(3) with the left invariant representation of derivatives leads to a tangent stiffness matrix $\mathbf {K}_t$ that can be considered as constant under the assumption of small local deformations, i.e. the tangent stiffness matrix is independent of the system configuration [127].

Another interesting characteristic of this formalism is that the equations of motion are expressed in the local frame defined for each node. Since the formulation is geometrically exact, the local frame expression of the internal forces of a body $\mathbf {g}_{int}^{b} \left( \mathbf {H}^b\right)$ is completely insensitive to rigid body motions. This property is decisive for the efficient formulation of the equivalent static problem. Indeed, the ESL vector for body b is merely the internal force vector acting on this body, i.e.

$$\begin{aligned} \mathbf {g}_{eq}^{b} = \mathbf {g}_{int}^{b} \left( \mathbf {H}^b\right) . \end{aligned}$$

(57)

It is remarkable that the evaluation of the ESL $\mathbf {g}_{eq}^{b}(t)$ from the dynamic response does not require the definition of local displacements. It is computed directly from the configuration with respect to the inertial frame represented by the variable $\mathbf {H}^b(t)$.

However, the static problem (57) is not well-posed because, for a given static load $\mathbf {g}_{eq}^{b}$, the solution $\mathbf {H}^b$ is only defined up to a rigid body motion of the body $\mathbf {H}^b_{rig}$, i.e. if $\mathbf {H}^{b*}$ is a solution of (57), then $\mathbf {H}^b_{rig}\mathbf {H}^{b*}$ is also a solution. This non-uniqueness issue is fixed by enforcing some boundary conditions to prevent rigid body motions. Mathematically, the boundary conditions restrict the variations of $\mathbf {H}^b$ to a reduced nonlinear space $G^b_{e}$. These boundary conditions are selected such that they are verified in the reference configuration, i.e. $\mathbf {H}_{ref}^{b}\in G^b_{e}$. Finally, the equivalent static equilibrium equation is defined as

$$\begin{aligned} \text {SEE}^b(\mathbf {p},\mathbf {H}^{b}_{e},\mathbf {g}_{eq}^{b}) := \mathbf {g}^{b}_{int}(\mathbf {H}^{b}_{e}) - \mathbf {g}_{eq}^{b}\; \text {with}\;\mathbf {H}^{b}_{e}\in G^b_{e}. \end{aligned}$$

(58)

The resulting static problem is represented by a nonlinear equation whose solution $\mathbf {H}^{b}_{e}$ is interpreted as a local displacement field with respect to the reference configuration $\mathbf {H}_{ref}^{b}$ as illustrated in Fig. 11.

Referring to the general procedure described in Sect. 6.2, the extraction of the local displacements $\mathbf {H}^{b}_{e}$ from the dynamic response $\mathbf {H}^{b}$ could be obtained by finding the rigid transformation $\mathbf {H}^b_{rig}$ such that $\mathbf {H}^{b}=\mathbf {H}^b_{rig}\mathbf {H}^{b}_{e}$ and $\mathbf {H}^{b}_{e}\in G^b_{e}$. However, this step is not necessary since the ESLs can be computed directly from $\mathbf {H}^{b}$ as explained before.

Fig. 11

ESL evaluation in a Lie group formalism

As small deformations are usually assumed, it is appealing to derive an equivalent linear static problem by performing a linearization of (58) around the undeformed configuration, producing

$$\begin{aligned} \text {SEE}^b_{lin}(\mathbf {p},\Delta \mathbf {n}^{b}_{e},\mathbf {g}_{eq}^{b}):=\mathbf {K}_t^{b} \Delta \mathbf {n}^{b}_{e} - \mathbf {g}_{eq}^{b}\; \text {with}\;\Delta \mathbf {n}^{b}_{e}\in \mathfrak {g}^b_{e}. \end{aligned}$$

(59)

The term $\Delta \mathbf {n}^{b}_{e}$ can be interpreted as a small increment vector that binds the locally deformed configuration $\mathbf {H}^{b}_{e}$ to the reference configuration $\mathbf {H}_{ref}^{b}$ (see Fig. 11).

7 Discussions

This paper presented and reviewed the two main methods that are currently used to couple MBS analysis and structural optimization. Both methods have been employed with conclusive results to solve the challenging design problem of flexible mechanisms.

The choice of an optimization method is not trivial and strongly depends on the targeted application. When the optimization problem formulation enables to use both methods, the same optimized design may be achieved. References [128, 138] discuss the equivalence between the optimization problem formulations resulting from the weakly and the fully coupled methods. It is shown that both methods can converge towards the same optimized design when the optimization problem can be formulated in an identical manner.

The weakly coupled method generally lessens the CPU time as it avoids the expensive computation of the dynamic response gradients. Also, mechanical systems with a rather moderate flexibility generally require less dynamic analyses to converge when employing the weakly coupled approach. However, this reduction is partly counterbalanced by inner iterations performed by the static response optimization at each cycle albeit these are based on static computations.

The weakly coupled method as presented in this paper concerns the optimization of isolated components even though the loading stems from the analysis of the whole system. As a consequence, the static equivalent optimization problem must be strictly formulated with respect to the component response. In other words, if the optimization problem incorporates multicomponent-based constraints, i.e. not limited to the response of a lone component, these constraints must be translated into component-based constraints to be applicable to the weakly coupled method. This limitation results from the ESL definition that is established at the component level. An interesting future development may be to derive the ESLs at a system-level in order to formulate the optimization problem with respect to the system itself and not limited to isolated components.

In comparison, the fully coupled method is completely general and accommodates any types of constraints at the price of a more complex optimization process. For systems, which are highly flexible or in which inertial forces dominate the loading, the fully coupled method may experience a faster convergence than the weakly coupled method. This is due to the fact that in these systems, the ESLs can change drastically from one cycle to another, hindering the convergence. However, the designer must have a strong knowledge of the mechanical system dynamics to properly formulate the optimization problem. An inappropriate formulation usually results in poor convergence properties. The impact of the optimization problem formulation has been investigated in [137]. The discussion on the treatment of time-dependent constraints started decades ago, see for instance [70], and the discussion is still open today. While dealing with time-dependent constraints seems to be only an issue in the fully coupled method, this question also arises employing the weakly coupled method since the number of ESLs and the treatment of the responses resulting from the ESLs is directly related to the treatment of time-dependent constraints.

A close connection can be established between the problem of treating time-dependent constraints and the incorporation of stress constraints in structural topology optimization. Stress constraints are also incorporated using either a local formulation or an aggregated formulation and similar conclusions are drawn. A local formulation wherein the stress value of each element is factored in, offers a precise control of the stresses but it drastically increases the size and the complexity of the problem. Aggregating the local responses in a unique constraint lead to a smooth convergence at the cost of losing the precise control of stresses.

The fully coupled method adopts the nested approach to formulate the optimization problem. In this approach, most of the computational effort is invested to solve the equilibrium equations [6]. Conversely, the SAND (Simultaneous ANalysis and Design) approach does not solve the equilibrium equations apart from the optimization process but incorporates them into the optimization process. Consequently, the size of the optimization problem is largely increased. Moreover, the size can even be larger, e.g. when the time integration formulae are added to the optimization problem. However, matrices exhibit interesting properties such as sparsity that enable to obtain an efficient optimization process. The SAND approach could be an interesting way to solve a combined structural optimization and optimal control problem. In robotics, optimal control can be achieved through the “Direct transcription method” [9] that is similar to the SAND approach. Simple examples demonstrated the capability of employing the “Direct transcription method” to solve the aforementioned coupled problem [8]. It is concluded that the formulation of the problem is essential to reduce the influence of local minima which hinder and may even prevent the convergence of deterministic optimization algorithms. The use of deterministic algorithms is important since each function evaluation requires a costly MBS simulation which restrains the use of heuristic methods. Despite this fact, the SAND approach seems to be an interesting perspective and merits to be investigated as a possibility to solve the coupled design problem. Such coupled problems have also been investigated using different approaches [4, 113].

Cost and constraint functions are generally formulated in terms of displacement variables. However, it can be desired to formulate some constraints with respect to velocity variables. For instance, in a trajectory tracking problem, the designer may not only want to follow a prescribed path but may also want to follow it at a prescribed speed. This combination should further be studied as it will even more complicate the optimization problem. In that case, the fully coupled method is the only possibility as a static analysis cannot predict the speed.

Flexible MBS analyses are in essence highly nonlinear. As a result, structural optimization problems of MBS are even more nonlinear. It is thus appealing to work with an optimization problem parameterization that limits the introduction of new nonlinearities while still being efficient. In that goal, an implicit description of the geometry based on the level set method and a geometry mapping based on a volume fraction has been proposed [138]. This geometrical description enables deep modifications of the geometry while keeping the optimization process simple. The resulting method is classified as a generalized shape optimization method wherein the component topology can change in a limited manner.

So far, most studies employ algorithms based on the sequential convex programming approach. As explained in Sect. 5.3, this approach relies on local approximations of the original complex problem and turns out to be extremely efficient to solve structural static response optimization problems [41, 120]. However, the fully coupled method combined with a local formulation of time-dependent constraints can lead to tortuous design space so that these approximation schemes may not be relevant. Thereby, other more sophisticated approximations or other types of algorithms could be investigated to study their potential in solving efficiently the complex design problem of MBS. For small to medium scale optimization problems surrogate-based optimization algorithms could be potential candidates [38, 56, 108, 124]. These methods rely on an approximated model that is constructed from data drawn from a high-fidelity model. The approximated model mimics the behavior of the simulation model as closely as possible and provide fast approximations of the objectives and constraints. This may be an attractive option especially when dealing with intensive simulations as encountered in flexible MBS analysis.

The choice of a MBS formalism to carry out the analysis of flexible mechanisms is out-of-the scope of the paper. However, the weakly coupled method is directly impacted by this choice since the ESL derivation depends on the formalism as presented in Sect. 6.2. It is quite convenient to derive the equivalent static subproblem from the floating frame of reference formulation. Indeed, the equivalent static subproblem already exists as part of the equations of motion. In contrast, if a nonlinear finite element approach is used to model the flexible multibody system, the ESL derivation can be more demanding and a linearization step is often required to obtain an efficient procedure if small deformations are assumed. Nonetheless, nonlinear finite element approaches have the capability of accounting for large deformations in the static equivalent subproblems without major difficulties.

Considering a nonlinear finite element approach, the local frame formalism presented in this paper possesses interesting features, notably to deal with the weakly coupled method. This local frame formalism stems from the particular choice of the special Euclidean group SE(3). When combining this Lie group with the left invariant representation of derivatives, it results in the tangent stiffness matrix $\mathbf {K}_t$ which can be considered as constant under the assumption of small deformations [127]. This characteristic is fundamental because a constant tangent stiffness matrix $\mathbf {K}_t$ is thus readily accessible to formulate the equivalent static optimization problems. This contrasts with a nonlinear finite element formulation which requires additional steps to formulate efficiently static equivalent problems.

Regarding numerical applications, standard mechanisms have been mainly considered such as a 2-dof robot, a 4-bar mechanism or a slider-crank mechanism (Fig. 12). This can be easily explained as most studies focused on developing and investigating new methods to tackle the complex design problem of flexible MBS. Nowadays, the methods become well-established and it would be interesting to compare the benefit that can be collected from a system-based approach compared to a traditional component-based approach on more elaborated design problems.

Fig. 12

Some standard MBS design problems

8 Concluding Remarks

The design of innovative and lightweight mechanical systems requires accounting for the influence of the entire system since the interactions between components strongly affect the optimal design. While most of the structural optimization developments have been conducted under (quasi-)static loadings or vibration design criteria, the methods reviewed in this paper aim at considering as precisely as possible the effects of nonlinear dynamic loading in mechanical systems under service conditions.

For the purpose, the discussed methods incorporate a MBS simulation within the optimization loop to accurately predict the dynamic behavior of the entire system. This leads to a system-based optimization approach that supersedes the traditional component-based approach, wherein the optimization is carried out on components that have been previously isolated from the system.

This article reviewed the two main state-of-the-art methods that are used to couple structural optimization techniques and MBS simulation tools. The method named “the weakly coupled method” was up to recently limited to the floating frame of reference formulation. However, as reviewed in this paper, recent research studies extended the definition of the Equivalent Static Load to other formalisms. Nowadays, this method is implemented in commercial software tools. The fully coupled method leads to a more challenging design problem as it relies on the time response coming directly from the MBS analysis. However, this method results in a totally general approach that can accommodate any types of cost and constraint functions.

A lot of developments have been achieved these years and some methods have become mature for industrial applications. Nonetheless, many open questions and perspectives are still worth being investigated in the field of flexible mechanism design.