Abstract
This review article summarizes the basis and recent developments on the combined interface boundary condition (CIBC) method for the numerical simulation of fluid–structure interaction (FSI) problems. To represent the continual reciprocity between both media better, the CIBC method employs a Gauss–Seidel-like procedure to transform the traditional interface conditions into the velocity and traction corrections. A free parameter is adopted to control the effect of such a treatment on the fluid–structure interface. The thorough derivation of the CIBC method is presented, hence providing the theoretical basis of two improved formulations of the method. The relevant issues are deeply discussed for the numerical implementation. The CIBC method is subsequently introduced into various partitioned solution schemes. After describing all ingredients of our coupling strategies in detail, intensive FSI examples are tested to justify the feasibility, robustness and efficiency of the developed methodologies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In real world, fluid–structure interaction (FSI) is inevitably encountered in a rich variety of engineering realms, such as civil engineering, ocean engineering, aerospace engineering, mechanical engineering, biomedical engineering and so on. To be specific, the wind action over a high-rise building or a suspension bridge is frequently met in civil engineering, and in ocean engineering marine risers subjected to ocean currents are always stimulated to vibrate violently. Self-excited vibrations of an engineering structure will be triggered once one of their natural frequencies gets close to the vortex-shedding frequency and the structural damping is small enough. The structures’ safety may not be guaranteed in that case. A terrible catastrophe is learnt from the collapse the old Tacoma Narrows Bridge in the 1940s. As a result, FSI is a significant consideration for the design of engineering structures experiencing intensive flow-induced oscillations. Accurate prediction of FSI dynamics can help people to find the formation mechanism and to work out countermeasures to suppress the adverse aerodynamic responses.
As a representative of multi-physical fields, FSI characterizes the persistent interplay of an incompressible viscous fluid with a submerged structure. This mixed interaction originates from the reality that, the fluid’s impact on the structure is thought as a fluctuating force which causes the structural movement that alters the flow patterns near the structure in turn. From the perspective of fundamentals, FSI is seized of strong nonlinearity and high uncertainty. The complexities rely upon not only the governing equations of fluid flows but also the behaviors of the coupled FSI system. They will be surely aggravated if structural nonlinearities (e.g. geometrical and/or material) are taken into account. Unfortunately, FSI is so complicated that its analytical solution remains almost unavailable, except for those extremely simplified cases.
Nowadays the numerical resolution of FSI has received massive attention from the research community because of its scientific and practical significance. Since FSI contains sophisticated principles of mathematics and abundant essences of physics, its computer assessment has become one of challenging topics in computational fluid dynamics for decades. Substantial progresses of mathematical theories in tandem with the advanced computer science enable this task. Conversely, FSI investigations have long promoted developments and interchanges of multidiscipline. Numerically, FSI comprises three ingredients: computational fluid dynamics, computational structural dynamics and computational mesh dynamics [131]; in other words, it is dominated by the three-field nonlinear formulation [47]. Several comprehensive reviews on diverse solution techniques of FSI can be consulted in [33, 50, 71, 95, 125, 126, 129]. Here we exclusively concentrate on those methods developed under the arbitrary Lagrangian–Eulerian (ALE) description [43]. Therefore, current numerical approaches to solve FSI problems are mainly grouped into two categories: monolithic coupling method [20, 72, 93] and partitioned (or staggered) coupling method [48, 52, 87]. In the former method the fluid and structural governing equations are assembled into a single block which is iteratively solved. In spite of excellent property of energy conservation, the monolithic approach demands notable efforts to recast the existing codes, entangling the mathematical management and losing the code modularity. It turns out that the computational expense is still a matter. By contrast, the latter method strategically solves different disciplines in a sequential manner. Accordingly, the partitioned method facilitates the marriage of available programs with minimal changes and allows for flexible choices of various efficient solvers. These traits make the partitioned coupling approach a very appealing solution technique in practice.
The partitioned coupling method may be stretched back to the early work of Park et al. [108] in the 1970s or even earlier. It is further classified into explicit coupling technique [5, 57, 62] and implicit coupling technique [35, 40, 87]. The partitioned explicit coupling technique works in the subiteration-free fashion, thus it achieves conceptual clarity and high efficiency. However, this technique does not assure exact satisfaction of the equilibrium on the fluid–structure interface such that cumulated errors may produce a spurious solution or even failure. In the cases of strong added-mass effect [23, 24, 54], the partitioned explicit coupling technique suffers from the severely numerical instability initiated by the inherent time lag. By comparison, the partitioned implicit coupling technique is numerically stable as it preserves energy balance by subiterations per time step. This technique is physically rigorous and is necessary if the overall solution accuracy is not expected to deteriorate. Its outstanding weakness rests with the time consumption, though it is efficient in aeroelasticity [6].
Apart from the above two, a third category of the partitioned method has been proposed by Fernández et al. [52] within the classical Chorin-Témam projection framework [26, 128]. To be specific, the ALE advection-diffusion step is explicitly treated with the predicted mesh whereas the fluid projection step is implicitly coupled with the structural motion on the frozen mesh. The method characterizes an intrinsic explicit-implicit or partially-implicit treatment for predicting FSI, thus it is designated as the projection-based partitioned semi-implicit coupling algorithm. In comparison to the fully implicit algorithm, the major advantage of the semi-implicit algorithm lies in the improved numerical efficiency without affecting stability too much [52]. Apparently, the semi-implicit method is somewhat distinguished from the three-field FSI formulation [47]. The comprehensive literature survey in regard to the partitioned semi-implicit coupling method is completed in the Introduction of our recent work [65].
Exploring partitioned coupling algorithms is essential and meaningful for both FSI theories and engineering practice. A relatively new partitioned solution procedure for modeling FSI has been proposed by Jaiman and his colleagues since a decade ago [75–77]. The procedure is termed the combined interface boundary condition (CIBC) method which depends on a higher-order treatment for better accuracy and stability of the global FSI system. The velocity and momentum flux corrections are constructed at two successive time levels in order to minimize numerical instability and to damp out energy residual on the interface. The interfacial corrections are adjusted by a free parameter that plays a vital role in this method. The CIBC method is developed on the ground of the characteristic interface boundary conditions [51] and the transformation of traditional interface conditions of a linearized FSI model [80]. The purpose of this technique consists in contriving an interfacial compensation mechanism for separate computation of partitioned solution procedure. The CIBC method was formally presented by Jaiman et al. [75]. In this conference article the interaction between a compressible fluid and a linear elastic structure is numerically analyzed, involving the one-dimensional (1D) elastic piston in closed and open fluid domains and the 2D subsonic flow-shell problem. Remarkable improvements are uncovered in the piston problems. The good adaptability is endorsed by equipping the non-collocated partitioned procedure [48] and the fluid subcycling technique [49, 111] with the method. Roe et al. [115] simulated a 1D conjugate heat-transfer process by way of exploiting the CIBC method. Their careful verification implies that, with the help of the CIBC method, the partitioned explicit coupling procedure generates more stable and accurate results. The optimal non-dimensional coupling constant is approximately suggested for a wider stability region of the coupled system via the Godunov–Ryabenkii method. Encouraged by that study, one may furnish the CIBC algorithm with the Dirichlet/Neumann averaging method [113, 130] to further improve the accuracy, stability or efficiency of partitioned coupling computation. Jaiman et al. [82] devised a multi-iterative coupling (MIC) scheme of the CIBC method for estimating a 2D flexible baffle problem, and for predicting the complicated interaction of 3D incompressible turbulent flows with a long marine riser. A much lower mass ratio (i.e. the ratio of the structural density to the fluid one) is achieved, showing the potential of this variation in practical applications. Unfortunately, the numerical description of the MIC scheme seems limited. Badia et al. [7] designed the Robin transmission conditions for FSI later. The similarity among the CIBC method and the approaches from [7, 51] is perceived from the formulae as such. The former utilizes one coupling parameter whereas the rest require two. In a word, applying the CIBC method to a relatively easy FSI event, such as the 1D interaction of an inviscid compressible fluid with a linearly flexible structure, presents manifest superiority over the direct use of partitioned coupling approach. Further considerations are however demanded in the multi-dimensional cases [76]. The nonlinear iterative force correction (NIFC) scheme is briefly presented in [78] as an extension of the MIC scheme, which may compute the predictor in terms of the CIBC method. In this conference paper, realistic simulations of flexible risers are addressed and the desirably low mass ratio is achieved. The NIFC method is then detailed in [81] based on the Aitken’s extrapolation for stabilizing the coupled partitioned system. The CIBC method inspires the derivation of stabilization parameter of the NIFC method. The mass ratio effect is investigated for a freely oscillating circular cylinder to demonstrate the approach’s merit. The CIBC predictor is not carried out in [78, 81] yet. For the moment, the CIBC method has mainly concentrated on two 1D model problems as well as an incomplete 2D FSI problem, thus fetching marginal achievements accompanied by mere applications. We also notice from the aforementioned articles several deficiencies of the method summarized below
-
The CIBC formulation is structured based on \(\varvec{\sigma }^{\mathrm{F}} = p\mathbf {I}\);
-
The structural traction rate is avoided before it is renewed;
-
The method fails to be applicable to the fluid-rigid body interaction owing to the traction term;
-
The displacement continuity is not maintained on the interface.
Up to now, the first author and his colleagues have performed a series of studies to enhance the CIBC method. We have extended the method to the frontier of the incompressible viscous fluid interacting with a rigid/flexible body. The relevant theoretical modifications have been made for it. In what follows, we briefly recall our accomplishments. He et al. [68] proposed a new formulation of the CIBC method where the uncorrected structural traction was discarded when establishing the CIBC terms. The crucial contribution depends upon the fluid-rigid body computation rescued by the improved method. Afterwards, the CIBC method is combined with the partitioned subiterative coupling schemes for aeroelastic simulations [69]. Nevertheless, it is found that the structural displacement predictor [111] results in the lagged field variables in calculating the CIBC corrections [63]. The structural force predictor [41, 117] is then put into use within the partitioned implicit coupling algorithm, ensuring that the latest quantities belonging to different subdomains are adopted for the CIBC method [63]. We justified our methodologies in [63, 68, 69] through various flow-induced vibration of a bluff body at low Reynolds numbers. It is worth mentioning that, Jaiman et al. [79] have recently extended the NIFC procedure based on our improved CIBC corrections [63, 68, 69] to the freely oscillating square cylinders at subcritical Reynolds number. Their study confirms that the developed scheme is able to cope with flow-induced vibrations of light offshore structures exposed to turbulent flows. Reference [79] is the first effort on the complex FSI simulation under condition of the 3D turbulent flows. Motivated by the projection-based semi-implicit coupling method [52], the author has recently developed a CBS-based partitioned semi-implicit coupling algorithm for simulating various FSI problems [65]. In the coupling algorithm, the CBS scheme serves not only for the fluid component but also for the entire coupling algorithm. The CIBC method that interprets the reciprocity between both physical fields is re-derived in a more concise fashion. Hence no extra equations yield on the interface for the traction increment. A weak implementation is proposed to avoid deteriorating the numerical results as follow: the displacement rather than the velocity is corrected on the interface. For the elastic solid, the traction correction term is imported into the Galerkin weak formulation while the velocity increment is properly simplified. The programming effort is consequently alleviated. The proposed method rectifies the limitations of its original counterpart, making itself applicable to fluid-rigid/flexible body interaction. The CIBC method is recoined in view of the complete fluid stress tensor by He and Zhang [67]. They analyzed the instability source arising from the CIBC compensation and proposed an approach to regain the two-sided corrections for Dirichlet and Neumann interface conditions. In particular, for the torsional rigid-body motion, the pitching moment is implicitly corrected by using the CIBC method. The proof is clearly shown on the basis of the theory of the generalized inverse matrix.
The remainder of this paper is organized as follows. The fluid governing equations are depicted in Sect. 2 whereas the structural dynamics is settled in Sect. 2.2. Section 2.3.1 demonstrates the mesh updating strategy. Section 3 is devoted to the derivation of the CIBC method. The steps of partitioned coupling schemes are presented in Sect. 4. Numerical examples are intensively investigated in Sect. 5. Concluding remarks and open issues are stated in the Sect. 6
2 Governing Equations
2.1 The Fluid Problem
2.1.1 Incompressible Flows on Moving Mesh
Let \(\varOmega ^{\mathrm{F}}_t \subset \mathbb {R}^2\) and \((0, \ T)\) be the fluid and temporal domains, respectively. \(\varOmega ^{\mathrm{F}}_t\) is bounded by \(\varGamma ^{\mathrm{F}}_t\) which is decomposed into three complementary subsets, i.e., the Dirichlet-type boundary \(\varGamma ^{\mathrm{F}}_{\mathrm{D}}\), the Neumann-type boundary \(\varGamma ^{\mathrm{F}}_{\mathrm{N}}\) and the fluid–structure interface \(\varSigma\). The spatial and temporal coordinates are denoted by \(\mathbf {x}\) and t. The incompressible Navier–Stokes equations in the arbitrary Lagrangian–Eulerian (ALE) description governing the fluid flows on a moving domain read as
where the primitive variables are the fluid velocity \(\mathbf {u}\) and the pressure p, \(\rho\) denotes the fluid density, \(\mathbf {c} = \mathbf {u} - \mathbf {w}\) is the convective velocity, \(\mathbf {w}\) is the mesh velocity, \(\mathbf {f}\) represents the body force, \(\varvec{\sigma }\) is the fluid stress tensor and \(\nabla\) means the gradient operator.
The constitutive equation for a Newtonian fluid is written as
where \(\mathbf {I}\) indicates the identity matrix, \(\mu\) is the fluid viscosity, \(\varvec{\epsilon }\) is the rate-of-strain tensor and superscript T indicates transpose.
The fluid problem is completed by prescribing the boundary and initial conditions below
where \(\mathbf {t}^{\mathrm{F}}\) is the fluid traction and \(\mathbf {n}^{\mathrm{F}}\) is the unit outward normal of \(\varGamma ^{\mathrm{F}}_{\mathrm{N}}\).
In order to facilitate the fluid simulation, the following dimensionless scales are defined
based on the free stream velocity U and the characteristic length D. By employing these scales and dropping all asterisks, the dimensionless version of the incompressible Navier–Stokes equations is obtained as follows
together with the constitutive relation
where \(Re =\rho ^{\mathrm{F}} UD / \mu\) is the Reynolds number. Note that the boundary and initial conditions Eqs. (4a–4c) should also be nondimensionalized [2].
2.1.2 Characteristic-Based Split (CBS) Scheme
A general algorithm for fluid dynamics has been originally proposed by the trilogy of Zienkiewicz et al. [28, 142, 143] since 1995, and in 1999 it was formally named as the CBS scheme [144]. In this paper, the semi-implicit CBS scheme is employed to solve Eqs. (5–7). The resulting procedure is actualized by the following steps:
- Step 1: :
-
Calculate the auxiliary velocity
$$\begin{aligned} \widetilde{\mathbf {u}} - \mathbf {u}^n = \varDelta t \left( -\mathbf {c}^n \cdot \nabla \mathbf {u}^n + \frac{1}{Re}\nabla ^2 \mathbf {u}^n + \frac{\varDelta t}{2} \mathbf {c}^n \cdot \nabla (\mathbf {c}^n \cdot \nabla \mathbf {u}^n) \right) , \end{aligned}$$(8) - Step 2: :
-
Update the pressure
$$\begin{aligned} \nabla ^2 p^{n+1} = \frac{1}{\varDelta t} \nabla \cdot \widetilde{\mathbf {u}}, \end{aligned}$$(9) - Step 3: :
-
Correct the velocity
$$\begin{aligned} \mathbf {u}^{n+1} - \widetilde{\mathbf {u}} = -\varDelta t \left( \nabla p^{n+1} - \frac{\varDelta t}{2} \mathbf {c}^n \cdot \nabla ^2 p^n \right) , \end{aligned}$$(10)
where superscripts n and \(n + 1\) denote the nth and \((n+1)\)th time slices respectively, the time step size is expressed as \(\varDelta t = t^{n+1} - t^n\) within the time interval \([ t^n, t^{n+1} ]\), and \(\mathbf {f}\) and the third-order terms are neglected.
It is emphasized that the CBS scheme can work in the matrix-free way [101, 102]. Also, the stabilizing parameter \((\varDelta t)^2/2\) is independent of local element size in the CBS scheme, thus leading to some computational savings for the ALE computation. The stabilization mechanism via the time step is described in [29]. The imposition of boundary conditions for the scheme are discussed in [28, 100]. The boundary condition treatment follows the suggestion of Ref. [100]. The use of the stabilization technique via dual time steps in FSI is inspired by Nithiarasu and Zienkiewicz [102, 104]. The impact of this technique shall be discussed later. The thorough derivation and versatile applications of the CBS scheme are summarized in the textbook [145]. The review on the CBS scheme is presented by Nithiarasu et al. [103], and the comparison of different versions is found in [18]. A variant of the CBS scheme is successfully applied to flow-induced oscillations of multiple cylinders [59, 60].
After the temporal discretization, the standard Galerkin finite element method (FEM) is employed to discretize Eqs. (8–10) in space [146]. Three-node triangular (T3) element is adopted as the CBS scheme allows for low-order and equal-order interpolation for both velocity and pressure variables. The mass matrix is lumped in a spirit of compromise between numerical accuracy and efficiency. The lumped mass approximation causes no significant errors [144].
Since the semi-implicit CBS scheme is conditional stable, the permissible time step is governed by the stability limitations [145] below
where the local convective time step \(\varDelta t_{\mathrm{CONV}}\) and the local diffusive time step \(\varDelta t_{\mathrm{DIFF}}\) are defined by
where \(\bar{\varDelta }\) indicates the characteristic element size.
2.2 The Structural Problem
We consider that a structure occupies the domain \(\varOmega ^{\mathrm{S}}_t \subset \mathbb {R}^2\) and the boundary \(\varGamma ^{\mathrm{S}}_t\) is composed of a union of three non-overlapped parts, namely, \(\varGamma ^{\mathrm{S}}_t = \varGamma ^{\mathrm{S}}_{\mathrm{D}} \cup \varGamma ^{\mathrm{S}}_{\mathrm{N}} \cup \varSigma\). The structural dynamics is expressed in the Lagrangian description and the isotropic assumption is made for the structural problem.
2.2.1 Rigid-Body Dynamics
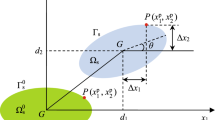
A rigid body immersed in a fluid is modeled as a spring-damper-mass system since it sustains the fluctuating fluid force. The rigid body undergoes the generalized planar motion, as shown in Fig. 1. The structural displacement is signified as \(\mathbf {d} = \{ d_1, \ d_2, \ \theta \}^{\mathrm{T}}\) where all components are defined at the center of gravity, G, and subscripts 1, 2 and \(\theta\) designates the horizontal, vertical and rotational directions. The equation governing such a structural motion reads as
where the dot illuminates the temporal derivative, \(m_i\), \(c_i\) and \(k_i\) stand for the mass, damping and stiffness of the structure, \(\mathbf {P} = \{F_{\mathrm{D}}, \ F_{\mathrm{L}}, \ F_{\mathrm{M}}\}^{\mathrm{T}}\) is the fluid force vector, \(F_{\mathrm{D}}\), \(F_{\mathrm{L}}\) and \(F_{\mathrm{M}}\) mean the drag, lift and pitching moment, respectively. The fluid forces are evaluated by means of
where \(\mathbf {n}^{\mathrm{S}}\) represents the unit outward normal of \(\varGamma ^{\mathrm{S}}\), \(\varDelta \mathbf {x}\) is the distance between the surface point and the center of gravity, and \(\mathbf {t}^{\mathrm{S}}\) stands for the structural traction whose components are illuminated by the first two subequations.
Schematic view of the generalized 2D rigid-body motion
The compatibility condition [5, 106, 120] must be satisfied between the center of gravity G and the surface point P. As pictured in Fig. 1, the geometric relation between \(\mathbf {d}^{\mathrm{P}}\) and \(\mathbf {d}\) is written in the component form as follow
where \(\mathbf {d}^{\mathrm{P}} = \{ d_1^{\mathrm{P}}, \ d_2^{\mathrm{P}} \}^{\mathrm{T}}\) and \(\mathbf {x}^{\mathrm{P}} = \{ x_1^{\mathrm{P}}, \ x_2^{\mathrm{P}} \}^{\mathrm{T}}\) are the displacement and coordinates of Point P.
By differentiating Eq. (15) with respect to t, the velocity relation between both points is expressed as
where \(L_1^{\mathrm{P}} = x_1^{\mathrm{P}} \cos \theta - x_2^{\mathrm{P}} \sin \theta\) and \(L_2^{\mathrm{P}} = x_1^{\mathrm{P}} \sin \theta + x_2^{\mathrm{P}} \cos \theta\) are the angle-dependent coefficients. Similarly, the acceleration relation is obtained below by differentiating Eq. (16) in terms of time
The dimensionless scales
and the reduced parameters
are computed to nondimensionalize Eq. (13), where the drag coefficient \(C_{\mathrm{D}}\), the lift coefficient \(C_{\mathrm{L}}\) and the moment coefficient \(C_{\mathrm{M}}\) are the dimensionless applied forces, the mass ratio \(m_i^*\) is the dimensionless mass, \(\xi _i\) is the damping ratio, \(f_{\mathrm {R} i}\) is the reduced natural frequency, and \(f_{\mathrm {N} i}\) is the natural frequency. By considering the above variables without superscript asterisks, the dimensionless equation of structural motion is written as
2.2.2 Flexible-Body Dynamics
For a geometrically nonlinear solid, the elastodynamics equation describes the law of momentum conservation by
where \(\rho ^{\mathrm{S}}\) is the structural density, \(\mathbf {f}^{\mathrm{S}}\) is the structural body force, \(\varvec{\sigma }^{\mathrm{S}}\) is the Cauchy stress tensor and the structural damping is omitted. By assuming a linear-elastic St. Venant–Kirchhoff material, the constitutive equation is obtained between the second Piola–Kirchhoff stress \(\mathbf {S}\) and the Green–Lagrange strain \(\mathbf {E}\) by
where \(\mathbf {C}\) signifies the constitutive tensor and \(\mathbf {F}\) represents the deformation gradient. \(\mathbf {S}\) is related to \(\varvec{\sigma }^{\mathrm{S}}\) through the geometric transformation
where \(J = \mathrm {det} (\mathbf {F})\). Young’s modulus E and Poisson’s ratio \(\nu\) should be prescribed for the elastic solid problem. Finally, the following boundary and initial conditions are applied to the problem statement
Similarly, the nondimensional scales
are computed in order to nondimensionalize Eq. (19) as
Note that the dimensionless Young’s modulus can be viewed as the inverse of the Cauchy number [30]. Equation (23) holds the geometric nonlinearity, or, in other words, it accounts for the finite deformation of the solid. For this reason, the linearization of the equilibrium equation is implemented via the Newton–Raphson procedure using total Lagrangian formulation [15, 62].
The finite element discretization is executed by the quadratic nine-node quadrilateral (Q9) plane stress element in space [146]. Also, the so-called celled-based smoothed finite element method (CS-FEM) is applied to the solid subsystem in this work.
2.2.3 Smoothed Finite Element Technique
The CS-FEM was developed by Liu et al. [92] for solid mechanics based on the gradient smoothing technique. This method subsequently was extended to the geometrically nonlinear analyses [31, 32]. The CS-FEM owns higher accuracy in results and faster convergence in energy without remarkably increasing computational expenditure. It is quite straightforward to execute such a technique since just trivial modifications are required in conventional FEM codes. In view of these merits, the CS-FEM is considered as an alternative approach for the geometrically nonlinear analysis. The basic idea of the CS-FEM is briefly recalled below.
Based on the gradient smoothing operation, the gradient of a scalar displacement d is approximated in the form of
where \(\varOmega _{\mathrm{C}}\) is the smoothing domain (SD) and \(\varPhi\) indicates the Heaviside-type smoothing function. Applying Gauss theorem into the right-hand side of Eq. (24) leads to
where \(\varGamma _{\mathrm{C}}\) is the boundary of \(\varOmega _{\mathrm{C}}\) and \(\mathbf {n}\) is the unit outward normal of \(\varGamma _{\mathrm{C}}\). The smoothing function \(\varPhi\) is given by
where \(A_{\mathrm{C}}\) is the area of \(\varOmega _{\mathrm{C}}\). Substituting Eq. (26) into Eq. (25), we have
Note that a constant’s gradient vanishes in the above equation.
The flexible solid is discretized with bilinear four-node quadrilateral (Q4) plane stress elements which are adopted to set up the smoothed shape functions for CS-FEM. No extra degrees of freedom are introduced into the numerical calculation. The construction of the SDs and smoothed shape functions will be shown in the example section. Interested readers can refer to [31, 32, 92] for more details. The author has successfully applied the CS-FEM to FSI problems [64, 65].
2.2.4 Time Marching Procedure
Concerning the time marching procedures, multiple choices can be made available for advancing the structural equation in time, such as the Newmark-\(\beta\) method [99], the Hibert–Hughes–Taylor-\(\alpha\) method [70], the Generalized-\(\alpha\) method [27], the composite implicit time integration method [12–14] (also known as the Bathe method), etc. A vivid application can be consulted with reference to the Bathe method in [61]. Among these methods, we adopt here the classical Newmark-\(\beta\) method [99].
The Newmark approximations to the velocity and displacement are written as follow
where \(\gamma \geqslant \frac{1}{2}\) and \(\beta \geqslant \frac{1}{4}\). The trapezoidal rule (\(\gamma = \frac{1}{2}\) and \(\beta = \frac{1}{4}\)) is extensively applied to structural dynamics, which brings the unconditionally stable and second-order time accurate scheme.
2.3 The ALE Mesh Kinematics
2.3.1 Mesh Deformation Method
An essential aspect of FSI computation involves the fluid ALE mesh deformation caused by the structural movement. Our mesh deformation method adopts a blend of the moving submesh approach (MSA) [88] and the ortho-semi-torsional spring analogy method (OST-SAM) [96] so as to significantly depress the time consumption.
The basic idea behind the MSA lies in putting a layer of sparse submesh (zones) over the fluid ALE mesh (elements) which is then dynamically rearranged through specific interpolation formulae, see Fig. 2. A node on the fluid mesh is distinctively referred to as a point, whereas that on the MSA submesh is still called a node. The principle of this technique is outlined below
- Step 1: :
-
Extract information of the mesh and submesh
- Step 2: :
-
Collect all fluid points falling into each MSA zone
- Step 3: :
-
Calculate interpolation formulae for each point in the zone
- Step 4: :
-
Begin time loop
- 4.1::
-
Gain boundary nodes’ displacement from the structural motion
- 4.2::
-
Invoke the OST-SAM to assess interior nodes’ motion (skip this substep if no interior nodes occur);
- 4.3::
-
Update the submesh
- 4.4::
-
Interpolate the ALE mesh based on the new submesh
- 4.5::
-
Check MSA zones and fluid elements’ areas
- Step 5: :
-
End time loop
Diagrammatic sketch of the MSA technique
According to Lefrançois [88], several keypoints should be noticed. Firstly, only the triangle is available for the zone and thus the resulting interpolation or mapping function is actually the shape function of T3 element. This seems to be the major limitation of the MSA. Despite that, the fluid element can adopt either a triangle or quadrangle. Secondly, the first three steps need to be implemented just once at initial state. Thirdly, either the absolute or relative displacement can be used in the approach. Finally, a capsule is adopted to encapsulate those complex structures whose geometries are composed of segments or curves. We can also use more than one capsules if necessary.
A submesh without any interior nodes permits the immediate application of the MSA (see Step 4.2). When interior nodes arise, the pseudo-structural equation of elastodynamics has to be dealt with by appropriate measures. The MSA works in conjunction with the OST-SAM in this case. The resulting quasi-static equilibrium equations are settled by the simple successive over-relaxation technique of Zeng and Ethier [139], other than the complex preconditioned solver. It is emphasized that the MSA is far more economical than the SAM since (1) the MSA possesses the very simple interpolation functions; (2) the MSA utilizes a fast interpolation process whereas the SAM requires the massive iterations; (3) the MSA demands the remarkably fewer iterations only if it has to.
Since the MSA preserves the quality of ALE mesh topology quite well, there is no need to smooth nodes’ coordinates [124]. In fact, the MSA is a variant of the approach proposed by Liu et al. [94] who made use of the Delaunay triangulation for structures of arbitrary profile. This technique is much simpler for those users who are not familiar with Delaunay graph tools.
2.3.2 Geometric Conservation Law
The geometric conservation law (GCL) is inevitably encountered in the moving boundary problems. Its general depiction is that an ALE computation must exactly reproduce the constant solution of a uniform flow [89]. The conclusions about the practical impact of the GCL on a time marching scheme are found to be controversial in a number of published papers. These incompatible statements have been compiled in the book chapter [43]. Nonetheless, numerous researchers are apt to believe that satisfying the GCL is conducive to the stability and accuracy of the considered numerical schemes.
As pointed out by Lesoinne and Farhat [89], the popular midpoint rule
automatically satisfies the GCL in the 2D FEM. Although Eq. (30) is merely first-order accurate, it outstrips higher order scheme [54].
For the fluid fractional-step-type method, it is not trivial to construct the differencing scheme of mesh velocity to fulfill the GCL (see [45] for instance). To reach this goal, a mass source term (MST) [83] is implanted into Step 2 of the CBS scheme as follow
with
where \(A_e\) indicates the area of element e, superscript i (\(i =\) 1, 2 and 3) in \(\mathbf {w}\) means point i of element e and subscript j (\(j =\) 1 and 2) component j of the coordinates. It is worth pointing out that the MST is rigorously derived within the T3 element context and it vanishes on the Eulerian mesh.
2.4 Conventional Interface Conditions
In the partitioned FSI calculation, the interplay between the fluid and structure is accomplished via separately enforcing the velocity continuity and the traction equilibrium on the interface \(\varSigma\) as follows
where \(\mathbf {t}^{\mathrm{F}} = \varvec{\sigma }^{\mathrm{F}} \cdot \mathbf {n}^{\mathrm{S}}\) and \(\mathbf {t}^{\mathrm{S}} = \varvec{\sigma }^{\mathrm{S}} \cdot \mathbf {n}^{\mathrm{S}}\) are the fluid and structural tractions respectively, \(\mathbf {n}^{\mathrm{S}}\) represents the unit outward normal of \(\varSigma\) pointing from the structure to the fluid and \(\mathbf {n}^{\mathrm{F}} = -\mathbf {n}^{\mathrm{S}}\). Note that the fluid traction differs from that defined in Eq. (4b). Also, the geometric continuity should be supplemented owing to the dynamic mesh motion
The majority of partitioned approaches exert Eq. (33) immediately, or by extrapolation [41, 111, 117], or by relaxation [85, 87]. Other efforts are dedicated to the non-standard enforcement of interface coupling conditions. Farhat and Lesoinne [48] proposed a conserving partitioned coupling algorithm through offsetting half a time step to satisfy the GCL without violating the continuity condition on the interface. This notion was later extended by Braun et al. [21] to the generalized-\(\alpha\) time marching method. A transpiration condition was derived from the truncated Taylor expansion of the fluid velocity in the reference interface’s neighborhood [37, 46]. This intermediate interface forms a fixed boundary on which the fluid subsystem can be settled, decreasing the computational cost. Because of this trait, Bekka et al. [17] applied the transpiration condition to the aeroelastic stability analysis of a flexible over-expanded rocket nozzle. Besides the CIBC method, numerical treatments that are tailored to building specific interface conditions seem limited. In this aspect, one of well-known artworks is the Robin transmission conditions developed by Badia et al. [7].
Under the consideration of the elastic solid, the matching finite element discretizations are generated at both sides of the interface in order to avoid loss of computational accuracy. For the pair of T3 and Q9 elements, partially incompatible finite element discretizations are adopted along the fluid–structure interface.
3 Combined Interface Boundary Condition Method
The asynchrony is caused by separate enforcement of the Dirichlet and Neumann conditions on the interface in the partitioned coupling algorithm. In order to rule out this asynchrony, two combined residual operators for the Dirichlet and Neumann interface conditions are established as
which is enlightened by the variational symplectic integrators [22] and the characteristic interface boundary conditions [51]. In Eq. (35) \(\partial /\partial t\) and \(\partial /\partial n\) represent the temporal and normal derivatives of the interfacial variables, respectively. The main idea consists of building up a local discrete energy-preserving property for the staggered stencil between the pair of differential equations on the interface. A coupling parameter is thus required for allying the spatial and temporal derivatives of Neumann and Dirichlet quantities in the forthcoming CIBC method. Once gaining the aforementioned residual operators \(\mathscr {R}^{\mathrm{D}}\) and \(\mathscr {R}^{\mathrm{N}}\), the increments will be utilized to correct the conventional interface conditions. Next, the combined interface conditions that result from both operators will be illustrated.
3.1 The CIBC Formulation I
3.1.1 Combined Interface Conditions
Within the continuum framework, the momentum conservation of the coupled FSI system is consolidated by
where subscript I (I = F and S) denotes the quantity coming from the fluid or structural field, and the symbol \(\dot = \mathrm {d}/\mathrm {d} t\) represents the material derivative in regard to time t. Details on the material, spatial and referential time derivatives are well written in [43]. Equation (36) is closed with the interface conditions. For the sake of the better understanding, all formulae of this section are written in the dimensional form. The dimensionless CIBC terms will be given later.
Following the definition of [76, 80], we write here the fluid traction as \(\mathbf {t}^{\mathrm{F}} = \varvec{\sigma }^{\mathrm{F}} \cdot \mathbf {n}^{\mathrm{F}}\). Considering Eq. (36), the Dirichlet velocity continuity condition in Eq. (33) is rewritten as follow
where the external force \(\mathbf {f}^{\mathrm{i}}\) is ignored on \(\varSigma\) and the normals are time-invariant along \(\varSigma\) for the infinitesimal deformation [80]. We can simplify Eq. (37) as
Multiplying on both sides by \(\mathbf {u}^{\mathrm{S}}\) and adopting \(\mathbf {t}^{\mathrm{F}} = \varvec{\sigma }^{\mathrm{F}} \cdot \mathbf {n}^{\mathrm{F}}\), Eq. (38) is transformed into
By differentiating the Neumann traction compatibility condition in Eq. (33) with respect to time t, we obtain
Equations (39) and (40) are the specific expression of the residual operators \(\mathscr {R}^{\mathrm{D}}\) and \(\mathscr {R}^{\mathrm{N}}\) on the interface, respectively. Now these two equations are the foundation of the transformation of the conventional interface conditions into the combined interface conditions.
By combining Eqs. (39) and (40) and considering \(\mathbf {n}^{\mathrm{F}} = -\mathbf {n}^{\mathrm{S}}\), one new relation for the velocity on the dry interface \(\varSigma ^{\mathrm{S}}\) is given by
and the other one for the traction on the wet interface \(\varSigma ^{\mathrm{F}}\) is derived by
where \(\omega\) is a positive coupling parameter which should be small enough to make sure that the interfacial energy is always stable [80].
In light of the Gauss–Seidel iterations, Eqs. (41) and (42) are rewritten on two consecutive time levels as follows [76]
for the velocity on \(\varSigma ^{\mathrm{S}}\), and
for the traction on \(\varSigma ^{\mathrm{F}}\). If the fluid density is constant, the corrections for velocity and traction are constructed on two sides of \(\varSigma\) as follows
Finally, the traditional interface conditions (33) are severally calibrated by the increments (45) and (46) as follows
The CIBC method is made up of Eqs. (45) and (46) where the coupling parameter \(\omega\) provides a suitable acceleration-traction joint. As explained in [76], the CIBC corrections are justified by the fact that the weak imposition of the boundary conditions may neglect certain physical processes on the FSI. Hence introducing these corrections back into the conventional interface conditions increases the physical relevance of the FSI solution. By solving the additional correction terms, the CIBC method can also attain the improved stability and accuracy of the coupled FSI system which the partitioned coupling algorithm may undermine. The similar derivative process is found in [51, 80] for a simplified linear FSI model, where the stability and conservation of the proposed combined boundary conditions are analyzed. Equation (46) requires the structural traction term which does not appear in rigid-body dynamics. Therefore, the original CIBC method cannot be applied to the fluid-rigid body interaction.
3.1.2 Modifications for the CIBC Method
In [76] the displacement field that is solved at time \(n + 1\) is used to update the structural stress on the dry interface. After that, the traction rate is easily acquired by differencing the structural traction. This process however leads to an unnatural fact that the new structural traction has to be applied to Eq. (46) before it is corrected by Eq. (48). To amend this fault, a new mathematical formulation of the CIBC method is proposed in this subsection.
The time derivative of Eq. (48) is simply obtained by
which also holds at time n, namely
Inserting Eq. (50) into Eq. (43) and considering the style adopt by Jaiman et al. [76], the following velocity increment is obtained
where the incremental traction rate is estimated by the first order backward differencing scheme
Similarly, two temporary equations are gained by individually inserting Eq. (49) into Eqs. (44) and (46). With the proper operations on the two temporary equations, the ordinary differential equations (ODEs) of order 1 yield below
where the solution vector, coefficients and right-hand vector are expressed by
The general solution of Eq. (53) is sought via
where \(\mathbf {D}\) is a constant and bound vector. Given the initial conditions, we can determine
where all quantities are finite at the initial state. \(\mathbf {D} e^{-\frac{2t}{\varDelta t}} = \mathbf {0}\) therefore holds when \(t \rightarrow \infty\). Finally, the traction increment is obtained by
As a result, Eqs. (51) and (57) constitute our new CIBC formulae where \(\mathbf {t}^{\mathrm{S}}\) does not appear any more. No need to compute \((\mathbf {t}^{\mathrm{S}})^{n+1}\) is provoked in constructing the traction increment before the structural traction is corrected. Using the above procedure, the dimensionless CIBC formulae are written as
where the normal is normalized by the characteristic scale.
In addition, the displacement continuity ought to be maintained on \(\varSigma\) by
Alternatively, we can derive the equation below if the relative displacement is used
Based on the above analysis, the differences between the original and the present CIBC methods are summarized as follows: (1) the structural traction is avoided before it is updated by the corrective term; (2) the ratio \(\omega /\varDelta t\) is suggested for calibrating the interfacial corrections; (3) the displacement continuity is guaranteed on the interface; (4) the present formulation can be applied to the fluid-rigid body interaction immediately.
3.2 The CIBC Formulation II
3.2.1 Reformulation of Combined Interface Conditions
The original CIBC method [76, 80] is derived from the convention \(\varvec{\sigma }^{\mathrm{F}} = p \mathbf {I}\), making the method run in an awkward way for fluid solvers. Here, the fluid stress takes the form of Eq. (3) to readily re-formulate the CIBC method. The inclusion of the full fluid stress is especially important to low Re flows in which the viscosity plays a significant role. Therefore, the combined interface conditions are reformulated in this subsection.
We still make use of the unified formulation (36). From the velocity continuity (33), we can obtain the following relation
where the body force is ignored on \(\varSigma\). Note that the interfacial normal is not assumed to be time-independent for the infinitesimal deformation. By differentiating the second equation of Eq. (33) with respect to t, we derive
Equations (61) and (62) set up the foundation of converting the conventional interface conditions into the combined interface conditions. As a result, one new relation for the velocity on the structural side of the interface \(\varSigma ^{\mathrm{S}}\) is given by
and the other one for the traction on the fluid side of the interface \(\varSigma ^{\mathrm{F}}\) is written by
where \(\omega\) is a positive coupling parameter which should be small enough to make sure that the interfacial energy is always stable [80].
In terms of Gauss–Seidel iterations, Eqs. (63) and (64) can be rewritten on two consecutive time levels as
for the velocity on \(\varSigma ^{\mathrm{S}}\), and
for the traction on \(\varSigma ^{\mathrm{F}}\). If the fluid density is constant, the corrections for velocity and traction are constructed on two sides of \(\varSigma\) as follows
where the coupling parameter \(\omega\) provides a suitable acceleration-traction joint.
The new CIBC method is composed of the corrective increments (67) and (68) that compensate the separate enforcement of the interface conditions via Eqs. (47) and (48).
3.2.2 A Simple Revision
As seen above, the new CIBC traction increment also needs the structural traction rate by updating the structural stress field on \(\varSigma ^{\mathrm{S}}\). The lack of consistency is thus realized in the interfacial treatment of the structural traction. Specifically, the new structural traction has to be applied to Eq. (68) before it is corrected by Eq. (48). This device poses two major deficiencies: (1) the incapability to deal with fluid-rigid body interaction where no internal stress occurs inside the rigid body and (2) special procedure may be required for stress prediction in structural dynamics [110]. To circumvent the restricted use of the CIBC method, a simple revision is made in this subsection.
Replacing Eq. (50) into Eq. (67) yields the velocity increment as follow
Inserting Eq. (49) into Eq. (66), we have the traction increment as follow
Equations (69) and (70) constitute the new CIBC formulae where \(\dot{\mathbf {t}}^{\mathrm {S}}\) does not appear any more. Both the consistency in the treatment of the interfacial traction and the solvability of fluid-rigid body interaction are recovered in the CIBC method. Differing from [63, 68, 69], the current CIBC method does not address the first-order ODEs on the interface for traction correction. In most situations Formulation II is favored, by which we present our results in the numerical examples.
3.2.3 Computational Sequence
We mark Eqs. (48) and (49) as Correction I, while the reverse amendments
with
are labeled as Correction II. In the latter condition, the interfacial displacement is correspondingly compensated by
or
The two corrections correspond to the force and displacement predictors typically adopted in the partitioned subiterative coupling schemes. Equations (73) utilizes \(\nabla \cdot \varvec{\sigma }^{\mathrm{F}}\) at time n rather than \(n + 1\) although the latest fluid variables have already been evaluated. On the other hand, Eq. (74) has to employ \(\dot{\mathrm {\delta } \mathbf {t}}^n\) because \(\dot{\mathrm {\delta } \mathbf {t}}^{n+1}\) is not obtained yet. Some hysteresis values are therefore used for Correction II. In a sense, the nuance between Correction I and Correction II resembles that between the block Jacobi iterations and the block Gauss–Seidel iterations [51]. At present, the sequence of the CIBC corrections appears irrelevant in partitioned FSI computations. Especially, the iterating subproblems’ resolutions will lead the difference between two consecutive subiterations to zero.
3.2.4 Weak Treatment of CIBC Corrections
The numerical tests in [115] show that correcting both interface conditions by the CIBC method may exhibit worse stability properties than correcting either one does. The reasons for this behavior are not clear yet. We also confirm that the FSI calculation will deteriorate or even fail when both interface conditions are corrected. To work out this issue, a possible option is to limit the velocity increment, but it is nontrivial to determine the reduction factor. Similar to the displacement predictor-traction corrector scheme [78, 82], a weak treatment of the CIBC corrections is proposed here. In particular, the velocity increment is used not to correct the structural velocity but to estimate the displacement increment. The traction correction is performed as usual.
Regarding the elastic solid, we can further decrease the numerical effort by directly introducing the traction increment into the Galerkin weak formulation of the structural equation to obtain the following equivalent force
where \(\mathbf {N}\) is the shape function of the structural element and \(\varGamma ^{\mathrm{S}}_{\mathrm{N}}\) is the Neumann segment of the structural boundary, and by approximating the velocity increment as
into which Eq. (69) degenerates if convergent.
3.2.5 Instability Source Caused by Two-Sided Corrections
Technically, two-sided corrections on the interface are supposed to be made for both velocity continuity and stress equilibrium, see [76, 80]. As stated above, Roe et al. [115] reported that in the coupled thermal simulations the modifications for Dirichlet and Neumann interface conditions would deteriorate stability. Instead, they suggested correcting one interface condition at each time step to secure stable computations. Our early studies have also shown such a destabilizing effect. The dependence of several nondimensional parameters on numerical instability was illustrated by computer experiments in [76, 115]. Here we are about to disclose the source of instability pertaining to the CIBC expressions themselves and to propose the sound CIBC method for suppressing the interfacial inconsistency which may be apperceived in Sect. 3.2.4.
Seen from Eqs. (69) and (70), the effect of CIBC corrections is regulated by the coupling parameter \(\omega\) and its reciprocal \(1/\omega\), respectively. It is easy to observe that
where either \(\omega\) or \(1/\omega\) definitely serves as the amplification factor. Here we specify that all quantities are finite except \(\omega\). The spectrum \(\omega > 1\) must be advocated in Eq. (70) to refrain from the potential divergence while it will amplify \(\dot{\mathrm {\delta } \mathbf {t}}\) in Eq. (69). The theoretical observation and numerical tests indicate that, the underlined term of Eq. (69) is the source of instability when carrying out two-sided corrections for velocity and traction. The underlined term even leads the partitioned implicit coupling scheme to divergence at times. To settle this dilemma, we streamline Eq. (69) as
Provided that the equilibrium or convergent state is reached, the temporal rate of traction increment, \(\dot{\mathrm {\delta } \mathbf {t}}\), will naturally disappear. The above simplification is therefore reasonable. Note that Eq. (77) is solely utilized for the elastic solid whereas Eq. (78) is applicable to both rigid and flexible bodies.
3.2.6 Application to the Rigid Body
It is straightforward by now to apply the CIBC method to the flexible body. The way of modeling a rigid body immersed in a fluid is somewhat tortuous since the external force acting on the rigid body is a concentrated load vector. For this reason, the stress equilibrium on \(\varSigma\) becomes
where \(\varDelta \mathbf {x}\) is the distance between the surface point and the center of gravity, see Fig. 1 for reference.
If the rotational degree of freedom is overlooked, we can immediately integrate Eqs. (62) and (63) along \(\varSigma\) as follows
Likewise, the two expressions of Eq. (80) are employed to educe the CIBC method for the vibrating rigid body. After several operations, the velocity and traction increments are readily obtained at two consecutive time steps
where \(S = \int _{\varSigma } \mathrm {d}\varGamma\). The CIBC corrections are hereby given via Eq. (48) for velocity and the equation below
for the applied force.
Next, we will interpret that the applied moment (79b) is only corrected in an implicit manner. From the compatibility condition [5, 106], the displacement and velocity relations between \(\mathbf {d}^{\mathrm{P}}\) and \(\mathbf {d}\) are written by Eqs. (15) and (16), the latter of which is equivalently expressed in the compact form of
where \(\mathbf {T}\) is the transformation matrix that explicitly depends upon the rotational component \(\theta\) as follow
In this special case, Eq. (62) is rewritten as
which is integrated within one time interval \(\varDelta t\) as follow
Substituting Eq. (84) into Eq. (86) produces
Now the problem of interest reads: find the left inverse matrix \(\mathbf {T}_{\mathrm{L}}^{-1}\) such that
Unfortunately, \(\mathbf {T}_{\mathrm{L}}^{-1}\) does not exist because the transformation matrix \(\mathbf {T}\) formulated in Eq. (16) is full-rank in row. This reality is also exposed by the expression of the left inverse matrix
where \(| \mathbf {T}^{\mathrm{T}} \mathbf {T} | = 0\) under the current circumstance. In fact only the right inverse matrix \(\mathbf {T}_{\mathrm{R}}^{-1}\) is attainable, which is easily evaluated as
which amounts to \(\mathbf {T} \mathbf {T}_{\mathrm{R}}^{-1} = \mathbf {I}_{2 \times 2}\). As a result, Eq. (88) does not hold and the applied moment is bound to be implicitly corrected by
3.2.7 Nondimensionalization
In what follows, the CIBC formulae are nondimensionalized for the flexible and rigid bodies, respectively.
Let us take a look at the right-hand sides of rigid-body Eqs. (13) and (18) and then we can have
where \(\mathbf {P} = \{ \mathrm {\delta } P_1, \ \mathrm {\delta } P_2, \ \mathrm {\delta } P_\theta \}^{\mathrm{T}}\) is the total external force and \(\{ \mathrm {\delta } t_1, \ \mathrm {\delta } t_2, \ \mathrm {\delta } t_\theta \}^{\mathrm{T}}\) is the CIBC traction increment.
Substituting the afore-defined nondimensional scales and \(\varGamma ^*= \frac{\varGamma }{D}\) into Eq. (81b) without temporal discretization, we are able to proceed with the equation below
which is nondimensionalized as
Also, it is straightforward to nondimensionalize \(\mathrm {\delta } t_\theta\) in terms of Eq. (94a) and \(\varDelta \mathrm {x}^*= \mathrm {x} / D\) below
Concerning the velocity increment, we can derive the following relation
which is simplified as
We observe that the Cauchy stress of the elastic solid is nondimensionalized by \(\rho ^{\mathrm{F}} U^2\) whereas the velocity by U. Utilizing the dimensionless scales, the traction increment is expressed as
which amounts to the nondimensional version of
where \(\bar{\omega } = U \omega\) and all asterisks are dropped.
Equally, the velocity increment is rewritten as
which is nondimensionalized as
3.2.8 Assessment of the Coupling Parameter
In the CIBC method the coupling parameter plays an important part in the accuracy and stability of the coupled FSI system. It works as the Courant-Friedrichs-Lewy-like limit through the explicit combination of velocity and traction on \(\varSigma\). For the present, it is almost impossible to estimate the optimal value of the coupling parameter in theory, especially for the multi-dimensional case. Alternatively, one must have recourse to numerical experiments to determine it. Our previous experience [68] indicates that \(10 \leqslant \bar{\omega } < +\infty\) and it is advisable to adpot \(\bar{\omega } = 100\). This scenario is partially coincident with the one-dimensional conjugate heat-transfer process [115] where \(10 \leqslant \omega \leqslant 50\) is suggested by the Godunov-Ryabenkii stability analysis, but different from the one-dimensional elastic piston problem [76] where \(5.0 \times 10^{-4} \leqslant \omega \leqslant 3.0 \times 10^{-3}\) is attained via numerical experiments. The difference may be attributed to the conjugate heat-transfer model that is expected to be applicable to multi-dimensional Navier–Stokes equations [115].
4 Partitioned Solution Procedures
Based on previous sections, partitioned coupling strategies consist of the explicit, implicit and semi-implicit coupling schemes. A detailed description of each coupling algorithm is provided in succedent subsections, providing the flexible choices to solve FSI problems. As mentioned before, other techniques can be used in the partitioned solution procedures to further improve the numerical simulations.
4.1 Explicit Coupling Algorithm
The partitioned explicit scheme possesses the desirable conceptual clarity. The staggered solution of each physical field is advanced in time without the imperative satisfaction of the interfacial conservation. The overall procedure of this scheme is written by a sequence of operations below. The relevant flowchart is illustrated in Fig. 3.
- Step 1: :
-
Initialize all variables
- Step 2: :
-
Solve the structural equation
- Step 3: :
-
Rearrange the fluid mesh by the MSA
- Step 4: :
-
Calculate the mesh velocity and other geometric quantities
- Step 5: :
-
Computate the MST for the GCL
- Step 6: :
-
Settle the fluid problem via the CBS scheme
- Step 7: :
-
Obtain the fluid force
- Step 8: :
-
Proceed to the next time step
Flowchart of the partitioned explict coupling algorithm
4.2 Implicit Coupling Algorithm
When advancing the FSI solution in time, it is imperative to require that the equilibrium conditions should be exactly satisfied on the interface at every time step for the implicit coupling of the interacting fields. The present partitioned implicit coupling scheme employs the fixed-point algorithm with Aitken’s \(\varDelta ^2\) accelerator [85, 98]. This technique is of simple operability with good convergence. The steps of the implicit scheme are well described below. Also, the flowchart of the algorithm is displayed in Fig. 4.
- Step 1: :
-
Initialize all variables and set \(iter = 0\)
- Step 2: :
-
Extrapolate the position of the interface
$$\begin{aligned} \left( \widetilde{\mathbf {x}}_\varSigma \right) ^{n+1}_{iter} = \mathbf {x}^{n}_\varSigma + \varDelta t \left( \frac{3}{2} \dot{\mathbf {x}}^{n}_\varSigma - \frac{1}{2} \dot{\mathbf {x}}^{n-1}_\varSigma \right) \end{aligned}$$ - Step 3: :
-
Start fixed-point iterations and set \(iter \leftarrow iter + 1\)
- Step 4: :
-
Rearrange the fluid mesh by the MSA
- Step 5: :
-
Calculate the mesh velocity and other geometric quantities
$$\begin{aligned} \mathbf {w}^{n+1}_{iter-1} = \dfrac{\widetilde{\mathbf {x}}^{n+1}_{iter-1} - \mathbf {x}^n}{\varDelta t} \end{aligned}$$ - Step 6: :
-
Obtain the MST for satisfying the GCL
$$\begin{aligned} \left( S_{\mathrm{MST}} \right) ^{n+1}_{iter-1} = \left( \frac{1}{2 A_e} \left|\begin{array}{cc} w^2_1 - w^1_1&w^2_2 - w^1_2 \\ w^3_1 - w^1_1&w^3_2 - w^1_2 \end{array}\right| \right) ^{n+1}_{iter-1} \end{aligned}$$ - Step 7: :
-
Compute the intermediate velocity
$$\begin{aligned} \widetilde{\mathbf {u}} - \mathbf {u}^n = \varDelta t \left( -\mathbf {c}^n \cdot \nabla \mathbf {u}^n + \frac{1}{Re}\nabla ^2 \mathbf {u}^n + \frac{\varDelta t}{2} \mathbf {c}^n \cdot \nabla (\mathbf {c}^n \cdot \nabla \mathbf {u}^n) \right) \end{aligned}$$ - Step 8: :
-
Update the fluid pressure
$$\begin{aligned} \nabla ^2 p^{n+1}_{iter} = \frac{1}{\varDelta t} \nabla \cdot \widetilde{\mathbf {u}} + \left( S_{\mathrm{MST}} \right) ^{n+1}_{iter-1} \end{aligned}$$ - Step 9: :
-
Correct the fluid velocity
$$\begin{aligned} \mathbf {u}^{n+1}_{iter} - \widetilde{\mathbf {u}} = -\varDelta t \left( \nabla ^2 p^{n+1}_{iter} - \frac{\varDelta t}{2} \mathbf {c}^n \cdot \nabla ^2 p^n \right) \end{aligned}$$ - Step 10: :
-
Deduce the fluid load and pass it to the structure
- Step 11: :
-
Solve the structural equation
$$\begin{aligned} \begin{aligned} \left( \frac{1}{\beta \varDelta t^2} \mathbf {M} + \frac{\gamma }{\beta \varDelta t} \mathbf {C} + \mathbf {K} \right) \mathbf {d}^{n+1}_{iter}&= \mathbf {F}^{n+1}_{iter} + \mathbf {M} \left( \frac{1}{\beta \varDelta t^2} \mathbf {d}^n + \frac{1}{\beta \varDelta t} \dot{\mathbf {d}}^n + \frac{1-2\beta }{2\beta } \ddot{\mathbf {d}}^n \right) \\&\quad + \mathbf {C} \left( \frac{\gamma }{\beta \varDelta t} \mathbf {d}^n + \frac{\gamma -\beta }{\beta } \dot{\mathbf {d}}^n + \frac{\gamma -2\beta }{2\beta } \varDelta t \ddot{\mathbf {d}}^n \right) \end{aligned} \end{aligned}$$ - Step 12: :
-
Estimate the interfacial residuals
$$\begin{aligned} \mathbf {g}_{iter} = \big | \left( \mathbf {x}_\varSigma \right) ^{n+1}_{iter} - \left( \widetilde{\mathbf {x}}_\varSigma \right) ^{n+1}_{iter-1} \big | \end{aligned}$$ - Step 13: :
-
Check the convergence and the maximum number of subiterations:
if not convergent, then go ahead;
otherwise, proceed to the next time step
- Step 14: :
-
Determine Aitken factor \(\lambda ^{n+1}_{iter}\)
- Step 15: :
-
Relax the interface’s position
$$\begin{aligned} \left( \widetilde{\mathbf {x}}_\varSigma \right) ^{n+1}_{iter} = \lambda ^{n+1}_{iter} \left( \mathbf {x}_\varSigma \right) ^{n+1}_{iter} + (1 - \lambda ^{n+1}_{iter}) \left( \widetilde{\mathbf {x}}_\varSigma \right) ^{n+1}_{iter-1} \end{aligned}$$ - Step 16: :
-
Return
Instead, we can predict the external force for the structural equation [63]. The modifications of the implicit procedure are very trivial. As pointed out in [63], such an action refrains from the lagged field variables used for the CIBC formulae. This feature may be important to the acceleration of subiterations under some conditions. Moreover, the incremental form written in total or updated Lagrangian formulation should be applied to the temporal discretization of structural equation in the algorithm to take finite deformation into account.
Flowchart of the partitioned implict coupling algorithm
4.3 Semi-implicit Coupling Algorithm
The CBS-based partitioned semi-implicit coupling algorithm is suggested in the similar fashion of [65, 67]. Interestingly, the CBS scheme serves not only for the fluid component but also for the entire coupling algorithm. The fixed-point iteration with Aitken’s \(\varDelta ^2\) accelerator is carried out to partially couple the fluid projection step and the structural motion. The procedure of the proposed algorithm is particularized in the following.
- Step 1: :
-
Initialize all variables and set \(iter = 0\)
- Step 2: :
-
Perform the explicit coupling step
- 2.1::
-
Extrapolate the position of the interface
$$\begin{aligned} \left( \widetilde{\mathbf {x}}_\varSigma \right) ^{n+1}_{iter} = \mathbf {d}^{n}_\varSigma + \left( \frac{3}{2} \dot{\mathbf {d}}^{n}_\varSigma - \frac{1}{2} \dot{\mathbf {d}}^{n-1}_\varSigma \right) \varDelta t \end{aligned}$$ - 2.2::
-
Rearrange the fluid mesh by MSA
- 2.3::
-
Calculate the mesh velocity and
$$\begin{aligned} \mathbf {w}^{n+1}_{iter} = \dfrac{\widetilde{\mathbf {x}}^{n+1}_{iter} - \mathbf {x}^n}{\varDelta t} \end{aligned}$$ - 2.4::
-
Obtain the MST for satisfying the GCL
$$\begin{aligned} \left( S_{\mathrm{MST}} \right) ^{n+1}_{iter} = \left( \frac{1}{2 A_e} \left|\begin{array}{cc} w^2_1 - w^1_1&w^2_2 - w^1_2 \\ w^3_1 - w^1_1&w^3_2 - w^1_2 \end{array}\right| \right) ^{n+1}_{iter} \end{aligned}$$ - 2.5::
-
Compute the intermediate velocity
$$\begin{aligned} \widetilde{\mathbf {u}} - \mathbf {u}^n = \varDelta t \left( -\mathbf {c}^n \cdot \nabla \mathbf {u}^n + \frac{1}{Re}\nabla ^2 \mathbf {u}^n + \frac{\varDelta t}{2} \mathbf {c}^n \cdot \nabla (\mathbf {c}^n \cdot \nabla \mathbf {u}^n) \right) \end{aligned}$$ - 2.6::
-
Assess the force increment when computing the rigid body
- Step 3: :
-
Perform the implicit coupling step
- 3.1::
-
Set \(iter \leftarrow iter + 1\)
- 3.2::
-
Update the fluid pressure
$$\begin{aligned} \nabla ^2 p^{n+1}_{iter} = \frac{1}{\varDelta t} \nabla \cdot \widetilde{\mathbf {u}} + \left( S_{\mathrm{MST}} \right) ^{n+1}_{iter-1} \end{aligned}$$ - 3.3::
-
Correct the fluid velocity
$$\begin{aligned} \mathbf {u}^{n+1}_{iter} - \widetilde{\mathbf {u}} = -\varDelta t \left( \nabla ^2 p^{n+1}_{iter} - \frac{\varDelta t}{2} \mathbf {c}^n \cdot \nabla ^2 p^n \right) \end{aligned}$$ - 3.4::
-
Deduce the fluid load
- 3.5::
-
Correct the structural force
$$\begin{aligned} \left( \int _{\varSigma } \mathbf {t}^{\mathrm{S}} \mathrm {d}\varGamma \right) ^{n+1}_{iter}& = \left( \int _{\varSigma } \mathbf {t}^{\mathrm{F}} \mathrm {d}\varGamma \right) ^{n+1}_{iter} + \left( \int _{\varSigma } \mathrm {\delta } \mathbf {t} \mathrm {d}\varGamma \right) ^n \quad \text{ for } \text{ the } \text{ rigid } \text{ body; }\\ \overline{\mathbf {F}}^{n+1}_{iter} & = \widetilde{\mathbf {F}}^{n+1}_{iter} + \int _{\varSigma } \left( \left( \mathbf {N}^{\mathrm{T}} \mathbf {t}^{\mathrm {F}} \right) ^{n+1}_{iter} + \left( \mathbf {N}^{\mathrm{T}} \right) ^{n+1}_{iter} \mathrm {\delta } \mathbf {t}^n \right) \mathrm {d}\varGamma \quad \text{ for } \text{ the } \text{ flexible } \text{ body } \end{aligned}$$ - 3.6::
-
Solve equation of the structural motion
$$\begin{aligned} \begin{aligned} \left( \frac{1}{\beta \varDelta t^2} \mathbf {M} + \frac{\gamma }{\beta \varDelta t} \mathbf {C} + \mathbf {K} \right) \mathbf {d}^{n+1}_{iter}&= \mathbf {F}^{n+1}_{iter} + \mathbf {M} \left( \frac{1}{\beta \varDelta t^2} \mathbf {d}^n + \frac{1}{\beta \varDelta t} \dot{\mathbf {d}}^n + \frac{1-2\beta }{2\beta } \ddot{\mathbf {d}}^n \right) \\&\quad + \mathbf {C} \left( \frac{\gamma }{\beta \varDelta t} \mathbf {d}^n + \frac{\gamma -\beta }{\beta } \dot{\mathbf {d}}^n + \frac{\gamma -2\beta }{2\beta } \varDelta t \ddot{\mathbf {d}}^n \right) \end{aligned} \end{aligned}$$ - 3.7::
-
Evaluate the velocity increment
$$\begin{aligned} \mathrm {\delta } \mathbf {u}^{n+1}_{iter}&= \frac{\varDelta t}{S} \int _{\varSigma } \left( \left( \nabla \cdot \varvec{\sigma }^{\mathrm{F}} \right) ^{n+1}_{iter} - \bar{\omega } \dot{\mathrm {\delta } \mathbf {t}}^n \right) \mathrm {d}\varGamma \quad \text{ for } \text{ the } \text{ rigid } \text{ body; }\\ \mathrm {\delta } \mathbf {u}^{n+1}_{iter}&= \varDelta t \left( \nabla \cdot \varvec{\sigma }^{\mathrm{F}} \right) ^{n+1}_{iter} \quad \text{ for } \text{ the } \text{ flexible } \text{ body } \end{aligned}$$ - 3.8::
-
Maintain the interfacial displacement continuity
$$\begin{aligned} (\mathbf {x}_\varSigma )^{n+1}_{iter} = \mathbf {d}^{n+1}_\varSigma + \mathrm {\delta } \mathbf {u}^{n+1}_{iter} \varDelta t \end{aligned}$$ - 3.9::
-
Estimate the interfacial residuals
$$\begin{aligned} \mathbf {g}_{iter} = \big | \left( \mathbf {x}_\varSigma \right) ^{n+1}_{iter} - \left( \widetilde{\mathbf {x}}_\varSigma \right) ^{n+1}_{iter-1} \big | \end{aligned}$$ - 3.10::
-
Check the convergence and the number of iterations:
If not convergent, then go ahead;
Otherwise, proceed to the next time step
- 3.11::
-
Assess Aitken factor \(\lambda ^{n+1}_{iter}\)
- 3.12::
-
Relax the interface’s position
$$\begin{aligned} \left( \widetilde{\mathbf {x}}_\varSigma \right) ^{n+1}_{iter} = \lambda ^{n+1}_{iter} \left( \mathbf {x}_\varSigma \right) ^{n+1}_{iter} + (1 - \lambda ^{n+1}_{iter}) \left( \widetilde{\mathbf {x}}_\varSigma \right) ^{n+1}_{iter-1} \end{aligned}$$ - 3.13::
-
Calculate the new mesh velocity on \(\varSigma\) as the fluid boundary condition
$$\begin{aligned} \left( \mathbf {w}_\varSigma \right) ^{n+1}_{iter} = \dfrac{ \left( \widetilde{\mathbf {x}}_\varSigma \right) ^{n+1}_{iter} - \mathbf {x}^n_\varSigma }{\varDelta t} \end{aligned}$$ - 3.14::
-
Renew the MST for those elements adjacent to the interface
- 3.15::
-
Return
For the sake of better understanding, the flowchart of the semi-implicit algorithm is also displayed in Fig. 5. As mentioned before, the semi-implicit coupling scheme is more economical than its implicit peer. This virtue can be aware in the next section.
Flowchart of the partitioned semi-implict coupling algorithm
4.4 Aitken Relaxation
The Aitken’s \(\varDelta ^2\) method [74] enjoys immense popularity in accelerating FSI subiterations which are employed to deal with the instability caused by the coupling of fluid and structural domains. The vector extrapolation of the Aitken method is described in [86]. At each subiteration per time step, the dynamic Aitken factor is estimated by the following recursion formula
where \(\lambda _{\mathrm{MAX}} = 0.1\) and \(\lambda ^0_1 = 0.5\). The limit of the Aitken factor may be outlined into the range \((0, \ 1)\) [8].
5 Numerical Examples
5.1 Transverse Oscillations of a Circular Cylinder
This example numerically replicates the physical experiment conducted by Anagnostopoulos and Bearman [4], where an elastically mounted circular cylinder is allowed to transversely oscillate in the laminar flow region. The problem settings are schematically demonstrated in Fig. 6 where D is the diameter of the circular cylinder. The system properties are consistent with [4]: the fluid density \(\rho ^{\mathrm{F}} = 0.01\) g/(cm s), the fluid viscosity \(\mu ^{\mathrm{F}} = 1.0\) g/cm\(^3\), the mass \(m_2 = 2.979\) g, the diameter \(D = 0.16\) cm, the spring stiffness \(k_2 = 5790.9\) g/s\(^2\) and the damping factor \(c = 0.325\) g/s. Correspondingly, the mass ratio \(m^*_2 = 116.37\), the damping ratio \(\xi _2 = 1.237 \times 10^{-3}\), the natural frequency \(f_{\mathrm{N2}} = 7.016\) Hz, the reduced natural frequency \(f_{\mathrm{R2}} = 17.961 / Re\) and \(90 \leqslant Re \leqslant 140\) due to various inflow velocities.
Sketch of geometry and boundary conditions for the transversely oscillating circular cylinder
For the sake of computational efficiency, the entire computational domain is divided into three parts: the Eulerian subdomain A1, the ALE subdomain A2 and the Lagrangian subdomain A3. The size of A2 is \(6D \times 6D\) while that of A3 is \(1.2D \times 1.2D\). The points in A1 keep fixed at all time while those in A3 move along with the circular cylinder. In A2 the points are instantaneously updated by MSA. To further lower the numerical cost, some time-invariant matrices in A1 are calculated only once at the beginning of the simulation. In Fig. 7a the finite element mesh constitutes 8092 T3 elements and 4141 points, and the corresponding submesh is plotted in Fig. 7b. Three tpyes of submeshes are discussed in [69], deferring to two criteria: (1) the fewer zones and (2) the (biaxial) symmetry. The time step is \(\varDelta t = 1.0 \times 10^{-2}\) and the convergence tolerance is \(tol = 1.0 \times 10^{-6}\). Since all coupling methods engender almost equal results, the implicit coupling algorithm is adopted here.
Mesh and submesh for the transversely oscillating circular cylinder. a Finite element mesh for the fluid field. b MSA submesh for the ALE domain
Dual time steps are referred back to the pioneering work of Zienkiewicz et al. [143] for seeking the optimal steady-state solution of the compressible fluid flows. Dual time steps were attempted for two Stokes problems in order to enhance the pressure stabilization [102, 104]. The second-order terms multiplied by \((\varDelta t)^2\) are responsible for stabilizing the pressure solution in Step 2 of the artificial compressibility(AC)-based CBS scheme. \((\varDelta t)^2\) is rewritten as \(\varDelta t_{\mathrm{EXT}} \varDelta t_{\mathrm{INT}}\) to maintain the numerical stability. The external time step \(\varDelta t_{\mathrm{EXT}}\) provides the temporal stability, while the internal time step \(\varDelta t_{\mathrm{INT}}\) takes charge of the spatial stability. The ratio is defined by \(\alpha = \varDelta t_{\mathrm{INT}} / \varDelta t_{\mathrm{EXT}}\) to quantify the effect of dual time steps. The stabilization technique hardly works in the elastic solid problem [102], but takes effect on the Stokes flow in a lid-driven cavity [104]. As \(\alpha > 1.0\) may be profitable for the deformable mesh problems (Nithiarasu and Zienkiewicz 2000), the present study adopts dual time steps as follows: \(\alpha = 1.0\) is employed for the elements in A1 and A3 while variable values of \(\alpha\) are applied for the elements in A2. The flows past the vertically oscillating circular cylinder at \(Re = 100\) is attempted for the influence of dual time steps. The obtained results are listed in Table 1 including the maximum value of vertical amplitude \(d_{\mathrm{MAX2}}\), the mean value of drag coefficient \(C_{\mathrm{D,MEAN}}\) and its root mean square (RMS) value \(C_{\mathrm{D,RMS}}\), the amplitude of lift coefficient \(C_{\mathrm{L,MAX}}\) and its RMS value \(C_{\mathrm{L,RMS}}\), the Strouhal number \(St (= f_{\mathrm{V}} D/U)\) and the ratio of the vortex-shedding frequency to the natural frequency \(f_{\mathrm{V}}/f_{\mathrm{N2}}\).
Seen from Table 1, the tiny difference of the calculated results are appreciated for various \(\alpha\). Overall, a larger \(\alpha\) causes a steady increase the computed parameters but it seldom infects St. Unfortunately, a large \(\alpha\), such as \(\alpha = 3.0\), leads to the oscillatory graphs of the aerodynamic parameters and delays lock-in. The interpretation is given as follow: (1) the Stokes equation without nonlinear convective term is a simplified case of the Navier–Stokes equations; (2) unlike the AC-based CBS scheme [102, 104], \(\varDelta t_{\mathrm{EXT}} \varDelta t_{\mathrm{INT}}\) does not appear in the second step of the present fully incompressible CBS scheme, failing to stabilize the latest pressure (see Eq. (31)); (3) in the incompressible CBS scheme enlarging \(\alpha\) is equivalent to using a stabilization parameter that improperly stabilizes the numerical solution of the Navier–Stokes equations. Based on the above analysis, \(\alpha = 1.0\) is employed for the current calculations.
The critical aerodynamic parameters of the \(Re = 100\) flow are compared among different articles [1, 38, 90, 121, 132, 136, 137] in Table 2. A good agreement between the present and previous data is fairly realized from the table. However, at this Re the lock-in phenomenon is not aroused in a few papers. Table 3 summarizes the cylinder amplitude and the corresponding Re from other investigations [1, 3, 4, 34, 38, 90, 105, 118, 121, 132, 137]. \(d_{\mathrm{MAX2}}\) bounds from 0.29 to 0.54, while the relevant Re varies from 95 to 115. It is clearly seen that our approach produce the rational \(d_{\mathrm{MAX2}}\) and Re at resonance.
In Fig. 8 \(d_{\mathrm{MAX2}}\) and \(f_{\mathrm{V}}/f_{\mathrm{N2}}\) of the transversely oscillating circular cylinder are further examined at various Re. Owing to the complexity of vortex-induced vibrations (VIV) and various approaches people used, there exists some scatter between the present results and previously published data [4, 34, 38, 118]. For the sake of comparison, Fig. 8 is also overlaid with the \(Re-St\) function [116]
for a rigid circular cylinder, where St is the Strouhal number. It is noticed that, a narrow lock-in range computed by the author and his colleagues covers \(97 \leqslant Re \leqslant 108\) which is nearly coincident with those of [34, 38, 118, 138]. Despite the narrow lock-in range, the trend of the cylinder amplitude is identical to the others. The cylinder oscillation is very faint when Re lies outside the lower end of the lock-in region. On this occasion, the vortices are shedding at the Strouhal frequency lower than its natural frequency. Since the cylinder amplitude is modulated, the phenomenon is called beating, as plotted in Fig. 9a for \(Re = 92\). The oscillation amplitude suddenly jumps to a high value once Re reaches the lower end. In general, the maximum amplitude is observed around the lower end. Within the lock-in region, the circular cylinder undergoes the large-scale and strong motion, and its amplitude declines smoothly as Re rises. At the same time, the frequency ratio \(f_{\mathrm{V}}/f_{\mathrm{N2}}\) roams around unity, implying the synchronization of the oscillation frequency and the vortex-shedding frequency. The synchronization is responsible for large-scale and strong motions of the cylinder. Figure 9b depicts the time history of the cylinder displacement at \(Re = 100\) where lock-in clearly takes place. The amplitude abruptly descends once Re migrates the outside of the upper end of the lock-in region. The cylinder keeps on imperceptibly oscillating with the growth of Re. \(f_{\mathrm{V}}\) reaches a high level as Re increases further. We see that \(f_{\mathrm{V}}\) becomes unlocked again during the period. As displayed in Fig. 9c, the beating phenomenon at \(Re = 120\) is more modulated than that at those Reynolds numbers outside the lower end. This behavior is opposite to the study of Anagnostopoulos and Bearman [4].
Amplitude and frequency ration of the transversely oscillating circular cylinder
Time histories of the transversely oscillating circular cylinder at three selected Re. a \(Re = 92\). b \(Re = 100\). c \(Re = 120\)
The corresponding vorticity fields for these Reynolds numbers are illustrated in Fig. 10. The cylinder undergoes low-amplitude oscillation at \(Re = 92 \ \text {and} \ 120\), whereas high-amplitude oscillation is perceived at \(Re = 100\). Unlike [9], the three vortex-shedding modes behind the cylinder wake are of the 2S type and the C(2S) vortex-shedding mode [133] is not detected here. In addition, the vortex spacing is somehow reduced at \(Re = 100\). The associated mode therefore seems closer to the standard 2S mode for a rigid circular cylinder. This reality is justified by Fig. 8 where the frequency ratio almost tallies with the Roshko curve if Re is absent within the lock-in region.
Vorticity fields of the transversely oscillating circular cylinder at three selected Re. a \(Re = 92\). b \(Re = 100\). c \(Re = 120\)
5.2 Free Oscillations of a Circular Cylinder
We consider here a freely vibrating circular cylinder under fully laminar flow conditions. The system parameters are set as follows [112]: the mass ratio \(m^*= 2.5\pi\), the damping ratio \(\xi = 0\), the reduced natural frequency \(f_{\mathrm{R}} = 16.6/ Re\) and \(60 \leqslant Re \leqslant 200\). The direction subscripts are ignored in these variables to account for the isotropic assumption. The problem statement and meshing are demonstrated by Figs. 6 and 7. The time step is \(\varDelta t = 1.0 \times 10^{-2}\) and Newmark parameters are \(\beta = 0.25\) and \(\gamma = 0.5\).
The preliminary study is conducted by means of the flow past the circular cylinder at \(Re = 100\). The computed results are listed in Table 4, including the mean value of horizontal amplitude \(d_{\mathrm{MEAN1}}\) and its RMS \(d_{\mathrm{RMS1}}\), the amplitude of vertical amplitude \(d_{\mathrm{MAX2}}\), the mean value of drag coefficient \(C_{\mathrm{D,MEAN}}\) and its RMS \(C_{\mathrm{D,RMS}}\), the amplitude of lift coefficient \(C_{\mathrm{L,MAX}}\) and the Strouhal number St. In Table 4 an excellent agreement is observed among the available data [65, 68, 69, 112], establishing the validation for further calculations. As to the efficiency issue, the \(Re = 100\) flow is chosen to be the model. We can quantify the time consumption of the semi-implicit and fully implicit coupling techniques with reference to Fig. 11. The figure fairly reports that the semi-implicit technique offers roughly 20% savings in run time. In connection with Table 4 and Fig. 11, the semi-implicit method is as accurate as the widely used implicit coupling method but achieves higher efficiency. This trait is valuable for large-scale computations.
Time cost of the implicit and semi-implicit methods for the freely oscillating circular cylinder
Figure 12 displays the variation of \(d_{\mathrm{RMS1}}\) and \(d_{\mathrm{MAX2}}\) of the cylinder with Re. We see from the two pictures that the lock-in region covers \(80 \leqslant Re \leqslant 130\) while that of [112] ranges from \(Re = 81\) to \(Re = 137\). In Fig. 12a, the horizontal oscillation of the cylinder is extraordinarily weak, compared with its vertical counterpart. The portrait of the \(d_{\mathrm{RMS1}}\) curve looks like that of [112] very much. Nevertheless, two peaks of the \(d_{\mathrm{RMS1}}\) curve are not observed near the two ends of the lock-in region. Possible causes are drawn as: (1) the hysteretic effect is not studied by increasing and decreasing Re herein; and (2) the Re resolution may be insufficient. In Fig. 12b the vertical amplitude is up to 0.566D, a little larger than that of [36]. At the lower end the graphs accord with those by increasing and decreasing Re [112], while they are coincident with that by decreasing Re at the upper end. A small rebound however arises at the upper end in advance, according to the trend in Fig. 12a.
Variation of statistical values of the cylinder response with Re. a RMS value of the horizontal amplitude. b Peak of the vertical amplitude
The computed force coefficients of the cylinder are plotted in Fig. 13. The freely oscillating circular cylinder undergoes significantly large drag and lift forces around the lower end of the lock-in region. Both peaks of \(C_{\mathrm{D,RMS}}\) and \(C_{\mathrm{L,RMS}}\) take place at \(Re = 83\), complying with those of \(d_{\mathrm{RMS1}}\) and \(d_{\mathrm{MAX2}}\) in Fig. 12. The associated Re is around 88 in [112], posterior to ours. Especially, the maximum value of \(C_{\mathrm{D,RMS}}\) is about 0.4, tallying very well with the value provided by Prasanth and Mittal [112]. At the upper end, the rebound of \(C_{\mathrm{D,RMS}}\) is faint whereas \(C_{\mathrm{L,RMS}}\) climbs on a large-scale, showing a trend similar to [112]. Stepping out of the upper end, both \(C_{\mathrm{D,RMS}}\) and \(C_{\mathrm{L,RMS}}\) experience a smooth and slow growth.
Variation of RMS values of fluid force coefficients with Re. a Drag coefficient. b Lift coefficient
Figure 14 illustrates the variation of St and \(f_{\mathrm{V}}/f_{\mathrm{N}}\) with Re. The Roshko function [116], the reduced natural frequency \(f_{\mathrm{R}} = 16.6/Re\) and the vortex shedding frequency for a rigid circular cylinder calculated by He et al. [68] are also revealed in Fig. 14a. As mentioned in [112], St of the oscillating circular cylinder is dramatically affected by both the Reynolds number effect and the cylinder oscillation. We see that, St evidently departs from that of a rigid cylinder within the lock-in region, whereas such departure remarkably reduces once Re locates outside the lock-in region. In addition, a very small offset between St and \(f_{\mathrm{R}}\) is perceived during lock-in. The main reason for the above behaviors has been given by Prasanth and Mittal [112]. Two jumps of \(f_{\mathrm{V}}/f_{\mathrm{N}}\) are obviously seen in Fig. 14b. The first jump occurs at \(Re = 81\), as the same as [112]. As mentioned before, the second jump emerges at \(Re = 83\), predating Prasanth and Mittal’s [112]. Similarly, \(Re = 81 \ \text {and} \ 83\) indicate the initial and lower branches, according to Govardhan and Williamson [56]. Based on Figs. 12 and 14, the whole lock-in region spans \(81 \leqslant Re \leqslant 130\).
Variation of Strouhal number and frequency ratio with Re. a Strouhal number. b Frequency ratio
In Fig. 15 vorticity fields are illustrated at two selected Reynolds numbers. The 2S vortex-shedding mode is seen in Fig. 15a since the cylinder goes through low-amplitude oscillations at \(Re = 75\). Although the cylinder experiences high-amplitude oscillations at \(Re = 90\), the C(2S) vortex-shedding mode [133] is not explicitly observed in Fig. 15b.
Vorticity fields of the freely oscillating circular cylinder at two selected Re. a \(Re = 75\). b \(Re = 90\)
A more challenging case is numerically simulated by the newly-proposed CBS-based partitioned semi-implicit coupling method. The considered problem is a light circular cylinder oscillating in uniform flows [141]. The physical properties are taken from [141]: the mass ratio \(m^*= 1\), the damping ratio \(\xi = 3.42849 \times 10^{-3}\), the reduced natural frequency \(f_{\mathrm{R}} = 0.24986\) and the Reynolds number \(Re = 200\). The finite element mesh consists of 13,870 T3 elements and 7040 points. The time step is chosen as \(\varDelta t = 5.0 \times 10^{-3}\). The very low mass ratio largely accounts for the strong added-mass effect in VIV of an oscillating bluff body. The influence of mass ratio is investigated in [68] on the coupled fluid-cylinder system.
Figure 16 displays the X-Y trajectory of the oscillating circular cylinder, illustrating the self-limiting VIV [141]. As subjected to the uniform flow at low Re, the cylinder trajectory remains nearly symmetrical and the classical Lissajous figure of 8 is clearly observed in this figure. According to Sarpkaya [119], when the cylinder vibrates in the horizontal and vertical directions, the common frequencies of the cylinder and driving forces in their respective directions may result in lock-in and the cylinder’s axis traces the path of the Lissajous figure. The eight-type loop is due to the significant variation of drag force within large amplitude oscillations. Thanks to the mean drag force imposed on the circular cylinder from the fluid, the equilibrium position of the cylinder’s oscillations is not situated at the origin in the in-line direction. In the present paper, the equilibrium position seems slightly far away from the origin. Seen from [141], the equilibrium position shifts to the point \((0.4, \ -0.2)\) from the current coordinates during different cycles. We can also see from Fig. 16 that the vertical amplitude is larger than its horizontal counterpart. Time histories of the force coefficients and vertical displacement are shown in Fig. 17. The basic characteristics of the present curves are similar to those in [141].
The trajectory of the freely oscillating light circular cylinder
Time histories of the force coefficients and vertical displacement
The vorticity field is illustrated in Fig. 18. As the circular cylinder experiences high-amplitude oscillations, the lateral spacing between two parallel rows of shedding vortices is much wider than the limit for the stable Karman vortex street of the fixed circular cylinder. Therefore, the von Karman vortex street is not obvious in Fig. 18. As interpreted by Zhou et al. [141], the two vortex rows will not persist for a long distance and a von-Karman-type vortex street occurs at a distance of approximately 20L far from the cylinder wake.
Vorticity contour of the freely oscillating light circular cylinder
5.3 Transverse Oscillations of a Square Cylinder
The transverse flow-induced oscillations of a square cylinder is analyzed at various Re in this subsection. The representation of this problem is schematically illustrated in Fig. 19. The square cylinder is laid at zero angle of attack and D is the edge length. The parameter conditions are as follows [38, 114]: the mass ratio \(m^*_2 = 20\), the damping ratio \(\xi _2 = 3.7 \times 10^{-3}\), the reduced natural frequency \(f_{\mathrm{R2}} = 6.25 / Re\) and \(40 \leqslant Re \leqslant 250\). The Re range allows us to explore both lock-in and galloping phenomena. According to Blevins [19], galloping will be triggered when a bluff body has the non-circular cross section and the velocity of the incident flow exceeds a certain critical value. Unlike lock-in, galloping drives the vortex-shedding frequency and the oscillation amplitude of the bluff body to be several times larger than the natural frequency and the characteristic dimension, respectively.
Sketch of geometry and boundary conditions for the transversely oscillating square cylinder
The entire computational domain is split into the Eulerian subdomain A1 and the ALE subdomain A2. The size of A2 is \(6D \times 6D\). The finite element mesh encompasses 7932 T3 elements and 4061 points. Figure 20 displays the corresponding finite mesh and MSA submesh. The time step is \(\varDelta t = 2.0 \times 10^{-2}\) and the trapezoidal rule is adopted.
Mesh and submesh for the transversely oscillating square cylinder. a Finite element mesh for the fluid field. b MSA submesh for the ALE domain
As the validation case, the flow past the square cylinder at \(Re = 250\) is analyzed first. The obtained results alongside with the existing data are summarized in Table 5. It is noticed that the partitioned explicit coupling method in [68] generates the slightly larger transverse amplitude but the same oscillation frequency. In view of the listed data, the transverse galloping phenomenon is activated at the selected Re by all methods. In sum, the good agreement among different partitioned approaches is observed from Table 5.
The Re effect is taken into account via analyzing the amplitude and two frequency ratios of the suqare cylinder against various Re, as plotted in Fig. 21. Generally speaking, the good agreement is uncovered among [38, 63, 69]. Both lock-in and galloping are clearly perceived in Fig. 21a. The present lock-in region covers \(48 \leqslant Re \leqslant 55\) but it is slightly larger than that of [38]. The peak of the transverse amplitude is around 0.23 at \(Re = 48\), while in [38] the peak is 0.186 at \(Re = 50\). Galloping is awakened at \(Re = 155\) here but at \(Re = 150\) in [38]. According to Barrero-Gil et al. [11], the lower limit of Re for the onset of transverse galloping depends on the expression of the polynomial coefficients employed in the quasisteady theory, and thus multiple values are possible. For example, the quantity is predicted to be 158.8 in [11] or 140.3 in [84] for a square cylinder with extremely low values of elastic properties. Similarly, the critical Re of the present case, if we consider the elastic properties, is approximate to 159.5 or 140.9 based on [11, 84]. This is very close to the afore-mentioned observation. As expected in Fig. 21b, \(f_{\mathrm{V}}/f_{\mathrm{N2}}\) approaches to unity within the lock-in region and it goes on ascending with the increase of Re. However, \(f_{\mathrm{O}}/f_{\mathrm{N2}}\) gets close to unity once galloping is observed. On this occasion, \(f_{\mathrm{V}}/f_{\mathrm{N2}}\) and the cylinder displacement become much larger. That is to say, galloping is a flow-induced motion along with both low frequency and high amplitude.
Time histories of the cylinder displacement at \(Re = 48, \ 100, \ \text {and} \ 250\) are shown in Fig. 22. The relevant flow patterns at the same Reynolds numbers are exhibited in Fig. 23. The vortex-shedding modes at \(Re = 48 \ \text {and} \ 100\) are of 2S types in the first two panels. The flow pattern at \(Re = 250\) which stimulates the transverse galloping is still 2S mode but shows a bit chaotic. Although the longitudinal spacing between vortices apparently decreases near the cylinder wake, it trends to increase far from the cylinder wake in the third panel. Neither lock-in nor galloping takes place at \(Re = 100\) where the vortex sheds in the manner a rigid square cylinder does alike. Robertson et al. [114] reported the similar results of a vibrating rectangular cylinder of aspect ratio \(\varLambda = 1.5\) under different flow conditions.
5.4 Free Oscillations of a Square Cylinder
This subsection is concerned with free oscillations of a flexible square cylinder under consideration of various Re. The problem definition and the associated MSA submesh are in accordance with those of last subsection. According to Sen and Mittal [122], the system parameters are defined as follows: the mass ratio \(m^*= 10\), the damping ratio \(\xi = 0\), the reduced natural frequency \(f_{\mathrm{R}} = 14.39 / Re\) and \(60 \leqslant Re \leqslant 250\). The fluid mesh of 16254 T3 elements and 8232 points and \(\varDelta t = 2.0 \times 10^{-2}\) are chosen in this example.
The flow past the cylinder at \(Re = 90\) is computed for validation. A detailed comparison among different studies are found in Table 6. Although the developed methods create the larger \(C_{\mathrm{D,MEAN}}\) but smaller \(C_{\mathrm{L,RMS}}\) than those of Sen and Mittal [122], an excellent agreement is observed in Table 6.
Variation of the cylinder amplitude and two frequency ratios with Re. a Transverse amplitude. b Frequency ratios
Time histories of the transversely oscillating square cylinder at three selected Re. a \(Re = 48\). b \(Re = 100\). c \(Re = 250\)
Vorticity fields of the transversely oscillating square cylinder at three selected Re. a \(Re = 48\). b \(Re = 100\). c \(Re = 250\)
The lock-in and galloping phenomena are distinctly perceived within the considered Re scope. The variation of the response, aerodynamic coefficients and oscillation frequency of the freely oscillating square cylinder with Re is plotted in Figs. 24, 25, 26, respectively.
Variation of the statistical values of the cylinder response with Re. a RMS value of the horizontal amplitude. b Peak of the vertical amplitude
Variation of the statistical values of fluid force coefficients with Re. a Drag coefficient. b Lift coefficient
Variation of the oscillation frequency and frequency ratio with Re. a Oscillation frequency. b Frequency ratio
The displacement response of the square cylinder is plotted in Fig. 24. As a whole, the deviation is tiny among all data. The two panels of the figure follow the similar variation trend, the behavior of which is mainly characterized by lock-in and galloping. Galloping is also referred to as secondary lock-in [122]. In Fig. 24a \(d_{\mathrm{RMS1}}\) is hardly visible prior to the onset of galloping, and \(d_{\mathrm{MAX2}}\) evidently forecasts lock-in in Fig. 24b. The peaks of transverse amplitude and their associated Re within the lock-in and galloping regions are reported in Table 7, where a good agreement is observed between the computed and published results. Within the lock-in region, \(d_{\mathrm{MAX2}}\) is closer to that of [122] by increasing Re. At the same time, \(d_{\mathrm{MAX2}}\) in [122] is about half the one for a freely vibrating circular cylinder [112], but the percentage becomes 41.6 %s here. The maximum transverse amplitude is plotted in Fig. 24b. The explicit method estimates a slightly larger peak of transverse amplitude when \(100 \leqslant Re \leqslant 200\) [68]. The second jump of displacement response takes place at \(Re = 220\) in all studies. That is to say, galloping will be waken if \(Re \geqslant 220\) for the given properties. The cylinder displacement rapidly ascends during galloping as Re continues to increase. This is explained by the widely known fact that the galloping instability results from the appearance of the negative aerodynamic damping [109].
The fluid force coefficients \(C_{\mathrm{D,MEAN}}\) and \(C_{\mathrm{L,RMS}}\) are illustrated in Fig. 25. In accordance with [122], an oscillating cylinder always yields more drag than the rigid one. Such a comparison is not yet made here. In Fig. 25a, the obtained \(C_{\mathrm{D,MEAN}}\) is larger than Sen and Mittal’s when Re lies outside of the galloping regions. Seen from Fig. 25b, the afore-mentioned situation happens to \(C_{\mathrm{L,RMS}}\) when \(105 \leqslant Re \leqslant 180\). The first jumps of these two parameters emerge at \(Re = 87\), coinciding with those of the cylinder responses. Sen and Mittal [122] reported the first jump of \(C_{\mathrm{D,MEAN}}\) at the same Re. Before galloping comes out, the \(C_{\mathrm{D,MEAN}}\) graph evenly mounts up after a steep fall in Fig. 25a. From Fig. 25b, \(C_{\mathrm{L,RMS}}\) bottoms out at \(Re = 96\) and then begins to rise. The significant rises of \(C_{\mathrm{D,MEAN}}\) and \(C_{\mathrm{L,RMS}}\) are realized when galloping occurs. As Re increases further, the growth of \(C_{\mathrm{D,MEAN}}\) is slowing but \(C_{\mathrm{L,RMS}}\) undergoes a slight fall.
\(f_{\mathrm{O}}\) versus Re is displayed in Fig. 26a. St for a rigid square cylinder [68, 123] and \(f_{\mathrm{R}}\) are also elaborated in this figure. The lock-in region initiates at \(Re = 87\) and terminates at \(Re = 100\), forming the first jump of the curve. When \(100 < Re \leqslant 130\), \(f_{\mathrm{O}}\) keeps close to St of a stationary square cylinder. Our galloping starts from \(Re = 179\) whereas the outset of galloping stands at \(Re = 175\) in [122]. After a second abrupt decline, the \(f_{\mathrm{O}}\) curve exhibits a flat fall and gets close to \(f_{\mathrm{R}}\), following the same trend as Sen and Mittal’s [122]. The width of the lock-in area for a freely oscillating square cylinder reported in [122] is roughly a third of the one gained for a freely oscillating circular cylinder [112]. This fact is also confirmed by [63, 69]. The frequency ratio \(f_{\mathrm{O}} / f_{\mathrm{N}}\) versus Re is plotted in Fig. 26b. The frequency ratio remains a rising tendency until Re reaches 178, and then undergoes a sudden fall. If Re varies from 179 to 250, the \(f_{\mathrm{O}} / f_{\mathrm{N}}\) curve maintains a smooth relation, suggesting the galloping phenomena.
In Fig. 27 the vortex-shedding modes of the cylinder are shown at \(Re = 87, \ 150, \ 230 \ \text {and} \ 250\), respectively. In Fig. 27a, the square cylinder experiences the high-amplitude oscillation at \(Re = 87\). At this Re, the 2S mode is seen whereas Sen and Mittal [122] reported the C(2S) vortex-shedding mode [133]. The longitudinal spacing between vortices is somewhat reduced at \(Re = 150\) in Fig. 27b. The flow pattern is therefore much like the classical 2S mode for a rigid square cylinder. Sen and Mittal [122] suggested that the 2P mode [133] would appear for \(Re \geqslant 215\). This fact is confirmed by the vortex-shedding mode shown in Fig. 27c. However, our previous work [68] shows a distinct mode that is similar to the Y-only motion reported in [122]. As indicated in Fig. 27d, the vortex sheds at \(Re = 250\) in the manner similar to \(Re = 230\).
Vorticity fields of the freely oscillating square cylinder at four selected Re. a \(Re = 87\). b \(Re = 150\). c \(Re = 230\).d \(Re = 250\)
5.5 Free Torsions of a Rectangular Cylinder
The numerical evaluation for flow past a freely rotating rectangular cylinder at \(Re = 250\) is accomplished in this subsection. The set-up and meshing of this problem are plotted in Figs. 28 and 29, respectively. The height and depth of the rectangular cylinder are \(D = 1\) and \(B = 4\). Physical properties of the cylinder-spring system are defined as follows [38, 114]: the mass ratio \(m^*_\theta = 400\), the damping ratio \(\xi _\theta = 0.25\) and the reduced natural frequency \(f_{\mathrm {R} \theta } = 6.25 / Re\). The mesh resolution contains 7988 T3 elements and 4089 points, and the time step \(\varDelta t = 4.0 \times 10^{-2}\) is used here.
Sketch of geometry and boundary conditions for the freely rotating rectangular cylinder
Mesh and submesh for the freely rotating rectangular cylinder. a Finite element mesh for the fluid field. b MSA submesh for the ALE domain
Several computed parameters are compared with the existing ones [38, 63, 69, 114] in Table 8 where a reasonable agreement is observed. Time history of torsional displacement is illustrated in Fig. 30. A typical vorticity contour is plotted in Fig. 31. Based on these obtained results, the torsional galloping is aroused successfully by using the developed coupling algorithms.
Time history of the freely rotating rectangular cylinder at \(Re = 250\)
Vorticity field of the freely rotating rectangular cylinder at \(Re = 250\)
5.6 Flutter of a Bridge Deck with H Profile
Due to the uniform flows, an H-shaped bridge deck supported with a vertical spring and a rotational spring experices the coupled motion of the vertical translation and rotation. This problem was proposed by Hübner et al. [73] to illustrate the flutter instability of the old Tacoma Narrows Bridge in the 1940s. Although the considered Reynolds number is unrealistic for natural wind, the vortex shedding phenomena that are essential for the system behavior are almost independent of Re [73].
The problem definition is graphically demonstrated in Fig. 32. The system properties are specified below [53]: the fluid density \(\rho ^{\mathrm{F}} = 1.25\), the fluid viscosity \(\mu = 0.1\), the structural mass \(m_2 = 3000\), the mass moment of inertia \(m_\theta\) = 25,300, the translational damping factor \(c_2 = 100\), the rotational damping factor \(c_\theta = 2200\), the translational spring stiffness \(k_2 = 2000\) and the rotational spring stiffness \(k_\theta\) = 40,000. The characteristic scales are the inflow velocity \(U = 10\) and the deck’s width \(D = 12\). The natural frequencies of the deck are \(f_{\mathrm{N2}} = 0.1299\) and \(f_{\mathrm {N} \theta } = 0.2001\), respectively. The other parameters are computed as: the reduced natural frequencies \(f_{\mathrm{R2}} = 0.1559\) and \(f_{\mathrm {R} \theta } = 0.2401\), the damping ratios \(\xi _2 = 2.041 \times 10^{-2}\) and \(\xi _\theta = 3.458 \times 10^{-2}\), the mass ratios \(m^*_2 = 16.667\) and \(m^*_\theta = 0.976\), and the Reynolds number \(Re = 1500\).
Sketch of geometry and boundary conditions for the oscillating bridge deck
The domain decomposition is plotted in Fig. 32. The size of A2 is \(4D \times 4D\), while that of A3 is \(2 \times 0.95D \times 0.0875D\) comprising two rectangular parts. In the first panel of Fig. 33 the finite element mesh consists of 6486 T3 elements and 3329 points, whereas the corresponding submesh is demonstrated in the second panel. The time step is \(\varDelta t = 2.0 \times 10^{-2}\).
Mesh and submesh for the oscillating bridge deck. a Finite element mesh for the fluid field. b MSA submesh for the ALE domain
The computed results are listed in Table 9, including the amplitude of vertical displacement \(d_{\mathrm{MAX2}}\), the vertical oscillation frequency \(f_{\mathrm{O2}}\), the amplitude of rotational displacement \(\theta _{\mathrm{MAX}}\) and the rotational oscillation frequency \(f_{\mathrm {O} \theta }\). From Table 9, \(d_{\mathrm{MAX2}}\) and \(\theta _{\mathrm{MAX}}\) based on our partitioned coupling methods are nearly identical, but they are larger than those of [53]. The simple geometry of this problem does not mean that the comparable data can be acquired by researchers. In the case of zero damping, the data from [25, 38, 55, 62, 73] vary significantly. For example, Cebral and Löhner [25] gave a rather small rotation whereas a large amplitude is seen in [38]. The simulation is even terminated at \(t=55s\) in [73]. Due to the demonstrated complexity of deck flutter, the difference in Table 9 between the vertical amplitudes is acceptable. We notice that the vertical oscillation frequency coincides with its rotational counterpart in [61, 67] when the flutter occurs. The relevant power spectra is shown in Fig. 34 by using a fast Fourier transform on the time history of rotation from [67]. The time histories of two displacement components of the bridge deck are shown in Fig. 35. Combined Table 2 with Fig. 35, it is noticed that the rotational oscillation frequency of the deck is quite close to its natural rotational frequency, and the vertical oscillation is feeble. As a consequence, the rotation is the dominant motion and the flutter phenomenon is obviously seen in this case. The force coefficients are illustrated in Fig. 36 as a function of nondimensional time. Three typical vorticity contours during one vibration period are displayed in Fig. 37.
Power spectra of the rotational time history
Time history of the deck displacement. a Vertical component. b Rotational component
Time histories of the force coefficients of the oscillating bridge deck. a Drag coefficient. b Lift coefficient. c Moment coefficient
Vorticity contours of the oscillating bridge deck during one cycle. a Time slice 1. b Time slice 2. c Time slice 3
5.7 Vortex-Induced Vibrations of a Cantilever Attached to a Square Obstacle
This model problem has been originally presented by Wall and Ramm [131] and now becomes the numerical benchmarking to test the capability of FSI solution strategy. The problem settings are schematically demonstrated in Fig. 38. A geometrically nonlinear cantilever is attached to a fixed square cylinder in the center of the downstream face. Due to the unsteady separation of the incompressible viscous flows past the square cylinder, the swirling vortices shed from the cylinder’s salient edges with a certain frequency. The vortex formation in the wake of the obstacle generates the time-dependent drag and lift which excite the flexible cantilever to vibrate in the fluid field. The no-slip boundary condition is applied on the surfaces of the cantilever and obstacle. The measuring point is placed in the middle of the right edge of the cantilever. Material parameters of the fluid and solid are specified as [131]: the fluid density \(\rho ^{\mathrm{F}} = 1.18 \times 10^{-3}\), the fluid viscosity \(\mu = 1.82 \times 10^{-4}\), the structural density \(\rho ^{\mathrm{S}} = 1.0 \times 10^{-1}\), Young’s modulus \(E = 2.5 \times 10^6\) and Poisson’s ratio \(\nu = 0.35\). The length scale of the square cylinder is \(D = 1\) and the inflow velocity is \(U = 51.3\), corresponding to \(Re = 332.6\) in this example.
Sketch of geometry and boundary conditions for the cantilever attached to a square cylinder
The fluid field is decomposed into the Eulerian subdomain A1 and the ALE subdomain A2. A2 is a square box of size \(6D \times 6D\). T3 elements are used for the fluid mesh and MSA submesh. The flexible cantilever is discretized with nine-node quadrilateral (Q9) plane stress elements for the FEM, and four-node quadrilateral (Q4) plane stress elements for the CS-FEM. The meshing information is summarized in Table 10. Figure 39 exhibits the fluid mesh and MSA submesh for Case 1. In Fig. 40 a Q4 element is typically subdivided into four exactly equivalent rectangular smoothing domains (SDs), relying on the stability condition of the CS-FEM [32, 92]. Of total nine points, extra five points are generated to compute the so-called smoothed shape functions by simply averaging the values at four corners. The time step is set as \(\varDelta t = 1.0 \times 10^{-2}\) and the tolerance is \(tol = 1.0 \times 10^{-6}\). Newmark parameters \(\beta = 0.5\) and \(\gamma = 0.8\) are chosen to eliminate the high-frequency noise in the structural vibrations. The cantilever problem is solved by means of the semi-implicit coupling scheme.
Mesh and submesh for Case 1. a Finite element mesh for the fluid field. b MSA submesh for the ALE domain
Construction of the SDs and smoothed shape function in a Q4 element
Two key parameters are calculated to assess the performance of the proposed partitioned coupling algorithms. Table 11 lists the time-averaged vertical deflection \(d_{\mathrm{MEAN2}}\) and the time-averaged oscillation frequency \(f_{\mathrm{O,MEAN}}\) of the measuring point, as well as those data well documented in the open literature [16, 21, 39, 58, 73, 91, 97, 107, 127, 131, 134, 135]. The data of Case 1 are identical with most of available ones. In Case 2 \(d_{\mathrm{MEAN2}} = 0.92\) is acceptable, compared with the values in [58, 73, 107]. \(f_{\mathrm{O,MEAN}} = 0.0586\) in Case 1 and \(f_{\mathrm{O,MEAN}} = 0.0622\) in Case 2 are very close to the first eigenfrequency of the cantilever \(f^{\mathrm{S}}_1 = 0.0591\) that predominates the structural oscillations. Based on the above analysis, a good agreement is observed from Table 11. Likewise, Table 11 and Fig. 41 suggest that the semi-implicit method shows the good accuracy and the improved efficiency, especially for the stringent convergence tolerance.
Time cost of the implicit and semi-implicit methods for the flexible cantilever. a \(tol = 1.0 \times 10^{-6}\). b \(tol = 1.0 \times 10^{-7}\)
Figure 42 plots the smooth and undamped time histories of tip displacement for both cases, where the unsteady periodic long-term oscillatory movements of the geometrically nonlinear solid are produced correctly. In accordance with [39, 135], the violent structural vibrations commences roughly at dimensionless time 100 or at real time of 2s. Nevertheless, the unsteady long-periodic response of the cantilever was established much later in [91]. Observed from Fig. 42, the amplitude of tip displacement in Case 2 is smaller than that in Case 1, and the slightly longer time is required to reach the characteristic amplitude in this case. The number of Q4 elements and linear shape function are possibly responsible for the underestimated tip deflection. It should be noticed that the amplitudes are still small in [58, 107] even if much denser finite volume cells are adopted for the cantilever.
Time history of the vertical displacement of the measuring point. a Case 1. b Case 2
According to [91], the displacement history is partitioned into two stages: lock-in and beating. The structural displacement is gradually amplified within the first stage. Meanwhile, the cantilever’s oscillation frequency gets close to its first eigenfrequency, inspiring the so-called lock-in or resonance. At the second stage, the structural response converges to the stable long-term oscillatory motion, forming the beating or modulation phenomenon. During the whole course, vortex shedding induces lock-in and drives the cantilever to oscillate sharply. Correspondingly, the violent oscillations of the flexible cantilever significantly alter the vortex-shedding mode whose frequency deviates from the cantilever’s first eigenfrequency.
When the stable structural oscillations are fully built up, three typical snapshots of vorticity and pressure fields are graphically displayed in Fig. 43. It is seen that the unsteady features of flow patterns and structural oscillations are evidently distinguished in different phases during an oscillation period. In Fig. 43a, vortices act on the cantilever surface while being alternatively shed from two lateral sides of the square cylinder. The strong structural oscillations are therefore motivated. Note that the vortices on one side towards which the flexible cantilever starts to move are weakened and are eventually suppressed by the flows near the cantilever. High compression is perceived on this side as well. However, vortices on the opposite side are strengthened and advect downstream from the cantilever. These vortices are generated by velocity gradient at the tip of the flapping cantilever [58]. In Fig. 43b the pressure distribution on the frontal side of the square cylinder is positive because of the immediate exposure of the obstacle to the flows, but high suction (the blue zone) is detected along the lateral sides of the square cylinder. The pressure distribution on the cantilever surface opposite to the direction of the structural motion is negative but results in the lower suction.
Instantaneous contours of the flexible cantilever. a Vorticity. b Pressure
5.8 A Restrictor Flap in a Uniform Channel Flow
The last example is a flexible restrictor flap in a uniform channel flow [107]. The problem definition is sketched in Fig. 44. The measuring point is put at the flap’s upper left corner. Systematic properties are set as follows [107]: the fluid density \(\rho ^{\mathrm{F}} = 1.0\), the fluid viscosity \(\mu = 1.0 \times 10^{-3}\), the structural density \(\rho ^{\mathrm{S}} = 1000\) for Case A and \(\rho ^{\mathrm{S}} = 62.5\) for Case B, Young’s modulus \(E = 6.0 \times 10^4\) and Poisson’s ratio \(\nu = 0.45\), the inflow velocity \(U = 1\), the flap’s height \(D = 1\) and the resulting Reynolds number is \(Re = 1000\).
Sketch of geometry and boundary conditions for the restrictor flap in a channel
The fluid domain is divided into the Eulerian subdomain A1 and the ALE subdomain A2. Given the feature of the structural motion, the proportion of A2 is designated as \(2.5D \times 1.5D\). Eight-node quadrilateral (Q8) plane stress element is utilized to discretize the restrictor flap for the FEM. The mesh information is listed in Table 12. The fluid mesh and MSA submesh for Case 1 are exposed in Fig. 45. The time step \(\varDelta t = 5.0 \times 10^{-3}\), the tolerance \(tol = 1.0 \times 10^{-6}\) and Newmark parameters \(\beta = 0.5\) and \(\gamma = 0.8\) are employed here. The semi-implicit coupling scheme is used for the restrictor flap problem.
Mesh and submesh for Case 1. a Finite element mesh for the fluid field. b MSA submesh for the ALE domain
The time evolutions of horizontal displacements among various cases are depicted in Fig. 46. Consistent with [107], the obtained magnitudes of the tip deflection are approximately 0.6 in both the FEM and CS-FEM. Case 1 and Case 2 produce the almost identical amplitudes for two structural densities. This may be caused by the small Young’s modulus. Based on the further observation of Fig. 46, the computed results of Case A agree better with that of [107], whereas the curves of Case B diverge from that of [107] very soon. For Case A, the decaying oscillations are observed between [107] and this paper. This phenomenon is explained as follows: when the structural density is large, the vibrations of the restrictor flap are mainly excited by the structural inertia and the fluid serves as the damped oscillator. The decay of tip oscillations in Case B is fairly rapid in this study, although the structural oscillations sustained by the tip vortex shedding remain significant in [107]. When the structural density decreases, our restrictor flap’s motion is damped sharply by the fluid action and soon its vibrations tend to be feeble. This behavior has been seen in an analogous example [10] where the structural movement becomes nearly stationary over an expanded period of time. The typical contours of the horizontal fluid velocity at different time slices are displayed in Fig. 47 for Case A.
Time history of the horizontal displacement of the measuring point
Horizontal velocity contours of the flexible flap for Case A
6 Concluding Remarks and Open Issues
We have looked over the basis and recent developments of the CIBC method in this review. The following advantages of the CIBC methods are acknowledged from its previous applications: (1) this scheme achieves the accuracy and stability of the coupled system as high as those of individual fields; (2) the low mass ratio is reached for VIV of a vibrating bluff body; (3) the expanded stability is obtained for coupled thermal simulations by explicit coupling computation; and (4) its good adaptability is seen by furnishing other techniques. We also re-derive the CIBC formulae. Especially, two enhanced CIBC formulations are proposed to repair the defects of the original method. The global FSI system is established in the ALE-FEM context and all of its components are well depicted. The proposed methodologies are validated against the available data for different FSI problems. Overall, good agreement is realized between the present and well-documented results. Some well-known flow phenomena, such as lock-in, beating, galloping and flutter, are reproduced successfully. The major contributions are summarized as follows:
-
1.
The CIBC method is re-derived on the basis of the definition \(\varvec{\sigma }^{\mathrm{F}} = p\mathbf {I}\) and the full-blown fluid Cauchy stress tensor, respectively. The latter brings about the simpler formulae.
-
2.
The CIBC Formulation I is proposed by using \(\varvec{\sigma }^{\mathrm{F}} = p\mathbf {I}\) in order to eliminate the structural traction term which disables the initial CIBC method in the computation of the fluid-rigid body interaction. After some algebraic manipulation, the first order ODEs are gained to achieve the above goal. Despite several improvements, the developed method runs in an awkward way, leading to certain inconvenience.
-
3.
In view of the full fluid stress, the CIBC Formulation II is developed to circumvent the restricted use of the CIBC method. The simplified derivation leads to no ODEs on the interface and the natrual application to diverse FSI problems.
-
4.
Both formulations retrieve the consistency in the treatment of the interfacial traction and the solvability of the fluid-rigid body interaction. Common issues are also discussed, such as the computational order of velocity and traction corrections, the weak treatment of the CIBC method, the instability source caused by two-sided corrections and its remedy, the implicit correction for rigid-body torsion testified via the generalized inverse matrix, the nondimensionalization and the assessment of the coupling parameter.
-
5.
The CIBC method is introduced into the partitioned explicit, implicit and semi-implicit coupling schemes. Other useful techniques can be jointly furnished for the sake of improved accuracy and efficiency.
Although the comprehensive argumentation of the CIBC method has been reported in this presentation, extra comments may be made on the constraints of the method as follows:
-
1.
Although a one-dimensional piston has been solved for an inviscid compressible fluid before, it is quite difficult to find another one-dimensional model problem that can represent both convection and diffusion of an incompressible flow. Without presenting such a model problem, we cannot justify the advantages of the CIBC method.
-
2.
It is essential to quantify or highlight the acceleration, stabilization and energy conservation of the method in multidimensional cases.
-
3.
Undoubtedly, the CIBC method is applicable to aeroelasticity and computational wind engineering where the pressure is the major driving force to excite the structure to oscillate [140]. However, the performance of the CIBC method needs to be re-examined for the fluid flows with large viscosity (such as haemodynamics), and the higher-order finite element meshing.
-
4.
The three dimensional extension seems a natural consideration as well as convincing.
Based on the above comments, the top priority may depend on presenting a new model problem to testify the strengths of the method, analytically or numerically. For the moment, one possible candidate is the model proposed in [42, 44]. It is also interesting to adopt a quadratic or higher-order finite element for both physical fields to precisely reflect the CIBC method. Enlightened by the first author’s finished work [66], the CIBC method may be able to stabilize the sensitive pressure which is in general acquired in the artificial compressibility FSI approach. More investment is demanded to exploit the CIBC method in the future.
References
Abdullah MM, Walsh KK, Grady S, Wesson GD (2005) Modeling flow around bluff bodies. J Comput Civil Eng ASCE 19(1):104–107
Afrasiab H, Movahhedy MR, Assempour A (2012) fluid–structure interaction analysis in microfluidic devices: a dimensionless finite element approach. Int J Numer Meth Fluids 68(9):1073–1086
Anagnostopoulos P (1994) Numerical investigation of response and wake characteristics of a vortex-excited cylinder in a uniform stream. J Fluids Struct 8(4):367–390
Anagnostopoulos P, Bearman PW (1992) Response characteristics of a vortex-excited cylinder at low Reynolds numbers. J Fluids Struct 6(1):39–50
Anju A, Maruoka A, Kawahara M (1997) 2-D fluid–structure interaction problems by an arbitrary Lagrangian–Eulerian finite element method. Int J Comput Fluid Dyn 8(1):1–9
Badia S, Codina R (2007) On some fluid–structure iterative algorithms using pressure segregation methods. Application to aeroelasticity. Int J Numer Meth Eng 72(1):46–71
Badia S, Nobile F, Vergara C (2008) fluid–structure partitioned procedures based on Robin transmission conditions. J Comput Phys 227(14):7027–7051
Baek H, Karniadakis GE (2012) A convergence study of a new partitioned fluid–structure interaction algorithm based on fictitious mass and damping. J Comput Phys 231(2):629–652
Bahmani MH, Akbari MH (2010) Effects of mass and damping ratios on VIV of a circular cylinder. Ocean Eng 37(5):511–519
Baiges J, Codina R (2010) The fixed-mesh ALE approach applied to solid mechanics and fluid–structure interaction problems. Int J Numer Meth Eng 81(12):1529–1557
Barrero-Gil A, Sanz-Andres A, Roura M (2009) Transverse galloping at low Reynolds numbers. J Fluids Struct 25(7):1236–1242
Bathe KJ (2007) Conserving energy and momentum in nonlinear dynamics: a simple implicit time integration scheme. Comput Struct 85(7):437–445
Bathe KJ, Baig MMI (2005) On a composite implicit time integration procedure for nonlinear dynamics. Comput Struct 83(31):2513–2524
Bathe KJ, Noh G (2012) Insight into an implicit time integration scheme for structural dynamics. Comput Struct 98:1–6
Bathe KJ, Ramm E, Wilson EL (1975) Finite element formulations for large deformation dynamic analysis. Int J Numer Meth Eng 9(2):353–386
Bazilevs Y, Calo VM, Hughes TJR, Zhang Y (2008) Isogeometric fluid–structure interaction: theory, algorithms, and computations. Comput Mech 43(1):3–37
Bekka N, Sellam M, Chpoun A (2015) Aeroelastic stability analysis of a flexible over-expanded rocket nozzle using numerical coupling by the method of transpiration. J Fluids Struct 56:89–106
Bevan RLT, Boileau E, van Loon R, Lewis RW, Nithiarasu P (2016) A comparative study of fractional step method in its quasi-implicit, semi-implicit and fully-explicit forms for incompressible flows. Int J Numer Methods Heat Fluid Flow 26(3/4):595–623
Blevins RD (1990) Flow-induced vibration, 2nd edn. Van Nostrand Reinhold Co. Inc., New York
Blom FJ (1998) A monolithical fluid–structure interaction algorithm applied to the piston problem. Comput Methods Appl Mech Eng 167(3):369–391
Braun AL, Awruch AM (2009) A partitioned model for fluid–structure interaction problems using hexahedral finite elements with one-point quadrature. Int J Numer Meth Eng 79(5):505–549
Bridges TJ (1997) Multi-symplectic structures and wave propagation. Math Proc Camb Philos Soc 121(1):147–190
van Brummelen EH (2009) Added mass effects of compressible and incompressible flows in fluid–structure interaction. J Appl Mech ASME 76(2):021,206
Causin P, Gerbeau JF, Nobile F (2005) Added-mass effect in the design of partitioned algorithms for fluid–structure problems. Comput Methods Appl Mech Eng 194(42):4506–4527
Cebral JR, Löhner R (2005) On the loose coupling of implicit time-marching codes. In: Proceedings of the 43th AIAA aerospace sciences meeting and exhibit. American Institute of Aeronautics and Astronautics, Reno, Nevada, pp 1–15
Chorin AJ (1968) Numerical solution of the Navier–Stokes equations. Math Comput 22(104):745–762
Chung J, Hulbert GM (1993) A time integration algorithm for structural dynamics with improved numerical dissipation: the generalized-\(\alpha\) method. J Appl Mech ASME 60(2):371–375
Codina R, Vázquez M, Zienkiewicz OC (1998) A general algorithm for compressible and incompressible flows. Part III: the semi-implicit form. Int J Numer Meth Fluids 27(1–4):13–32
Codina R, Zienkiewicz OC (2002) CBS versus GLS stabilization of the incompressible Navier–Stokes equations and the role of the time step as stabilization parameter. Commun Numer Methods Eng 18(2):99–112
Cori JF, Etienne S, Garon A, Pelletier D (2015) High-order implicit Runge–Kutta time integrators for fluid–structure interactions. Int J Numer Meth Fluids 78(7):385–412
Cui XY, Liu GR, Li GY, Zhao X, Nguyen TT, Sun GY (2008) A smoothed finite element method (SFEM) for linear and geometrically nonlinear analysis of plates and shells. Comput Model Eng Sci 28(2):109–126
Dai KY, Liu GR (2007) Free and forced vibration analysis using the smoothed finite element method (SFEM). J Sound Vib 301(3):803–820
De Boer A, Van Zuijlen AH, Bijl H (2007) Review of coupling methods for non-matching meshes. Comput Methods Appl Mech Eng 196(8):1515–1525
De Rosis A, Falcucci G, Ubertini S, Ubertini F, Succi S (2013) Lattice Boltzmann analysis of fluid–structure interaction with moving boundaries. Commun Comput Phys 13(03):823–834
Degroote J (2013) Partitioned simulation of fluid–structure interaction. Arch Comput Methods Eng 20(3):185–238
DeJong A, Liang C (2014) Parallel spectral difference method for predicting 3D vortex-induced vibrations. Comput Fluids 98:17–26
Deparis S, Fernández MA, Formaggia L (2003) Acceleration of a fixed point algorithm for fluid–structure interaction using transpiration conditions. ESAIM. Math Model Numer Anal 37(4):601–616
Dettmer W, Perić D (2006) A computational framework for fluid-rigid body interaction: finite element formulation and applications. Comput Methods Appl Mech Eng 195(13):1633–1666
Dettmer W, Perić D (2006) A computational framework for fluid–structure interaction: finite element formulation and applications. Comput Methods Appl Mech Eng 195(41):5754–5779
Dettmer WG, Perić D (2007) A fully implicit computational strategy for strongly coupled fluid–solid interaction. Arch Comput Methods Eng 14(3):205–247
Dettmer WG, Perić D (2013) A new staggered scheme for fluid–structure interaction. Int J Numer Meth Eng 93(1):1–22
Döerfel MR, Simeon B (2013) Fluid–structure interaction: acceleration of strong coupling by preconditioning of the fixed-point iteration. In: Numerical mathematics and advanced applications 2011. Springer, Berlin, pp 741–749
Donea J, Huerta A, Ponthot JP, Rodriguez-Ferran A (2004) Chapter 14: arbitrary Lagrangian–Eulerian Methods. In: Stein E, de Borst R, Hughes TJR (eds) Encyclopedia of computational mechanics vol 1: fundamentals. Wiley, West Sussex, pp 413–437
Dörfel MR, Simeon B (2010) Analysis and acceleration of a fluid–structure interaction coupling scheme. In: Numerical mathematics and advanced applications 2009. Springer, Uppsala, pp 307–315
Étienne S, Garon A, Pelletier D (2009) Perspective on the geometric conservation law and finite element methods for ALE simulations of incompressible flow. J Comput Phys 228(7):2313–2333
Fanion T, Fernández M, Le Tallec P (2000) Deriving adequate formulations for fluid–structure interaction problems: from ALE to transpiration. Revue Européenne des Élém 9(6–7):681–708
Farhat C, Geuzaine P, Brown G (2003) Application of a three-field nonlinear fluid–structure formulation to the prediction of the aeroelastic parameters of an F-16 fighter. Comput Fluids 32(1):3–29
Farhat C, Lesoinne M (2000) Two efficient staggered algorithms for the serial and parallel solution of three-dimensional nonlinear transient aeroelastic problems. Comput Methods Appl Mech Eng 182(3):499–515
Farhat C, Lesoinne M, Maman N (1995) Mixed explicit/implicit time integration of coupled aeroelastic problems: three-field formulation, geometric conservation and distributed solution. Int J Numer Meth Fluids 21(10):807–835
Felippa CA, Park KC, Farhat C (2001) Partitioned analysis of coupled mechanical systems. Comput Methods Appl Mech Eng 190(24):3247–3270
Feng X (2000) Analysis of finite element methods and domain decomposition algorithms for a fluid–solid interaction problem. SIAM J Numer Anal 38(4):1312–1336
Fernández MA, Gerbeau JF, Grandmont C (2007) A projection semi-implicit scheme for the coupling of an elastic structure with an incompressible fluid. Int J Numer Meth Eng 69(4):794–821
Filippini G, Dalcin L, Nigro N, Storti M (2008) Fluid-rigid body interaction by PETs-FEM driven by Python. Mecánica Computac XXVII(8):489–504
Förster C, Wall WA, Ramm E (2007) Artificial added mass instabilities in sequential staggered coupling of nonlinear structures and incompressible viscous flows. Comput Methods Appl Mech Eng 196(7):1278–1293
Fourestey G, Piperno S (2004) A second-order time-accurate ALE Lagrange–Galerkin method applied to wind engineering and control of bridge profiles. Comput Methods Appl Mech Eng 193(39):4117–4137
Govardhan R, Williamson CHK (2000) Modes of vortex formation and frequency response of a freely vibrating cylinder. J Fluid Mech 420:85–130
Guidoboni G, Glowinski R, Cavallini N, Canic S (2009) Stable loosely-coupled-type algorithm for fluid–structure interaction in blood flow. J Comput Phys 228(18):6916–6937
Habchi C, Russeil S, Bougeard D, Harion JL, Lemenand T, Ghanem A, Valle DD, Peerhossaini H (2013) Partitioned solver for strongly coupled fluid–structure interaction. Comput Fluids 71:306–319
Han Z, Zhou D, He T, Tu J, Li C, Kwok KC, Fang C (2015) Flow-induced vibrations of four circular cylinders with square arrangement at low Reynolds numbers. Ocean Eng 96:21–33
Han Z, Zhou D, Tu J, Fang C, He T (2014) Flow over two side-by-side square cylinders by CBS finite element scheme of Spalart–Allmaras model. Ocean Eng 87:40–49
He T (2015) On a partitioned strong coupling algorithm for modeling fluid–structure interaction. Int J Appl Mech 7(2):1550,021
He T (2015) Partitioned coupling strategies for fluid–structure interaction with large displacement: explicit, implicit and semi-implicit schemes. Wind Struct 20(3):423–448
He T (2015) A partitioned implicit coupling strategy for incompressible flow past an oscillating cylinder. Int J Comput Methods 12(2):1550,012
He T (2015) Semi-implicit coupling of CS-FEM and FEM for the interaction between a geometrically nonlinear solid and an incompressible fluid. Int J Comput Methods 12(5):1550,025
He T (2016) A CBS-based partitioned semi-implicit coupling algorithm for fluid–structure interaction using MCIBC method. Comput Methods Appl Mech Eng 298:252–278
He T, Wang T (2016) The use of artificial compressibility to improve partitioned semi-implicit FSI coupling within the classical Chorin-Témam projection framework (submitted)
He T, Zhang K (2015) Combined interface boundary condition method for fluid–structure interaction: some improvements and extensions. Ocean Eng 109:243–255
He T, Zhou D, Bao Y (2012) Combined interface boundary condition method for fluid-rigid body interaction. Comput Methods Appl Mech Eng 223:81–102
He T, Zhou D, Han Z, Tu J, Ma J (2014) Partitioned subiterative coupling schemes for aeroelasticity using combined interface boundary condition method. Int J Comput Fluid Dyn 28(6–10):272–300
Hilber HM, Hughes TJ, Taylor RL (1977) Improved numerical dissipation for time integration algorithms in structural dynamics. Earthq Eng Struct Dyn 5(3):283–292
Hou G, Wang J, Layton A (2012) Numerical methods for fluid–structure interaction—a review. Commun Comput Phys 12(2):337–377
Hu Z, Tang W, Xue H, Zhang X (2016) A SIMPLE-based monolithic implicit method for strong-coupled fluid–structure interaction problems with free surfaces. Comput Methods Appl Mech Eng 299:90–115
Hübner B, Walhorn E, Dinkier, D (2001) Strongly coupled analysis of fluid–structure interaction using space-time finite elements. In: Proceedings of the 2nd European conference on computational mechanics. Cracow, Poland, pp 546–547
Irons BM, Tuck RC (1969) A version of the Aitken accelerator for computer iteration. Int J Numer Meth Eng 1(3):275–277
Jaiman R, Geubelle P, Loth E, Jiao X (2007) Stable and accurate loosely-coupled scheme for unsteady fluid–structure interaction. In: Proceedings of the 45th AIAA aerospace sciences meeting and exhibit. American Institute of Aeronautics and Astronautics, Reno, Nevada, pp 1–28
Jaiman R, Geubelle P, Loth E, Jiao X (2011) Combined interface boundary condition method for unsteady fluid–structure interaction. Comput Methods Appl Mech Eng 200(1):27–39
Jaiman R, Geubelle P, Loth E, Jiao X (2011) Transient fluid–structure interaction with non-matching spatial and temporal discretizations. Comput Fluids 50(1):120–135
Jaiman RK (2012) Advances in ALE based fluid–structure interaction modeling for offshore engineering applications. In: Eberhardsteiner J, Böhm H, Rammerstorfer F (eds) Proceedings of the 6th European congress on computational methods in applied sciences and engineering (ECCOMAS 2012). Austria, Vienna, pp 1–11
Jaiman RK, Guan MZ, Miyanawala TP (2016) Partitioned iterative and dynamic subgrid-scale methods for freely vibrating square-section structures at subcritical Reynolds number. Comput Fluid 133:68–89
Jaiman RK, Jiao X, Geubelle PH, Loth E (2006) Conservative load transfer along curved fluid-solid interface with non-matching meshes. J Comput Phys 218(1):372–397
Jaiman RK, Pillalamarri NR, Guan MZ (2016) A stable second-order partitioned iterative scheme for freely vibrating low-mass bluff bodies in a uniform flow. Comput Methods Appl Mech Eng 301:187–215
Jaiman RK, Shakib F, Oakley OH, Constantinides Y (2009) Fully coupled fluid–structure interaction for offshore applications. In: Proceedings of the 28th international conference on ocean., offshore and arctic engineering. American Society of Mechanical Engineers, Honolulu, Hawaii, pp 757–765
Jan YJ, Sheu TWH (2004) Finite element analysis of vortex shedding oscillations from cylinders in the straight channel. Comput Mech 33(2):81–94
Joly A, Etienne S, Pelletier D (2012) Galloping of square cylinders in cross-flow at low Reynolds numbers. J Fluids Struct 28:232–243
Küttler U, Wall WA (2008) Fixed-point fluid–structure interaction solvers with dynamic relaxation. Comput Mech 43(1):61–72
Küttler U, Wall WA (2009) Vector extrapolation for strong coupling fluid–structure interaction solvers. J Appl Mech ASME 76(2):021,205
Le Tallec P, Mouro J (2001) Fluid structure interaction with large structural displacements. Comput Methods Appl Mech Eng 190(24):3039–3067
Lefrançois E (2008) A simple mesh deformation technique for fluid–structure interaction based on a submesh approach. Int J Numer Meth Eng 75(9):1085–1101
Lesoinne M, Farhat C (1996) Geometric conservation laws for flow problems with moving boundaries and deformable meshes, and their impact on aeroelastic computations. Comput Methods Appl Mech Eng 134(1):71–90
Li L, Sherwin S, Bearman PW (2002) A moving frame of reference algorithm for fluid/structure interaction of rotating and translating bodies. Int J Numer Meth Fluids 38(2):187–206
Liew KM, Wang WQ, Zhang LX, He XQ (2007) A computational approach for predicting the hydroelasticity of flexible structures based on the pressure Poisson equation. Int J Numer Meth Eng 72(13):1560–1583
Liu GR, Dai KY, Nguyen TT (2007) A smoothed finite element method for mechanics problems. Comput Mech 39(6):859–877
Liu J, Jaiman RK, Gurugubelli PS (2014) A stable second-order scheme for fluid–structure interaction with strong added-mass effects. J Comput Phys 270:687–710
Liu X, Qin N, Xia H (2006) Fast dynamic grid deformation based on Delaunay graph mapping. J Comput Phys 211(2):405–423
Löhner R, Haug E, Michalski A, Muhammad B, Drego A, Nanjundaiah R, Zarfam R (2015) Recent advances in computational wind engineering and fluid–structure interaction. J Wind Eng Ind Aerodyn 144:14–23
Markou GA, Mouroutis ZS, Charmpis DC, Papadrakakis M (2007) The ortho-semi-torsional (OST) spring analogy method for 3D mesh moving boundary problems. Comput Methods Appl Mech Eng 196(4):747–765
Matthies HG, Steindorf J (2003) Partitioned strong coupling algorithms for fluid–structure interaction. Comput Struct 81(8):805–812
Mok DP, Wall WA (2001) Partitioned analysis schemes for the transient interaction of incompressible flows and nonlinear flexible structures. In: Wall WA, Bletzinger KU, Schweizerhof K (eds) Trends in computational structural mechanics. CIMNE, Barcelona, pp 689–698
Newmark NM (1959) A method of computation for structural dynamics. J Eng Mech ASCE 85(3):67–94
Nithiarasu P (2002) On boundary conditions of the characteristic based split (CBS) algorithm for fluid dynamics. Int J Numer Meth Eng 54(4):523–536
Nithiarasu P (2004) A fully explicit characteristic based split (CBS) scheme for viscoelastic flow calculations. Int J Numer Meth Eng 60(5):949–978
Nithiarasu P (2006) A matrix free fractional step method for static and dynamic incompressible solid mechanics. Int J Comput Methods Eng Sci Mech 7(5):369–380
Nithiarasu P, Codina R, Zienkiewicz OC (2006) The Characteristic-Based Split (CBS) scheme—a unified approach to fluid dynamics. Int J Numer Meth Eng 66(10):1514–1546
Nithiarasu P, Zienkiewicz OC (2000) On stabilization of the CBS algorithm: internal and external time steps. Int J Numer Meth Eng 48(6):875–880
Nomura T (1993) Finite element analysis of vortex-induced vibrations of bluff cylinders. J Wind Eng Ind Aerodyn 46:587–594
Normura T, Hughes TJR (1992) An arbitrary Lagrangian–Eulerian finite element method for interaction of fluid and a rigid body. Comput Methods Appl Mech Eng 95(1):115–138
Olivier M, Dumas G, Morissette J (2009) A fluid–structure interaction solver for nano-air-vehicle flapping wings. In: Proceedings of the 19th AIAA computational fluid dynamics conference. American Institute of Aeronautics and Astronautics, San Antonio, Texas, pp 1–15
Park KC, Felippa CA, DeRuntz JA (1977) Stabilization of staggered solution procedures for fluid–structure interaction analysis. In: Belytschko T, Geers TL (eds) Computational methods for fluid–structure interaction problems, New York, pp 95–124
Parkinson GV, Smith JD (1964) The square prism as an aeroelastic non-linear oscillator. Quart J Mech Appl Math 17(2):225–239
Payen DJ, Bathe KJ (2012) A stress improvement procedure. Comput Struct 112–113:311–326
Piperno S (1997) Explicit/implicit fluid/structure staggered procedures with a structural predictor and fluid subcycling for 2D inviscid aeroelastic simulations. Int J Numer Meth Fluids 25(10):1207–1226
Prasanth TK, Mittal S (2008) Vortex-induced vibrations of a circular cylinder at low Reynolds numbers. J Fluid Mech 594:463–491
Rice JR, Tsompanopoulou P, Vavalis E (2000) Interface relaxation methods for elliptic differential equations. Appl Numer Math 32(2):219–245
Robertson I, Li L, Sherwin SJ, Bearman PW (2003) A numerical study of rotational and transverse galloping rectangular bodies. J Fluids Struct 17(5):681–699
Roe B, Jaiman R, Haselbacher A, Geubelle PH (2008) Combined interface boundary condition method for coupled thermal simulations. Int J Numer Meth Fluids 57(3):329–354
Roshko A (1954) On the development of turbulent wakes from vortex streets. Technical Report NACA TN 1191, National Advisory Committee for Aeronautics
Rossi R, Oñate E (2010) Analysis of some partitioned algorithms for fluid–structure interaction. Eng Comput 27(1):20–56
Samaniego C, Houzeaux G, Samaniego E, Vázquez M (2015) Parallel embedded boundary methods for fluid and rigid-body interaction. Comput Methods Appl Mech Eng 290:387–419
Sarpkaya T (2004) A critical review of the intrinsic nature of vortex-induced vibrations. J Fluids Struct 19(4):389–447
Sarrate J, Huerta A, Donea J (2001) Arbitrary Lagrangian–Eulerian formulation for fluid-rigid body interaction. Comput Methods Appl Mech Eng 190(24):3171–3188
Schulz KW, Kallinderis Y (1998) Unsteady flow structure interaction for incompressible flows using deformable hybrid grids. J Comput Phys 143(2):569–597
Sen S, Mittal S (2011) Free vibration of a square cylinder at low Reynolds numbers. J Fluids Struct 27(5):875–884
Sen S, Mittal S, Biswas G (2011) Flow past a square cylinder at low Reynolds numbers. Int J Numer Meth Fluids 67(9):1160–1174
Souli M, Ouahsine A, Lewin L (2000) ALE formulation for fluid–structure interaction problems. Comput Methods Appl Mech Eng 190(5):659–675
Surana KS, Blackwell B, Powell M, Reddy JN (2014) Mathematical models for fluid-solid interaction and their numerical solutions. J Fluids Struct 50:184–216
Takagi S, Sugiyama K, Ii S, Matsumoto Y (2012) A review of full Eulerian methods for fluid structure interaction problems. J Appl Mech ASME 79(1):010,911
Teixeira PRF, Awruch AM (2005) Numerical simulation of fluid–structure interaction using the finite element method. Comput Fluid 34(2):249–273
Témam R (1968) Une méthode d’approximation de la solution des équations de Navier–Stokes. Bull la Société Math France 96:115–152
Tezduyar TE (2007) Finite elements in fluids: stabilized formulations and moving boundaries and interfaces. Comput Fluid 36(2):191–206
Tsompanopoulou P, Vavalis E (2008) An experimental study of interface relaxation methods for composite elliptic differential equations. Appl Math Model 32(8):1620–1641
Wall WA, Ramm E (1998) fluid–structure interaction based upon a stabilized (ALE) finite element method. In: Idelsohn SR, Oñate E, Dvorkin EN (eds) Proceedings of the 4th world congress on computational mechanics: new trends and applications. CIMNE, Barcelona, pp 1–20
Wei R, Sekine A, Shimura M (1995) Numerical analysis of 2D vortex-induced oscillations of a circular cylinder. Int J Numer Meth Fluids 21(10):993–1005
Williamson CHK, Roshko A (1988) Vortex formation in the wake of an oscillating cylinder. J Fluids Struct 2(4):355–381
Wood C, Gil AJ, Hassan O, Bonet J (2010) Partitioned block-Gauss–Seidel coupling for dynamic fluid–structure interaction. Comput Struct 88(23):1367–1382
Yamada T, Yoshimura S (2008) Line search partitioned approach for fluid–structure interaction analysis of flapping wing. CMES. Comput Model Eng Sci 24(1):51–60
Yang FL, Chen CH, Young DL (2011) A novel mesh regeneration algorithm for 2D FEM simulations of flows with moving boundary. J Comput Phys 230(9):3276–3301
Yang J, Preidikman S, Balaras E (2008) A strongly coupled, embedded-boundary method for fluid–structure interactions of elastically mounted rigid bodies. J Fluids Struct 24(2):167–182
Young DL, Chang JT, Eldho TI (2001) A coupled BEM and arbitrary Lagrangian–Eulerian FEM model for the solution of two-dimensional laminar flows in external flow fields. Int J Numer Meth Eng 51(9):1053–1077
Zeng D, Ethier CR (2005) A semi-torsional spring analogy model for updating unstructured meshes in 3D moving domains. Finite Elem Anal Des 41(11):1118–1139
Zhang K, Katsuchi H, Zhou D, Yamada H, Han Z (2016) Numerical study on the effect of shape modification to the flow around circular cylinders. J Wind Eng Ind Aerodyn 152:23–40
Zhou CY, So RMC, Lam K (1999) Vortex-induced vibrations of an elastic circular cylinder. J Fluids Struct 13(2):165–189
Zienkiewicz OC, Codina R (1995) A general algorithm for compressible and incompressible flow. Part I: the split, characteristic-based scheme. Int J Numer Meth Fluids 20(8–9):869–885
Zienkiewicz OC, Morgan K, Sai BVK, Codina R, Vasquez M (1995) A general algorithm for compressible and incompressible flow. Part II: tests on the explicit form. Int J Numer Meth Fluids 20(8–9):887–913
Zienkiewicz OC, Nithiarasu P, Codina R, Vazquez M, Ortiz P (1999) The characteristic-based-split procedure: an efficient and accurate algorithm for fluid problems. Int J Numer Meth Fluids 31(1):359–392
Zienkiewicz OC, Taylor RL, Nithiarasu P (2005) The finite element method for fluid dynamics, 6th edn. Butterworth-Heinemann, Oxford
Zienkiewicz OC, Taylor RL, Zhu JZ (2005) The finite element method: its basis and fundamentals, 6th edn. Butterworth-Heinemann, Oxford
Acknowledgments
The authors thank anonymous referees for their insightful comments in improving this paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of Interest
The authors declare that they have no conflict of interest.
Funding
This study was funded by National Natural Science Foundation of China (grant number 51508332), Innovation Program of Shanghai Municipal Education Commission (grant number 14ZZ129) and Capacity Building Program for Local Universities of Shanghai Municipal Science and Technology Commission (Grant number 14200503000).
Rights and permissions
About this article
Cite this article
He, T., Zhang, K. An Overview of the Combined Interface Boundary Condition Method for Fluid–Structure Interaction. Arch Computat Methods Eng 24, 891–934 (2017). https://doi.org/10.1007/s11831-016-9193-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-016-9193-0