Modified viscosity implicit rules for nonexpansive mappings in Hilbert spaces

Abstract

In this paper, we study a modified viscosity implicit rule of a nonexpansive mapping in Hilbert spaces. Strong convergence theorems are obtained under some suitable assumptions imposed on the parameters. As applications, we obtain some strong convergence theorems for solving fixed-point problems of strict pseudocontractive mappings and finite equilibrium problems in Hilbert spaces. We also give some numerical examples to support our main results.

1 Introduction

Let H be a real Hilbert space with the inner product $\left<\cdot \right>$ and let C be a nonempty closed convex subset of H. We denote by F(T) the set of fixed points of a nonlinear mapping T. Now, we recall some concepts.

A mapping $f: C\rightarrow C$ is called a strict contraction if there exists a constant $\alpha \in (0,1)$ satisfying

$$\begin{aligned} \left\| f(x)-f(y)\right\| \le \alpha \left\| x-y\right\| ,\quad \forall \, x,y\in C. \end{aligned}$$

(1.1)

A mapping $T:C\rightarrow H$ is called nonexpansive if

$$\begin{aligned} \left\| Tx-Ty\right\| \le \left\| x-y\right\| ,\quad \forall \,x,y\in C. \end{aligned}$$

(1.2)

A mapping $A:C\rightarrow H$ is called monotone if

$$\begin{aligned} \left<Ax-Ay,x-y\right>\ge 0,\quad \forall \, x,y\in C. \end{aligned}$$

(1.3)

A mapping $A:C\rightarrow H$ is called $\alpha$-inverse strongly monotone if there exists a positive real number $\alpha$, such that

$$\begin{aligned} \left<Ax-Ay,x-y\right>\ge \alpha \left\| Ax-Ay\right\| ^2,\quad \forall \, x,y\in C. \end{aligned}$$

(1.4)

A mapping $F:C\rightarrow H$ is called k-Lipschitzian if there exists a positive constant k, such that

$$\begin{aligned} \left\| Fx-Fy\right\| \le k\left\| x-y\right\| ,\quad \forall \, x,y\in H. \end{aligned}$$

(1.5)

A mapping $F:C\rightarrow H$ is called $\eta$-strongly monotone if there exists a positive constant $\eta$, such that

$$\begin{aligned} \left<Fx-Fy,x-y\right>\ge \eta \left\| x-y\right\| ^2,\quad \forall \, x,y\in H. \end{aligned}$$

(1.6)

$A:C\rightarrow H$ is called a strongly positive bounded linear operator if there exists a constant $\gamma >0$ such that

$$\begin{aligned} \left<Ax,x\right>\ge \gamma \left\| x\right\| ^2,\quad \forall \, x\in H. \end{aligned}$$

(1.7)

Remark 1.1

It is easy to see that strongly positive bounded linear operator A is $\left\| A\right\|$-Lipschitzian and $\gamma$-strongly monotone.

Recently, viscosity iterative algorithms for approximating a common element of the set of fixed points of nonexpansive mappings and the set of solutions of equilibrium problems have been investigated extensively by many authors, see [1,2,3,4,5,6,7,8,9] and the references therein. For instance, Moudafi [1] studied the viscosity technique for nonexpansive mappings in Hilbert spaces. Moreover, Xu [2] refined the main results of [1] in Hilbert spaces and extended them to more general uniformly smooth spaces.

Very recently, the implicit midpoint rule has become a powerful numerical method for solving ordinary differential equations; see [10,11,12,13,14,15,16] and the references therein. Xu et al. [14] introduced the following viscosity implicit midpoint rule:

$$\begin{aligned} x_{n+1}=\alpha _nf(x_n)+(1-\alpha _n)T\left( \frac{x_n+x_{n+1}}{2}\right) ,\quad n\ge 0. \end{aligned}$$

(1.8)

Precisely, they proved the following theorem.

Theorem 1.2

(Xu et al. [14]). Let H be a Hilbert space, C a closed convex subset of H, $T:C\rightarrow C$ a nonexpansive mapping with $S:=F(T)\ne \emptyset$, and $f:C\rightarrow C$ a contraction with coefficient $\alpha \in [0,1)$. Let $\left\{ x_n\right\}$ be generated by the viscosity implicit midpoint rule (1.8), where $\left\{ \alpha _n\right\}$ is a sequence in (0, 1) satisfying

• (C1) $\lim _{n\rightarrow \infty }\alpha _n=0$,

• (C2) $\sum _{n=0}^\infty \alpha _n=\infty$,

• (C3) either $\sum _{n=0}^\infty \left| \alpha _{n+1}-\alpha _n\right| <\infty$ or $\lim _{n\rightarrow \infty }\frac{\alpha _{n+1}}{\alpha _n}=1$. Then, $\left\{ x_n\right\}$ converges in norm to a fixed point q of T, which is also the unique solution of the variational inequality:

  $$\begin{aligned} \left<(I-f)q,x-q\right>\ge 0, \quad \forall \, x\in S. \end{aligned}$$

Motivated and inspired by Xu et al. [14], Ke and Ma [16] studied the following generalized viscosity implicit rule:

$$\begin{aligned} x_{n+1}=\alpha _nf(x_n)+(1-\alpha _n)T(s_nx_n+(1-s_n)x_{n+1}),\quad \forall \, n\ge 0. \end{aligned}$$

(1.9)

More precisely, they obtained the followings results.

Theorem 1.3

(Ke and Ma [16]). Let C be a nonempty closed convex subset of the real Hilbert space H. Let $T:C\rightarrow C$ be a nonexpansive mapping with $F(T)\ne \emptyset$ and $f:C\rightarrow C$ be a contraction with coefficient $\theta \in [0,1)$. Pick any $x_0\in C$, let $\left\{ x_n\right\}$ be a sequence generated by (1.9), where $\left\{ \alpha _n\right\}$ and $\left\{ s_n\right\}$ are two sequences in (0, 1) satisfying the following conditions:

• (1) $\lim _{n\rightarrow \infty }\alpha _n=0$,

• (2) $\sum _{n=0}^\infty \alpha _n=\infty$,

• (3) $\sum _{n=0}^\infty \left| \alpha _{n+1}-\alpha _n\right| <\infty$,

• (4) $0<\varepsilon \le s_n\le s_{n+1}<1$ for all $n\ge 0$. Then, $\left\{ x_n\right\}$ converges strongly to a fixed point q of the nonexpansive mapping T, which is also the unique solution of the variational inequality:

  $$\begin{aligned} \left<(I-f)q,x-q\right>\ge 0,\quad \forall \, x\in F(T). \end{aligned}$$

  In other words, q is the unique fixed point of the contraction $P_{F(T)}f$, that is, $P_{F(T)}f(q)=q$.

The purpose of this paper is to study a modified viscosity implicit rule of a nonexpansive mapping in Hilbert spaces. Under some suitable assumptions imposed on the parameters, we prove some strong convergence theorems. As applications, we obtain some strong convergence theorems for solving fixed-point problems of strict pseudocontractive mappings and finite equilibrium problems in Hilbert spaces. Some numerical examples are also given to support our main results.

2 Preliminaries

Let C be a nonempty closed convex subset of H. For all $x\in H$, there exists a unique nearest point in C, denoted by $P_Cx$, such that

$$\begin{aligned} \left\| x-P_Cx\right\| \le \left\| x-y\right\| \,\,\text{ for } \text{ all }\,\,y\in C. \end{aligned}$$

(2.1)

P is called a metric projection of H onto C. We know that $P_C$ is a nonexpansive mapping of H onto C and satisfies

$$\begin{aligned} \left<x-y,P_Cx-P_Cy\right>\ge \left\| P_Cx-P_Cy\right\| ^2,\quad \forall \, x,y\in H. \end{aligned}$$

(2.2)

Moreover, $P_Cx$ is characterized by the following properties: $P_Cx\in C$ and

$$\begin{aligned} \left<x-P_Cx,y-P_Cx\right>\le 0, \end{aligned}$$

(2.3)

$$\begin{aligned} \left\| x-y\right\| ^2\ge \left\| x-P_Cx\right\| ^2+\left\| y-P_Cx\right\| ^2,\quad \forall \,x\in H,\,y\in C. \end{aligned}$$

(2.4)

For properties of the metric projection, we refer the readers to [17] and the reference therein.

We need the following lemmas for proving our main results.

Lemma 2.1

([2, 18]). Assume that $\left\{ a_n\right\}$ is a sequence of nonnegative real numbers, such that

$$\begin{aligned} a_{n+1}\le (1-\alpha _n)a_n+\delta _n,\quad n\ge 0, \end{aligned}$$

where $\left\{ \alpha _n\right\}$ is a sequence in (0, 1) and $\left\{ \delta _n\right\}$ is a sequence in $\mathbb {R}$, such that

• (i) $\sum _{n=0}^\infty \alpha _n=\infty$,

• (ii) either $\limsup _{n\rightarrow \infty }\frac{\delta _n}{\alpha _n}\le 0$ or $\sum _{n=1}^\infty \left| \delta _n\right| <\infty$. Then, $\lim _{n\rightarrow \infty }a_n=0$.

Lemma 2.2

([19]). Let C be a nonempty closed convex subset of a real Hilbert space H. Let S be a nonexpansive self-mapping on C with $F(T)\ne \emptyset$. Then, $I-S$ is demiclosed, that is, whenever $\left\{ x_n\right\}$ is a sequence in C weakly converging to some $x\in C$ and the sequence $\left\{ (I-S)x_n\right\}$ strongly converges to some y, it follows that $(I-S)x=y$, where I is the identity operator of H.

Lemma 2.3

([20]). Let $\lambda$ be a number in (0, 1] and $T:C\rightarrow H$ be a nonexpansive mapping, we define the mapping $T^\lambda :C\rightarrow H$ by

$$\begin{aligned} T^\lambda x:=Tx-\lambda \mu F(Tx),\quad \forall \ x\in C, \end{aligned}$$

where $F:H\rightarrow H$ is k-Lipschitzian and $\eta$-strongly monotone. Then, $T^\lambda$ is a contraction provided $0<\mu <\frac{2\eta }{k^2}$, that is

$$\begin{aligned} \left\| T^\lambda x-T^\lambda y\right\| \le (1-\lambda \tau )\left\| x-y\right\| ,\quad \forall \, x,y\in C, \end{aligned}$$

where $\tau =1-\sqrt{1-\mu (2\eta -\mu k^2)}\in (0,1]$.

3 Main results

Theorem 3.1

Let C be a nonempty closed convex subset of a real Hilbert space H. Let $T:C\rightarrow C$ be a nonexpansive mapping with $F(T)\ne \emptyset$ and $f:C\rightarrow C$ a strict contraction with coefficient $\alpha \in [0,1)$. Let $F:C\rightarrow H$ be k-Lipschitzian and $\eta$-strongly monotone with constants $k,\eta >0$, such that $\alpha <\tau$ and $0<\mu <\frac{2\eta }{k^2}$, where $\tau =1-\sqrt{1-\mu (2\eta -\mu k^2)}\in (0,1]$. For arbitrarily given $x_{0}\in C$, let $\left\{ x_{n}\right\}$ be a sequence generated by

$$\begin{aligned} x_{n+1}=P_C[\alpha _{n}f(x_{n})+(I-\alpha _n\mu F)T(s_nx_{n}+(1-s_n)x_{n+1})], \end{aligned}$$

(3.1)

where $\{\alpha _{n}\}$ and $\{s_{n}\}$ are two sequences in (0, 1] satisfying the following conditions:

• (i) $\lim _{n\rightarrow \infty }\alpha _{n}=0$;

• (ii) $\sum _{n=0}^{\infty }\alpha _{n}=\infty$ and $\sum _{n=0}^{\infty }\left| \alpha _{n+1}-\alpha _n\right| <\infty$;

• (iii) $0<\varepsilon \le s_n\le s_{n+1}<1$ for all $n\ge 0$.

Then, $\left\{ x_{n}\right\}$ converges strongly to a fixed point $q\in F(T)$, which also solves the variational inequality:

$$\begin{aligned} \left<f(q)-\mu F(q),y-q\right>\le 0,\text { for all } y\in F(T). \end{aligned}$$

Proof

First, we show that $\{x_{n}\}$ is bounded. Indeed, take $p\in F(T)$ arbitrarily, it follows from Lemma 2.3 and (3.1) that

$$\begin{aligned}&\left\| x_{n+1}-p\right\| \\&\quad =\left\| P_C[\alpha _{n}f(x_{n})+(I-\alpha _n\mu F)T(s_nx_{n}+(1-s_n)x_{n+1})]-p\right\| \\&\quad \le \left\| \alpha _n(f(x_n)-\mu F(p))+(I-\alpha _n\mu F)(T(s_nx_{n}+(1-s_n)x_{n+1})-p)\right\| \\&\quad \le \alpha _n\left\| f(x_n)-f(p)\right\| +(1-\alpha _n\tau )\left\| T(s_nx_{n}+(1-s_n)x_{n+1})-p\right\| \\&\quad \quad +\alpha _n\left\| f(p)-\mu F(p)\right\| \\&\quad \le \alpha _n\left\| f(x_n)-f(p)\right\| +(1-\alpha _n\tau )\left\| s_n(x_{n}-p)+(1-s_n)(x_{n+1}-p)\right\| \\&\quad \quad +\alpha _n\left\| f(p)-\mu F(p)\right\| \\&\quad \le \alpha _n\alpha \left\| x_n-p\right\| +(1-\alpha _n\tau )s_n\left\| x_{n}-p\right\| +(1-\alpha _n\tau )(1-s_n)\left\| x_{n+1}-p\right\| \\&\quad \quad +\alpha _n\left\| f(p)-\mu F(p)\right\| , \end{aligned}$$

which implies that

$$\begin{aligned} (s_n+\alpha _n\tau (1-s_n))\left\| x_{n+1}-p\right\| \le (\alpha _n\alpha +s_n-\alpha _ns_n\tau )\left\| x_{n}-p\right\| +\alpha _n\left\| f(p)-\mu F(p)\right\| . \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} \left\| x_{n+1}-p\right\|&\le \frac{\alpha _n\alpha +s_n-\alpha _ns_n\tau }{s_n+\alpha _n\tau (1-s_n)}\left\| x_{n}-p\right\| +\frac{\alpha _n\left\| f(p)-\mu F(p)\right\| }{s_n+\alpha _n\tau (1-s_n)}\\&=\left[ 1-\frac{\alpha _n(\tau -\alpha )}{s_n+\alpha _n\tau (1-s_n)}\right] \left\| x_{n}-p\right\| +\frac{\alpha _n(\tau -\alpha )}{s_n+\alpha _n\tau (1-s_n)} \frac{\left\| f(p)-\mu F(p)\right\| }{\tau -\alpha }. \end{aligned}$$

By induction, we have

$$\begin{aligned} \left\| x_{n+1}-p\right\| \le \max \left\{ \left\| x_0-p\right\| ,\frac{\left\| f(p)-\mu F(p)\right\| }{\tau -\alpha }\right\} ,\quad \forall \, n\ge 0. \end{aligned}$$

Hence we obtain that $\{x_{n}\}$ is bounded.

Second, we prove that $\lim _{n\rightarrow \infty }\Vert x_{n+1}-x_{n}\Vert =0$. We observe that

$$\begin{aligned}&\left\| x_{n+2}-x_{n+1}\right\| \\&\quad =\Vert P_C[\alpha _{n+1}f(x_{n+1})+(I-\alpha _{n+1}\mu F)T(s_{n+1}x_{n+1}+(1-s_{n+1})x_{n+2})]\\&\qquad -P_C[\alpha _{n}f(x_{n})+(I-\alpha _n\mu F)T(s_nx_{n}+(1-s_n)x_{n+1})\Vert \\&\quad \le \Vert \alpha _{n+1}f(x_{n+1})\!-\!\alpha _{n}f(x_{n})\!+\!(I-\alpha _{n+1}\mu F)T(s_{n+1}x_{n+1}+(1-s_{n+1})x_{n+2})\\&\qquad -(I-\alpha _n\mu F)T(s_nx_{n}+(1-s_n)x_{n+1})\Vert \\&\quad =\Vert \alpha _{n+1}(f(x_{n+1})\!-f(x_n))\!+\!(I-\alpha _{n+1}\mu F)[T(s_{n+1}x_{n+1}+(1-s_{n+1})x_{n+2})\\&\qquad -T(s_nx_{n}+(1-s_n)x_{n+1})]+(\alpha _{n+1}-\alpha _n)[f(x_n)\\&\qquad -\mu FT(s_nx_{n}+(1-s_n)x_{n+1})]\Vert \\&\quad \le \alpha _{n+1}\alpha \left\| x_{n+1}-x_n\right\| +(1-\alpha _{n+1}\tau )\Vert s_{n+1}x_{n+1}+(1-s_{n+1})x_{n+2}\\&\qquad -s_nx_{n}-(1-s_n)x_{n+1}\Vert +\left| \alpha _{n+1}-\alpha _n\right| M_1,\\&\quad =\alpha _{n+1}\alpha \left\| x_{n+1}-x_n\right\| +(1-\alpha _{n+1}\tau )\Vert (1-s_{n+1})(x_{n+2}-x_{n+1})\\&\qquad +s_n(x_{n+1}-x_n)\Vert +\left| \alpha _{n+1}-\alpha _n\right| M_1,\\&\quad \le (\alpha _{n+1}\alpha +(1-\alpha _{n+1}\tau )s_n)\left\| x_{n+1}-x_n\right\| \\&\qquad +(1-\alpha _{n+1}\tau )(1-s_{n+1})\Vert x_{n+2}-x_{n+1}\Vert +\left| \alpha _{n+1}-\alpha _n\right| M_1, \end{aligned}$$

where

$$\begin{aligned} M_1=\sup _{n\ge 0}\left\| f(x_n)-\mu FT(s_nx_{n}+(1-s_n)x_{n+1})\right\| . \end{aligned}$$

This implies that

$$\begin{aligned}&\left\| x_{n+2}-x_{n+1}\right\| \nonumber \\&\quad \le \frac{\alpha _{n+1}\alpha +(1-\alpha _{n+1}\tau )s_n}{1-(1-\alpha _{n+1}\tau )(1-s_{n+1})}\left\| x_{n+1}-x_n\right\| +\frac{\left| \alpha _{n+1}-\alpha _n\right| M_1}{1-(1-\alpha _{n+1}\tau )(1-s_{n+1})}\nonumber \\&\quad =[1-\frac{\alpha _{n+1}(\tau -\alpha )+(1-\alpha _{n+1}\tau )(s_{n+1}-s_n)}{1-(1-\alpha _{n+1}\tau )(1-s_{n+1})}]\left\| x_{n+1}-x_n\right\| \nonumber \\&\qquad +\frac{M_1}{1-(1-\alpha _{n+1}\tau )(1-s_{n+1})}\left| \alpha _{n+1}-\alpha _n\right| . \end{aligned}$$

(3.2)

From condition (iii), we have

$$\begin{aligned} 0<\varepsilon \le s_n\le 1-(1-\alpha _n)(1-s_n)<1. \end{aligned}$$

It follows that

$$\begin{aligned} \frac{\alpha _{n+1}(\tau -\alpha )+(1-\alpha _{n+1}\tau )(s_{n+1}-s_n)}{1-(1-\alpha _{n+1}\tau )(1-s_{n+1})}\ge \alpha _{n+1}(\tau -\alpha ). \end{aligned}$$

By (3.2), we get that

$$\begin{aligned} \left\| x_{n+2}-x_{n+1}\right\| \le [1-\alpha _{n+1}(\tau -\alpha )]\left\| x_{n+1}-x_n\right\| +\frac{M_1}{\varepsilon }\left| \alpha _{n+1}-\alpha _n\right| . \end{aligned}$$

From condition (ii) and Lemma 2.1, we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_{n+1}-x_{n}\Vert =0. \end{aligned}$$

(3.3)

It follows from condition (i) and (3.3) that

$$\begin{aligned}&\left\| x_n-Tx_n\right\| \nonumber \\&\quad =\left\| x_n-P_CTx_n\right\| \nonumber \\&\quad \le \left\| x_n-x_{n+1}\right\| +\left\| x_{n+1}-P_CTx_n\right\| \nonumber \\&\quad =\left\| x_n-x_{n+1}\right\| +\Vert P_C[\alpha _{n}f(x_{n})+(I-\alpha _n\mu F)T(s_nx_{n}+(1-s_n)x_{n+1})]\nonumber \\&\qquad -P_CTx_n\Vert \nonumber \\&\quad \le \left\| x_n-x_{n+1}\right\| +\alpha _n\left\| f(x_n)-\mu FT(s_nx_{n}+(1-s_n)x_{n+1})\right\| \nonumber \\&\qquad +\left\| T(s_nx_{n}+(1-s_n)x_{n+1})-Tx_n\right\| \nonumber \\&\quad \le \left\| x_n-x_{n+1}\right\| +\alpha _n\left\| f(x_n)-\mu FT(s_nx_{n}+(1-s_n)x_{n+1})\right\| \nonumber \\&\qquad +(1-s_n)\left\| x_n-x_{n+1}\right\| \nonumber \\&\quad =(2-s_n)\left\| x_n-x_{n+1}\right\| +\alpha _n\left\| f(x_n)-\mu FT(s_nx_{n}+(1-s_n)x_{n+1})\right\| \nonumber \\&\quad \rightarrow 0\text { as }n\rightarrow \infty . \end{aligned}$$

(3.4)

Third, we show that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\left<f(q)-\mu F(q),x_{n}-q\right>\le 0, \end{aligned}$$

(3.5)

where $q=P_{F(T)}(f+I-\mu F)(q)$. Indeed, there exists a subsequence $\{x_{n_i}\}$ of $\{x_{n}\}$, such that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\left<f(q)-\mu F(q),x_{n}-q\right>=\lim _{i\rightarrow \infty }\left<f(q)-\mu F(q),x_{n_i}-q\right>. \end{aligned}$$

Now, we prove that $P_{F(T)}(f+I-\mu F)$ is a contractive mapping. In fact, for any $x,y\in C$, by Lemma 2.3, we have

$$\begin{aligned}&\left\| P_{F(T)}(f+I-\mu F)(x)-P_{F(T)}(f+I-\mu F)(y)\right\| \\&\quad \le \left\| f(x)-f(y)\right\| +\left\| (I-\mu F)(x)-(I-\mu F)(y)\right\| \\&\quad \le \alpha \left\| x-y\right\| +(1-\tau )\left\| x-y\right\| \\&\quad =[1-(\tau -\alpha )]\left\| x-y\right\| , \end{aligned}$$

which implies that $P_{F(T)}(f+I-\mu F)$ is a contractive mapping. Banach’s Contraction Mapping Principle guarantees that $P_{F(T)}(f+I-\mu F)$ has a unique fixed point. Say $q\in C$, that is, $q=P_{F(T)}(f+I-\mu F)(q)$. Since $\left\{ x_n\right\}$ is a bounded in C, without loss of generality, we can assume that $x_{n_i}\rightharpoonup z\in C$. From (3.4) and Lemma 2.2, we have $z\in F(T)$. Then, it follows from (2.3) that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\left<f(q)-\mu F(q),x_{n}-q\right>&=\lim _{i\rightarrow \infty }\left<f(q)-\mu F(q),x_{n_i}-q\right>\\&=\left<f(q)-\mu F(q),z-q\right>\le 0, \end{aligned}$$

which implies that (3.5) holds. By (3.3), we obtain that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\left<f(q)-\mu F(q),x_{n+1}-q\right>\le 0, \end{aligned}$$

(3.6)

Finally, we prove that $x_n\rightarrow q$ as $n\rightarrow \infty$. Put $y_n=\alpha _{n}f(x_{n})+(I-\alpha _n\mu F)T(s_nx_{n}+(1-s_n)x_{n+1})$. Then, $x_{n+1}=P_Cy_n$. By (2.3) and (3.1), we have

$$\begin{aligned}&\left\| x_{n+1}-q\right\| ^2\\&\quad =\left<x_{n+1}-y_n,x_{n+1}-q\right>+\left<y_n-q,x_{n+1}-q\right>\\&\quad \le \left<y_n-q,x_{n+1}-q\right>\\&\quad =\left<\alpha _{n}f(x_{n})+(I-\alpha _n\mu F)T(s_nx_{n}+(1-s_n)x_{n+1})-q,x_{n+1}-q\right>\\&\quad =\alpha _n\left<f(x_n)-\mu F(q),x_{n+1}-q\right>\\&\quad \quad +\left<(I-\alpha _n\mu F)(T(s_nx_{n}+(1-s_n)x_{n+1})-q),x_{n+1}-q\right>\\&\quad =\alpha _n\left<f(x_n)-f(q),x_{n+1}-q\right>\\&\quad \quad +\left<(I-\alpha _n\mu F)(T(s_nx_{n}+(1-s_n)x_{n+1})-q),x_{n+1}-q\right>\\&\qquad +\alpha _n\left<f(q)-\mu F(q),x_{n+1}-q\right>\\&\quad \le \alpha _n\alpha \left\| x_n-q\right\| \left\| x_{n+1}-q\right\| \\&\quad \quad +(1-\alpha _n\tau )\left\| s_n(x_n-q)+(1-s_n)(x_{n+1}-q)\right\| \left\| x_{n+1}-q\right\| \\&\qquad +\alpha _n\left<f(q)-\mu F(q),x_{n+1}-q\right>\\&\quad \le (\alpha _n\alpha +(1-\alpha _n\tau )s_n)\left\| x_n-q\right\| \left\| x_{n+1}-q\right\| \\&\quad \quad +(1-\alpha _n\tau )(1-s_n)\left\| x_{n+1}-q\right\| ^2+\alpha _n\left<f(q)-\mu F(q),x_{n+1}-q\right>\\&\quad \le \frac{\alpha _n\alpha +(1-\alpha _n\tau )s_n}{2}\left\| x_n-q\right\| ^2\\&\quad \quad +\frac{\alpha _n\alpha +(1-\alpha _n\tau )s_n+2(1-\alpha _n\tau )(1-s_n)}{2}\left\| x_{n+1}-q\right\| ^2\\&\qquad +\alpha _n\left<f(q)-\mu F(q),x_{n+1}-q\right>,\\ \end{aligned}$$

which implies that

$$\begin{aligned} \frac{\alpha _n(2\tau -\alpha )+s_n(1-\alpha _n\tau )}{2}\left\| x_{n+1}-q\right\| ^2\le & {} \frac{\alpha _n\alpha +(1-\alpha _n\tau )s_n}{2}\left\| x_n-q\right\| ^2\\&+\alpha _n\left<f(q)-\mu F(q),x_{n+1}-q\right>. \end{aligned}$$

It follows that

$$\begin{aligned}&\left\| x_{n+1}-q\right\| ^2\nonumber \\&\quad \le \frac{\alpha _n\alpha +(1-\alpha _n\tau )s_n}{\alpha _n(2\tau -\alpha )+s_n(1-\alpha _n\tau )}\left\| x_n-q\right\| ^2+\frac{\alpha _n\left<f(q)-\mu F(q),x_{n+1}-q\right>}{\alpha _n(2\tau -\alpha )+s_n(1-\alpha _n\tau )}\nonumber \\&\quad =\left[ 1-\frac{2\alpha _n(\tau -\alpha )}{\alpha _n(2\tau -\alpha )+s_n(1-\alpha _n\tau )}\right] \left\| x_n-q\right\| ^2\nonumber \\&\qquad +\frac{2\alpha _n(\tau -\alpha )}{\alpha _n(2\tau -\alpha )+s_n(1-\alpha _n\tau )}\frac{\left<f(q)-\mu F(q),x_{n+1}-q\right>}{\tau -\alpha }. \end{aligned}$$

(3.7)

We note that

$$\begin{aligned} \frac{2\alpha _n(\tau -\alpha )}{\alpha _n(2\tau -\alpha )+s_n(1-\alpha _n\tau )}&\ge \frac{2\alpha _n(\tau -\alpha )}{\alpha _n(2\tau -\alpha )+(1-\alpha _n\tau )}\\&=\frac{2\alpha _n(\tau -\alpha )}{1+\alpha _n(\tau -\alpha )}\\&\ge \frac{2(\tau -\alpha )}{1+\tau -\alpha }\alpha _n. \end{aligned}$$

Apply Lemma 2.1 to (3.7), we conclude that $x_n\rightarrow q$ as $n\rightarrow \infty$. This finishes the proof. $\square$

The following results can be obtained by Theorem 3.1 easily, we omit the details.

Theorem 3.2

Let C be a nonempty closed convex subset of a real Hilbert space H. Let $T:C\rightarrow C$ be a nonexpansive mapping with $F(T)\ne \emptyset$ and $f:C\rightarrow C$ be a strict contraction with coefficient $\alpha \in [0,1)$. Let $F:C\rightarrow H$ be k-Lipschitzian and $\eta$-strongly monotone with constants $k,\eta >0$, such that $\alpha <\tau$ and $0<\mu <\frac{2\eta }{k^2}$, where $\tau =1-\sqrt{1-\mu (2\eta -\mu k^2)}\in (0,1]$. For arbitrarily given $x_{0}\in C$, let $\left\{ x_{n}\right\}$ be a sequence generated by

$$\begin{aligned} x_{n+1}=P_C\left[ \alpha _{n}f(x_{n})+(I-\alpha _n\mu F)T\left( \frac{x_{n}+x_{n+1}}{2}\right) \right] , \end{aligned}$$

(3.8)

where $\{\alpha _{n}\}$ is a sequence in (0, 1] satisfying the following conditions:

• (i) $\lim _{n\rightarrow \infty }\alpha _{n}=0$;

• (ii) $\sum _{n=0}^{\infty }\alpha _{n}=\infty$ and $\sum _{n=0}^{\infty }\left| \alpha _{n+1}-\alpha _n\right| <\infty$. Then, $\left\{ x_{n}\right\}$ converges strongly to a fixed point $q\in F(T)$, which also solves the variational inequality:

  $$\begin{aligned} \left<f(q)-\mu F(q),y-q\right>\le 0,\text { for all } y\in F(T). \end{aligned}$$

Theorem 3.3

Let C be a nonempty closed convex subset of a real Hilbert space H. Let $T:C\rightarrow C$ be a nonexpansive mapping with $F(T)\ne \emptyset$ and $f:C\rightarrow C$ a strict contraction with coefficient $\alpha \in [0,1)$. Let $A:C\rightarrow H$ be a strongly positive bounded linear operator with a constant $\gamma >0$, such that $\alpha <\tau$ and $0<\mu <\frac{2\gamma }{\left\| A\right\| ^2}$, where $\tau =1-\sqrt{1-\mu (2\gamma -\mu \left\| A\right\| ^2)}\in (0,1]$. For arbitrarily given $x_{0}\in C$, let $\left\{ x_{n}\right\}$ be a sequence generated by

$$\begin{aligned} x_{n+1}=P_C[\alpha _{n}f(x_{n})+(I-\alpha _n\mu A)T(s_nx_{n}+(1-s_n)x_{n+1})], \end{aligned}$$

(3.9)

where $\{\alpha _{n}\}$ and $\{s_{n}\}$ are two sequences in (0, 1] satisfying the following conditions:

• (i) $\lim _{n\rightarrow \infty }\alpha _{n}=0$;

• (ii) $\sum _{n=0}^{\infty }\alpha _{n}=\infty$ and $\sum _{n=0}^{\infty }\left| \alpha _{n+1}-\alpha _n\right| <\infty$;

• (iii) $0<\varepsilon \le s_n\le s_{n+1}<1$ for all $n\ge 0$. Then, $\left\{ x_{n}\right\}$ converges strongly to a fixed point $q\in F(T)$, which also solves the variational inequality:

  $$\begin{aligned} \left<f(q)-\mu A(q),y-q\right>\le 0,\text { for all } y\in F(T). \end{aligned}$$

4 Applications

In this section, we discuss some of the applications of our scheme.

4.1 Application to strict pseudocontractive mappings

A mapping $T:C\rightarrow H$ is called a k-strict pseudo-contraction if there exists a constant $k\in [0,1)$, such that

$$\begin{aligned} \left\| Tx-Ty\right\| ^2\le \left\| x-y\right\| ^2+k\left\| (I-T)x-(I-T)y\right\| ^2\text { for all }x,y\in C.\nonumber \\ \end{aligned}$$

(4.1)

Lemma 4.1

([21]). Let $T:C\rightarrow H$ be a k-strict pseudo-contraction with $F(T)\ne \emptyset$. Then, $F(P_CT)=F(T)$.

Lemma 4.2

([21]). Let $T:C\rightarrow H$ be a k-strict pseudo-contraction. Define $S:C\rightarrow H$ by $Sx=\delta x+(1-\delta )Tx$ for each $x\in C$. Then, as $\delta \in [k,1)$, S is nonexpansive, such that $F(S)=F(T)$.

Theorem 4.3

Let C be a nonempty closed convex subset of a real Hilbert space H. Let $T:C\rightarrow H$ be a $\nu$-strict pseudo-contraction with $F(T)\ne \emptyset$ and $f:C\rightarrow C$ a strict contraction with coefficient $\alpha \in [0,1)$. Let $F:C\rightarrow H$ be k-Lipschitzian and $\eta$-strongly monotone with constants $k,\eta >0$, such that $\alpha <\tau$ and $0<\mu <\frac{2\eta }{k^2}$, where $\tau =1-\sqrt{1-\mu (2\eta -\mu k^2)}\in (0,1]$. For arbitrarily given $x_{0}\in C$, let $\left\{ x_{n}\right\}$ be a sequence generated by

$$\begin{aligned} x_{n+1}= & {} P_C[\alpha _{n}f(x_{n})+(I-\alpha _n\mu F)P_C(\delta I+(1-\delta )T)\nonumber \\&\times (s_nx_{n}+(1-s_n)x_{n+1})], \end{aligned}$$

(4.2)

where $\delta \in [\nu ,1)$, $\{\alpha _{n}\}$, and $\{s_{n}\}$ are two sequences in (0, 1] satisfying the following conditions:

• (i) $\lim _{n\rightarrow \infty }\alpha _{n}=0$;

• (ii) $\sum _{n=0}^{\infty }\alpha _{n}=\infty$ and $\sum _{n=0}^{\infty }\left| \alpha _{n+1}-\alpha _n\right| <\infty$;

• (iii) $0<\varepsilon \le s_n\le s_{n+1}<1$ for all $n\ge 0$. Then, $\left\{ x_{n}\right\}$ converges strongly to a fixed point $q\in F(T)$, which also solves the variational inequality:

  $$\begin{aligned} \left<f(q)-\mu F(q),y-q\right>\le 0,\text { for all } y\in F(T). \end{aligned}$$

Proof

Define $S:C\rightarrow H$ by $Sx=\delta x+(1-\delta )Tx$ for each $x\in C$. Then, we can rewrite (4.2) as follows:

$$\begin{aligned} x_{n+1}=P_C[\alpha _{n}f(x_{n})+(I-\alpha _n\mu F)P_CS(s_nx_{n}+(1-s_n)x_{n+1})]. \end{aligned}$$

By Lemmas 4.1 and 4.2, we have $F(T)=F(P_CS)$. Therefore, we obtain the desired results by Theorem 3.1 immediately. $\square$

4.2 Application to equilibrium problems in Hilbert spaces

Let $\phi :C\times C\rightarrow \mathbb {R}$ be a bifunction, where $\mathbb {R}$ is the set of real numbers. The equilibrium problem for the function $\phi$ is to find a point $x\in C$ satisfying

$$\begin{aligned} \phi (x,y)\ge 0\quad \text{ for } \text{ all }\,y\in C. \end{aligned}$$

(4.3)

The set of solutions of (4.3) is denoted by $EP(\phi )$. It is well known that equilibrium problem contains fixed-point problems, variational inequality problems, and optimization problems as its special cases (see, Blum and Oetti [4]).

For solving the equilibrium problem, we assume that the bifunction $\phi$ satisfies the following conditions (see [4]):

• (A1) $\phi (x,x)=0$ for all $x\in C$;

• (A2) $\phi$ is monotone, i.e., $\phi (x,y)+\phi (y,x)\le 0$ for any $x,y\in C$;

• (A3) $\phi$ is upper-hemicontinuous, i.e., for each $x,y,z\in C$

  $$\begin{aligned} \limsup _{t\rightarrow 0^+}\phi (tz+(1-t)x,y)\le \phi (x,y); \end{aligned}$$

• (A4) $\phi (x,.)$ is convex and weakly lower semicontinuous for each $x\in C$.

Lemma 4.4

([4]). Let C be a nonempty closed convex subset of H and let $\phi$ be a bifunction of $C\times C$ into $\mathbb {R}$ satisfying (A1)-(A4). Let $r>0$ and $x\in H$. Then, there exists $z\in C$, such that

$$\begin{aligned} \phi (z,y)+\frac{1}{r}\left<y-z,z-x\right>\ge 0\quad \text{ for } \text{ all } \,y\in C. \end{aligned}$$

Lemma 4.5

([22]). Assume that $\phi :C\times C\rightarrow \mathbb {R}$ satisfies (A1)–(A4). For $r>0$ and $x\in H$, define a mapping $T_r:H\rightarrow C$ as follows:

$$\begin{aligned} T_r(x)=\left\{ z\in C:\phi (z,y)+\frac{1}{r}\left<y-z,z-x\right>\ge 0 \quad \forall \, y\in C\right\} \end{aligned}$$

for all $z\in H$. Then, the following holds:

• (1) $T_r$ is single-valued;

• (2) $T_r$ is firmly nonexpansive,i.e., for any $x,y\in H$, $\left\| T_rx-T_ry\right\| ^2\le \left<T_rx-T_ry,x-y\right>$. This implies that $\left\| T_rx-T_ry\right\| \le \left\| x-y\right\| ,\quad \forall \, x,y\in H$, i.e., $T_r$ is a nonexpansive mapping;

• (3) $F(T_r)=EP(\phi ),\quad \forall \, r>0$;

• (4) $EP(\phi )$ is a closed and convex set.

A mapping T is called to be attracting nonexpansive if it is nonexpansive and satisfies:

$$\begin{aligned} \left\| Tx-p\right\| <\left\| x-p\right\| \text { for all }x\notin \text {F(T) and }p\in \text {F(T)}. \end{aligned}$$

Lemma 4.6

([23]). Suppose that E is strictly convex, $T_1$ an attracting nonexpansive, and $T_2$ a nonexpansive mapping which have a common fixed point. Then, we have $F(T_1T_2)=F(T_2T_1)=F(T_1)\cap F(T_2)$.

Theorem 4.7

Let C be a nonempty closed convex subset of a real Hilbert space H. Let $\phi _i:C\times C\rightarrow \mathbb {R}$ be a bifunction satisfying the conditions (A1)–(A4), where $i\in \left\{ 1,2,\ldots ,M\right\}$ and M is a positive integer. Let $T:C\rightarrow C$ be a nonexpansive mapping with $\Omega =F(T)\cap \cap _{i=1}^MEP(\phi _i)\ne \emptyset$ and $f:C\rightarrow C$ a strict contraction with coefficient $\alpha \in [0,1)$. Let $F:C\rightarrow H$ be k-Lipschitzian and $\eta$-strongly monotone with constants $k,\eta >0$, such that $\alpha <\tau$ and $0<\mu <\frac{2\eta }{k^2}$, where $\tau =1-\sqrt{1-\mu (2\eta -\mu k^2)}\in (0,1]$. For arbitrarily given $x_{0}\in C$, let $\left\{ x_{n}\right\}$ be a sequence generated by

$$\begin{aligned} x_{n+1}= & {} P_C[\alpha _{n}f(x_{n})+(I-\alpha _n\mu F)TT_{r_M}T_{r_{M-1}}\cdots \nonumber \\&T_{r_1}(s_nx_{n}+(1-s_n)x_{n+1})], \end{aligned}$$

(4.4)

where $r_i>0$, $i\in \left\{ 1,2,\ldots ,M\right\}$; $\{\alpha _{n}\}$ and $\{s_{n}\}$ are two sequences in (0, 1] satisfying the following conditions:

• (i) $\lim _{n\rightarrow \infty }\alpha _{n}=0$;

• (ii) $\sum _{n=0}^{\infty }\alpha _{n}=\infty$ and $\sum _{n=0}^{\infty }\left| \alpha _{n+1}-\alpha _n\right| <\infty$;

• (iii) $0<\varepsilon \le s_n\le s_{n+1}<1$ for all $n\ge 0$. Then, $\left\{ x_{n}\right\}$ converges strongly to a fixed point $q\in \Omega$, which also solves the variational inequality:

  $$\begin{aligned} \left<f(q)-\mu F(q),y-q\right>\le 0,\text { for all } y\in \Omega . \end{aligned}$$

Proof

By Lemma 4.4, we have that $T_{r_i}$ is firmly nonexpansive. Moreover, we prove that $T_{r_i}$ is attracting nonexpansive. Indeed, For all $x\notin F(T_{r_i})$ and $y\in F(T_{r_i})$, we observe

$$\begin{aligned} \left\| T_{r_i}x-T_{r_i}y\right\| ^2&\le \left<T_{r_i}x-T_{r_i}y,x-y\right>\\&=\frac{1}{2}[\left\| T_{r_i}x-T_{r_i}y\right\| ^2+\left\| x-y\right\| ^2-\left\| T_{r_i}x-x\right\| ^2], \end{aligned}$$

which implies that

$$\begin{aligned} \left\| T_{r_i}x-T_{r_i}y\right\| ^2&\le \left\| x-y\right\| ^2-\left\| T_{r_i}x-x\right\| ^2\\&<\left\| x-y\right\| ^2. \end{aligned}$$

Therefore, $T_{r_i}$ is attracting nonexpansive. It follows from Lemma 4.5 that

$$\begin{aligned} F(TT_{r_M}T_{r_{M-1}}\cdots T_{r_1})=F(T)\cap \cap _{i=1}^MEP(\phi _i)=\Omega . \end{aligned}$$

Therefore, we obtain the desired result by Theorem 3.1 easily. This finishes the proof. $\square$

5 Numerical Examples

Fig. 1

Two dimension

Fig. 2

Three dimension

Example 5.1

We define the inner product $<\cdot ,\cdot >:\mathbb {R}^3\times \mathbb {R}^3\rightarrow \mathbb {R}$ by

$$\begin{aligned} \left<\mathbf x ,\mathbf y \right>=\mathbf x \cdot \mathbf y =x_1\cdot y_1+x_2\cdot y_2+x_3\cdot y_3 \end{aligned}$$

and the usual norm $\left\| \cdot \right\| :\mathbb {R}^3\rightarrow \mathbb {R}$ is defined by

$$\begin{aligned} \left\| \mathbf x \right\| =\sqrt{x_1^2+y_1^2+z_1^2},\quad \forall \, \mathbf x =(x_1,x_2,x_3),\, \mathbf y =(y_1,y_2,y_3)\in \mathbb {R}^3. \end{aligned}$$

Let $F,T,f:\mathbb {R}^3\rightarrow \mathbb {R}^3$ be defined by

$$\begin{aligned} F\mathbf x =\mathbf x ,\, T\mathbf x =\frac{1}{2}{} \mathbf x ,\, f(\mathbf x )=\frac{1}{4}{} \mathbf x ,\quad \forall \, x\in \mathbb {R}. \end{aligned}$$

Let

$$\begin{aligned} \alpha _n=\frac{1}{2n},\ s_n=\frac{1}{2},\quad \forall \, n\in \mathbb {N} \end{aligned}$$

and let $\left\{ x_n\right\}$ be a sequence generated by (3.1). It is easy to see that F is 1-Lipschitzian and 1-strongly monotone. Then, we can set $\mu =1$, it follows that $\tau =1$. It is easy to see that all conditions of Theorem 3.1 hold.

We can rewrite (3.1) as follows:

$$\begin{aligned} \mathbf x _{n+1}=\frac{2n}{6n+1}{} \mathbf x _n. \end{aligned}$$

(5.1)

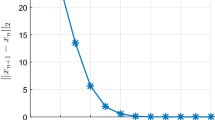
Choosing $\mathbf x _1=(1,2,4)$ in (5.1), we have the following numerical result in Figs. 1 and 2.

Example 5.2

Suppose that $C=H = L^2([0,1])$ with norm $\Vert x\Vert :=\left( \int _0^1 |x(t)|^2\mathrm{d}t\right) ^{\frac{1}{2}}$ and inner product $\langle x,y\rangle := \int _0^1 x(t)y(t)\mathrm{d}t,~~x,y \in H$. Let us define

$$\begin{aligned} Tx(t) = cos(x(t)) \quad \text {and}\quad Fx(t)=\frac{1}{t+1}x(t),~~t \in [0,1]. \end{aligned}$$

Table 1 Algorithm (5.2) with different cases

Fig. 3

Case I

Fig. 4

Case II

Then, it can be shown that T is a nonexpansive mapping and that F is $\frac{1}{2}$-strongly monotone and 1-Lipschitz continuous on C. Therefore, $F(T)\ne \emptyset$ and from Theorem 3.1, we have $k=1$ and $\eta =\frac{1}{2}$. We choose $\mu =\frac{1}{2}$. Then, it is clear that $0<\mu <\frac{2\eta }{k^2}$ and $\tau =1-\sqrt{1-\mu (2\eta -\mu k^2)}=1-\sqrt{\frac{3}{4}}$. Suppose that $\alpha _n:=\frac{1}{n+1},~~s_n:=\frac{n}{2(n+1)}$ and $f(x):=\frac{1}{4}x,~~x \in C$. Then, $\alpha :=\frac{1}{4}$, and it is clear that $\alpha =\frac{1}{4}<1-\sqrt{\frac{3}{4}}=\tau$. Therefore, all the conditions in Theorem 3.1 are satisfied and our Algorithm (3.1) becomes

$$\begin{aligned} x_{n+1}=\frac{1}{4(n+1)}x_n+\left( I-\frac{1}{2(n+1)} F\right) T\left( \frac{n}{2(n+1)}x_{n}+\left( 1-\frac{n}{2(n+1)}\right) x_{n+1}\right) . \end{aligned}$$

(5.2)

We choose different starting point $x_0(t)$ with stopping criterion $||x_{n+1}-x_n||<\varepsilon$ with $\varepsilon =10^{-2}$. The results are presented in Table 1 and Figs. 3 and 4.

Case I $x_1(t)=\frac{1}{50}e^{20t}$.

Case II $x_1(t)=\frac{1}{40}t^2+\frac{e^{-30t}}{40}$.