Abstract
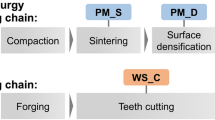
In gear production, resource efficiency considering material, energy and time can be achieved using a powder metallurgical process chain. Furthermore, powder metallurgical gears have a lower weight, which will improve the fuel efficiency of a gear box as well. Currently powder metallurgical gears are not used in series-production automobile gear boxes. The main reason for this is a lower expected tooth root fatigue strength, which can be increased using surface densification by rolling. The investigation of how the powder metallurgical (PM) gear manufacturing has to improve in order to gain the possible resource efficiency, is funded in the Priority Program "Resource efficient machine elements”. This paper considers a two-step approach to increase the tooth root fatigue strength of PM gears. The first step is to calculate the fatigue strength considering the density profile of the gear. This first step will result in a description of the optimal density profile. The second step is an investigation of how the density profile and the manufacturing properties can be influenced using different process designs. This step will result in a guideline to change the density profile to the one described in the first step. The combined knowledge of which density profile is necessary and how it can be achieved will give the chance to increase the tooth root fatigue strength of powder metallurgical gears. This paper considers the first part of both steps of the approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Using powder metallurgical (PM) process chain offers several benefits in comparison to the conventional one. By powder pressing, the areas of the gear with very low stresses can be substituted by free spaces. Additionally, the remaining volume has a lower density due to pores which are caused by manufacturing. Hence, the produced gears have a lower material consumption [1] and a lower weight. Furthermore, Strehl showed that the powder metallurgical production chain offers up to 20 % cost reduction potential [16].
Due to the porosity, PM gears have a lower Young’s modulus, Poisson ratio and strength [2]. As gears are mainly stressed at the surface, the near surface porosity is the main problem for the gears strength. A high improvement of the fatigue strength is possible by surface densification [11, 12, 15]. However, due to remaining doubts in their strength, PM gears are not used in series production of automobile gear boxes. In this paper, the surface densification by rolling is investigated. The increase of the tooth root fatigue strength of PM gears is considered with a two way approach. The necessary surface densification for the application and the way to achieve this densification by rolling are investigated.
The first part of this paper presents the first step of the approach, which seems to be suitable to predict the tooth root fatigue strength using only fatigue data of laboratory specimens and allows to derive information about an optimal density profile. In order to investigate the fatigue behavior of a surface densified powder metallurgical gear, the density and the highly loaded volume have to be investigated and described mathematically. The used material is Astaloy 85 Mo, see Table 1.
The second part of this paper evaluates the densification process by rolling. Surface densification by rolling is mostly performed with two gear shaped tools [7, 10, 14], see Fig. 1. The tools apply a load on the PM gear which leads to the densification of the stock. One part of the displaced material flows normally into the gear and leads to a densification. The other part flows tangentially. This leads to an increase of the tip diameter and to defects such as profile deviations and overlaps [17] on the surface. In order to improve the strength of PM gears, defects have to be avoided and a densification has to be achieved which is appropriate for the application.
All calculations on gears are made for the same gear geometry: The gear has \(z_2=27\) teeth, a helix angle of \(b=0^{\circ }\), a pressure angle of \(a=20^{\circ }\), a module of \(m=2.0\hbox { mm}\), a thickness of 14 mm and an addendum modification of \(x_2=-0.2\hbox { mm}\).
2 Fatigue strength and size effect
2.1 Wöhler fatigue tests and regression analysis
As a matter of principle, sinter metals are afflicted with pores; with regard to the components fatigue behavior, these pores are defects. By an enlargement of the stress exposed volume, the possibility of critical defects in this volume increases, thus reducing the locally endurable stress amplitude (size effect). For the numerical determination of the stress exposed volume, the highly loaded volume \(V_{90}\) (HLV) is used, which is the amount of volume, that is exposed to a minimum of 90 % of the maximum occurring first principal stress peak \(\sigma _{Imax}\). For the mathematical description of the size effect and the density dependence, the modified 3-parameter Weibull distribution is used, Eq. 1. For a detailed explanation of the fatigue strength assessment of sintered steels see Zafari and Beiss [4, 19].
In Eq. 1 the coefficients \(\varDelta \sigma _{A0}, \sigma _{A0\textit{ref}}, m\) and \(n\) have to be determined in a nonlinear least squares regression analysis (see Table 3 for explanation). For the necessary experimental data points, nine Wöhler fatigue tests have been carried out, each based on at least 25 specimens in the transition zone. Each influencing variable (size effect and density) is evaluated on the basis of three supporting points, Table 2. The specimens have been compacted with target density values of 7.0 and \(7.35\hbox { g}\hbox { cm}^{-3}\) . Half of the 7.35-specimens are compacted to full density by hot isostatic pressing. After sintering at \(1,120\,^{\circ }\hbox {C}\) for 20 min, the specimens have been austenitized at \(870\,^{\circ }\hbox {C}\) and quenched at 80 °C. The resulting coefficients are summarized in Table 3. Figure 2 presents Eq. 1 visually in a three dimensional plot.
Three dimensional plot of the fatigue strength of Astaloy 85 Mo with 0.25 % C according to Eq. 1
2.2 Finite element analysis
For the determination of the highly loaded volume—for the laboratory specimens and the gear—the finite element analysis is used. The model of the gear is build up by the use of symmetry constraints, to reduce computational costs, and a very fine meshing in the highly loaded zone. The characteristic element length in the tooth root region is down to ca. \(50\,\upmu \hbox {m}\), this is necessary to meet convergence criteria. The boundary conditions are modeled close to the arrangements in the pulsator, in which the gear will be tested. The applied load is a unit force of 1 N.
The density dependence of the Young’s Modulus is implemented in the material definition using the function \(E(\rho )=E_0 \cdot \left( \rho / \rho _0 \right) ^{3.52}\). The Young’s Modulus is changing with the surface distance; it is implemented according to the density gradient shown in Fig. 3. For the Young’s modulus \(E_0\) the value of full density material 210,000 \(\hbox { N }\hbox {mm}^{2}\) is set and the Poisson’s ratio \(\mu\) is set to a constant value of 0.27. [3]
2.3 Prediction of the fatigue strength of surface densified gears
Using the finite element analysis, the highly loded volume of the gear has been determined. The densification in the manufacturing process in the tooth root surface changes the value of the highly loaded volume, a fact, that is easily explained by visualizing the gradients of the first principle stresses over the surface distance, Fig. 4. The gear without the surface densification shows a lower stress peak in the surface and a gradient more plainly compared to the densified gear.
The finite element analysis of the gear with a constant density value in surface and core, shows a highly loaded volume of \(V_{90}=0.532\hbox { mm}^{3}\). The highly loaded volume of the surface densified gear adds up to a value of \(0.448\hbox { mm}^{3}\) reaching a depth of almost 0.05 mm, Fig. 5.
For the prediciton of the fatigue strength of the gear, Eq. 1 is used with the surface density of \(7.8\hbox { g }\hbox {cm}^{-3}\) (rounded down for safety purposes) and the highly loaded volume of the densified gear (Fig. 5) as input parameter. The coefficients of the equation have been determined as described in the previous chapter.
Figure 6 visualizes the fatigue strength according to Eq. 1 in a two dimensional plot, evaluated for both highly loaded volumes—the gear of a constant density and the surface densified gear. Figure 3 shows the density gradient and the depth of the highly loaded volume (including a factor of safety) in comparison. It is essential, that the zone of fully densified material reaches a higher depth than the highly stressed volume in the tooth root surface.
3 Geometry-independent description of densification rolling
In this section the densification process is investigated on a geometry-independent level. In order to do a geometry–independent investigation of the material flow, there are several steps which have to be performed:
-
The process conditions have to be analyzed and abstracted.
-
A simulation for the investigation has to be set-up.
-
The process results have to be analyzed.
-
A model has to be derived for calculating the material flow.
The first three steps will be discussed in this paper.
3.1 Process analysis
The contact of a gear with a rolling tool is shown in Fig. 7. The contact on the left is a convex-convex contact. On the right the concave tooth root of the workpiece is in contact with the convex tool tip. On top of Fig. 7 the resulting contact radiuses are shown. Due to the variable contact radiuses along the tooth height of both, tool and workpiece, the combinations of contact radiuses change continuously during the process.
Beside the contact geometries, the contact is defined also by the contact kinematics, eg. the slip. Considering the tangent of the contact point of tool and workpiece, the tangential velocities \(v_t\) can be derived of the rotational velocities and hence the slip \(s\) can be calculated by Eq. 2.
In order to evaluate the slip in the rolling process a contact analysis has been developed. Input to this contact analysis is the tool and workpiece geometry in rolling contact. In the contact analysis the gear is rolled by the tool, as shown in Fig. 8, and the slip is calculated incrementally. This is a two-flank contact of tool and workpiece with contact in tooth root. Due to these conditions no conventional contact analysis or the calculation according to DIN 3960 [5] can be used.
The contact analysis was used for the evaluation of two processes. In top of Fig. 9 the target geometry and the blank geometry of the gear are shown. The blank geometry has a positive allowance on flank and root and a negative allowance on the tip. The positive allowance provides material for the densification. The negative allowance gives space for the expected tip increase [9].
An overview of possibilities in tool design is given in [11]. It showed that the addendum modification of the tool is the main influencing parameter with a given gear geometry. Hence in this work, the evaluated tools have \(z_0=79\) teeth and different addendum modifications of \(x_{0A}=-0.70\) or \(x_{0B}=1.28\). The differences of the tool teeth are shown in top right of Fig. 9. The teeth have the same height from tip to root. However the tools have different diameters. The form of the teeth is different especially by the tip curvature were the dark plotted tool A is much more rounded with a tip radius of \(r_{tA}=2.0\hbox { mm}\) than the light plotted tool B with a tip radius of \(r_{tB}=1.4\hbox { mm}\).
The slip of these tools with the workpiece is shown in bottom of Fig. 9. On the gear flank, the slip is negative at the tip and positive near the tooth root. The rolling circle \((s=0\,\%)\) is moved to the tip with decreasing addendum modification of the tool. In the area were the convex flank merges into the concave root, the slip is considerably increased. This is due to the very steep tangent and the resulting very low tangential velocity of the gear. According to Eq. 2, the slip increases considerably. This is in agreement with the high deformation of the microstructure which was documented by Kauffmann [9]. The difference of the two tools considering the slip is foremost a longer area of negative slip for the tool with a negative addendum modification, which could indicate a lower tangential material flow to the top than to the root. With this contact analysis it is possible to analyze different process designs considering their contact conditions.
3.2 Simulation set-up
In order to do a geometrical-independent investigation on material flow in densification rolling of gears, the geometrical and kinematical analysis is used to set the boundary conditions of the experimental and simulative investigations. The geometrical-independent analogy of cylinder rolling is used. As seen in Fig. 7 there are concave-convex and convex-convex contacts in gear rolling. Hence, internal and external cylinder rolling has to be considered.
Using the analogy of cylinder rolling has several benefits in opposite to gear rolling. In gear rolling, both, the slip and the contact radius are changing constantly during the process and they are both depending on the tool and workpiece geometry. There is no way to find a general relation from the contact geometries to the resulted material flow. In cylinder rolling, both parameters can be kept constant. Therefore, all parameters can be changed independently from each other.
The used material model was developed and validated by Kauffmann [9]. The validation was repeated in this project with the investigated geometry again, which showed very good compliance. The used friction model is the shear stress model, as this process is a deforming process with high normal contact stresses [6, 8]. The friction changes due to contact conditions [13, 18].
The simulations, set up as described above, have to be evaluated concerning their material flow. The material flows normally—which results in the densification—and tangentially. One investigated value is the increase of the densification depth in comparison to the densification before the tool contact. According to Kaufmann [9] the densification depth \(t_{di}\) is defined as the depth where the relative density falls below the value of \(i\). The tangential material flow has to be evaluated as well: A straight line in the beginning of the process deforms during the process as shown in Fig. 10. This deformation is due to the tangential material flow and is described in this work by the angle of the deformed line to the surface the flow angle. The flow angle is between \(0^{\circ }\) and \(90^{\circ }\).
In order to understand the cause-and-effect of the material flow in the process, it is necessary to understand the material flow also during the process in opposite to only consider the end result.
The steady increase of the densification during the process is different for all process designs. Hence, the densification is a result as well as an input variable. Therefore, in this paper different densifications of the workpiece complemented with all according properties of this densification are pre-defined.
3.3 Possibilities to influence material flow
The process results can be influenced by contacting radiuses, kinematics, friction and stock. As described above, another parameter is the given densification depth. In the following figures the results are shown for “beginning of densification”— densification depth is zero—and “end of densification”—the densification depth for 95 % relative density is 2.3 mm. In Fig. 11 the flow angle and the increase of densification depth is shown for different densifications and stocks. The reference parameters are given in the figure caption. The shown stocks reflect the stock of one tool-workpiece contact. The workpieces at the end of densification show a considerably lower flow angle in opposite to the non-densified ones. The workpieces at the end of densification have less potential for further densification. Hence, the resistance against normal material flow is high, which leads to the increased tangential material flow. With increasing stock, more material has to be displaced. The flow angle decreases for the workpieces at the beginning and the end of densification, as not all material can be transferred in normal direction.
The increase of densification depth for a relative density of 95 % shows that with increase of stock not only the tangential material flow increases, but foremost the normal material flow which leads to the densification. The increase is however lower for the workpieces at the end of densification, due to the resistance against further densification which results of the high densification.
In Fig. 12 the influence of the tool diameter is shown for the flow angle and the increase of densification depth. In the beginning of the densification, the tool diameter has not a very high impact on the flow angle. At the end of the densification, the very small tool diameter results in a flow angle of zero. For the higher tool diameters the flow angle is still increasing, only with a lower difference.
A similar relation exists for increase of densification depth. The workpieces at the beginning of the densification show an increase, with only small difference for the different diameters. For the workpieces at the end of the densification, no normal material flow occurs for the smallest diameter. For the lager diameters an increase of the diameter leads to a small increase of densification depth.
In Fig. 13 the material flow is shown for varying friction factor. For the shown negative slip condition, high friction leads to a material displacement rather than to densification: for a higher shear friction factor, the tangential material flow increases, especially for the workpieces at the end of the densification. The densification depth increases less with higher friction factor. This effect reinforces with a given densification of the part.
In Fig. 14 the material flow is shown for varying slip. For a slip of zero and of 40, the results for both, densification and flow angle are equal. This is true at the beginning and at the end of densification. A high negative slip leads to a reduced flow angle at the beginning but even more at the end of densification. At the end of densification, the densification depth is also reduced for the negative slip condition. As the slip also influences the friction [18], a high negative slip could lead to a high friction factor and hence would have an high impact on the densification and flow angle.
In Fig. 15 the workpiece diameter is varied with negative (concave) and positive (convex) diameters. The tool has a diameter of 3 mm, as the tool diameter has to be smaller than the smallest negative diameter. For the positive diameters this leads to only tangential material flow for workpieces at the end of the densification as has been seen in Fig. 12 as well. From left to right, the workpiece geometry changes from concave to convex with the more flat geometries in the middle. For the tool-workpiece contact this means that the geometries on the right side have a lower wrap angle with the tool. This leads to a decreasing flow angle and an increasing densification. The results of Figs. 12 and 15 lead to the assumption that a large contact area with a high wrap angle lead to lower tangential material flow.
These results show that there are ways to influence the normal and tangential material flow. If the target is to decrease tangential material flow in order to avoid overlaps and profile deviations, and the densification should be held constant or be increased, the following statements can be held:
-
A tool design which avoids very small contact radiuses should be preferred.
-
Contact analysis should be used to evaluate tool–work-piece contact considering contact area and wrap angle.
-
Contact conditions with low shear friction and low negative slip should be picked.
-
An increase of the total stock would not lead to the target.
-
Higher densification leads to higher tangential material flow. Hence, the high density should only be as high as necessary. The densification does not have to be as high as possible (Fig. 3).
4 Outlook
The detailed analysis of the rolling process enabled statements how the material flow can be changed by size and direction. However the shown results cover only a small part of the possible process conditions. Hence, a model has to be developed which includes the different process parameters with their interactions.
Furthermore, this work showed that the fatigue strength of different PM gears can be calculated. This calculation has to be extended by carbon profile and residual stresses.
The two-step approach complements when gears with different stock designs are rolled and hardened, followed by pulsatory tests. This chain is used as a validation for the gained results as well.
References
Behrens BA, Gastan E, Vahed N, Lange F (2010) Numerical analysis of the process chain for the production of PM components with integrated information storage. Prod Eng 4(5):477–482
Beiss P (2003) Mechanische Eigenschaften von Sinterstählen
Beiss P (2013) Pulvermetallurgische Fertigungstechnik. Springer Vieweg
Beiss P, Zafari ALKBJ (2012) Fatigue behavior of a sintered steel containing 4 % Ni, 1.5 % Cu, 0.5 % Mo and 0.6 % C. Int J Powder Metal 48:19–34
DIN (1987) Begriffe und Bestimmungsgrößen für Stirnräder (Zylinderräder) und Stirnradpaare (Zylinderradpaare) mit Evolventenverzahnung
Doege E, Behrens BA (2007) Handbuch Umformtechnik: Grundlagen, Technologien, Maschinen; mit 55 Tabellen. Springer, Berlin
Felten K (2008) Verzahntechnik: Das aktuelle Grundwissen über Herstellung und Prüfung von Zahnrädern, 2nd edn. Expert-Verl, Renningen
Fereshteh-Saniee F, Pillinger I, Hartley P (2004) Friction modelling for the physical simulation of the bulk metal forming processes
Kauffmann P (2013) Walzen pulvermetallurgisch hergestellter Zahnräder. Ph.D. thesis, Rheinisch-Westfälische Technische Hochschule, Aachen
Klocke F, König W (2005) Fertigungsverfahren: Umformen. Springer, Berlin
Klocke F, Gorgels C, Gräser E (2011) Study of tool design for surface densification of PM Gears
Kotthoff G (2003) Neue Verfahren zur Tragfähigkeitssteigerung von gesinterten Zahnrädern. Ph.D. thesis, Rheinisch-Westfälische Technische Hochschule, Aachen
Neumaier T (2003) Zur Optimierung der Verfahrensauswahl von Kalt-, Halbwarm- und Warmmassivumformverfahren. Ph.D. thesis, Universität, Hannover
Neugebauer R, Klug D, Hellfritzsch U (2007) Description of the interactions during gear rolling as a basis for a method for the prognosis of the attainable quality parameters
Strehl R (1997) Tragfähigkeit von Zahnrädern aus hochfestem Sinterstählen. Ph.D. thesis, Rheinisch-Westfälische Technische Hochschule, Aachen
Strehl R (2012) Wirtschaftlichkeit von P/M-Verzahnungen. In Tagungsband zu: Aktuelle Entwicklungen beim Vorverzahnen 2012
Tiedemann I, Hirt G, Kopp R, Michl D, Khanjari N (2007) Material flow determination for radial flexible profile ring rolling. Prod Eng 1(3):227–232
Wimmer AJ (2006) Lastverluste von Stirnradverzahnungen: Konstruktive Einflüsse, Wirkungsgradmaximierung, Tribologie, FZG / FZG, Lehrstuhl für Maschinenelemente, Forschungsstelle für Zahnräder und Getriebebau, vol 152. Shaker, Aachen
Zafari A, Beiss PBCLK (2011) Assessing the fatigue strength of a sintered steel as affected by the highly stressed volume. pp 15–20. EPMA, Shrewsbury
Acknowledgments
This work is funded as the project “High-strength gears by powder metallurgical manufacturing processes” which is part of the Priority Program “Resource efficient machine elements” (SPP 1551) by the German Research Foundation (DFG). We thank GKN Sinter Metals for sintering and the institute “Werkstoffsynthese und Herstellungsverfahren (IEK-1)” of Forschungszentrum Jülich for hot isostatic pressing the fatigue specimen.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gräser, E., Hajeck, M., Bezold, A. et al. Optimized density profiles for powder metallurgical gears. Prod. Eng. Res. Devel. 8, 461–468 (2014). https://doi.org/10.1007/s11740-014-0543-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11740-014-0543-1