1 Introduction

Dynamical feed drives commonly used in machine tools and production units represent complex mechanical structures with multiple degrees of freedom (DOF) and various eigenmodes. Numerous scientific works have dealt with the simulation of such drive systems, using Finite-Element-Methods (FEM) and complex modeling techniques in order represent the dynamical behavior as detailed as possible [1–3]. Especially when describing the complex behavior of the ball screw shaft, FEM-based modeling techniques are commonly used. In contrary, the approach presented in this paper aims at identifying the dominant effects of the ball screw shaft and including them into a simple lumped mass model, capable of expressing the most relevant characteristics of feed drives with respect to their application in machine tools.

Generally spoken, a ball screw drive can be characterized as a system with three different types of eigenmodes: axial, rotational and flexural modes [4]. Typically the first axial and rotational mode of the ball screw show a dominant influence on the overall dynamics while the relevance of higher order modes for most technical applications is rather small. The excitation of the flexural modes and their effect on the feed motion greatly depends on fabrication and mounting tolerances as well as on the operating conditions of the drive system. Presuming proper mounting and operating conditions, the excitation of the flexural modes are considerably small and therefore will be neglected in the course of this paper. The two dominant vibrational DOF, namely the axial and the rotational mode, are primarily influenced by the geometrical dimensions and the pitch of the ball screw shaft and the table position. Depending on the transmission ratio as well as on the operating conditions, the system can behave qualitatively and quantitatively very different. In most cases however, the configuration of a feed drive allows for a simple approximation of the systems characteristics.

While the characteristic of the axial mode of a ball screw feed drive and its dependency to changing operating conditions are generally known, this work focuses on the rotational eigenmode and its integration into a lumped mass model. In the following, a practical and application-oriented modeling technique for ball screw feed drives will be derived. The physical context is explained and an extensive parameter analysis is provided. Finally the model is verified by measurement results conducted on an experimental test bench.

2 Ball screw feed drives for machine tools

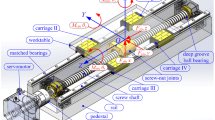
Figure 1 shows a typical ball screw assembly with its relevant components. In this case servomotor and bearings are fixed to the machine base and the torque of the servomotor is transmitted through an elastic coupling onto the ball screw shaft. Not depicted in Fig. 1 are the linear guideways constraining the movement of the machine table in axial direction. The transformation from the rotational into the linear motion is realized by the ball screw system with its transmission ratio i, defined as the distance of travel h during one revolution of the shaft.

$$ i\, = \,\frac{h}{2\pi } $$
(1)
Fig. 1
figure 1

Schematic configuration of a ball screw feed drive

Full size image

Manufacturers provide a great variety of ball screw systems with different constructive designs, dimensions and transmission ratios. The available pitches nowadays lie between 0.05 and 3 times the ball screw diameter, while for most applications in machine tools values between 0.25 and 1 are being used.

As already mentioned, the dynamical behavior of such a drive system is greatly influenced by the physical dimensions of the ball screw shaft. Diameter and length of the shaft have a decisive impact on the overall rigidity and therefore on the structural vibration modes of the drive system. Figure 2 shows a measured frequency response of a ball screw drive, derived from the comparison of motor and machine table velocity.

Fig. 2
figure 2

Measured frequency response of a ball screw feed drive

Full size image

Clearly noticeable are the two dominant eigenfrequencies f 1 and f 2 , characteristical for ball screw feed drives. The first eigenfrequency in Fig. 2 represents an axial oscillation of the machine table while the second eigenfrequency can be primarily ascribed to an angular deflection of the rotational system. Although each mode is a result of axial and angular deformations, it is convenient to classify an axial and a rotational mode depending on the predominant deformation. In both cases, the flexibility of the ball screw shaft has a major influence on the absolute value of the eigenfrequencies. This is due to the fact that the shaft represents the component with the least rigidity within the drive system [5]. At this point it should be noted, that for most technical applications the eigenfrequency of the axial mode is articulately smaller than that of the rotational mode. On this account the axial mode is often referred to as the first eigenfrequency of a ball screw feed drive. The interaction between the dominant eigenfrequencies of a ball screw drive is defined by the transmission ratio, describing the coupling between the axial and the rotational motion. Furthermore the properties of the ball screw shaft are not constant but change over the travel range of the machine table. This leads to a complex overall system with numerous variations and dependencies.

The structural vibration modes of the mechanical system are of particular importance when considering the dynamical behavior of a position controlled feed drive. Especially in high speed applications, high acceleration and jerk values can excite the mechanical structure and therefore have to be considered when tuning the controller. When using cascaded P-position PI-velocity controller, the closed loop bandwidth and tracking accuracy of a feed drive are directly limited by the first eigenfrequency of the mechanical system [6, 7]. In similar matter, external excitations e.g. cutting forces can excite the mechanical structure and cause unwanted oscillations and stability problems. On this account, the second eigenfrequency is equally important to the performance of feed drives. Susceptible to oscillations, the rotational mode has a decisive impact on the velocity control loop of a feed drive, and therefore often has to be compensated for by additional notch filters [13]. Figure 3 exemplarily shows the open-loop Nyquist plot for a PI velocity controller, measured on an actual feed drive. The characteristics of the two eigenmodes are clearly noticeable and the effect of the rotational mode on the phase margin of the control system becomes evident.

Fig. 3
figure 3

Measured open loop Nyquist plot for the velocity controller of a ball screw feed drive

Full size image

But especially when using more sophisticated control strategies, the relevance of accurate plant models becomes evident. A good understanding of the mechanical system and a detailed plant model are often basic requirements when implementing such control systems [8, 9]. The demand for even higher dynamics and better tracking accuracy therefore goes along with highly efficient and accurate feed drive models, equally valid for different operating conditions.

3 Comparison of two different modeling techniques

In order to examine the influence of the shaft on the overall dynamical behavior of a ball screw drive, two simplified models with different degrees of complexity are being introduced and compared to one other. The first model is built up in FEM using a combination of springs, dampers, mass-elements and Timoshenko beam elements. We call this model a hybrid model since we are using discrete and continuous formulation elements. The relevant axial and rotational flexibilities of the system, namely the axial rigidity of the fixed bearing including the mounting k bearing , the rigidity of the ball screw nut k nut and the torsional rigidity of the coupling k coupling are being expressed as linear springs. The individual damping values are treated in equal measure. The shaft including both, relevant axial and torsional characteristics, is modeled with Timoshenko beam elements and coupled with the surrounding springs and dampers. This provides the possibility of an exact examination of the structural behavior of the shaft and its influence on the overall dynamical behavior. In concordance to the real mechanical system, rotational and axial motion are coupled by the transmission ratio i, which is modeled using constraint equations on the involved DOF. Figure 4 depicts the composition of this hybrid model.

Fig. 4
figure 4

Hybrid model of a ball screw drive

Full size image

Following well established techniques [5, 12, 14], the second model entirely uses lumped physical features, and is therefore referred to as discrete model. Due to its simplicity it can be directly modeled with CACE-Tools (Computer-Aided-Control-Engineering-Tools), using available standard blocks like gains, integrators and basic mathematical operations. While discrete modeling approaches typically neglect the influence of the shaft on the rotational mode of the drive system, in this case, the dominant effects are explicitly included into the lumped mass model. Therefore, the shaft is separated into two different branches, an axial and a rotational branch while the coupling once more is realized using constrained equations. Since all components are expressed by discrete springs and dampers, the rigidity values of shaft, coupling and bearing are combined to an overall axial k ax and rotational value k rot :

$$ k_{rot} \, = \,\left( {\frac{1}{{k_{{shaft_{rot} }} }}\, + \,\frac{1}{{k_{coupling} }}} \right)^{ - 1} $$
(2)
$$ k_{ax} \, = \,\left( {\frac{1}{{k_{{shaft_{ax} }} }}\, + \,\frac{1}{{k_{bearing} }}} \right)^{ - 1} $$
(3)

Figure 5 shows the principle set up of the lumped mass model. The individual parameters in each model such as the mass of the machine table m t , the mass of the ball screw shaft m s , the rotary inertia of shaft J s and motor J m , as well as the rigidity and damping factors correspond to their physical values.

Fig. 5
figure 5

Discrete model of a ball screw feed drive

Full size image

Precondition for this approach is the definition of adequate, alternative values for the axial and rotational rigidity of the shaft. For this purpose the shaft is considered as a solid steel rod (Young modulus E = 210e9 N/m2, shear modulus G = 81e9 N/m2, density ρ = 7,800 kg/m2). With the dimensions of the ball screw, namely equivalent diameter d, length l and effective length l eff , the axial and rotational rigidity values of the shaft \( k_{{shaft_{ax} }} \) and \( k_{{shaft_{rot} }} \) can be approximated using Eqs. 4 through 6.

$$ k_{{shaft_{ax} }} \, = \,\frac{EA}{{l_{eff} }}\, = \,\frac{\pi }{{4l_{eff} }}\,d^{2} E $$
(4)
$$ k_{{shaft_{rot} }} \, = \,J_{s} (2\pi f_{s} )^{2} \, = \,\frac{\pi }{32}\,d^{4} lp\,(2\pi f_{s} )^{2} $$
(5)
$$ f_{s} \, = \,\frac{1}{4l}\,\sqrt {\frac{G}{\rho }} $$
(6)

Notice that the alternative rotational rigidity of the shaft has been approximated using the eigenfrequency f s of a solid, on one side fixed rod which can according to [10] be calculated using Eq. 6.

With this approach, the axial rigidity of the shaft depends on the distance between fixed bearing and table position l eff , while the rotational rigidity is considered constant throughout the travel range of the machine table. In the following, both models have been examined with an identical set of parameters according to Table 1.

Table 1 Parameter values used for the simulations
Full size table

It should be noted, that the assumption of the shaft being a solid rod is a simplified approximation. In reality all geometric parameters of the ball screw, including the screw pitch, have an effect on the axial and torsional stiffness values which in turn can be regarded in form of an equivalent diameter [11].

The simulation results, namely the first two eigenfrequencies of the feed drive at different operating and coupling conditions, are presented in Table 2.

Table 2 First two eigenfrequencies of the ball screw drive models for different mass, screw pitch and table positions
Full size table

As expected, the value of the first eigenfrequency greatly depends on the mass and the position of the machine table: The higher the mass and the greater the distance between machine table and fixed bearing the smaller the value of the first eigenfrequency. In comparison to that, the second eigenfrequency seems to change rather insignificantly with different operating conditions. Both models show that the rotational mode remains almost constant for a great range of parameters. The difference between hybrid and discrete model expressed in Fig. 6 can be ascribed to the simplified representation of the shaft in the discrete model.

Fig. 6
figure 6

Percental difference between hybrid and discrete model of the ball screw drive

Full size image

From Fig. 6 it can be seen that the absolute difference as well as the parameter sensitivity of the eigenfrequencies greatly depend on the interaction between axial and rotational mode, determined by the transmission ratio of the ball screw. With increasing transmission ratio the influence of the rotational rigidity of the shaft on the overall axial rigidity increases. The position dependent, effective axial rigidity \( k_{{ax_{eff} }} \) can be expressed as follows.

$$ k_{ax\_eff} \, \approx \,\left( {\frac{1}{{k_{{shaft_{ax} }} }}\, + \,\frac{1}{{k_{bearing} }}\, + \,\frac{1}{{k_{nut} }}\, + \,\frac{1}{{\frac{{k_{{shaft_{rot} }} }}{{i^{2} }}}}} \right)^{ - 1} $$
(7)

In many cases however, the influence of the rotational rigidity on the axial mode can be neglected due to the transmission ratio of the ball screw. With the effective axial rigidity and the knowledge of the consistency of the rotational mode, the two characteristic eigenfrequencies of a ball drive can be approximated using Eqs. 8 and 9.

$$ f_{1} \, \approx \,\frac{1}{2\pi }\,\sqrt {\frac{{k_{ax\_eff} }}{{m_{t} \, + \,m_{s} }}} $$
(8)
$$ f_{2} \, = \,\frac{1}{2\pi }\,\sqrt {\frac{{k_{rot} }}{{J_{s} }}} $$
(9)

Despite the chosen simplifications the discrete model shows good results for the first two eigenfrequencies of a ball screw system. This allows for an intuitive and clearly arranged simulation of the dynamical behavior, valid for a great range of parameters and well suitable for most practical applications. In the following chapter the simulation results of the discrete model depicted in Fig. 4 will be compared to measurements on an actual machine tool feed drive. Especially the numerically observed low dependency of the rotational eigenfrequency is to be validated by measurements.

4 Experimental verification of the model

At the Institute for Control Engineering of Machine Tools and Manufacturing Units (ISW) at the University of Stuttgart exists a great variety of test benches with different size ball screws and numerous transmission ratios. While the research on this topic is based on experiments with different ball screw types, the following measurements focus on a typical ball screw set up for machine tools according to the specifications in Table 3. The parameters used for the simulation comply with those of the experimental set-up. The values for rigidity and mass are based on manufacturer’s data while the damping factors correspond to empirical values.

Table 3 Specifications of the test bench
Full size table

With the given feed drive various measurements have been conducted and compared to the simulation results from the discrete model. Figures 7 and 8 exemplarily show simulated and measured frequency responses for the given feed drive at different operating conditions.

Fig. 7
figure 7

Simulated and measured frequency response for the feed drive at different machine table positions

Full size image
Fig. 8
figure 8

Simulated and measured frequency response for different machine table masses

Full size image

The discrete model used to describe the mechanical system shows good concordance with the behavior of the actual feed drive. Despite of the chosen simplifications and the impreciseness of the manufacturer’s data, a good predictability could be achieved. Furthermore, the predicted parameter dependency of the eigenfrequencies is confirmed by the measurement results. The frequency of the axial mode changes depending on machine table mass and position while the rotational mode of the ball screw drive remains almost constant. The invariance of the rotational mode towards operating conditions, as already detected in the foregoing simulations, can be explained by the low pass characteristic of the mechanical system. After the first eigenfrequency the system experiences an amplitude drop-off of 20 dB/decade. Hence the energy imposed by the servo drive at higher frequencies is merely transformed onto the machine table. The axial motion of the table at the second eigenfrequency is therefore quite small. Due to the kinematic coupling, the angular deflection of the shaft will still lead to an axial displacement which in this case is predominantly executed by the deflection of the shaft, bearing and mounting. Considering the minor changes in table position at the rotational mode of the ball screw system, it is intelligible that neither the mass nor the effective position of the table have a relevant influence on the second eigenfrequency of the oscillating system.

The predictability and simulation of the dominant eigenfrequencies of a ball screw drive and their dependency to different operating conditions provides a better understanding of the system dynamics and is beneficial for the design process of the mechanical components as well as for the implementation of adequate feedback controllers. In particular the consistency of the rotational eigenmode is an important inside, allowing for an adequate design of filter structures and compensational networks, and hence beneficial for both the field of research and industrial applications.

5 Conclusion

In this paper two well-structured and clearly arranged models for ball screw feed drives have been presented: a hybrid (discrete-continuum) and a lumped mass (discrete) model. The used modeling techniques are state of the art, however the chosen combination of the lumped physical features, the integration of additional system properties and the assignment of the physical parameters to the model describe a new approach. Of central interest to this work are the characteristics of the ball screw shaft and its dominant influence on the vibrational modes of a feed drive. By separating the physical characteristics of the shaft into an axial and a rotational system, the dominant effects of this complex flexural body could be projected onto the simple lumped mass model. Through comparison with the more complex hybrid model it could be shown, that the simplified discrete model is well suitable for predicting the relevant eigenfrequencies of a feed drive over a great range of parameters. Different coupling and operating conditions have been analyzed and the effect on the dominant eigenmodes has been illustrated. While the axial vibration mode shows the well know dependencies to the operating conditions, the rotational vibration mode proofs to be little sensitive with respect to table mass and table position. Finally the simulation results were validated by experimental measurements on a machine tool feed drive. The derived discrete model, using the actual physical parameters of the machine components, showed good concordance with the measurement results from the investigated feed drive. The simplicity and the intuitive composition of the model allow for a physical interpretation of the dominant effects and an effective simulation with preciseness high enough for most practical applications. Furthermore, the consistency of the rotational eigenmode is an important insight for the field of research and industrial applications.