1 Introduction

As an alternative to conventional drilling orbital drilling offers many advantages. The kinematics of orbital drilling allow different working steps for the production of different borehole geometries with one tool. Orbital drilling can optimize the drilling process in different forms. Cylindrical holes can be drilled independent of the tool diameter and without changing the tool. This makes it possible to drill complex tapered holes and perform finishing operations using the same cylindrical tool and settings. Another significant advantage of the orbital drilling process is the diameter variability without tool change. This fact offers the possibility for a dynamic correction of the bore diameter during the drilling process. This can be used for example, for the compensation of diameter deviations caused by different material properties in a CFRP/aluminium compound structure or arising tool wear [1, 2]. More advantages of orbital drilling are low burr formation, little delamination in CFRP, good chip transportation and cutting fluid conditions [3, 4].

2 Objective of the theoretical investigation

To maximize the productivity and cost-effectivness of orbital drilling a fundamental understanding of the removal process must exist. This understanding will lead to the optimization of the cutting parameters. To accomplish an optimized adjustment of the drilling parameters, it is necessary to deduce a theoretical model of the special removal kinematics of orbital drilling. With the help of this model theoretical considerations can be included into further development in addition to experimental and experience-based optimization of the orbital drilling process. Furthermore for the design of an orbital drilling simulation system a mathematical model of the cutting conditions is essential. The geometrical coherences of the cutting process, particularly for a conventional end mill the engagement conditions regarding the front and the peripheral cutting edge, are presented in this paper. These results can be used as a basic knowledge for further investigations with more complex milling cutter geometries.

3 Orbital drilling process

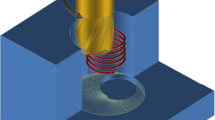
In orbital drilling the borehole is generated by a milling tool which executes a helical path into the workpiece (Fig. 1). The bore diameter is adjusted by the radius of the helix path in the NC-program [5–7].

Fig. 1
figure 1

Orbital drilling process

Full size image

In Fig. 2 the first cuts of an orbital drilling process are shown. Pictured is a 3 mm solid (cemented) carbide tool orbital drilling a 4.2 mm borehole. In position A the arrow 1 illustrates the spindle rotation and arrow 2 the orbital rotation. In picture B of Fig. 2 the two cutting zones of the orbital drilling process are pictured. There is a difference between drilling and milling. The ratio between drilling and milling plays a decisive role for the reached borehole qualities [1]. This ratio can be adjusted by the ratio between bore diameter and tool diameter.

Fig. 2
figure 2

First cut in the orbital drilling of an aluminium workpiece

Full size image

4 Geometic relation between periphery cutting zone and front cutting zone

The orbital drilling process is characterized by a simultaneous movement of the tool on a circular path and a superimposed movement in the axial direction. The superposition of these two movements forms a helical course. After a closer inspection of the geometrical conditions between the tool and the workpiece this course produces two different engagement zones into the workpiece volume. Figure 3 illustrates the two engagement zones of the helical course with an arbitrary inspection radius R i pierces the tool shape.

Fig. 3
figure 3

Cutting zones on a concentric circle to the borehole with an arbitrary inspection radius (R i )

Full size image

Based on the tool motion it is possible to distinguish between two types of machining which occur; a part of the workpiece which is machined by the periphery cutting edges (grey part of the helical course h 1i in Fig. 4) and a part machined by the front cutting edges (dark part of the helical course h 2i in Fig. 4).

Fig. 4
figure 4

Cutting zones

Full size image

Figure 5 shows additionally the curved tool path projected onto a plane (developed tool path). On the basis of this developed tool path fundamental geometrical relations which determine the orbital drilling process can be determined.

Fig. 5
figure 5

Developed tool path

Full size image

The aim of the following derivation is to calculate the two target values, periphery cutting depth (h 1i ) and front cutting depth (h 2i ) at each engagement point of the cutting edge for a cylindrical tool geometry as a function of the inputs (D W, D B, a p, R i ) (Fig 6).

Fig. 6
figure 6

Sought relation

Full size image

For the calculation the following variables are used:

Dw::

tool diameter

DB::

bore diameter

ap::

depth setting of the helical course

h1i ::

periphery cutting depth

h2i ::

front cutting depth

R i ::

arbitrary inspection radius

\( U_{R_i } \)::

circumference of R i

Uwi::

tool inspection arc

e::

eccentricity.

The difficulty of the engagement relations and the calculation increase with the complexity of the tool design, e.g. torus, ball, etc. [8].

For the determination of the periphery cutting depth (h 1i ) and front cutting depth (h 2i ). Figure 7 shows the situation for an arbitrary inspection radius (R i ). In this case the arbitrary inspection radius (R i ) pierces only partially the tool contour and builds thereby the tool inspection arc (U Wi) on the arbitrary inspection radius (R i ). With inspection radii below R i < R pfc with R pfc = D W/2 − e and e = (D B − D W)/2 the tool inspection arcs become full circles (dark circular area). In this range a pure front cut with a superimposed eccentric movement, which is similar to conventional drilling is obtained. Regarding the geometric values with the pure front cut radius (R pfc) the following statement for the dark range can be made: h 1i = 0, h 2i = a p. It is also important to consider that the cutting speed v c = 0 occurs caused by the front cutting zone. This fact might induce build-up edge in orbital drilling.

Fig. 7
figure 7

Dependency of the cutting zones (h 1i , h 2i ) on the arbitrary inspection radius (R i ) on the tool path

Full size image

For the inclination of the developed tool path regarding the inspection radius (R i ) the following mathematical relation for the angle η i can be obtained (Fig. 7).

$$ \eta _i = { \arctan }\left( {\frac{{a_{\text{p}} }}{{U_{R_i } }}} \right) $$
(4.1)

Due to this equation the range of η i can be calculated between two limits.

$$ \eta _{i{ \min }} = { \arctan }\frac{{a_{\text{p}} }}{{2\pi \left( {R_{i{ \max }} } \right)}}\quad R_{i{ \max }} = \frac{{D_{\text{B}} }}{2} $$
$$ \eta _{i{ \max }} = { \arctan }\frac{{a_{\text{p}} }}{{2\pi \left( {R_{i{ \min }} } \right)}} = 90^\circ \quad R_{i{ \min }} \to 0 $$

Furthermore the Eq. (4.2) can be developed with the projected toolpath triangle on the arbitrary inspection radius R i (Fig. 7).

$$ {\frac{{h_{2i} }}{{U_{{\text{Wi}}} }} = \frac{{a_{\text{p}} }}{{U_{R_i } }} \Rightarrow h_{2i} = a_{\text{p}} \cdot \frac{{U_{{\text{Wi}}} }}{{U_{R_i } }}} $$
(4.2)

Equation (4.2) describes the geometric dependence of the front cutting depth (h 2i ) on the arc length of the full circle with radius (R i ), the depth setting per orbital path (a p) and the tool inspection arc (U Wi). Assuming that h 2i is known h 1i can be calculated with the following equation (Fig. 7).

$$ h_{1i} = a_{\text{p}} - h_{2i} $$
(4.3)

Substituting Eqs. (4.2) into (4.3) gives:

$$ h_{1i} = a_{\text{p}} \left( {1 - \frac{{U_{{\text{Wi}}} }}{{U_{R_i } }}} \right) $$
(4.4)

The geometric relationship for the tool inspection arc angle β i shown in Fig. 8 enables the calculation of the unknown tool inspection arc (U Wi).

Fig. 8
figure 8

Graphic for the calculation of β i

Full size image
$$ {\frac{{U_{{\text{Wi}}} }}{{2\beta _i }} = \frac{{U_{R_i } }}{{2\pi }}} \Rightarrow U_{{\text{Wi}}} = \frac{{U_{R_i } }}{\pi } \cdot \beta _i $$
(4.5)

Equation (4.5) can be substituted into Eq. (4.2) for h 2i and in (4.4) for h 1i to obtain:

$$ h_{2i} = a_{\text{p}} \cdot \frac{{\beta _i }}{\pi } $$
(4.6)
$$ h_{1i} = a_{\text{p}} \left( {1 - \frac{{\beta _i }}{\pi }} \right) $$
(4.7)

The Eqs. (4.6) and (4.7) require the calculation of β i . Figure 8 pictures the geometrical relationships for this angle. Therefore the following auxiliary calculations are necessary because the value R iy is unknown.

$$ {\sin \beta _i = \frac{{R_{iy} }}{{R_i }}} $$
(4.8)
$$ {R_i^2 = R_{ix}^2 + }R_{iy}^2 \Rightarrow R_{iy}^2 = R_i^2 - R_{ix}^2 $$
(4.9)
$$ {R_{\text{W}}^2 } = R_{{\text{Wi}}x}^2 + R_{iy}^2 \Rightarrow R_{iy}^2 = R_{\text{W}}^2 - R_{{\text{Wi}}x}^2 $$
(4.10)

Setting (4.9) (4.8) and (4.10) (4.9) equal to another

$$ {R_i^2 - R_{ix}^2 = R_{\text{W}}^2 - R_{{\text{Wi}}x}^2 } \Rightarrow R_{ix}^2 = R_i^2 - R_{\text{W}}^2 + R_{{\text{Wi}}x}^2 $$
(4.11)

Also essential

$$ {R_{ix} = e + R_{{\text{Wi}}x} } $$
(4.12)

Squaring both sides of Eq. (4.12)

$$ R_{ix}^2 = \left( {e + R_{{\text{Wi}}x} } \right)^2 $$
(4.13)

Substituting (4.11) into (4.13)

$$ {R_i^2 - R_{\text{W}}^2 + R_{{\text{Wi}}x}^2 = \left( {e + R_{{\text{Wi}}x} } \right)^2 } $$
$$ R_i^2 - R_{\text{w}}^2 + R_{{\text{Wi}}x}^2 = e^2 + 2eR_{{\text{Wi}}x} + R_{{\text{Wi}}x}^2 $$
$$ R_i^2 - R_{\text{W}}^2 = e^2 + 2eR_{{\text{Wi}}x} $$
$$ R_{{\text{Wi}}x} = \frac{{R_i^2 - R_{\text{W}}^2 - e^2 }}{{2e}} $$
(4.14)

Extracting the root of (4.10)

$$ {R_{iy} = \sqrt {R_{\text{W}}^2 - R_{{\text{Wi}}x}^2 } } $$
(4.15)

Re-writing Eq. (4.8):

$$ \beta _i = { \arcsin }\left( {\frac{{R_{iy} }}{{R_i }}} \right) $$
(4.16)

For the final calculation of β i it is necessary to use the following:

$$ {e = \frac{{D_{\text{B}} - D_{\text{W}} }}{2}} $$
(4.17)
$$ {R_{\text{W}} = \frac{{D_{\text{W}} }}{2}} $$
(4.18)

Substituting Eqs. (4.17) and (4.18) into (4.16) gives:

$$ \beta _i = { \arcsin }\left( {\frac{{\sqrt {\left( {\frac{{D_{\text{W}} }}{2}} \right)^2 - \left( {\frac{{R_i^2 - \left( {\frac{{D_{\text{W}} }}{2}} \right)^2 - \left( {\frac{{D_{\text{B}} - D_{\text{W}} }}{2}} \right)^2 }}{{D_{\text{B}} - D_{\text{W}} }}} \right)^2 } }}{{R_i }}} \right) $$
(4.19)

The calculation of β i depends on the arbitrary inspection radius (R i ). With the calculated value β i and the known value a p, the periphery cutting depth (h 1i ) and the front cutting edge (h 2i ) can be determined. Figure 9 shows the process to determine h 1i and h 2i .

Fig. 9
figure 9

Process for the determination of the sought values

Full size image

For the determination of h 2i and h 1i Eq. (4.19) is used in Eqs. (4.6) and (4.7).

$$ h_{2i} = \frac{{a_{\text{p}} }}{\pi } \cdot { \arcsin }\left( {\frac{{\sqrt {\left( {\frac{{D_{\text{W}} }}{2}} \right)^2 - \left( {\frac{{R_i^2 - \left( {\frac{{D_{\text{W}} }}{2}} \right)^2 - \left( {\frac{{D_{\text{B}} - D_{\text{W}} }}{2}} \right)^2 }}{{D_{\text{B}} - D_{\text{W}} }}} \right)^2 } }}{{R_i }}} \right) $$
(4.20)
$$ h_{1i} = a_{\text{p}} \left( {1 - \frac{1}{\pi }{ \arcsin }\left( {\frac{{\sqrt {\left( {\frac{{D_{\text{W}} }}{2}} \right)^2 - \left( {\frac{{R_i^2 - \left( {\frac{{D_{\text{W}} }}{2}} \right)^2 - \left( {\frac{{D_{\text{B}} - D_{\text{W}} }}{2}} \right)^2 }}{{D_{\text{B}} - D_{\text{W}} }}} \right)^2 } }}{{R_i }}} \right)} \right) $$
(4.21)

Hence obtained relationships enable the calculation of h 1i and h 2i (periphery cutting depth and front cutting depth) for every inspection radius R i of the cutting edge with regard to the bore hole centre.

5 Application of the calculation results for the determination of engagement values in orbital drilling

Figure 10 shows the topography of the bore ground as a function of the radius R i over the calculation of the periphery cutting depth h 1i (simulated in a CAD model). The maximum engagement angle φ for the periphery cut amounts constantly 180° whereas the periphery cutting depth (h 1i ) increases from inside to outside. Furthermore it is possible to calculate the cross-section of undeformed chip A 1i over the periphery cut (h 1i ) and the engagement width (b i ) in consideration of the hypocycloidal cutting movement over the engagement angle φ i . The calculated cross-section of undeformed chip can be used for published cutting force models in the literature.

Fig. 10
figure 10

Simulated topography of the bore ground and the cross-section of undeformed chip of the periphery cut as a function of the engagement angle

Full size image

The following equation in a peripheral milling process for the engagement width b 1i is applied [9]:

$$ b_{1i} = f_z \cdot \sin \varphi_i $$
(5.1)

The equations for the periphery cutting depth (h 1i ) and front cutting depth (h 2i ) obtained in the previous section refer to the bore hole centre because of the geometrical dependence on the tool inspection arc (U Wi ). For the determination of the cross-section of undeformed chip A i for the peripheral cut [10],

$$ A_{1i} = h_{1i} \cdot b_{1i} $$
(5.2)

with \( h_{1i} = f(\beta {}_i) \) and \( b_{1i} = f(\varphi {}_i) \)which depends on the engagement angle. It is necessary to distinguish between a bore coordinate system in which we find the tool inspection arc angle β i and tool coordinate system in which we find the engagement angle φ i , to obtain a relationship between both angles (Fig. 8).

$$ R_{{\text{Wi}}x} = R_{\text{W}} \cdot \cos \varphi $$
(5.3)
$$ R_i = \sqrt {\left( {R_{\text{W}} \cdot \sin \varphi} \right)^2 + R_{ix} ^2 } $$
(5.4)
$$ R_{ix} = e + R_{{\text{Wi}}x} = e + R_{\text{W}} \cdot \cos \varphi $$
(5.5)

Substituting (5.5) into (5.4) gives

$$ R_{\text{i}} = \sqrt {\left( {R_{\text{W}} \cdot \sin \varphi} \right)^2 + \left( {e + R_{\text{W}} \cdot \cos \varphi } \right)^2 } $$
(5.6)

Substituting (5.3) into (4.15) gives

$$ R_{iy} = \sqrt {R_{\text{W}} ^2 - R_{{\text{Wi}}x} ^2 } = \sqrt {R_{\text{W}} ^2 - \left( {R_{\text{W}} \cdot \cos \varphi } \right)^2 } $$
(5.7)

Substituting (5.6) and (5.7) into (4.16) gives

$$ \beta = { \arcsin }\frac{{\sqrt {R_{\text{W}} ^2 - \left( {R_{\text{W}} \cdot \cos \varphi } \right)^2 } }}{{\sqrt {\left( {R_{\text{W}} \cdot \sin \varphi } \right)^2 + \left( {e + R_{\text{W}} \cdot \cos \varphi } \right)^2 } }} $$
(5.8)

For a complete consideration of the cross-section of undeformed chip A i in orbital drilling it is necessary to include in addition to the peripheral cross-section of undeformed chip A 1i the front cross-section of undeformed chip A 2i given by the front cutting depth h 2i in the calculation [11]. The cross-section of undeformed chip A 1i for the peripheral cut can be illustrated directly out of the bore ground topography in Fig. 10. On the other hand the cross-section of undeformed chip A 2i for the front cut in relation to the engagement angle φ i can not be visualized directly in the tool coordinate system (Fig. 10). The utilization of the cross-section of undeformed chip A i in a cutting force model requires the inclusion of the relationship between the tool and the bore coordinate system with Eq. (4.21). The detailed mathematical elaboration to use the cross-section of the front cut A 2i in a cutting force model is the object of a current investigation. Independent of this mathematical elaboration of the cross-section of undeformed chip A 2i for the front cut in the tool coordinate system it is possible to picture the volume which is removed by the front cutting edges over one bore hole depth (Fig. 11).

Fig. 11
figure 11

Cutting volume for the front and peripheral cut in different views

Full size image

In the first view of the front cutting edge volume in Fig. 11 the small disc pictures an approximated front cutting zone which is added over one borehole depth. Furthermore it is possible to show the volume which is removed by the peripheral cutting edges and the combined cutting volume (dark volume shows the front cut and the bright volume the peripheral cut).

6 Total ratio between front cut volume and peripheral cut volume over one orbital revolution

In addition a specific consideration of the ratio between the front cut and the peripheral cut over the total bore volume can be made. Figure 12 shows the developed (projected onto the plane) cutting plane for the derivation of the total ratio for one orbital revolution with the arbitrary inspection radius (R i ).

Fig. 12
figure 12

Mathematic derivation (integral formation)

Full size image

On the basis of the geometric ratios shown in Fig. 12 the removed area for the peripheral cut and the front cut is given in the form of two parallelograms on the radius R i . The areas can be calculated as follows.

6.1 Peripheral cut

$$ A_{1i} = h_{1i} \cdot 2\pi \cdot R_i = h_{1i} \cdot U_{R_i } $$
(6.1)

The total volume removed by the peripheral cutting edge is given by the summation of all partial areas over the radius R i . From this follows the intergral (6.2).

$$ V_1 = 2\pi \int {h_{1i} \cdot R_i \cdot {\text{d}}R_i } $$
(6.2)

Substituting (4.4) into (6.2) gives

$$ V_1 = 2\pi \int {a_{\text{p}} \cdot \left( {1 - \frac{{U_{{\text{Wi}}} }}{{U_{R_i } }}} \right) \cdot R_i \cdot {\text{d}}R_i } $$
$$ V_1 = a_{\text{p}} \int {2\pi \cdot R_i } - \frac{{U_{{\text{Wi}}} }}{{U_{R_i } }} \cdot 2\pi \cdot R_i \cdot {\text{d}}R_i $$
$$ \underline {V_1 = a_{\text{p}} \int {U_{R_i } - U_{{\text{Wi}}} \cdot {\text{d}}R_i } } $$
(6.3)
$$ V_1 = A_1 \cdot a_{\text{p}} \Rightarrow V_1 = \pi \cdot \left( {\frac{{D_{\text{B}} - D_{\text{W}}}}{2}} \right)^{2} \cdot a_{\text{p}} $$
(6.4)

6.2 Front cut

$$ A_{2i} = a_{\text{p}} \cdot U_{{\text{Wi}}} $$
(6.5)
$$ V_2 = a_{\text{p}} \cdot \int {U_{{\text{Wi}}} \cdot {\text{d}}R_i } $$
(6.6)
$$ A_2 = \int {U_{{\text{Wi}}} \cdot {\text{d}}R_i } $$
(6.7)
$$ V_2 = A_2 \cdot a_{\text{p}} \Rightarrow V_2 = \pi \cdot \left( {\frac{{D_{\text{W}} }}{2}} \right)^2 \cdot a_{\text{p}} $$
(6.8)

The value V 2 is identical to a cylindrical volume with the tool diameter and a depth setting per helical course (a p).

Substituting (6.6) into (6.3) gives

$$ V_1 = a_{\text{p}} \int {U_{R_i } \cdot {\text{d}}R_i - V_2 } $$
(6.9)

The Eq. (6.9) describes the differential volume (V 1) between the bore diameter and the tool diameter with the height of a p.

The total ratio (G) between peripheral cut and front cut (milling/drilling) in orbital drilling gives a constant value at every point of the helical course after the first cut. This ratio is independent of the axial feed velocity, the spindle speed or the orbital rotational speed; it is solely given by the ratio between bore diameter (D B) and tool diameter (D W). The total ratio (G) can be calculated as follows.

$$ G = \frac{{V_1 }}{{V_2 }} = \frac{{\pi \cdot \left( {\frac{{D_{\text{B}} - D_{\text{W}} }}{2}} \right)^2 \cdot a_{\text{p}} }}{{\pi \cdot \left( {\frac{{D_{\text{W}} }}{2}} \right)^2 \cdot a_{\text{p}} }} = \left( {\frac{{D_{\text{B}} - D_{\text{W}} }}{{D_{\text{W}} }}} \right)^2 $$
(6.10)

Hence the total ratio between drilling and milling in orbital drilling equals sequential drilling and subsequent milling on a circular path for the generation of the bore hole.

7 Conclusion

The results presented show that it is possible to calculate the peripheral cutting depth (h 1i ) as a function of the arbitrary inspection radius (R i ) and the engagement angle (φ i ) within that the front cutting depth (h 2i ). So a total ratio G of the both cuts can be given by Eq. (6.10). The theoretical description confirmed a change of the cutting characteristic over the engagement angle of the tool from drilling to milling. The total ratio G can be optimized regarding the borehole qualities. Furthermore the value of the peripheral cutting depth (h 1i ) can be used to predict the topography of the bore ground.

On the basis of this mathematical description further fundamental and qualitative statements regarding the cutting process of orbital drilling can be determined and applied for a cutting force model. For different tool geometries it is necessary to extend the determined geometrical coherences. In addition the proof of the theoretical description for the topography requires a comparison with a practical machined bore ground.

To get an overview of the pure front cutting force influence regarding the total cutting forces a view into the range of the pure front cut (h 2i = a p) is necessary. That requires a practical investigation of the area with the radius R pfc. This can be achieved by orbital drilling e.g. of workpiece pins with the radius R pfc. So an appraisal of the cutting forces for the pure front cut is possible.

The results for the orbital drilling process regarding the two cutting zones can be transfered to a conventional 3D milling process.

The final aim is to apply the calculations in a cutting force model to predict the deflection of the tool and thereby to calculate a correction for the tool path. This model will be also auxiliary to optimize the tool design in a simulation system for orbital drilling.