1 Introduction

Numerous research projects on the computer numerical controlled milling of complex or free formed workpieces are known [1–4]. Research projects on numerical controlled grinding according to DIN 8589 [5] for the production of free formed workpieces are rare. External cylindrical shape grinding for the production of rotationally symmetric workpieces is described in [6, 7]. Belt grinding for the production of free formed surfaces is presented in [8]. Belt grinding with high material removal is not possible. Therefore this grinding process is primarily used for finishing. Furthermore, according to DIN 8589, belt grinding is not assigned to NC-shape grinding.

Regarding shape grinding for the production of free formed surfaces the use of spherical mounted points and toroid grinding wheels are described in [9]. Because of their dimensions, mounted points are suitable for local workpiece machining. In comparison to mounted points, toroid grinding wheels can be considered as a universal shape grinding tool. The relevance of modelling and simulation of grinding processes are specially given for grinding of three-dimensional surfaces [10].

The Department of Machining Technology (ISF), University of Dortmund, in cooperation with the Chair for Scientific Computing (LSX), University of Dortmund, carries out a holistic consideration of the NC-shape grinding process with toroid grinding wheels. The process is investigated by applying extensive modelling and simulation methods within a project supported by the DFG*. The aim is to optimize the grinding process, i.e., to avoid grinding errors. The optimization is mainly done by modifying the NC-data. Therefore, all process relevant factors have to be known during the complete process and are determined by the simulation.

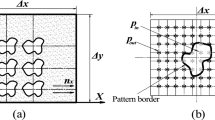
During these investigations toroid grinding wheels of the form 1F1 [11] are used. Unlike the grinding process with cylindrical tools, grinding wheel contact areas that can not be described analytically can occur, especially while grinding free formed surfaces. The different material removal volumes during one grinding wheel rotation are exemplarily shown in Fig. 1. In [12], the contact area between grinding wheel and workpiece is pointed out for its influence on the process, because this area represents the most important part in the entire closed loop interaction of the grinding operation. The material removal is carried out during the process line by line. It can vary both along a line and between two consecutive lines. The desired surface can be produced by multidimensional relative motions between grinding wheel and workpiece.

Fig. 1
figure 1

Material removal volume during one grinding wheel rotation for a a cylindrical and b a toroid grinding wheel

Full size image

The limits are given geometrically by the radius of the grinding wheel profile and by the grinding wheel radius. The smallest producable concave radius on the workpiece is given by the respective toolradius. Research into profile production by NC-shape grinding shows a dependency between the magnitude of the concave radius and the form deviation. The closer the profile radius of the grinding wheel resembles the target radius of the workpiece, the larger the deviations between the measured and the target radius on the workpiece [13].

2 Process description

For the investigations, ceramically bonded CBN grinding wheels are used, because these exhibit a long endurance and thus a high profile accuracy. The semicircular profile of the applied grinding wheel requires the use of an adapted shoe nozzle, because a tangential jet cannot ensure sufficient coolant supply along the grinding wheel profile.

For the selected tool-workpiece combination, the maximum appropriate grinding wheel infeed for grinding in full material at a feed rate of v f = 1,000 mm/min amounts to a e  = 0.25 mm. With a feed rate of v f = 30,000 mm/min infeeds are possible up to a e = 0.1 mm. Due to the small material removal rate and in order to guarantee an economic process the bigger feed rate is selected for the experiments.

Furthermore, high cutting speed is necessary for CBN grinding wheels, in order to keep the wear small. For the investigations a cutting speed of v c = 50 m/s was chosen. As material X210Cr12 is used. This material reacts sensitively to thermal stress, so that unsuitable process variables can be recognized quickly.

3 Simulation cycle

For modelling the numerically controlled (NC) shape grinding process, a holistic approach is chosen. Consequently the reciprocal effects between structure and process are considered. Present state of research is the simulation of the process by linking two simulation tools. The geometric-kinematic simulation describes the contact area A wgk between the grinding wheel and the workpiece under idealized conditions. A finite-element simulation takes the dynamics of the process into account. Investigations regarding the wear of the tools as well as temperature analyses are intended as a future work.

The complete simulation consists of three parts: the geometric-kinematic simulation, the finite-element simulation and the removal-predictor. The interaction of these three parts is illustrated in Fig. 2 and described in this section. More details are given in the following text. The geometry, the material properties and the NC-data are the main inputs of the simulation. The surface of the workpiece after the grinding process is the main output. It is mainly determined by the infeed a e,act. The displacement of the grinding wheel and the process forces are additional results.

Fig. 2
figure 2

The simulation cycle in a time step

Full size image

The simulation is controlled by the geometric-kinematic simulation. Consequently the global temporal discretization is implemented here. At the moment, equal time steps are used for the geometric-kinematic simulation and for the finite-element simulation. Later on, it may become necessary to use smaller time steps for the finite-element simulation in order to increase the accuracy.

After the initialization of the different simulations, consisting mainly of the reading of the geometric data and the usual finite-element preparations, time stepping starts. The simulation cycle displayed in Fig. 2 is passed through in each time step. It starts with the geometric-kinematic simulation. First, some preparation steps are necessary. The new position of the workpiece in relation to the grinding wheel is determined according to the NC-data. The result process force F res in the current time step is calculated from the geometric-kinematic data. For this purpose an empirical grinding force model is used, which is only able to predict a result process force. No local or microscopic effects are taken into account.

The part of the workpiece surface, which might be in contact with the grinding wheel is passed from the geometric-kinematic simulation to the finite-element simulation. This information is used to handle the contact constraints of the dynamic Signorini problem in the current time step. Then the discrete problem is solved and the current normal contact stress is determined. The resulting accumulated contact force F con is calculated subsequently from the normal contact stress and returned to the removal-predictor. The most important parts of the grinding machine, the grinding wheel and the spindle, are taken into account in the finite-element simulation. The stiffness of the other parts of the machine is modelled by additional elastic bearings.

The finite-element simulation is able to calculate the accumulated contact force F con. Thereby, the contact area is considered in detail. F con depends directly on the real infeed a e,act. So it is expected, that a good approximation of a e,act has been found, if F con and F res coincide. The predicted global process force F res is stored in the removal-predictor.

Two steps are performed in the removal-predictor. First, it tests if the accumulated contact force F con and the predicted process force F res match. In this case, the cycle is left and the next time step is started. Otherwise, a corrected value for the real infeed a e,act is predicted and passed to the geometric-kinematic simulation. Here, the surface of the workpiece is modified accordingly, and the cycle restarts.

4 Geometric-kinematic simulation

The geometric-kinematic simulation discribes the contact between grinding wheel and workpiece based on idealized process conditions, i.e., grinding takes place without wear, no temperature influences are present and the system is rigid. All relevant factors for the process analysis can be determined from this contact. In each time step the simulation calculates the contact area between grinding wheel and workpiece, the material removal rate as well as the effective infeed. The effective infeed a e,eff describes the radial infeed of the grinding wheel along the grinding wheel profile and varies accordingly over the contact area (Fig. 3).

Fig. 3
figure 3

The effective infeed along the grinding wheel profile

Full size image

Based on the experiences with the simulation of milling processes at the ISF, a nailblock-model of the workpiece is the basis of the geometric-kinematic simulation. Beginning and end of the nails represent in each case a part of the workpiece exterior surface. The material removal takes place via the time-discrete determination of the intersections of individual nails with the constructive-solid-geometry-model (CSG model) of the grinding wheel [14]. Here the grinding wheel is simplified as ring torus.

5 Empirical grinding force model

As already shown in Fig. 1, complex contact areas can be present in shape grinding under employment of toroid grinding wheels. The feed is not constant over the grinded volume. Conventional grinding-force models as presented in [15] cannot be used for the determination of the process forces of NC-shape grinding with toroid grinding wheels. Thus a new model was developed based on the measurements presented in Fig. 4.

Fig. 4
figure 4

Influence of removal rate and contact area to process forces

Full size image

For the investigations no variation of the workpiece material, grinding wheel geometry and cutting speed is intended. Therefore, these factors are not considered in the force model. For the sufficiently exact determination of the process forces, as they are needed for the FEM-simulation, an empirical model can be provided from measured data and the factors of the geometrical-kinematic simulation. Axial and tangential forces were found to primarily dependent on the contact area A wgk, radial force is mainly determined by the removal rate Q w .

$$ F_r =70.2+2.86 Q_W $$
$$ F_t =4.79+6.14 A_{\rm wgk} $$
$$ F_a =4.186+77.1 a_e +5.366 A_{\rm wgk} $$

6 Finite-element simulation

The most relevant parts of the machine, the grinding wheel and the spindle, constitute the domain of the finite-element model. Since their deformation is small during the grinding process, a linear elastic material law is used. In addition, contact constraints have to be included in the model, because the displacements of the grinding wheel are restricted by the workpiece. Finally, the dynamic behavior of the machine has to be taken into account, too. Therefore, an appropriate model is given by a dynamic Signorini problem. The mathematical formulation of this problem can be found in [16].

The discretization of the dynamic Signorini problem can be carried out either by finite difference schemes such as the Newmark method in time and finite elements in space [17] or by finite elements in space and time [18]. Both methods are implemented in the finite-element library SOFAR [19], which is the platform that was used for the presented calculations.

The precise knowledge of the workpiece surface is essential for the simulation. The workpiece surface is discretized by the nailblock model of the geometric-kinematic simulation. So the finite-element simulation has to evaluate this description of the surface at many different points. The nails, which lie in the possible contact area, are transferred to the finite-element simulation. Since the finite-element mesh is not equal to the nailblock, the evaluation has to be done via interpolation.

Two approaches seem to be reasonable for the calculation of the normal contact stress. The first one is to calculate the normal contact stress based on the displacement u by the equation

$$ \sigma _N \left(x \right)=n\left(x \right)^T\left({C\varepsilon \left( {u\left(x \right)} \right)} \right)n\left(x \right), $$

where x is an element of the possible contact boundary Γ C , n is the normal vector in x onto Γ C , C is the material tensor and

$$\varepsilon \left(u \right)=\frac{1}{2}\left({\nabla u+\nabla u^T} \right)$$

is the linearized strain tensor. The second possibility is to rewrite the variational inequality as a mixed problem. Here, the normal contact stress is just the Lagrangian multiplier in the mixed problem. Thus, it is calculated in combination with the displacements during the solution process. The second formulation is preferred, because a better accuracy is achieved.

In Fig. 5 the finite-element model and a drawing of the spindle and the grinding wheel are displayed. In the finite-element model the geometry has been slightly simplified and is discretized by hexahedral elements. The material is linear elastic in the whole domain. But the material parameters vary. The regions of the different material parameters are indicated in the finite-element model in Fig. 5. The first region consists of the spindle and the carrier of the grinding wheel. The second one contains the grinding layer. The third region is given by the bearings.

Fig. 5
figure 5

Drawing (a) and finite-element model (b) of the spindle and the grinding wheel

Full size image

The material parameters of the bearings are used to model the stiffness of the rest of the grinding machine. The displacement of the grinding wheel under a given load is measured in experiments.

The same load is applied in the simulation and the results are compared to the experiments. This is used to adjust the material parameters. Since the displacement of the grinding wheel in the finite-element solution strongly depends on the mesh width h, this step has to be done separately for every h.

7 Measurement of compliance

Due to the coolant and high rotation speed of the grinding wheel the measurement of the grinding wheel vibration in process is not possible. From the finished workpiece a first estimation of the structural compliance is possible through the difference of measured infeed a e,act and adjusted target infeed a e,ref. The difference in relation to the averaged radial force represents approximately the vertical compliance of the system. However, it is to be noted that friction and temperature-dependent as well as dynamic effects influence the measured factors. As represented in Fig. 6, the measurements show a more rigid machine behavior with smaller radial process force. At the same time the experiments prove that the balance condition of the grinding wheel exerts only a small influence on the result. Furthermore, there are smaller compliances, if the grinding wheel is completely ground in.

Fig. 6
figure 6

Difference between measured- and target-infeed

Full size image

Regardless of the dynamic effects, the compliance of the system is measured quasi-statically (Fig. 7). For this purpose the displacement of the grinding wheel is determined under the effect of static loads. A defined force is applied to the spindle in horizontal direction. By regarding the spindle without rotation, larger deflections can be observed. Because of this, the spindle rotates during the measurement with n = 6 min−1. Due to the tactile measurement, higher rotation speed is not realizable.

Fig. 7
figure 7

Quasi-static measurement of compliance

Full size image

Similar to the preceding results, these measurements show a stiffer machine behavior at smaller applied forces. Altogether the results of the measurements show a less stiff system than determined before. The comparison of both measurements shows the influence of effects, which are independent of the structural rigidity. By using the finite-element simulation for describing the dynamic effects, the compliance under quasi-static conditions are used for the modelling.

8 Removal-predictor

The infeed a e,ref is given by the NC-data. But the machine is not able to realize this infeed. Instead a real infeed a e,act is measured, which is smaller than the given infeed. The geometric-kinematic simulation is only able to simulate the given infeed. It is combined with the finite element simulation to obtain a better approximation of a e,act.

The process force F res is predicted by the geometric-kinematic simulation and the contact force F con is calculated by the finite-element simulation. A good approximation of the real infeed is found, if the contact force and the predicted process force are equal. The problem is to find such an approximation of the real infeed. The solution algorithm is described in this section.

The accumulated contact force F con is calculated from the given normal contact stress by the equation

$$F_{\rm con} =\int\limits_{\Gamma _C} {\sigma _N \, n\,{\rm d}x} .$$

The contact force F con is a function of the real infeed. It is known (see e.g., [20]) that approximately

$$ \sigma_{N}={C|(u_{N}-g)_{+}|}^{m} $$

holds with some C > 0 and m ∈[2,3.3]. The gap-function g measures the distance between the grinding wheel and the workpiece surface. The normal displacement of the grinding wheel is given by u N . So it is assumed that

$$ |F_{con}| \approx {C|a_{e,{\rm ref}}-a_{e,{\rm act}}}|^{m} $$

holds. This is a rough approximation, but it is accurate enough for the prediction of the removal.

The iterative algorithm predicts approximations a l of a e,act. The chosen starting value is a 0 = 0. The corresponding contact force F 0 is much larger than F res, since no removal takes place. Next a 1 is obtained by the equation

$$ \left| {a_{e,{\rm ref}} - a_1 } \right| = \left| {a_{e,{\rm ref}} - a_0 } \right| \left( {\frac{{F_{\rm res} }} {{F^0 }}} \right)^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}} . $$

In the next iteration cycle F 1 is calculated. The procedure is iterated until the condition

$$\left|F_{\rm res}-F^{n} \right|\leqslant {\rm tol}$$

holds for a given tolerance tol. Thereby, the equation

$$ \left| {a_{e,{\rm ref}} - a_l } \right| = \left| {a_{e,{\rm ref}} - a_{l - 1} } \right| \cdot \left( {\frac{{F_{\rm res} }} {{F^{l - 1} }}} \right)^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}} $$

is used to predict the corrected infeed a l from the values of the last simulation cycle.

In practice some additional rules are implemented to speed up the computation and to handle some problematic cases, e.g., if F i equals zero. The predicted process force is used to obtain a good starting value for the iteration. It is added to the load vector and then one unrestricted calculation is performed. This way a good starting value is given by the displacement after the unconstrained calculation. The highest and lowest values for the real infeed, which are used in the current iteration, are saved. In the exceptional cases, if for example, the predicted value is not within this interval or F i equals zero, the midpoint of the interval is taken as the next approximation.

9 Numerical results

The presented simulation is tested by means of a simple grinding process. The cutting speed was set to v c = 50 m/s and the feed rate was v f = 30 m/min. So the grinding wheel rotated with n = 5,100 min−1. The infeed was set to a e = 40 μm. An oil based coolant was used. The process kinematic was down-grinding.

The simulation was carried out as described above. The termination tolerance was set to tol = 10 N. This seems to lead to a rough approximation. But the experience with the simulation showed that a smaller tolerance changes the values of the real infeed a e,act by only about 0.001 μm. Thus the tolerance is accurate enough considering the other model errors. Three to four passes of the simulation cycle are necessary to reach the given tolerance. If the better starting values, as described in the last section, are not used, six to seven passes were necessary.

In Fig. 8 a cut through the workpiece is displayed. The profiles simulated with time step lengths of Δt = 0.000125 s and Δt = 0.0005 s look similar to the filtered measured profile, which does not contain the surface roughness of the workpiece. All three profiles show fluctuations during the initial and the final sections of the grinding pass.

Fig. 8
figure 8

The simulated and the real workpiece surface

Full size image

The best approximation of the displayed numerical results is achieved for a time step length Δ t = 0.000125 s. The result with Δt = 0.0005 s is displayed to demonstrate the convergence properties of the presented algorithm with respect to Δt. The third displayed approximation, named elastic, is only based on the predicted process forces, which are applied to the linear elastic model without considering the contact conditions. The length of the time step for the pure elastic simulation was also selected as Δt = 0.000125 s. The computing time for the pure elastic simulation is smaller, since only one elastic problem has to be solved in every time step. But the accuracy of the pure elastic simulation is significantly smaller than the accuracy of the simulation, which uses the above presented approach.

10 Conclusions and future work

A simulation of the grinding process with toroid grinding wheels is presented in this article. The simulation consists of three parts. The geometric-kinematic simulation discretizes the workpiece and the kinematics of the grinding machine. It is also able to approximately predict the grinding forces. The finite-element simulation describes the response of the grinding machine to the contact between the grinding wheel and the workpiece. The removal-predictor uses the contact forces to calculate an approximation of the real infeed.

The results of the simulation have been tested using a simple grinding process. Thereby a basic correspondence of the simulated with real experimental results is demonstrated. It is also shown, that the results of the presented simulation are more accurate than the results of a simulation, which uses only the predicted grinding forces as input for the finite-element simulation. Therefore the presented simulation is an improvement over the existing simulations.

The simulation takes the main interactions between the structure of the grinding machine and the process into account. But the simulation has to be improved further in order to achieve even better results, because the important effects of friction and temperature are missing. Therefore, the finite-element simulation will be extended to consider frictional and damping effects. This is mainly an extension of the dynamic Signorini problem. The temperature is closely related to the friction and also has an influence on the grinding process. So the effects of the temperature on the workpiece and on the structure will be considered later. Finally, a strategy for the grinding process, which prevents damage to the workpiece surface, can be developed using this knowledge.

The consideration of these additional effects will significantly increase the computational effort in every time step. Consequently techniques to decrease this effort have to be used. A posteriori error estimation and adaptive mesh refinement are techniques to increase the accuracy of the results with minimal additional cost. In addition to this, high performance computing techniques will be used to decrease the computing time.