Thermodynamic Assessment of the Fe-Mn-O System

Abstract

The C-Cr-Fe-Ni-O system has recently been studied with the intention to thermodynamically describe the influence of oxygen on high alloyed steels. In this study the ternary Fe-Mn-O system is assessed and part of the binary Mn-O system is reassessed. α- and β-hausmannite (Mn₃O₄) were earlier described as stoichiometric phases, but are here described using the compound energy formalism with a four sublattice model to be consistent with the preceding study of the Cr-Fe-Ni-O spinel. The liquid phase is assessed using the ionic two-sublattice model. Good agreement between calculated and experimental values is achieved.

Introduction

In a preceding study the C-Cr-Fe-Ni-O system[1,2] was described. It is a basic system for describing stainless steels. In this study the Fe-Mn-O system is assessed, a first step towards a consistent C-Cr-Fe-Mn-Ni-O database. In the present work both the metallic and the oxide liquid are modelled using the ionic two-sublattice model.[3,4] The ionic two-sublattice liquid model was developed within the framework of the compound energy formalism (CEF),[5] which is used to describe phases using two or more sublattices and is widely used in CALPHAD assessments.[6,7]

The Fe-O system was assessed by Sundman,[8] and later modified by Selleby and Sundman[9] (ionic liquid), Kowalski and Spencer[10] (fcc and bcc) and Kjellqvist et al.[1] (hematite). This modified description of Sundmans assessment is used in this study. The Mn-O system has been assessed by Grundy et al.,[11] and is here accepted after slight modifications. Grundy et al. described α- and β-hausmannite (Mn₃O₄) as stoichiometric phases where each component can reside in only one sublattice, thus without the possibility to describe any degree of inversion. Those phases are now treated using a more complex model, where the degree of inversion and also the deviation from stoichiometry are described. In their model for the ionic liquid they use a Mn⁺³ species which now is replaced by a neutral MnO_1.5 species equivalent to the description of the Fe-O system. For the third binary, Fe-Mn, the assessment of Huang[12] is accepted without modification. The ternary system, Fe-Mn-O, has been assessed by Weiland,[13] but is reassessed in this work. Weiland used a different description of the Mn-O system and the α- and β-spinel phases were modelled as stoichiometric phases with respect to oxygen. Pelton et al.[14] performed an assessment on the Fe₃O₄-Mn₃O₄ system.

Some phases undergo a magnetic transition characterized by a λ-peak in the heat capacity curve. The magnetic contribution to the Gibbs energy is given by a model proposed by Inden[15] and adapted by Hillert and Jarl.[16]

Thermodynamic Models

Liquid

Grundy et al.[11] applied the ionic two-sublattice liquid model[3,4] to the Mn-O system, using the formula $\left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} } \right)_{P} \left( {{\text{O}}^{{ 2 - }} ,{\text{Va}}^{{Q - }} } \right)_{Q}$. The liquid phase in the Fe-O system was first modelled with $\left( {{\text{Fe}}^{{ 2 + }} ,{\text{Fe}}^{{ 3 + }} } \right)_{P} \left( {{\text{O}}^{{ 2 - }} ,{\text{Va}}^{{Q - }} } \right)_{Q}$,[8] but later Fe³⁺ was replaced by a neutral species, FeO_1.5.[9] This change was imposed by an equivalent change for Al-containing system where Al³⁺ was replaced by AlO_1.5 in order to better control the unwanted reciprocal miscibility gaps that occurred in e.g. Al₂O₃-CaO-SiO₂. However, even though a new model for liquid Al₂O₃ (without AlO_1.5) has been developed,[17] the FeO_1.5 species has been kept. In the present work the formula $\left( {{\text{Fe}}^{{ 2 + }} ,{\text{Mn}}^{{ 2 + }} } \right)_{P} \left( {{\text{O}}^{{ 2 - }} ,{\text{Va}}^{{Q - }} ,{\text{FeO}}_{ 1. 5} ,{\text{MnO}}_{ 1. 5} } \right)_{Q}$ will be used. P and Q is the number of sites on each sublattice. P and Q vary so that electroneutrality is maintained. The same model can be used both for metallic and oxide melts. At low levels of oxygen, the model becomes equivalent to a substitutional solution model between metallic atoms. The Gibbs energy of the liquid phase is expressed by:

$$ \begin{aligned} G_{\text{m}} &=\,y_{{{\text{Fe}}^{{ 2 + }} }} y_{{{\text{O}}^{{ 2 - }} }}{}^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{O}}^{{ 2 - }} }} + y_{{{\text{Mn}}^{{ 2 + }} }} y_{{{\text{O}}^{{ 2 - }} }}{}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{O}}^{{ 2 - }} }} + Qy_{{{\text{Va}}^{{Q - }} }} \left( {y_{{{\text{Fe}}^{{ 2 + }} }}{}^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Va}}^{{Q - }} }} + y_{{{\text{Mn}}^{{ 2 + }} }}{}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Va}}^{{Q - }} }} } \right) + Q\left( {y_{{{\text{FeO}}_{ 1. 5} }}{}^{\text{o}}G_{{{\text{FeO}}_{ 1. 5} }} + y_{{{\text{MnO}}_{ 1. 5} }}{}^{\text{o}}G_{{{\text{MnO}}_{ 1. 5} }} } \right) + {\text{RTP}}\left( {y_{{{\text{Fe}}^{{ 2 + }} }} { \ln }\left( {y_{{{\text{Fe}}^{{ 2 + }} }} } \right)} \right) + y_{{{\text{Mn}}^{{ 2 + }} \, }} { \ln }\left( {y_{{{\text{Mn}}^{{ 2 + }} }} } \right) \hfill \\& + {\text{RTQ}}\left( {y_{{{\text{O}}^{{ 2 - }} }} { \ln }\left( {y_{{{\text{O}}^{{ 2 - }} }} } \right) + y_{{{\text{Va}}^{Q - } }} { \ln }\left( {y_{{{\text{Va}}^{{Q - }} }} } \right) + y_{{{\text{FeO}}_{ 1. 5} }} { \ln }\left( {y_{{{\text{FeO}}_{ 1. 5} }} } \right) + y_{{{\text{MnO}}_{ 1. 5} }} { \ln }\left( {y_{{{\text{MnO}}_{ 1. 5} }} } \right)} \right) +^{\text{E}}G_{\text{m}} \hfill \\ \end{aligned} $$

(1)

where y denotes the site-fraction and ${}^{\text{E}}G_{\text{m}}$ is the excess Gibbs energy which depends on the interaction between species within each sublattice. The interaction parameters used in this assessment are the following:

$$ \begin{aligned}{}^{\text{E}}G_{\text{m}} &= y_{{{\text{Fe}}^{{ 2 + }} }} y_{{{\text{Mn}}^{{ 2 + }} }} y_{{{\text{O}}^{{ 2 - }} }} \, \left( {{}^{0}L_{{{\text{Fe}}^{{ 2 + }} ,{\text{Mn}}^{{ 2 + }} :{\text{O}}^{{ 2 - }} }} +{}^{1}L_{{{\text{Fe}}^{{ 2 + }} ,{\text{Mn}}^{{ 2 + }} :{\text{Va}}}} \left( {y_{{{\text{Fe}}^{{ 2 + }} }} - y_{{{\text{Mn}}^{{ 2 + }} }} } \right)} \right) \hfill \\ &+Q \, y_{\text{Va}}^{ 2} y_{{{\text{Fe}}^{{ 2 + }} y{\text{Mn}}^{{ 2 + }} }} \left( {{}^{0}L_{{{\text{Fe}}^{{ 2 + }} ,{\text{Mn}}^{{ 2 + }} :{\text{Va}}}} +{}^{1}L_{{{\text{Fe}}^{{ 2 + }} ,{\text{Mn}}^{{ 2 + }} :{\text{Va}}}} \left( {y_{{{\text{Fe}}^{{ 2 + }} }} - y_{{{\text{Mn}}^{{ 2 + }} }} } \right)} \right) \hfill \\ &+y_{\text{Va}} y_{{{\text{Fe}}^{{ 2 + }} }} y_{{{\text{O}}^{{ 2 - }} }} \left( {{}^{0}L_{{{\text{Fe}}^{{ 2 + }} :{\text{O}}^{{ 2 - }} ,{\text{Va}}}} +{}^{1}L_{{{\text{Fe}}^{{ 2 + }} :{\text{O}}^{{ 2 - }} ,{\text{Va}}}} \left( {y_{{{\text{O}}^{{ 2 - }} }} - y_{\text{Va}} } \right)} \right) \hfill \\ &+y_{\text{Va}} y_{{{\text{Mn}}^{{ 2 + }} }} y_{{{\text{O}}^{{ 2 - }} }} \left( {{}^{0}L_{{{\text{Mn}}^{{ 2 + }} :{\text{O}}^{{ 2 - }} ,{\text{Va}}}} +{}^{1}L_{{{\text{Mn}}^{{ 2 + }} :{\text{O}}^{{ 2 - }} ,{\text{Va}}}} \left( {y_{{{\text{O}}^{{ 2 - }} }} - y_{\text{Va}} } \right)} \right) \hfill \\&+ y_{{{\text{Fe}}^{{ 2 + }} }} y_{{{\text{O}}^{{ 2 - }} }} y_{{{\text{FeO}}_{ 1. 5} }} \left( {{}^{0}L_{{{\text{Fe}}^{{ 2 + }} :{\text{O}}^{{ 2 - }} ,{\text{FeO}}_{ 1. 5} }} +{}^{1}L_{{{\text{Fe}}^{{ 2 + }} :{\text{O}}^{{ 2 - }} ,{\text{FeO}}_{ 1. 5} }} \left( {y_{{{\text{O}}^{{ 2 - }} }} - y_{{{\text{FeO}}_{ 1. 5} }} } \right)} \right) \hfill \\ &+y_{{{\text{Mn}}^{{ 2 + }} }} y_{{{\text{O}}^{{ 2 - }} }} y_{{{\text{FeO}}_{ 1. 5} }}{}^{0}L_{{{\text{Mn}}^{{ 2 + }} :{\text{O}}^{{ 2 - }} ,{\text{FeO}}_{ 1. 5} }} + y_{{{\text{Mn}}^{{ 2 + }} }} y_{{{\text{O}}^{{ 2 - }} }} y_{{{\text{MnO}}_{ 1. 5} }}{}^{0}L_{{{\text{Mn}}^{{ 2 + }} :{\text{O}}^{{ 2 - }} ,{\text{MnO}}_{ 1. 5} }} \hfill \\&+ Qy_{\text{Va}} (y_{{{\text{Fe}}^{{ 2 + }} }} y_{{{\text{FeO}}_{ 1. 5} }}{}^{0}L_{{{\text{Fe}}^{{ 2 + }} :{\text{FeO}}_{ 1. 5} ,{\text{Va}}}} + y_{{{\text{Fe}}^{{ 2 + }} }} y_{{{\text{MnO}}_{ 1. 5} }}{}^{0}L_{{{\text{Fe}}^{ + 2} :{\text{MnO}}_{ 1. 5} ,{\text{Va}}}} \hfill \\ &+y_{{{\text{Mn}}^{{ 2 + }} }} y_{{{\text{FeO}}_{ 1. 5} }}{}^{0}L_{{{\text{Mn}}^{{ 2 + }} :{\text{FeO}}_{ 1. 5} ,{\text{Va}}}} + y_{{{\text{Mn}}^{{ 2 + }} }} y_{{{\text{MnO}}_{ 1. 5} }}{}^{0}L_{{{\text{Mn}}^{{ 2 + }} :{\text{MnO}}_{ 1. 5} ,{\text{Va}}}} ) \hfill \\ \end{aligned} $$

(2)

A colon is used to separate species on different sublattices and a comma is used to separate species on the same sublattice.

Spinel: Cubic and Tetragonal

There are two types of spinel phases in the Fe-Mn system; cubic and tetragonal spinels (Strukturbericht H1₁ for cubic spinel). Hausmannite (Mn₃O₄) is a tetragonal spinel (α-Mn₃O₄) at low temperatures and transforms to a cubic spinel (β-Mn₃O₄) at higher temperatures. α-Mn₃O₄ dissolves small amounts of Fe, while β-Mn₃O₄ extend up to magnetite (Fe₃O₄). The tetragonal distortion originates from the Jahn-Teller distortion[18] of octahedral sites occupied by Mn³⁺ ions.

Dorris and Mason[19] found that α- and β-Mn₃O₄ have different ionic configuration. They believe that α-Mn₃O₄ has the same ionic configuration as cubic ${\text{Fe}}_{ 3} {\text{O}}_{ 4}{:}\; \left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} } \right)_{ 1} \left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} } \right)_{ 2} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 4}$, while in the case of β-Mn₃O₄ Mn²⁺ resides on tetrahedral sites and Mn²⁺, Mn³⁺ and Mn⁴⁺ on octahedral sites: $\left( {{\text{Mn}}^{{ 2 + }} } \right)_{ 1} \left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} ,{\text{Mn}}^{{ 4 + }} } \right)_{ 2} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 4}$. Other authors conclude that these charge states are Mn²⁺ and Mn³⁺ for both phases, see for example Ref 20-23. Taking other manganese containing spinels into consideration, e.g. the Mn-Ni system, the model with Mn⁴⁺ ions is preferred. β-Spinel dissolve more nickel than NiMn₂O₄, thus β-spinel in Mn-Ni can not sufficiently be described without using Mn⁴⁺ ions on octahedral sites. In this work it is assumed that α- and β-Mn₃O₄ have different ionic configurations: stoichiometric α-Mn₃O₄ is described by $\left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} } \right)_{ 1} \left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} } \right)_{ 2} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 4}$ and β-Mn₃O₄ by $\left( {{\text{Mn}}^{{ 2 + }} } \right)_{ 1} \left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} ,{\text{Mn}}^{{ 4 + }} } \right)_{ 2} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 4}$.

Cubic Hausmannite (β-Mn₃O₄)

The complete description of the spinel phase is rather complicated why a stoichiometric spinel is considered as a first approach, which is modelled using the formula $\left( {{\text{Mn}}^{{ 2 + }} } \right)_{ 1} \left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} ,{\text{Mn}}^{{ 4 + }} } \right)_{ 2} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 4}$. The first sublattice represents tetrahedral sites and the second sublattice represents octahedral sites. A normal spinel has the trivalent ions on the octahedral sites and the divalent ions on the tetrahedral sites. If the octahedral sites are occupied by divalent and tetravalent ions the spinel is referred to as inverse. The three ^o G parameters $\left( {{}^{\text{o}}G_{{{\text{Mn}}^{2 + } :{\text{Mn}}^{2 + } }}^{\upbeta } ,\;{}^{\text{o}}G_{{{\text{Mn}}^{2 + }:{\text{Mn}}^{3 + } }}^{\upbeta } ,\;{\text{and}}\;{}^{\text{o}}G_{{{\text{Mn}}^{2 + } :{\text{Mn}}^{4 + } }}^{\upbeta } } \right)$ are from now on denoted ${}^{\text{o}}G_{22}^{\upbeta } ,\;{}^{\text{o}}G_{23}^{\upbeta } ,\;{\text{and}}\;{}^{\text{o}}G_{24}^{\upbeta }$. The Gibbs energy of stoichiometric β-Mn₃O₄ is given by

$$ {}^{\text{o}}G_{\text{m}}^{\upbeta } = y_{2}^{\prime } y_{2}^{\prime \prime\, \text{o}}G_{22}^{\upbeta } + y_{2}^{\prime } y_{3}^{\prime \prime\, \text{o}}G_{23}^{\upbeta } + y_{2}^{\prime } y_{4}^{\prime \prime\, \text{o}}G_{24}^{\upbeta } - {\text{TS}}_{\text{m}} +{}^{\text{E}}G_{\text{m}} $$

(3)

where the superscripts ′ and ′′ denote tetrahedral and octahedral sites, respectively. This is a system with a neutral line between the ${}^{\text{o}}G_{23}^{\upbeta }$ corner and the middle of the ${}^{\text{o}}G_{22}^{\upbeta } - {}^{\text{o}}G_{24}^{\upbeta }$ side. All points on the neutral line between the normal and inverse spinels represent the stoichiometric composition, but with different distributions of ions on the octahedral sublattice. Only one point on the line represents the equilibrium composition at a given temperature. Only two parameters can normally be evaluated since there are two pieces of information, the Gibbs energy of the equilibrium phase and the degree of inversion. The site fractions in Eq 3 are replaced by a variable describing the disorder, ξ. ξ = 0 yields the normal state $\left( {{\text{Mn}}^{{ 2 + }} } \right)_{ 1} \left( {{\text{Mn}}^{{ 3 + }} } \right)_{ 2}$ and ξ = 1 yields the inverse state $\left( {{\text{Mn}}^{{ 2 + }} } \right)_{ 1} \left( {{\text{Mn}}_{0. 5}^{2 + } ,{\text{Mn}}_{0.5}^{4 + } } \right)_{ 2}$. ξ is an expression of the degree of inversion and can be used to express all site fractions, $\upxi = 1- y_{3}^{\prime \prime } = 2y_{2}^{\prime \prime } = 2y_{4}^{\prime \prime } ,\;y_{2}^{\prime } = 1$. All interaction energies in Eq 3 should be neglected since there already are more compound energies than experimental information, i.e. ^E G _m is set to zero. Rearranging Eq 3 and expressing all site fractions in terms of ξ yields:

$$ G_{\text{m}}^{\upbeta } + {\text{TS}}_{\text{m}} \left( \upxi \right) = {}^{\text{o}}G_{23}^{\upbeta } + J_{234}^{\upbeta } \upxi $$

(4)

$$ J_{234}^{\upbeta } = 0. 5{}^{\text{o}}G_{22}^{\upbeta } + 0. 5{}^{\text{o}}G_{24}^{\upbeta } - {}^{\text{o}}G_{23}^{\upbeta } $$

(5)

Gibbs energy of β-Mn₃O₄ is given by the parameter ${}^{\text{o}}G_{23}^{\upbeta }$ and $J_{234}^{\upbeta }$ is used to model the degree of inversion. ${}^{\text{o}}G_{22}^{\upbeta }$ is used as a reference and can adopt any value. If Mn-O was assessed without the intention to include the description in a larger system the easiest choice would be to put ${}^{\text{o}}G_{22}^{\upbeta } = 0$. But since a reference already is chosen in Fe₃O₄, ${}^{\text{o}}G_{22}^{\upbeta }$ will adopt a value from the Fe-Mn-O assessment that is compatible with the reference in Fe-O. This gives the following parameters for stoichiometric β-Mn₃O₄:

$$ {}^{\text{o}}G_{22}^{\upbeta } \quad {\text{reference}} $$

(6)

$$ {}^{\text{o}}G_{23}^{\upbeta } = 7G_{{_{{{\text{Mn}}_{ 3} {\text{O}}_{ 4} }} }}^{\upbeta } $$

(7)

$$ {}^{\text{o}}G_{24}^{\upbeta } = 1 4G_{{{\text{Mn}}_{ 3} {\text{O}}_{ 4} }}^{\upbeta } + J_{{{\text{Mn}}_{ 3} {\text{O}}_{ 4} }}^{\upbeta } -{}^{\text{o}}G_{22}^{\upbeta } $$

(8)

β-Mn₃O₄ shows a small deviation from stoichiometry. Vacant sites are formed in the octahedral sublattice to maintain electroneutrality when excess Mn⁴⁺ is introduced to model the deviation towards oxygen in equilibrium with Mn₂O₃. The extended spinel model is then $\left( {{\text{Mn}}^{{ 2 + }} } \right)_{ 1} \left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} ,{\text{Mn}}^{{ 4 + }} ,{\text{Va}}} \right)_{ 2} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 4}$. Several combinations to form neutral Mn₂O₃ with spinel structure are found in this formula. One of them is used to describe the deviation from stoichiometry towards oxygen. Gibbs energy of this Mn₂O₃ is

$$ {}^{\text{o}}G_{\text{m}}^{\upbeta } = \left( { 2^{\text{o}}G_{23}^{\upbeta } + 3^{\text{o}}G_{24}^{\upbeta } +{}^{\text{o}}G_{{ 2 {\text{V}}}}^{\upbeta } - 2 {\text{RT}}\left( { 6\;{ \ln }\left( 6\right) - 3 {\text{ ln}}\left( 3\right) - 2 {\text{ ln}}\left( 2\right)} \right)} \right)/ 6 $$

(9)

where ${}^{\text{o}}G_{{ 2 {\text{V}}}}^{\upbeta }$ is used to describe the solubility of O in the spinel. To model deviation towards manganese in equilibrium with halite, Mn²⁺ is assumed to enter interstitial sites normally filled with vacancies. The final spinel model for β-Mn₃O₄ is $\left( {{\text{Mn}}^{{ 2 + }} } \right)_{ 1} \left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} ,{\text{Mn}}^{{ 4 + }} ,{\text{Va}}} \right)_{ 2} \left( {{\text{Mn}}^{{ 2 + }} ,{\text{Va}}} \right)_{ 2} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 4}$. A new neutral endpoint is found, a hypothetical metastable MnO with spinel structure. Gibbs energy of this endpoint is

$$ {}^{\text{o}}G_{\text{m}}^{\upbeta } = \left( {{}^{\text{o}}G_{{ 2 2 {\text{V}}}}^{\upbeta } + {}^{\text{o}}G_{ 2 2 2}^{\upbeta } - 4\;RT\;{ \ln }\left( 2\right)} \right)/ 2 $$

(10)

where ${}^{\text{o}}G_{222}^{\upbeta }$ is used to describe the solubility of Mn in the spinel. The remaining three ^o G parameters $\left( {{}^{\text{o}}G_{232}^{\upbeta } , \, {}^{\text{o}}G_{242}^{\upbeta } ,\;{\text{and}}\;{}^{\text{o}}G_{{ 2 {\text{V2}}}}^{\upbeta } } \right)$ are obtained from reciprocal reactions (ΔG _223:2V2, ΔG _224:2V2, ΔG _22V:2V2), where all reactions are assumed to have ΔG = 0.

Tetragonal Hausmannite (α-Mn₃O₄)

The stoichiometric tetragonal spinel is modelled using the formula $\left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} } \right)_{ 1} \left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} } \right)_{ 2} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 4}$. The four ^o G parameters $\left( {{}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Mn}}^{{ 2 + }} }}^{\upalpha } ,\;{}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Mn}}^{{ 3 + }} }}^{\upalpha } ,\;{}^{\text{o}}G_{{{\text{Mn}}^{{ 3 + }} :{\text{Mn}}^{{ 2 + }} }}^{\upalpha}\; {\text{and}}\;{}^{\text{o}}G_{{{\text{Mn}}^{{ 3 + }} :{\text{Mn}}^{{ 3 + }} }}^{\upalpha } } \right)$ are from now on denoted ${}^{\text{o}}G_{22}^{\upalpha } ,\;{}^{\text{o}}G_{23}^{\upalpha } , \, {}^{\text{o}}G_{32}^{\upalpha}\; {\text{and}}\;{}^{\text{o}}G_{33}^{\upalpha }$. Gibbs energy of stoichiometric α-Mn₃O₄ is given by

$$ {}^{\text{o}}G_{\text{m}}^{\upalpha } = y_{2}^{\prime } y_{2}^{\prime \prime\, \text{o}}G_{22}^{\upalpha } + y_{2}^{\prime } y_{3}^{\prime \prime\, \text{o}}G_{23}^{\upalpha } + y_{3}^{\prime } y_{2}^{\prime \prime\, \text{o}}G_{32}^{\upalpha } + y_{3}^{\prime } y_{3}^{\prime \prime\, \text{o}}G_{33}^{\upalpha } - {\text{TS}}_{\text{m}} + {}^{\text{E}}G_{\text{m}} $$

(11)

This is a reciprocal system, with a neutral line between the ${}^{\text{o}}G_{23}^{\upalpha }$ corner and the middle of the ${}^{\text{o}}G_{32}^{\upalpha } - {}^{\text{o}}G_{33}^{\upalpha }$ side. How to choose the optimizing parameters for a 23-spinel is discussed in detail by Hillert et al.[24] The site fractions in Eq 11 are replaced by a variable describing the disorder, ξ. ξ = 0 yields the normal state $\left( {{\text{Mn}}^{{ 2 + }} } \right)_{ 1} \left( {{\text{Mn}}^{{ 3 + }} } \right)_{ 2}$ and ξ = 1 yields the inverse state $\left( {{\text{Mn}}^{{ 3 + }} } \right)_{ 1} \left( {{\text{Mn}}_{0.5}^{2 + } ,{\text{Mn}}_{0.5}^{3 + } } \right)_{ 2}$. α-Mn₃O₄ is a normal spinel with low degree of inversion. ξ is an expression of the degree of inversion and can be used to express all site fractions, $\upxi = y_{3}^{\prime } = 1- y_{2}^{\prime } = 2y_{2}^{\prime \prime } = 2\left( { 1- y_{3}^{\prime \prime } } \right)$. Rearranging Eq 11, neglecting all interaction energies and expressing all site fractions in terms of ξ yields:

$$ G_{\text{m}}^{\upalpha } + {\text{TS}}_{\text{m}} \left( \upxi \right) = {}^{\text{o}}G_{23}^{\upalpha } + 0. 5J_{23}^{\upalpha } \upxi + 0. 5\Updelta G_{ 2 3: 2 3} \upxi^{ 2} $$

(12)

$$ J_{23}^{\upalpha } = {}^{\text{o}}G_{22}^{\upalpha } - 3^{\text{o}}G_{23}^{\upalpha } + 2^{\text{o}}G_{33}^{\upalpha } $$

(13)

$$ \Updelta G_{ 2 3: 2 3} = {}^{\text{o}}G_{23}^{\upalpha } + {}^{\text{o}}G_{32}^{\upalpha } - {}^{\text{o}}G_{22}^{\upalpha } - {}^{\text{o}}G_{33}^{\upalpha } $$

(14)

Gibbs energy of α-Mn₃O₄ is given by the parameter ${}^{\text{o}}G_{23}^{\upalpha }$ and $J_{23}^{\upalpha }$ is used to model the degree of inversion. ${}^{\text{o}}G_{33}^{\upalpha }$ is used as a reference and will adopt a value from the Fe-Mn-O assessment that is compatible with the reference in the Fe-O assessment. The last parameter, ${}^{\text{o}}G_{32}^{\upalpha }$, is determined by the reciprocal reaction, where ΔG _23:23 = 0 is chosen. This gives the following parameters for stoichiometric α-Mn₃O₄:

$$ {}^{\text{o}}G_{22}^{\upalpha } = 2 1G_{{{\text{Mn}}_{ 3} {\text{O}}_{ 4} }}^{\upalpha } + 2J_{{{\text{Mn}}_{ 3} {\text{O}}_{ 4} }}^{\upalpha } - 2^{\text{o}}G_{33}^{\upalpha } $$

(15)

$$ {}^{\text{o}}G_{23}^{\upalpha } = 7G_{{{\text{Mn}}_{ 3} {\text{O}}_{ 4} }}^{\upalpha } $$

(16)

$$ {}^{\text{o}}G_{\;32}^{\upalpha } = 1 4G_{{{\text{Mn}}_{ 3} {\text{O}}_{ 4} }}^{\upalpha } + 2J_{{{\text{Mn}}_{ 3} {\text{O}}_{ 4} }}^{\upalpha } - {}^{\text{o}}G_{33}^{\upalpha } $$

(17)

$$ {}^{\text{o}}G_{33}^{\upalpha } \quad {\text{reference}} $$

(18)

In the same way as β-Mn₃O₄, α-Mn₃O₄ also shows a small deviation from stoichiometry. The complete model is $\left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} } \right)_{ 1} \left( {{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} ,{\text{Va}}} \right)_{ 2} \left( {{\text{Mn}}^{{ 2 + }} ,{\text{Va}}} \right)_{ 2} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 4}.$

Two new neutral endpoints are found, hypothetical metastable Mn₂O₃ and MnO with spinel structure. The Gibbs energy of these endpoints are

$$ {}^{\text{o}}G_{\text{m}}^{\upalpha } = \left( { 5^{\text{o}}G_{{ 3 3 {\text{V}}}}^{\upalpha } +{}^{\text{o}}G_{{ 3 {\text{VV}}}}^{\upalpha } - 2RT\left( { 6\;{ \ln }\left( 6\right) - 5 {\text{ ln}}\left( 5\right)} \right)} \right)/ 6 $$

(19)

$$ {}^{\text{o}}G_{\text{m}}^{\upalpha } = \left( {{}^{\text{o}}G_{{ 2 2 {\text{V}}}}^{\upalpha } +{}^{\text{o}}G_{222}^{\upalpha } - 4\;RT\;{ \ln }\left( 2\right)} \right)/ 2 $$

(20)

where ${}^{\text{o}}G_{{ 3 {\text{VV}}}}^{\upalpha }$ and ${}^{\text{o}}G_{222}^{\upalpha }$ are used to describe the solubility of O and Mn respectively in α-spinel. The remaining ^o G parameters $\left( {{}^{\text{o}}G_{{ 2 {\text{VV}}}}^{\upalpha } ,\;{}^{\text{o}}G_{232}^{\upalpha } ,\;{}^{\text{o}}G_{{ 2 {\text{V2}}}}^{\upalpha } ,\;{}^{\text{o}}G_{ 3 2 2}^{\upalpha } ,\;{}^{\text{o}}G_{332}^{\upalpha } ,\;{}^{\text{o}}G_{{ 3 {\text{V2}}}}^{\upalpha } } \right)$ are obtained from reciprocal reactions, where all reactions are assumed to have ΔG = 0.

The high temperature β-Mn₃O₄ is modelled relative to α-Mn₃O₄ by:

$$ {}^{\text{o}}G_{{ 2 3 {\text{V}}}}^{\upalpha } = {}^{\text{o}}G_{{ 2 3 {\text{V}}}}^{\upbeta } + A + BT $$

(21)

Cubic Fe-Mn Spinel

The complete cubic Fe-Mn spinel, which besides magnetite and hausmannite consists of jacobsite (MnFe₂O₄), is thus modelled as:

$$ \left( {{\text{Fe}}^{{ 2 + }} ,{\text{Fe}}^{{ 3 + }} ,{\text{Mn}}^{{ 2 + }} } \right)_{ 1} \left( {{\text{Fe}}^{{ 2 + }} ,{\text{Fe}}^{{ 3 + }} ,{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} ,{\text{Mn}}^{{ 4 + }} ,{\text{Va}}} \right)_{ 2} \left( {{\text{Fe}}^{{ 2 + }} ,{\text{Mn}}^{{ 2 + }} ,{\text{Va}}} \right)_{ 2} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 4} $$

The subsystem used to model stoichiometric jacobsite is $\left( {{\text{Fe}}^{{ 3 + }} ,{\text{Mn}}^{{ 2 + }} } \right)_{ 1} \left( {{\text{Fe}}^{{ 3 + }} ,{\text{Mn}}^{{ 2 + }} } \right)_{ 2} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 4}$. This reciprocal system will generate equivalent expressions as in Eq 12-14. As in the model for stoichiometric α-Mn₃O₄, two parameters can be obtained from experiments: Gibbs energy of MnFe₂O₄ and the degree of inversion. ${}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Fe}}^{{ 3 + }} }}^{\upbeta }$ is used to model the Gibbs energy of jacobsite $\left( {G_{{{\text{MnFe}}_{ 2} {\text{O}}_{ 4} }}^{\upbeta } } \right), \, {}^{\text{o}}G_{{{\text{Fe}}^{{ 3 + }} :{\text{Mn}}^{{ 2 + }} }}^{\upbeta }$ the degree of inversion $\left( {J_{{{\text{MnFe}}_{ 2} {\text{O}}_{ 4} }}^{\upbeta } } \right)$ and ${}^{\text{o}}G_{{{\text{Fe}}^{{ 3 + }} :{\text{Fe}}^{{ 3 + }} }}^{\upbeta }$ is already fixed from the Fe-O assessment. The reciprocal reaction, $\Updelta G_{{{\text{Mn}}^{{ 2 + }} ,{\text{Fe}}^{{ 3 + }} :{\text{Mn}}^{{ 2 + }} ,{\text{Fe}}^{{ 3 + }} }} = 0$ will give us the ${}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Mn}}^{{ 2 + }} }}^{\upbeta }$ parameter which is used in the model for Mn₃O₄. This gives the following parameters for stoichiometric MnFe₂O₄:

$$ {}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Mn}}^{{ 2 + }} }}^{\upbeta } = 2 1G_{{{\text{MnFe}}_{ 2} {\text{O}}_{ 4} }}^{\upbeta } + 2J_{{{\text{MnFe}}_{ 2} {\text{O}}_{ 4} }}^{\upbeta } - 1 4G_{{{\text{Fe}}_{ 3} {\text{O}}_{ 4} }}^{\upbeta } + 2B_{{{\text{Fe}}_{ 3} {\text{O}}_{ 4} }}^{\upbeta } $$

(22)

$$ {}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Fe}}^{{ 3 + }} }}^{\upbeta } = 7G_{{{\text{MnFe}}_{ 2} {\text{O}}_{ 4} }}^{\upbeta } $$

(23)

$$ {}^{\text{o}}G_{{{\text{Fe}}^{{ 3 + }} :{\text{Mn}}^{{ 2 + }} }}^{\upbeta } = 7G_{{{\text{Fe}}_{ 3} {\text{O}}_{ 4} }}^{\upbeta } - B_{{{\text{Fe}}_{ 3} {\text{O}}_{ 4} }}^{\upbeta } - 7G_{{{\text{MnFe}}_{ 2} {\text{O}}_{ 4} }}^{\upbeta } + {}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Mn}}^{{ 2 + }} }}^{\upbeta } $$

(24)

$$ {}^{\text{o}}G_{{{\text{Fe}}^{{ 3 + }} :{\text{Fe}}^{{ 3 + }} }}^{\upbeta } = 7G_{{{\text{Fe}}_{ 3} {\text{O}}_{ 4} }}^{\upbeta } - B_{{{\text{Fe}}_{ 3} {\text{O}}_{ 4} }}^{\upbeta } $$

(25)

It may seem strange that the ${}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Mn}}^{{ 2 + }} }}^{\upbeta }$ compound involve parameters evaluated in the assessment of both Fe₃O₄ and MnFe₂O₄ although it does not contain any Fe. This arises because there could only be one ^o G parameter acting as reference in a phase and the reference in the spinel phase is agreed to be ${}^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Fe}}^{{ 3 + }} }}^{\upbeta } = {}^{\text{o}}G_{{{\text{Fe}}^{{ 3 + }} :{\text{Fe}}^{{ 2 + }} }}^{\upbeta }$. It would be possible to choose another reference, i.e. ${}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Mn}}^{{ 2 + }} }}^{\upbeta } = 0$, and adjust the Fe₃O₄ and the MnFe₂O₄ values accordingly. This would give different values on all ^o G parameters that have a net charge, but the description would be identical.

There are still six parameters in the Fe-Mn system needed to be fixed in a proper way $\left( {{}^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Mn}}^{{ 2 + }} }}^{\upbeta } ,\;{}^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Mn}}^{{ 3 + }} }}^{\upbeta } ,\;{}^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Mn}}^{{ 4 + }} }}^{\upbeta } ,\;{}^{\text{o}}G_{{{\text{Fe}}^{{ 3 + }} :{\text{Mn}}^{{ 3 + }} }}^{\upbeta } ,\;{}^{\text{o}}G_{{{\text{Fe}}^{{ 3 + }} :{\text{Mn}}^{{ 4 + }} }}^{\upbeta }\; {\text{ and }}\;{}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Fe}}^{{ 2 + }} }}^{\upbeta } } \right)$. Some of these parameters could be obtained by setting reciprocal reactions equals zero, while others need to be evaluated using some other expressions. Another subsystem in stoichiometric Fe-Mn spinel is $\left( {{\text{Fe}}^{{ 2 + }} ,{\text{Mn}}^{{ 2 + }} } \right)_{ 1} \left( {{\text{Fe}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} ,{\text{Mn}}^{{ 4 + }} } \right)_{ 2} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 4}$, which can be used to model one more possible neutral spinel, FeMn₂O₄. Gibbs energy of this subsystem is given by

$$ G_{\text{m}}^{\upbeta } + {\text{TS}}_{\text{m}} \left( \upxi \right) = {}^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Mn}}^{{ 3 + }} }}^{\upbeta } + J_{{{\text{FeMn}}_{ 2} {\text{O}}_{ 4} }}^{\upbeta } \upxi + D_{{{\text{FeMn}}_{ 2} {\text{O}}_{ 4} }}^{\upbeta } \upxi^{ 2} $$

(26)

$$ J_{{{\text{FeMn}}_{ 2} {\text{O}}_{ 4} }}^{\upbeta } = 0. 5^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Fe}}^{{ 2 + }} }}^{\upbeta } + 0. 5^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Mn}}^{{ 4 + }} }}^{\upbeta } - 2^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Mn}}^{{ 3 + }} }}^{\upbeta } + G_{{{\text{Mn}}^{{ 2 + }} :{\text{Mn}}^{{ 3 + }} }}^{\upbeta } $$

(27)

$$ D_{{{\text{FeMn}}_{ 2} {\text{O}}_{ 4} }}^{\upbeta } = - 0. 5^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Fe}}^{{ 2 + }} }}^{\upbeta } - 0. 5^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Mn}}^{{ 4 + }} }}^{\upbeta } +{}^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Mn}}^{{ 3 + }} }}^{\upbeta } + 0. 5^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Fe}}^{{ 2 + }} }}^{\upbeta } + 0. 5^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Mn}}^{{ 4 + }} }}^{\upbeta } - {}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Mn}}^{{ 3 + }} }}^{\upbeta } $$

(28)

where ξ is the degree of inversion. This is a system with a neutral line between the ${}^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Mn}}^{{ 3 + }} }}^{\upbeta }$ corner and the ${}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Fe}}^{{ 2 + }} }}^{\upbeta } - {}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Mn}}^{{ 4 + }} }}^{\upbeta }$ side. If $D_{{{\text{FeMn}}_{ 2} {\text{O}}_{ 4} }}^{\upbeta }$ is assumed to be equal to zero, Eq 27 will reduce to

$$ J_{{{\text{FeMn}}_{ 2} {\text{O}}_{ 4} }}^{\upbeta } = 0. 5^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Fe}}^{{ 2 + }} }}^{\upbeta } + 0. 5^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Mn}}^{{ 4 + }} }}^{\upbeta } - {}^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Mn}}^{{ 3 + }} }}^{\upbeta } $$

(29)

which is rather obvious the parameter describing the degree of inversion of FeMn₂O₄. The Gibbs energy of FeMn₂O₄ is given by the parameter ${}^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Mn}}^{{ 3 + }} }}^{\upbeta }$ and the third parameter, ${}^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Mn}}^{{ 4 + }} }}^{\upbeta }$, is given by Eq 28.

The remaining three ^o G parameters in the stoichiometric system $\left( {^{\text{o}}G_{{{\text{Fe}}^{{ 2 + }} :{\text{Mn}}^{{ 2 + }} }}^{\upbeta } ,\;{}^{\text{o}}G_{{{\text{Fe}}^{{ 3 + }} :{\text{Mn}}^{{ 3 + }} }}^{\upbeta } \;{\text{and}}\;{}^{\text{o}}G_{{{\text{Fe}}^{{ 3 + }} :{\text{Mn}}^{{ 4 + }} }}^{\upbeta } } \right)$ are related to the previously mentioned parameters by reciprocal reactions $(\Updelta G_{{{\text{Fe}}^{{ 2 + }} ,{\text{Mn}}^{{ 2 + }} :{\text{Fe}}^{{ 3 + }} ,{\text{Mn}}^{{ 2 + }} }} = \Updelta G_{{{\text{Fe}}^{{ 3 + }} ,{\text{Mn}}^{{ 2 + }} :{\text{Fe}}^{{ 3 + }} ,{\text{Mn}}^{{ 3 + }} }} = \Updelta G_{{{\text{Fe}}^{{ 3 + }} ,{\text{Mn}}^{{ 2 + }} :{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 4 + }} }} = 0$. For the nonstoichiometric system, all 26 parameters are evaluated using ΔG = 0.

Tetragonal Fe-Mn Spinel

Fe has a low solubility in the tetragonal α-spinel, but to be able to correctly model the tetragonal phase, it is in this assessment described all the way to the metastable α-Fe₃O₄. It makes very little difference what values are chosen for the majority of those parameters. We choose, rather arbitrarily, the same functions for many parameters in the tetragonal spinel as we did in the cubic spinel.

Wustite, Manganosite, Hematite, β-Bixbyite and Pyrolusite

The wustite (Fe_1−x O) and manganosite (Mn_1−x O) phases are isomorphous both having the NaCl-type structure (Strukturbericht B1), with generic name halite. The halite phase is described using a model within the CEF with two sublattices; one for metal ions and one for oxygen. Both Fe_1−x O and Mn_1−x O have a considerable solid solubility, due to the oxidation of Fe²⁺ to Fe³⁺ and Mn²⁺ to Mn³⁺ respectively and the formation of cation vacancies. The phase is thus represented as:

$$ \left( {{\text{Fe}}^{{ 2 + }} ,{\text{Fe}}^{{ 3 + }} ,{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} ,{\text{Va}}} \right)_{ 1} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 1} $$

Hematite (Fe₂O₃) with the generic name corundum (Strukturbericht D5₁) is described with a small deviation from stoichiometry with a model within the CEF using three sublattices. The solubility of Mn in hematite is modelled by adding Mn³⁺ ions on the first sublattice. The phase is thus represented as:

$$ \left( {{\text{Fe}}^{{ 2 + }} ,{\text{Fe}}^{{ 3 + }} ,{\text{Mn}}^{{ 3 + }} } \right)_{ 2} \left( {{\text{Fe}}^{{ 3 + }} ,{\text{Va}}} \right)_{ 1} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 3} $$

The end member Mn³⁺:Va:O²⁻ is used to model the solubility of Mn in hematite. Mn³⁺:Fe³⁺:O²⁻ is derived using the reciprocal reaction:

$$ {}^{\text{o}}G_{{{\text{Mn}}^{{ 3 + }} :{\text{Fe}}^{{ 3 + }} }} - {}^{\text{o}}G_{{{\text{Mn}}^{{ 3 + }} :{\text{Va}}}} = {}^{\text{o}}G_{{{\text{Fe}}^{{ 3 + }} :{\text{Fe}}^{{ 3 + }} }} - {}^{\text{o}}G_{{{\text{Fe}}^{{ 3 + }} :{\text{Va}}}} $$

α-Bixbyite (α-Mn₂O₃) transforms to β-Mn₂O₃ (Strukturbericht D5₃) at around 300 K. The α-modification was not considered due to the low transformation temperature. The solubility of Fe in β-bixbyite is modelled by adding Fe³⁺ ions on the cation sublattice. The phase is thus represented as:

$$ \left( {{\text{Fe}}^{{ 3 + }} ,{\text{Mn}}^{{ 3 + }} } \right)_{ 2} \left( {{\text{O}}^{{ 2 - }} } \right)_{ 3} $$

Pyrolusite (MnO₂) with the generic name rutile (Strukturbericht C4) is described as a stoichiometric phase. There are no reports on solubility of Fe in pyrolusite.

The description of Fe_1−x O is taken from Sundman[8] and the description of Fe₂O₃ is from Kjellqvist et al.[1] The descriptions for Mn_1−x O, β-Mn₂O₃ and MnO₂ are all from Grundy et al.[11]

Experimental Data

Mn₃O₄

With increasing temperature, Mn₃O₄ transforms from tetragonal α-Mn₃O₄ to cubic β-Mn₃O₄. The measured temperatures at which this transformation takes place varies between 1403 and 1473 K in air at 1 atmosphere total pressure, with a larger group between 1443 and 1450 K.[20,25-34] The transformation enthalpy has been measured by three authors ranging from 18 to 22.82 kJ/mole.[26-28] The nonstoichiometry of hausmannite has been investigated by a number of authors, some of them find it to be stoichiometric Mn₃O₄,[35-39] while others find different degree of nonstoichiometry.[20,30,31,40-46] β-Mn₃O₄ melts according to β-Mn₃O₄ → liquid + gas. The measured temperatures ranging from 1835 to 1863 K.[32,33,36,42,47] The eutectic between liquid β-Mn₃O₄ and halite[33,35,36,42] and the reaction Mn₂O₃ → β-Mn₃O₄ + gas[25,34,36,39,48-52] have also been measured numerous times.

There are many determinations on the enthalpy of formation, $\Updelta_{\text{f}}^{\text{o}} H_{ 2 9 8}$,[25,38,53-62] the entropy at 298.15 K, ${}^{\text{o}}S_{ 2 9 8}$,[25,37,59,62-65] and heat capacity, c _p,[37,64,65] see Table 1. The heat content of α-Mn₃O₄ has been measured by Southard and Moore[28] and Fritsch and Navrotsky.[66] The magnetic transition temperature was measured by two authors[64,65] with excellent agreement between their values, 43.15 and 43.12 K respectively.

Table 1 Thermodynamic data of Mn₃O₄

The non-configurational free energy change on converting a normal to an inverse α-spinel $\left( {\Updelta G_{\text{D}} = G_{\text{i}} - G_{\text{n}} + {\text{TS}}_{\text{m}} = 0. 5J_{23}^{\upalpha } } \right)$ has been calculated from crystal field theory by several authors.[21,22,67] Dorris and Mason[19] measured the ionic configuration for β-Mn₃O₄.

Fe-Mn-O

The nonstoichiometry of (Fe_1−x Mn _x )_1−δO has been investigated at different temperatures and compositions.[68-72] There are a number of investigations on the two-phase region between halite and fcc[52,68,69,72-77] and halite and spinel.[52,68,69,72,74-80] Ref 52, 69, 73, 77, 81-83 measured the activity of FeO at the two-phase equilibrium fcc/halite.

The phase relations in the system Fe₂O₃-Mn₂O₃ have been examined by several authors.[75,84-88] Bixbyite has large solubility of iron, approximately 70% at the peritectoid reaction between bixbyite, corundum and β-spinel in air, while the solubility of Mn in corundum at the same reaction is approximately 13%.

The two-phase region between corundum and spinel at 1273 K has been investigated by Ref 69, 75, 76.

Fe₃O₄ and β-Mn₃O₄ forms a continuous solid solution down to 1443 K at the manganese side, where β-Mn₃O₄ transforms to α-Mn₃O₄. While β-Mn₃O₄ is isomorph with Fe₃O₄, α-Mn₃O₄ has a limited solubility of iron. The miscibility limits of the α-Mn₃O₄/β-Mn₃O₄ transformation has been determined by Ref 32, 79, 86, 89-92. Jacobsite (MnFe₂O₄) is a normal spinel at low temperatures, with an increasing degree of inversion at higher temperatures. The cation distribution of jacobsite has been studied by several authors.[93-99] The oxygen nonstoichiometry of β-spinel has been measured by Bulgakova and Rozanov[74] and Terayama et al.[100]

The enthalpy of formation, $\Updelta_{\text{f}}^{\text{o}}H_{ 2 9 8}$, and the entropy at 298.15 K, ${}^{\text{o}}S_{ 2 9 8}$, for MnFe₂O₄ are tabulated by Kubaschewski et al.[62] Heat content, H-H ₂₉₈, and heat capacity, c _p, for temperatures ranging from 298 to 1000 K have been measured by Reznitskii.[101] Naito et al.[102] measured c _p for the spinels MnFe₂O₄, Mn_1.5Fe_1.5O₄ and Mn₂FeO₄ between 200 and 740 K. Curie temperatures in Fe₃O₄-Mn₃O₄ at different compositions are determined with good agreement between the authors.[101-106]

Nölle[107] measured the phase boundary between liquid oxide and halite at 1823 K. The phase boundary between liquid oxide and spinel has been measured by Muan and Somiya.[84] A number of studies report the solubility of oxygen in liquid Fe-Mn alloys at 1873 K,[52,84,108-114] with a wide scatter in the different data.

Optimization and Results

The optimization of the parameters was performed using the PARROT module of the Thermo-Calc software.[115] The values for the interaction parameters assessed in this work are listed in Table 2. Data for the pure elements were taken from Dinsdale.[116]

Table 2 Assessed parameters (in SI units: J, mole, K)

Mn-O

The descriptions of all phases in Mn-O from Grundy et al.[11] except the liquid, α- and β-Mn₃O₄ are unchanged. The calculated phase diagram is shown in Fig. 1.

Fig. 1

Calculated Mn-O phase diagram at 1 atmosphere total pressure

α-Mn₃O₄ is known to be a normal spinel[19,20,117] with Mn²⁺ occupying the tetrahedral sites and Mn³⁺ occupying the octahedral sites. Some interchange between the sites will however occur. The calculated stabilization energies from Dunitz and Orgel[22] were used to evaluate a parameter to describe the cation distribution between tetrahedral and octahedral sites. The cation distribution for β-Mn₃O₄ is consistent with experiments from Dorris and Mason.[19]

The investigation on the nonstoichiometry of α- and β-Mn₃O₄ from Keller and Dieckmann[30] was then used to evaluate the two parameters in each phase describing the deviation from stoichiometry towards lower and higher oxygen contents by formation of cation interstitials and octahedral vacancies. The assessed heat capacity from Grundy et al.[11] was kept, but the enthalpy of formation and entropy at 298.15 K needed to be adjusted in order to fit the nonstoichiometry data, the enthalpy of the α-Mn₃O₄/β-Mn₃O₄ transformation and the transition temperature. The enthalpy of formation, the entropy at 298.15 K and the enthalpy of the α-Mn₃O₄/β-Mn₃O₄ transformation from literature are compared to this assessment in Table 1. The magnetic transition temperature was fixed to the experimental value of 43.15 K measured by Chhor et al.[65]

In Fig. 2 the enthalpy of α-Mn₃O₄ is plotted against experimental data. The calculated oxygen potential inside the two spinel phases is shown in Fig. 3 and 4.

Fig. 2

Calculated and experimental[28,66] enthalpy of Mn₃O₄

Fig. 3

Calculated and experimental[30] oxygen potential in α-Mn_3−δO₄

Fig. 4

Calculated and experimental[30] oxygen potential in β-Mn_3−δO₄

The liquid parameters for the Mn-O system using the MnO_1.5 species instead of the Mn³⁺ species, are obtained from the previous description without any reassessment using

$$ {}^{\text{o}}G_{{{\text{MnO}}_{ 1. 5} }} = 0. 5^{\text{o}}G_{{{\text{Mn}}^{{ 3 + }} :{\text{O}}^{{ 2 - }} }} $$

(30)

$$ L_{{{\text{Mn}}^{{ 2 + }} :{\text{O}}^{{ 2 - }} ,{\text{MnO}}_{ 1. 5} }} = L_{{{\text{Mn}}^{{ 2 + }} ,{\text{Mn}}^{{ 3 + }} :{\text{O}}^{{ 2 - }} }} $$

(31)

Equivalent to the Fe-O system, an additional parameter, $L_{{{\text{Mn}}^{{ 2 + }} :{\text{Va}}^{{Q - }} ,{\text{MnO}}_{ 1. 5} }}$, was introduced and optimized to obtain an almost identical fit to the phase diagram as the previous model using Mn³⁺.

Fe-Mn-O

Data for the Fe-Mn and Fe-O systems were taken from existing assessments from Huang[12] and Sundman[8] (modified by Selleby and Sundman,[9] Kowalski and Spencer,[10] Kjellqvist et al.[1]) respectively.

When optimizing the cubic spinel phase, the parameter ${}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Fe}}^{{ 3 + }} }}$ is first determined against the enthalpy of formation, $\Updelta_{\text{f}}^{\text{o}} H_{ 2 9 8}$,[62] the entropy at 298.15 K, ${}^{\text{o}}S_{ 2 9 8}$,[62] heat content, H-H ₂₉₈,[100] and heat capacity, c _p,[100] for MnFe₂O₄. The magnetic transition temperature was fixed to the experimental value of 577 K, and the Bohr magneton number, ⁰β, was used as the optimizing parameter to fit the λ-peak in the heat capacity curve. The enthalpy and heat capacity together with experimental data is shown in Fig. 5 and 6.

Fig. 5

Calculated and experimental[101] enthalpy of MnFe₂O₄

Fig. 6

Calculated and experimental[101,102] heat capacity of MnFe₂O₄

Curie temperatures for Fe-Mn-O spinels have been measured and an excess parameter for the Curie temperature between Mn₃O₄ and MnFe₂O₄ is needed to reproduce the correct behavior. The calculated and experimental Curie temperature between Fe₃O₄ and Mn₃O₄ is shown in Fig. 7.

Fig. 7

Calculated and experimental[89-91,101-106] phase diagram and Curie temperature between Fe₃O₄ and Mn₃O₄

Tetragonal MnFe₂O₄ is not stable at normal conditions and the parameter ${}^{\text{o}}G_{{{\text{Mn}}^{{ 2 + }} :{\text{Fe}}^{{ 3 + }} }}^{\upalpha }$ is used to reproduce the solubility limit of Fe in tetragonal spinel. The calculated phase diagram Fe₃O₄-Mn₃O₄ is shown in Fig. 7.

The distribution of cations between tetrahedral and octahedral sites in MnFe₂O₄ has been studied by a number of authors, with different results. Jirák and Vratislav[97] did neutron diffraction investigations at elevated temperatures between 603 and 1443 K. Hasting and Corliss[93] found the degree of inversion to be independent of preparation conditions and temperature. Other authors found a very low degree of inversion.[118,119] Faller and Birchenall[120] showed that in some cases even rapid quenching is not sufficient to retain the equilibrium distribution of cations corresponding to the annealing temperature. Therefore, the experimental data on the degree of inversion (fraction of Mn ions in octahedral sites) from Jirák and Vratislav was used to evaluate the cation distribution in MnFe₂O₄. MnFe₂O₄ is known to be an almost normal spinel at room temperature with Mn²⁺ ions on tetrahedral sites and Fe³⁺ ions on octahedral sites. At increasing temperature the degree of inversion increases. The distribution of cations is determined by the formula Mn_1−λFe_λ[Mn_λFe_2−λ]O₄, where the cations inside the square brackets are in octahedral sites while the cations in front of the brackets are in tetrahedral sites. The calculated degree of inversion is shown in Fig. 8. The calculated cation distribution in cubic Fe_3−x Mn _x O₄ at 1000 K is shown in Fig. 9, where the tetragonal spinel phase was excluded in the calculation. Terayama et al.[100] found a wide nonstoichiometric range in MnFe₂O₄ at 1153 K, corresponding to −0.2258 ≤ δ ≤ 0 in (Fe _x Mn_1−x )_3−δO₄. This huge deviation from stoichiometry seems very unlikely and disagrees with the measurements from Bulgakova and Rozanov,[74] whose results agree well with our calculated values, even though they were not taken into account in this optimization, see Fig. 10.

Fig. 8

Calculated and experimental[97] degree of inversion of MnFe₂O₄ (Mn_1−λFe_λ[Mn_λFe_2−λ]O₄)

Fig. 9

Calculated cation distribution in cubic Fe₃O₄-Mn₃O₄ at 1000 K

Fig. 10

Calculated and experimental[74] oxygen potential at 1242 K in MnFe _n O _x

The nonstoichiometry of (Fe_1−x Mn _x )_1−δO at 1273 and 1473 K for different values on x, investigated by Subramanian and Dieckmann[72] and Franke and Dieckmann,[69] were used to optimize the interaction parameters in halite. The calculated partial pressure of oxygen in nonstoichiometric halite is shown in Fig. 11 and 12. It could be noted that the slope of the calculations does not perfectly align with the experiments. To change the slope of the calculated curves, the model for the manganowustite phase needs to be changed to also include Mn⁴⁺ ions.

Fig. 11

Calculated and experimental[69] oxygen potential in (Fe_1−x Mn _x )_1−δO at 1273 K

Fig. 12

Calculated and experimental[72] oxygen potential in (Fe_1−x Mn _x )_1−δO at 1473 K

When reasonable parameters had been given to the halite and spinel phases, experimental information on invariant equilibria was included in the assessment. Information from Subramanian and Dieckmann,[72] Franke and Dieckmann[69] and Schwerdtfeger and Muan[52] of the two-phase regions of halite/fcc and halite/spinel at two temperatures (1273 and 1473 K) were used to further improve the description of halite and spinel. Figure 13 shows the calculated composition-oxygen activity phase diagram at 1273 K together with experimental data.

Fig. 13

Calculated and experimental[52,69,73,75-77,85,121] phase diagram at 1273 K

The investigations of the two-phase regions of corundum/bixbyite and corundum/spinel from Ref 69, 75, 84, 86, 121 were used to describe the solubility of Mn in Fe₂O₃. The data from Bergstein and Kleinert[85] on the β-spinel/corundum phase boundary at 1273 K could not be reproduced. To correctly describe the solubility of Fe in Mn₂O₃, an excess parameter was required to be able to reproduce the experimental data. A phase diagram calculated in air (P = 0.21 bar) is shown in Fig. 14 together with experimental data.

Fig. 14

Calculated and experimental[75,84,86] phase diagram for a fixed oxygen partial pressure of 0.21 bar

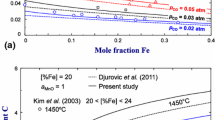
The liquid phase is optimized using the data from Muan and Somiya[84] and Nölle[107] on the phase boundaries between liquid oxide and spinel/halite respectively. The experiments on the solubility of oxygen in the metallic melt are not taken into consideration in this assessment due to the large scattering. The experimental and calculated oxygen content of the metallic liquid in equilibrium with the halite phase are shown in Fig. 15.

Fig. 15

Calculated and experimental[108,109,112] oxygen solubility in liquid Fe-Mn in equilibrium with halite and liquid oxide at 1873 K

Calculated isothermal sections at two different temperatures are shown in Fig. 16 and 17.

Fig. 16

Calculated isothermal section of the Fe-Mn-O system at 1273 K

Fig. 17

Calculated isothermal section of the Fe-Mn-O system at 1823 K with experimental data from Nölle[107]

Conclusions and Discussion

The present assessment gives a good description of the available experimental information in the ternary Fe-Mn-O system. A complete list of all parameters is found in Table 2. Part of the Mn-O system has been revised. In the liquid phase the Mn³⁺ ion has been replaced by a neutral MnO_1.5 species equivalent to the Fe-O system. The spinel phases (α- and β-Mn₃O₄) are here modelled using a more complex description than the previous assessment from Grundy et al.[11] The new model describes the cation distribution of ions between tetrahedral and octahedral sites and the nonstoichiometry of the phases. The description of the spinel phases in the Fe-Mn-O system is consistent with the description of the Fe-Cr-Ni-O spinel from an earlier work,[1] but to be able to do thermodynamic calculations in the Fe-Cr-Mn-Ni-O system the Cr-Mn-O and Mn-Ni-O systems need to be assessed. The models in this work are compatible with the models used in a parallel work on the Al₂O₃-CaO-Fe-O-MgO-SiO₂ system.[122,123]