Introduction

The concept of cohesive zone model, proposed by [1, 2], has been used to handle the process zone ahead of the crack tip where linear elastic fracture mechanics (LEFM) does not work well if the process zone is not sufficiently small compared to the structural size. It treats the process zone as a cohesive zone where there exists traction between two virtual surfaces ahead of the crack tip and the traction–separation relationship follows a cohesive law (Fig. 1).

Fig. 1
figure 1

Cohesive zone at crack tip and cohesive law

Full size image

A cohesive law describes the relationship between traction and separation within the cohesive zone. Thus, it is also called the traction–separation law. There are various cohesive laws in literature, and the commonly used ones are bilinear cohesive law by [3], exponential cohesive law by [4], and trapezoidal cohesive law by [5]. These cohesive laws have different shapes but share common features like:

  1. 1.

    The area under the traction–separation curve corresponds to the critical energy release rate of the material. This gives the cohesive zone model a physical meaning.

  2. 2.

    They all have a descending part where traction decreases as separation increases, and when traction drops to zero, the cohesive zone model is considered failed and crack forms.

Research has been carried out to study the influence of cohesive law shape. Volokh [6] simulated a block peel test using various cohesive laws, and he showed that influence of cohesive law shape is not negligible. However, [7] conducted a comprehensive study of the cohesive law’s shape and concluded that for a typical double cantilever beam test the solution is practically independent of the shape of the cohesive law.

Despite the many choices of cohesive laws, cohesive zone model is straightforward and powerful and can be used to handle many fracture problems. It is especially useful for crack initiation problems in geometries that don’t have initial cracks, where LEFM doesn’t work well. It can also be used to predict crack propagation, whether it is in composite [3, 8, 9] or concrete [10] or metal [11]. Xu and Needleman [4] used a cohesive element approach to insert zero-thickness cohesive elements into every element interfaces to predict arbitrary crack propagation. Wells and Sluys [12] used the cohesive model in combination with XFEM to predict crack propagation which is mesh independent. Recently, cohesive zone model has also gained popularity in fatigue simulation.

Cohesive zone model has been used in cyclic loading and fatigue simulation by many authors [13,14,15,16,17,18]. It has been used to simulate the fatigue failure of adhesively bonded joints [13, 15], polymeric materials [19], composite [17, 18] and crystal superalloys [14]. The fatigue crack growth within cohesive zone often combines the theory of damage mechanics and fracture mechanics. Roe and Siegmund [13] predict fatigue by degrading the strength and stiffness in the cohesive model using a damage evolution law. (It will be referred to as Roe’s damage law in this paper.) Roe’s damage law applies Xu and Needleman’s exponential cohesive law [4] and a constant unloading and reloading slope. The damage accumulation rate is considered by combining endurance limit, separation threshold, and deformation rate. It is calculated in each loading cycle and integrated over time to get the damage parameter. Roe’s damage law provides a deep insight into fatigue simulation using cohesive zone model, and the general form of Roe’s damage law has been used by many people [14].

Despite the extensive usage of Roe’s damage law, it suffers from two limitations: (1) the adoption of constant unloading and reloading slope limits its application to only pure mode loading or mixed mode loading with the constant mixed mode ratio. However, in engineering problems a model that can consider arbitrary mixed mode ratio is needed; (2) calculating the damage parameter cycle by cycle makes Roe’s damage law computationally expensive, especially in explicit time integration. The first limitation, for the best of our knowledge, has not been appropriately handled in the literature, and it will be the focus of this paper. The solution to the second limitation has been attempted by using extrapolation scheme [20]. In this paper, a scale factor is added into Roe’s damage law to accelerate the damage accumulation process, and it will be shown that the fatigue failure time and the scale factor are inversely proportional.

The paper is structured as follows: In section “The Discontinuity Issue and a New Formulation”, scenarios are presented where the discontinuity in traction–separation curve happens, and the reason is explained. In section “Modified Roe’s Damage Evolution Law”, new formulations for exponential law’s unloading and reloading behaviors are proposed. In section “Verification of the Cyclic Loading Formulation and Modified Roe’s Damage Law”, a scale factor is introduced to Roe’s damage law to make it computationally cost-efficient, and the feasibility of this approach is discussed. In section “Conclusion”, Roe’s damage law and the new formulation are combined in two numerical examples to show the robustness of the new formulation. The inversely proportional relationship between the scale factor and fatigue failure time is illustrated using a small numerical example.

The Discontinuity Issue and a New Formulation

Limitation of the Constant Unloading and Reloading Slope in Exponential Cohesive Law

Exponential cohesive law by [21] is used to illustrate possible discontinuity if constant unloading and reloading slope is used. This exponential law is based on the cohesive model of [4] and is improved to eliminate possible energy inconsistency under mixed mode loading. Thus, it will be called improved Xu–Needleman’s cohesive law in this paper. The improved Xu–Needleman’s cohesive law is derived from an energy form:

$$\phi \left( {\Delta _{\text{n}} ,\Delta _{\text{t}} } \right) = \phi \left[ {1 - \left( {1 + \frac{{\Delta _{n} }}{{\delta_{n} }}} \right)\exp \left( { - \frac{{\Delta _{n} }}{{\delta_{n} }}} \right)\exp \left( { - \frac{{\Delta _{t}^{2} }}{{\delta_{t}^{2} }}} \right)} \right]$$
(1)

where the characteristic separations δn, δt are calculated by:

$$\delta_{\text{n}} = \phi_{\text{n}} /\left( {eT} \right),\quad \delta_{\text{t}} = \phi_{\text{t}} /\left( {S\sqrt {e/2} } \right).$$
(2)

The traction is obtained by taking derivatives of energy release rate against separations:

$$T_{\text{n}} = \frac{\partial \phi }{{\partial\Delta _{\text{n}} }} = \frac{{\phi_{\text{n}} }}{{\delta_{\text{n}} }}\left( {\frac{{\Delta _{\text{n}} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{\text{n}} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{\text{t}}^{2} }}{{\delta_{\text{t}}^{2} }}} \right)$$
(3)
$$T_{\text{t}} = \frac{\partial \phi }{{\partial\Delta _{\text{t}} }} = 2\frac{{\phi_{\text{t}} }}{{\delta_{\text{t}} }}\left( {\frac{{\Delta _{\text{t}} }}{{\delta_{\text{t}} }}} \right)\left( {1 + \frac{{\Delta _{\text{n}} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{\text{n}} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{\text{t}}^{2} }}{{\delta_{\text{t}}^{2} }}} \right).$$
(4)

The unloading and reloading behavior of the improved Xu–Needleman cohesive law in [13] is done by linear interpolation, or secant method, like in the paper of [22]. It is done using a constant unloading and reloading slope calculated using the ratio between traction (Tn or Tt) and separation (Δn or Δn) at the point unloading starts. It is also based on the assumption that no plastic deformation occurs and the traction–separation curve will return to the origin point. The unloading and reloading slope for normal and tangential separations is different from each other: It is Tn/Δn for normal separation and Tt/Δt for tangential separation:

$$\frac{{T_{\text{n}} }}{{\Delta _{\text{n}} }} = \frac{{\phi_{\text{n}} }}{{\delta_{\text{n}}^{2} }}\exp \left( { - \frac{{\Delta _{\text{n}} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{\text{t}}^{2} }}{{\delta_{\text{t}}^{2} }}} \right)$$
(5)
$$\frac{{T_{\text{t}} }}{{\Delta _{\text{t}} }} = 2\frac{{\phi_{\text{t}} }}{{\delta_{\text{t}}^{2} }}\left( {1 + \frac{{\Delta _{\text{n}} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{\text{n}} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{\text{t}}^{2} }}{{\delta_{\text{t}}^{2} }}} \right).$$
(6)

Replace \(\phi\)n/δ 2n and 2\(\phi\)t/δ 2t by Kn and Kt, respectively, where Kn and Kt represent the initial slope of the exponential cohesive law in normal and tangential directions. If there is no healing during the cyclic loading process, the maximum separation (Δn,max and Δt,max) in each loading cycle is used to calculate the unloading and reloading slope:

$$\frac{{T_{\text{n}} }}{{\Delta _{\text{n}} }} = K_{\text{n}} \exp \left( { - \frac{{\Delta _{{{\text{n}},\hbox{max} }} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{{{\text{t}},\hbox{max} }}^{2} }}{{\delta_{\text{t}}^{2} }}} \right)$$
(7)
$$\frac{{T_{\text{t}} }}{{\Delta _{\text{t}} }} = K_{\text{n}} \left( {1 + \frac{{\Delta _{{{\text{n}},\hbox{max} }} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{{{\text{n}},\hbox{max} }} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{{{\text{t}},\hbox{max} }}^{2} }}{{\delta_{\text{t}}^{2} }}} \right).$$
(8)

To further simplify it, the terms following Kn and Kt can be represented as a damage factor in normal and tangential directions:

$$d_{\text{n}} = 1 - \exp \left( { - \frac{{\Delta _{{{\text{n}},\hbox{max} }} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{{{\text{t}},\hbox{max} }}^{2} }}{{\delta_{\text{t}}^{2} }}} \right)$$
(9)
$$d_{\text{t}} = 1 - \left( {1 + \frac{{\Delta _{{{\text{n}},\hbox{max} }} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{{{\text{n}},\hbox{max} }} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{{{\text{t}},\hbox{max} }}^{2} }}{{\delta_{\text{t}}^{2} }}} \right)$$
(10)

where dn ∊ [0, 1] and dt ∊ [0, 1]. 0 means no reduction of the initial slope, and 1 means complete reduction in the slope value to 0, which also means the model has reached a failure point. Tractions during the unloading and reloading processes are calculated using:

$$\left\{ {\begin{array}{*{20}c} {T_{\text{n}} = \left( {1 - d_{\text{n}} } \right)K_{\text{n}} \Delta_{\text{n}} } \\ {T_{\text{t}} = \left( {1 - d_{\text{t}} } \right)K_{\text{t}} \Delta_{\text{t}} } \\ \end{array} } \right.\,\,{\text{when}}\,\,\,\Delta \le\Delta _{\hbox{max} }$$
(11)

where \(\Delta = \sqrt {\Delta _{\text{n}}^{2} +\Delta _{\text{t}}^{2} }\) is the mixed mode separation and Δmax is the maximum mixed mode separation in a loading cycle. The unloading and reloading paths are linear because Δn,max and Δt,max for loading cycles are fixed values. It works well when the mixed mode ratio β = Δt/Δn does not change in cyclic loadings (Fig. 2). However, when the mixed mode ratio β = Δt/Δn if different from the first and the second loading cycle, a jump in the traction–separation curve becomes inevitable (Fig. 3).

Fig. 2
figure 2

Traction–separation curve in two loading cycles with a constant β value. (a) 3D plot. (b) 2D plot

Full size image
Fig. 3
figure 3

Discontinuity in traction–separation curve happens when β in the first loading cycle is different from the second loading cycle. (a) 3D plot. (b) 2D plot

Full size image

The normal and tangential separations are plotted in the same figure (Fig. 4) so that the mixed mode ratio change can be better visualized. The envelope represents Δmax value and only points within the envelope are controlled by the unloading and reloading formulation. The intersection of loading path and envelope corresponds to a point whose coordinates are Δn,max and Δt,max, and these values are used to calculate the unloading and reloading slope. For a constant β throughout the loading cycles, the displacement curve remains a straight line (Fig. 4a), and the corresponding traction–separation curve is continuous (Fig. 2). Furthermore, with the help of Fig. 4b, it is evident that if β in reloading process is different from unloading process, a different pair of Δn,max and Δt,max is needed to calculate a new slope for reloading process. However, the existing formulation in Eqs 9 and 10 cannot reflect such change, thus resulting in a jump in traction–separation law in Fig. 3.

Fig. 4
figure 4

Loading paths of two different scenarios. (a) β is the same for unloading and reloading and (b) β is different for unloading and reloading

Full size image

Kregting [23] noticed the phenomenon described above and used an extrapolation method to predict a new pair of Δn,max and Δt,max values for the reloading process. However, extrapolation is only applicable to linear cases. For cases where β value changes throughout the simulation (reloading curves in Fig. 5), the accuracy cannot be guaranteed. A robust cyclic loading behavior requires a formulation that could consider the β change during the whole process and be path dependent, like the damage parameter in bilinear cohesive model.

Fig. 5
figure 5

Loading paths when β is nonlinear in reloading process

Full size image

New Cyclic Loading Formulations for Exponential Cohesive Law

The new formulation is constructed with the help of a surface that connects the maximum separation envelope and the origin (it will be referred to as cutting surface in this paper). A point on the maximum separation envelope has a coordinate of (Δn, Δt, Tn) for normal direction (Fig. 6a) and (Δn, Δt, Tt) for tangential direction (Fig. 6b), where \(\Delta _{\hbox{max} } = \sqrt {\Delta _{\text{n}}^{2} +\Delta _{\text{t}}^{2} }\). Our method states that within one loading cycle, all the points during the unloading and reloading processes fall on this surface, and since the surface is first-order continuous, the traction–separation curve is also first-order continuous. Furthermore, this method also guarantees no healing during the unloading and reloading process, as all points (Δn, Δt, T) on cohesive law will not go beyond the cutting surface, which is consisted of straight lines directly connecting the origin and envelope points.

Fig. 6
figure 6

Cutting surface and mixed mode separation envelope. (a) Traction in normal direction. (b) Traction in tangential direction

Full size image

The traction at any point of the unloading and reloading process can be obtained by finding the z coordinate of a point on the cutting surface. Instead of deriving the formulation of cutting surface, which can be complicated, only the formulation of lines is needed that connects points on the envelope to the origin. Let the traction be z-axis, normal and tangential separation be x- and y-axis, respectively. For a point on the envelope, denote the (x, y) coordinates by (Δn0, Δt0). Express (Δn0, Δt0) as functions of Δmax and β ∊ [0, ∞), and the following relationship can be obtained:

$$\left( {\Delta _{{{\text{n}}0}} ,\Delta _{{{\text{t}}0}} } \right) = \left( {\Delta _{\hbox{max} } /\sqrt {1 + \beta^{2} } ,\beta\Delta _{\hbox{max} } /\sqrt {1 + \beta^{2} } } \right).$$
(12)

And the z coordinate is Tn0 in the normal direction and Tt0 in the tangential direction:

$$T_{\text{n0}} = \frac{{\phi_{\text{n}} }}{{\delta_{\text{n}} }}\left( {\frac{{\Delta _{{{\text{n}}0}} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{{{\text{n}}0}} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{{{\text{t}}0}}^{2} }}{{\delta_{\text{t}}^{2} }}} \right)$$
(13)
$$T_{\text{t0}} = \frac{{2\phi_{\text{t}} }}{{\delta_{\text{t}} }}\frac{{\Delta _{{{\text{t}}0}} }}{{\delta_{\text{t}} }}\left( {1 + \frac{{\Delta _{{{\text{n}}0}} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{{{\text{n}}0}} }}{{\delta_{\text{n}} }}} \right)\exp \left( { - \frac{{\Delta _{{{\text{t}}0}}^{2} }}{{\delta_{\text{t}}^{2} }}} \right).$$
(14)

Thus, these lines can be expressed as:

$$\frac{x}{{\Delta _{\hbox{max} } /\sqrt {1 + \beta^{2} } }} = \frac{y}{{\beta\Delta _{\hbox{max} } /\sqrt {1 + \beta^{2} } }} = \frac{z}{{T_{{{\text{n}}0}} }}$$
(15)
$$\frac{x}{{\Delta _{\hbox{max} } /\sqrt {1 + \beta^{2} } }} = \frac{y}{{\beta\Delta _{\hbox{max} } /\sqrt {1 + \beta^{2} } }} = \frac{z}{{T_{{{\text{t}}0}} }}$$
(16)

where z is the normal traction in Eq 15 and tangential traction in Eq 16. Thus, the traction of a point inside the envelope can be calculated from Eqs 15 and 16 using its (x, y) = (Δn, Δt) values.

The traction curves are plotted for displacement paths in Fig. 5 to show how our method guarantees the continuity. For Fig. 5a, the 3D and 2D plots of normal and tangential traction–separation curves are shown in Figs. 7 and 8, respectively. Figures 9 and 10 show the normal and tangential traction–separation curves for the displacement path in Fig. 5b.

Fig. 7
figure 7

3D plot of traction–separation curve for loading path in Fig. 5a. (a) Normal traction. (b) Tangential traction

Full size image
Fig. 8
figure 8

2D plot of traction–separation curve for loading path in Fig. 5a. (a) Normal traction. (b) Tangential traction

Full size image
Fig. 9
figure 9

3D plot of traction–separation curve for loading path in Fig. 5b. (a) Normal traction. (b) Tangential traction

Full size image
Fig. 10
figure 10

2D plot of traction–separation curve for loading path in Fig. 5b. (a) Normal traction. (b) Tangential traction

Full size image

Modified Roe’s Damage Evolution Law

In this section, Roe’s damage evolution law will be briefly described, and a method to make it computationally affordable for cyclic loading is described. Roe’s damage evolution law considers fatigue through damage accumulation. It combines endurance limit, deformation rate, and separation threshold to obtain the damage accumulation rate [13]:

$$\dot{D}_{\text{c}} = \frac{{\left| {{\dot{\Delta }}} \right|}}{{\delta_{\sum } }}\left( {\frac{{\bar{T}}}{{\sigma_{\hbox{max} ,0} }} - C_{f} } \right)H\left( {\Delta - \delta_{0} } \right)\,\,\,\,{\text{and}}\,\,\,\,\dot{D}_{c} > 0$$
(17)

where \({{\left| {{\dot{\Delta }}} \right|} \mathord{\left/ {\vphantom {{\left| {{\dot{\Delta }}} \right|} {\delta_{\sum } }}} \right. \kern-0pt} {\delta_{\sum } }}\) considers the influence of deformation rate, \(\left( {\frac{{\bar{T}}}{{\sigma_{\hbox{max} ,0} }} - C_{f} } \right)\)defines the endurance limit requirement, and H(Δ − δ0) is a Heaviside function that controls the separation threshold. In these terms,

$${\dot{\Delta }} =\Delta ^{t} -\Delta ^{{t -\Delta t}}$$
(18)

where Δt and Δt−Δt are the mixed mode separation at time t and t − Δt. \(\bar{T}\) is the resultant traction:

$$\bar{T} = \sqrt {T_{\text{n}}^{2} + T_{\text{t}}^{2} }$$
(19)

And σmax,0 is the mixed mode cohesive strength and its value depends on the mixed mode ratio β. σmax,0 is a normalization factor that is calculated using the following equation:

$$\sigma_{\hbox{max} ,0} = T \cdot S\sqrt {\frac{{1 + \beta^{2} }}{{S^{2} + \beta^{2} T^{2} }}} .$$
(20)

Roe [13] introduced C f (0 < C f  < 1) to relate to the physical meaning of endurance limit. \(\left( {\frac{{\bar{T}}}{{\sigma_{\hbox{max} ,0} }} - C_{f} } \right)\) is not less than zero to avoid any negative damage accumulation. δ0 is the mixed mode separation calculated by the following equation:

$$\delta_{0} = \delta_{\text{n}} \cdot \delta_{\text{t}} \sqrt {\frac{{1 + \beta^{2} }}{{\delta_{\text{t}}^{2} + \beta^{2} \delta_{\text{n}}^{2} }}}$$
(21)

After the damage accumulation rate is calculated, the fatigue damage can be calculated by integrating over time:

$$D = \int {\dot{D}_{\text{c}} {\text{d}}t}$$
(22)

In discrete form:

$$D = \sum {\dot{D}_{\text{c}} {\text{d}}t}$$
(23)

Fatigue failure happens when \(\left( {1 - D} \right)\sigma_{\hbox{max} } < \overline{T}\) for force control and D = 1 for displacement control. During the unloading and reloading processes, the traction is calculated using our proposed formulations:

$$\frac{x}{{\Delta _{\hbox{max} } /\sqrt {1 + \beta^{2} } }} = \frac{y}{{\beta\Delta _{\hbox{max} } /\sqrt {1 + \beta^{2} } }} = \frac{z}{{T_{{{\text{n}}0}} \left( {1 - D} \right)}}$$
(24)
$$\frac{x}{{\Delta _{\hbox{max} } /\sqrt {1 + \beta^{2} } }} = \frac{y}{{\beta\Delta _{\hbox{max} } /\sqrt {1 + \beta^{2} } }} = \frac{z}{{T_{t0} \left( {1 - D} \right)}}.$$
(25)

Although Roe’s damage parameter provides a way to consider the endurance limit and deformation rate into the damage accumulation, it suffers from high computational cost because fatigue is calculated cycle by cycle, which means the simulation must go through all the loading cycles to obtain a desired amount of damage. It becomes especially hard for explicit time integration because of the small time step.

To make it feasible for cyclic loading, we use a scale factor C to accelerate the fatigue accumulation process. For a cyclic loading with constant amplitude and frequency, if the damage accumulated for each cycle is approximately the same (Fig. 11a), we can multiply it by a constant scale factor C (Eq 26) to scale the damage accumulation rate, and the time it takes to fatigue failure should be scaled down linearly. This can be illustrated by plotting the damage accumulated per cycle versus time (Fig. 11b), and the area under the curve is the total damage accumulated. By multiplying a scale factor of 2, the damage accumulated per cycle is doubled (shown as the dotted line in Fig. 11b), and the failure time is reduced to half because the total damage to reach failure is the same.

$$\dot{D}_{c} = C\frac{{\left| {\dot{\Delta }} \right|}}{{\delta_{\sum } }}\left( {\frac{{\bar{T}}}{{\sigma_{\hbox{max} ,0} }} - C_{f} } \right)H\left( {\Delta - \delta_{0} } \right)\,\,\,\,{\text{and}}\,\,\,\,\dot{D}_{c} > 0.$$
(26)

If we use T0 as fatigue failure time without the scale factor, and T c as a failure time with a scale factor, then their relationship should approximately be T0 = T c  × C because the damage accumulation rate is scaled up linearly. Verifications are given in section “Verification of the Cyclic Loading Formulation and Modified Roe’s Damage Law” to prove this concept.

Fig. 11
figure 11

(a) Damage accumulation rate vs. time. (b) Damage per cycle vs. time

Full size image

Verification of the Cyclic Loading Formulation and Modified Roe’s Damage Law

Verification of Proposed Cyclic Loading Formulation

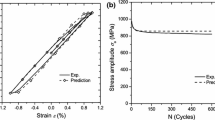
In this section, Roe’s damage evolution law combined with the proposed exponential formulation is tested on two types of cyclic loadings. The cyclic loading is made in a way that normal and tangential separations change nonlinearly with each other, as shown in Fig. 12. Moreover, a big scale factor is used so that visible damage accumulation can be observed in a few cycles.

Fig. 12
figure 12

Cyclic loading history. (a) Case (a). (b) Case (b)

Full size image

Traction versus separation curves for loading case (a) are plotted in Fig. 13, in which Fig. 13a uses a constant unloading and reloading slope, and Fig. 13b uses the proposed cyclic loading formulation. Discontinuity is observed using the constant unloading and reloading slope as expected, while the proposed cyclic loading formulation captures the mixed mode ratio change very well. Monotonic loading curve is also plotted to show the effect of damage accumulation. The same result behavior is observed in case (b), whose traction–separation curves are plotted in Fig. 14.

Fig. 13
figure 13

Traction–separation curves for cyclic loading (case a). (a) Constant unloading and reloading slope is used. (b) Proposed formulation is used

Full size image
Fig. 14
figure 14

Traction–separation curve for cyclic loading (case b). (a) Constant unloading and reloading slope is used. (b) Proposed formulation is used

Full size image

Verification of Modified Roe’s Damage Law

A three-element model is built to verify the modified Roe’s damage law: two solid elements and one zero-thickness cohesive element in between (Fig. 15a). The modified Roe’s damage model is programmed as a user-defined material in LS-DYNA, with the scale factor and endurance limit as input parameters. The material used for solid elements is aluminum substrates (E = 70,000 MPa, v = 0.3) and for the cohesive element is high-density polyethylene (HDPE). We use cohesive strength T = 6.66 MPa and δ n  = δ t  = 0.203 mm [13] for both mode I, mode II and mixed mode loading. The critical energy release rate can be calculated using relationships δn = \(\phi\)n/(eT) and \(\delta_{\text{t}} = \phi_{\text{t}} /\left( {S\sqrt {e/2} } \right)\), so \(\phi\)n = 3.67 kJ/m2 and \(\phi\)n = 1.57 kJ/m2 are used. In mixed mode loading, load in mode I is the same as mode II. The load has a form of sine wave function with a frequency of 50 Hz (Fig. 15b). Load ratio r = σmin/σmax is 0.25, and σmean/T is 0.5. The endurance limit is assumed to be 0.1 in this simulation.

Fig. 15
figure 15

(a) Illustration of the model (left) and (b) cyclic loading history (right)

Full size image

Different cases are run with the scale factor varying from 5 to 600, and the number of cycles to reach fatigue failure is recorded for each case. The number of cycles versus scale factor is plotted in a log–log chart (Fig. 16), and power law curve fitting is used to obtain their relationship. The curve fitting equation can be interpreted as

$$N_{\text{c}} \cong N_{0} C^{ - n}$$
(27)

where Nc is the number of loading cycles to fatigue failure for a scale factor C, N0 is the number of cycles without a scale factor, and n can be approximated as − 1, with an average error of 2.9%. This proves our assumption that the scale factor and number of cycles it takes to failure have an inversely linear relationship. The number of loading cycles along with the scale factors is listed in Table 1. It can be observed from Table 1 that for the error becomes larger when there is a fewer number of cycles before fatigue failure. Thus, we suggest doing a parameter study to make sure the error is within an acceptable range when this method is used on engineering problems.

Fig. 16
figure 16

Scale factor vs. number of loading cycles to fatigue failure. (a) Mode I loading. (b) Mode II loading. (c) Mixed mode loading

Full size image
Table 1 Scale factors and the corresponding number of loading cycles
Full size table

To further verify this method, the same model is tested for different mode I cyclic loading conditions (Table 2) and their results are plotted in Fig. 17. The load ratio r = σmin/σmax varies for different loading cases, and σmax/T is kept the same. Power law curve fitting shows that the slope values for these curves are all around − 1 with an average of 6% error. And R2 > 0.99 for all these curves indicates excellent curve fitting. The results from Table 2 shows that the loading ratio r = σmin/σmax doesn’t influence the scalability of damage accumulation.

Table 2 Different loading cases and the corresponding fitted curve equations
Full size table
Fig. 17
figure 17

Scale factor vs. number of cycles to fatigue failure for Mode I cyclic loading under different load ratios

Full size image

Conclusion

The widely used exponential cohesive law and its cyclic loading formulation in Roe’s damage model are found to have a possible discontinuity in the traction–separation curve. The discontinuity happens if the mixed mode ratio changes with time. The reason of that discontinuity is explored and explained. A new cyclic loading formulation is proposed for the exponential cohesive law. Its ability to keep the traction–separation law continuous and irreversible under arbitrary mixed mode cyclic loading is proved through several numerical models. The proposed formulation can be combined with Roe’s damage evolution law to simulate fatigue accumulation. Roe’s damage law is also modified by adding scale factor to accelerate the damage accumulation rate. It is also demonstrated that the predicted fatigue life and the scale factor are inversely proportional.