Introduction

Formation of a two-phase flow is a key problem in thermal spraying of coatings, as characteristics of this flow determine both values of productivity and stability of the spraying process and quality of the resulting coatings (Ref 1). Successful solution of this problem depends in many respects on the conditions of introduction of a spraying material into the gas or plasma flow. Whereas traditionally much consideration is given to the introduction of powder materials (Ref 1, 2), the processes of spraying of wire materials remain little studied, in a number of cases, e.g., in electric-arc metalizing (wire-arc spraying) (Ref 3), this leading to certain difficulties in formation of a concentrated flow of particles. At the same time, new promising methods are being developed now for thermal spraying using wire materials (Ref 4-7). An example of such a method is plasma-arc spraying of coatings (Ref 7), where the current-conducting anode wire continuously fed to the plasma arc behind the plasmatron nozzle section is sprayed, as shown in Fig. 1. Therefore, it is of high scientific and practical interest to comprehensively investigate the physical processes occurring in dispersion of the molten wire materials.

Fig. 1
figure 1

Appearance of the plasmatron (a) and flow diagram of the process (b) of plasma-arc wire spraying using external anode wire

Full size image

Dispersion of the anode wire in spraying is a complex intricate process, which includes heating and melting of the wire, formation of a liquid film at its tip, entrainment of the molten material by the plasma flow leading to formation of a jet flow, and its decomposition into droplets, i.e., dispersed particles of the spraying materials. Up to now the majority of the efforts dedicated to theoretical studies and mathematical modelling of interaction of the electric arc, gas flow, and anode wire leading to formation of droplets have made in the field of the arc-welding process. For example, the mathematical models describing the processes of formation and transfer of the electrode metal droplets in metal-arc welding are available (Ref 8-11). However, results obtained in the aforementioned studies are not applicable to the process of plasma-arc spraying, as it differs by the position of sprayed wire relative to the arc which formed angle from 70 to 90o, as well as more high values of temperature (up to 30,000 K) and velocity (up to 4000 m/s) of plasma flow (Ref 12). As to the theoretical investigation of the processes of wire thermal spraying, it is worthy to note here studies on mathematical modelling of plasma-arc (Ref 12-15) and wire-arc (Ref 16-18) spraying. Mathematical models of the plasma flow generated by the arc plasmatron with an external anode wire (Ref 12, 13), as well as of the processes of heating and melting of the anode wire, and formation of a liquid film at its tip (Ref 14, 15) have been developed. Papers (Ref 16-18) are devoted to the modelling of the formation of the gas flow, as well as thermal and dynamic interaction of the gas flow sprayed liquid particles during wire-arc spraying. However, there are lack of detailed understanding of the mechanisms controlling the primary atomization of liquid metal from the wire tips. Therefore, usually researchers are used the experimental droplet-size distributions (Ref 17, 18), or the simplified relation (Ref 16), allowing to estimate the size of detaching droplets according to parameters of spray operation mode, and polarity of the electrode wire (cathode or anode). There are only few studies dedicated to investigation of the effect of the forces acting on the spraying material (Ref 3, 19) during wire-arc spraying. At the same time, processes of formation of droplets under conditions of wire and rod spraying are little studied as yet. Therefore, this study will present the mathematical model and detailed numerical investigations of the processes of formation and detachment of droplets of the molten wire material under conditions of plasma-arc spraying.

Mathematical Model

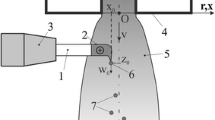
To develop the mathematical model of the process of dispersion of the spraying wire, we will use the diagram shown in Fig. 2. The solid metal wire of a circular section with radius R w is fed to the constricted (plasma) arc at speed \( v_{\text{w}} \) normal to the plasma flow symmetry axis. The plasma arc is fixed to the tip of the wire serving as anode. The wire is heated and melted (Ref 14) under the effect of the anode spot of the arc and high-temperature plasma flow around the wire, and the molten metal layer with characteristic thickness \( L_{\text{b}} \), which can be determined by the procedure described in (Ref 15), is formed at the wire tip. Assume that the melting front is flat and located parallel to the plasma flow symmetry axis (see Fig. 2), and the wire melting rate is equal to its feed speed. In this case the molten material of the wire is entrained by the plasma flow to form a jet of the molten metal, the axis of which is located at distance L p from the plasma flow axis, which can be determined by the procedure in (Ref 15). Assume also that the main force affecting the melt on the side of the plasma flow is a viscous friction force. Considering that flowing of the melt jet occurs in a wake plasma flow, the viscous forces near the molten metal-arc plasma interface will accelerate the melt in a plasma motion direction. While further flowing, this jet will split into droplets, i.e., dispersed particles of the spraying material.

Fig. 2
figure 2

Schematic of formation of the molten wire metal jet in plasma-arc spraying: 1 non-melted wire, 2 melting front, 3 melt, 4 melt-plasma flow interface, 5 plasma flow region, 6 symmetry axis of plasma flow generated by plasmatron

Full size image

To describe flowing and splitting of the jet of the molten wire metal, we will assume that the hydrodynamic system under consideration is axisymmetric and jet flow of a molten metal is laminar. In this case we can show that flowing of the molten metal jet can be described to a high degree of accuracy by the system of one-dimensional Navier-Stokes equations for a thin jet (Ref 20, 21), which is written down allowing for the viscous friction force affecting the melt on the side of the plasma flow:

$$ \frac{\partial v}{\partial t} + v\,\frac{\partial v}{\partial z} = - \frac{1}{{\rho_{\rm w} }}\frac{\partial p}{\partial z} + 3\upsilon_{\rm w} \,\frac{1}{{h^{2} }}\frac{\partial }{\partial z}\left( {h^{2} \frac{\partial v}{\partial z}} \right) - \frac{{2\,\uptau_{\rm p} \left( v \right)}}{{h\,\rho_{\rm w} }},\,\,\quad \,\, - L_{\rm d} < z < 0; $$
(1)
$$ \frac{\partial F}{\partial t} + \frac{\partial (vF)}{\partial z} = 0, $$
(2)

where \( v = v(z,t) \) is the axial component of the flow rate of the melt; p is the pressure in the melt; \( h = h(z,t) \) is the radius of the cross section of the jet; \( F(z,t) = {{\uppi}}h^{2} (z,t) \) is its cross-section area; \( \uptau_{p} \left( v \right) \) is the friction stress on the streamlined surface; \( \rho_{w} \) and \( {{\upupsilon}}_{\text{w}} \) are the density and kinematic viscosity of the molten wire metal; and \( L_{\text{d}} \) is the full length of the jet.

The value of pressure in the jet is determined by the following expression:

$$ p = 2\sigma K + p_{ext} , $$
(3)

where \( {{\upsigma}}\, \) is the surface tension coefficient; \( K = 0.5\,(K_{1} + K_{2} ) \) is the mean, and \( K_{1} ,\,K_{2} \) are main curvatures of the jet surface; and \( p_{\text{ext}} \) is the pressure in the external environment. In turn, the curvatures of the surface can be expressed in terms of such parameters as length of the arc of generatrix s of the jet surface counted out from point \( z = - L_{\text{d}} \), angle \( {{\uptheta}} \) formed by the tangent to this surface and r-axis (see Fig. 2), and jet radius h:

$$ K_{1} = {\text{d}}{\uptheta}/{\text{d}}s;\,K_{2} = h^{ - 1} \sin {{\uptheta}}. $$
(4)

The values of \( s \) and \( {{\uptheta}} \) are related to each other by the following equations:

$$ \frac{{{\text{d}}z}}{{{\text{d}}s}} = {\text{sin}}{{\uptheta}};\quad \,\,\,\frac{{{\text{d}}h}}{{{\text{d}}s}} = {\text{cos}}{\uptheta}. $$
(5)

For justification of applicability of model of the thin jet used for the description of the jet flow of a molten wire material, instead of full system of the hydrodynamic equations, comparison of experimental profiles of a water drop at the stage of its formation before detachment at the slow expiration from a tube with a diameter of 5.2 mm (Ref 22) with results of calculations on the specified model were carried out (Fig. 3). Thus, instead of volume force \( F_{\text{z}} = - {{2 \cdot {{\uptau}}_{\text{p}} \left( v \right)} \mathord{\left/ {\vphantom {{2 \cdot {{\uptau}}_{\text{p}} \left( v \right)} h}} \right. \kern-0pt} h} \) in Eq. 1 gravity force \( F_{\text{z}} = - {{\uprho}}g \) was used. As can be seen from Fig. 3, results of calculations agree with the experimental observations.

Fig. 3
figure 3

Comparison of the calculated and experimental profiles of a water drop

Full size image

To close the system of Eqs (1) and (2) it is necessary to set an expression for viscous stresses in the plasma on the streamlined surface of the molten metal jet \( {{\uptau}}_{\text{p}} \left( z \right) \). For this we use the results of (Ref 15). Thus, considering that the boundary layer in the plasma flow along the surface of liquid metal is turbulent (Ref 12), distribution of the velocity of the plasma near the medium interface can be described using a logarithmic near-wall function (Ref 15, 23)

$$ v^{ + } = \frac{1}{\text{Kar}}\ln \left( {Ey^{ + } } \right). $$
(6)

Here, \( v^{ + } = {{\bar{v}_{\text{p}} } \mathord{\left/ {\vphantom {{\bar{v}_{\text{p}} } {v^{*} }}} \right. \kern-0pt} {v^{*} }} \) is the dimensionless tangential (relative to melt surface) velocity of plasma; \( \bar{v}_{\text{p}} \left( r \right) = v_{\text{p}} \left( r \right) - v \) is the velocity of plasma flow relative to the melt flow velocity; \( v^{*} \) is the dynamic velocity determined as

$$ v^{ * } = \,\,\sqrt {{{\uptau_{p} } \mathord{\left/ {\vphantom {{\uptau_{p} } {\rho_{p} }}} \right. \kern-0pt} {\rho_{p} }}} ; $$
(7)

where \( \uptau_{p} = \left( {\upeta_{p} \frac{{\partial {\kern 1pt} v_{p} }}{{\partial {\kern 1pt} r}}} \right) \), \( {{\upeta}}_{\text{p}} \) is the coefficient of dynamic viscosity of plasma; \( {{\uprho}}_{\text{p}} \) is the plasma density; Kar ≈ 0.41 is Karman constant; E is the constant determining the degree of wall roughness [for smooth wall E = 8.8 (Ref 15)]; \( y^{ + } \) is the dimensionless distance from the interface \( h\left( z \right) \), determined as \( y^{ + } = \frac{{{{\uprho}}_{\text{p}} \left( {r - h} \right)}}{{{{\upeta}}_{\text{p}} }}v^{*} \). Assume that the transition from the melt flowing velocity (“sticking” condition) to the velocity of the undisturbed plasma flow, which can be determined, for instance, by model (Ref 12), occurs in region \( 0 \le y^{ + } < 400 \) (Ref 23). Then, based on expression (6) tangential stress in the plasma can be presented as follows:

$$ {{\uptau}}_{\text{p}} \left( z \right) = \frac{{\bar{v}_{\text{ext}}^{2} \left( z \right)}}{{\left( {\frac{1}{\text{Kar}} \cdot \ln \left( {Ey^{ + } } \right)} \right)^{2} }} \cdot {{\uprho}}_{\text{p}} = \frac{{\bar{v}_{\text{ext}}^{2} \left( z \right) \cdot {{\uprho}}_{\text{p}} }}{396.71}, $$
(8)

where \( \bar{v}_{\text{ext}} \left( v \right) = v_{\text{ext}} - v \) is the flow velocity of undisturbed plasma stream near the metal/plasma boundary surface of thin metal jet, relative to the melt velocity \( v \).

Equations (1) and (2) should be supplemented with initial and boundary conditions. In particular, at the initial section (\( z = 0 \)) it is necessary to set the jet radius and rate of arrival of the molten wire metal. Here, we will allow for the assumption made in (Ref 15) that the liquid film held at the wire tip takes the shape of a spherical segment with thickness \( L_{\text{b}} \) (see Fig. 2) under the effect of the ambient plasma flow. We will assume that the liquid film carried away from the wire tip is transformed near the edge of the melted wire tip into the axisymmetric jet of a circular section. Then the area of the jet in initial section F(0, t) and, hence, \( h_{0} = h\left( {0,t} \right) \) can be determined from the equivalent value of the cross-section area of the spherical segment held at the wire tip:

$$ h_{0} = \sqrt {\frac{2}{{{\uppi}}}\int\limits_{0}^{{L_{\text{b}} }} {\int\limits_{0}^{{y\left( {z_{\text{b}} } \right)}} {{\text{d}}y{\text{d}}z_{\text{b}} } } } , $$
(9)

where \( y\left( {z_{\text{b}} } \right) = \sqrt {R_{\text{w}}^{2} - 2\left( {{{\left( {R_{\text{w}}^{2} - L_{\text{b}}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {R_{\text{w}}^{2} - L_{\text{b}}^{2} } \right)} {\left( {2L_{\text{b}} } \right)}}} \right. \kern-0pt} {\left( {2L_{\text{b}} } \right)}}} \right)z_{\text{b}} - z_{\text{b}}^{2} } \) is the generatrix of the spherical segment boundary; and \( z_{\text{b}} \) is the symmetry axis of the spherical segment (on the melting boundary \( z_{\text{b}} = 0 \), i.e. at \( r = - L_{{{\text{b}}/2}} \)). In turn, the mass rate of melting of the anode wire being known

$$ G_{1} = {{\uprho}}_{\text{w}} v_{\text{w}} S_{\text{w}} , $$
(10)

where \( S_{\text{w}} = {{\uppi}}R_{\text{w}}^{2} \) is the cross-section area of the wire, the rate of arrival of the molten metal to the jet can be determined using the following expression:

$$ v_{0} = v(0,t) = {{G_{1} } \mathord{\left/ {\vphantom {{G_{1} } {\left( {{{\uppi}}h_{0}^{2} {{\uprho}}_{\text{w}} } \right)}}} \right. \kern-0pt} {\left( {{{\uppi}}h_{0}^{2} {{\uprho}}_{\text{w}} } \right)}}. $$
(11)

The model related to estimation of the thickness of the molten metal film L b, at the tip of sprayed anode-wire described in detail in paper (Ref 15). For this we consider the mass balance of molten wire material. Taking into account the assumption (Ref 15) that the molten metal in the upper part of the wire tip takes the shape of a segment of a sphere, flow rate of liquid wire material passing through circular segment in the line of plasma flow can be determined as

$$ G_{2} = 2{{\uprho}}_{\text{w}} \int\limits_{0}^{{L_{\text{b}} }} {v_{\text{liq}} \left( {z_{\text{b}} } \right)} \int\limits_{0}^{{y\left( {z_{\text{b}} } \right)}} {{\text{d}}y{\text{d}}z_{\text{b}} } . $$
(12)

Dependence \( v_{\text{liq}} \left( {z_{\text{b}} } \right) \) describes the distribution of melt flow velocity in the liquid interlayer at the wire tip along the axis z b. Considering the smallness of liquid interlayer thickness, flowing of liquid metal in it can be considered to be practically laminar, and a linear dependence of tangential component of velocity can be assumed here (Ref 15)

$$ v_{\text{liq}} \left( {z_{\text{b}} } \right) = \frac{{z_{\text{b}} }}{{L_{\text{b}} }} \cdot v_{\text{m}} , $$
(13)

where \( v_{\text{m}} \) is the melt flow velocity on the medium interface (at \( z_{\text{b}} = L_{\text{b}} \)).

Considering that half of the molten wire material flow through the half of the segment of a sphere under study, we will come to the following relationship:

$$ {{G_{1} } \mathord{\left/ {\vphantom {{G_{1} } 2}} \right. \kern-0pt} 2} = G_{2} . $$
(14)

Substituting expressions (10) and (12) into (14), and considering assumption (13), we can obtain the dependence of maximum melt flow velocity on its melt layer thickness on the wire tip:

$$ v_{\text{m}} \left( {L_{\text{b}} } \right) = \frac{{S_{\text{w}} }}{4}\frac{{v_{\text{w}} L_{\text{b}} }}{{\int\limits_{0}^{{L_{\text{b}} }} {z_{\text{b}} } \int\limits_{0}^{{y\left( {z_{\text{b}} } \right)}} {{\text{d}}y{\text{d}}z_{\text{b}} } }}. $$
(15)

Then, proceeding from the assumption that tangential stresses in the plasma and melt on the medium interface are equal:

$$ {{\upeta}}_{\text{W}} \left. {\frac{{\partial v_{\text{liq}} }}{{\partial z_{\text{b}} }}} \right|_{{L_{\text{b}} }} = {{\upeta}}_{\text{p}} \left. {\frac{{\partial v_{\text{p}} }}{{\partial z_{\text{b}} }}} \right|_{{L_{\text{b}} }} , $$
(16)

where \( {{\upeta}}_{\text{W}} \) is the dynamic viscosity of molten metal of the wire, Eq 14 can be rewritten as follows:

$$ \frac{{v_{w} S_{\text{w}} }}{2} = 2\frac{{{{\uptau}}_{\text{p}} \left( {v_{\text{m}} \left( {L_{\text{b}} } \right)} \right)}}{{{{\upeta}}_{\text{W}} }}\int\limits_{0}^{{L_{\text{b}} }} {z_{\text{b}} } \int\limits_{0}^{{y\left( {z_{\text{b}} } \right)}} {{\text{d}}y{\text{d}}z_{\text{b}} } . $$
(17)

The last equation can be used to determine the thickness of a liquid interlayer on the wire tip.

The following boundary conditions are set for the lower end of the jet:

$$ v( - L_{\text{d}} ,t) = - \frac{{{\text{d}}L_{\text{d}} }}{{{\text{d}}t}};\,\,\,\;h( - L_{\text{d}} ,t) = 0;\,\;\,\,{{\uptheta}}( - L_{\text{d}} ,t) = 0. $$
(18)

The shape of a droplet being in hydrostatic equilibrium is used as the initial conditions

$$ h(z,0) = \tilde{h}(z);\,\;\;v(z,0) = 0;\,\,\,\,\,{{\uptheta}}(z,0) = {\tilde{{\uptheta}}}(z);\,\,\,\,z \in ( - L_{\text{d}}^{(0)} ,0), $$
(19)

where \( L_{\text{d}}^{(0)} \) is the height of the droplet, the volume of which was selected to be sufficiently small; \( \tilde{h} = \tilde{h}(z) \) and \( {\tilde{{\uptheta}}} = {\tilde{{\uptheta}}}(z) \) are calculated using the equilibrium model (Ref 24).

Detachment of the droplet at point \( z = z^{*} \) was fixed when the following condition was met:

$$ h(z^{*} ) \le h^{*} , $$
(20)

where \( h^{*} \to 0 \). In this case, the volume of the detaching droplet can be determined by the following relationship:

$$ V^{*} = \pi \int\limits_{{ - L_{\text{d}} }}^{{z^{*} }} {h^{2} (z,t){\text{d}}z} $$
(21)

and it is assumed that the following conditions are met:

$$ h\left( {z^{*} } \right) = 0;\,\,\,\,\,L_{\text{d}} = z^{*} . $$
(22)

Numerical Method

The posed boundary problem was solved numerically by the finite difference method. The numerical solution procedure is described in detail in (Ref 21). Let discuss the main approaches used at creation of algorithms of the numerical solution of the equations of a thin jet (1-5, 9, 11, 18), and (19).

In the present problem the domain of integration over the space of Eq 1 changes in time, therefore it is expedient to pass to the dimensionless variables. Let \( {{\bar{z} = z} \mathord{\left/ {\vphantom {{\bar{z} = z} {L_{\text{d}} }}} \right. \kern-0pt} {L_{\text{d}} }} \), \( {{\bar{f} = F} \mathord{\left/ {\vphantom {{\bar{f} = F} {a^{2} }}} \right. \kern-0pt} {a^{2} }} \), \( \bar{L}_{\text{d}} = {{L_{\text{d}} } \mathord{\left/ {\vphantom {{L_{\text{d}} } a}} \right. \kern-0pt} a} \), \( \bar{K} = aK\,,\, \) \( \bar{t} = t\sqrt {{g \mathord{\left/ {\vphantom {g a}} \right. \kern-0pt} a}} \), \( \bar{v} = {v \mathord{\left/ {\vphantom {v {\sqrt {ga} }}} \right. \kern-0pt} {\sqrt {ga} }} \), where \( a = h_{0} \) is the jet base. Then, the equations of flow of a thin jet under the influence of the cocurrent gas stream, recorded relatively to the dimensionless variables take the form

$$ \left( {\frac{a}{\alpha }} \right)^{2} \frac{{D\bar{v}}}{{D\bar{t}}} = - \frac{1}{{\overline{{L_{\text{d}} }} }}\frac{{\partial 2\bar{K}}}{{\partial \bar{z}}} + \frac{\chi }{{\bar{L}_{\text{d}}^{2} \bar{f}}}\frac{\partial }{{\partial \bar{z}}}\left( {\bar{f}\,\frac{{\partial \bar{v}}}{{\partial \bar{z}}}} \right) - \frac{{2a \cdot {{\uptau}}_{\text{p}} }}{{{{\upsigma}} \cdot \bar{h}}},\,\,\,\, - 1 < \bar{z} < 0, $$
(23)
$$ \frac{{\partial \left( {\bar{L}_{\text{d}} \bar{f}} \right)}}{{\partial \bar{t}}} + \frac{\partial }{{\partial \bar{z}}}\left( {\bar{f} \cdot \bar{v} - \frac{{{\text{d}}\bar{L}_{\text{d}} }}{{{\text{d}}\bar{t}}}\bar{f} \cdot \bar{z}} \right) = 0, $$
(24)
$$ \frac{1}{{\bar{L}_{\text{d}} }}\sin (\uptheta )\frac{{\partial \left( {\sqrt {\bar{f}} } \right)}}{\partial z} = \cos ({{\uptheta}}), $$
(25)
$$ \bar{v}( - \bar{L}_{\text{d}} ,\bar{t}) = - \frac{{{\text{d}}\bar{L}_{\text{d}} }}{{{\text{d}}\bar{t}}},\,\,\,\,\bar{v}(0,\bar{t}) = - \frac{{v_{0} }}{{\sqrt {ga} }},\;\;\bar{f}( - 1,\bar{t}) = 0,\;\;\bar{f}(0,\bar{t}) = 1,\,\uptheta \left( { - 1,\bar{t}} \right) = 0, $$
(26)
$$ \bar{f}(\bar{z},0) = \bar{f}_{0} (\bar{z}),\;\;\bar{v}(\bar{z},0) = 0,\,\,\,\bar{z} \in ( - \bar{L}_{\text{d}}^{(0)} ,0), $$
(27)

where \( 2\bar{K} = - \frac{1}{{\bar{L}_{\text{d}} }}\frac{{\partial \left( {\cos \left( {{\uptheta}} \right)} \right)}}{{\partial \bar{z}}} + \frac{{\sin \left( {{\uptheta}} \right)}}{{\sqrt {\bar{f}} }} \), \( \frac{D}{{D\bar{t}}} = \frac{\partial }{{\partial \bar{t}}} + \bar{v}\frac{\partial }{{\partial \bar{z}}} \) is the substantial derivative, \( {{\upchi}} = {{3\nu {{\uprho}}\sqrt {ga} } \mathord{\left/ {\vphantom {{3\nu {{\uprho}}\sqrt {ga} } {{{\upsigma}}\,\,}}} \right. \kern-0pt} {{{\upsigma}}\,\,}} \), \( {{\upalpha}} = \sqrt {{{{\upsigma}} \mathord{\left/ {\vphantom {{{\upsigma}} {{{\uprho}}g}}} \right. \kern-0pt} {{{\uprho}}g}}} \) is the capillary constant.

On the integration interval \( - 1 \le \bar{z} \le 0 \) introduce an uniform spatial mesh \( \omega_{{\bar{z}}} = \{ \bar{z} = - 1 + (i - 1)\Updelta \bar{z},i = \overline{1,N} ,\,\,(N - 1)\Updelta \bar{z} = 1\} \) with step \( \Updelta \bar{z} \), as the dimensionless time step \( {\bar{{\uptau }}} \) can be introduced. The substantial derivative in (23) is approximated by a local Lagrangian grid. Difference analogs of Eqs (23-27) can be written as

$$ - \frac{1}{{\bar{L}_{\text{d}} }}\frac{{\cos ({{\uptheta}}_{i + 1} ) - \cos ({{\uptheta}}_{i} )}}{{\Updelta \bar{z}^{2} }} + \frac{1}{{2\Updelta \bar{z}}}\left( {\frac{{\sin ({{\uptheta}}_{i + 1} )}}{{\sqrt {\bar{f}_{i + 1} } }} - 3\bar{K}_{0} } \right) + \frac{{\bar{L}_{\text{d}} }}{2}\left( {\frac{\text{a}}{{{\upalpha}}}} \right)^{2} \frac{{\bar{v}_{i} - \tilde{v}_{i} }}{{{\bar{{\uptau }}}}} + \frac{{2a \cdot {{\uptau}}_{i} }}{{{{\upsigma}} \cdot \sqrt {\bar{f}_{i} } }} = 0,\;\;i = 1 $$
(28)
$$ \begin{aligned} \frac{1}{{2\Updelta \bar{z}}}\left( {\frac{{\sin ({{\uptheta}}_{i + 1} )}}{{\sqrt {\bar{f}_{i + 1} } }} - \frac{{\sin ({{\uptheta}}_{i - 1} )}}{{\sqrt {\bar{f}_{i - 1} } }}} \right) - \frac{1}{{\bar{L}_{\text{d}} \Updelta \bar{z}^{2} }}\left( {\cos \left( {{{\uptheta}}_{i + 1} } \right) - 2\cos \left( {{{\uptheta}}_{i} } \right) + \cos \left( {{{\uptheta}}_{i - 1} } \right)} \right) \hfill \\ + \bar{L}_{\text{d}} \left( {\frac{a}{\alpha }} \right)^{2} \left( {1 + \frac{{\bar{v}_{i} - \tilde{v}_{i} }}{{{\uptau}}}} \right) - {{\upchi}}\left( {\frac{{\bar{v}_{i + 1} - 2\bar{v}_{i} + \bar{v}_{i - 1} }}{{\bar{L}_{\text{d}} \Updelta \bar{z}^{2} }} + \frac{{ctg({{\uptheta}}_{i} )}}{{\sqrt {\bar{f}_{i} } }}\frac{{\left( {\bar{v}_{i + 1} - \bar{v}_{i - 1} } \right)}}{{\Updelta \bar{z}}}} \right) \hfill \\ + \frac{{2a \cdot {{\uptau}}_{i} }}{{{{\upsigma}} \cdot \sqrt {\bar{f}_{i} } }} = 0,\;\;\,i = \overline{2,N - 1} \hfill \\ \end{aligned} $$
(29)
$$ \begin{aligned} \frac{{\Updelta \bar{z}}}{{{\bar{{\uptau }}}}}\left( {\bar{L}_{\text{d}} \frac{{\bar{f}_{i + 1} + \bar{f}_{i} }}{2} - {\breve{L}}_{\text{d}} \frac{{{\breve{f}}_{i + 1} + {\breve{f}}_{i} }}{2}} \right) + \bar{f}_{i + 1} \left( {\bar{v}_{i + 1} - \bar{z}_{i + 1} \frac{{\bar{L}_{\text{d}} - {\breve{L}}_{\text{d}} }}{{{\bar{{\uptau }}}}}} \right) \hfill \\ + \bar{f}_{i} \left( {\bar{z}_{i} \frac{{\bar{L}_{\text{d}} - {\breve{L}}_{\text{d}} }}{{{\bar{{\uptau }}}}} - \bar{v}_{i} } \right) = 0,\;\,\;i = \overline{1,N - 1} \hfill \\ \end{aligned} $$
(30)
$$ \frac{{\sin ({{\uptheta}}_{i + 1} ) + \sin ({{\uptheta}}_{i} )}}{2}\frac{{\bar{f}_{i + 1} - \bar{f}_{i} }}{\Updelta z} - \bar{L}_{\text{d}} \left( {\sqrt {\bar{f}_{i + 1} } \cos ({{\uptheta}}_{i + 1} ) + \sqrt {\bar{f}_{i} } \cos ({{\uptheta}}_{i} )} \right) = 0,\,\;\;i = \overline{1,N - 1} $$
(31)
$$ \bar{v}_{1} = - \frac{{\bar{L}_{\text{d}} - {\breve{L}}_{\text{d}} }}{{{\bar{{\uptau }}}}},\;\;\bar{v}_{N} = - \frac{{v_{\text{e}} }}{{\sqrt {ga} }},\;\;\bar{f}_{1} = 0,\;\;\bar{f}_{N} = 1,\;\;\uptheta_{1} = 0, $$
(32)
$$ {\breve{v}}_{i} = 0,\;\;{\breve{f}}_{i} = \bar{f}_{0} \left( {\bar{z}_{i} } \right),\;\;i = \overline{1,N} $$
(33)

In Eqs (28-33) the following notation for grid functions were introduced: \( g_{i} = g(\bar{z}_{i} ,\bar{t}_{k} ),\, \) \( g = \bar{v},\bar{f},{{\uptheta}} \); \( {\breve{g}}_{i} = g(\bar{z}_{i} ,\bar{t}_{k - 1} ), \) \( g = \bar{v},\bar{f} \); \( {{\uptau}}_{i} = {{\uptau}}_{\text{p}} \left( {v_{i} } \right) \); \( \tilde{v}_{i} = v(\tilde{z}_{i} ,\bar{t}_{k - 1} ) \). Here, \( \tilde{z}_{i} \) is the local Lagrangian mesh node at the time \( \bar{t} = \bar{t}_{k - 1} \). The solving of the system of nonlinear Eqs (28-32), in which unknowns are \( \bar{K}_{0} ,\;\bar{L}_{\text{d}} ,\;\bar{f}_{1} ,{{\uptheta}}_{1} ,\bar{v}_{1} , \ldots ,\bar{f}_{N} ,{{\uptheta}}_{N} ,\bar{v}_{N} \), was done by Newton’s method.

Results and Discussions

Now, we will consider peculiarities of formation of droplets of the molten wire metal based on the results of numerical modelling by using the described mathematical model. Calculations were made for a steel wire, whose thermal-physical characteristics were taken from study (Ref 8), at the following spraying parameters: arc current I = 160-240 A, plasma gas (Ar) flow rate G = 1.0-1.5 m3/h, wire feed speed 6-15 m/min, and wire diameter 1.2-1.6 mm. Characteristics of the plasma flow were calculated by the procedure described in (Ref 12, 13). The values of thickness and metal flow rate \( v_{\text{m}} \) in the liquid film held at the tip of the wire, its position relative to the plasma jet axis, and corresponding initial characteristics of the melt jet for different spraying parameters are given in Table 1 (Ref 15).

Table 1 Parameters of flow of the melt in liquid film at the wire tip and in the initial section of the jet at different spraying parameters
Full size table

It is of interest to analyse the very mechanism of formation of droplets from a thin jet of the melt under conditions of plasma-arc wire spraying. For example, Fig. 4 shows distributions of the rate of the molten metal flow in the jet, as well as profiles of cross-section of the jet at different time moments in formation of the first droplet. As follows from the presented calculation data, at the initial stage of the flow the rate decreases from that of the molten metal arriving to the jet to that at its end equal to the rate of elongation of the jet (see curves 1 and 2 in Fig. 4a). As a result, the metal coming to the jet is gradually transported to its end, and a neck forms near the jet base (see curve 3 in Fig. 4b). Moreover, decrease in radius of the jet within the neck region leads to increase in Laplace pressure in the liquid metal and intensification of viscous forces on the side of the plasma flow. The metal from the neck region starts actively flowing out into the forming droplet (see curves 3 and 4 in Fig. 4a) until the radius of the neck reaches a critical value, at which the surface tension forces can no longer hold the droplet at the jet end (see curve 4 in Fig. 4b). It is in this way that detachment of the droplet, i.e., the dispersed spraying material particle, takes place.

Fig. 4
figure 4

Distributions of flow rate (a) and radius of the molten wire metal jet (b) along the jet axis at different time moments of formation of the first droplet: 1, 0; 2, 0.347; 3, 0.708; 4, 0.874 ms; plasma arc current 200 A; Ar flow rate 1 m3/h; wire diameter 1.4 mm; wire feed speed 9 m/min

Full size image

The results of modelling dynamics of formation of molten metal droplets for different wire feed speeds are shown in Fig. 5. As follows from the calculation results presented in this figure, characteristics of flowing of the jet can differ substantially for different values of the feed speed. For instance, each set of values of the spraying process parameters has certain boundary values of the wire feed speed, at which the volume consumption of the molten metal arriving to the jet coincides with the rate of growth of the droplet volume (see, e.g. Fig. 5, at v w = 9 m/min). In this case the forming droplets have approximately identical sizes, and length of the jet varies but insignificantly, thus reflecting the process of growth of the volume and detachment of the droplet. At higher values of the wire feed speed, the volume of the molten metal arriving to the jet exceeds the rate of growth of the volume of the droplet at the jet end, this resulting in a gradual increase of its length (see Fig. 5, at v w = 12 and 15 m/min). Disturbances caused by the effect of the surface tension forces start accumulating on the jet surface. Propagation of the disturbances leads to formation of many necks and regions of expansion of the jet. As a rule, this is accompanied by breaking of the jet near the wire tip, as shown in Fig. 6, i.e., the forming droplet has a rather big volume and, upon getting into the plasma flow, it may split into finer droplets due to the effect of the gas-dynamic forces. Plots of time variations in the jet length related to detachment of the droplets are shown in Fig. 7 for a number of values of the wire feed speed.

Fig. 5
figure 5

Dynamics of formation of the first (a), second (b), and third (c) droplets at different wire feed speeds (9, 12, and 15 m/min): plasma arc current 200 A; Ar flow rate 1 m3/h; wire diameter 1.4 mm

Full size image
Fig. 6
figure 6

Profile of the molten metal jet at a moment of its breaking near the wire tip: arc current 200 A; Ar flow rate 1 m3/h; wire diameter 1.4 mm; wire feed speed 12 m/min; t = 3.86 ms

Full size image
Fig. 7
figure 7

Variations in length of the molten metal jet with time: 1 wire feed speed 6; 2, 9; 3, 12 m/min; arc current 200 A; Ar flow rate 1 m3/h; wire diameter 1.4 mm

Full size image

While generalising the results of modelling of flowing of the molten metal jet and formation of droplets, i.e., spraying particles, note that three, most characteristic types of the melt flow can be distinguished in plasma-arc wire spraying. The first one, as a rule, is typical of small-diameter wires (1.2-1.4 mm) fed at relatively low speeds (5-7 m/min), spraying material consumption of 0.7-1.3 g/s, arc current of about 200 A, and plasma gas flow rate of 1 m3/h. In this case the molten wire tip is located at a distance of 0.7-1.0 mm from the plasma jet axis (see Table 1), i.e., outside the zone of the intensive gas-dynamic and thermal effect on the side of the plasma flow. Under such conditions the molten metal jet starts extending in length (see curve 1 in Fig. 7), and actually the jet-type metal transfer without atomization takes place.

The second type of flowing and splitting of the jet occurs at a wire feed speed of 8-12 m/min and wire diameter of 1.4-1.6 mm, this corresponding to a consumption of 1.3-2.1 g/s and being characterised by a stable process of formation of droplets, i.e., their stable sizes and detachment intervals (see curve 2 in Fig. 7, 5 at v w = 9 m/min). This type of wire spraying is most preferable in terms of formation of droplets of an identical size and, hence, homogeneous coatings.

Finally, the third type of the flow takes place at high wire feed speeds (12-15 m/min), when the jet length varies in a cyclic manner, i.e., formation of droplets occurs at a regular alternation of the processes of growth of the length of the jet and processes of its breaking (see Fig. 5 at v w = 12 and 15 m/min, and curve 3 in Fig. 7). In the latter case formation of satellite droplets accompanying detachment of the course droplets and, as a rule, preceding breaking of the jet is observed.

Consider now some statistical characteristics of the processes of formation and detachment of droplets in plasma-arc wire spraying. Figure 8 shows the calculated distributions of the detaching droplets in size and initial velocities for the above three types of flowing of the molten wire metal. For example, Fig. 8a, corresponds to a case of extension of the melt jet with its periodic breaking. In this case the coarse droplets, 750 μm or more in diameter, are formed, their initial velocity being 0.7-0.8 m/s. At a wire feed speed of 9 m/min (see Fig. 8b) practically similar droplets with an average diameter of 670 μm detach from the wire tip at a velocity of about 1.31 m/s. At the higher wire feed speeds (see Fig. 8c) the forming droplets may be substantially different in size and initial velocity. Droplets with a diameter of 600-800 μm form in breaking of the extending melt jet held at the wire tip. Breaking of the main jet (see Fig. 7) is often accompanied by subsequent detachment of finer satellite droplets with a diameter of 400-500 μm or less.

Fig. 8
figure 8

Distribution of forming droplets in size and initial velocity depending on the wire feed speed: (a), 7; (b), 9; (c), 12 m/min; arc current 200 A; Ar flow rate 1 m3/h; wire diameter 1.4 mm

Full size image

The averaged characteristics of the process of formation of droplets, i.e., spraying particles, in plasma-arc spraying are shown in Fig. 9. As seen from the calculation data presented in this figure, spraying of the steel wire results in formation of mostly the droplets that correspond in volume to the spherical droplets 600-750 μm in diameter at a breaking interval of 0.4-0.8 ms. The highest effect on parameters of the forming droplets in plasma-arc wire spraying is exerted by the amount of the material melted and arriving into the jet per time unit, i.e., diameter of the spraying wire and its feed speed, as well as operation mode of the plasmatron. For example, the temperature and rate of the plasma flow grow with increase in the arc current and plasma gas flow rate. This leads to increase in the intensity of the viscous friction forces on the plasma side acting on the melt that forms at the wire tip. Size of the liquid film held at the tip and, hence, thickness of the jet and diameter of the forming droplets decrease. The interval of detachment of the droplets depends most significantly on the wire feed speed, increase in the values of which leads to intensification of the processes occurring in the molten metal jet.

Fig. 9
figure 9

Effect of the wire feed speed on the average diameter (a) and interval of detachment (b) of forming droplets: 1, wire diameter 1.4; 2, 1.2; 3, 1.6 mm; arc current 200 A; 4, wire diameter 1.4 mm; arc current 240 A

Full size image

Comparisons with Experimental Data

An important stage in the development of the mathematical model is comparison of obtained calculated results with the experimental data. Note that carrying out the experimental work on the study of the formation of droplets in plasma-arc spraying is complicated by the rapidity of taking place processes, as well as a high level of radiation of arc plasma in studied area, and other factors. In this regard, it is possible to note only a relatively small number of papers devoted to the experimental studies of spraying of wires during related process of wire-arc spraying. For example, in (Ref 25-28) investigations of the process of wire-arc spraying by high-speed imaging of the formation and transport of droplets from the tip of the electrodes were conducted. It is shown that during wire-arc spraying the size of droplets detached from the cathode wire is much smaller than the size of droplets detached from the anode wire. In the case of the anode (Ref 25, 26), the diffuse arc attachment heats a large part of the wire surface, creating a small layer of molten metal on the wire. When the molten metal on the wire electrode is stretched in the direction parallel to the jet axis the forces acting on the liquid sheet in opposing directions lead to its breakup. Disturbance on the liquid metal/gas surface of anode sheet which is enhanced by aerodynamic forces leading to the breakup of the thin metal sheet (primary atomization) and formation of ligaments (larger liquid drops), which may break up in gas stream into smaller drops (secondary atomization) (Ref 25). This scheme of wire atomization qualitatively corresponds to the calculated results received for the plasma-arc spraying. In (Ref 25) in addition to a qualitative description of the formation of droplets, effects of operation parameters on length of anode and cathode sheets, as well as on anode and cathode breakup time were experimentally investigated. It is established that length of an anode sheet is 3.2-4.7 mm, with the breakup time 0.63-2.8 ms, and length of a cathode sheet is 1.3-3.7 mm with the breakup time 0.48-0.9 ms. Unfortunately, obtained in (Ref 25) experimental data cannot be used to estimate the volume or medium-volume diameter of the produced drops after its breaks away from wire tips. Results of calculations (see Fig. 6, 7) show that during plasma-arc spraying the melt jet is pulled at the length of 0.4 - 3 mm. These results is close to obtained in (Ref 25) experimental data, however incorrectly to carry out their direct comparison, in view of various conditions of spraying processes.

Another approach to the experimental investigation of the formation of droplets during wire-arc spraying used in (Ref 3) and consisted of measurement of arc voltage trace behavior by oscillograph. This allowed to detect the moments of droplets breakup, and, assuming a constant speed of wire fed to the arc, to estimate the sizes of formed droplets. Thus, according to study (Ref 3), during wire-arc spraying the droplets corresponding in mass to the 500-800-μm diameter ones detach from the steel electrode tips at a detachment interval of 0.5-0.8 ms. The values are in good agreement with the calculated results shown in Fig. 9. Let’s note, also, that in contrast to the wire-arc spraying oscillography for plasma-arc spraying does not allow to interpret received results unambiguously. This is due to the fact that during plasma-arc spraying is only one wire atomizing and changes of the thickness of the melt at the wire tip does not significantly affected on the length of the plasma arc. So by the signals latched by oscilloscope it is difficult to separate the moments the droplets breakup from the failure of random fluctuations in the arc voltage.

Conclusions

  1. 1.

    The mathematical model was developed, describing hydrodynamic processes occurring in flowing of the jet and formation of liquid metal droplets in a wake high-velocity plasma flow. Using it in combination with the earlier developed models of the plasma jet and thermal state of the wire allows stating the development of the complete mathematical model of the physical processes occurring in spraying of the anode wire under conditions of plasma-arc wire spraying. This provides the possibility of conducting a detailed quantitative analysis of the processes of heating and melting of the wire, as well as formation and detachment of the molten metal droplets depending on the spraying process parameters.

  2. 2.

    As shown by the conducted numerical analysis, plasma-arc spraying of steel wire results in formation of droplets with a diameter of 600-750 μm and detachment interval of 0.4-0.8 ms. Parameters of the process of formation of the droplets can be adjusted by varying the spraying material consumption (wire feed speed and diameter) and operation mode of the plasmatron.

  3. 3.

    Three types of flowing and splitting of the molten wire metal jet may occur in plasma-arc spraying: jet flow of metal (at wire feed speeds of 5-7 m/min and arc current of about 200 A); formation of droplets of almost identical sizes (at wire feed speeds of 8-12 m/min), and, finally, formation of droplets substantially differing in size (at wire feed speeds of 12-15 m/min).

  4. 4.

    To predict thermal and dynamic characteristics of the particles flying to the workpiece surface, it is necessary to analyse the processes of heating, acceleration, deformation, and splitting of the molten metal droplets in a turbulent plasma flow.