Numerical Study of Fatigue Crack Propagation in a Residual Stress Field Induced by Shot Peening

Abstract

Shot peening (SP) is a relatively traditional but highly effective mechanical surface treatment that produces a compressive residual stress field in a shot-peened (SPed) surface, which can effectively delay fatigue crack propagation (FCP) and prolong the service life of engineering materials and structures. A multistep analysis method was developed by combining a numerical simulation of the SP process and the LEFM-based (linear elastic fracture mechanics) superposition principle to study FCP behavior in an SP-induced residual stress field. The SP-induced residual stresses were first simulated by a symmetric cell model and then introduced into a finite element model of the CT specimen. The total stress intensity factors and stress ratios with respect to different crack lengths were calculated according to the LEFM-based superposition principle. The influences of external applied load ratios and SP conditions, including one-sided and double-sided SP, on the FCP behavior of the SPed CT specimen were investigated in detail.

Introduction

Engineering materials and structures that are subjected to variable amplitude loading during service often experience fatigue failure (Ref 1, 2), which consists of three phases: fatigue crack initiation, propagation and fracture. Considering that fatigue cracks mostly initiate on material surfaces, many surface enhancement treatment techniques have emerged to improve the fatigue performance and prolong the service life of engineering components (Ref 3), including SP (Ref 4), deep rolling (DR) (Ref 5) and laser shock processing (LSP) (Ref 6).

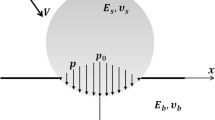
SP is a relatively traditional but highly effective mechanical surface enhancement treatment technique that is widely used in the aerospace, automotive and power generation industries (Ref 7, 8). As shown in Fig. 1, during the SP process, a large number of small spherical shots are fired at a metal surface, and the resultant impacts produce inhomogeneous elastic–plastic deformation in the SPed materials. As a result, beneficial compressive residual stresses are produced in the surface layer of metallic materials. A large number of experiments have confirmed that SP-induced compressive residual stresses can considerably improve the surface integrity and fatigue resistance of metallic materials (Ref 9, 10).

Fig. 1

Schematic of the SP process

Numerical simulations with the finite element method (FEM) are inexpensive and easy to perform; moreover, this approach can provide insight into the compressive residual stress strengthening mechanism of SP. For numerical simulations of the SP process, many finite element models have been developed, such as the single-shot impact model (Ref 11), multiple-shot random-impact model (Ref 12, 13), DEM-FEM coupled model (Ref 14), SPH-FEM coupled model (Ref 15) and symmetric cell model (Ref 16, 17). The residual stresses predicted by these SP models are in good agreement with the experimental results.

Additionally, FCP behavior in a residual stress field has been studied by researchers based on finite element simulations (Ref 18,19,20), and there are two main methods widely used to compute the FCP rate. The first approach, as proposed by Elber (Ref 21), is based on plasticity-induced crack closure and requires a calculation of the crack opening stress intensity factor (K_op) by using elastic–plastic finite element analyses (Ref 22, 23) or empirical formulas (Ref 24, 25). The effective stress intensity factor range ($\Delta K_{\text{eff}}$), which is used to describe FCP behavior in the combined stress field of external applied loads and residual stresses, can be calculated by $\Delta K_{\text{eff}} = K_{{\hbox{max} ,{\text{tot}}}} - K_{\text{op}}$. The other approach is the (modified) superposition based on the principle of LEFM (Ref 26). According to the LEFM-based superposition principle, provided that the material behavior is linear elastic, the total stress intensity factor ($K_{\text{tot}}$), which is used to describe the stress state next to the crack tip, is the sum of two separate stress intensity factors, associated with the external applied loads and residual stresses. The second approach generally consists of the following four steps:

• 1. Calculation or measurement of the residual stresses induced by material processing technology, such as SP.

• 2. Calculation of $K_{\text{tot}}$, which is related to the external applied loads and residual stresses, by using the modified virtual crack closure technique (MVCCT) (Ref 27).

• 3. Calculation of $\Delta K_{\text{tot}}$ and the total stress ratio ($R_{\text{tot}}$).

• 4. Calculation of the FCP rate (da/dN) by using $\Delta K_{\text{tot}}$ and $R_{\text{tot}}$ in the empirical crack growth laws, such as Paris’ law (Ref 28), Walker’s equation (Ref 29) and Nasgro’s equation (Ref 30).

The LEFM-based superposition principle has been widely used in recent years. Keller et al. (Ref 31) proposed a multistep simulation strategy to predict the FCP rate in LSP-induced residual stress fields, and the predictions were validated through a comparison with the results of FCP tests. A linear elastic finite element crack growth prediction model was developed by Pavan el at. (Ref 32) to simulate FCP behavior in an LSP-induced residual stress field, and the predicted results are in excellent agreement with experimental data. Zhao et al. (Ref 33) used a numerical method combining FEM and residual stress intensity factor analysis to investigate the influence of the LSP pattern on the FCP behavior of compact tension (CT) samples. Schnubel et al. (Ref 34) used a quantitative numerical approach that was similar to the multistep analysis method to predict the delay in FCP of AA2198-T8 specimens containing one line of laser heating. Jacob et al. (Ref 35) and Servetti et al. (Ref 36) employed the MVCCT incorporating FEM to study the FCP behavior in a welding-induced residual stress field.

SP-induced compressive residual stresses are very beneficial for improving fatigue performance. Although a large number of experiments have been conducted to investigate FCP behavior in SP-induced residual stress fields, the influence mechanism of SP-induced residual stress on FCP has not yet been comprehensively and quantitatively studied, as this task is difficult to complete using experiments alone. Therefore, in this work, by combining the LEFM-based superposition principle and finite element simulation of the SP process, a multistep analysis method was developed and used to investigate FCP behavior in an SP-induced residual stress field. The CT specimens in this study were composed of AISI 304 stainless steel, which is widely used in industrial applications due to its excellent corrosion resistance, good strength and high toughness. The influences of the external applied load ratios and SP conditions, including one-sided and double-sided SP, on the FCP behavior of the SPed CT specimens were investigated in detail.

Numerical Modeling and Prediction Methodology

The AISI 304 stainless steel CT specimen was used to numerically investigate FCP behavior in an SP-induced residual stress field. The CT specimen geometry and the multistep simulation strategy are shown in Fig. 2. The length, width and height of the CT specimen were 125, 120 and 4.5 mm, respectively. The center area with dimensions of 15 mm × 60 mm on the top (or bottom) surface of the CT specimen was impacted by multiple shots, which produced beneficial compressive residual stresses in the local region of the surface layer.

Fig. 2

CT specimen geometry and the multistep simulation strategy

To minimize the computational cost, a symmetric cell model taken from the local region to be peening was created to simulate the SP process. Both the length and width of the symmetric cell model were equal to the shot radius, $R = 0.3\;{\text{mm}}$, and the height of the symmetric cell model was equal to the height of the CT specimen. The residual stresses resulting from the symmetric cell model were transferred to the finite element model of CT specimen by means of the analytical stress field.

Considering the symmetry of CT specimen model, a 1/2 symmetric finite element model of CT specimen was created to simulate FCP behavior according to the LEFM-based superposition principle, as shown in Fig. 2. The external loads were applied over an area in the loading hole by a distributed force of $F_{\hbox{max} } = 8$ and $F_{ \hbox{min} } = 0.8$ and 0.08 kN, which correspond to the external applied load ratios of $R_{\text{load}} = 0.1$ and 0.01, respectively. FCP behavior was simulated by progressively releasing the symmetric boundary conditions applied on the nodes ahead of the crack tip. Depending on the crack length, the symmetric boundary conditions were replaced by the contact conditions of a rigid plate with no friction in the x–z plane. The contact with the rigid plate simulates fatigue crack closure behavior and prevents the crack faces from exhibiting negative displacement. The crack tip was assumed to be a straight line perpendicular to the specimen surface, and the crack uniformly extended during its propagation process. Note that SP-induced residual stresses were assumed to be constant during the FCP process. Hence, the dynamic redistribution of residual stresses during the FCP process was not taken into consideration, this phenomenon is related to elastic–plastic deformation and is a subject for further investigation in the future.

Symmetric Cell Model

The symmetric cell model is widely used to predict SP-induced residual stresses due to the lower computational cost. The symmetric cell model can be theoretically regarded as a representative volume element (RVE) model for the numerical simulation of the SP process, which assumes that multiple shots impact the target surface with a symmetric layout, row by row at normal incidence (Ref 16). As shown in Fig. 3, four shots were used to impact four corresponding corner regions of the symmetric cell model in an anti-clockwise direction, which can be regarded as one peening series, and eight shots constitute two peening series. Symmetric boundary conditions were imposed on the four side surfaces of the symmetric cell model, and a normal displacement constraint was imposed on the bottom (or top) surface. For the interaction between the shots and the target surface, when compared with the target material, the shots sustained very little plastic deformation and were therefore treated as the rigid spherical bodies. An initial shot velocity of 50 m/s was applied to the reference point of the rigid body, which is located at the center of the spherical shot. The penalty method with a Coulomb friction coefficient of 0.3 was used to calculate the contact between the shots and the target surface.

Fig. 3

Symmetric cell model used to simulate the SP process

Three-dimensional eight-node linear brick elements with reduced integration and hourglass control (C3D8R elements in ABAQUS/Explicit codes) were used to mesh the target and shot models. To obtain more accurate gradient distributions of residual stresses in the thickness direction of the SPed target model, the element size close to the contact surface was set to be increasingly refined, wherein the finest element size was 20 µm, as shown in Fig. 3.

The Johnson–Cook (JC) model was employed to characterize the dynamic mechanical responses under shot impact, wherein this model can be expressed as,

$$ \bar{\sigma } = \left[ {A + B\bar{\varepsilon }_{\text{p}}^{n} } \right] \cdot \left[ {1 + C\ln \left( {\frac{{\dot{\bar{\varepsilon }}_{\text{p}} }}{{\dot{\bar{\varepsilon }}_{{{\text{p}},0}} }}} \right)} \right] \cdot \left[ {1 - \left( {\frac{{T - T_{\text{r}} }}{{T_{\text{m}} - T_{\text{r}} }}} \right)^{\text{m}} } \right] $$

(1)

where A is the initial yield strength of the material at room temperature of T_r; B is the strain hardening coefficient; C represents the strain rate sensitivity; $\bar{\varepsilon }_{\text{p}}$, $\dot{\bar{\varepsilon }}_{\text{p}}$ and $\dot{\bar{\varepsilon }}_{{{\text{p}},0}}$ represent the equivalent plastic strain, equivalent plastic strain rate and reference plastic strain rate, respectively; T represents the temperature; $T_{\text{m}}$ is the melting temperature; and n and m are related to the strain hardening and thermal softening effects, respectively. The JC model parameters of AISI304 stainless steel are listed in Table 1 (Ref 37).

Table 1 JC model parameters of AISI304 stainless steel (Ref 37)

To validate the symmetric cell model, the experimental conditions of SP taken from the literature (Ref 38) were resimulated, and the resultant in-depth residual stresses are shown in Fig. 4, where S11 and S22 represent the in-plane stress components of $\sigma_{x}$ and $\sigma_{y}$, respectively. The in-depth residual stresses were calculated by using the “area-averaged” method (Ref 17, 39), which could eliminate the influences of the shot impacting sequence for one peening series (i.e., each four shot impacts). Figure 4 shows that for the different peening series, the area-averaged values of the two in-plane residual stress components are approximately equal, $\sigma_{x} \approx \sigma_{y}$. The in-depth residual stresses in the SPed surface and subsurface are in good agreement with the experimental data (Ref 38) in the cases of two and three peening series, although there are some differences in the maximum compressive residual stresses, which may be related to the material constitutive model or the dispersion of experimental data. The experimentally measured values of SP-induced residual stresses correspond to 100% coverage (Ref 38), and according to the calculation method of 100% coverage used for the symmetric cell model (Ref 17), two or more peening series are needed to predict the residual stresses corresponding to 100% coverage. Figure 4 demonstrates that the symmetric cell model has the capability of predicting SP-induced residual stresses. For simplicity, the SP coverage was not taken into consideration in this work, and one peening series was used to investigate FCP behavior in an SP-induced residual stress field.

Fig. 4

Validation of the symmetric cell model

Simulation of Residual Stresses

Numerical simulations of one-sided and double-sided SP processes were carried out to investigate FCP behavior in an SP-induced residual stress field. In the case of one-sided SP, four shots (one SP series) were used to impact the bottom surface of the symmetric cell model, which is the surface at $z = 0.0\;{\text{mm}}$. For double-sided SP, two peening series were used: the first four shots (the first peening series) were used to impact the bottom surface of the symmetric cell model ($z = 0.0\;{\text{mm}}$), and the other four shots (the second peening series) were used to subsequently impact the top surface of the symmetric cell model ($z = 4.5\;{\text{mm}}$).

The residual stress distributions resulting from the symmetric cell model are shown in Fig. 5. For one-sided SP, the resultant compressive residual stresses are located in the SPed surface layer, and the larger compressive residual stresses are close to the indentations produced by the shot impacts. For double-sided SP, both the top and the bottom surfaces of the symmetric cell model were strengthened with compressive residual stresses, as shown in Fig. 5(b). In the case of double-sided SP, significant residual stress relaxation occurred in the surface layer impacted by the first four shots after the second peening series was carried out; this phenomenon is likely related to the propagation and attenuation of elastic waves induced by the second peening series (Ref 40).

Fig. 5

SP-induced residual stresses: (a) one-sided SP and (b) double-sided SP

As seen in Fig. 5, in the SPed symmetric cell model, some local regions on the target surface are impinged by the shots, while some local regions are never impinged. The larger elastic–plastic deformation would be produced in the impacted region, which results in the larger compressive residual stresses. The un-uniform residual stresses in Fig. 5 are not consistent with the experimental measured results, an “area-averaged” method (Ref 17, 39) was therefore used to calculate the averaged value of the residual tresses, as shown in Fig. 6, and the area-averaged values of the residual stresses agree well with the experimental measured results (Ref 17, 39). The in-depth residual stresses in Fig. 6 are the results of the area-averaged the residual stresses in Fig. 5, and the function proposed by Robertson (Ref 41) was used to fit the area-averaged values of the in-depth residual stresses.

Fig. 6

Area-averaged in-depth residual stresses: (a) one-sided SP and (b) double-sided SP

For one-sided SP [shown in Fig. 5(a)],

$$ \bar{\sigma }\left( z \right) = - 452.23\exp \left( { - \frac{{2\left( {z - 0.09} \right)^{2} }}{{0.25^{2} }}} \right) + 24.08 $$

(2)

whereas for double-sided SP [shown in Fig. 5(b)],

$$ \bar{\sigma }\left( z \right) = \left\{ {\begin{array}{*{20}c} { - 1849.5\exp \left( { - \frac{{2\left( {z + 1.59} \right)^{2} }}{{1.47^{2} }}} \right) + 25.42} & {0 \le z < 2.25} \\ { - 464.88\exp \left( { - \frac{{2\left( {4.4 - z} \right)^{2} }}{{0.26^{2} }}} \right) + 25.54} & {2.25 \le z \le 4.5} \\ \end{array} } \right. $$

(3)

where $\bar{\sigma }\left( z \right)$ represents the area-averaged values of in-depth residual stresses and z represents the z-axis coordinates. Note that the origin of the Cartesian coordinate system is located on the bottom surface of CT specimen and the z-axis is along the thickness direction.

CT Specimen Model

The 1/2 symmetric finite element model of the CT specimen is shown in Fig. 7. The model was meshed with a total of 402600 C3D8R elements with the following linear elastic material mechanical parameters: Young’s modulus $E = 200\;{\text{GPa}}$ and Poisson’s ratio $\upsilon = 0.3$. To account for the gradient distributions of SP-induced in-depth residual stresses, the element size was increasingly refined close to the SPed surface in the thickness direction of the CT specimen, which is consistent with the element size of the symmetric cell model in Fig. 3.

Fig. 7

1/2 symmetric finite element model of CT specimen

The in-depth residual stresses outputted from the symmetric cell model were introduced into the 1/2 symmetric finite element model of CT specimen through the ABAQUS user subroutine SIGINI, wherein the values are associated with the fitting equations for the in-depth residual stresses, i.e., Eq 2 and 3. After the in-depth residual stresses were introduced, the initial residual stress states of CT specimen were obtained by a self-balancing calculation and are shown in Fig. 8, which are in good agreement with the residual stress distributions in Fig. 6. A comparison of Fig. 6 and 8 reveals that some differences in the maximum compressive residual stresses, which are mainly attributed to the self-balancing calculation, and the differences were not taken into consideration in this work.

Fig. 8

Residual stress fields of CT specimen: (a) one-sided SP and (b) double-sided SP

Results and Discussion

Distributions of Von Mises Stress

The distributions of von Mises stress were used to describe the stress state next to the crack tip in the FCP process. Under the maximum external applied load of $F_{\hbox{max} } = 8\;{\text{kN}}$, with respect to a crack length of 40 mm, the distributions of von Mises stress without SP are shown in Fig. 9 associated with $K_{\hbox{max} } = 37.24\; {\text{MPa}}\sqrt {\text{m}}$, which were used as a reference. The distributions of von Mises stress in Fig. 10 and 11, associated with $K_{\hbox{max} } = 3 7. 7 3$ and $3 7. 7 5\;{\text{MPa}}\sqrt {\text{m}}$, respectively, correspond to the cases of one-sided and double-sided SP, which were used to investigate the influences of SP-induced residual stresses on the stress state next to the crack tip.

Fig. 9

Distributions of von Mises stress in the x–y plane with regard to different z-axis coordinates without SP: (a) z = 0 mm, (b) z = 2.0 mm, (c) z = 4.1 mm and (d) z = 4.5 mm

Fig. 10

Distributions of von Mises stress in the x–y plane with regard to different z-axis coordinates for one-sided SP: (a) z = 0 mm, (b) z = 0.63 mm, (c) z = 2.5 mm and (d) z = 4.5 mm

Fig. 11

Distributions of von Mises stress in the x–y plane with regard to different z-axis coordinates for double-sided SP: (a) z = 0 mm, (b) z = 2.0 mm, (c) z = 3.87 mm and (d) z = 4.5 mm

Figure 9 shows that without introducing residual stresses, next to the crack tip, a relatively uniform distribution of von Mises stress can be observed in the thickness direction of CT specimen. The slight differences in the von Mises stresses in the x–y plane with regard to different z-axis coordinates are focused on the crack tip, the relatively larger von Mises stresses are on the top/bottom surfaces, and the relatively smaller von Mises stresses are located in the middle region along the thickness direction of CT specimen.

Different from the results shown in Fig. 9, for one-sided SP, the larger von Mises stresses are close to the SPed surface, as seen in Fig. 10. In Fig. 10, the x–y plane at $z = 0.0\;{\text{mm}}$ is the SPed surface, the relatively larger von Mises stresses are in the x–y plane at $z = 0.63\;{\text{mm}}$, the von Mises stresses in the middle region are shown in the x–y plane at $z = 2.5\;{\text{mm}}$, and the x–y plane at $z = 4.5\;{\text{mm}}$ is the unpeened surface. By careful observation, the following conclusions can be obtained: (1) the von Mises stresses are obviously smaller on the SPed surface, which is attributed to SP-induced compressive residual stresses; (2) the maximum von Mises stress is in the subsurface close to the SPed surface; and (3) the distributions of von Mises stress in the x–y plane become increasingly similar to Fig. 9 with increases in the z-axis coordinates. Therefore, these results reveal that SP is capable of improving the stress state of material surface and causing fatigue crack initiation and propagation to occur in the subsurface instead of the surface.

For double-sided SP, as shown in Fig. 11, the bottom surface ($z = 0.0\;{\text{mm}}$) and top surface ($z = 4.5\;{\text{mm}}$) were successively peened by two peening series, wherein the first peening series was applied on the bottom surface, and the second peening series was applied on the top surface. As a result, the distributions of von Mises stress in the x–y planes with respect to $z = 0.0\;{\text{mm}}$ and $z = 4.5\;{\text{mm}}$ are significantly different from Fig. 9 due to the introduction of double-sided SP-induced compressive residual stresses. Distributions of von Mises stress similar to Fig. 9 can be observed in the x–y plane at $z = 2.0\;{\text{mm}}$, which corresponds to the middle region in the thickness direction and is only slightly affected by SP-induced residual stresses. The relatively larger von Mises stresses are close to the top surface, as shown in Fig. 11(c), which presents the distribution of von Mises stress in the x–y plane at $z = 3.87\;{\text{mm}}$. Therefore, the introduction of SP-induced compressive residual stresses can effectively improve the surface properties and fatigue performance of metallic materials.

Predictions of FCP Behavior

Regarding $\Delta K_{\text{tot}}$ as a crack-driving quantity, the FCP rate can be calculated by Paris’ law

$$ {{{\text{d}}a} \mathord{\left/ {\vphantom {{{\text{d}}a} {{\text{d}}N}}} \right. \kern-0pt} {{\text{d}}N}} = C_{P} \Delta K_{\text{tot}}^{{m_{P} }} $$

(4)

where a is the crack length, N is the number of loading cycles, $C{}_{P}$ and $m_{P}$ are two material constants and $\Delta K_{\text{tot}}$ is the total stress intensity factor range, which is calculated by

$$ \Delta K_{\text{tot}} = K_{{\hbox{max} ,{\text{tot}}}} - K_{{\hbox{min} ,{\text{tot}}}} $$

(5)

The total stress ratio, which is based on the linear elastic superposition principle, is defined as

$$ R_{\text{tot}} = {{K_{{\hbox{min} ,{\text{tot}}}} } \mathord{\left/ {\vphantom {{K_{{\hbox{min} ,{\text{tot}}}} } {K_{{\hbox{max} ,{\text{tot}}}} }}} \right. \kern-0pt} {K_{{\hbox{max} ,{\text{tot}}}} }} $$

(6)

In Eq 5 and 6, $K_{{\hbox{max} ,{\text{tot}}}}$ and $K_{{\hbox{min} ,{\text{tot}}}}$ are the maximum and minimum crack-driving stress intensity factors, respectively, which are determined by the MVCCT. Considering that the thickness of the CT specimen is 4.5 mm, which is significantly smaller than the length (125 mm) and width (120 mm), therefore, the subjected stresses of the CT specimens in the process of fatigue crack propagation can be reasonably regarded as the plane stress state, and the value of $K_{\text{tot}}$ can be calculated as

$$ K_{\text{tot}} = \sqrt {G_{\text{tot}} \cdot E} $$

(7)

where $G_{tot}$ is the total energy release rate for a certain crack length and is approximately calculated by finite element computation and finite crack extension $\Delta a$

$$ G_{tot} = - \frac{1}{b\Delta a}\sum {F_{y} u_{y} } $$

(8)

where b is the specimen thickness, $F_{y}$ are the reaction forces of the crack tip nodes and $u_{y}$ are the nodal displacements of the nodes located on the crack faces at a distance $\Delta a$ behind the crack tip. Further details about the approach of the MVCCT can be found in the literature (Ref 27, 31,32,33,34,35,36). In Eq 8, if $F_{y}^{i} u_{y}^{i} \ge 0$, then $G^{i} = 0$, which means that the crack closure would lead to a delay in FCP, and the superscript (i) represents the number of nodes at the one-dimensional crack tip.

To validate the multistep analysis method combining the LEFM-based superposition principle and finite element simulation, the FCP in an LSP-induced residual stress field taken from literature (Ref 32) was simulated herein, and the prediction results are shown in Fig. 12. Figure 12(a) presents the finite element model of the LSPed specimen, for which a detailed introduction can be found in the literature (Ref 32). Figure 12(b) shows the distribution of von Mises stress with respect to a crack length of 52 mm in the combined stress filed resulting from a maximum external applied load of 113 MPa and LSP-induced residual stresses. Figure 12(c) and (d) compares the prediction results with computational data from the literature (Ref 32) in terms of the maximum (minimum) stress intensity factors and effective stress intensity factor ranges. The effective stress intensity factor range was calculated by Walker’s equation $\Delta K_{\text{eff}} = {{\Delta K_{\text{tot}} } \mathord{\left/ {\vphantom {{\Delta K_{\text{tot}} } {\left( {1 - R_{\text{tot}} } \right)^{1 - \gamma } }}} \right. \kern-0pt} {\left( {1 - R_{\text{tot}} } \right)^{1 - \gamma } }}$, where $\gamma$ is a fitting parameter that is experimentally determined. Figure 12(c) and (d) shows that the prediction results are in good agreement with the computational data from the literature (Ref 32), which validated the multistep analysis method used for predicting FCP in a residual stress field.

Fig. 12

Simulation of FCP in an LSP-induced residual stress field: (a) finite element model of the LSPed specimen, (b) distribution of von Mises stress with regard to a crack length of 52 mm, (c) $K_{\hbox{max} }$ and $K_{\hbox{min} }$ and (d) $\Delta K_{\text{eff}}$

Effects of External Applied Load Ratio

To investigate the effects of the external applied load ratio ($R_{\text{load}} = {{F_{\hbox{min} } } \mathord{\left/ {\vphantom {{F_{\hbox{min} } } {F_{\hbox{max} } }}} \right. \kern-0pt} {F_{\hbox{max} } }}$), in the case of one-sided SP, the maximum external applied load remained constant at $F_{\hbox{max} } = 8\;{\text{kN}}$ and the minimum external applied loads were set to $F_{\hbox{min} } = 0.8\;{\text{kN}}$ and 0.08 kN, which correspond to external applied load ratios of $R_{\text{load}} = 0.1$ and 0.01, respectively.

According to Eqs 5, 6, 7 and 8, $\Delta K_{\text{tot}}$ is proportional to $\Delta \sqrt {\sum {F_{y} u_{y} } }$ since b, $\Delta a$ and E are constants. Figure 13 shows the calculation results of $\Delta \sqrt {F_{y}^{1} u_{y}^{1} }$ and $R_{\text{tot}}^{1}$ ($R_{\text{tot}}^{1} = {{\left( {\sqrt {F_{y}^{1} u_{y}^{1} } } \right)_{{F_{\hbox{min} } }} } \mathord{\left/ {\vphantom {{\left( {\sqrt {F_{y}^{1} u_{y}^{1} } } \right)_{{F_{\hbox{min} } }} } {\left( {\sqrt {F_{y}^{1} u_{y}^{1} } } \right)_{{F_{\hbox{max} } }} }}} \right. \kern-0pt} {\left( {\sqrt {F_{y}^{1} u_{y}^{1} } } \right)_{{F_{\hbox{max} } }} }}$) with respect to different crack lengths on the SPed surface. Note that $F_{y}$ and $u_{y}$ were outputted from the first element layer on the SPed surface and represented by the superscript “1”. In Fig. 13(a), the values of $\Delta \sqrt {F_{y}^{1} u_{y}^{1} }$ within the SPed region are obviously smaller than that in the reference cases without SP, which indicates that SP-induced surface compressive residual stresses can effectively delay surface FCP. As shown in Fig. 13(a), the external applied load ratios have no influence on the values of $\Delta \sqrt {F_{y}^{1} u_{y}^{1} }$ within the SPed region. This phenomenon can be explained by the fact that the crack is closed and $\left( {\sqrt {F_{y}^{1} u_{y}^{1} } } \right)_{{F_{\hbox{min} } }} = 0$ (i.e., $K_{\hbox{min} } = 0$) under the combined effects of SP-induced residual stresses and the minimum external applied loads ($F_{\hbox{min} } = 0.8$ or 0.08 kN). Moreover, the values of $\left( {\sqrt {F_{y}^{1} u_{y}^{1} } } \right)_{{F_{\hbox{max} } }}$ are the same due to the same maximum external applied load ($F_{\hbox{max} } = 8\;{\text{kN}}$). As a result, the values of $\Delta \sqrt {F_{y}^{1} u_{y}^{1} }$ within the SPed region are the same for different $R_{\text{load}}$. Figure 13(b) shows $R_{\text{tot}}^{1}$ with respect to different crack lengths on the SPed surface. Within the SPed region, $R_{\text{tot}}^{1} = 0$ can be observed, which is consistent with $\left( {\sqrt {F_{y}^{1} u_{y}^{1} } } \right)_{{F_{\hbox{min} } }} = 0$ in Fig. 13(a).

Fig. 13

Calculated values of $\Delta \sqrt {F_{y}^{1} u_{y}^{1} }$ and $R_{\text{tot}}^{1}$ with different crack lengths on the SPed surface under different $R_{\text{load}}$: (a) $\Delta \sqrt {F_{y}^{1} u_{y}^{1} }$ and (b) $R_{\text{tot}}^{1}$

Figure 14 shows the calculated values of $K_{\hbox{max} }$, $K_{\hbox{min} }$, $\Delta K_{\text{tot}}$, $R_{\text{tot}}$, $\Delta K_{\text{eff}}$ and da/dN with respect to different crack lengths, and the $F_{y}^{i}$ and $u_{y}^{i}$ used for calculation were outputted from all elements at the one-dimensional crack tip along the thickness direction of CT specimen, where i represents the number of nodes at the crack tip. In Fig. 14(a), under different $R_{\text{load}}$, there is no difference in $K_{\hbox{max} }$ for the SPed (or unpeened) CT specimens due to the same $F_{\hbox{max} }$. However, the influences of SP-induced residual stresses on $K_{\hbox{min} }$ are relatively significant, particularly for the case of $R_{\text{load}} = 0.01$, as shown in Fig. 14(b). The larger values of $K_{\hbox{min} }$ are produced within the SPed region due to the tensile residual stresses in the middle region of CT specimen along the thickness direction, which are different from the values of $K_{\hbox{min} }$ on the SPed surface in Fig. 13. With the known $K_{\hbox{max} }$ and $K_{\hbox{min} }$, $\Delta K_{\text{tot}}$ can be calculated, as shown in Fig. 14(c), which has a good consistency with $K_{\hbox{min} }$ in Fig. 14(b), i.e., a larger $K_{\hbox{min} }$ corresponds to a smaller $\Delta K_{\text{tot}}$, particularly for the case of $R_{\text{load}} = 0.01$. Figure 14(d) presents $R_{\text{tot}}$ with respect to different crack lengths. The results show that $R_{\text{tot}} = 0.1$ and 0.01 correspond to $R_{\text{load}} = 0.1$ and 0.01 for the reference cases without SP, whereas $R_{\text{tot}} > R_{\text{load}}$ within the SPed region and the increase in $R_{\text{tot}}$ is more obvious in the case of $R_{\text{load}} = 0.01$. The increase in $R_{\text{tot}}$ for the SPed CT specimen is related to the tensile residual stresses in the middle region of CT specimen along the thickness direction, which could cause the fatigue crack to initiate in the middle of the CT specimen thickness instead of the material surface, and that have been validated by many experimental investigations. For the smaller external applied load, the tensile residual stresses result in a larger increase of $K_{{\hbox{min} ,{\text{tot}}}}$, when compared with the case of the larger external applied load which corresponds to $K_{{\hbox{max} ,{\text{tot}}}}$; as a result, the value of $R_{\text{tot}}$ is increased by SP. Therefore, these results reveal that the total stress ratio effects of FCP would be produced by SP, and the total stress ratio effects would become more obvious for smaller $R_{\text{load}}$.

Fig. 14

Influences of $R_{\text{load}}$ on FCP in a SP-induced residual stress field: (a) $K_{\hbox{max} }$, (b) $K_{\hbox{min} }$, (c) $\Delta K_{\text{tot}}$, (d) $R_{\text{tot}}$, (e) $\Delta K_{\text{eff}}$, (f) da/dN without SP and (g) da/dN with SP

With the known $K_{\hbox{max} }$ and $\Delta K_{\text{tot}}$ (or $R_{\text{tot}}$), the effective stress intensity factor range can be calculated as $\Delta K_{\text{eff}} = K_{\hbox{max} }^{\alpha } \cdot \Delta K_{\text{tot}}^{1 - \alpha }$ (Ref 42, 43), where $\alpha$ is a material constant and $\alpha = 0.36$ for AISI 304 stainless steel (Ref 43). Figure 14(e) shows $\Delta K_{\text{eff}}$ with respect to different crack lengths, wherein the values are consistent with those of $\Delta K_{\text{tot}}$ in Fig. 14(c). By using the Paris type power law, the FCP rate can be calculated as ${\text{d}}a / {\text{d}}N = C_{1} \left( {\Delta K_{\text{eff}} } \right)^{{n_{1} }}$, where $C{}_{1}$ and $n_{1}$ are both material constants: $C_{1} = 1.25 \times 10^{ - 10}$ and $n_{1} = 3.97$ for AISI 304 stainless steel (Ref 43). Figure 14(f) compares the predicted da/dN values with experimental data in the case of $R_{\text{load}} = 0.1$ without SP, and a good agreement is found between them. Under different $R_{\text{load}}$, the FCP rates accounting for SP are shown in Fig. 14(g), which indicates that SP-induced residual stresses are beneficial to delaying FCP, and the delaying effect would be more effective in the case of a smaller $R_{\text{load}}$, which is in agreement with the experimental results and conclusions (Ref 44,45,46).

By comparing Fig. 13(b) and 14(d), it is observed that $R_{\text{tot}}$ on the SPed surface decreases and even equals zero, whereas $R_{\text{tot}}$ accounting for the whole stress field at the crack tip increases and becomes larger than the corresponding $R_{\text{load}}$ within the SPed region. The difference between Fig. 13(b) and 14(d) is attributed to the distribution of $F_{y}^{i} u_{y}^{i}$ along the thickness direction of CT specimen. Figure 15 shows the distributions of $F_{y}^{i} u_{y}^{i}$ and $R_{\text{tot}}^{i}$ along the thickness direction with respect to a crack length of 40 mm. In Fig. 15(a), under $F_{\hbox{max} } = 8\;{\text{kN}}$, the maximum value of $F_{y}^{i} u_{y}^{i}$ is in the middle region, and $F_{y}^{i} u_{y}^{i}$ decreases closer to the top (or bottom) surface. In contrast to the reference cases without SP, the values of $F_{y}^{i} u_{y}^{i}$ are smaller close to the SPed surface, whereas the values of $F_{y}^{i} u_{y}^{i}$ are larger in the middle region. This phenomenon becomes much more significant under $F_{\hbox{min} } = 0.8$ or 0.08 kN, as shown in Fig. 15(b), where $F_{y}^{i} u_{y}^{i} = 0$ close to the SPed surface. With the known $F_{y}^{i} u_{y}^{i}$ associated with $F_{\hbox{max} }$ and $F_{\hbox{min} }$, the distribution of $\Delta \sqrt {F_{y}^{i} u_{y}^{i} }$ at the crack tip along the thickness direction of CT specimen is shown in Fig. 15(c). There are almost no differences in the $\Delta \sqrt {F_{y}^{i} u_{y}^{i} }$ close to the SPed (or unpeened) surface, whereas larger differences can be observed in the middle region for different $R_{\text{load}}$, which is responsible for the distributions of $\Delta K_{\text{tot}}$ in Fig. 14(c). Figure 15(d) shows the distributions of $R_{\text{tot}}^{i}$ at the crack tip along the thickness direction of CT specimen, $R_{\text{tot}}^{i} = R_{\text{load}}^{i}$ for the reference cases without SP, whereas $R_{\text{tot}}^{i} = 0$ close to the SPed surface and $R_{\text{tot}}^{i} > R_{\text{load}}^{i}$ close to unpeened surface, $R_{\text{tot}}^{i}$ increases to the maximum first and then decreases to zero from the unpeened surface to the SPed surface, and more significant changes can be observed in the case of $R_{\text{load}} = 0.01$. Therefore, these results reveal that SP-induced residual stresses have a larger influence on $\Delta K_{\text{tot}}$ and $R_{\text{tot}}$ in the case of $R_{\text{load}} = 0.01$ than $R_{\text{load}} = 0.1$, when $F_{\hbox{max} }$ remains a constant.

Fig. 15

Distributions of $F_{y}^{i} u_{y}^{i}$ and $R_{\text{tot}}^{i}$ at the crack tip along the thickness direction of CT specimen with respect to the crack length of 40 mm under different $R_{\text{load}}$: (a) $\left( {F_{y}^{i} u_{y}^{i} } \right)_{{F_{\hbox{max} } }}$, (b) $\left( {F_{y}^{i} u_{y}^{i} } \right)_{{F_{\hbox{min} } }}$, (c) $\Delta \left( {F_{y}^{i} u_{y}^{i} } \right)$ and (d) $R_{\text{tot}}^{i}$

Effects of Different SP Conditions

With $R_{\text{load}} = 0.1$, the effects of different SP conditions, including one-sided and double-sided SP, on $\Delta \sqrt {F_{y}^{1} u_{y}^{1} }$ and $R_{\text{tot}}^{1}$ with respect to different crack lengths on the SPed surface are shown in Fig. 16. From Fig. 16(a), when compared with the reference case without SP, $\Delta \sqrt {F_{y}^{1} u_{y}^{1} }$ becomes significantly smaller due to SP. In the two cases of one-sided and double-sided SP, $\Delta \sqrt {F_{y}^{1} u_{y}^{1} }$ on the top surface, which was peened by the second peening series in the case of double-sided SP, are equal to $\Delta \sqrt {F_{y}^{1} u_{y}^{1} }$ on the one-sided SPed surface because $\left( {\sqrt {F_{y}^{1} u_{y}^{1} } } \right)_{{F_{\hbox{min} } }} = 0$ (i.e., $K_{\hbox{min} } = 0$) and $\Delta \sqrt {F_{y}^{1} u_{y}^{1} } = \left( {\sqrt {F_{y}^{1} u_{y}^{1} } } \right)_{{F_{\hbox{max} } }} - \left( {\sqrt {F_{y}^{1} u_{y}^{1} } } \right)_{{F_{\hbox{min} } }}$; whereas $\Delta \sqrt {F_{y}^{1} u_{y}^{1} }$ on the bottom surface, which was peened by the first peening series in the case of double-sided SP, is much larger than $\Delta \sqrt {F_{y}^{1} u_{y}^{1} }$ on the top surface due to the relaxation of residual stresses induced by the first peening series. Figure 16(b) presents $R_{\text{tot}}^{1}$ with respect to different crack lengths on the SPed surface, and $R_{\text{tot}}^{1} = 0$ can be observed in the SPed region, which is a result of $\left( {\sqrt {F_{y}^{1} u_{y}^{1} } } \right)_{{F_{\hbox{min} } }} = 0$.

Fig. 16

Calculation results of and with different crack lengths on the SPed surface under different SP conditions: (a) and (b)

Taking into account the whole stress field at the crack tip along the thickness direction of CT specimen, the computation results of $K_{\hbox{max} }$, $K_{\hbox{min} }$, $\Delta K_{\text{tot}}$, $R_{\text{tot}}$, $\Delta K_{\text{eff}}$ and da/dN with respect to different crack lengths are shown in Fig. 17. In Fig. 17(a), with regard to the same crack length in the SPed region, there is almost no difference in $K_{\hbox{max} }$ resulting from one-sided and double-sided SP, whereas the $K_{\hbox{max} }$ without SP is slightly smaller. However, as shown in Fig. 17(b), the $K_{\hbox{min} }$ values resulting from one-sided and double-sided SP are larger than the $K_{\hbox{min} }$ without SP, and the $K_{\hbox{min} }$ resulting from double-sided SP is larger than that in the case of one-sided SP. As a result, the $\Delta K_{\text{tot}}$ in the case of double-sided SP is smallest, followed by that in one-sided SP, and both of them are smaller than the $\Delta K_{\text{tot}}$ without SP, as shown in Fig. 17(c). Figure 14(d) compares the $R_{\text{tot}}$ resulting from the three simulation cases. The SPed $R_{\text{tot}}$ values are larger than the unpeened $R_{\text{tot}}$ values, and the $R_{\text{tot}}$ values resulting from double-sided SP are largest.

Fig. 17

Influences of SP conditions on FCP in an SP-induced residual stress field: (a) $K_{\hbox{max} }$, (b) $K_{\hbox{min} }$, (c) $\Delta K_{\text{tot}}$, (d) $R_{\text{tot}}$, (e) $\Delta K_{\text{eff}}$, (f) da/dN and (g) differences of da/dN between SPed and unpeened conditions

With the known $\Delta K_{\text{tot}}$ and $K_{\hbox{max} }$, $\Delta K_{\text{eff}}$ was calculated as shown in Fig. 17(e), and then da/dN was obtained, as shown in Fig. 17(f). The distributions of $\Delta K_{\text{eff}}$ and da/dN are highly similar, and the double-sided SP results in the smaller $\Delta K_{\text{eff}}$ and da/dN than that in the case of one-sided SP. Figure 17(g) presents the differences in da/dN within the SPed region between the SPed and unpeened conditions. The SPed conditions include one-sided and double-sided SP, and larger differences can be observed in the case of double-sided SP. Therefore, these results reveal that double-sided SP would be more beneficial to delaying FCP than one-sided SP.

The computation results in Fig. 17 are dependent on the distributions of $F_{y}^{i} u_{y}^{i}$ and $R_{\text{tot}}^{i}$ at the crack tip along the thickness direction of CT specimen, as shown in Fig. 18, which corresponds to a crack length of 40 mm. In Fig. 18(a), under $F_{\hbox{max} } = 8\;{\text{kN}}$, compared with the reference case without SP, the $F_{y}^{i} u_{y}^{i}$ values close to the SPed surface are smaller. However, $F_{y}^{i} u_{y}^{i}$ is larger in the middle region, and the maximum value of $F_{y}^{i} u_{y}^{i}$ is largest in the case of double-sided SP, followed by that in the case of one-sided SP, and this value is smallest in the reference case without SP. The differences in $F_{y}^{i} u_{y}^{i}$ are more significant under $F_{\hbox{min} } = 0.8\;{\text{kN}}$, as shown in Fig. 18(b), wherein $F_{y}^{i} u_{y}^{i} = 0$ close to the SPed surface. With the known distributions of $F_{y}^{i} u_{y}^{i}$ under $F_{\hbox{max} }$ and $F_{\hbox{min} }$, the distributions of $\Delta \sqrt {F_{y}^{i} u_{y}^{i} }$ at the crack tip along the thickness direction of CT specimen are shown in Fig. 18(c). There are almost no differences in $\Delta \sqrt {F_{y}^{i} u_{y}^{i} }$ in the middle region, whereas the larger differences can be observed close to the SPed surface for different SP conditions, which is responsible for the distributions of $\Delta K_{\text{tot}}$ in Fig. 17(c). For the distributions of $R_{\text{tot}}^{i}$ in Fig. 18(d), $R_{\text{tot}}^{i} = 0$ close to the SPed surface, and the maximum value of $R_{\text{tot}}^{i}$ is largest in the case of double-sided SP, followed by that in the case of one-sided SP, and the value is smallest in the reference case without SP, which is consistent with the distributions of $F_{y}^{i} u_{y}^{i}$ under $F_{\hbox{min} }$.

Fig. 18

Distributions of $F_{y}^{i} u_{y}^{i}$ and $R_{tot}^{i}$ at the crack tip along the thickness direction of CT specimen with respect to the crack length of 40 mm under different SP conditions: (a) $\left( {F_{y}^{i} u_{y}^{i} } \right)_{{F_{\hbox{max} } }}$, (b) $\left( {F_{y}^{i} u_{y}^{i} } \right)_{{F_{\hbox{min} } }}$, (c) $\Delta \left( {F_{y}^{i} u_{y}^{i} } \right)$ and (d) $R_{\text{tot}}^{i}$

Conclusions

To investigate FCP behavior in an SP-induced residual stress field, a multistep analysis method was developed by combining a finite element simulation of the SP process and LEFM-based superposition principle. The SP-induced residual stress field was predicted by the symmetric cell model and validated through a comparison with experimental results. Two SP conditions, including one-sided and double-sided SP, were simulated, and the resultant residual stress fields outputted from the symmetric cell model were introduced into the finite element model of CT specimen through the user subroutine SIGINI. Then, the total stress intensity factors and stress ratios with respect to different crack lengths were calculated according to the LEFM-based principle. The following conclusions can be drawn from this study:

• 1. The SP-induced residual stresses are capable of improving the stress state of the SPed surface next to the crack tip and transferring the larger von Mises stress to the material subsurface.

• 2. The SP-induced residual stresses can contribute to delaying FCP, and the delaying effect is more obvious in the double-sided SP-induced residual stress field.

• 3. The external applied load ratio has an impact on FCP behavior in an SP-induced residual stress field, and a smaller external applied load ratio results in a smaller FCP rate.