Introduction

As a type of age-hardening alloy, Cu-Cr alloys have been widely used in electric and heat exchange fields, such as railway contact wires (Ref 1,2,3), lead frames (Ref 4,5,6), and heat exchange devices (Ref 3, 7, 8). Cu-Cr-Zr (Ref 1, 3, 5), Cu-Cr-Sn (Ref 9), Cu-Cr-Ag (Ref 10, 11), and Cu-Cr-In (Ref 12) alloys have been developed because of their excellent mechanical properties and thermal and electrical performance. Hot processing, such as hot extrusion and hot rolling, is an important process for Cu-Cr-based alloy production. Due to the low stacking fault energy of copper and copper alloys, the hot working of alloys is always accompanied by work hardening, dynamic recovery and recrystallization (Ref 13), and these will have a great influence on the performance of the alloys. So it is often used to improve the alloy structure and obtain a fine and uniform grain structure. The thermoplastic deformation ability of a material has an important effect on the stability of alloys, and this deformation ability is related to the flow stress, strain rate, and deformation temperature (Ref 14,15,16). Based on dynamic material models, the processing maps can be structured, and the instability and stability domains are visualized and hot workability can be realized from them (Ref 17,18,19,20). Zhang et al. (Ref 19) observed that the rare-earth element Y can be used to refine grains and promote nucleation of dynamic recrystallization. Elongated grains and shear bands were observed in Cu-0.6Cr-0.03Zr alloys deformed at 550 and 650 °C, and the dynamically recrystallized grain size increased with decreasing strain rate and increasing deformation temperature (Ref 16). In addition, the cracks formed in a compressed specimen at a deformation temperature of 650 °C and strain rate of 10 s−1 were in good agreement with the processing map predictions for a Cu-Cr-Zr alloy (Ref 21).

A Cu-Cr-In alloy (Ref 12) studied in the early stage exhibited excellent comprehensive performance with facile preparation and production and showed potential for more widespread application in the future. In this study, the hot deformation behavior of a Cu-Cr-In alloy was studied by performing compression tests on a Gleeble thermomechanical simulator in the temperature range of 700-900 °C and strain rate range of 0.01-10 s−1. The flow behavior, dynamic recrystallization behavior, and processing map of the Cu-Cr-In alloy were investigated. Constitutive equations were established, the hot deformation activation energy was determined, and the dynamic recrystallization microstructural evolution was investigated in detail.

Materials and Experimental Procedure

The chemical composition (wt.%) of the Cu-Cr-In alloy used in this study was 0.45 Cr, 0.093 In, and Cu balance. The alloy was melted in a medium-frequency furnace (ZP-45, Jiangyin Ruibang) in an air atmosphere. After holding at 950 °C for 1 h, the alloy ingot was quenched into water. And then, the ingot was cut into cylindrical specimens with 10 mm diameter and 15 mm length using an electro-discharge cutting machine. With a heating rate of 10 °C/s, the specimens were heated to the deformation temperatures and held for 3 min. Isothermal compression tests were performed on a Gleeble MMS-100 thermomechanical simulator with deformation temperatures of 700, 750, 800, 850, and 900 °C and strain rates of 0.01, 0.1, 1, and 10 s−1. The specimens were compressed by 60% and quenched in water immediately to room temperature to obtain the deformed microstructure.

Metallographic specimens along the compression direction were prepared using the electro-discharge cutting machine. Etching was conducted with a solution of HNO3 (30 ml) + H2O (80 ml). Optical microscope (OM, BMM-90AE, Shanghai Bimu) and transmission electron microscope (TEM, Tecnai-G2-F20, FEI) were used to examine the microstructures of the samples.

Results and Discussion

Stress–Strain Curves of Cu-Cr-In Alloy

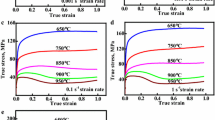
Figure 1 presents the true stress–strain curves of the Cu-Cr-In alloy at different deformation temperatures and strain rates. It can been seen that the flow stress was found to be closely related to both the deformation temperature and strain rate. The flow stress decreased with increasing deformation temperature under constant strain rate. The flow stress increased with increasing strain rate under constant deformation.

Fig. 1
figure 1

True stress–strain curves of the Cu-Cr-In alloy deformed at: (a) \(\dot{\varepsilon }\) = 0.01 s−1; (b) \(\dot{\varepsilon }\) = 0.1 s−1; (c) \(\dot{\varepsilon }\) = 1 s−1; and (d) \(\dot{\varepsilon }\) = 10 s−1

Full size image

As shown in Fig. 1, the flow stress rapidly increased with increasing true strain at 700, 750, 800, and 850 °C. In addition, there was no peak flow stress until a strain of 0.9; this finding is attributed to the presence of a work-hardening stage and the effect of work hardening is greater than that of dynamic softening. As shown in Fig. 1(a) and (b), the flow stress increased to a maximum value and then reached a steady state at 900 °C for strain rates of 0.01 and 0.1 s−1; this behavior is attributed to the interaction between the work hardening and dynamic recrystallization. Dynamic recrystallization clearly occurred at 900 °C for strain rates of 0.01 and 0.1 s−1 during hot deformation, and the softening effect of dynamic recrystallization was in balance with the work-hardening effect (Ref 22). However, the work-hardening effect was greater than the softening effect and the flow stress increased continuously for the alloy deformed at 900 °C for strain rates of 1 and 10 s−1. There was insufficient time for completion of dynamic recovery and dynamic recrystallization at high strain rate, and a higher activation energy of the alloy was required (Ref 19).

Activation Energy and Constitutive Equations

The strain rate and deformation temperature greatly affected the flow stress during hot deformation. The relationship between the flow stress, strain rate, and deformation temperature can be represented by the following Arrhenius equation (Ref 22):

$$\dot{\varepsilon } = A \cdot F\left( \sigma \right)\exp \left\{ { - \frac{Q}{RT}} \right\}$$
(1)

Here, \(\dot{\varepsilon }\), A, \(\sigma\), R, Q, and T are the strain rate, material constant, the flow stress or peak stress, the universal gas constant, the activation energy of dynamic recrystallization, and the absolute temperature, respectively.

\(F\left( \sigma \right)\) can be expressed as follows:

$$F\left( \sigma \right) = \left\{ {\begin{array}{*{20}l} {A_{1} \sigma^{{n_{1} }} ,} \hfill & {\alpha \sigma < 0.8} \hfill \\ {A_{2} \exp \left( {\beta \sigma } \right), } \hfill & {\alpha \sigma > 1.2} \hfill \\ {A_{3} \left\{ {\sinh \left( {\alpha \sigma } \right)} \right\}^{n} ,} \hfill & {{\text{for}}\,{\text{all}}\,\sigma } \hfill \\ \end{array} } \right.$$
(2)

Here, A1, A2, A3, α, β are the material constants, \(\alpha = \beta /n_{1}\).

No peak stress or steady flow stress for the true stress was reached for the hot deformation of the Cu-Cr-In alloy. Therefore, the peak stress and steady flow stress could not be used in the calculation. If the effect of strain is considered (Ref 23), Eq 1 can be expressed as:

$$\sigma = f\left( {\dot{\varepsilon },T} \right)f\left( \varepsilon \right)$$
(3)

The relationships among the deformation temperature, strain rate, and flow stress represented by the Zener–Hollomon parameter (Ref 24) can be analyzed using the following equation:

$$Z = \dot{\varepsilon }\exp \left( {\frac{Q}{RT}} \right) = A\left[ {\sinh \left( {\alpha \sigma } \right)} \right]^{n}$$
(4)

The material constants A1, A2, A3, α, β must be determined before the constitutive equation can be established. In order to determine the material constants, an example has been chosen for the strain (0.4) to introduce the solution procedures.

According to Eq 1 and 2, the strain rate \(\dot{\varepsilon }\) can be expressed as follows:

For low stress, \(\alpha \sigma < 0.8\):

$$\dot{\varepsilon } = {\text{A}}_{1} \sigma^{{n_{1} }} { \exp }\left[ { - \frac{Q}{RT}} \right]$$
(5)

For high stress, \(\alpha \sigma > 1.2\):

$$\dot{\varepsilon } = {\text{A}}_{2} { \exp }\left( {\beta \sigma } \right){ \exp }\left[ { - \frac{Q}{RT}} \right]$$
(6)

And thus for all stress,

$$\dot{\varepsilon } = {\text{A}}_{3} \left[ {{ \sinh }\left( {\alpha \sigma } \right)} \right]^{n} { \exp }\left[ { - \frac{Q}{RT}} \right]$$
(7)

Taking natural logarithms of both sides of Eq 1 and 2 yields

$${ \ln }\left( {\dot{\varepsilon }} \right) = {\text{n}}_{1} { \ln }\sigma + { \ln }A_{1} - \frac{Q}{RT}$$
(8)
$${ \ln }\left( {\dot{\varepsilon }} \right) = \beta \sigma + { \ln }A_{2} - \frac{Q}{RT}$$
(9)

The values of n1 and β are determined to be n1 = 7.75 and β = 0.1547 from the slope of the linear regression lines in Fig. 2. The value of α of the Cu-Cr-In alloy was calculated to be \(\alpha = \beta /n_{1}\) = 0.02 MPa−1.

Fig. 2
figure 2

Relationships between: (a) \(\ln \dot{\varepsilon } - \ln \sigma\) and (b) \(\ln \dot{\varepsilon } - \sigma\)

Full size image

Taking natural logarithms of both sides of Eq 7 yields

$$\ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right] = \frac{{\ln \dot{\varepsilon }}}{n} + \frac{Q}{nRT} - \frac{\ln A}{n}$$
(10)

For a constant strain rate \(\dot{\varepsilon }\), by taking the partial derivative of both sides of Eq 7 with respect to 1/T, Q can be expressed as

$$Q = Rn\frac{{\partial \ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right]}}{{\partial \left( {1/T} \right)}}$$
(11)

The value of n can be determined from the slope of a plot of \(\ln \dot{\varepsilon } - \ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right]\) by substituting the values of the stress and strain rate for all the tested temperatures into Eq 10 and the regressed analysis results from Fig. 3.

Fig. 3
figure 3

Relationship between lnε − ln[sinh(ασ)]

Full size image

By plotting \(\ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right]\)−\(1000/T\) at different temperatures, the average slope was calculated to be 8.3085. Consequently, when the strain of the Cu-Cr-In alloy is 0.4, the value of Q for the alloy was determined to be Q = 460.827 kJ/mol (Fig. 4).

Fig. 4
figure 4

Relationship between ln[sinh(ασ)] − 1000/T

Full size image

Taking natural logarithms of both sides of Eq 4 yields

$$\ln Z = \ln A + n\ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right]$$
(12)

The relationship between \({ \ln }Z\) and \(\ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right]\) is shown in Fig. 5. The correlation coefficient for the linear regression is 0.982, which confirms the accuracy of Eq 12 for describing the hot deformation behavior of the Cu-Cr-In alloy. As ln A is the intercept of the \({ \ln } Z\) − \({ \ln }\left[ {{ \sin }h\left( {\alpha \sigma } \right)} \right]\) plot, the value of A was determined to be e46.8828.

Fig. 5
figure 5

Relationship between lnZ − ln[sinh(ασ)]

Full size image

Based on the above analysis, the following constitutive equation of the Cu-0.45 Cr-0.093 In alloy with the strain 0.4 was established:

$$\dot{\varepsilon } = {\text{e}}^{46.8828} \left[ {\sinh \left( {0.02\sigma } \right)} \right]^{6.6712} \exp \left( { - \frac{460827}{RT}} \right)$$
(13)

The value of Q can be determined from the slope of a plot of \(\ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right]\) − \(1000/T\), as shown in Fig. 4.

We recorded 16 points of true strain from 0.1 to 0.85 at an interval of 0.05. The same methods were used to calculate the values of α, n, Q, and lnA in Eq 10 from experiments performed under different strains.

The data points in Fig. 6 were used to fit the following eighth polynomial function of strain (\(\varepsilon\)):

$$\begin{aligned} \alpha & = A_{0} + A_{1} \varepsilon^{1} + A_{2} \varepsilon^{2} + A_{3} \varepsilon^{3} + A_{4} \varepsilon^{4} + A_{5} \varepsilon^{5} + A_{6} \varepsilon^{6} + A_{7} \varepsilon^{7} + A_{8} \varepsilon^{8} \\ n & = B_{0} + B_{1} \varepsilon^{1} + B_{2} \varepsilon^{2} + B_{3} \varepsilon^{3} + B_{4} \varepsilon^{4} + B_{5} \varepsilon^{5} + B_{6} \varepsilon^{6} + B_{7} \varepsilon^{7} + B_{8} \varepsilon^{8} \\ Q & = C_{0} + C_{1} \varepsilon^{1} + C_{2} \varepsilon^{2} + C_{3} \varepsilon^{3} + C_{4} \varepsilon^{4} + C_{5} \varepsilon^{5} + C_{6} \varepsilon^{6} + C_{7} \varepsilon^{7} + C_{8} \varepsilon^{8} \\ \ln A & = D_{0} + D_{1} \varepsilon^{1} + D_{2} \varepsilon^{2} + D_{3} \varepsilon^{3} + D_{4} \varepsilon^{4} + D_{5} \varepsilon^{5} + D_{6} \varepsilon^{6} + D_{7} \varepsilon^{7} + D_{8} \varepsilon^{8} \\ \end{aligned}$$
(14)

where the values of the coefficients Ai, Bi, Ci, and Di (i = 0, 1, 2, 3, 4, 5, 6, 7, 8) are summarized in Table 1.

Fig. 6
figure 6

Polynomial fit of variations of (a) α, (b) n, (c) Q, and (d) lnA with true strain

Full size image
Table 1 Coefficients of the polynomial for α, n, Q, and lnA
Full size table

The plots of experimental values and predicted values predicted by the constitutive equations with seventh-, eighth-, and ninth-order polynomials are shown in Fig. 7. The predicted values calculated from the constitutive equation that fitted eighth-order polynomials are the most consistent with the experimental plots. The correlation between experimental and predicted flow stress from the different constitutive equations with seventh-, eighth-, and ninth-order polynomials is shown in Fig. 8. The values of correlation coefficients (R) for the constitutive equations with eighth-order polynomials are 0.99689, higher than the other two. It indicates that the constitutive equation fitted by eighth-order polynomials should be used.

Fig. 7
figure 7

Comparison between experimental and predicted flow stress at various order polynomials

Full size image
Fig. 8
figure 8

Correlation between experimental and predicted flow stress by (a) seventh polynomial, (b) eighth polynomial, and (c) ninth polynomial

Full size image

Processing Map

The dynamic material model proposed by Prasad (Ref 25, 26) and established based on continuum mechanics and irreversible thermodynamics was used in this study. The hot deformation process can be regarded as a closed system and a nonlinear energy dissipater. And the plastic deformation and microstructure evolution are the two ways to transform and dissipate energy. Therefore, the total energy input (P) of the system can be separated into plastic deformation dissipation (G) and microstructural evolution dissipation (J), which can be mathematically defined as

$$G = \mathop \smallint \limits_{0}^{{\dot{\varepsilon }}} \sigma {\text{d}}\dot{\varepsilon }$$
(15)
$$J = \mathop \smallint \limits_{0}^{\sigma } \dot{\varepsilon }{\text{d}}\sigma$$
(16)
$$P = G + J = \sigma \dot{\varepsilon } = \mathop \smallint \limits_{0}^{\sigma } \dot{\varepsilon }{\text{d}}\sigma + \mathop \smallint \limits_{0}^{{\dot{\varepsilon }}} \sigma {\text{d}}\dot{\varepsilon }$$
(17)

And the ratio of microstructure evolution dissipation (J) to ideal linear dissipated energy of microstructure (Jmax) can be defined as the efficiency of power dissipation (η), which can be expressed as

$$\eta = \frac{J}{{J_{\hbox{max} } }}$$
(18)

When the deformation temperature and strain remain constant, the relationship between G and J can be expressed by the parameter m (the strain rate sensitivity index) as

$$m = \frac{{{\text{d}}J}}{{{\text{d}}G}} = \left[ {\frac{{\partial \left( {\ln \sigma } \right)}}{{\partial (\ln \dot{\varepsilon })}}} \right]_{\varepsilon ,T}$$
(19)

For an ideal linear dissipation process, m = 1, \(J = J_{\hbox{max} } = \sigma \dot{\varepsilon }/2 = P/2\). And the efficiency of power dissipation (η) can be expressed as

$$\eta = \frac{J}{{J_{\hbox{max} } }} = \frac{m}{2m + 1}$$
(20)

A power dissipation diagram of the alloy could be constructed by calculating the value of η. According to the extremum principles of irreversible thermodynamics, a continuum instability criterion can be developed (Ref 21). The value of power dissipation is higher, and the hot deformation ability is better, but the premise is that the deformation conditions cannot be located in the unstable zone. According to the principle of maximum entropy, the instability criterion for flow instabilities was developed, which can be expressed as

$$\xi \dot{\varepsilon } = \frac{{\partial \ln \left[ {\frac{m}{m + 1}} \right]}}{{\partial \ln \left( {\dot{\varepsilon }} \right)}} + m < 0$$
(21)

The alloy becomes unstable when \(\xi \dot{\varepsilon } < 0\). An instability diagram of the material can be drawn by the instability criterion. And the processing maps of the material can be constructed by combining the instability diagram and power dissipation diagram.

The traditional method of drawing a processing map is based on the power function relation of the constitutive relation of the alloy. However, Eq 20 and 21 are suitable for the constitutive equations which are power-defendant functions of the alloy. But the constitutive equations obtained in this work are hyperbolic sine function and do not satisfy the power function relation, so Eq 20 and 21 does not apply. In this work, another method was used to draw the processing maps.

The constitutive equation was substituted into Eq 16, and then, the values of J were obtained by integration. The values of J and \(J_{\hbox{max} } = \sigma \dot{\varepsilon }/2\) were substituted into Eq 18, the values of η were calculated and the power dissipation map could be drawn.

The instability criterion of any constitutive relation was proposed by Murty (Ref 27), and the basic formula of material instability can be expressed as

$$\frac{{{\text{d}}D}}{{{\text{d}}\dot{\varepsilon }}} < \frac{D}{{\dot{\varepsilon }}}$$
(22)

Here, D is a dissipative function connected with the strain rate.

Combining Eq 16 and 18, the following expression can be obtained:

$$\frac{\partial J}{{\partial \dot{\varepsilon }}} = \frac{\partial \sigma }{{\partial \dot{\varepsilon }}}\dot{\varepsilon } = \sigma \frac{{\frac{\partial \sigma }{\sigma }}}{{\frac{{\partial \dot{\varepsilon }}}{{\dot{\varepsilon }}}}} = \sigma \frac{\partial \ln \sigma }{{\partial \ln \dot{\varepsilon }}} = m\sigma$$
(23)
$$\eta = \frac{J}{{J_{\hbox{max} } }} = \frac{J}{{\frac{{\sigma \dot{\varepsilon }}}{2}}}$$
(24)

Combining Eq 22, 23, and 24, Murty’s instability criterion can be expressed as

$$2m < \eta$$
(25)

Thus, the flow instabilities can be defined by the instability parameter

$$\xi = 2m - \eta < 0$$
(26)

The instability map can be developed based on the values of η and ξ.

Using Eq 1, 2, and 14, the constitutive equations of the alloy deformed at strains of 0.4 and 0.8 were obtained, and the associated processing maps are presented in Fig. 9.

Fig. 9
figure 9

Processing maps for the Cu-Cr-In alloy at a true strain of (a) 0.4 and (b) 0.8

Full size image

The processing maps of the Cu-Cr-In alloy deformed at strains of 0.4 and 0.8 are presented in Fig. 9(a) and (b), respectively. The shaded areas represent the unstable regions, and areas with darker shades indicate more severe instability. The contour lines represent the dissipative efficiency of energy, and the data points are the values of energy dissipation efficiency (η). At a strain of 0.4, a stable domain of high temperature and low strain rate is shown in Fig. 9(a). The energy dissipation efficiency increased with the increasing temperature and the decreasing strain rate. Larger energy dissipation values indicate improved hot deformation performance and the maximum efficiency of energy dissipation on domain A. For a strain of 0.4, the flow instability domain consisted of two parts: a low-temperature and low-strain-rate domain (domain B) and a high-strain-rate domain in the temperature range of 760-880 °C (domain C). The energy dissipation was low in domains B and C; the high-density dislocation areas were easily formed during deformation at high strain rates and low-temperature domains (Ref 28). At the same time, lattice distortion occurred at the interface, which can easily cause stress concentration. And cracks formed in the grain boundary when the stress exceeded the alloy strength. As shown in Fig. 9(b), a similar area of flow instability domain was observed at low temperature and high strain rate (domain D), where the energy dissipation was low in this domain at a strain of 0.8. As the temperature increased and the strain rate decreased, the energy dissipation efficiency increased, and the energy dissipation was higher and the workability was better in these deformation conditions. The efficiency of energy dissipation peaked at 36% in 880 °C and 0.1 s−1 (domain E). Therefore, according to the processing maps in Fig. 9, the optimal hot deformation conditions lie in the range of 850-900 °C and strain rate range of 0.01-0.1 s−1.

Microstructural Evolution

As shown in Fig. 10, the optical images of the Cu-Cr-In alloy microstructure for a true strain 0.4 under different deformation conditions are presented. As observed in Fig. 10(a) and (b), the original grains retained deformation structure which was elongated during hot deformation. No obvious recrystallized grains were observed, and some deformation bands appeared inside the grain. At 800 °C and a strain rate of 10 s−1, a large number of fibrous deformation bands were observed inside and through the grain and the inhomogeneity of the microstructure was more severe. The deformation conditions of the instability microstructure correspond to the metastable domain point a1 and severe instability domain point a2 in Fig. 9(a), and the results are consistent with the hot processing maps. These findings indicate that a large number of deformation bands will form during hot deformation at low temperature and high strain rate and that some elongated grains remain with no recrystallization. In addition, the microstructure of the alloy consisted of mixed grains and facilitated cracking during deformation. Therefore, it is necessary to avoid deformation under these deformation conditions in industrial practice. The microstructure of the alloy deformed at point a3 (900 °C, 10 s−1) is shown in Fig. 10(c). The new recrystallized grains take the place of the deformed grains. It indicates that the dynamic recrystallization process was complete, and the driving force and time were sufficient for nucleation and growth of the recrystallized grains under the deformation conditions (Ref 29). Therefore, the deformation temperature and strain rate significantly affected the microstructure of the deformed alloy.

Fig. 10
figure 10

Optical micrographs of the microstructure of the true strain 0.4 specimens deformed at different temperatures and strain rates: (a) 750 °C, 1 s−1; (b) 800 °C, 10 s−1; and (c) 900 °C, 0.01 s−1

Full size image

Optical images of the microstructure of the Cu-Cr-In alloy at a true strain of 0.8 deformed under different deformation conditions are presented in Fig. 11. The grains were obviously elongated at 700 °C and a strain rate of 10 s−1, as shown in Fig. 11(a). No obvious recrystallized grains were observed, except for the parallel deformation bands in the grains. In addition, the deformation conditions of the instability microstructure correspond to the metastable domain point b1. Only a few small recrystallized grains are observed in the grain boundaries in Fig. 11(b), which indicates that the dynamic recrystallization occurred in the alloy at point b2 (850 °C, 10 s−1) and that the structure of the alloy tended to be stable. Typical recrystallization with uniform and fine grains is observed in Fig. 11(c), which indicates that full dynamic recrystallization was achieved at point b3 (900 °C, 0.01 s−1). In addition, a sufficient level of dynamic recrystallization occurred that the softening effect of dynamic recrystallization reached a balance with the work-hardening effect. Therefore, the flow stress rapidly increased to the critical stress and continued to slowly increase to the peak stress, reaching a steady stress, as observed in Fig. 1(a).

Fig. 11
figure 11

Optical micrographs of the microstructure of the true strain 0.8 specimens deformed at different temperatures and strain rates: (a) 700 °C, 1 s−1; (b) 850 °C, 10 s−1; and (c) 900 °C, 0.01 s−1

Full size image

Figure 12 presents TEM micrographs of the Cu-Cr-In alloy deformed under different deformation conditions (true strain 0.8). As shown in Fig. 12(a), the elongated deformation banded structure formed at 700 °C and a strain rate of 10 s−1. A lot of dislocation formed during hot deformation, and a larger number of dislocation walls and tiny dislocation sliding bands formed because of the motion and entanglement of the dislocation. There are no significant recrystallization occurred and insufficient energy for dislocation annihilation at this deformation condition. Therefore, the flow stress of the alloy increased continuously, and the effect of work hardening was greater than that of dynamic softening. As shown in Fig. 12(b), uniform recrystallized grains were clearly observed and the dislocations tangled in the grain and formed a dislocation cell structure. Under the conditions of low temperature and high strain rate, only dynamic recovery with no dynamic recrystallization occurred due to low atom diffusion rate and low amount of energy stored. Therefore, the flow stress increased with the rise of deformation, and the hardening effect continued to strengthen. The alloy has enough heat and time for energy storage at high temperature and low strain rate. And when the stored energy reaches its critical value, the dynamic recrystallization will start up and the softening of recrystallization will be enhanced.

Fig. 12
figure 12

TEM micrographs of the true strain 0.8 specimens deformed at: (a) 700 °C and 10 s−1; (b) 900 °C and 0.1 s−1

Full size image

The processing maps and corresponding microstructures suggest that the instability mechanisms are connected with shear deformation bands. Therefore, these deformation conditions and corresponding microstructures should be avoided in industrial practice.

Conclusions

The hot deformation behavior of a Cu-0.45 Cr-0.093 In alloy was studied in the temperature range of 700-900 °C and strain rate range of 0.01-10 s−1. Based on the experimental and modeling results, the following conclusions can be drawn:

  1. (1)

    The Cu-Cr-In alloy was sensitive to the deformation temperature and strain rate. The flow stress increased with the rise of the strain rate and decreased with the rise of the deformation temperature during hot deformation.

  2. (2)

    The hot deformation activation energy of the Cu-Cr-In alloy at a strain of 0.4 was 460.827 kJ/mol, and the constitutive equation of the alloy can be expressed as

    $$\dot{\varepsilon } = {\text{e}}^{46.8828} \left[ {\sinh \left( {0.02\sigma } \right)} \right]^{6.6712} \exp \left( { - \frac{460827}{RT}} \right).$$
  3. (3)

    Based on the dynamic material model principles, the processing maps at true strains of 0.4 and 0.8 were structured. The optimal hot deformation conditions of the Cu-Cr-In alloy lie in the range of 850-900 °C and strain rate range of 0.01-0.1 s−1.