Introduction

Beam-type porous biological implant as an advanced 3D-printed architecture has been extensively received attention by bioengineers for clinical approaches. Addition of tough and hard bioceramic material as an additive/reinforcement with proper biological behavior to a damaged bone leads to a new generation of porous bio-nanocomposites with crystallographic properties similar to calcified tissues of vertebrates (Ref 1,2,3). Recent researches have shown a great demand of artificial organs to replace them with a damaged tissue of traumatic diseases like cancer and fracture (Ref 4, 5). The artificial synthetic bones that are usually encapsulated with fibrous tissues have a certain drawback, and that is its inability to adhere adequately to its bone host. The mechanical, thermal, and surface properties (e.g., surface roughness and contact angle) of advanced Ca-Si-Mg-based bioceramics and biopolymer like polycaprolactone (PCL) need to be drastically enhanced for biomedical applications (Ref 6,7,8,9).

Biodegradable PCL bio-nanocomposites with the addition of bioceramic nanoparticles can be used for bone tissue engineering. The effect of the components composition on the chemical and mechanical properties of composites is essential to investigate. In order to successfully boost the orthopedic, dentistry, and cancer therapy applications, calcium silicate structures can be fused by bioinorganic trace elements like zinc, titanium, magnesium, zirconium, and magnetite nanoparticles (MNPs) after metallurgic characterization (Ref 10,11,12,13). Magnetic porous scaffolds have recently attracted significant attention in bone tissue engineering due to the prospect of improving bone tissue formation by conveying soluble factors such as growth factors, hormones, and polypeptides directly to the site of implantation, and also because of the possibility of improving implant fixation and stability (Ref 10). Superparamagnetic nanoparticles have a high sensitivity to receiving the electromagnetic wave from their surrounding area and beside AC magnetic field by receiving electromagnetic signals from the medium. The scaffolds should have excellent compressive strength, thermal and chemical stability, vibrational response, and biological behavior to substitute with the destroyed part of bone (Ref 11,12,13,14).

Additive manufacturing (AM) products like 3D printing bring up some interesting bio-intrusive innovations that can be designed in 3D architecture. However, other techniques such as freeze drying (Ref 4), space holder (Ref 12), lost foam casting (Ref 9), and polyurethane polymeric sponge technique (Ref 9) may do not have the capability to produce complex shapes with near neat architecture. As remarked above, the printed bone from a synthetic material that is in triplicate is strong enough in their mechanical properties; however, it has a porous structure that facilitates the “osseointegration” to grow throughout the bone implantation. Biomaterials that are 3D-printed are biocompatible with living tissues and capable of having proper decomposition rate (they will not be repulsed from the body). Incremental manufacturing technology enables researchers to produce three-dimensional implants from a 3D virtual model, which simplifies the process of surgery and reduces its risks. Additionally, there is an increasing demand for fabrication of customized implants for each individual patient.

The surface roughness of the bone implant’s microphotography can affect its biological and cellular response. The vital role of proper roughness of implant in the cellular response may increase cell attachment, wetting properties, and formation of new bone. It has been demonstrated that the synthesis of extracellular matrix and subsequent mineralization cause to enhance the efficiency of a porous bone implant. An essential situation for a fitting bone implant is to have active osteopenia and continues mechanical and chemical stability on its surface. Bioceramic scaffolds have been implanted and applied for bone beam-type implants, because of their efficient compounds and elements due to their crystal growth and lattice constant close to human’s bone. The wettability of a bone beam-type implant involves physicochemical and cellular functions, like cellular attachment to the extracellular matrix proteins. The combination of surface and structure changes leads to activate the protein absorption as well as the formation of dissolved proteins. However, there are no valid data about the influence of surface roughness of bioceramics and generally surface tissue on the cellular response such as wettability and bioactivity. Therefore, some bioceramics are faced with high dissolution rate in a biological environment and poor corrosion resistance in acid solutions subjected to high load bearing (Ref 15). Moreover, bioceramics have a poor thermal stability which causes to decompose to other phases. As a result, they have undesirable fast dissolution rate in vivo environment (Ref 14,15,16). On the other hand, the mechanical properties of silicate bioceramics such as natural graft, forsterite, baghdadite, akermanite, diopside, diopside-magnetite, and bredigite are generally more adequate for many load-carrying applications rather than conventional bioceramics like hydroxyapatites or bioglasses (Ref 14, 17). The required technique to synthesize the above-mentioned materials is unique, simple, and economical rather than other additive or other conventional techniques; for example, the high-energy ball milling process is a simple dry method to obtain any quantity of powder with controlled microstructure (Ref 17, 18). Usually, the powder obtained by the mechanochemical/mechanical activation technique has a suitable structure because of the disorderliness of surface-bonded species resulted by the procedure. The benefits of ease, reprocessing capability, and low processing cost are the most significant advantages of this type of technique. Moreover, it is not necessary to control the melting conditions precisely, and the obtained powders have nanostructure characteristics.

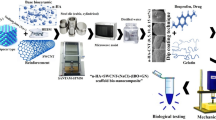
The interconnected porosity, permeability, chemical and mechanical strength are important parameters that define the performance and life span of a scaffold which are monitored by a 3D setting. Recent studies have shown that bredigite bioceramic is highly bioactive, induces regeneration, and possesses apatite formation ability due to the existence of Ca, Mg, and Si ions in its composition (Ref 10, 19). The hyperthermia term (41 °C ≤ temperature ≤ 43 °C) in MNPs has emerged as promising mediators for localized magnetic hyperthermia treatment as shown in Fig. 1 (Ref 11, 12, 20,21,22,23,24,25,26,27). Cancer is a lethal fatal disease, and efforts to treat it continue. Magnetic hyperthermia or heat therapy is one of the effective techniques for treating hard tissue biopsy by magnetic bone replacement, which is used to treat cancer. In this hyperthermia treatment, the nanofluid containing magnetite nanoparticles is injected into the cancerous tissue with magnetic nanoparticles and penetrates into the cancerous tissue in the AC magnetic field and increases the temperature of the infected tissue. Hyperthermia can be combined with other treatment types such as chemotherapy and radiotherapy. The minerals which arise from this method of treatment are Ca2MgSi2O7, CaMgSi2O6, and Ca3ZrSi2O9. It has been found that these minerals have a high degree of enhancement within the in vivo and in vitro circle. On the other hand, several studies have been performed in recent years to predict the nonlinear mechanical characteristics of structures made of nanocomposite materials (Ref 28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44). Silicate calcium-magnetic bio-nanocomposites have proper characteristics due to their biocompatibility and mechanical properties similar to mineral parts of the bone in biomedical fields. The magnetite nanoparticle also improves the properties of bioceramics and can be used in drug delivery, MRI, and thermal therapy applications. In the previous works, the bending strength and vibrational response of novel bredigite-magnetite bio-nanocomposite scaffold have been simulated using the experimental analysis values such as elastic modulus from compression test, Poisson ratio, and mass density values (Ref 45, 46). The resonance response is the tendency of a bone scaffold microstructure to respond at prominent amplitude while the frequency of its oscillations equals the structure’s natural frequency of vibration. The prime aim of the current study is to investigate the nonlinear primary resonance of a beam-type bone implant relevant to its surfaces roughness and wettability properties for the first time. To this end, based upon the experimental data, an analytical solution using the multiple-timescale method is presented to explore the nonlinear primary resonance characteristics of the 3D-printed porous beam-type biological implant under uniform-distributed external load (Table 1).

Fig. 1
figure 1

Hyperthermia phenomenon using magnetic bio-nanocomposite material for thermal therapy under AC magnetic field to treat cancer cells

Full size image
Table 1 Values of Young’s modulus obtained via the experimental analysis for the fabricated bio-nanocomposite material with different MNP weight fractions (Ref 45, 46)
Full size table

3D-Printed Porous Bio-nanocomposites

Materials Preparation

In this work, the bredigite nanopowders are synthesized using Mg3Si4O10(OH)2), SiO2, and CaCO3 as starting materials according to the procedure described in the previous works (Ref 10, 11, 45, 46). Subsequently, the bredigite nanopowders are composed of magnetite nanoparticles (MNPs) which are synthesized via the sol–gel technique using Fe2+ Ions. In order to synthesize the bredigite powder, planetary high-energy ball milling (HEBM) technique is employed including several milling hours (zirconia vial and ball, speed = 650 rpm, ball–powder ratio 10:1) and then sintering under ambient temperature of 1300–1350 °C for 4 h with heating and cooling rate of 10 °C/min. The prepared bredigite bioceramic is composed of MNPs with various weight fractions (0, 10, 20, and 30 wt.%), and then the composite material is milled for 1 h to obtain a homogenized bio-nanocomposites as shown schematically in Fig. 2. To design the 3D structure, the obtained bio-nanocomposite material is inserted into a 3D-printing machine with Zb63 as a binder with specific amount of polycaprolactone (PCL) polymer to build a beam-type implant with circular cross section according to the ASTM standard (Ref 9) using SolidWorks®2012 software. There is a growing need to improve the bone cancer therapy and bone regeneration discussed in most articles and reports in the field of biomaterials as shown schematically in Fig. 1. After 3D-printing four scaffolds, the samples are depowered and inserted into furnace to compact their powders. The four scaffolds containing various amounts of MNP are then sintered at 650 °C for 2 h.

Fig. 2
figure 2

Schematic of materials preparation, 3D-printed structure of a bredigite-MNPs scaffold nanocomposite, and the applications of MNPs on therapy of human body disease

Full size image

Wettability Study

It is shown that the surface wetting in simulated body fluid (SBF: produced according to the procedure explained by Kokubo et al.) solution can be affected by the roughness of the surface. There are two main parameters in wettability of surfaces including: (1) surface roughness, (2) charge (zeta potential). Therefore, in biomaterial engineering, two important issues including roughness and wettability are required for bone regeneration of host and guest tissue, as well as conjunction of cells with proteins. It is essential that all silicate bioceramics have negative zeta potentials, which is indicative of a negative surface charge. Herein, the contact angle/wettability test is performed to investigate the wettability value of bio-nanocomposite scaffolds. The 3D-printed bio-nanocomposite scaffolds are tested using the sessile drop method to consider the wettability by depositing SBF on scaffold surface. The results are captured using optical tools and camera to analyze \(\theta\) angle. Also, the theoretical wettability formula is utilized as below:

$$\cos \theta = \frac{{\gamma_{\text{SV}} - \gamma_{\text{SL}} }}{{\gamma_{\text{LV}} }}$$
(1)

where \(\gamma_{\text{SV}}\), \(\gamma_{\text{SL}}\), and \(\gamma_{\text{LV}}\) are interfacial surface tensions of solid–gas, solid–liquid, and V liquid–gas, respectively. The wettability test is performed at room temperature (25 ± 1 °C) and relative humidity (RH) of 35 ± 5%, with the aid of a low-energy electron beam irradiation for various exposition times 400–1200 s with time step of 120 s.

Surfaces Profilometry

Four measurements are performed for each sample, and then their average is determined. The roughness of the surface can be described based on different measures such as \(R_{\text{a}}\) used by roughness tester. The surface roughness of the bio-nanocomposite scaffold with cylindrical shape is measured by profilometry using a Mitutoyo SURFTEST 301 profilometer. Three slices of the scaffold are measured for each surface condition to obtain an average roughness value (\(R_{\text{a}}\)).

Materials Characterization

The prepared 3D-printed bio-nanocomposite scaffolds are characterized by size, geometry, and different mechanical properties such as roughness, surface morphology using scanning electron microscope (SEM) (Seron Technologies, AIS2100, coated with Quorum Technologies-EMITECH SC7620, and Amirkabir University of Technology). To this end, the samples are coated with gold (Au) for 3 min using spraying, in a high vacuum environment with 30 kV accelerating voltage. Thereafter, phase structure analysis is performed using x-ray diffraction (XRD) analysis with a Philips X’Pert Pro MPD diffractometer using Cu Kα radiation (λ1 = 0.1541 nm) over a 2θ range of 20°–55°. The obtained experimental patterns are then compared with the standard ones compiled by the Joint Committee on Powder Diffraction and Standards (JCDPS). With the aid of XRD patterns and the modified Scherrer equation, the crystalline size of the prepared powders is determined. The thermal characterization of the bredigite nanopowder is also anticipated using thermogravimetric analysis (TGA) together with the differential scanning calorimetric (DSC) analysis (CRL, New Technology Research Centre and Amirkabir University of Technology). Samples with weights of 5 and 7 mg are tied separately in aluminum crucibles via lids. The surface roughness is achieved using atomic force microscopy (AFM) at Isfahan University Technology. The TGA and DSC analyses are done at a heating rate of 10 °C/min in the nitrogen atmosphere. TGA analysis is conducted by raising the temperature slowly and proposing weight against temperature. On the other hand, DSC analysis is carried out within dry condition using a heating ramp rate of 10 °C/min, starting form 50 °C up to 1500 °C as a heating temperature. The basic data show that through the temperature increment within the range of 500–1000 °C, the mass of sample reduces to about 0.2 mg. Therefore, it can be concluded that the contents of the prepared material remain almost constant at higher temperature.

Experimental results

Figure 3a shows the XRD patterns of the prepared bio-nanocomposite scaffold made of the sintered bredigite composed of 30 wt.% MNPs. It can be seen that the only existing phase is related to the bredigite at 32°. It is observed that the presence of 30 wt.% MNPs causes to create a new phase. However, the presence of Fe3O4 results in a reduction in the peak intensity and a slight increment in the peak width of the bredigite due to the presence of Si and Mg ions. Also, in Fig. 3b, the MNPs sharp peaks can be found within the range of 30°–32°. The XRD analysis indicates that in case there are several different peaks for a nanocrystal within the range of 0°–90° (θ), then all of these N peaks must present identical L values for the crystal size as below:

$$L = \frac{K\lambda }{\beta \cos \theta }$$
(2)

As a result, if \(L\) is assumed to be a fixed value for different peaks of a substance, and with consideration of this point that \(K\) and λ and therefore \(K\lambda\) are fixed values, then it required the value of \(\beta \cos \theta\) to be fixed within the range of 0 < 2θ < 180°. So, in order to reduce the error and obtain the average value of L through all of the peaks (or any number of selected peaks), the least squares method is employed to decrease mathematically the source of errors (Ref 2, 47).

Fig. 3
figure 3

XRD comparison of (a) bredigite, Fe3O4, and bredigite containing 30 wt.% Fe3O4, (b) magnified angle between 30 to 32°

Full size image

The basic Scherrer formula can be rewritten as

$$\beta = \frac{K\lambda }{L\cos \theta } = \frac{K\lambda }{L}.\frac{1}{\cos \theta }$$
(3)

Now by taking logarithm on both the sides, one can obtain the modified Scherrer equation (Ref 47) (4a) and Williamson-Hall Eq 4b as below

$$\ln \beta = \ln \left( {\frac{K\lambda }{L\cos \theta }} \right) = \ln \left( {\frac{K\lambda }{L}} \right) + \ln \left( {\frac{1}{\cos \theta }} \right)\quad {\text{Modified}}\;{\text{Scherer}}$$
(4a)
$${\text{FW(S)}} \times \text{Cos} \theta \, = \frac{K \times \lambda }{\text{Size}} + \, 4 \times {\text{strain}} \times \text{Sin}\, \theta \quad {\text{Williamson-Hall}}$$
(4b)

The XRD extracted data are gathered in Table 2 using Scherrer and Williamson-Hall equations. However, as shown in Fig. 4(a) and (b), Scherer and Williamson-Hall equation, since errors are associated with experimental data, the least squares method leads to the best slope. After getting the intercept, then the exponential of the intercept can be obtained as

$$e^{{\ln \left( {\frac{K\lambda }{L}} \right)}} = \frac{K\lambda }{L}$$
(5)

The above interpretation changes through the addition of MNPs to the bredigite. In fact, MNPs can prevent the decomposition of bredigite, so they cause to strengthen the interactions between the apatite particles, which leads to enhance the compaction as shown in Fig. 5(a)-(d). As the MNPs are added to the bredigite, the materials crystalline size increased, which is proved in the SEM micrographs.

Table 2 Data extracted from XRD analysis using Scherrer and Williamson-Hall equations
Full size table
Fig. 4
figure 4

Curve for (a) Scherrer equation results, and (b) Williamson-Hall for the sample with 30 wt.% MNPs and 70 wt.% bredigite

Full size image
Fig. 5
figure 5

SEM micrographs of the bredigite-MNP bio-nanocomposite samples with (a) 0 wt.%, (b) 10 wt.%, (c) 20 wt.%, and (d) 30 wt.% MNPs

Full size image

In Fig. 6, the SEM of a sample of bredigite-MNPs (30 wt.%) bio-nanocomposite scaffold sintered at 650 °C for 2 h is shown. It is revealed that the surfaces of the bio- nanocomposite sample are not smooth and some small pores can be spotted (Fig. 6a and b). On closer inspection, it can be realized that the sample containing 30 wt.% MNPs has glassy surface which is suitable for bone formation and mechanical behavior of scaffolds surface. The main attention goes to investigate the particle size as an important factor, because the mobility of the charged particles is proportional to the size of the particles. The PSA distribution can be rationally justified according to SEM results to introduce the increasing particle size distribution by increasing the MNPs content.

Fig. 6
figure 6

SEM micrographs of (a) bredigite 30% MNPs and (b) magnified cross section of bredigite 30% MNPs scaffold (see the glassy surface)

Full size image

Figure 7(a)-(d) shows the EDS images of the fabricated bio-nanocomposite samples which are necessary for cell infiltration and unrestricting the cell–cell communication. All bio-nanocomposite scaffolds have similar pore sizes, within the range of 300–500 nm, which are ideal for many tissue engineering purposes. At high magnification, the samples containing 30 wt.% MNP have more irregular porous architecture as the associated SEM evident illustrates. The observation shows that the sintering process causes to destroy the pores and changed the surface morphology obtained by the complete sintering process. The EDS results confirm this fact that addition of magnetite nanoparticles may lead to some peaks in the samples composition. Some intensify peaks are related to Fe and Mg ions as shown in Fig. 7(b)-(d) related to samples with 10, 20 and 30 wt.% MNPs in the bredigite microstructure.

Fig. 7
figure 7

EDS micrographs of (a) bredigite 0 wt.% MNPs and (b) bredigite 10 wt.% MNPs, (c) bredigite 20 wt.% MNP, and (d) bredigite 30 wt.% MNPs bio-nanocomposite scaffolds (corresponding to Fig. 5, the shiny region)

Full size image

Superparamagnetic nanoparticles have a high sensitivity to receiving the electromagnetic wave from their surrounding area, or receiving electromagnetic signals from the medium. Electromagnetic signals in the medium affect the alive cells and infected cells by altering cytoplasmic enzymatic reactions as well as wall permeability. This phenomenon increases the rate of cell proliferation and enhances the hyperthermia treatment in the presence of magnetite nanoparticles. From AFM results and roughness test, it is clear that the smaller particle size distribution is related to the sample containing 30 wt.% MNPs, but it contains higher agglomeration of the particles. The images clearly confirm that as the weight fraction of MNPs increases, the “Texture” diagram is almost superimposed on the “Waviness” diagram and the “Roughen” diagram fluctuates between the range of 0.04 and + 0.05 μm when the MNP content reaches 30 wt.% (see Fig. 8a-d).

Fig. 8
figure 8

Two-dimensional images of AFM analysis of the prepared bio-nanocomposites with (a) 0 wt.% MNPs, (b) 10 wt.% MNPs, (c) 20 wt.% MNPs, (d) 30 wt.% MNPs after sintering at 650 °C for 2 h, and (e) wettability and surface roughness values of the samples corresponding to various amounts of MNPs

Full size image

The surface hydrophilicity of the bio-nanocomposite scaffold is investigated by measuring its wettability value after dropping SBF on the surfaces of it. In the current work, an electron irradiation (low energy) is employed to obtain a tuneable contact angle for bredigite-magnetite bio-nanocomposite scaffold. The obtained results indicate that the sample with 30 wt.% MNPs has a contact angle ranging from 58° to 23° and explain this fact that by increasing the time of the scaffold exposure (containing 30 wt.% MNPs), the contact angle (wetting response) moves slowly toward a lower angle. Moreover, by adding more MNPs, an increment in the surface roughness of the scaffold is occurred; subsequently, an upward trend is also observed (excluding the pure bredigite scaffold) as shown in Fig. 8e. For example, in the bio-nanocomposite scaffold containing 30 wt.% MNPs, the values of roughness and wettability are measured at 33.23 (μm) and 23.3°. However, in the sample without MNPs, the values are 30 (μm) and 58.3°. Therefore, by adding MNPs, a higher roughness value is achieved; In contrast, the wettability of the surface is reduced. Additionally, the bredigite-magnetite bio-nanocomposite scaffold is deposited with a bigger particle size on the surface of scaffold, which can be related to the nanocomposite agglomeration and cluster particles.

Thermal properties are also important which can affect the properties of ceramics. These thermal properties include the duration of applied heat treatment and its temperature. Several studies have shown that synthetic ceramics like HA having a Ca/P ratio close to 1.67 remain steady even below the 1200 °C when sintered at a moist or dry atmosphere (Ref 21). The stability of ceramics is compromised due to their poor thermal resistance, which results in breaking down to tricalcium phosphate form, i.e., TCP, when temperature exceeds 1200 °C (Ref 22). Therefore, great care must be taken when working with ceramics at high or low temperatures. With respect to this fact, materials that portray different stoichiometries, morphologies, and crystallinities have been designed (Ref 23). Moreover, these new properties cause a profound effect on the biomaterial quality because of mechanical integrity, dissolution behavior, and thermal stability (Ref 22). Another study conducted by Dezfuli et al. (Ref 23) showed that the creation of Mg-bredigite composites is not the only thermal event that occurred during the heating process, but the cold magnesium oxide heated at 600 °C leads to an exothermic reaction which commenced at 550 °C and peaked at 592 °C and results in an abrupt mass loss (Ref 24). Khandan et al. (Ref 11) fabricated bredigite-magnetite bio-nanocomposite scaffold and represented that the sample with 30 wt.% MNPs has highest heat transfer during hyperthermia test about 27 °C for 50 s. In our previous study (Ref 10, 11), addition of magnetite nanoparticles up to 30 wt.% leads to better magnetic saturation and energy release (heat) from the magnetite nanoparticles under AC magnetic field to the bredigite bioceramic. These ongoing researches were targeted at devising a fabrication methodology viable for structural bioceramics housing with MNPs-matrix composite. It is no surprise that an in-depth comprehension of the mechanism for degrading as well as the rate of degradation with respect to the decline in MNPs-bredigite mechanical property will help to improve the MNPs-matrix composites’ degradation to control mechanical properties.

The mechanisms of the thermal, mechanical, biological, electrical, and degradation of the bredigite-magnetite bio-nanocomposites are proposed in this work. However, another critical important issue, i.e., their cell culture behavior in relation to degradation behavior, has not been addressed. The thermal conductivity of the magnetite-bioceramic bio-nanocomposite scaffold introduces two advantages such as the microstructural assistance, which may help the matrix with appropriate functionalizing, and presenting thermal and magnetic behavior to the host tissues. The magnetite has the capability to release heat when it is inserted in the AC field; therefore, the bio-nanocomposite scaffolds including MNPs can properly release heat because of cortical bone thickness, which limits the thermal conductivity for tumor therapy. The obtained data from the current work indicate that incorporation of MNPs with various amounts can lead to some crystalline changes and effects on the surface modification of the samples. The results demonstrate that addition of MNPs to the bredigite nanopowder causes to enhance the roughness of the samples and also to decrease the wettability and creation of non-uniform struts.

The graphs of DSC and TGA for thermal analyses of the prepared bredigite nanopowder composed of various amounts of MNPs (0, 10, 20, and 30 wt.%) are presented in Fig. 9. It can be concluded that the four graphs are typically similar to each other. In the thermal test, the heat change indicates that the calculated degree of crystallinity is 90%, which is close to full growth of the crystals. The presence of magnetite nanoparticles in the bioceramics can lead to two possible mechanisms. It can accelerate the crystallization which has a strong dependence on the amount of magnetite nanoparticles in the microstructure of the basic material. As it can be observed from Fig. 9(a)-(d), changes in the weight can be detected in TG curve which proves the microstructural architecture of an endothermic peak for water loss. Two obvious decomposition steps of weight loss are observed in the TG curve, accompanied by endothermic peak and a sharp exothermic peak on the DSC diagram.

Fig. 9
figure 9

DSC/TG analysis for the prepared bredigite-MNP bio-nanocomposite material corresponding to different MNPs weight fractions (a) 0 wt.% (reproduced from Ref 11), (b) 10 wt.%, (c) 20 wt.%, and (d) 30 wt.%

Full size image

Figure 9 illustrates that the weight loss of the bio-nanocomposite samples containing various amounts of MNPs within the temperature range of 0-1000 °C may be related to the desorption of water in the Ca7MgSi4O16. It is observed that the highest weight loss is related to the temperature range of 800-900 °C due to the loss of lattice water. The results from other samples show similar behavior to that of the sample without MNPs. However, some peaks become sharper. For example, the initial endothermic peak happens before 500 °C for sample without MNPs, while for the samples with various amounts of MNPs, it is shown that endothermic peak shifts to the right side. It can be concluded that maybe some additional compounds such as magnesium nitrate coming from incomplete sintering procedure are removed. It is seen that the second endothermic peak occurs before 900-1000 °C. It means that MNPs lead to a slow decomposition of water in the composition of the bredigite nanopowder.

Nonlinear Resonance Analysis of Beam-Type Biological Implants

In Fig. 2, the prepared 3D-printed porous beam-type biological implant of length \(L\), radius \(R\), and thickness \(h\) is represented schematically. Based on the classical Euler–Bernoulli beam theory, the displacement field can be written as

$$u_{x} \left( {x,t} \right) = - z\frac{{\partial w\left( {x,t} \right)}}{\partial x} ,\quad u_{z} \left( {x,t} \right) = w\left( {x,t} \right)$$
(6)

in which \(w\) stands for the middle surface displacements along \(z\)-axis, and \(t\) denotes time.

In accordance with the von Karman kinematics of nonlinearity, the strain–displacement relationship can be written as

$$\varepsilon_{xx} = - z\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2}$$
(7)

Moreover, on the basis of the elastic constitutive law, the stress component of the beam-type implant can be expressed as

$$\sigma_{xx} = \left( {\lambda + 2\mu } \right)\left( {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} - z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)$$
(8)

in which \(\lambda = E\nu /\left( {1 - \nu^{2} } \right)\), \(\mu = E/\left( {2\left( {1 + \nu } \right)} \right)\) are Lame’s constants. The associated Young’s modulus corresponding to different morphology shapes and MNPs weight fractions is extracted from the experimental results presented in the previous section. Also, with the aid of the rule of mixture, the Poisson’s ratio of the bio-nanocomposite material can be estimated as

$$\nu = \nu_{\text{MNP}} V_{\text{MNP}} + \nu_{b} \left( {1 - V_{\text{MNP}} } \right)$$
(9)

where \(\nu_{\text{MNP}}\) and \(\nu_{b}\) are the Poisson’s ratios of MNPs and bredigite phases of the bio-nanocomposite material. Also, \(V_{\text{MNP}}\) represents the volume fraction of MNPs as given in Table 1.

Following the classical continuum theory of elasticity, the total strain energy of the implant can be obtained as

$$\varPi_{s} = \frac{1}{2}\mathop \int \limits_{x} \mathop \int \limits_{S} \sigma_{ij} \varepsilon_{ij} {\text{d}}x{\text{d}}S = \frac{1}{2}\mathop \int \limits_{x} \left\{ {N_{xx} \left( {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right) - M_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right\}{\text{d}}x$$
(10)

in which

$$N_{xx} = 2\pi R\mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \sigma_{xx} {\text{d}}z = \frac{{2\pi Rh\left( {\lambda + 2\mu } \right)}}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2}$$
$$M_{xx} = 2\pi R\mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \sigma_{xx} z{\text{d}}z = - \frac{{2\pi Rh^{3} \left( {\lambda + 2\mu } \right)}}{12}\frac{{\partial^{2} w}}{{\partial x^{2} }}$$
(11)

Moreover, the external work \(\varPi_{P}\) done by the external distributed load \(f\) can be introduced in the following form

$$\varPi_{P} = \mathop \int \limits_{x} fw{\text{d}}x$$
(12)

Furthermore, the kinetic energy of the biological implant can be calculated as

$$\varPi_{T} = \frac{1}{2}\mathop \int \limits_{x} \mathop \int \limits_{S} \rho \left\{ {\left( {\frac{{\partial u_{x} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{z} }}{\partial t}} \right)^{2} } \right\}{\text{d}}x\,{\text{d}}S = \frac{1}{2}\mathop \int \limits_{x} \left\{ {2\pi \rho Rh\left( {\frac{\partial w}{\partial t}} \right)^{2} + \frac{{\pi \rho Rh^{3} }}{6}\left( {\frac{{\partial^{2} w}}{\partial x\partial t}} \right)^{2} } \right\}{\text{d}}x$$
(13)

Now, by using the Hamilton principle as below

$$\delta \mathop \int \limits_{{t_{1} }}^{{t_{2} }} \left( {\varPi_{T} - \varPi_{s} + \varPi_{P} } \right){\text{d}}t = 0$$
(14)

one will have

$$\frac{\partial }{\partial x}\left[ {N_{xx} \frac{\partial w}{\partial x}} \right] + \frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} = f + 2\pi \rho Rh\frac{{\partial^{2} w}}{{\partial t^{2} }} - \frac{{\pi \rho Rh^{3} }}{6}\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}$$
(15)

Substitution of Eq 11 into Eq 15 leads to the nonlinear governing differential equation of motion in terms of the displacement field as below:

$$D_{11}^{*} \frac{{\partial^{4} w}}{{\partial x^{4} }} + \left[ {\left( {\frac{{A_{11}^{*} }}{2}} \right)\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right]\frac{{\partial^{2} w}}{{\partial x^{2} }} + \left[ {A_{11}^{*} \frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right]\frac{\partial w}{\partial x} = f + I_{1}^{*} \frac{{\partial^{2} w}}{{\partial t^{2} }} + I_{3}^{*} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}$$
(16)

where

$$A_{11}^{*} = 2\pi Rh\left( {\lambda + 2\mu } \right) ,\quad D_{11}^{*} = - \frac{{\pi Rh^{3} \left( {\lambda + 2\mu } \right)}}{6},\quad I_{1}^{*} = 2\pi \rho Rh ,\quad I_{3}^{*} = - \frac{{\pi \rho Rh^{3} }}{6}$$
(17)

To perform the solution methodology in a more general form, the following dimensionless parameters are defined as

$$W = \frac{w}{h},\quad X = \frac{x}{L},\quad \vartheta = \frac{h}{L},\quad T = \frac{t}{L}\sqrt {\frac{{\left( {\lambda + 2\mu } \right)}}{\rho }} ,\quad \left\{ {\hat{I}_{1} ,\hat{I}_{3} } \right\} = \left\{ {\frac{{I_{1}^{*} }}{\rho bh},\frac{{I_{3}^{*} }}{{\rho bh^{3} }}} \right\}$$
$$F = \frac{{fL^{2} }}{{bh^{2} \left( {\lambda + 2\mu } \right)}} ,\quad a_{11}^{*} = \frac{{A_{11}^{*} }}{{bh\left( {\lambda + 2\mu } \right)}} ,\quad d_{11}^{*} = \frac{{D_{11}^{*} }}{{bh^{3} \left( {\lambda + 2\mu } \right)}}$$
(18)

Consequently, the dimensionless form of the nonlinear governing differential equation of motion can be expressed as

$$d_{11}^{*} \vartheta^{2} \frac{{\partial^{4} W}}{{\partial X^{4} }} + \frac{3}{2}\vartheta^{2} a_{11}^{*} \left( {\frac{\partial W}{\partial X}} \right)^{2} \frac{{\partial^{2} W}}{{\partial X^{2} }} = F + \hat{I}_{1} \frac{{\partial^{2} W}}{{\partial T^{2} }} + \hat{I}_{3} \vartheta^{2} \frac{{\partial^{4} W}}{{\partial X^{2} \partial T^{2} }}$$
(19)

With the aid of the Galerkin method, the differential equation of motion can be written in discretized form. To accomplish this purpose, it is assumed that \(W\left( {X,T} \right)\) can be introduced separately as follows:

$$W\left( {X,T} \right) = \varphi \left( X \right)q\left( T \right)$$
(20)

By inserting Eq 20 in Eq 19, it yields

$$d_{11}^{*} \vartheta^{2} \frac{{{\text{d}}^{4} \varphi }}{{{\text{d}}X^{4} }}q + \frac{3}{2}\vartheta^{2} a_{11}^{*} \left( {\frac{{{\text{d}}\varphi }}{{{\text{d}}X}}q} \right)^{2} \frac{{{\text{d}}^{2} \varphi }}{{{\text{d}}X^{2} }}q = F + \hat{I}_{1} \varphi \frac{{{\text{d}}^{2} q}}{{{\text{d}}T^{2} }} + \hat{I}_{3} \vartheta^{2} \frac{{{\text{d}}^{2} \varphi }}{{{\text{d}}X^{2} }}\frac{{{\text{d}}q^{2} }}{{{\text{d}}T^{2} }}$$
(21)

On the basis of the Galerkin technique, the Duffing-type equation of motion can be extracted in the following form:

$$\ddot{q} + 2\beta \dot{q} + \omega^{2} q + \alpha q^{3} = \tilde{F}$$
(22)

in which

$$\omega^{2} = - \frac{{\mathop \int \nolimits_{0}^{1} \left\{ { - d_{11}^{*} \vartheta^{2} \varphi \left( {\frac{{{\text{d}}^{4} \varphi }}{{{\text{d}}X^{4} }}} \right)} \right\}{\text{d}}X}}{{\mathop \int \nolimits_{0}^{1} \left\{ {\hat{I}_{1} \varphi^{2} - \hat{I}_{3} \vartheta^{2} \varphi \left( {\frac{{{\text{d}}^{2} \varphi }}{{{\text{d}}X^{2} }}} \right)} \right\}{\text{d}}X}}$$
$$\alpha = - \frac{{\mathop \int \nolimits_{0}^{1} \left\{ {\frac{{a_{11}^{*} \vartheta^{2} }}{2}\left[ {\mathop \int \nolimits_{0}^{1} \left( {\frac{d\varphi }{dX}} \right)^{2} {\text{d}}X} \right]\varphi \left( {\frac{{{\text{d}}^{2} \varphi }}{{{\text{d}}X^{2} }}} \right)} \right\}{\text{d}}X}}{{\mathop \int \nolimits_{0}^{1} \left\{ {\hat{I}_{1} \varphi^{2} - \hat{I}_{3} \vartheta^{2} \varphi \left( {\frac{{{\text{d}}^{2} \varphi }}{{{\text{d}}X^{2} }}} \right)} \right\}{\text{d}}X}}$$
(23)
$$\tilde{F} = - \frac{F}{{\mathop \int \nolimits_{0}^{1} \left\{ {\hat{I}_{1} \varphi^{2} - \hat{I}_{3} \vartheta^{2} \varphi \left( {\frac{{{\text{d}}^{2} \varphi }}{{{\text{d}}X^{2} }}} \right)} \right\}{\text{d}}X}}$$

In addition, it is assumed that the external distributed load is a dissipative one, so the damping parameter takes the following form (Ref 48, 49):

$$\beta = \frac{{\eta \omega^{2} }}{{\omega_{L} }}$$
(24)

where \(\omega_{L}\) denotes the linear frequency of the system and \(\eta\) is a constant.

The analytical expression for \(\varphi \left( X \right)\) corresponding to clamped boundary conditions can be considered in the following forms:

$$\varphi (x) = \sinh \left( {4.73X} \right) - \sin \left( {4.73X} \right) + \left( {\frac{{\sin \left( {4.73} \right) - \sinh \left( {4.73} \right)}}{{\cos \left( {4.73} \right) - \cosh \left( {4.73} \right)}}} \right)\left( {\cos \left( {4.73X} \right) - \cosh \left( {4.73X} \right)} \right)$$
(25)

For the resonance analysis, the damping and nonlinear terms are assumed to be small and they are in the order of a small parameter, \(\in\). Thereby, Eq 22 can be rewritten as

$$\ddot{q} + 2\beta \in \dot{q} + \omega^{2} q + \alpha \in q^{3} = \tilde{F}$$

According to the soft excitation, the order of the external distributed load can be considered similar to that of damping and nonlinear terms. Thus, for a periodic type of excitation, one will have

$$\ddot{q}\left( T \right) + 2\beta \int \dot{q}\left( T \right) + \omega^{2} q\left( T \right) + \alpha \int q^{3} \left( T \right) = 2\int \tilde{F}\cos \left( {\varOmega T} \right)$$
(27)

where \(\varOmega\) is the excitation frequency.

On the other hand, the multiple-time-scale summation for \(q\) results in

$$q\left( T \right) = q_{0} \left( {T_{0} ,T_{1} } \right) + \int q_{1} \left( {T_{0} ,T_{1} } \right)$$
(28)

in which \(T_{0} = T\) and \(T_{1} = \in T\). Substitution Eq 28 into Eq 27 gives

$$\left\{ {\begin{array}{*{20}l} {O\left( {\int^{0} } \right): {\mathcal{D}}_{0}^{2} q_{0} + \omega^{2} q_{0} = 0} \hfill \\ {O\left( {\int^{1} } \right): {\mathcal{D}}_{0}^{2} q_{1} + \omega^{2} q_{1} = - 2{\mathcal{D}}_{0} {\mathcal{D}}_{1} q_{0} - 2\beta {\mathcal{D}}_{0} q_{0} - \alpha q_{0}^{3} + \tilde{F}e^{i\varOmega T} } \hfill \\ \end{array} } \right.$$
(29)

where \({\mathcal{D}}_{i}^{j} = \frac{{d^{j} }}{{dT_{i}^{j} }}\) represents the time derivatives.

In accordance with the first relation of Eq 29, one will have

$$q_{0} = {\mathcal{A}}\left( {T_{1} } \right)e^{{i\omega T_{0} }}$$
(30)

Thereafter, by substituting Eq 30 into the second relation of Eq 29, one will obtain

$${\mathcal{D}}_{0}^{2} q_{1} + \omega^{2} q_{1} = - \left[ {2i\omega_{0} \left( {\frac{{d{\mathcal{A}}}}{{dT_{1} }} + {\mathcal{A}}\beta } \right) + 3\alpha {\mathcal{A}}^{2} {\mathcal{B}}} \right]e^{{i\omega T_{0} }} - \alpha {\mathcal{A}}^{3} e^{{3i\omega T_{0} }} + \tilde{F}e^{{i\varOmega T_{0} }} + \ldots$$
(31)

where \({\mathcal{B}}\left( {T_{1} } \right)\) stands for the complex conjugate part of the expression.

Within the range of soft excitation, it is possible to assume

$$\varOmega = \omega + \int \varGamma$$
(32)

in which \(\varGamma\) stands for the detuning parameter. By eliminating the secular and small divisor terms, one will have

$$- \;2i\omega_{0} \left( {\frac{{{\text{d}}{\mathcal{A}}}}{{{\text{d}}T_{1} }} + {\mathcal{A}}\beta } \right) - \;3\alpha {\mathcal{A}}^{2} {\mathcal{B}} + \tilde{F}e^{{i\varOmega T_{0} }} = 0$$
(33)

For \({\mathcal{A}}\left( {T_{1} } \right)\), a polar function can be defined as below:

$${\mathcal{A}}\left( {T_{1} } \right) = \frac{1}{2}a\left( {T_{1} } \right)e^{{i\xi \left( {T_{1} } \right)}}$$
(34)

Through inserting Eq 34 in Eq 33, each of the real and imaginary parts yields

$$\frac{{{\text{d}}a}}{{{\text{d}}T_{1} }} = - \;\beta a + \frac{{\tilde{F}}}{\omega }\sin \left( {\varGamma T_{1} - \xi } \right)$$
(35a)
$$a\frac{{{\text{d}}\xi }}{{{\text{d}}T_{1} }} = \frac{{3\alpha a^{3} }}{8\omega } - \frac{{\tilde{F}}}{\omega }\cos \left( {\varGamma T_{1} - \xi } \right)$$
(35b)

By setting the derivative terms on the left side of Eq 35 equal to zero, the steady-state solution (Ref 50) can be achieved as

$$\beta a = \frac{{\tilde{F}}}{\omega }\sin \left( {\varGamma T_{1} - \xi } \right)$$
(36a)
$$\frac{{3\alpha a^{3} }}{8\omega } = \frac{{\tilde{F}}}{\omega }\cos \left( {\varGamma T_{1} - \xi } \right)$$
(36b)

As a result, the frequency response and amplitude response associated with the nonlinear primary resonance of the 3D-printed porous beam-type biological implant can be expressed in analytical explicit forms, respectively, as

$$\varGamma = \frac{{3\alpha a^{2} }}{8\omega } \pm \sqrt {\frac{{\tilde{F}^{2} }}{{a^{2} \omega^{2} }} - \beta^{2} }$$
(37)
$$\tilde{F} = a\omega \sqrt {\beta^{2} + \left( {\varGamma - \frac{{3\alpha a^{2} }}{8\omega }} \right)^{2} }$$
(38)

Firstly, the validity of the present solution methodology is checked. For this purpose, the fundamental frequency of an isotropic beam are calculated and compared with those reported by Sheng and Wang (Ref 51) using the method of multiple scales. As presented in Table 3, a very good agreement is found which confirms the validity as well as accuracy of the current solving process of problem.

Table 3 Comparison of the dimensionless fundamental frequencies of an isotropic beam corresponding to various length to thickness ratios
Full size table

In Fig. 10, the frequency response and amplitude response associated with the nonlinear primary resonance of a beam-type biological implant made of the porous bio-nanocomposite material are depicted corresponding to different MNPs weight fractions (Ref 52,53,54). It is found that by increasing the MNP percent, the height of jump phenomenon decreases. It is demonstrated that by increasing the forcing amplitude related to the external excitation, the maximum deflection of the response increases up to the first bifurcation point. After that, reduction of the forcing amplitude leads to increase the response amplitude until reaching the second bifurcation point. For higher values of MNPs weight fraction, the response amplitudes of the porous bio-nanocomposite implant associated with the both bifurcation points increase.

Fig. 10
figure 10

Nonlinear resonance response of the porous beam-type implant corresponding to various MNPs weight fractions: (a) frequency response; (b) amplitude response

Full size image

Figure 11 and 12 illustrate the frequency response and amplitude response of the 3D-printed porous beam-type biological implant with different morphology shapes relevant to various values of MNPs weight fractions used from work (Ref 45, 46). It is found that for lower MNPs weight fraction, the height of jump phenomenon related to the nonlinear resonance response is maximum and minimum for, respectively, irregular and mesoporous shapes of morphology, but their associated forcing amplitudes of the bifurcation points in order are minimum and maximum. For higher MNPs weight fraction, the height of jump phenomenon is maximum and minimum for, respectively, spongy and porous shapes of morphology, but their associated forcing amplitudes of the bifurcation points in order are minimum and maximum.

Fig. 11
figure 11

Nonlinear resonance response of the porous beam-type implant corresponding to various morphology shapes (MNPs wt.% = 0.42): (a) frequency response; (b) amplitude response

Full size image
Fig. 12
figure 12

Nonlinear resonance response of the porous beam-type implant corresponding to various morphology shapes (MNPs wt.% = 0.48): (a) frequency response; (b) amplitude response

Full size image

It should be noted that bone exemplifies the organic–inorganic composite structures inherent in mineralized tissues (Ref 52). Suitable bending strength and vibrational response of the cell can be useful for chemoradiation as well as better glioma oxygenation (Ref 45, 46). Investigation of reinforcements like carbon nanotube (CNT) (single-wall and multi-wall), nanosilica, or functionally graded nanocomposite plates using molecular dynamics simulation has received researchers’ attention during recent decades to predict mechanical properties of materials before any experimental testing (Ref 55,56,57,58,59). Therefore, in this work, we evaluated the resonance behavior of bredigite-magnetite scaffolds using analytical data.

Conclusion

In the present work, through addition of MNPs to the bredigite bioceramic using HEBM method, a new bio-nanocomposite material was prepared having the hyperthermia application potential. After that, with the aid of a 3D-printer design tool, a biological scaffold as a beam-type porous bone implant was manufactured made of the bio-nanocomposite material. Also, the surface properties, morphology, and size of the composed powder were evaluated using Scherrer and Williamson-Hall equation. Afterward, via the experimentally obtained mechanical properties, the nonlinear primary resonance response of the beam-type bone implant was predicted analytically.

The results of the surface roughness indicated that the pores region on the scaffold sample produced after sintering process is occurred by the thermal and kinematic coefficients changes of the biomaterials. In addition, by surface hydrophilicity of the bio-nanocomposite scaffold, it was found that the sample with 30 wt.% MNPs has a contact angle ranging from 58.3° to 23°, indicating this fact that by increasing the time of exposure of the bio-nanocomposite scaffold (30 wt.% MNPs), the contact angle moves slowly toward a lower angle. Moreover, it was observed that by increasing the forcing amplitude related to the external excitation, the maximum deflection of the response increases up to the first bifurcation point. After that, reduction of the forcing amplitude leads to increase the response amplitude until reaching the second bifurcation point. For higher values of MNPs weight fraction, the response amplitudes of the porous bio-nanocomposite implant associated with the both bifurcation points increase. Also, for higher MNPs weight fraction, the height of jump phenomenon is maximum and minimum for, respectively, spongy and porous shapes of morphology, but their associated forcing amplitudes of the bifurcation points in order are minimum and maximum.