Introduction

NiTi shape memory alloy (SMA) has attracted increasing attention because of its shape memory effect and superelasticity (Ref 1, 2). The phase transformation temperature plays an important role in the engineering application of NiTi SMA (Ref 3). In general, the addition of a third element to binary NiTi SMA has a significant influence on the phase transformation temperature (Ref 4, 5). The substitution of Fe element for Ni element in the binary NiTi SMA contributes to lowering the martensitic transformation start temperature (Ref 6, 7). As a consequence, NiTiFe SMA has been a primary candidate for pipe coupling. However, the microstructure and the texture have a significant influence on shape memory effect and superelasticity of NiTiFe SMA (Ref 8, 9). In particular, plastic deformation plays a predominant role in microstructure evolution and texture evolution of NiTiFe SMA (Ref 10, 11). Therefore, it is of great importance to investigate microstructure evolution and texture evolution of NiTiFe SMA during plastic deformation.

It is well known that during plastic deformation of metals, the preferential orientations of the grains lead to a strong crystallographic texture, which affects seriously the mechanical properties of metals. The numerical modeling and simulation techniques have become the efficient tools to investigate the formation mechanism and the texture evolution during plastic deformation of metals. Most of numerical studies on texture evolution are based on polycrystal plasticity models, such as full-constraints Taylor model (Ref 12), relaxed-constraints model and visco-plastic self-consistent (VPSC) polycrystal model (Ref 13, 14). The Taylor model is reasonable for materials comprising crystals with many slip systems of comparable strength, but it can lead to prediction of excessively high stresses and incorrect texture components in other situations. The relaxed-constraints model often results in imprecise texture predictions due to highly concentrated deformation in a small number of crystals. VPSC model has been successfully used to predict plastic anisotropy and texture evolution of various metals, and it can also be refined by converting modeling parameters to better correlate assumed microscopic interactions with macroscopic behavior or with the results of crystal plasticity finite element simulation. The crystal plasticity finite element method (CPFEM) is the best model for detailed simulation of texture evolution under realistic mechanical boundary conditions and in consideration of texture updating (Ref 15-18). In addition, CPFEM has also the advantage of capturing geometrical change, grain interaction, grain topology, microstructure information and so on (Ref 19).

It is very important for employing CPFEM to establish an appropriate polycrystalline model. As rigorous studies have revealed, the mean grain size and the grain size distribution seriously affect the macroscopic plastic flow stress as well as the local stress and strain development (Ref 20, 21). In some studies, each grain is represented either with a single finite element (Ref 22) or an integration point (Ref 23), which neither reflects the diversity of shape and the size of grains nor describes the inhomogeneous deformation in the grains. Currently, the Voronoi tessellations which are able to provide planar boundaries separating grains have been widely used to represent polycrystalline materials (Ref 17, 24, 25). The Voronoi tessellations divide the space into Voronoi regions, which are defined as non-overlapping zone assigned to each nucleus. Under the assumption of isotropic and steady growth, a natural geometrical description of a grain structure that originates from a homogeneous crystallization process is developed based on Voronoi polygons. Voronoi polygons are viewed as the influence zones of a given set of randomly distributed points. The simplest way to distribute these central points is to use Poisson process (Ref 26), which is used to control the distribution of grain size. Although the model based on space tessellation into Voronoi polygons can describe grain structure very well, the established polycrystalline model is different from the real polycrystal to some extent. Therefore, it is very necessary to adopt the advanced microstructure characterization technology for obtaining the genuine microstructure information in the undeformed and deformed polycrystal. Electron back-scattered diffraction (EBSD) has been the superior candidate for capturing grain size, grain morphology and grain orientation in the undeformed polycrystal, which can provide an input for microstructure parameters of crystal plasticity finite element model (Ref 27, 28). In particular, EBSD can be combined with digital image correlation (DIC) to capture microstructures and microstrains in the deformed polycrystal, which provides an approach to compare the experimental results with the simulation ones (Ref 29-31). In general, crystal plasticity constitutive model is based on three-dimensional stress tensor. Therefore, in terms of crystal plasticity finite element simulation, three-dimensional model works better than two-dimensional one and it is able to reveal the microstructure evolution more genuinely (Ref 19, 32). However, it is a complicated task to establish three-dimensional crystal plasticity finite element model and especially it is a challenge to implement the appropriate boundary conditions. Consequently, two-dimensional crystal plasticity finite element model still has an advantage in terms of model establishment, computation cost and so on, but it is restricted to plane strain compression, uniaxial compression and uniaxial tension (Ref 33, 34).

In the present work, CPFEM is used to simulate the microstructural evolution, the texture evolution and the macroscopic stress-strain response of NiTiFe SMA during compression deformation, where a novel two-dimensional polycrystalline finite element model based on electron back-scattered diffraction (EBSD) experiment data is developed to represent virtual grain structures of polycrystalline NiTiFe SMA, which has never been reported in the literatures.

Materials and Methods

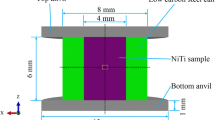
In the present study, the as-received material was an Ni47Ti50Fe3 (in at.%) SMA bar, which was prepared by means of vacuum induction melting method and multi-pass rolling at 850 °C. Subsequently, all the specimens for the following experiments were cut from the as-received NiTiFe SMA bar by means of wire electrical discharge machining (WEDM). In order to identify the crystal structures and phase composition of the polycrystalline NiTiFe SMA, the x-ray diffraction (XRD) experiment was conducted on a PANalytical X′Pert Pro diffractometer using Cu target Kα radiation at ambient temperature, where the NiTiFe SMA sample for XRD analysis possessed the height of 5 mm and the diameter of 8 mm. The NiTiFe SMA sample with the height of 9 mm and the diameter of 6 mm was used for compression test, which was carried out on an Instron 5500R testing machine at the strain rate of 0.001 s−1 at room temperature, in order to capture the stress-strain curve. Furthermore, the NiTiFe SMA sample for compression test was subjected to the compression deformation degree by 50%, namely the reduction in height by 50%.

The cross section of the as-received NiTiFe SMA bar and the compressed NiTiFe SMA sample, which is parallel to rolling direction (RD), was used to prepare the samples for electron back-scattered diffraction (EBSD) measurements. The NiTiFe SMA samples for EBSD were mechanically polished and subsequently electropolished in a solution of 30% HNO3 and 70% CH3OH by volume fraction at −30°C. EBSD experiments are conducted on the NiTiFe SMA samples using a Zeiss Ultra plus scanning electron microscope (SEM) equipped with Oxford Instruments AZtec integrated energy-dispersive spectroscopy (EDS) and EBSD system. The patterns were acquired using Aztec data acquisition software compatible with the EBSD detector with a binning of 2 × 2 pixels. The software indexes the diffraction patterns to evaluate the crystallographic orientation of the selected region. The scan step size is chosen to be 1.5 μm for obtaining a scan area of 231 μm × 172.5 μm for the cross section. Prior to analyzing EBSD data, a modified procedure was used to remove inaccurate orientation measurements with a mean angular deviation (MAD) standardization, followed by neighbor orientation correlation with a maximum MAD of 0.8. EBSD analysis was carried out using MTEX toolbox in MATLAB software.

Constitutive Model of Crystal Plasticity

The advantage of CPFEM is that the constitutive model of crystal plasticity is based on not only dislocation slip mechanism, but also other mechanisms such as mechanical twinning and martensite formation (Ref 32, 35, 36). In the present study, neither stress-induced martensite transformation nor mechanical twinning is observed by means of experiments during uniaxial compression of NiTiFe SMA. As a consequence, the constitutive model of crystal plasticity is based on dislocation slip.

The kinematics used commonly in the field of crystal plasticity may be traced back to the works of Rice (Ref 37), Hill and Rice (Ref 38), Peirce, Asaro and Needleman (Ref 39, 40). The basic characteristic of crystal plasticity is based on the fact that the deformation of a grain is attributed to the result of two distinct physical mechanisms, which deal with crystallographic slip caused by dislocation motion on the active slip systems and elastic lattice distortion (as well as rigid-body rotations). Accordingly, the deformation gradient tensor F can be decomposed into two components according to the following equation:

$${\varvec{F}} = {\varvec{F}}^{e} {\varvec{F}}^{p}$$
(1)

where \({\varvec{F}}^{p}\) represents solely the plastic deformation part and \({\varvec{F}}^{e}\) represents the elastic deformation part, as illustrated in Fig. 1. In Fig. 1, the vectors \({\varvec{m}}_{0}^{(\alpha )}\) and \({\varvec{n}}_{0}^{(\alpha )}\) are regarded as lattice vectors so that they can stretch and rotate by

$${\varvec{m}}^{(\alpha )} = {\varvec{F}}^{e} {\varvec{m}}_{0}^{(\alpha )} ,\quad {\varvec{n}}^{(\alpha )} = {\varvec{n}}_{0}^{(\alpha )} {\varvec{F}}^{e - 1}$$
(2)
Fig. 1
figure 1

Multiplicative decomposition of deformation gradient tensor

Full size image

Correspondingly, the vectors \({\varvec{m}}_{0}^{(\alpha )}\) and \({\mathbf{n}}_{0}^{(\alpha )}\) are unchanged during plastic deformation part and their relationship with \({\varvec{F}}^{p}\) can be written as

$${\varvec{F}}^{P} = \sum\limits_{\alpha = 1}^{N} {\left( {{\varvec{I}} + \gamma^{(\alpha )} {\varvec{m}}_{0}^{(\alpha )} \otimes {\varvec{n}}_{0}^{(\alpha )} } \right)}$$
(3)

where I is the second-order identity tensor. According to Eq 1, the spatial gradient of velocity L can be written as

$${\varvec{L}} = {\dot{\varvec{F}F}}^{ - 1} = {\varvec{L}}^{e} + {\varvec{L}}^{p}$$
(4)

where

$${\varvec{L}}^{e} = {\dot{\varvec{F}}}^{e} {\varvec{F}}^{e - 1} ,\quad {\varvec{L}}^{p} = {\varvec{F}}^{e} {\dot{\varvec{F}}}^{p} {\varvec{F}}^{p - 1} \varvec{F}^{e - 1}$$
(5)

For the constitutive model of rate-dependent materials, the dependence of the slip rate on the resolved shear stress and the resistance to shear is given in the form of a power law (Ref 39) to describe the shear kinetics on the active slip systems as follows:

$$\dot{\gamma }^{(\alpha )} = \dot{\gamma }_{0}^{(\alpha )} \text{sgn} (\tau^{(\alpha )} )\left| {\frac{{\tau^{(\alpha )} }}{{{\text{g}}^{(\alpha )} }}} \right|^{{\frac{1}{\text{m}}}}$$
(6)

where \(\dot{\gamma }_{0}^{(\alpha )}\) is the reference shear rate for plastic slip, \(\uptau^{(\alpha )}\)is the resolved shear stress, \(g^{(\alpha )}\)is the reference shear stress on the α-th slip system and m is the strain rate sensitivity exponent.

The strain hardening is characterized by the evolution of the strength \(g^{(\alpha )}\)through the incremental relation:

$$\dot{g}^{(\alpha )} = \sum\limits_{\beta = 1}^{N} {h_{\alpha \beta } \dot{\gamma}^{(\beta )} }$$
(7)

where \(h_{\alpha \beta }\) is the slip hardening modulus. In addition, \(h_{\alpha \alpha }\) and \(h_{\alpha \beta }\) are called self and latent hardening moduli, respectively. The self-hardening modulus proposed by Peirce et al. (Ref 40) is adopted in the present work.

$$h_{\alpha \alpha } = h(\gamma ) = h_{0} \text{sech}^{2} \left| {\frac{{h_{0} \gamma }}{{\tau_{s} - \tau_{0} }}} \right|$$
(8)

where \(h_{0}\) is the initial hardening modulus, \(\tau_{0}\) is the yield stress which is equal to the initial value of current strength \(g^{(\alpha )}\), \(\tau_{s}\) is the saturation stress where large plastic flow initiates, and \(\gamma\) is the Taylor cumulative shear strain on all the slip systems. The latent hardening modulus is given by the following equation.

$$h_{\alpha \beta } = qh(\gamma ) + (1 - q)h(\gamma )\delta_{\alpha \beta }$$
(9)

where \(\delta_{\alpha \beta }\) is the Kronecker delta and q=1.4 was used for analyzing the texture of polycrystals in the present work (Ref 17, 41). Table 1 illustrates the values of the corresponding parameters during CPFEM simulation of NiTiFe SMA under uniaxial compression in the present study, where the elastic constants of NiTiFe SMA are approximately determined according to the literature (Ref 42). The values of \(\tau_{0}\), \(\tau_{s}\) and \(h_{0}\) are obtained by fitting the compression strain-strain curve of NiTiFe SMA. In other words, the preset values of \(\tau_{0}\), \(\tau_{s}\) and \(h_{0}\) are put into crystal plasticity finite element model in order to obtain the simulated strain-strain curve. In the case of given simulation accuracy, when the simulated strain-strain curve agrees well with the experimental one, the corresponding values of \(\tau_{0}\), \(\tau_{s}\) and \(h_{0}\) are finally determined as the ones of parameters for crystal plasticity constitutive model.

Table 1 Values of parameters for crystal plasticity constitutive model
Full size table

It has been reported in the literatures (Ref 43-45) that B2 austenite phase of NiTi SMA possesses 12 slip systems, which include six 〈100〉/{110} slip systems and six 〈100〉/{010} slip systems. Recently, twelve 〈111〉/{110} slip systems were reported to be the second most likely slip systems after 〈100〉 slip systems (Ref 46, 47). In the present work, it can be accepted that NiTiFe SMA possesses the same slip systems as NiTi SMA. Therefore, the crystallographic slip is considered based on the six 〈100〉/{110} slip systems, six 〈100〉/{010} slip systems and twelve 〈111〉/{110} slip systems, and consequently the total number of slip systems is determined as 24.

Polycrystal Representation and Meshing

Initial microstructures of NiTiFe SMA can be characterized by means of EBSD experiment, where morphology, size and orientation of each grain are captured, as shown in Fig. 2. It can be accepted generally that an EBSD map can be viewed as a list of pixels, where each pixel contains information about the location in the form of (x, y) coordinates as well as the crystallographic orientation in the form of three Euler angles at each point (Ref 48). Each grain can be regarded as the aggregation of many pixels according to the function of calcGrains in MTEX toolbox of MATLAB software, where a threshold is imparted to the misorientation between adjacent pixels. In the present study, the threshold of misorientation between grain boundaries is defined as 15°, above which the different colors are assigned to the grains according to mean orientation of EBSD data. The distribution of grain size is given according to equivalent diameter of grain, which is defined as follows.

$$d = 2\sqrt {A/\pi }$$
(10)

where \(d\) is the equivalent diameter of grain, and A is the area of a grain. The mean equivalent diameter of grain is about 9.4 μm. Furthermore, EBSD experiment indicates that NiTiFe SMA is mainly composed of B2 austenite phase and is nearly free of precipitate phase, which is also validated by XRD experiment, as shown in Fig. 3.

Fig. 2
figure 2

Microstructures, grain size and orientation distribution of NiTiFe SMA based on EBSD experiment: (a) initial microstructure; (b) inverse pole figure; (c) grain size distribution

Full size image
Fig. 3
figure 3

XRD pattern of NiTiFe SMA

Full size image

Based on EBSD data, the two-dimensional finite element model of polycrystalline NiTiFe SMA is established according to the mean orientation of grain, where x is parallel to the normal direction (ND) of sample and y is parallel to the rolling direction (RD) of sample, as shown in Fig. 4. The location coordinates of pixels, (x, y), correspond directly to mesh coordinates in ABAQUS software. In other words, a pixel in the grain of EBSD map corresponds to a mesh in the grain of finite element model, where the size of finite element model is the same as the EBSD scan area. The size of each mesh in the finite element is 1.5 μm × 1.5 μm, which is equal to the size of EBSD scan step. As a consequence, the number of elements in the finite element model is 154 × 115. Then, the following algorithm is used to establish the relationship between the identity number of each grain and the label number of each element. First, the labels of all the indexed pixels belonging to a grain are identified and the unindexed pixels (less than 2% of total number of pixels) are assigned to the neighboring grains. Subsequently, the grains containing less than 2 pixels would be assigned to the neighboring grains in order to avoid singularity and reduce the computational cost. Finally, 454 element sets were created based on the labels of the pixels belonging to a grain.

Fig. 4
figure 4

Polycrystalline finite element model of NiTiFe SMA

Full size image

It is well known that the Voronoi tessellations have been traditionally used to represent polycrystalline materials in metallurgy. In general, Voronoi polygons are dependent upon a given set of randomly distributed points, which can be viewed as the centers of Voronoi polygons. It is assumed that\(S \subset {\varvec{R}}^{2}\)is a real domain, and \(E = \{ A_{i} \}\) is a set of N random points, so\(A_{i} \in S\). If \(d(P_{1} ,\;P_{2} )\)is the Euclidean distance between two points, the influence zone of a point \(A_{i}\) is defined as the set of points P(x, y), namely

$$V(A_{i} ) = \{ P(x,y) \in S|d(P,A{}_{i}) < d(P,A_{j} )\;\;\;\;\;\;\;\;\forall j \ne i\}$$
(11)

On the assumption that a homogeneous crystallization process is described by Voronoi tessellations, the distribution of grain morphology and size is completely determined by the initial centers of Voronoi polygons. In the present study, a new simple method is used to control the distributions of the centers of Voronoi polygons, as shown in Fig. 5. Firstly, the plane is divided into many congruent rectangles, the number of which is equal to the number of Voronoi polygons. It can be assumed that the center of rectangle (i, j) is (x, y), and the dimension of the rectangle is 2a × 2b. Consequently, \(\delta {\text{x}} = \alpha \times a\), \(\delta {\text{y}} = \alpha \times b\), where \(\alpha\) is defined as the size control factor. Accordingly, the center of Voronoi polygon is distributed randomly in the rectangle determined by the points (\(x + \delta x\),\(y + \delta y\)) and (\(x - \delta x\),\(y - \delta y\)).

Fig. 5
figure 5

Schematic diagram with respect to the distribution of the centers of Voronoi polygons

Full size image

According to the aforementioned method, the different regularity of Voronoi tessellations with \(\alpha = 0\), \(\alpha = 0.5\), \(\alpha = 1\), \(\alpha = 2\) and completely random tessellation is established in ABAQUS software, where each one contains 450 Voronoi polygons, as shown in Fig. 6. It can be seen from Fig. 6(a), (b), (c) and (d) that the regularity of Voronoi polygons gradually decreases with the increase in the value of α. Figure 6(g) shows the relationship between the standard deviation of equivalent diameter and the size control factor α. It can be seen from Fig. 6(g) that when α ranges from 0 to 2, there is an approximately linear relationship between standard deviation and α. When α ranges from 2 to 4, the standard deviation exhibits a slow increase and finally approaches to a steady state. However, when α is beyond 4, the standard deviation is between 2.8 and 2.9 and is almost equal to that of completely random tessellation. However, the standard deviation of equivalent diameter for EBSD-based model is about 4.83, which is much larger than that of size-controlled Voronoi tessellations. In fact, it is difficult to make the standard deviation of equivalent diameter for size-controlled Voronoi tessellations reach a level of the genuine grains. Therefore, EBSD-based polycrystalline aggregate is able to better reflect the variety of grains and thus represent the real microstructures. As a consequence, EBSD-based polycrystalline aggregate is used as a crystal plastic finite element model in the present work. In addition, according to the symmetry of uniaxial compression, the two-dimensional polycrystalline finite element model is used in order to save the computational cost. Simultaneously, half of polycrystalline finite element model is employed based on the symmetric axis, where the bottom edge of finite element model is restricted in the axial displacement, and the symmetric axis of finite element model is restricted in the radial displacement.

Fig. 6
figure 6

Illustration of the relationship between the regularity of Voronoi tessellations and the size control factor α: (a) α=0; (b) α=0.5; (c) α=1; (d) α=2; (e) completely random tessellation; (f) microstructure based on EBSD data; (g) relationship between the standard deviation of equivalent diameters and the size control factor α, where the dark spots correspond to (a-f)

Full size image

Results and Discussion

Texture Evolution

Figure 7 indicates the equal area pole figures of {100}, {110} and {111} of NiTiFe SMA based on full-constraint Taylor model, CPFEM and EBSD experiment in the case of the compression deformation degree by 50%. It is worth noting that the axisymmetric compression axis is y-axis (TD) rather than z-axis (ND) in ABAQUS software. Therefore, the orientations should be rotated by 90 degrees along x-axis (RD) to unify the coordinate system of specimen. It can be observed from Fig. 7 that the three pole figures exhibit a similar regularity. It is obvious that the texture intensity derived from the Taylor model is highly overestimated compared with the experimental result, which is attributed to the fact that the strain for all the grains should meet the requirement for homogenization assumption in the Taylor model. However, the texture predicted by CPFEM is in good agreement with that obtained by the experimental measure, which is attributed to the fact that the CPFEM is capable of taking into account the intergranular interactions among the neighboring grains and allows for the occurrence of the intragranular orientation gradient within a grain. Therefore, it is important for predicting the texture evolution to consider the heterogeneity caused by orientation-dependent deformation at a local position over the microstructure. It can be generally accepted that the preferential orientations resulting from uniaxial compression are quite different from those produced by simple tension. It is well known that the 〈111〉/{110} slip system plays a dominant role in plastic deformation of BCC metals, whereas plastic deformation of FCC metals are dominated by the 〈110〉/{111} slip system. As a consequence, compression textures for BCC metals are similar to tension textures for FCC metals (Ref 18).

Fig. 7
figure 7

Equal area pole figures of NiTiFe SMA subjected to the compression deformation degree by 50%: (a) full-constraint Taylor model; (b) CPFEM; (c) EBSD measurement

Full size image

In order to clarify the texture evolution of NiTiFe SMA in the case of the compression deformation degree by 50%, the orientation distribution function (ODF) is illustrated in Fig. 8, where the section of \(\varphi_{2} = 45^\circ\)is given. ODF contributes to extracting the overlapped components in the pole figure. It can be found that the main texture of NiTiFe SMA subjected to compression deformation is composed of the γ-fiber texture, where the 〈111〉 axis is parallel to the ND. In the same manner, the γ-fiber texture exhibits a higher intensity in the Taylor model than in the CPFEM and EBSD experiment. Furthermore, compared to the Taylor model, the simulated result based on CPFEM is in better agreement with the experimental one in terms of the intensity of fiber texture. However, it is difficult to precisely capture the specific local position that reinforces the ideal components along the fiber texture.

Fig. 8
figure 8

\(\varphi_{2} = 45^\circ\)section of ODF of NiTiFe SMA subjected to the compression deformation degree by 50%: (a) full-constraint Taylor model; (b) CPFEM; (c) EBSD measurement; (d) ideal orientation

Full size image

According to the aforementioned results, it can be concluded that CPFEM is a powerful candidate for predicting the texture evolution of NiTiFe SMA during compression deformation. As a consequence, the microstructure evolution and the texture evolution of NiTiFe SMA subjected to the various plastic deformation degrees are captured by means of CPFEM, as shown in Fig. 9. It can be found from Fig. 9 that when NiTiFe SMA is subjected to the compression deformation degree by 10%, the texture is mainly characterized by a duplex texture of [111] and [101]. With the progression of plastic deformation, [111] texture becomes stronger and stronger and it becomes a major component finally, which means that the [111] rotates gradually toward the compression direction. The simulation results are in good accordance with the general texture evolution of BCC metals (Ref 18).

Fig. 9
figure 9

Microstructure and texture evolutions based on the various compression deformation degrees: (a) 10%; (b) 30%; (c) 50% (The small black circle in the inverse pole figure represents the mean orientation of a grain)

Full size image

In addition, it can be found from the microstructure evolution in Fig. 9 that the free surface of the compressed specimen exhibits a certain distortion, which results from the texture-induced anisotropy and the orientation-dependent heterogeneity. Furthermore, most of grains are elongated along X direction with the progression of plastic deformation. A scatter plot of aspect ratio against shape factor is shown in Fig. 10 to represent the relationship between change of grain shape and plastic deformation degree. The aspect ratio is defined as the ratio of the length of grain along X direction to the length of grain along Y direction. Shape factor is designated as the ratio of the perimeter of a genuine grain to the perimeter of an assumed round grain, where the area of the assumed round grain is equal to that of the genuine grain. It can be found from Fig. 10 that the aspect ratio and the shape factor increase with the increase of plastic strain. The phenomenon indicates that with the progression of plastic deformation, the grains are gradually elongated to be far from the initial equiaxed ones, where shape factor is greater than 1.

Fig. 10
figure 10

Relationship between shape factor and aspect ratio at the various compression deformation degrees (The circles stand for the relative size of the area of the grains)

Full size image

In order to better understand the influence of the orientation-dependent heterogeneity on the microstructure evolution and the texture evolution, the rotation angle, which is relative to the initial orientation, is calculated with respect to each integration point. The corresponding contour maps are shown in Fig. 11(a), (b), and (c). The rotation angle can be calculated by the misorientation matrix R:

$${\varvec{R}} = {\varvec{g}}_{2}\cdot {\varvec{g}}_{1}^{ - 1}$$
(12)

where g 1 and g 2 are the orientation matrix. The rotation angle \(\Delta \theta\) can be extracted from the misorientation matrix R as follows:

Fig. 11
figure 11

Microstructure evolution and texture evolution in terms of rotation angle maps based on the various compression deformation degrees: (a) 10%; (b) 30%; (c) 50%; (d) statistic distribution of rotation angles

Full size image
$$\Delta \theta = \arccos \{ [{\text{tr}}({\varvec{R}}) - 1]/2\}$$
(13)

The rotation angle can be viewed as an approximate measure of the deformation accumulation amount except for the rigid-body rotation (Ref 17). As can be seen in Fig. 11(a), (b), and (c), the rotation angle within a grain is also inhomogeneous, which indicates that inhomogeneous deformation depends on the initial orientation. The statistic distribution of rotation angle is plotted based on the various compression deformation degrees, as shown in Fig. 11(d). It can be found that the rotation angle basically meets the requirement for Gaussian distribution during compression deformation of NiTiFe SMA.

In order to further understand the variation of orientations, the distribution of rotation angles is captured according to the threshold values of 10° and 20° in the case of the compression deformation degree by 50%, as shown in Fig. 12. It can be found from Fig. 12 that as for the grains whose rotation angles are less than 10°, their initial orientations are nearly close to [111] direction, while as for the grains whose rotation angles are greater than 20°, their initial orientations obviously deviate from [111] direction. The phenomenon indicates that the grains which initially deviate from [111] texture are more liable to rotating toward [111] direction.

Fig. 12
figure 12

Inverse pole figure established based on the different threshold values of rotation angle in the case of the compression deformation degree by 50%: (a) rotation angles less than 10°; (b) rotation angles greater than 20°

Full size image

Intragranular and Intergranular Deformation Heterogeneity

Figure 13 indicates comparison of stress and strain of NiTiFe SMA under uniaxial compression by 50% at a strain rate of 0.001 s−1 at the macroscopic level and in each grain. It can be found from Fig. 13(a) that the macroscopic stress-strain curve obtained by CPFEM is in good agreement with the one obtained by the experiment. The phenomenon indicates that CPFEM plays an important role in predicting the macroscopic stress-strain response of NiTiFe SMA. In addition, it can be found that the average stress-strain response in each grain is different due to the orientation-dependent heterogeneity.

Fig. 13
figure 13

Comparison of stress and strain of NiTiFe SMA under uniaxial compression by 50% at a strain rate of 0.001 s−1 at the macroscopic level and in each grain: (a) macroscopic stress and strain curves based on experiment and simulation; (b) average stress-strain curves in each grain based on simulation

Full size image

Figure 14 indicates the distributions of Von Mises stress and accumulative shear strain on all the slip systems for NiTiFe SMA subjected to uniaxial compression by 50% based on CPFEM. It can be found from Fig. 14 that NiTiFe SMA exhibits an inhomogeneous plastic deformation both among the grains and in the grain interior. Furthermore, CPFEM plays a significant role in predicting intragranular and intergranular deformation heterogeneities during compression deformation of NiTiFe SMA. It can be concluded that the intragranular and intergranular deformation heterogeneities are of great importance in guaranteeing the compatibility between the grains during compression deformation of NiTiFe SMA.

Fig. 14
figure 14

Von Mises stress and accumulative shear strain of NiTiFe SMA subjected to uniaxial compression by 50% based on crystal plastic finite element simulation: (a) mises stress distribution; (b) shear strain distribution

Full size image

It is well known that grain boundaries play a predominant role during plastic deformation of a polycrystalline aggregate. In the case of cold plastic deformation of a polycrystalline aggregate, in particular, some substructures, such as subgrain boundaries, frequently occur due to the interaction between the dislocations. In the present study, though the constitutive model of CPFEM is based on dislocation slip, CPFEM is not capable of capturing the interactions between the dislocations and the grain boundaries and between the dislocations. However, CPFEM is able to give the simulation results with respect to the grain boundaries in the case of the various compression deformation degrees. The centroid coordinates of finite meshes and the Euler angles of integration points can be extracted from the simulation results obtained by CPFEM. The corresponding data are used to generate the EBSD data from external files by using the function of loadEBSD in MTEX toolbox of MATLAB software. As a consequence, the evolution of grain boundaries with the various misorientation angles for NiTiFe SMA subjected to the various compression deformation degrees is captured, as shown in Fig. 15. It can be found from Fig. 15 that when NiTiFe SMA is subjected to the compression deformation degree by 10%, the subgrain boundaries of 5°~15° begin to arise. When NiTiFe SMA is subjected to the compression deformation degree by 30%, the subgrain boundaries of 2°~5° appear. However, in the case of the compression deformation degree by 50%, plenty of subgrain boundaries of 2°~5° and 5°~15° are induced in the large plastic deformation zone of NiTiFe SMA. It can be concluded that during uniaxial compression of polycrystalline NiTiFe SMA, the microstructure evolves into high-energy substructure and consequently the well-defined subgrains are formed. In addition, the grain boundaries and the subgrain boundaries are approximately aligned with the direction in which metal flows (Ref 49).

Fig. 15
figure 15

Evolution of grain boundaries with the various misorientation angles for NiTiFe SMA subjected to the various compression deformation degrees: (a) 10%; (b) 30%; (c) 50%

Full size image

Conclusions

  1. 1.

    CPFEM is a powerful candidate for predicting the texture evolution of NiTiFe SMA subjected to compression deformation. The texture predicted by CPFEM is in good agreement with that obtained by the experimental measure, which is attributed to the fact that the CPFEM is capable of taking into account the intergranular interactions among the neighboring grains and allows for the occurrence of the intragranular orientation gradient within a grain.

  2. 2.

    CPFEM plays an important role in predicting the macroscopic stress-strain response of NiTiFe SMA under uniaxial compression. The macroscopic stress-strain curve obtained by CPFEM is in good agreement with the one obtained by the experiment. In addition, the average stress-strain response in each grain is different due to the orientation-dependent heterogeneity, which indicates that NiTiFe SMA is characterized by the inhomogeneous plastic deformation at the grain scale. The intragranular and intergranular deformation heterogeneities are of great importance in guaranteeing the compatibility between the grains during compression deformation of NiTiFe SMA.

  3. 3.

    The evolution of grain boundaries with the various misorientation angles for NiTiFe SMA subjected to the various compression deformation degrees is captured by means of CPFEM. During uniaxial compression of polycrystalline NiTiFe SMA, the microstructure evolves into high-energy substructure and consequently the well-defined subgrains are formed. In addition, the grain boundaries and the subgrain boundaries are approximately aligned with the direction in which metal flows.