Introduction

Friction stir welding (FSW) is a relatively new solid-state metal-joining process that was invented at The Welding Institute in the United Kingdom (Ref 1). FSW can be used to produce butt, corner, lap, T, spot, fillet, and hem joints, as well as to weld hollow objects, such as tanks and tubes/pipes, stock with different thicknesses, tapered sections, and parts with three-dimensional (3D) contours. This welding process is particularly suited for butt and lap joining of aluminum alloys which are otherwise quite difficult to join using conventional arc/fusion welding processes. FSW has established itself as a preferred joining technique for aluminum components, and its application for joining other difficult-to-weld metals is gradually expanding. Currently, this joining process is being widely used in many industrial sectors such as shipbuilding/marine, aerospace, railway, land transportation, etc.

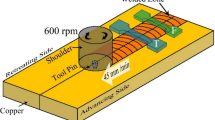
The basic concept behind the FSW process for the case of butt welding is displayed schematically in Fig. 1(a). Essentially, a non-consumable rotating tool, Fig. 1(b), consisting of a pin (usually conically shaped and containing threads, flutes, and flats) and a shoulder (usually containing scrolls or spirals) is forced to move along the contacting surfaces of two rigidly butt-clamped plates (the work-piece). Heat dissipation associated with frictional sliding at the shoulder/work-piece and pin/work-piece interfaces as well as the plastic deformation caused by the rotating and advancing tool causes the work-piece material to soften to a temperature near the respective solidus temperature. This, in turn, enables the tool to stir the surrounding material and cause its extrusion around the tool and its forging in the wake of the tool. Since, the tool is rotating as it traverses along the butted surfaces, the FSW process is essentially asymmetric, i.e., one typically makes a distinction between the so-called advancing side of the weld (the side on which the peripheral velocity of the rotating tool coincides with the transverse velocity of the tool) and the retreating side (the side on which the two velocities are aligned in the opposite directions).

Fig. 1
figure 1

(a) A schematic of the friction stir welding (FSW) process; and (b) a typical design of the FSW tool

Full size image

Relative to the traditional fusion-welding technologies, FSW offers a number of advantages. Since a fairly detailed discussion pertaining to these advantages can be found in recent studies (Ref 2-4), a similar detailed account will not be given here. Instead, it should be noted that most of these advantages arise from the fact that FSW is associated with lower temperatures, does not involve fusion and re-solidification of the weld material, and that no filler metal, flux, or fuel/oxidizer is used.

FSW normally involves complex interactions and competition between various mass and heat transport phenomena, plastic deformation and damage/fracture mechanisms, and microstructure evolution processes (Ref 2-9). Consequently, the material microstructure (and mechanical properties) in the weld region are highly complex and spatially diverse. Metallographic examinations of the Friction stir-welded (FSWed) joints typically reveal the existence of the following four zones, Fig. 2: (a) An unaffected (base-metal) zone which is far enough from the weld so that material microstructure/properties are not altered by the joining process; (b) The heat-affected zone (HAZ) in which material microstructure/properties are effected only by the thermal effects associated with FSW. While this zone is normally found in the case of fusion welds, the nature of the microstructural changes may be different in the FSW case due to generally lower temperatures and a more diffuse heat source; (c) The thermo-mechanically affected zone (TMAZ) which is located closer than the HAZ zone to the butting surfaces. Consequently, both the thermal and the mechanical aspects of the FSW affect the material microstructure/properties in this zone. Typically, the original grains are retained in this zone although they may have undergone severe plastic deformation; and (d) the weld nugget which is the innermost zone of an FSWed joint. As a result of the way the material is transported from the regions ahead of the tool to the wake regions behind the tool, this zone typically contains the so called onion-ring features. The material in this region has been subjected to most severe conditions of plastic deformation and high temperature exposure, and consequently contains a very fine dynamically recrystallized (equiaxed grain microstructure).

Fig. 2
figure 2

A schematic of the four microstructural zones associated with the typical FSW joint

Full size image

Despite the fact that FSW was discovered less than 20 years ago, this joining process has found a wide scale application in many industries. Among the most notable examples in which full advantage of the FSW process was taken to reduce production cost and fabricate durable structures are: (a) FSW is being used in a serial production of aluminum alloy-based ferryboat deck structures in Finland; (b) Al-Mg-Si-based alloy bullet-train cabins are commonly fabricated in Japan using FSW as the primary joining process; (c) Boeing predominantly utilizes FSW in the manufacture of Al-Cu-based rocket launch systems; (d) NASA has almost completely replaced conventional fusion welding processes with FSW for critical joints in the space-shuttle’s external fuel-tanks which are manufactured using Al-Li-based alloy; and (e) General Electric has begun to use FSW in very demanding jet engine applications.

Recent efforts of the U.S. Army have been aimed at becoming more mobile, deployable, and sustainable while maintaining or surpassing the current levels of lethality and survivability. Current battlefield vehicles have reached in excess of 70 tons due to ever increasing lethality of ballistic threats which hinders their ability to be readily transported and sustained. Therefore, a number of research and development programs are under way to engineer light-weight, highly mobile, transportable, and lethal battlefield vehicles with a target weight under 20 tons. To attain these goals, significant advances are needed in the areas of light-weight structural- and armor-materials development (including aluminum-based structural/armor-grade materials).

Historically, aluminum alloy AA5083-H131 has been used in military-vehicle systems such as the M1113 and the M109, in accordance with the MIL-DTL-46027J specification (Ref 5). The main reasons for the selection of this alloy are its lighter weight, ease of joining by various welding techniques, a relatively high level of performance against fragmentation-based threats, and superior corrosion resistance. In recent years, FSW is being increasingly used during construction/fabrication of various military vehicle AA5083 welded structures (e.g., vehicle hulls). In previous studies (Ref 2-4), the effect of FSW process parameters on the blast/ballistic performance/survivability of such structures was discussed. It should be also recognized that in addition to meeting blast/ballistic survivability requirements, such structures should also meet (corrosion-based and fatigue-based) durability requirements. The main objective of this study is to address the issue of the effect of FSW and its process parameters on the fatigue behavior of AA5083-H321. Specifically, the issues regarding the statistical analysis of the high-cycle fatigue results obtained for AA5083-H321 FSW joints as described in Ref 6 are discussed.

One of the main advantages of FSW over the traditional fusion welding techniques is a significantly reduced defect content within the weld. The two most common defects found within the FSW joints are: (a) lack of penetration (caused by an insufficient length of the tool pin), Fig. 3(a); and (b) voids and root defects (also known as kissing bonds), Fig. 3(b). While the former defects can be readily eliminated by properly designing the FSW tool, the true origin for the latter type of defects is not well understood and/hence/they are more challenging to deal with. To make the situation worse, these defects are generally difficult to detect using conventional techniques like radiography and ultrasonics (Ref 7), since they can occur in any orientation. The presence and the concentration of these defects is affected both by the type of the alloys being welded and by the FSW process parameters, while they generally profoundly affect fatigue strength/life of the welded joints (Ref 6). Due to stochastic nature of the void/root-defect generation process (e.g., the material flow underneath the tool-shoulder on the advancing side is often of a chaotic nature and is associated with singularities which may lead to the formation of defects), the resulting fatigue strength/life data typically show a relatively wide distribution and, hence, they must be analyzed using statistical tools. An example of such a statistical analysis of the AA5083-H321 high-cycle fatigue results (Ref 6) is presented in this study.

Fig. 3
figure 3

Two most often observed FSW flaws: (a) incomplete welds; and (b) voids

Full size image

The organization of the article is as follows: A summary of the high-cycle fatigue experimental testing procedure used and the experimental results obtained in Ref 6 for the case AA5083-H321 FSW-joints is presented in section 2.1. A new three step statistical-analysis procedure is introduced in section 2.2. The application of this procedure to the AA5083-H321 FSW-joint high-cycle fatigue data as reported in Ref 6 is carried out in section 3. Specifically, in section 3.1, the optimal type of the probability distribution function is identified. Determination of the most-likely estimates for the selected probability-distribution function is carried out in section 3.2. Statistical significance of the effect of the two controlled variates (the tool translational speed and the fatigue specimen surface condition) is assessed in section 3.3. A brief summary of the study carried out and the conclusions resulting from this study are presented in section 4.

Analyses and Procedures

High-Cycle Fatigue Results from Ref 6

As mentioned earlier, the main objective of this study is to introduce and apply a statistical analysis to the AA5083-H321 high-cycle fatigue results reported in Ref 6. In this section, a brief description is provided regarding the details of the FSW joining process and of the high-cycle fatigue strength/life experimental assessment procedure.

The as-rolled AA5083-H321 plates of dimensions: L × W × H (1000 mm × 500 mm × 8 mm) were used in the experiment described in Ref 6. Two such plates were welded at a time to form a FSWed workpiece from which the fatigue specimens were machined. Chemical and mechanical property characterizations of the base material yielded the following results: 4.20 wt.% Mg, 0.60 wt.% Mn, 0.25 wt.% Si, 0.15 wt.% Fe, 0.09% Cr and 0.09% Zn; yield strength = 264 MPa and Ultimate Tensile Strength = 350 MPa. The H321 temper designation denotes a strain-hardened and stabilized condition of the alloy with the final strength level corresponding to roughly a quarter of that observed in the material before the stabilization heat treatment. Typically, the yield strength of the FSW joint material is circa 160 MPa (i.e., around 40% lower than that in the base metal).

The FSW tool used was made of tool steel, had a 25 mm-diameter shoulder and a 10 mm diameter 7.9 mm length pin. The tool rotational speed was kept constant at a value of 500 rpm while four different (80, 95, 130, and 200 mm/min) tool translational speeds were used. The tool was tilted by 2.5° in the direction of travel, and had a plunge depth of 0.2 mm. Rectangular section, hourglass-shaped fatigue specimens were machined from the FSWed workpieces. Gauge length and width of the fatigue specimens were 40 and 16 mm, respectively, while the gage thickness was kept as close as possible to the original 8 mm plate thickness. Fatigue (cyclic loading) testing was done at a frequency of 112 Hz in the fully reversed uniaxial loading mode with the (algebraically) lowest stress to (algebraically) highest stress ratio = −1.0.

In addition to investigating the effect of tool translational velocity on the fatigue strength/life of the AA5083-H321 FSW joints, the effect of the fatigue-sample surface condition was also studied. Specifically, two types of surface conditions were considered: (a) the so-called as-welded condition in which small burrs at the edges of the weld region were removed while ~0.2-mm-high tool shoulder ledges were left; and (b) the so-called polished condition in which both burrs at the edges and the tool shoulder ledges were removed leaving a fatigue sample with smooth surfaces and free of stress concentrators. This portion of the study enabled separate assessment of the relative contributions of surface and interior defects to the fatigue strength/life of FSWed joints.

A summary of the high-cycle fatigue strength/life results for the as-welded and polished conditions of the specimen surface are displayed in Fig. 4(a) and (b), respectively. In each figure, stress amplitude versus number of cycles to failure results are presented at four different tool translational speeds. A quick examination of the results displayed in these figures shows (a) significant spread in the number of cycles to failure at nominally identical FSW-processing, specimen-surface and fatigue-testing conditions; and (b) a generally larger value of the number of cycles to failure for the case of polished fatigued samples.

Fig. 4
figure 4

Stress amplitude vs. number of cycles to failure results for AA5083-H321 FSW joints at four different tool translational speeds and for two fatigue-specimen surface conditions: (a) as-welded; and (b) polished

Full size image

Statistical Analysis of the FSW-Joint Fatigue Results

In this section, a simple statistics-based analysis is described which would be used to address the issue of the spread in the FSW-joint fatigue results associated with the stochastic nature of the location, orientation, and size of the welding-induced defects. The proposed procedure is depicted, in Fig. 5, using a flow chart type of diagram. As seen, the first step in this procedure is the identification of the appropriate probability distribution function which best accounts for the observed spread in the results. This is typically accomplished using the so-called “chi-square goodness of fit” method (Ref 8). Once the type of the appropriate probability density function is identified, the so-called maximum likelihood estimation (MLE) procedure (Ref 9) is invoked to obtain the optimal estimates for the probability density function parameters and their respective ranges for a given statistical level of confidence. The information obtained at this point is sufficient, at a given level of confidence, to enable the determination of the fatigue life at a prescribed level of the service stress or determination of the maximum allowable surface stress which guarantees the desired fatigue life. Finally, one can investigate the magnitude of the effect of the FSW process parameters and fatigue-sample surface condition, in a statistical sense, on the fatigue strength/life of the FSW joints. This is typically done using the so-called likelihood ratio method (Ref 10). In the remaining subsections of this section, a brief description is provided for the three statistical-analytical tools identified above, i.e., the chi-square goodness of fit method, the MLE method, and the likelihood ratio method.

Fig. 5
figure 5

A flow chart of the proposed three-step procedure for statistical analysis of FSW joint fatigue data

Full size image

Chi-Square Goodness of Fit

As mentioned earlier, the chi-square goodness of fit test (Ref 8), is used to identify the appropriate type of probability distribution function for a given set of data. This method can be applied to any univariate distribution for which the cumulative distribution function can be calculated. Before the method could be applied, the data have to be binned, i.e., grouped into classes. Once this is done, the mean and the standard deviation for the bin data can be calculated and, for a given type of the probability, the values of the cumulative density function evaluated at the variate levels corresponding to the bin edges. Then, for a given bin, a product of the total number of data points and the positive difference in the cumulative distribution function values at the two edges of the bin are used to calculate the expected number of observations in a given bin, E i (i = 1, …, number of bins(N)). The corresponding experimental observations are denoted as O i . To assess the appropriateness of the given distribution, the following null hypothesis is formulated:

H 0

The experimental data follow the assumed distribution.

To test this hypothesis, the following chi-square test statistic is defined:

$$ \upchi^{2} = \sum\limits_{i = 1}^{N} {\left( {O_{i} - E_{i} } \right)^{2} } /E_{i} $$
(1)

The test statistic follows, approximately, a chi-square distribution with (k − c) degrees of freedom, where, k is the number of non-empty bins, and c is the number of parameters in the assumed probability function plus one. The null hypothesis given above is rejected, at the confidence level of (1 − α) when the following condition is satisfied:

$$ \upchi^{2} > \upchi^{2}_{(\upalpha ,k - c)} $$
(2)

where \( \upchi^{2}_{(\upalpha ,k - c)} \), corresponds to the test-statistic evaluated at (k − c) degrees of freedom chi-square cumulative distribution function value of (1 − α). To aid in the understanding of this procedure, the case of a chi-squared distribution function for a three degrees-of-freedom and at a confidence level of (1 − α) = 0.95 is depicted in Fig. 6(a) and (b).

Fig. 6
figure 6

Three degree-of-freedom chi-squared: (a) probability density; and (b) cumulative distribution functions used for testing the hypothesis H0 at a confidence level of (1 − α) = 0.95

Full size image

The aforementioned procedure can be used to determine whether the chosen probability function accounts well for the given set of data. On the other hand, when two or more probabilities are found to be appropriate for a given set of data, the one associated with the lowest value of the test statistic is considered the most appropriate.

Maximum Likelihood Estimation

Maximum likelihood estimation (MLE) is a common statistical method used for fitting a pre-selected type of the probability density function (PDF) to a given set of data, and for providing the estimates for the function parameters. The basic idea behind the MLE method is that, for a given type of PDF, it computes the values of function parameters which maximize the likelihood that the given set of data belongs to the population PDF associated with these parameters. Toward that end, a likelihood function is defined in terms of the preselected-PDF with yet-undetermined parameters. The function is next maximized with respect to the unknown parameters resulting in their “most likely” estimates.

In this study, the likelihood function, L, is defined as

$$ \ln [L] = \mathop \sum \limits_{i = 1}^{R} \ln \left[ {f\left( {N_{i} ,p_{1} ,p_{2} , \ldots } \right)} \right] + \mathop \sum \limits_{j = 1}^{U} \ln \left[ {1 - F\left( {S_{j} ,p_{1} ,p_{2} , \ldots } \right)} \right] $$
(3)

where f and F are the failure probability density function (PDF) and cumulative distribution function (CDF), respectively, R is the number of failed specimens, U is the number of survived specimens, N i is the number of cycles at failure for the ith specimen, S j is the number of cycles at which the un-failed jth specimen test was suspended, and p 1, p 2, … are the unknown parameters in f and F.

The MLE method described above yields the most likely values of the parameters for the assumed probability density function. However, these parameters themselves are statistical variables and in the limit of a large sample size they are distributed in accordance with the normal distribution function. Consequently, in-order to assess the error associated with the computed value of the likelihood function, one needs to know the confidence limits for each of the parameters (i.e. the range for each parameter associated with a given level of statistical confidence). To determine these confidence limits, one can employ the so-called Fisher Matrix method (Ref 11). In the remainder of this section, some of the details of the Fisher Matrix method for the case of a two-parameter weibull distribution function is provided. The two parameters are commonly referred to as the scale factor θ and shape factor. Following the procedure outlined in Ref 11, the confidence limits at a confidence level of (1 − α) for these two parameters can be calculated as follows:

$$ \upbeta_{\text{U}} = \hat{\upbeta }e^{{{\frac{{K_{\upalpha } \sqrt {{\text{Var}}(\hat{\upbeta })} }}{{\hat{\upbeta }}}}}} $$
(4)
$$ \upbeta_{\text{L}} = {\frac{{\hat{\upbeta }}}{{e^{{{\frac{{K_{\upalpha } \sqrt {{\text{Var}}(\hat{\upbeta })} }}{{\hat{\upbeta }}}}}} }}} $$
(5)
$$ \upeta_{\text{U}} = \hat{\upeta }e^{{{\frac{{K_{\upalpha } \sqrt {{\text{Var}}(\hat{\upeta })} }}{{\hat{\upeta }}}}}} $$
(6)
$$ \upeta_{\text{L}} = {\frac{{\hat{\upeta }}}{{e^{{{\frac{{K_{\upalpha } \sqrt {{\text{Var}}(\hat{\upeta })} }}{{\hat{\upeta }}}}}} }}} $$
(7)

where K α is implicitly defined by

$$ \upalpha = {\frac{1}{{\sqrt {2\uppi } }}}\int\limits_{{K_{\upalpha } }}^{\infty } {e^{{ - {\frac{{t^{2} }}{2}}}} } dt = 1 - \upphi (K_{\upalpha } ) $$
(8)

To determine variances and covariances of the two parameters, the value of the local inverse fisher matrix is calculated as follows:

$$ \left( {\begin{array}{*{20}c} {{\text{Var}}(\hat{\upbeta })} \hfill & {{\text{Cov}}(\hat{\upbeta },\hat{\upeta })} \hfill \\ {{\text{Cov}}(\hat{\upbeta },\hat{\upeta })} \hfill & {{\text{Var}}(\hat{\upeta })} \hfill \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - \partial^{2} { \ln }(L)/\partial \upbeta^{2} } \hfill & { - \partial^{2} { \ln }(L)/\partial \upbeta \partial \upeta } \hfill \\ { - \partial^{2} { \ln }(L)/\partial \upbeta \partial \upeta } \hfill & { - \partial^{2} { \ln }(L)/\partial \upeta^{2} } \hfill \\ \end{array} } \right)^{ - 1} \quad \upbeta = \hat{\upbeta },\;\upeta = \hat{\upeta } $$
(9)

To compute the second-order partial derivatives appearing in Eq 9, the chain rule has to be applied (e.g., \( - \partial^{2} { \ln }(L)/\partial \upbeta^{2} = - \partial^{2} { \ln }(L)/\partial f^{2} *\partial f^{2} /\partial \upbeta^{2} \)), since, the two parameters are functionally related to f, while, f is functionally related to L. Mathematical expressions for the weibull probability density, f, and cumulative distribution functions, F, are given later in this document.

Likelihood Ratio Method

When two or more data sets are each analyzed using the MLE method and the corresponding parameter-estimate and likelihood-function values computed, the likelihood ratio method can be used to determine whether the data are associated with the same population. In this study, this method is employed to determine if the variations in the FSW process parameters, and the fatigue specimen surface conditions impart a statistically significant effect to the fatigue strength/life of the FSW joints. Toward that end, the null hypothesis is formulated as

H 0

The fatigue strength/life data obtained under different combinations of the FSW process parameters and fatigue-specimen surface conditions are all associated with the same population.

In this case, the test statistic is defined as

$$ T = 2\left[ {\mathop \sum \limits_{i = 1}^{K} \left( {{ \ln }(L_{i} ) - { \ln }(L_{\text{P}} )} \right)} \right] $$
(10)

where K is the total number of different data sets, L i is the maximum likelihood for the ith sample and L P is the maximum likelihood for the pooled data. The data pool is obtained by combining all K data sets into a single data set and by applying the MLE method to it. Since the test statistic is again assumed to follow a chi-square distribution function, the procedure analogous to that employed in the chi-square goodness of fit method is utilized. In other words, if the computed test statistic is larger than its counter part associated with the value of chi-square cumulative distribution function (with the number of degrees of freedom equal to the number of parameters in the PDF) of (1 − α), then the null hypothesis is rejected at the confidence level of (1 − α).

Results and Discussion

In this section, the results of the statistical analysis of the fatigue strength/life data as reported in Ref 6 are presented and discussed. The section is organized in such a way that it fully complies with the three-step procedure depicted in Fig. 5.

Identification of the Appropriate Probability Distribution Function

In accordance with the three-step procedure depicted in Fig. 5, the first task is to employ the chi-square goodness of fit method in-order to identify the appropriate type of the probability distribution function which best represents the statistical variation in the given data set. Unfortunately, the chi-square goodness of fit method requires a relatively large data set which was not available in this study. To overcome this problem, it was assumed that the same type of probability distribution function identified as appropriate in other alloy systems will also be appropriate in the case of AA5083-H321. Specifically, in Ref 12, it was demonstrated that a two parameter weibull distribution function is the appropriate choice for the case of the fatigue strength/life data for many metallic systems. Consequently, this type of distribution function was adopted in this study.

An examination of the results displayed in Fig. 4(a) and (b) revealed that at a given stress-amplitude and for a given combination of the tool translational speed and the fatigue-specimen surface condition, the data set is way too small to carry-out any meaningful statistical analysis. To overcome this problem, and in accordance with the suggestions presented in Ref 12, the natural logarithm of the scaling parameter, ln(θ), in the weibull distribution function is assumed to be a linear function of the stress-amplitude, σ, as

$$ \ln (\uptheta ) = C_{1} + C_{2} \upsigma $$
(11)

while, the shape parameter, β, is defined as

$$ \upbeta = e^{{D_{1} }} $$
(12)

where C 1, C 2 , and D 1 are the unknown coefficients/parameters. This procedure increased the number of parameters in the weibull distribution to three but enabled the data associated with different stress amplitudes, at the same combination of the tool translational speed and the fatigue specimen surface condition, to be combined into a single data set. This, in-turn, enabled us to provide a more meaningful statistical analysis of the fatigue strength/life data.

The weibull probability density and the cumulative distribution functions in-terms of the two original parameters θ and β are defined, respectively, as

$$ f(N) = {\frac{\upbeta }{\uptheta }}\left( {{\frac{N}{\uptheta }}} \right)^{\upbeta - 1} e^{{ - \left( {{\frac{N}{\uptheta }}} \right)^{\upbeta } }} $$
(13)

and

$$ F(N) = 1 - e^{{ - \left( {{\frac{N}{\uptheta }}} \right)^{\upbeta } }} $$
(14)

where the variate N in this case denotes the number of cycles to failure.

An example of the effect of the values of the scale and shape parameters on the weibull probability density and cumulative distribution functions is displayed in Fig. 7(a) and (b). It is seen, that at a constant value of the shape parameter, an increase in the scale parameter value stretches the PDF curve in the horizontal direction. This will also cause a reduction in the peak value of the PDF, since the area under the PDF curve is constant and equal to one. As far as the effect of the shape parameter is concerned, it is seen that it could be quite large, markedly changing the shape of the PDF curve.

Fig. 7
figure 7

The effect of the scale and shape parameters on the weibull: (a) probability density; and (b) cumulative distribution functions

Full size image

Estimation of the Weibull Distribution Parameters and their Confidence Limits

In the previous section, it was established that a two-parameter weibull distribution function with a stress-dependent scale parameter is the appropriate choice for the statistical analysis of the fatigue strength/life data considered. In this section, the MLE method is employed to determine the values of these parameters and their confidence limits. As discussed in the previous section, stress dependency of the scale parameter makes the weibull distribution effectively a three-parameter function.

The results of the MLE analyses for the four tool translational speeds (80, 95, 130, and 200 mm/min) and the as-welded surface condition for the fatigue specimens are summarized in Table 1. The corresponding MLE results for the case of the polished surface condition for the fatigue specimens are summarized in Table 2. These results are used in the remainder of this section to show the relationship between the fatigue strength and fatigue life at a given confidence level. In addition, these results will be used in the next section to assess the magnitude of the effect of the tool translational speed and the fatigue-specimen surface condition on the fatigue strength/life of the FSW joints.

Table 1 The results of the maximum likelihood estimation (MLE) analyses for the fatigue strength/life data of AA5083-H321 FSWed joints and for an as-welded surface condition of the fatigue samples
Full size table
Table 2 The results of the maximum likelihood estimation (MLE) analyses for the fatigue strength/life data of AA5083-H321 FSWed joints and a polished surface condition of the fatigue samples
Full size table

An example of the resulting stress amplitude and the number of cycles to failure-dependent probability density function for the case of the tool translational speed of 80 mm/min and as-welded surface condition of the fatigue sample is depicted in Fig. 8. The results displayed in this figure clearly show that, as expected, the peak in the probability density curve moves toward a lower number of cycles to failure as stress amplitude is increased. At the same time, the distribution variance is reduced, while the peak value is increased. The practical significance of these changes in the probability density function is discussed below.

Fig. 8
figure 8

Stress amplitude and number of cycles to failure-dependent probability density function for the case of the tool translational speed of 80 mm/min and as-welded surface condition of the fatigue sample

Full size image

The functional relationship between the fatigue strength (as represented by the stress amplitude) and the fatigue life (as represented by the number of cycles to failure) at a given confidence level is demonstrated using a contour plot as shown in Fig. 9. For the case of a 80 mm/min tool translational speed and the as-welded surface condition of the fatigue specimen, the confidence levels indicated in this figure are computed as (1 − F), where F is the corresponding weibull cumulative distribution function. The results displayed in Fig. 9 show that (a) at a given level of confidence, higher fatigue strength is associated with a lower level of fatigue life; and (b) at a constant fatigue-strength level, a longer fatigue life can be obtained at the expense of a reduction in the statistical confidence. Alternatively, at a given fatigue-life level, higher fatigue strengths can be expected only if the level of statistical confidence is reduced.

Fig. 9
figure 9

Trade-off between the fatigue strength (as represented by the stress amplitude) and the fatigue life (as represented by the number of cycles to failure) at three different levels of the statistical confidence for the case of tool translational speed of 80 mm/min and as-welded surface condition of the fatigue sample

Full size image

Statistical Significance of the Effects of FSW Process and Specimen Surface Condition

In this section, the results displayed in Table 1 and 2 are combined with additional pooled samples’ MLE results and used within the Likelihood Ratio method to determine the statistical significance of the FSW tool translational speed and the fatigue-specimen surface condition on the fatigue strength/life of the FSW joints. Specifically, the following two questions were addressed: (a) Do the variations in the tool translational speed in a 80-200 mm/min range have a statistically significant effect on the materials fatigue strength/life when the surface condition of the fatigue specimen is kept constant? and (b) Does the variation of the fatigue specimen surface condition at a constant tool translational speed have a statistically significant effect on the materials fatigue strength/life?

The Effect of Tool Translational Speed

The null-hypothesis in this case is defined as:

H 0

The variation of tool translational speed in an 80-200 mm/min range does not have a statistically significant effect on the FSW-joint fatigue strength/life. In other words, at the same surface condition of the fatigue specimens, the data sets associated with different values of the tool translational speed belong to the same population.

To test this hypothesis, the following test statistic is defined

$$ T = 2\left[ {\mathop \sum \limits_{i = 1}^{K} \left( {\ln (L_{i} ) - \ln (L_{\text{Pool}} )} \right)} \right] $$
(15)

where the number of data sets, K(=4), is equal to the number of tool-translational velocities at the same fatigue specimen surface condition. The maximum likelihood function for the pooled data set is obtained by combining all the data sets at the same fatigue-specimen surface condition into a single data set and by performing the MLE analysis on it.

The results of the aforementioned procedure are summarized in Table 3. It is seen that the T-statistic values for the as-welded and the polished surface conditions are 20.72 and 24.23, respectively. To determine if the null hypothesis defined earlier in this section should be rejected, these T-statistic values should be compared with the chi-square value associated with the given number of degrees of freedom and a statistical confidence level. In this case, a chi-square distribution function associated with the number of degrees of freedom equal to the number of weibull distribution function parameters (=3) is used. For this chi-square distribution function, the critical chi-square value associated with a 0.95 confidence level is computed as, \( \upchi_{(0.05,3)}^{2} \)(=7.81). When employing the procedure described in section 2.2, it is found that the null hypothesis should be rejected for both surface conditions of the fatigue specimen. This finding is simply based on the fact that both T values mentioned earlier in this section are greater than 7.81. To summarize, the results obtained in this section simply suggest that a variation of the tool translational speed in a 80-200 mm/min range gives rise to the changes in the weld microstructure, defect content, and properties, which are reflected in first-order changes of the FSW joint fatigue strength/life.

Table 3 The results of the likelihood ratio analyses of the effect of the tool translational speed on the fatigue strength/life of AA5083-H321 FSWed joints for the as-welded and polished surface conditions
Full size table

The Effect of the Fatigue Specimen Surface Condition

The null-hypothesis in this case is defined as

H 0

The variation of the fatigue specimen surface condition at a constant tool translational speed does not have a statistically significant effect on the FSW-joint fatigue strength/life. In other words, at the same tool translational speed, the data sets associated with the two fatigue specimen surface conditions belong to the same population.

To test this hypothesis, a procedure analogous to the one presented in the previous section is employed. The test statistic used in this case is also defined by Eq 15, but the number of data sets K is equal to two. That is, the pooled data set in this case is obtained by combining two data sets associated with the same value of the tool translational speed but having different fatigue specimen surface conditions. As a consequence, the procedure yielded four T values, one for each of the four tool translational speeds.

The results of the aforementioned procedure are summarized in Table 4. It is seen that the T-statistic values associated with the 80, 95, 130, and 200 mm/min tool translational speeds, are 3.67, 7.76, 4.33, and 6.76, respectively. Since all the four T-statistic values are smaller then the critical chi-square value, \( \upchi_{(0.05,3)}^{2} \)(=7.81), at a confidence level of 0.95, the null hypothesis defined earlier in this section cannot be rejected. To summarize, the results obtained in this section simply suggest that the surface condition of the fatigue specimen may not have a first-order effect on the FSW-joint fatigue strength/life in a range of weld-material microstructure, defect content, and properties brought about by a variation in the tool translational speeds between 80 and 200 mm/min. In other words, crack initiation occurring predominantly on the specimen surface may not have a dominant effect on the overall FSW-joint fatigue strength/life.

It should be recalled that all the fatigue data used in this study were obtained under uniaxial loading conditions under which stress distribution across the specimen cross-sectional area is uniform. Fatigue testing is often also carried out under cyclic bending/torsional loading conditions. In this case, the highest stresses are located in the surface regions of the tensile specimen and, hence, the role of surface condition can be expected to be more significant.

Table 4 The results of the likelihood ratio analyses of the effect of the fatigue-specimen surface condition on the fatigue strength/life of AA5083-H321 FSWed joints for four tool translational speeds
Full size table

Summary and Conclusions

Based on the study reported and discussed in this article, the following main summary remarks and conclusions can be made:

  1. 1.

    Owing to intrinsic variability and stochastic nature of the workpiece material microstructure/properties, the use of statistical methods and tools in the analysis of friction stir welding (FSW) joints is highly critical. This is particularly the case when one deals with fatigue strength and life properties of these joints since these properties are highly affected by the material microstructure and defect content as well as by the surface condition of the welds.

  2. 2.

    A three-step FSW-joint fatigue-strength/life statistical-analysis procedure is proposed in this study. Within this procedure, the type of the most appropriate probability distribution function is first identified. Then, the parameters of the selected probability distribution function are computed along with their confidence limits. Finally, the statistical significance of the effect of the variates (the tool translational speed and the fatigue-specimen surface condition) is assessed.

  3. 3.

    This procedure showed that, within their respective ranges of variation, while the tool translational speed has a first-order effect on the FSW-joint fatigue strength/life, the effect of the fatigue specimen surface condition is less pronounced.