Thermodynamic Analysis of TiN Precipitation in SWRH92A High Carbon Tire Cord Steel Under the Influence of Solute Micro-segregations During Solidification

Abstract

The precipitation of TiN inclusion during the solidification of SWRH92A high carbon tire cord steel has been thermodynamically calculated. The influence of solute micro-segregations calculated by Ohnaka and Clyne–Kurz models, respectively, on the thermodynamic parameters is considered. The TiN precipitation module is coupled with the Ti and N micro-segregations when the condition of TiN precipitation is satisfied. Furthermore, the TiN growth is predicted based on the thermodynamic calculation results. The results first show that the solute elements of molten steel segregate to different extents during solidification. The carbon concentration increases most significantly by about 1.8 wt pct due to its highest original content. By coupling TiN precipitation module with solute micro-segregation module, the segregated ratios of Ti and N decrease after the TiN inclusion starts precipitating. With cooling rate increasing from 0.17 to 1.67 K/s, TiN precipitation starts earlier, but the TiN particle size decreases from about 10 to about 3 μm. The TiN inclusion sizes calculated in the Ohnaka and Clyne–Kurz model cases are close and well validated by the metallographic images of TiN inclusions and the statistical data of TiN particle size distribution in high carbon tire cord steels. This agreement encourages the proposed calculation method and provides guidance for the future thermodynamic studies of nonmetallic inclusions of steel.

Introduction

The non-oxide inclusions of steel products, such as nitride and sulfide inclusions, normally precipitate in the liquid–solid mushy zone during the solidification process due to the micro-segregations of solute elements. With the enrichment of these elements in the inter-dendrite liquid pool, the actual activity products of some non-oxide inclusions tend to be larger than their equilibrium activity products as the temperature decreases to certain values. As a result, the corresponding inclusions would begin to precipitate and then grow up. Therefore, the non-oxide inclusions normally form under a non-isothermal, concentration-varying, and finite “time and space” condition. Once these inclusions precipitate in the steel products, they cannot be effectively removed.

Non-oxide inclusions are generally harmful to the quality of steel products. TiN, a typical nitride inclusion, is non-deformable and has extremely high strength.[1,2] The formation of TiN in tire cord steel, especially in hypereutectoid high carbon tire cord steel, would significantly increase the chances of filament break and delamination during the wire drawing process and deteriorate the fatigue properties of the final products. The specific hazards of TiN for tire cord steel have been illustrated in many studies.[3,4,5,6] Even though a series of strict steelmaking and refining process measures have been applied so far to decrease the concentrations of Ti and N, micrometer-scale TiN inclusions can be still observed in the tire cord steel samples.[7] With the tire cord steel strength improving through increasing carbon content, e.g., from 0.7 to 0.9 wt pct, the hazards of TiN inclusion for the material properties of steel products would become more serious.[8,9] Therefore, how to control the precipitation of TiN inclusion has become an urgent issue in the steelmaking industry.

To look inside the mechanisms of TiN precipitation and growth behavior during solidification, a series of thermodynamic and kinetic studies has been conducted in former studies.[10,11,12,13,14] In these studies, various kinds of solute micro-segregation models (e.g., Scheil model, Lever-rule model and Ohnaka model, etc.) were used to quantify the enrichment of Ti and N during solidification. Then by calculating the actual activity product of TiN and the equilibrium activity product which is a function of the temperature at solidifying front, the solidification fraction at which TiN starts precipitating was thermodynamically determined. However, in these studies, the micro-segregations of other solute elements, such as carbon, phosphorus, and sulfur, were rarely taken into account. In fact, during the solidification of molten steel, the concentration of each solute element keeps varying in the inter-dendrite space due to micro-segregation. The variations in the solute concentrations would affect the thermodynamic calculation of TiN precipitation via affecting the liquidus and solidus temperatures of steel, the activity coefficients of Ti and N, and other thermodynamic parameters. Within each solidification fraction step, these variations would definitely affect the solute micro-segregations in its next step. Therefore, this iterative influence on the thermodynamic calculation of TiN precipitation would be non-negligible.

In this paper, the thermodynamic calculation of TiN precipitation in SWRH92A super-strength high carbon tire cord steel is conducted, especially considering the micro-segregations of carbon and other solute elements during the solidification of molten steel. Furthermore, the TiN precipitation calculation is coupled with the calculations of the Ti and N micro-segregations at the late stage of solidification to mimic the actual precipitation of TiN. In the end, the radius of the precipitated TiN inclusion is calculated based on the thermodynamic calculation results. The TiN particle size is compared with the values measured in the metallographic images published in previous studies to prove the calculation reasonability.

Thermodynamic Theory of TiN Precipitation

Basic Thermodynamic Condition of TiN Precipitation

The chemical reaction of TiN formation in molten steel and the corresponding standard Gibbs free energy change are expressed as follows[15]:

$$ \left[ {\text{Ti}} \right]\,{ + }\, \left[ {\text{N}} \right] \,{ = }\,{\text{TiN}}_{{ ( {\text{s)}}}} \quad \Delta G^{\theta } \, = \, - \,RT \cdot \ln K_{\text{TiN}} \, = \, - \,291,000\, + \,107.91T \left( {{\text{J}}\,{\text{mol}}^{ - 1} } \right) $$

(1)

where K_TiN denotes the reaction equilibrium constant; R is the ideal gas constant with value of 8.314 J/(mol K); T is the temperature of molten steel, K. During the precipitation of TiN inclusion, the actual change of Gibbs free energy can be calculated as follows:

$$ \Delta G = \Delta G^{\theta } + RT \ln \frac{{a_{\text{TiN}} }}{{a_{{\left[ {\text{Ti}} \right]}} \cdot a_{{\left[ {\text{N}} \right]}} }} = \Delta G^{\theta } + RT \ln \frac{1}{{f_{\text{Ti}} \cdot \omega_{{\left[ {\text{Ti}} \right]}} \cdot f_{N} \cdot \omega_{{\left[ {\text{N}} \right]}} }} $$

(2)

where a_TiN, a_[Ti], and a_[N] denote the activities of TiN, Ti, and N in molten steel, respectively. For pure TiN inclusion, a_TiN= 1. ω_[Ti] and ω_[Ti] denote the mass fractions of Ti and N in molten steel, respectively; f_[Ti] and f_[N] denote the activity coefficients of Ti and N, respectively. The values of f_[Ti] and f_[N] can be calculated by Eqs. [3] and [4][16]:

$$ \lg f_{{\left[ {\text{Ti}} \right]}} = \lg f _{{\left[ {\text{Ti}} \right]}}^{1873K} \cdot \left( {\frac{2557}{T} - 0.365} \right) $$

(3)

$$ \lg f_{{\left[ {\text{N}} \right]}} = \lg f _{{\left[ {\text{N}} \right]}}^{1873K} \cdot \left( {\frac{3280}{T} - 0.75} \right) $$

(4)

where $f _{{ [ {\text{Ti]}}}}^{{ 1 8 7 3 {\text{K}}}}$ and $f _{{ [ {\text{Ti]}}}}^{{ 1 8 7 3 {\text{K}}}}$ are the activity coefficients of Ti and N at 1873 K, which can be calculated by Eqs. [5] and [6]:

$$ \lg f _{{\left[ {\text{Ti}} \right]}}^{{1873\,{\text{K}}}} = \sum {e_{\text{Ti}}^{i} \cdot \omega_{[i]} } $$

(5)

$$ \lg f _{{\left[ {\text{N}} \right]}}^{{1873\,{\text{K}}}} = \sum {e_{\text{N}}^{i} \cdot \omega_{[i]} } $$

(6)

where $e_{\text{Ti}}^{i}$ and $e_{N}^{i}$ are the interaction coefficients of solute element i for Ti and N at 1873 K, respectively. For the studied SWRH92A tire cord steel, its main chemical composition is shown in Table I. The specific values of first-order interaction coefficients of the main solute elements in the molten steel for Ti and N at 1873 K are listed in Table II.[16,17] Since the mass fraction of Fe in molten steel is more than 90 wt pct, the impact of second-order interaction coefficients can be ignored.

Table I Chemical Composition of Studied SWRH92A Tire Cord Steel, Wt Pct

Table II First-Order Interaction Coefficients $e_{j}^{i}$ of Solute Elements in Molten Steel at 1873 K.[16,17]

By combining Eqs. [1] through [6], it can be seen that with the temperature of molten steel decreasing during the solidification process, the actual Gibbs free energy change ΔG varies as well. When $\Delta G \le 0$, the precipitation of TiN is thermodynamically possible. Based on the combination of Eqs. [1] and [2], the thermodynamic condition of TiN precipitation is expressed as follows:

$$ K_{\text{TiN}} \ge \frac{1}{{f_{\text{Ti}} \cdot \omega_{{ [ {\text{Ti] }}}} \cdot f_{\text{N}} \cdot \omega_{{ [ {\text{N]}}}} }} $$

(7)

By introducing the activity product of TiN, Q_TiN, and defining $K^{\prime}_{\text{TiN}}$ as the reciprocal of $K_{\text{TiN}}$, Eq. [7] can be reformulated as follows:

$$ K^{\prime}_{\text{TiN }} \le Q_{\text{TiN}} = f_{\text{Ti}} \cdot \omega_{{ [ {\text{Ti]}}}} \cdot f_{\text{N}} \cdot \omega_{{ [ {\text{N]}}}} $$

(8)

The equilibrium activity product $K^{\prime}_{\text{TiN }}$ is a function of the temperature at the solid–liquid mushy zone in a dendrite cell, T_s−l. Q_TiN is the product of the concentrations and activity coefficients of Ti and N. Due to the micro-segregations of solute elements, the concentrations of solute elements are not constants as the original values shown in Table I, but variants during solidification. Therefore, the key points of solving Eq. [8] are the accurate determinations of T_s−l and the real-time solute concentrations during solidification.

Calculation of T _s−l During Solidification of Molten Steel

Based on the previous thermodynamic studies, T_s−l is a function of liquidus temperature, T_l, solidus temperature, T_s, and solidification fraction, g. The specific relationship is expressed as Eq. [9][18]:

$$ T_{s - l} = T_{m} - \frac{{T_{m} - T_{l} }}{{1 - g \cdot \frac{{T_{l} - T_{s} }}{{T_{m} - T_{s} }}}} $$

(9)

where T_m is the melting point of pure iron (1811 K). The values of T_l and T_s are usually estimated based on the following empirical expressions:

$$ T_{l} = T_{m} - \sum {\Delta t_{l} \cdot \omega_{[i]} } $$

(10)

$$ T_{s} = T_{m} - \sum {\Delta t_{s} \cdot \omega_{[i]} } $$

(11)

where Δt_l and Δt_s denote the reduced temperature values for solute element i of 1.0 wt pct. The detailed formation is listed in Table III.[16]

Table III Values of Δt_l and Δt_s for Solute Elements in Molten Steel, K[16]

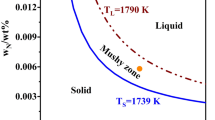
Based on Eqs. [10] and [11] and Table III, it can be seen that the concentrations of solute elements significantly affect the values of T_l and T_s of molten steel and thus further affect T_s−l during solidification. The studied SWRH92A high carbon tire cord steel has a relatively high carbon content (> 0.9 wt pct) and, therefore, the effect of carbon enrichment due to micro-segregation in the inter-dendrite space on T_l and T_s is paid particular attention. Figure 1 shows an example comparison of T_l and T_s of SWRH92A steel between the calculation cases considering and not considering carbon enrichment. In the carbon segregation case (Case 1), Lever-rule model is used for calculating the carbon micro-segregation ratio. The comparison results indicate that because of carbon enrichment in Case 1, there are obvious decreasing trends in T_l and especially T_s with increasing solidification fraction, which causes a more significant drop of T_s–l compared with the trend of T_s–l in Case 2. The decreased T_s−l at a certain solidification fraction would undoubtedly affect the precipitation equilibrium of TiN and thus shift the precipitation point along the solidification fraction axis. Furthermore, the decrease in T_s–l also affects the calculations of other thermodynamic parameters, e.g., the diffusion coefficients and activity coefficients of solute elements. Since the values of T_l and T_s during solidification are closely related to the real-time concentrations of solute elements, as shown in Eqs. [10] and [11], the accurate determination of the segregated solute concentrations in the dendrite cell zone becomes the most important part in the thermodynamic calculation.[19]

Fig. 1

Comparison of T_l, T_s, and T_s–l between the calculation cases considering (Case 1) and not considering (Case 2) carbon micro-segregation during solidification

Micro-segregation Models for Solute Elements

During the actual solidification of molten steel, the redistribution of solute atoms takes place because of the solubility difference between the solid and liquid phases. As a result, the micro-segregation of solute element occurs between the dendrite arms. The enrichment of solute element occurring in the inter-dendrite liquid pools can be quantified by the segregation ratio which is defined as the ratio of the segregated solute concentration in liquid phase to its original value. To date, there have been several models proposed for calculating the segregation ratio of solute elements. In these models, solute elements are assumed to diffuse completely in liquid phase. While, regarding the solute diffusion in solid phase, the model assumptions are categorized into three types, i.e., (I) complete diffusion; (II) no diffusion; and (III) partial diffusion. For each Category III model, the method of calculating the partial diffusion in solid phase differs. A summary of the micro-segregation models for solute elements during solidification is shown in Table IV.

Table IV Summary of Micro-segregation Models for Solute Elements During Solidification

In some former studies,[8,25,26,27] the combination of Lever-rule and Scheil models (generally called LRSM) is used. In LRSM, the solute elements are applied to either Lever-rule model or Scheil model according to their diffusion coefficients in solid phase, $D_{i}^{\text{s}}$. For example, $D_{\text{Ti}}^{\text{s}}$ is normally much lower than $D_{\text{N}}^{\text{s}}$ over the solidification process. So the segregated concentration of Ti is calculated using Scheil model and that of N using Lever-rule model. LRSM provides a convenient way of choosing segregation models for solute elements, but this combination of extreme models would inevitably overestimate or underestimate the actual segregated concentrations of the studied elements. This is because in the actual solidification process, the diffusion of one solute element in solid phase can be neither absolutely complete nor negligible. Some solute elements may be neither suitable for Scheil model nor Lever-rule model due to their intermediate values of $D_{i}^{\text{s}}$, and thus the usage of LRSM may lead to a significant deviation from the real segregated solute concentration.

Compared to Category I and II models, Category III models considering partial element diffusion in solid phase are relatively moderate and flexible. The advantage of Category III models is their flexibility and wide applicability for the inclusion precipitation calculations. The main features of three typical Category III models are simply discussed as below. Brody–Fleming model is proposed based on the analysis of Scheil model and first takes the finite diffusion in solid phase into account by introducing back diffusion coefficient ($\alpha$ in Table I). When $\alpha$ equals to 0 and 0.5 (i.e., ϕ is equal to 0 and 1), this model would become the Scheil model and the Lever-rule model, respectively. However, for some interstitial solutes with high $D_{i}^{\text{s}}$, the values of $\alpha$ may be higher than 0.5 and this would make the calculated segregated concentration unreasonable. This limitation is overcome by the Clyne–Kurz model where ϕ is reformulated based on an approximate analytical treatment of the back diffusion. With this treatment, when $\alpha$ equals to 0 and infinite, the model approaches to the Scheil model and the Lever-rule model, respectively. Ohnaka model analyses the solute redistribution during solidification by a profile method which approximately considers the two-dimensional diffusion in solid phase. In this model, the columnar and plate dendrites are, respectively, considered and hence the two ϕ expressions are, respectively, provided in Table I. Note that in this study, the dendrites are assumed as columnar, so ϕ₂ is used in the following calculations by Ohnaka model. Although all these three models assume incomplete solute back diffusion in solid phase, the different expressions of ϕ would theoretically result in different segregated solute concentrations. Therefore, the selection of appropriate segregation model for each solute element is worth being discussed.

Discussion of Applicability of Category III MODELS for Solute Elements

For this thermodynamic calculation of TiN precipitation in SWRH92A tire cord steel, eight main solute elements are considered, which are carbon, silicon, manganese, phosphorous, sulfur, titanium, nitrogen, and oxygen. The expression of $D_{i}^{\text{s}}$ as a function of T_s-l, together with the solid/liquid equilibrium partition coefficient k_i, of each studied element is shown in Table V.[28,29,30] Herein, the solid phase of steel refers to γ-Fe because the original carbon content of the studied steel is 0.92 wt pct, and based on the iron-carbon equilibrium diagram, only γ-Fe will be formed during the whole solidification process. The back diffusion coefficients of these solute elements during solidification are first compared in Figure 2 under the condition that the effect of solute micro-segregation on the liquidus and solidus temperatures of molten steel is temporally neglected. The comparison in Figure 2 indicates that sequence of $D_{i}^{\text{s}}$ of the studied solute elements is O >> N > C > other solute elements (i.e., Si, Mn, P, S and Ti). Based on this sequence, it is clear that oxygen, nitrogen, and carbon have relatively high values of $D_{i}^{\text{s}}$ and in comparison, the remaining five solute elements have relatively lower diffusivity in solid phase.

Table V Equilibrium Partition Coefficients Between Solid and Liquid Steel of Solute Element and Their Diffusion Coefficients in Solid Phase.[17,28,29]

Fig. 2

Comparison of $D_{i}^{\text{s}}$ for the studied solute elements during solidification provided that the effect of element segregation on T_l and T_s is not considered

To investigate the appropriate Category III models for each element, the values of ϕ(α) calculated by different segregation models are further compared. To do this comparison, the local solidification time, τ, and the secondary dendrite arm space, λ, should be calculated beforehand, as shown in Table IV. The expressions of τ and L are given in Eqs. [12] and [13], respectively.[30,31]

$$ \tau = \left( {T_{l} - T_{s} } \right)/ R_{c} $$

(12)

$$ \lambda = 143.9R_{c}^{ - (0.3616)} \cdot \omega_{C}^{{(0.5501 - 1.996*\omega_{C} )}} $$

(13)

where R_c is the cooling rate of molten steel, K/s. In this test case, R_c is set as 1.67 K/s. The original carbon concentration is temporarily substituted into ω_C in Eq. [13]. The detailed comparison of ϕ(α) calculated by Brody–Fleming (abbrev. B–F), Clyne–Kurz (abbrev. C–K), and Ohnaka models for each solute element is shown in Figure 3.

Fig. 3

Comparison of ϕ(α) calculated by Brody–Fleming, Clyne–Kurz, and Ohnaka models for each solute element

The comparison results in Figure 3 mainly indicate two conclusions. First, for the solute elements with high diffusivity in solid phase (i.e., C, N and O), B–F model generally predicts an unreasonable higher ϕ(α) than C–K and Ohnaka models, and the other two models predict the very close values of ϕ(α) near 1.0. Second, for the solute elements with low diffusivity in solid phase (i.e., Si, Mn, P and Ti), the values of ϕ(α) calculated by all three models are generally low. Among them, B–F and C–K models almost predict the same value and in comparison Ohnaka model provides a relatively higher ϕ(α). For S which has an intermediate diffusivity, the values of ϕ(α) calculated by C–K and Ohnaka models keep lower than 1.0 over the solidification process but differ slightly. Therefore, for C, N and O, either C–K or Ohnaka model can be used in the segregation calculation. For Si, Mn, P and Ti, either C–K (or B–F) or Ohnaka model is applicable. Based on the above analysis, a summary is shown in Table VI.

Table VI Summary of the Applicability of Category III Models for Solute Element

In general, both C–K and Ohnaka models are applicable for all the studied solute elements and these two models can be even regarded as equivalent for the elements of C, N, and O. While for the remaining elements, it is difficult to determine which model is more appropriate. Considering this issue, C–K and Ohnaka models are, respectively, applied to the following thermodynamic calculations in this study and then the corresponding calculation results will be compared between these two model cases

Calculation Procedures of TiN Precipitation and Growth

Thermodynamic Calculation of Solute Micro-segregation

The calculation unit starts from the center axis of one secondary dendrite in the mushy zone and ends at the length of half secondary dendrite arm space, as shown in Figure 4. Through applying the finite volume method, the calculation proceeds by every solidification fraction of 0.001, Δg. In each calculation step, the solidification is assumed at a steady state where the temperature of molten steel and solute concentrations are uniform. As solidification proceeds, the solid–liquid interface slowly moves towards the center of the inter-dendrite liquid pool.

Fig. 4

Schematic of calculation unit considered in the finite volume method and the illustration of the solidification of sub-unit i within Δt

The variations in solute concentrations due to the solute micro-segregations during solidification would consequently keep updating the values of T_s–l, ${\text{D}}_{\text{i}}^{\text{s}}$, τ, λ and f_i in the calculation. Based on Eq. [9], T_s–l is a function of the liquidus and solidus temperatures (T_l, T_s) which are normally estimated via the actual concentrations of solute elements, as shown in Eqs. [10] and [11]. As the solute concentrations vary, T_l and T_s would keep changing and this change further affects the value of T_s–l. As a result, the updated T_s–l, T_l and T_s affect the values of $D_{i}^{\text{s}}$and τ based on the expressions shown in Table V and Eq. [12]. λ is a function of actual carbon concentration (see Eq. [13]) so the secondary dendrite arm space also keeps varying during the solidification. Furthermore, f_i is also a variant according to Eqs. [3] through [6].

As the calculation proceeds by Δg, the values T_l, T_s and λ are first updated by the segregated solute concentrations calculated in the previous step (for the first step, the original concentrations are used), then T_l–s, f_i, $D_{i}^{\text{s}}$ and τ are updated, followed by the update of back diffusion coefficient, α. Finally, the segregated solute concentrations in this step are calculated by segregation model. In each step, the calculated activity product of TiN (i.e., Q_TiN in Eq. [7]) is compared with the equilibrium activity product $K^{\prime}_{\text{TiN}}$ which is a function of T_s–l to determine the solidification fraction at which TiN precipitation starts, g_TiN. Figure 5 shows the thermodynamic calculation procedure as solidification fraction increases by Δg. The whole calculation process (0 → g → 1) is conducted using the commercial software MATLAB.

Fig. 5

Illustration of thermodynamic calculation procedure as solidification fraction increases by Δg

Coupling of Micro-segregation and TiN Precipitation

If Q_TiN> $K^{\prime}_{\text{TiN}}$ is detected in one calculation step, TiN starts precipitating and then grows up in the following calculation steps. As a result, the concentrations of Ti and N in the molten steel would be partially consumed. This is realized in the thermodynamic calculation by coupling the TiN precipitation module with the solute micro-segregation module. In this study, the precipitated TiN inclusions are assumed to be uniformly dispersed in the liquid phase. When TiN precipitation occurs, there exists an equilibrium between the inclusion and liquid steel phases, which can be expressed by the following equations[32,33]:

$$ f_{\text{Ti}} \cdot \left( {\omega_{{\left[ {\text{Ti}} \right]}} - \Delta \omega_{{\left[ {\text{Ti}} \right]}} } \right) \cdot f_{\text{N}} \cdot \left( {\omega_{{\left[ {\text{N}} \right]}} - \Delta \omega_{{\left[ {\text{N}} \right]}} } \right) = K^{\prime}_{\text{TiN}} $$

(14)

$$ {{\Delta \omega_{{\left[ {\text{Ti}} \right]}} } \mathord{\left/ {\vphantom {{\Delta \omega_{{\left[ {\text{Ti}} \right]}} } {\Delta \omega_{{\left[ {\text{N}} \right]}} }}} \right. \kern-0pt} {\Delta \omega_{{\left[ {\text{N}} \right]}} }} = {{M_{\text{Ti}} } \mathord{\left/ {\vphantom {{M_{\text{Ti}} } {M_{\text{N}} }}} \right. \kern-0pt} {M_{\text{N}} }} $$

(15)

where $\Delta \omega_{{\left[ {\text{Ti}} \right]}}$ and $\Delta \omega_{{\left[ {\text{N}} \right]}}$ are the consumed Ti and N concentrations due to TiN precipitation, respectively; M_Ti and M_N are molar mass of Ti and N, respectively. After TiN precipitates within one calculation step, Ti and N would reach their equilibrium concentrations, respectively, in the molten steel. Equation [14] can be also reformulated as:

$$ f_{\text{Ti}} \cdot \omega_{{\left[ {\text{Ti}} \right]}}^{\text{e}} \cdot f_{\text{N}} \cdot \omega_{{\left[ {\text{N}} \right]}}^{\text{e}} = K^{\prime}_{\text{TiN}} $$

(16)

where $\omega_{{\left[ {\text{Ti}} \right]}}^{\text{e}}$ and $\omega_{{\left[ {\text{N}} \right]}}^{\text{e}}$ are the equilibrium concentrations of Ti and N, respectively, which is equal to $\left( {\omega_{{\left[ {\text{Ti}} \right]}} - \Delta \omega_{{\left[ {\text{Ti}} \right]}} } \right)$ and $\left( {\omega_{{\left[ {\text{N}} \right]}} - \Delta \omega_{{\left[ {\text{N}} \right]}} } \right)$ ,respectively.

The values of $\omega_{{\left[ {\text{Ti}} \right]}}$ and $\omega_{{\left[ {\text{N}} \right]}}$ in Eq. [14] are obtained based on the Ti and N micro-segregation calculations by segregation model. Before TiN starts precipitation, Ti and N are continuously enriched in the inter-dendrite space. In (n − 1)th and nth calculation steps, the segregated concentrations of either Ti or N are normally calculated by the general expression of Category III models:

$$ \omega_{\left[ i \right]}^{n} = \omega_{\left[ i \right]}^{0} \cdot \left[ {1 - \left( {1 - \varPhi_{(n)} k_{i} } \right)g} \right]^{{\left( {k_{i} - 1} \right)/\left( {1 - \varPhi_{(n)} k_{i} } \right)}} $$

(17)

$$ \omega_{\left[ i \right]}^{n - 1} = \omega_{\left[ i \right]}^{0} \cdot \left[ {1 - \left( {1 - \varPhi_{(n - 1)} k_{i} } \right)g} \right]^{{\left( {k_{i} - 1} \right)/\left( {1 - \varPhi_{(n - 1)} k_{i} } \right)}} $$

(18)

where $\omega_{\left[ i \right]}^{n - 1}$ and $\omega_{\left[ i \right]}^{n}$ are the segregated concentrations of Ti or N in the (n − 1)th and nth steps, respectively; $\omega_{\left[ i \right]}^{0}$ refers to the original concentration of Ti or N; $\varPhi_{(n - 1)}$ and $\varPhi_{{\left( {n - 1} \right)}}$ are the values of ϕ(α) calculated in the (n − 1)th and nth steps, respectively; k_i represents for the partition coefficient of Ti or N and its value is assumed to be constant during the solidification process. By combining Eqs. [17] and [18], $\omega_{\left[ i \right]}^{n}$ can be expressed as follows:

$$ \omega_{\left[ i \right]}^{n} = \omega_{\left[ i \right]}^{n - 1} \cdot \frac{{\left[ {1 - \left( {1 - \varPhi_{(n)} k_{i} } \right)g} \right]^{{\left( {k_{i} - 1} \right)/\left( {1 - \varPhi_{(n)} k_{i} } \right)}} }}{{\left[ {1 - \left( {1 - \varPhi_{(n - 1)} k_{i} } \right)g} \right]^{{\left( {k_{i} - 1} \right)/\left( {1 - \varPhi_{(n - 1)} k_{i} } \right)}} }} $$

(19)

Note that in the TiN precipitation module, the actual concentration of Ti or N in the (n − 1)th step, $\omega_{\left[ i \right]}^{n - 1}$, would finally reach the corresponding equilibrium concentration, $\omega_{\left[ i \right]}^{\text{e}}$, in the (n − 1)th step instead of the segregated value calculated by Eq. [18].

Kinetic Calculation of TiN Inclusion Growth

To estimate the TiN inclusion size at the end of solidification, the principal mechanism controlling the growth rate of TiN should be clear. In general, the potential mechanisms that control the growth rate of TiN include the chemical reaction rate at the TiN/steel interface and the mass transport rates of Ti and N from the liquid phase to the interface. The interfacial reaction rate within the molten steel temperature range is very fast so the inclusion growth is assumed to be diffusion-controlled. The diffusion coefficients of Ti and N in the molten steel are, respectively, calculated as follows[34]:

$$ D_{\text{Ti}}^{\text{L}} \left( {{\text{m}}^{ - 2} \,{\text{s}}^{ - 1} } \right) = 3.10 \times 10^{ - 7} \exp \left( { - 11500/\left( {RT_{s - l} } \right)} \right) $$

(20)

$$ D_{N}^{L} \left( {{\text{m}}^{ - 2} \,{\text{s}}^{ - 1} } \right) = 3.25 \times 10^{ - 7} \exp \left( { - 11500/\left( {RT_{s - l} } \right)} \right) $$

(21)

Equations [20] and [21] indicate that $D_{\text{Ti}}^{\text{L}}$ and $D_{\text{N}}^{\text{L}}$ are very close within the molten steel temperature range. Since the original concentration of Ti in the molten steel is lower than the value of N by an order of magnitude, as shown in Table I, the diffusion of Ti can be assumed as the controlling mechanism for the growth rate of TiN inclusion.

According to the previous kinetics research,[35] the diffusion flux of Ti towards the TiN particle is proportional to the Ti concentration gradient, so for a TiN particle with the radius of r, there is

$$ J_{\text{Ti}} = \frac{{D_{\text{Ti}}^{L} \cdot \rho_{\text{Fe}} }}{{100M_{\text{Ti}} \cdot r}} \cdot \left( {\omega_{{ [ {\text{Ti]}}}} - \omega_{{ [ {\text{Ti]}}}}^{e} } \right) $$

(22)

where J_Ti is the diffusion flux of Ti, mol m⁻² s⁻¹; r is the radius of TiN particle, m; ρ_Fe is the iron density (7.07×10³ kg m⁻³), and M_Ti is the molecular weight of Ti (0.048 kg mol⁻¹). $\omega_{{\left[ {\text{Ti}} \right]}}$ is the Ti concentration calculated by the coupling of Ti micro-segregation and TiN precipitation during solidification, wt pct, and $\omega_{{[{\text{Ti]}}}}^{\text{e}}$ is the Ti concentration in equilibrium with TiN particle, wt pct. Assuming that the TiN particle is spherical and each TiN particle grows independently without interaction with others at a stationary diffusion state, the relationship between the Ti diffusion flux and the TiN particle radius is expressed by Eq. [23]:

$$ 4\pi r^{2} \cdot M_{\text{TiN}} \cdot J_{\text{Ti}} \cdot \Delta t = \frac{4}{3}\pi \rho_{\text{TiN}} \cdot \left[ {\left( {r + \Delta r} \right)^{3} - r^{3} } \right] $$

(23)

where M_TiN is the molecular weight of TiN (0.062 kg mol⁻¹), ρ_TiN is the TiN density (5.43 × 10³ kg m⁻³), Δt refers to the unit growing time, s, and Δr denotes the increase in TiN particle radius within Δt, m. Combining Eqs. [22] and [23], the growth of TiN particle can be expressed by Eq. [24]:

$$ r\frac{{{\text{d}}r}}{{{\text{d}}t}} = \frac{{M_{{{\text{TiN}} \cdot \rho_{\text{Fe}} }} }}{{100M_{\text{Ti}} \cdot \rho_{\text{TiN}} }} \cdot D_{\text{Ti}}^{\text{L}} \cdot \left( {\omega_{{ [ {\text{Ti]}}}} - \omega_{{ [ {\text{Ti]}}}}^{e} } \right) $$

(24)

Through integration for r and t in Eq. [24], the radius of TiN particle can be calculated by Eq. [25]:

$$ \mathop \smallint \limits_{0}^{{r_{t} }} r{\text{d}}r = \frac{{M_{\text{TiN}} \cdot \rho_{\text{Fe}} }}{{100M_{\text{Ti}} \cdot \rho_{\text{TiN}} }} \cdot \mathop \smallint \limits_{0}^{t} D_{\text{Ti}}^{\text{L}} \cdot \left( {\omega_{{ [ {\text{Ti]}}}} - \omega_{{ [ {\text{Ti]}}}}^{e} } \right){\text{d}}t $$

(25)

where r_t refers to the radius of TiN particle after time t since the TiN precipitation starts. Note that $D_{\text{Ti}}^{\text{L}}$ actually varies with the TiN growth time, t, due to the variation in the temperature of molten steel, as shown in Eq. [20], and the driving force for TiN precipitation, $\left( {\omega_{{ [ {\text{Ti]}}}} - \omega_{{ [ {\text{Ti]}}}}^{e} } \right)$, in each calculation step is also a variant with growth time, t. Therefore, these two parameters should be treated as functions of growth time rather than constants. Although ρ_Fe actually also changes during solidification, its value is temporarily regarded as a constant in this study for calculation simplicity.

In general, the overall calculation procedures described in Section III are shown in Figure 6. Please note an assumption that in the current calculation model, the precipitations of other types of inclusions from liquid steel during solidification are currently not considered. In reality, for the chemical composition of the studied SWRH92A tire cord steel, it is thermodynamically possible that other types of inclusions may also precipitate sequentially during the solidification process.[36] As a result, the consumptions of the constituent solute elements would affect the calculated solute concentrations.[37] In our future work, the calculation model will be improved by taking this influence into account.

Fig. 6

Overall flow chart of TiN precipitation calculation in the molten steel during solidification

Results and Discussions

Micro-segregations of Solute Elements

The micro-segregation of each solute element during solidification (R_c = 1.67 K/s) was calculated by Ohnaka and C–K models, respectively, and the calculation results are compared in Figure 7. Since the micro-segregations of Ti and N may be affected by TiN precipitation, their results were temporarily not discussed in this comparison. The results in Figure 7 firstly indicate that Ohnaka and C–K models predicted similar solute segregation ratios. As shown in Table VI, for C and O the micro-segregation ratios calculated by Ohnaka and C–K models were regarded as equivalent. For Si, Mn, P and S, the segregation ratios of these solute elements were also very close in both Ohnaka and C–K model cases. The specific segregation ratios of these four elements at several solidification fractions were compared between the Ohnaka and C–K model cases (see Table VII).

Fig. 7

Comparison of the solute segregation ratios calculated by Ohnaka and C–K models. (Ti, N are not included.)

Table VII Segregated Ratios of Si, Mn, P and S Calculated by Ohnaka (Left) and C–K (Right) Models

Second, the sequence of the micro-segregation ratios of these solute elements is O > S > P > C > Si > Mn. Considering the equilibrium partition coefficient, k_i, and the diffusion coefficient in solid phase, $D_{i}^{\text{s}}$, of each element (see Table V and Figure 2), this sequence indicates that k_i probably affects the solute micro-segregation more significantly than $D_{i}^{\text{s}}$. The smaller k_i is, the larger micro-segregation ratio of element i would be. The main reason is that the sequence of k_i is O < S < P < C < Si < Mn, which perfectly matches the sequence of the reciprocal of solute micro-segregation ratio, while the sequence of $D_{i}^{\text{s}}$ does not have a clear correlation with the sequence of solute micro-segregation ratio. For example, although $D_{\text{O}}^{\text{s}}$ is obviously larger than the values of other elements (see Figure 2), the segregation ratio of oxygen is the highest because k_O is the lowest among the solute elements.

The segregated solute concentrations calculated by Ohnaka and C–K models, respectively, are shown in Figure 8. It is clearly seen that although the segregation ratio of carbon is in the medium level among the solute elements, the increase in carbon concentration is very obvious because the original carbon concentration in the molten steel is the highest among the solute elements. In comparison, the increases in other solute concentrations are smoother since their original concentrations are relatively lower than carbon’s. Based on this result, it is noticeable that for high carbon steel the micro-segregation of carbon would lead to a huge increase in carbon concentration (by about 1.8 wt pct in this study) in the inter-dendrite space during solidification. Therefore, the effect of carbon micro-segregation on the thermodynamic parameters, such as liquidus and solidus temperatures (T_l and T_s) and secondary dendrite arm (λ), should be seriously considered.

Fig. 8

Comparison of the solute concentrations calculated by Ohnaka and C–K models. (Ti, N are not included.)

Thermodynamic Calculation of TiN Precipitation

The Ti and N micro-segregation ratios and solute concentrations calculated by Ohnaka and C–K models, respectively, are shown as the solid lines in Figure 9. The dash lines represent for the corresponding imaginary segregation ratios and solute concentrations provided that TiN precipitation is not coupled in the thermodynamic calculations. It is noticeable that if the micro-segregation module is not coupled with the TiN precipitation module, the calculated results would dramatically deviate from the results of the coupled cases. In Figure 9, the turning point refers to the solidification fraction where the TiN precipitation started. As the TiN precipitation proceeded, the micro-segregation of Ti dropped more sharply compared with that of N. This is because that the original concentration of Ti is lower than the value of N by about one order of magnitude. Furthermore, the mass consumption of Ti is more than three times (about 3.43) of the value of N due to TiN precipitation according to stoichiometry.

Fig. 9

Ti and N segregation ratios and solute concentrations under the influence of TiN precipitation. Dash lines represent the imaginary counterparts provided that the TiN precipitation is not coupled in the calculation

The curves in Figure 10 show the variations in the liquidus temperature, T_l, solidus temperature, T_s, and the solid/liquid interface temperature, T_s–l, of the molten steel with increasing solidification fraction. Due to the micro-segregations of solute elements, the liquidus and solidus temperatures of molten steel decreased obviously instead of keeping as constants. Especially due to the dramatic decrease in T_s, the temperature range within which the mushy zone of molten steel existed was extended. As a result, the solid/liquid interface temperature, as a function of T_l and T_s, dropped to the values near 1200 K.

Fig. 10

Variations in T_l, T_s, and T_s–l of molten steel during solidification in Ohnaka and C–K model cases. (R_c= 1.67 K/s)

Figure 11 indicates the precipitation point where the actual activity product of TiN, Q_TiN, became larger than the corresponding equilibrium activity product, $K^{\prime}_{\text{TiN}}$. Due to the sharp decrease in T_s–l as shown in Figure 10, $K^{\prime}_{\text{TiN}}$ as a function of T_s–l also dropped significantly. In the Ohnaka and C–K model cases, the trendlines of Q_TiN and $K^{\prime}_{\text{TiN}}$ intersected at 0.892 and 0.888, respectively (R_c= 1.67 K/s). These two TiN precipitation points were quite close so that the Ohnaka and C–K models could be also treated as equivalent in this thermodynamic calculation. After TiN precipitation, Q_TiN decreased but kept closely above the value of $K^{\prime}_{\text{TiN}}$. This is because that due to the TiN precipitation, $\omega_{{\left[ {\text{Ti}} \right]}}$ and $\omega_{{\left[ {\text{N}} \right]}}$ in one calculation step were re-calculated by Eq. [19] based on $\omega_{{\left[ {\text{Ti}} \right]}}^{\text{e}}$ and $\omega_{{\left[ {\text{N}} \right]}}^{\text{e}}$ obtained in its previous step. The difference between $\omega_{{\left[ {\text{Ti}} \right]}}$ and $\omega_{{\left[ {\text{Ti}} \right]}}^{\text{e}}$ formed the driving force of the growth of TiN particle.

Fig. 11

Variations in Q_TiN and $K^{\prime}_{\text{TiN}}$ during solidification in Ohnaka and C–K model cases. (R_c = 1.67 K/s)

Kinetic Calculation of TiN Particle Growth

To estimate the radius of growing TiN particle during solidification, $D_{\text{Ti}}^{\text{L}}$ and $\left( {\omega_{{\left[ {\text{Ti}} \right]}} - \omega_{{[{\text{Ti]}}}}^{\text{e}} } \right)$ as functions of growing time should be first determined as indicated by Eq. [25]. In this section, three molten steel cooling rates, i.e., 1.67, 0.83 and 0.17 K/s, were, respectively, considered in the calculations, aiming to investigate the effect of cooling rate on the TiN inclusion growth behavior.

Based on the thermodynamic calculation data, the variations in $D_{\text{Ti}}^{\text{L}}$ and $\left( {\omega_{{ [ {\text{Ti]}}}} - \omega_{{ [ {\text{Ti]}}}}^{\text{e}} } \right)$ with growing time under these three cooling rate conditions are shown in Figure 12. The specific fitting functions for $D_{\text{Ti}}^{\text{L}}$ and $\left( {\omega_{{ [ {\text{Ti]}}}} - \omega_{{ [ {\text{Ti]}}}}^{\text{e}} } \right)$ are listed in Table VIII. It is shown that the diffusion coefficient of Ti in the liquid phase, $D_{\text{Ti}}^{\text{L}}$, decreased almost linearly due to the decreasing temperature with TiN growing time. The driving force $\left( {\omega_{{ [ {\text{Ti]}}}} - \omega_{{ [ {\text{Ti]}}}}^{\text{e}} } \right)$ first decreased sharply at the early stage of TiN growth and then the decreasing slope gradually became smoother and finally reached a relatively stable level. This trend was similar to that of $\omega_{{ [ {\text{Ti]}}}}$ during the TiN precipitation period, as shown in Figure 9. When TiN precipitation started, the segregated Ti concentration in the liquid steel was still relatively high, which made the driving force $\left( {\omega_{{ [ {\text{Ti]}}}} - \omega_{{ [ {\text{Ti]}}}}^{\text{e}} } \right)$ large and benefited the TiN particle growth. Due to the consumption of Ti concentration, $\omega_{{ [ {\text{Ti]}}}}$ dropped significantly and this sharply decreased the Ti concentration gradient between the liquid phase and the region near TiN particle. As a result, the TiN growth gradually became slowly, which in turn limited the consumption of Ti concentration in the liquid phase. Consequently, as TiN growth proceeded, the driving force $\left( {\omega_{{ [ {\text{Ti]}}}} - \omega_{{ [ {\text{Ti]}}}}^{\text{e}} } \right)$ decreased more smoothly and gradually reached a relative equilibrium state until the steel solidification process finished. By substituting the expressions of ${\text{D}}_{\text{Ti}}^{\text{L}}$ and $\left( {\omega_{{ [ {\text{Ti]}}}} - \omega_{{ [ {\text{Ti]}}}}^{\text{e}} } \right)$ into Eq. [25], the variation in TiN particle radius with solidification fraction in each cooling rate case was obtained and the relevant result is shown in Figure 13.

Fig. 12

Variations in $D_{\text{Ti}}^{\text{L}}$ and $\left( {\omega_{{\left[ {\text{Ti}} \right]}} - \omega_{{[{\text{Ti]}}}}^{\text{e}} } \right)$ with increasing growing time under three cooling rate conditions

Table VIII Fitting Functions for $D_{\text{Ti}}^{\text{L}}$ and $\left( {\omega_{{ [ {\text{Ti]}}}} - \omega_{{ [ {\text{Ti]}}}}^{e} } \right)$ in the Ohnaka and C–K Model Cases

Fig. 13

Variation in TiN particle size with increasing solidification fraction

The trendlines of all three cooling rate cases in Figure 13 indicate that as solidification proceeded since TiN precipitation started, the growth curves of TiN particle followed a parabolic relationship with growth time. The particle first grew quickly at the early stage of precipitation and then the growth rate gradually slowed down and finally the particle radius reached a relatively stable value. With R_c increasing from 0.17 to 0.83 K/s, the solidification fraction at which the precipitation started, g_TiN, shifted from 0.895 to 0.893 for Ohnaka model case and from 0.892 to 0.889 for C–K model case, respectively. The TiN particle size at the end of solidification, d_g=1, decreased from about 10 to about 4 μm. With R_c further increasing from 0.83 to 1.67 K/s, g_TiN shifted from 0.893 to 0.892 for Ohnaka model case and from 0.889 to 0.888 for C–K model case, respectively. The value of d_g=1 decreased from about 4 to about 3 μm. The above analysis first indicates that as the cooling rate increased, the TiN precipitation became earlier but the final particle size got smaller. Furthermore, as R_c increased from 0.83 to 1.67 K/s, the change in d_g=1 was less significantly than that as R_c increased from 0.17 to 0.83 K/s. This illustrates that when R_c is above a certain value, d_g would probably be within a narrow range and hence further increasing R_c may be not a cost-effective way of decreasing TiN inclusion size.

The calculated TiN inclusion radius under different cooling rate conditions were compared with the reference values measured in the metallographic images of TiN inclusions published in the previous studies relating to TiN precipitation in high carbon tire cord steel.[9,12, 38,39,40,41,42,43] Some typical images showing the morphologies of TiN inclusions precipitated in SWRH82A tire cord steel were referenced as displayed in Figure 14. Based on these images, it can be seen that the TiN inclusion sizes are not uniform. The larger particle (left) is about 6.0 μm and the smaller ones (right) are about 3.0 μm. Considering that the observed individual TiN particles cannot represent all the TiN inclusions in the steel, a summary of the TiN particle size distribution in the tire cord steels with different carbon contents was also referenced as shown in Table IX. It can be seen that for the tire cord steel with 0.93 wt pct carbon content (R_c =1.5 K/s), the average size of measured TiN inclusions is 3.32 μm which basically agrees with the calculated size of 3.15 μm (green line: R_c =1.67 K/s) shown in Figure 13. These TiN inclusion images and statistical data generally validate the kinetic calculations in this study and this agreement provides a substantial support for the thermodynamic studies of nonmetallic inclusions of steel in the future work.

Fig. 14

Morphologies of TiN inclusions observed in the samples of SWRH82A tire cord steel. (R_c was about 1.5 K/s) Reprinted with permission from Ref. [38]

Table IX TiN Particle Size Distribution in the Tire Cord Steels With Different Carbon Contents

Conclusions

A systematic thermodynamic analysis of the precipitation of TiN inclusion during the solidification of SWRH92A high carbon tire cord steel was conducted in this paper. Finite volume method was used in the calculation to mimic the dynamic solute variation in the inter-dendrite space as the solidifying front pushed forward during solidification. In the thermodynamic calculation, the micro-segregations of solute elements and their influence on thermodynamic parameters were particularly taken into account. Ohnaka and Clyne–Kurz models were, respectively, applied to the solute micro-segregation calculations. To consider the influence of TiN precipitation on the micro-segregations of Ti and N, the coupling calculation between TiN precipitation and solute micro-segregation was activated when the condition of TiN precipitation was satisfied. Furthermore, the kinetic calculation of TiN growth was conducted based on the thermodynamic calculation results. The main conclusions are listed as follows:

• 1. The sequence of the micro-segregation ratios of the solute elements (excluding Ti and N) in the SWRH92A molten steel is O > S > P > C > Si > Mn. The micro-segregation ratio of each solute element is mainly dependent on its equilibrium partition coefficient between the solid and liquid steel phases, k_i. The smaller k_i is, the larger micro-segregation ratio of element i would be.

• 2. The concentration of carbon increased most significantly (by about 1.8 wt pct) among the solute elements in the inter-dendrite space during solidification of its highest original content. This result indicates that the effect of carbon micro-segregation on the thermodynamic calculations of high carbon steel products should be seriously considered.

• 3. By coupling the solute micro-segregation module with the TiN precipitation module, the segregated ratios of Ti and N decreased to different extents after the TiN precipitation, which obviously differed from the trends in the calculation case where the TiN precipitation module was not coupled with the segregation module.

• 4. When the Ohnaka model and Clyne–Kurz model were, respectively, applied in the thermodynamic calculation, the TiN precipitation point, g_TiN, was 0.892 and 0.888, respectively. The close values indicate that these two micro-segregation models can be regarded as equivalent in this thermodynamic study.

• 5. With R_c increasing from 0.17 to 1.67 K/s, g_TiN shifted from 0.895 to 0.892 for Ohnaka model case and from 0.892 to 0.888 for Clyne–Kurz model case, respectively. This indicates that TiN precipitation would occur earlier as R_c increased. However, the TiN particle size decreased from about 10 to about 3 μm as R_c increased within this range.

• 6. The calculated TiN inclusion size was well validated by the metallographic images of TiN inclusions and the statistical data of TiN particle size distribution in high carbon tire cord steel published in the previous studies. This agreement encourages the proposed thermodynamic calculation method and sets an example for the future thermodynamic studies of nonmetallic inclusions of steel.