Motion and Detachment Behaviors of Liquid Inclusion at Molten Steel–Slag Interfaces

Abstract

The fundamental physics of particles adsorbed at the liquid interfaces has numerous applications in a wide field. In the current study, the motion and detachment behaviors of the liquid nonmetallic inclusion from molten steel–slag interfaces were theoretically studied by developing a force balance model. According to the model calculations, the thin-film drainage is the main stage of the inclusion separation. The capillary force is the main driving force of the inclusion rebounding at the drainage stage. The effect of triple interface among the steel, slag, and inclusion after the film rupture does not seem to be the main factor for the inclusion detachment. The current model can predict the critical inclusion size of the detachment. The vertical terminal velocities of the inclusion, inclusion size, and slag surface tension are the key factors of the detachment.

Introduction

When a microscopic fluid droplet or spherical rigid particle moves toward a liquid–liquid interface, the interface can be deformed by the droplet or particle. The body might transport the interface between two immiscible fluids, and move into the second fluid. In the reverse process, the body might be rebounded back into the first fluid by the interface. These processes of different types of droplets or particles have attracted a large amount of attention of the researchers in the past few decades. In the metallurgical process, transfer of undesirable nonmetallic particles from liquid metal into slag is hastened through different stirring methods such as gas stirring, induction stirring, among others. A similar situation arises in biochemical reactions, in which agitation by ways other than jetting might not be feasible. Many experimental studies[1,2,3,4,5] under the room temperature are performed to obtain insights into the particle/droplet behavior at liquid–liquid interfaces. However, it is quite difficult to study such phenomenon using experimental means in high-temperature industrial field. Of specific interest in the current study is the theoretical analysis on the motion and detachment behaviors of the dispersed nonmetallic droplets, referred to as ‘inclusion’ from hereon, at the liquid steel–slag interfaces.

To date, it is well known that the separation of the nonmetallic inclusions is one of the most important objectives in steelmaking. The cluster formation in steel is considered to be detrimental for both the casting process (clogging) and mechanical properties of the final product. Many efforts have been done to analyze the mechanism of inclusion agglomeration and evolution[6,7,8,9,10] so as to optimize the inclusion control. The separation procedure can mainly be summarized as (i) inclusion coalescence–collision,[11,12,13,14] (ii) inclusion detachment through the steel–slag interface[15,16,17,18,19,20,21] and (iii) inclusion dissolution into slag.[22,23,24] When a liquid inclusion passes through steel–slag interface, the dissolution rate in slag phase is much faster, compared with solid inclusions such as Al₂O₃ and MgAl₂O₄. This is due to the fact that the liquid diffusion is much more facile than the solid dissolution. Thus, the liquid inclusion dissolution into slag does not seem to be a challenging subject. More studies should focus on the first two processes. Numerous experimental and simulation studies[11,12,13,14,25,26,27,28,29] have been conducted regarding the inclusion motion and coalescence–collision in the liquid metal. Inclusion characters such as number density, size distribution, etc. have been systematically analyzed. However, the liquid inclusion behavior at the steel–slag interfaces is rarely studied.

Nakajima and Okamura[15] developed a mathematic model to describe the solid inclusion detachment at the steel–slag interface. Introducing the inclusion viscosity into the Nakajima model,[15,16] Strandeh et al.[17] studied the liquid inclusion motion at the steel–slag interfaces.

Valdez et al.[18] and Bouris et al.[19] used the same model to calculate the capture of inclusions at the steel–slag interfaces. More recently, Liu et al.[20] and Yang et al.[21] in addition considered the influence of Reynolds number into Nakajima model.[15] According to above-mentioned previous study, in both the liquid and solid inclusion cases, the liquid film will form only when the inclusion diameter is larger than about 150 to 180 [μm].[17] Since most of the inclusions in the modern steel manufacturing are smaller than this size range, it indicates that the effect of the liquid film seems to be negligible. Moreover, the model shows that the vertical terminal velocity of inclusion has minor effect on the inclusion detachment.[19] Nakajima model is based on an initial assumption about two cases. First, if the Reynolds number (Re) is smaller than 1, no film will be formed. In the second case, when the Reynolds number (Re) is larger than 1, a liquid film can exist between the inclusion and steel–slag interface. However, according to previous experimental observations and simulations,[2,30,31,32,33,34] it is more common to recognize that the film formation occurs even though the Reynolds number (Re) is much smaller than 1. Thus, Nakajima model might underestimate the film effect due to its initial assumption. More fundamental study is needed to better understand the liquid inclusion behavior at the steel–slag interfaces.

In the current study, a new theoretical model is developed, in which it is assumed that the deformable thin film will exist if the liquid inclusion/bubble approaches to the steel–slag interfaces. This postulation is based on reported experimental and simulation work.[2,30,31,32,33,34] The liquid droplets with small diameters might be assumed to be rigid spheres.[35,36] In the present case we are dealing with the rigid spherical droplets without the internal circulation. The interfacial deformation at the stage of thin-film drainage, which is not considered in previous studies,[15,16,17,18,19,20,21] is included in the current model. All the model parameters are derived from a vacuum degassing trial in the industry. The predicted critical size of liquid inclusion for detaching is validated by means of experimental analysis of inclusion size density. The current study pointed out that the thin-film drainage stage, which is considered to be negligible in previous studies,[15,16,17,18,19,20,21] is the main stage of inclusion detachment. The terminal velocity of inclusion has important influence on inclusion detachment according to current study. This finding is also different from previous study using Nakajima’s model. In addition, a small slag surface tension is favorable to aid in the liquid inclusion detachment. The slag composition can be optimized using the current model. The understanding gained can be applied in a comprehensive kinetic study without restriction in the steelmaking.

Theoretical Consideration

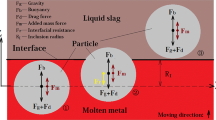
When a rigid sphere penetrates through a liquid–liquid interface, the thin-film behavior can be mainly classified into two types, as shown in Figure 1.

Fig. 1

Schematic illustration of the tailing behavior and draining behavior

Tailing Behavior

When a rigid sphere arrives at a liquid–liquid interface, the interface near the sphere can have a deformation. The deformed interface and film drainage have effects on the sphere’s motion. The film drainage can continue with the sphere movement, but the film cannot rupture immediately. When the sphere after completely immersing in the liquid 1 moves into the liquid 2, a column region attached to the back of the sphere will be formed. The column region becomes thinner and longer with the increasing sphere-movement time. According to the research of Maru et al.,[2] the column region is subjected to instability by the effect of different forces. Finally, both the film and the upper column will detach from the sphere.

Draining Behavior

In the “Draining behavior” case, the interface near the sphere has a deformation as well. However, the thin film can rupture when the film drainage arrives at a certain degree during the sphere’s upward movement. Then the sphere directly and simultaneously makes contact with the liquid 1 and liquid 2 at the interface. With the increasing movement time, the sphere will fully leave the liquid 1 and immerse into the liquid 2.

Whether the thin film should have “Tailing behavior” or “Draining behavior” depends on the density relationship among the rigid spheres, liquid 1 and liquid 2. Geller et al.[34] pointed out that no tails will occur if the rigid-sphere density is in between those of the two immiscible fluids. According to the density estimation of the liquid inclusion, steel and slag (see Section IV), the film behavior in the current study fits the “Draining behavior.”

The displacement (Z) of the inclusion motion is defined using the distance between top point of the inclusion and steel–slag interface. It is defined that the steel–slag interface is the initial point of the displacement (Z = 0). The inclusion radius equals R_o. The starting point of inclusion motion is defined at the steel–slag interface (Z/R_o= 0). At the starting point, the vertical velocity of the inclusion has reached the terminal velocity. According to the inclusion displacement, three positions are existing in this system.

Position 1 → Z/R_o< 0: The inclusion is in the steel phase.

Position 2 → 0≤ Z/R_o≤ 2: The inclusion is at the steel–slag interface.

Position 3 → Z/R_o> 2: The inclusion is in the slag phase.

When the inclusion displacement is smaller than zero, it indicates that the inclusion is completely re-entrained back into the steel phase. Thus, the force analysis at “Position 1” will not be included in the model. When the inclusion has been completely immersed into the slag side (Z/R_o> 2), whether the inclusion will be re-entrained back to interface or not depends on the densities of different phases and interfacial tension. The re-entrainment will occur if the inclusion can reach a critical size that is expressed as[2]

$$ R_{\text{crit}} = \frac{1.27}{{\sqrt {\frac{{\Delta \rho_{\text{SM}} \cdot g}}{{\sigma_{\text{SM}} }} \cdot \left( {\frac{{\Delta \rho_{\text{IS}} }}{{\Delta \rho_{\text{SM}} }} - 1} \right)} }}, $$

(1)

where g = 9.81 [m/s²] is the gravitational acceleration. Δρ_SM, Δρ_IS, Δρ_IM are the interfacial density differences of the slag–steel, inclusion–slag and inclusion–steel, respectively. The sign of “Δ” in density terms denotes the absolute value of density difference between two different phases. σ_SM denotes the slag–steel interfacial tension. The calculation of the above-mentioned parameters is discussed in detail in Section IV. It is found that the value of R_crit in the current study is approximately 6 [mm], which is much larger than the observed inclusions in the secondary metallurgical process. It indicates that if the inclusion can immerse into the slag phase, it cannot be re-entrained back into the steel phase. Since the re-entrainment due to turbulent flow is not the main focus in the current study, the displacement position Z/R_o> 2 is not included in the current model. Thus, the model calculation only focuses on the “Position 2.”

The motion of a small particle dispersed in a flow with a nonuniform velocity field has been well formulated by Maxey and Riley[37] with the equation below:

$$ m_{\text{P}} \cdot \frac{{{\text{d}}U_{\text{I}} }}{{{\text{d}}t}} = F_{\text{G}} + F_{\text{A}} + F_{\text{D}} + F_{\text{B}}. $$

(2)

The left-hand side of the equation indicates the total acceleration force of the particle. The forces on the right-hand side of the equation denote the (I) Gravitational force (F_G), (II) added mass force (F_A), (III) Drag force (F_D), and (IV) Basset history force (F_B), respectively. The Basset history force is governed by the unsteady diffusion of vorticity at the boundary layer around the particle. Namely, it describes the deviations of flow pattern from the steady state. The fluid near the steel–slag interface region is postulated to fit the property of “steady creeping flow/Stokes flow.” Thus, the term of Basset history force is neglected in the current study. The pressure force (F_P) due to the thin-film formation is added into the force balance. The capillary force (F_C) is also added into the equation due to the effect of the steel–slag interface deformation. Consequently, the force balance in the present model is rewritten as

$$ \frac{4}{3}\pi R_{\text{o}}^{3} \cdot \rho_{\text{I}} \cdot \frac{{{\text{d}}^{2} Z}}{{{\text{d}}^{2} t}} = F_{\text{G}} + F_{\text{P}} + F_{\text{C}} + F_{\text{A}} + F_{\text{D}} $$

(3)

Film drainage model

The schematic illustration of the film drainage model is developed, as shown in Figure 2. The assumptions and descriptions of the model are given as

Fig. 2

Proposed film drainage model

• (1) The fluid near the steel–slag interface region fits the property of “steady creeping flow/Stokes flow,” in which the advective inertial forces are much smaller than viscous forces.

• (2) The deformation of the steel–slag interface needs to be considered when the inclusion displacement (Z) is larger than zero.

• (3) The contact area (“C–D–E region” in Figure 2) between the inclusion and steel–slag interface is exactly the same as the thin-film area, and the thickness of the film is negligible compared to the inclusion dimension. The shapes of the “C–D–E region” and bulk interface are symmetrical around the Z-axis symmetry.

• (4) The portion “A–C region” of the bulk interface is approximated by a circular arc with center point “B,” and the radius equals r_o. The rest of the steel–slag interface is assumed to be plane. This approximation is based on the theoretical work and experimental observation of Reference 2.

• (5) The effects of the electrical and molecular forces on the inclusion motion near/at the steel–slag interface are negligible.

Gravitational Force

The gravitational force (positive in the upward direction) is due to the inclusion–steel/slag density difference, and it is expressed as

$$ F_{\text{G}} = V_{\text{IM}} \cdot \left( {\Delta \rho_{\text{IM}} } \right)g + V_{\text{IS}} \cdot \left( {\Delta \rho_{\text{IS}} } \right)g, $$

(4)

where V_IM and V_IS denote the immersed volumes of inclusion in steel and slag, respectively. According to the geometry in Figure 2, the following equations can be obtained as

$$ V_{\text{inlcusion}} = \frac{4}{3}\pi R_{\text{o}}^{3} = V_{\text{IM}} + V_{\text{IS}} $$

(5)

$$ V_{\text{IS}} = \frac{1}{3}\pi R_{\text{o}}^{3} (1 - { \cos }\theta )^{2} (2 + { \cos }\theta ) $$

(6)

$$ { \cos }\theta = \frac{{r_{\text{o}} + R_{\text{o}} - Z}}{{r_{\text{o}} + R_{\text{o}} }}, $$

(7)

where θ is the angle at which the thin film has the same shape as the inclusion itself. Using the above-mentioned set of equations, the final set of the gravitational force gives

$$ F_{\text{G}} = \frac{4}{3}\pi R_{\text{o}}^{3} \cdot \left\{ {\rho_{\text{S}} \cdot \left[ {\frac{1}{4}\left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }} - 1} \right)\left( {\frac{Z}{{R_{\text{o}} + r_{\text{o}} }}} \right)^{3} - \frac{3}{4}\left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }} - 1} \right)\left( {\frac{Z}{{R_{\text{o}} + r_{\text{o}} }}} \right)^{2} + \left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }}} \right)} \right] - \rho_{\text{I}} } \right\}g, $$

(8)

where ρ_M and ρ_S are the steel and slag densities, respectively.

Pressure Force

According to Figure 2, a small region of the liquid steel near the inclusion is dragged up above the steel–slag interface. The dragged distance is named as “Z_c.” A pressure force on the inclusion is driven by the “dragged region” due to the difference in the steel–slag densities. The effective area equals the projected area of the thin-film region in the Z-axis direction. The pressure force (positive in upward direction) is formulated as

$$ F_{\text{P}} = - \left( {\rho_{\text{s}} - \rho_{\text{m}} } \right)g \cdot Z_{\text{c}} \pi (R_{\text{o}} \cdot { \sin }\theta )^{2} $$

(9)

The dragged distance (Z_c) is expressed as

$$ Z_{\text{c}} = r_{\text{o}} \cdot \left( {1 - { \cos }\theta } \right) = \frac{{r_{\text{o}} \cdot Z}}{{r_{\text{o}} + R_{\text{o}} }} $$

(10)

Substituting Eqs. [9] and [10], the pressure force gives

$$ F_{\text{P}} = \pi R_{\text{o}}^{2} \cdot r_{\text{o}} \cdot \left( {\rho_{\text{m}} - \rho_{\text{s}} } \right)g \cdot \left[ {2\left( {\frac{Z}{{R_{\text{o}} + r_{\text{o}} }}} \right)^{2} - \left( {\frac{Z}{{R_{\text{o}} + r_{\text{o}} }}} \right)^{3} } \right] $$

(11)

Capillary Force

The interfacial energy change of the system is formed due to the steel–slag interfacial deformation. The effective area of the interfacial energy change equals the cross-sectional area of the thin film, as is shown in Figure 2. The interfacial energy change acting on the inclusion is expressed as

$$ E_{\text{inter}} = \pi (R_{\text{o}} \cdot { \sin }\theta )^{2} \sigma_{\text{MS}}, $$

(12)

where σ_MS is the steel–slag interfacial tension. Thus, the capillary force equation (positive in upward direction) gives

$$ F_{\text{C}} = - \frac{{{\text{d}}E_{\text{inter}} }}{{{\text{d}}Z}} = \frac{{ - 2\pi R_{\text{o}}^{3} \cdot \sigma_{\text{MS}} }}{{(R_{\text{o}} + r_{\text{o}} )^{2} }} \cdot \left( {1 + \frac{{r_{\text{o}} }}{{R_{\text{o}} }} - \frac{Z}{{R_{\text{o}} }}} \right) $$

(13)

Added Mass Force

As a body moves in a fluid, some amount of fluid moves around it. If the body has acceleration, the fluid will have the acceleration as well. Thus, more force is needed to accelerate the body in fluid, compared with that in vacuum. We can think of the additional force in terms of an imaginary “added mass” of the body in the fluid. The added mass force is derived from the Bernoulli’s equation that is given as

$$ F_{\text{A}} = - \frac{2}{3}\pi R_{\text{o}}^{3} \cdot \rho_{\text{M}} \cdot \frac{{{\text{d}}^{2} Z}}{{{\text{d}}^{2} t}} $$

(14)

Drag Force

According to the Hadamard–Rybezynski theory,[38,39] the drag force (positive in upward direction) acting on the liquid sphere in a creeping flow equals

$$ F_{\text{D}} = - 2\pi U_{\text{I}} \cdot \mu_{\text{f}} \cdot R_{\text{o}} \left( {\frac{2 + 3\tau }{1 + \tau }} \right) = - 2\pi U_{\text{I}} \cdot \mu_{\text{M}} \cdot R_{\text{o}} \left( {\frac{{2\mu_{\text{M}} + 3\mu_{\text{I}} }}{{\mu_{\text{M}} + \mu_{\text{I}} }}} \right), $$

(15)

where U_I is the inclusion velocity relative to the flow, µ_f is the viscosity of the fluid (it equals the steel viscosity at the draining stage). τ = µ_I/µ_M is the viscosity ratio of the inclusion and fluid. It is clear that for a solid sphere case, the viscosity ratio (τ) is close to the positive infinity. Then Eq. [15] can be changed to the Stokes equation as

$$ F_{\text{D}} = - 6\pi U_{\text{I}} \cdot \mu_{\text{f}} \cdot R_{\text{o}} $$

(16)

From the theoretical perspective, Eq. [15] is available only when the Reynolds number (Re) is much smaller than 1. However, according to the experimental results,[40,41] the Hadamard–Rybezynski analysis satisfies the complete Navier–Stokes equation, which means that Eq. [15] can be used to predict the high speed motion of the inclusion (Re >> 1) in a creeping flow. Thus, the standard correlation of the high Reynolds number is unnecessary to be included in the current model.

Substituting Eqs. [8], [11], [13] [14] and [15] into Eq. [3], the force balance equation is rewritten as

$$ \frac{4}{3}\pi R_{\text{o}}^{3} \cdot \left( {\rho_{\text{I}} + \frac{1}{2}\rho_{\text{M}} } \right) \cdot \frac{{{\text{d}}^{2} Z}}{{{\text{d}}^{2} t}} = \frac{4}{3}\pi R_{\text{o}}^{3} \cdot \left\{ {\rho_{\text{S}} \cdot \left[ {\frac{1}{4}\left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }} - 1} \right)\left( {\frac{Z}{{R_{\text{o}} + r_{\text{o}} }}} \right)^{3} - \frac{3}{4}\left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }} - 1} \right)\left( {\frac{Z}{{R_{\text{o}} + r_{\text{o}} }}} \right)^{2} + \left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }}} \right)} \right] - \rho_{\text{I}} } \right\}g + \pi R_{\text{o}}^{2} \cdot r_{\text{o}} \cdot \left( {\rho_{\text{m}} - \rho_{\text{s}} } \right)g \cdot \left[ {2\left( {\frac{Z}{{R_{\text{o}} + r_{\text{o}} }}} \right)^{2} - \left( {\frac{Z}{{R_{\text{o}} + r_{\text{o}} }}} \right)^{3} } \right] - \frac{{2\pi R_{\text{o}}^{3} \cdot \sigma_{\text{MS}} }}{{(R_{\text{o}} + r_{\text{o}} )^{2} }} \cdot \left( {1 + \frac{{r_{\text{o}} }}{{R_{\text{o}} }} - \frac{Z}{{R_{\text{o}} }}} \right) - 2\pi \mu_{\text{M}} \cdot \left( {\frac{{2\mu_{\text{M}} + 3\mu_{\text{I}} }}{{\mu_{\text{M}} + \mu_{\text{I}} }}} \right)R_{\text{o}} \cdot \frac{{{\text{d}}Z}}{{{\text{d}}t}} $$

(17)

According to the hydrostatic balance at the point “C” in Figure 2, the pressure balance equation is given as

$$ \frac{{\sigma_{\text{MS}} }}{{r_{\text{o}} }} - \frac{{\sigma_{\text{MS}} }}{{R_{\text{o}} }} = \Delta \rho_{\text{SM}} \cdot g \cdot Z_{\text{c}} $$

(18)

Combining Eqs. [10] and [18], it leads to:

$$ r_{\text{o}} = \left( {\frac{{\sigma_{\text{MS}} \cdot R_{\text{o}}^{2} }}{{\sigma_{\text{MS}} + \Delta \rho_{\text{SM}} \cdot g \cdot R_{\text{o}} \cdot Z}}} \right)^{0.5} $$

(19)

Consequently, the inclusion displacement at the film draining stage can be obtained by solving Eqs. [17] and [19].

Critical displacement of film rupture

When the thin-film drainage approaches to a critical degree, the film will rupture if the inclusion/bubble can further move toward the slag phase. The critical inclusion/bubble displacement (Z_crit) of the film rupture is assumed to be proportional to the inclusion/bubble radius, and can be expressed as

$$ Z_{\text{Crit}} = K_{\text{o}} \cdot R_{\text{o}}, $$

(20)

where K_o is a film-rupture constant that is assumed to the same for both the liquid inclusion and gas bubble with a same size. The value of K_o can be estimated by using a gas bubble model, as is shown in Figure 3. The model is almost the same as the film drainage model. The only difference is that the sphere is a gas bubble instead of a liquid inclusion. The bubble shape is assumed to be a rigid sphere for simplification. When a bubble reaches to a steel–slag interface, the bubble stability can be described by the equation below[42]:

Fig. 3

Proposed bubble model

$$ \xi = \frac{{\sigma_{\text{S}} }}{{\sigma_{\text{MS}} + \sigma_{\text{S}} + \sigma_{\text{M}} }}, $$

(21)

where ξ is the thin-film stability. σ_S and σ_M are the slag and steel surface tension. If the ξ value is smaller than 0.5,[42] the thin film will be unstable, and it can be followed by rupture. The calculation of the surface tension and interfacial tension is detailed introduced in Section IV. Based on the calculation, the ξ value is about 0.14 which means that the bubble can rupture in the current study.

It has been well known that steel droplet can be immersed into the slag phase when the gas bubbles rupture at the steel–slag interfaces.[43,44] The thin-film thickness is negligible due to the initial model assumption. According to Figure 3, the shadow region is assumed to be the effective region of the steel droplet formation. The volume of the effective region is approximately given as

$$ V_{\text{d}} = \frac{1}{3}\pi { \sin }\theta^{2} Z_{\text{Crit}} \cdot \frac{{\left( {R_{\text{o}} + r_{\text{o}} } \right)^{3} - R_{\text{o}}^{3} }}{{\left( {R_{\text{o}} + r_{\text{o}} } \right)}} - \frac{1}{3}\pi Z_{\text{Crit}} \left( {2R_{\text{o}} - Z_{\text{Crit}} } \right)\left( {3R_{\text{o}} - Z_{\text{Crit}} } \right) + \frac{1}{3}\pi R_{\text{o}}^{3} (1 - { \cos }\theta )^{2} (2 + { \cos }\theta ) $$

(22)

Deng[45] reported the immersed weight of the steel droplet changed with the Ar-bubble radius, using the bubbling experiments of the molten steel–slag system. Based on the Deng’s experimental results, the relation between the steel droplet (m_d) and bubble radius is estimated as

$$ m_{\text{d}} = \rho_{m} \cdot V_{d} = 4.241 \times 10^{6} R_{\text{o}}^{3.455} $$

(23)

Combining Eqs. [19], [22] and [23], the film-rupture constant K_o= 0.085 is obtained.

Film rupture model

The schematic illustration of the film rupture model is shown in Figure 4. The interface is simplified as flat that is the same as References 15,16,17,18,19,20, through 21. After film rupture, the inclusion contacts simultaneously with the slag and steel. In the film rupture model, both r_o and the pressure force (F_P) equal 0. The force balance equation of the film rupture model is given by

Fig. 4

Proposed film rupture model

$$ F_{\text{total}} = \frac{4}{3}\pi R_{\text{o}}^{3} \cdot \rho_{\text{I}} \cdot \frac{{{\text{d}}^{2} Z}}{{{\text{d}}^{2} t}} = F_{\text{B}} + F_{\text{C}} + F_{\text{A}} + F_{\text{D}} $$

(24)

Gravitational Force

Changing the r_o to 0, Eq. [8] is rewritten as

$$ F_{\text{G}} = \frac{4}{3}\pi R_{\text{o}}^{3} \cdot \left\{ {\rho_{\text{S}} \cdot \left[ {\frac{1}{4}\left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }} - 1} \right)\left( {\frac{Z}{{R_{\text{o}} }}} \right)^{3} - \frac{3}{4}\left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }} - 1} \right)\left( {\frac{Z}{{R_{\text{o}} }}} \right)^{2} + \left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }}} \right)} \right] - \rho_{\text{I}} } \right\}g $$

(25)

Capillary Force

According to Pieranski,[46] when a sphere contacts with two different phases, the contributions to the overall interfacial energy are given as

$$ E_{1} = 2\pi R_{\text{o}} \cdot \left( {2R_{\text{o}} - Z} \right)\sigma_{\text{IM}} $$

(26)

$$ E_{2} = 2\pi R_{\text{o}} \cdot Z \cdot \sigma_{\text{SI}} $$

(27)

$$ E_{3} = - \pi \left( {2R_{\text{o}} \cdot Z - Z^{2} } \right)\sigma_{\text{MS}}, $$

(28)

where E₁ and E₂ are the contributions of the inclusion–steel and inclusion–slag interface. E₃ is the energy that gets released due to the penetration of inclusion through the steel–slag interface. The sum of the interfacial energy gives

$$ E_{\text{inter}} = - \pi \left( {2R_{\text{o}} \cdot Z - Z^{2} } \right)\sigma_{\text{MS}} + 2\pi R_{\text{o}} \cdot \left( {2R_{\text{o}} - Z} \right)\sigma_{\text{IM}} + 2\pi R_{\text{o}} \cdot Z \cdot \sigma_{\text{SI}} $$

(29)

Thus, the capillary force (positive in upward direction) is expressed as

$$ F_{\text{C}} = - \frac{{{\text{d}}E_{\text{inter}} }}{{{\text{d}}Z}} = - 2\pi R_{\text{o}} \cdot \sigma_{\text{MS}} \cdot \left( {\frac{Z}{{R_{\text{o}} }} - 1 - \frac{{\sigma_{\text{IM}} - \sigma_{\text{IS}} }}{{\sigma_{\text{MS}} }}} \right) $$

(30)

Added Mass Force

The added mass force (positive in upward direction) driven by the slag and steel is given as

$$ F_{\text{A}} = - \frac{2}{3}\pi R_{\text{o}}^{3} \cdot \rho_{\text{S}} \cdot \left[ {\frac{1}{4}\left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }} - 1} \right)\left( {\frac{Z}{{R_{\text{o}} }}} \right)^{3} - \frac{3}{4}\left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }} - 1} \right)\left( {\frac{Z}{{R_{\text{o}} }}} \right)^{2} + \left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }}} \right)} \right] \cdot \frac{{{\text{d}}^{2} Z}}{{{\text{d}}^{2} t}} $$

(31)

Drag Force

The drag force (positive in upward direction) is given as

$$ F_{\text{D}} = - 2\pi V_{\text{p}} \cdot \mu_{\text{f}} \cdot R_{\text{o}} \left( {\frac{2 + 3\tau }{1 + \tau }} \right) $$

(32)

The fluid viscosity combining the effects of both the steel and slag is expressed as

$$ \mu_{\text{f}} = \mu_{\text{S}} \cdot \left[ {\left( {\frac{{\mu_{\text{M}} }}{{\mu_{\text{S}} }} - 1} \right)\left( {\frac{Z}{{R_{\text{o}} }}} \right)^{2} - 2\left( {\frac{{\mu_{\text{M}} }}{{\mu_{\text{S}} }} - 1} \right)\left( {\frac{Z}{{R_{\text{o}} }}} \right) + \left( {\frac{{\mu_{\text{M}} }}{{\mu_{\text{S}} }}} \right)} \right] $$

(33)

Substituting the above-mentioned set of equations, the force balance equation is rewritten as

$$ \frac{4}{3}\pi R_{\text{o}}^{3} \cdot \left( {\rho_{\text{I}} + \frac{1}{2}\rho_{\text{f}} } \right) \cdot \frac{{{\text{d}}^{2} Z}}{{{\text{d}}^{2} t}} = \frac{4}{3}\pi R_{\text{o}}^{3} \cdot \left( {\rho_{\text{f}} - \rho_{\text{I}} } \right)g - 2\pi R_{\text{o}} \cdot \sigma_{\text{MS}} \cdot \left( {\frac{Z}{{R_{\text{o}} }} - 1 - \frac{{\sigma_{\text{IM}} - \sigma_{\text{IS}} }}{{\sigma_{\text{MS}} }}} \right) - 2\pi \mu_{\text{f}} \cdot \left( {\frac{{2\mu_{\text{f}} + 3\mu_{\text{I}} }}{{\mu_{\text{f}} + \mu_{\text{I}} }}} \right)R_{\text{o}} \cdot \frac{{{\text{d}}Z}}{{{\text{d}}t}}, $$

(34)

where the ρ_f term is given as

$$ \rho_{\text{f}} = \rho_{\text{S}} \cdot \left[ {\frac{1}{4}\left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }} - 1} \right)\left( {\frac{Z}{{R_{\text{o}} }}} \right)^{3} - \frac{3}{4}\left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }} - 1} \right)\left( {\frac{Z}{{R_{\text{o}} }}} \right)^{2} + \left( {\frac{{\rho_{\text{M}} }}{{\rho_{\text{S}} }}} \right)} \right] $$

(35)

Combining Eqs. [33], [34] and [35], the inclusion displacement can be simulated.

The computer-code flow chart to implement the model is plotted in Figure 5. The new displacement (Z) is updated after each time step (1 × 10⁻⁷ [seconds]) and is used as the initial displacement for the next step iteration. The equations in the model are solved by using the commercial software MATLAB with the fourth-order Runge–Kutta (R–K) method (Figure 5).

Fig. 5

Model flow chart

Experimental Procedure

One industrial trial study was done at Uddeholms AB’s steel plant in Hagfors, Sweden. The samples come from the vacuum degassing stage in the ladle treatment process.

Process Description

Uddeholms AB is a scrap-based steel company, and the steel scrap is melted in an electric arc furnace with a nominal capacity of about 65 [ton]. When the melting and refining procedures are completed, the steel melt is tapped into a ladle and then transferred to the heating station. After the refining in the heating station, the ladle is transported to the vacuum degassing station, where a vacuum lid is placed on the top of the ladle. The stirring during vacuum is to promote the removal of the undesired elements, gases, and nonmetallic inclusions.

Sampling Procedure

Three types of samplings were performed as (i) steel sampling, (ii) slag sampling and (iii) temperature measurement. The sampling was made at three different time t = 0 [minutes], t = 20 [minutes] and t = 50 [minutes] during the vacuum degassing. The vacuum degassing was considered to start when the vacuum pressure reached 4 mbar. The average argon flow rate was about 150 [NL/min], and the inductive stirring power was 900 [A]. An automatic sampler[47] was applied for the steel sampling and temperature measurements. The slag samples were taken with a slag scoop in manual.

Analyses of Steel, Slag, and Inclusion

The carbon and sulfur contents in the steel samples were analyzed by the fusing method (CS-444 LS Leco Corporation in St. Joseph, MI, USA). The total oxygen content in the steel sample was also determined by the fusing method (TC-436 Leco Corporation in St. Joseph, MI, USA). The other elements in the steel samples were measured using a Phillips Perl X-2 XRF analyzer and an optical emissions spectrometer. The slag samples were ground and cast into small disks. Afterward, the samples were analyzed using an X-ray fluorescence meter (Siemens SRS 303). The identified slag basicity (= pct CaO/pct SiO₂) is between 5.1 and 6.2 in vacuum degassing process. The inclusion composition was determined using scanning electron microscope (SEM) (FEI-QUANTA600FEG-D8366) combined with commercial INCA-feature software. The INCA-feature enables the SEM to automatically scan the steel sample surface. When the system detects a gray scale difference compared to the metal matrix, supposedly an inclusion, it will perform an EDS-scan of the area and take a SEM image, and then continue the scanning procedure. The total scanning area for each sample in the current study is about 500 mm². The inclusion number is analyzed by means of CSD-corrections program. The reader is referred to Reference 48 for more details. Due to the uncertainties of the light elements (e.g., O) with this technique, only the metallic elements contents were used for the evaluation. At least 30 spherical liquid inclusions were analyzed in each sample, and the average composition is used in the model calculation. The contents of significant elements in steel, inclusions, and temperatures at different sampling times are summarized in Tables I and II. The averaged composition of inclusion is inserted into 6MgO-CaO-Al₂O₃-SiO₂ phase diagram[49] at 1873 K, as shown in Figure 6. It can be seen that the composition points are located in the liquid zone. Since the production temperature is higher than 1873 K, it is reasonable to estimate that the inclusions are in liquid state.

Table I Chemical Compositions of Significant Elements in Steel and Temperatures at Different Vacuum Degassing Times

Table II Chemical Compositions of Liquid Inclusions at Different Vacuum Degassing Times

Fig. 6

Distribution of averaged compositions of inclusion at different vacuum degassing time-points

Parameters Determination

Surface Tension of Slag and Liquid Inclusion

The surface tensions of the slag and liquid inclusion are calculated using the model of Tanaka et al.[50] based on the Butler’s equation. The surface tension of the 4-component molten slag can be expressed as

$$ \sigma_{\text{S}} = \sigma_{{{\text{SiO}}_{2} }}^{\text{Pure}} + \frac{\text{RT}}{{{{A}}_{{{\text{SiO}}_{2} }} }}{ \ln }\frac{{M_{{{\text{SiO}}_{2} }}^{\text{Surf}} }}{{M_{{{\text{SiO}}_{2} }}^{\text{Bulk}} }} $$

$$ \sigma_{\text{S}} = \sigma_{{{\text{Al}}_{2} {\text{O}}_{3} }}^{\text{Pure}} + \frac{\text{RT}}{{A_{{{\text{Al}}_{2} {\text{O}}_{3} }} }}{ \ln }\frac{{M_{{{\text{Al}}_{2} {\text{O}}_{3} }}^{\text{Surf}} }}{{M_{{{\text{Al}}_{2} {\text{O}}_{3} }}^{\text{Bulk}} }} $$

$$ \sigma_{\text{S}} = \sigma_{\text{CaO}}^{\text{Pure}} + \frac{\text{RT}}{{A_{\text{CaO}} }}{ \ln }\frac{{M_{\text{CaO}}^{\text{Surf}} }}{{M_{\text{CaO}}^{\text{Bulk}} }} $$

$$ \sigma_{\text{S}} = \sigma_{\text{MgO}}^{\text{Pure}} + \frac{\text{RT}}{{A_{\text{MgO}} }}{ \ln }\frac{{M_{\text{MgO}}^{\text{Surf}} }}{{M_{\text{MgO}}^{\text{Bulk}} }}, $$

(36)

and

$$ M_{\text{i}}^{\text{P}} = \frac{{\left( {\frac{{R_{\text{A}} }}{{R_{\text{X}} }} \cdot X_{\text{i}}^{\text{P}} } \right)}}{{\left( {\frac{{R_{{{\text{Si}}^{4 + } }} }}{{R_{{{\text{SiO}}_{4}^{4 - } }} }} \cdot X_{{{\text{SiO}}_{2} }}^{\text{P}} + \frac{{R_{{{\text{Al}}^{3 + } }} }}{{R_{{{\text{O}}^{2 - } }} }} \cdot X_{{{\text{Al}}_{2} {\text{O}}_{3} }}^{\text{P}} + \frac{{R_{{{\text{Ca}}^{2 + } }} }}{{R_{{{\text{O}}^{2 - } }} }} \cdot X_{\text{CaO}}^{\text{P}} + \frac{{R_{{{\text{Mg}}^{2 + } }} }}{{R_{{{\text{O}}^{2 - } }} }} \cdot X_{\text{MgO}}^{\text{P}} } \right)}}, $$

(37)

where R is the gas constant, T is the absolute temperature, σ ^Pure_i is the surface tension of pure component, and A_i is the surface area of each element, which can be calculated as follows:

$$ A_{i} = 1.091N_{\text{AV}}^{{\frac{1}{3}}} \cdot V_{i}^{{\frac{2}{3}}}, $$

(38)

where N_AV is Avogadro’s number of atoms N_AV= 6.02 × 10²³; V_i is the molar volume of each element. The subscripts “A” and “X” indicate the cation and anion of component “i,” respectively. M ^P _i is the mole fraction of compound “i” in phase P (P = “Surf” or “Bulk”). “Surf” and “Bulk” indicate the surface and bulk materials, respectively. R_i is the radius of cation or anion. The molar volume and surface tension of each pure oxide component are summarized in Table III, and the radii of different cations and anions are listed in Table IV.

Table III Molar Volumes and Surface Tensions of Oxide Components

Table IV Radii of Ion

Surface Tension of Liquid Steel

The surface tension of liquid steel is estimated as

$$ \sigma_{\text{M}} = \sigma_{0} - RT\varphi_{\text{O}} \ln \left( {1 + K_{\text{O}} \cdot [{\text{mass }}\,{\text{pct }}\,{\text{O}}] \cdot {\text{fo}}} \right) - RT\varphi_{\text{S}} \ln \left( {1 + K_{\text{S}} \cdot [{\text{mass}}\;{\text{pct S}}] \cdot {\text{f}}_{\text{S}} } \right), $$

(39)

where σ₀ is the overall surface tension of the metal components. φ_o and φ_s are the saturated surface excess concentrations of O and S, respectively. K_o and K_s denote the adsorption coefficients, respectively. f_o and f_s are the activity coefficients of O and S, respectively. The overall surface tension (σ₀) is obtained using the model of Hajra et al.,[55] and is given as

$$ 1 = \mathop \sum \nolimits X_{\text{i}} \cdot { \exp }\left[ {\frac{{(\sigma_{0} - \sigma_{\text{i}} )A_{\text{i}} }}{RT}} \right], $$

(40)

where X_i is the molar fraction of each metallic component in the steel. σ_i is the surface tension of pure metal component. A_i is the surface area of each element that can be obtained using Eq. [38]. The molar volume and surface tension of each element component are listed in Table V.

Table V Molar Volumes and Surface Tensions of the Pure Metals[56]

The adsorption coefficients (K_O and K_S) of S and O can be, respectively, given as[57]

$$ \log K_{\text{O}} = \frac{11370}{\text{T}} - 4.09 $$

(41)

$$ \log K_{\text{S}} = \frac{10013}{\text{T}} - 2.87 $$

(42)

The saturated surface excess concentrations of O and S, which changed with the Cr content are summarized based on the literature and are plotted in Figure 7. The values of φ_o and φ_s for the current steel grade (pct Cr ≈ 5 [mass pct]) are estimated as 2.06 × 10⁻⁵ and 1.26 × 10⁻⁵, respectively.

Fig. 7

Saturated surface excess concentration of O and S which changed with Cr content in steel.[58,59,60,61,62,63]

The activity coefficients (f_o and f_s) can be determined by means of the Wagners equation:

$$ \log f_{\text{s}} = \mathop \sum \limits_{j} e_{\text{s}}^{j} [{\text{mass}}\,{\text{pct}}\,j] $$

(43)

$$ \log f_{\text{O}} = \mathop \sum \limits_{j} e_{\text{O}}^{j} [{\text{mass}}\,{\text{pct }}j]. $$

(44)

The interaction parameters are summarized in Table VI.

Table VI Interaction Parameters[64,65,66,67]

Interfacial Tension Between Two Different Phases

The interfacial tension between two liquids is described using the equation of Girifalco and Good,[68] which is given by

$$ \sigma_{{{\text{liquid}}1 - {\text{liquid}}2}} = \sigma_{{{\text{liquid}}1}} + \sigma_{{{\text{liquid}}2}} - 2\phi \cdot (\sigma_{{{\text{liquid}}1}} \cdot \sigma_{{{\text{liquid}}2}} )^{0.5}, $$

(45)

where ϕ is the interaction coefficient. For the cases of the slag–steel and liquid inclusion–steel interaction, the interaction coefficient is taken as ϕ= 0.5 + 0.3X_FeO.[69] In the case of the slag–liquid inclusion interaction, the interaction coefficient is assumed to be 0.5.

Density of Slag and Steel

The slag and steel density can be calculated using the equation given below:

$$ \rho = \frac{M}{V} = \frac{{\mathop \sum \nolimits X_{i} \cdot M_{i} }}{{\mathop \sum \nolimits X_{i} \cdot V_{i} }}, $$

(46)

where M_i is the molar weight of each metallic/oxide component. The molar volumes (V_i) are listed in Tables III and V.

Viscosities of Steel and Slag

The slag viscosity is calculated by means of Thermo-slag software.[70] The viscosity of liquid steel is estimated as[71]

$$ \mu_{\text{M}} = 21.24 - 0.0102 \cdot (T - 273) [{\text{mpa}}\,{\text{seconds}}] $$

(47)

Results and Discussions

The calculated parameters based on information in Section IV are summarized in Table VII. Using Table VII and the current developed model, the liquid inclusion behavior at the steel–slag interface can be predicted. The vertical terminal velocity of the inclusion is estimated to be about 1.0 [m/s].

Table VII Calculated Values of Surface Tension, Interfacial Tension, Density, and Viscosity

Inclusion Motion Behavior at Film Drainage Stage

Figure 8 shows the motion behavior of the liquid inclusion at the initial stage of the vacuum degassing (t = 0). Five different inclusion sizes (5, 10, 20, 50, and 100 [μm]) are selected for the analysis. According to Figure 8(a), when the vertical terminal velocity of the liquid inclusion is 1.0 [m/s], the maximum inclusion displacement increases with the increased inclusion size. In the cases of R = 50 [μm] and R = 100 [μm], the maximum inclusion displacements are much larger than the critical displacement of the film rupture. This means that the liquid inclusions can penetrate the thin film, and then simultaneously contact with the slag and steel. However, for the R = 5 [μm], R = 10 [μm] and R = 20 [μm] cases, the maximum displacements are smaller than the critical displacement, which indicates that the film rupture cannot occur. After arriving at the maximum displacements, the inclusions are rebounded back, and finally return to the liquid steel (Z/R_o = 0). Figure 8(b) shows the inclusion motion with the terminal velocity of 0.5 [m/s]. The larger inclusions can obtain a larger maximum displacement, compared the smaller inclusions. Meanwhile, the rebounding time of the larger inclusions is longer than that of the smaller inclusions. However, the maximum displacements in all the cases decrease to certain positions below the critical displacement. It indicates that none of them can pass through the thin film.

Fig. 8

Dimensionless displacements of inclusions with the terminal velocity as (a) 1.0 [m/s] and (b) 0.5 [m/s]

The above-mentioned analysis shows that both the vertical terminal velocity and inclusion size play important roles on the inclusion detachment. An inclusion needs to have a large vertical terminal velocity or/and a large size to pass through the thin film. Figure 9 shows the critical inclusion radius of the film rupture changing with the increased vertical terminal velocity. The critical inclusion radius of the detachment is almost the same during the vacuum degassing (t = 0 to 50 [minutes]). Moreover, the decrease rate of the critical radius decreases with the increased vertical terminal velocity. In order to validate the predicted critical inclusion size, the results of average inclusion size and inclusion size distribution are analyzed, as shown in Figure 10. According to Figure 10(a), the averaged inclusion size increases from about 6 [μm] to 16 [μm] during the first 20 minutes vacuum treatment. When the time increases from 20 to 50 minutes, the average inclusion size increases to about 10 [μm]. Based on the inclusion size distribution in Figure 10(b), all the observed inclusions are smaller than 20 [μm] at the initial stage of vacuum treatment. After 20 minutes, the number of inclusions, which are smaller than about 6 [μm], considerably decreases. Meanwhile, the larger inclusions (> 20 [μm]) appear. It indicates that the agglomerations among inclusions occur. After 50 minutes vacuum treatment, the larger inclusions (> 20 [μm]) cannot be identified, and the observed maximum inclusion is about 20 [μm]. At the current production condition, the predicted critical radius of liquid inclusion for detaching is approximately 25 to 30 [μm] that is slightly larger than the observed maximum value (≈ 20 [μm]). The current model shows a good potential to predict the maximum size of inclusion for detachment.

Fig. 9

Relationship between critical radii of inclusion changes and terminal velocity during vacuum treatment

Fig. 10

Time-dependent (a) average inclusion size and (b) inclusion size distribution during the vacuum degassing treatment

In order to understand the motion mechanism of the liquid inclusion at the film drainage stage, different forces acting on the inclusions need to be further analyzed. Figure 11 shows the forces in the cases of R = 5 [µm] and R = 100 [µm] at the time t = 0. An average pressure (= force/ inclusion cross-sectional area) is used for the comparison convenience. Figure 11(a) shows that the gravitational force term (F_G) is constant and equals 0.26 [Pa] for R = 5 [µm] and 5.13 [Pa] for R = 100 [µm]. According to Figure 11(b), the pressure force term (F_P) of R = 5 [µm] increases to 8.54 × 10⁻⁵ [Pa] when the inclusion approaches to the maximum displacement. Afterward, the average pressure decreases to zero when the inclusion is rebounded back to the initial position. In the case of R = 100 [µm], the average pressure keep increasing, and then reaches 0.03 [Pa] at the film rupture position. The capillary force term (F_C) almost maintains a constant at the film drainage stage with the downward direction, as is shown in Figure 11(c). Meanwhile, the average pressure in the case of R = 5[µm] (= 2.75 × 10⁵ [Pa]) is much larger than that in the case of R = 100 [µm] (=1.38 × 10⁴ [Pa]). As for the added mass force term (F_A) in Figure 11(d), the average pressure in the case of R = 5[µm] and R = 100[µm] slightly decreases from 1.50 × 10⁵ to 1.45 × 10⁵ [Pa] and from 7.52 × 10³ to 7.19 × 10³ [Pa] at the drainage stage. In the case of the drag force term (F_D) in Figure 11(e), the downward pressure of R = 5[µm] decreases from 5.49 × 10³ to 0 [Pa] when the inclusion arrives at the maximum displacement. After that, the average pressure increases reversely to 5.56 × 10³ [Pa] when the inclusion is rebounded back to the initial position. In the case of R = 100 [µm], the average downward pressure gradually decreases from 274 to 244 [Pa] at the film drainage stage.

Fig. 11

Average pressures of different force terms as (a) gravitational force, (b) pressure force, (c) capillary force, (d) added mass force and (e) drag force changing with the increased time at film drainage stage

According to the force analysis, it shows that the gravitational force and pressure force can be negligible, compared with the other forces. The main contribution to the lift net force during the film drainage is the added mass force. If the inclusion can be rebounded back by the thin film, the drag force acting on small size inclusions also makes contribution to the lift net force in the rebounding process. The contributions to the downward net force at the film drainage stage are capillary force and drag force (before reaching at the maximum displacement). The main force influencing the inclusion motion at the film drainage stage is the capillary force in the downward direction. According to Eq. [13], it is clear that if other parameters are kept fixed, a lower slag surface tension will be helpful to decrease the capillary force.

Figure 12 shows the decreasing percentage of the inclusion velocity after the film rupture. It shows that the velocity decrease is almost the same when the vacuum degassing time increases from t = 0 to t = 50 [min]. A larger inclusion has a smaller velocity decrease, compared with a smaller inclusion. Based on the above-mentioned force analysis, the difference between the large and small inclusion sizes is mainly due to different capillary force and added mass force. After the film rupture, the inclusions can further move with the decreased terminal velocity at the steel–slag interface.

Fig. 12

Decreasing percentage of the inclusion velocity with the increasing inclusion size during vacuum treatment after film rupture

Inclusion Motion Behavior After Film Rupture

If the inclusion can penetrate into the thin film, it will further move at the steel–slag interface. The time point, which film rupture occurs, is set to be the initial time. In Section V–A, it shows that the critical inclusion radius of the film rupture is about 21 [µm] in the current study. It is interesting to select a little larger inclusion (= 23 [µm]) than this critical value, and analyze the motion behavior. The inclusion radius R = 50 [µm] and R = 100 [µm] are also selected as the examples. Figure 13 shows the dimensionless inclusion displacement in different vacuum degassing time. It shows that in all the three cases the inclusions can be detached (Z/R_o = 2), and the detachment time is increased with the increasing inclusion size. It also shows that the detachment time of R = 23 [µm] remains almost constant with the increasing time. However, for both the R = 50 and R = 100 [µm] cases, the detachment time becomes longer when the time increases from t = 0 to t = 20 [min]. When the time further increases from t = 20 to t = 50 [min], the detachment time maintains constant.

Fig. 13

Dimensionless displacement of different size inclusions during vacuum degassing after film rupture at the vacuum time (a) 0 [min], (b) 20 [min] and (c) 50 [min]

According to the current model, the velocity decrease of R = 23 [µm] after the film rupture is about 68 to 77 pct during the vacuum degassing. However, the inclusion still can be immersed into the slag and even has a shorter detachment time than that of R = 50 [µm] and R = 100 [µm]. One reason is that the detachment–displacement of a small inclusion is smaller than that of a large inclusion. Another reason is the contribution of the net force that depends on the inclusion size. Figure 14 shows the overall average pressure driven by the net force and inclusion velocity at the initial stage of the vacuum degassing. It can be seen that at the initial stage of the inclusion motion, the average pressure is in the upward direction and accelerate the inclusion. The average pressures of R = 23 [µm] and R = 50 [µm] are much larger than that of R = 100 [µm]. It indicates that the velocity of a smaller inclusion can be increased much faster than that of a bigger inclusion. The average pressure decreases with the inclusion movement. The decreasing rates of R = 23 [µm] and R = 50 [µm] are higher, compared with that of R = 100 [µm]. When the inclusion arrives at certain displacements, the average pressure increases reversely and decreases the inclusion velocity. The inclusions in all the three cases can be detached into the slag before the velocities decrease to zero.

Fig. 14

(a) Average pressures of combined force and (b) inclusion motion speed which changed with the increasing time after film rupture

Figure 15 shows the average pressure of the difference force terms. It is found that the gravitational force term (F_G) is much smaller than the other force terms. The initial average pressure of the capillary force term (F_C) decreases in the order of (i) 1.92×10⁵ [Pa] for R = 23 [µm], (ii) 0.89×10⁵ for R = 50 [µm] and (iii) 0.44×10⁵ for R = 100 [µm]. With inclusion movement, the average pressure decreases to zero and then increases reversely in all the three cases. In the case of the added mass force term (F_A), the average pressures of R = 50 [µm] and R = 100 [µm] decrease firstly and then reversely increase with the downward direction. As for the case of 23, the initial average pressure (= 0.56 × 10⁴ [Pa]) has a downward direction and has a decrease and increase oscillation. When the inclusion arrives at the detachment position, the average pressure becomes almost zero. In the case of the drag force term (F_D), the average pressure with the downward direction increases to maxima as 0.63 × 10⁵ for R = 23 [µm], 0.40 × 10⁵ for R = 50 [µm] and 0.19 × 10⁵ [Pa] for R = 100 [µm]. Thereafter, the average pressure decreases to certain values near zero. According to the above-mentioned force analysis, it is concluded that the inclusion acceleration is mainly due to the capillary force and added mass force. And the inclusion deceleration is driven by the contributions of the capillary force, added mass force and drag force.

Fig. 15

Average pressures of different force terms as (a) gravitational force, (b) capillary force, (c) added mass force and (d) drag force which changed with the increasing time after film rupture

Conclusions

The motion and detachment behaviors of liquid inclusion at the steel–slag interface were theoretically studied. A mathematical model using the force balance equation was developed. It was found that the thin-film drainage is the main stage of the inclusion detachment. If the inclusion can penetrate into the thin film, it can be detached into the slag. At the drainage stage, the main force is the capillary force, and the impacts of the gravitational force and pressure force are negligible. If the film rupture can occur, the triple interface among the liquid inclusion, steel, and slag can affect the inclusion detachment time. However, this stage does not seem to be the key factor of the detachment. At a given physical condition (e.g., steel and slag composition, temperature, etc.), the critical inclusion size of the detachment can be calculated using the current proposed model. A high upward terminal velocity, a large inclusion size, and a small slag surface tension are conducive to the liquid inclusion detachment.