Solid Phase Equilibrium Relations in the CaO-SiO₂-Nb₂O₅-La₂O₃ System at 1273 K

Abstract

Silicate slag system with additions Nb and RE formed in the utilization of REE-Nb-Fe ore deposit resources in China has industrial uses as a metallurgical slag system. The lack of a phase diagram, theoretical, and thermodynamic information for the multi-component system restrict the comprehensive utilization process. In the current work, solid phase equilibrium relations in the CaO-SiO₂-Nb₂O₅-La₂O₃ quaternary system at 1273 K (1000 °C) were investigated experimentally by the high-temperature equilibrium experiment followed by X-ray diffraction, scanning electron microscope, and energy dispersive spectrometer. Six spatial independent tetrahedron fields in the CaO-SiO₂-Nb₂O₅-La₂O₃ system phase diagram were determined by the Gibbs Phase Rule. The current work combines the mass fraction of equilibrium phase and corresponding geometric relation. A determinant method was deduced to calculate the mass fraction of equilibrium phase in quaternary system according to the Mass Conservation Law, the Gibbs Phase Rule, the Lever’s Rule, and the Cramer Law.

Introduction

China’s Inner Mongolia contains a large rare earth element-Nb-Fe complex ore deposit: Bayan Obo REE-Nb-Fe. Extracting valuable elements from the REE-Nb-FE ore deposit imposes difficulties due to the multiple-element symbiotic specificity. Until now, niobium and rare earth resources were wasted as tailings in the ore dressing process, which led to a huge waste of resources.[1] Processes and techniques to smelt metal niobium and enrich rare earth resources from the tailings have been proposed, but the processes have flaws in the low metal yield and high cost. The uncertainties of thermodynamic property especially the phase diagram data for the tailings with niobium and rare earth severely restrict the development of above mentioned processes.[2] In correlative slag phase diagrams, CaO-SiO₂-Nb₂O₅ ternary system had been investigated by Jongejan and Wilkins.[3] Previous work did not study the phase diagram for the slag system with Nb and REE. Phase relations for the slag system with REE and Nb remain unclear, making it necessary to update the fundamental thermodynamic information for the development and application of processing the slag. The CaO-SiO₂-Nb₂O₅-La₂O₃ system contains the most directly related slag system during the pyrometallurgy extraction process of niobium and rare earth resources in REE-Nb-Fe ore deposit.

The most common scientific method for the investigation of silicate system phase diagrams uses the high-temperature equilibrium experiment.[4,5,6,7] Relations between equilibrium phases and the corresponding proportion relation contain important thermodynamic information in phase diagram.[8] Little research exists for the proportion relation of equilibrium phases in a multi-component system. This also limits the study on multi-component system phase diagram.

In the current work, solid phase equilibrium relations and corresponding proportion relation in the CaO-SiO₂-Nb₂O₅-La₂O₃ system within the specified region were determined experimentally by the high-temperature equilibrium experiment followed by the X-ray diffraction (XRD), the scanning electron microscope (SEM), and the energy dispersive spectroscope (EDS) analysis. The current research provides significant results for the quaternary system and application of multi-component system phase diagram with benefits to the comprehensive utilization for niobium and rare earth resources.

Experiment

In this section, we describe the preparation and equilibrium experiments for determining solid phase equilibrium relations in the CaO-SiO₂-Nb₂O₅-La₂O₃ quaternary system.

Sample Preparation

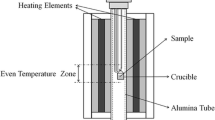
Reagent grade oxide powders (provided by the Sinopharm Chemical Reagent Co., Ltd.) of CaO (99.99 mass fraction pure), SiO₂ (99.99 mass fraction pure), Nb₂O₅ (99.99 mass fraction pure), and La₂O₃ (99.99 mass fraction pure) were used to prepare the slags, which were calcined at 1273 K (1000 °C) for 14,400 seconds to evaporate the moisture and impurities. 0.015 kg mixtures were carefully weighed, fully mixed, and pre-melted in air atmosphere using MoSi₂ furnace. The mixtures were placed inside platinum crucibles and placed inside the furnace at 1873 K (1600 °C) for 21,600 seconds to completely homogenize the slags. The size of platinum crucibles for pre-melt has an upper diameter 0.04 m, bottom diameter 0.03 m, and height 0.038 m. The pre-melt time was decided by pre-experiment by determining that 21,600 seconds was enough to achieve the homogenization of slag. After homogenization of the slag, the samples were quenched into ice-water, dried, crushed, and ground to 200 meshes for further use. Temperature was monitored by a B-type thermocouple placed next to the samples with an overall temperature accuracy estimated to 2 K.

The pre-melt slag was analyzed by XRD and SEM to ensure the effect of pre-melt experiments, the EDS result, as listed in Table I, was used as the initial composition of pre-melt slag. Quenching by ice-water ensured that the quenched slags showed glassy phase, as shown in Figures 1 and 2. The pre-melt results showed that 1873 K (1600 °C) achieved the homogenization of slag samples. The compositions of pre-melt slag measured by EDS are projected on the CaO-SiO₂-Nb₂O₅-10 wt pct La₂O₃ pseudo-ternary phase diagram, as shown in Figure 3.

Table I The Comparison of Designed and EDS Measured Compositions of Pre-melt Slags (Mass Pct)

Fig. 1

XRD result of typical pre-melt slag

Fig. 2

Backscattered electron image of typical pre-melt slag

Fig. 3

The projection of pre-melt compositions on CaO-SiO₂-Nb₂O₅-10 wt pct La₂O₃ pseudo-ternary phase diagram

Equilibrium Experiments

The MoSi₂ furnace used for the pre-melt was also used for the equilibrium experiment. The pre-melt slag (0.0015 kg for each slag) was placed in the platinum crucible and placed into the hot zone of the MoSi₂ furnace. The curve of controlled temperature was shown in Figure 4. It was found that the complete crystallization temperature of each slag was above 1273 K in pre-experiment, in order to ensure that each slag could crystallize completely, the equilibrium temperature in the equilibrium experiment was determined to be 1273 K (1000 °C). The equilibration time lasted 86,400 seconds based on experiences reported by previous authors,[9,10,11,12] repeat experiments with 172,800 seconds were performed for some samples to check whether the equilibrium was achieved. There was no significant difference between the equilibrium phases with longer equilibration time. After the equilibrium, the sample was rapidly taken out from the furnace and quenched to 273 K (0 °C) by ice-water, the quenching process was completed in 2 seconds to ensured that all samples maintained the high-temperature equilibrium phase composition and construction. Quenched samples were dried and embedded in epoxy resin and polished for analysis. SEM, XRD, and EDS were used to identify the phase equilibrium relations and analyze the composition of each phase in the samples.

Fig. 4

Curve of controlled temperature in high-temperature equilibrium experiment

Results and Discussion

We discuss details related to the equilibrium phase relations at 1273 K, determine independent tetrahedron, and perform quantitative analysis on each equilibrium phase.

Equilibrium Phase Relations at 1273 K

The microstructure and composition of the equilibrium phases at 1273 K (1000 °C) are shown in Table II and Figure 5, respectively. The composition of the equilibrium phase has been composed of the average values calculated from six different analysis points in the sample. Figure 5(a) shows the four phases that were detected by SEM for sample #1, based on the XRD result of sample #1 we can confirm that the black phase consists of SiO₂, the deep gray phase consists of CaO·Nb₂O₅, the white phase consists of La₂O₃·6Nb₂O₅, and the light gray phase consists of Nb₂O₅. Based on the EDS results, elemental calcium was found in the composition of La₂O₃·6Nb₂O₅, and elemental lanthanum was found in the composition of CaO·Nb₂O₅ and 2CaO·Nb₂O₅. Frolov and Evdokimov[13] found that elemental calcium can be dissolved in La₂O₃·6Nb₂O₅ and elemental lanthanum can be dissolved in CaO·Nb₂O₅ and 2CaO·Nb₂O₅ within a certain composition range. In Figure 5(b), four phases were detected by SEM for sample #2, we confirm that the light gray with strip shape consists of CaO·Nb₂O₅, the black phase consists of SiO₂, the white phase with block shape consists of La₂O₃·Nb₂O₅, and the deep gray phase consists of CaO·SiO₂. In Figure 5(c), four phases were detected by SEM for sample #3, based on the XRD result, we confirm that the black phase consists of CaO·SiO₂, the gray phase with strip shape consists of CaO·Nb₂O₅ and 2CaO·Nb₂O₅, the white phase consists of La₂O₃·Nb₂O₅. The SEM microphotographs show no difference in morphology and contrast between CaO·Nb₂O₅ and 2CaO·Nb₂O₅. In Figure 5(d), four phases were detected by SEM for sample #4, based on the XRD result of #4, we confirm that the gray phase with strip shape consists of 2CaO·Nb₂O₅, the black phase consists of CaO·SiO₂, the white phase with block shape consists of La₂O₃·Nb₂O₅, and the deep gray phase consists of 10CaO·6SiO₂·Nb₂O₅. The CaO-SiO₂-Nb₂O₅ ternary compound, known as “Niocalite”, was first discovered by Nickel.[14] Elemental lanthanum was detected in the 10CaO·6SiO₂·Nb₂O₅ using EDS in the current experiment.

Table II Experimental Determined Phase Compositions of Equilibrium Phase at 1273 K (1000 °C) in CaO-SiO₂-Nb₂O₅-La₂O₃ System

Fig. 5

SEM microphotographs of equilibrium phases at 1273 K (1000 °C)

Determination of Independent Tetrahedron

Under the constant pressure condition, the Gibbs Phase Rule for the system can be expressed as Formula (1).

$$ F = C - P + 1. $$

(1)

The terms F, C, and P in Formula (1) are the number of degrees of freedom, components, and equilibrium phases,[15] respectively. The completely crystallized temperature for the system approaches T _s under constant pressure conditions. When T is less than T _s and the solid phase decomposition did not appear in the system, the degree of freedom could be represented as the uniform function of the temperature, implying that the number of components equal the number of equilibrium phases. Table III shows the relationship between “C”, “F”, and “P”. It can be seen that four equilibrium solid phases coexist in the CaO-SiO₂-Nb₂O₅-La₂O₃ system at T < T _s.

Table III Relationship Between C and P in Silicate System with Constant Pressure and T < T _s

According to the equilibrium experiment results and the compatibility of phase diagram, six independent tetrahedron fields in the CaO-SiO₂-Nb₂O₅-La₂O₃ system were determined, as shown in Table IV and Figure 6. The Tetrahedrons ⑤ and ⑥ were determined by the Tetrahedrons ① and ② according to the existing phase information in related sub-systems[16,17] and the compatibility of phase diagram.

Table IV Independent Tetrahedron Fields in the CaO-SiO₂-Nb₂O₅-La₂O₃ System

Fig. 6

Positions of the independent tetrahedrons field in the spatial quaternary phase diagram

Quantitative Analysis of Each Equilibrium Phase

After the determination of an independent tetrahedron field in the spatial phase diagram, for any component point in it at T lower than T _s, proportion relation of the equilibrium solid phases could be calculated by the relative position of the initial component point and the related equilibrium phase. However, due to the quaternary tetrahedral phase, diagram cannot be represented by a flat graphic. In the current work, we present a determinant calculation method to evaluate whether a given component point exists in a certain tetrahedral field in the quaternary system phase diagram. Using the determinant calculation, the proportion relation of the equilibrium phases can also be calculated. The relevant steps and principles of the determinant calculation method will be introduced using the example quaternary system.

As shown in Figure 7, A, B, C, and D represent the four hypothetical basic phases of the A–B–C–D quaternary system. M, N, P, and Q represent the equilibrium phases involved in the related tetrahedron field. The initial composition of sample E, involved in the discussion as an example, is that mass pct A = A _E, mass pct B = B _E, mass pct C = C _E, and mass pct D = D _E. Table V shows the theoretical composition of phases M, N, P, and Q. We can then construct the determinant V as represented in Formula (2).

$$ V = \left| {\begin{array}{ccccc} 1 & 1 & 1 & 1 & 1 \\ {A_{\text{M}} } & {A_{\text{N}} } & {A_{\text{P}} } & {A_{\text{Q}} } & {A_{\text{E}} } \\ {B_{\text{M}} } & {B_{\text{N}} } & {B_{\text{P}} } & {B_{\text{Q}} } & {B_{\text{E}} } \\ {C_{\text{M}} } & {C_{\text{N}} } & {C_{\text{P}} } & {C_{\text{Q}} } & {C_{\text{E}} } \\ {D_{\text{M}} } & {D_{\text{N}} } & {D_{\text{P}} } & {D_{\text{Q}} } & {D_{\text{E}} } \\ \end{array} } \right|. $$

(2)

Fig. 7

A spatial illustration of the relationship in the A–B–C–D quaternary system phase diagram

Table V The Theoretical Composition of Phases M, N, P, and Q

Set V _M = |A ₁₁|, V _N = |A ₁₂|, V _P = |A ₁₃|, V _Q = |A ₁₄|, and V _E = |A ₁₅|, that are the absolute value of the “algebraic cofactor” of each element in the first row of the determinant in Formula (2), as shown in Formula (3) for example.

$$ \left| {A_{11} } \right| = \left\| {\begin{array}{cccc} {A_{\text{N}} } & {A_{\text{P}} } & {A_{\text{Q}} } & {A_{\text{E}} } \\ {B_{\text{N}} } & {B_{\text{P}} } & {B_{\text{Q}} } & {B_{\text{E}} } \\ {C_{\text{N}} } & {C_{\text{P}} } & {C_{\text{Q}} } & {C_{\text{E}} } \\ {D_{\text{N}} } & {D_{\text{P}} } & {D_{\text{Q}} } & {D_{\text{E}} } \\ \end{array} } \right\|. $$

(3)

When the equation V _M + V _N + V _P + V _Q = V _E holds, sample E exists inside the tetrahedral field M–N–P–Q and its low temperature equilibrium phases are M, N, P, and Q. (Of course the equation holds in the discussion due to the initial setup.) Moreover, the equilibrium mass fraction of phases M, N, P, and Q is $\frac{{V_{\text{M}} }}{{V_{\text{E}} }} \times 100\,{\text{pct}},\;\frac{{V_{\text{N}} }}{{V_{\text{E}} }}{{\times}}100\,{\text{pct}},\;\frac{{V_{\text{P}} }}{{V_{\text{E}} }}{{\times}}100\,{\text{pct}}$ and $\frac{{V_{\text{Q}} }}{{V_{\text{E}} }} \times 100\,{\text{pct}},$ respectively. The equilibrium mass fraction of the M phase equals the volume ratio of the tetrahedron N–P–Q–E and the tetrahedron M–N–P–Q. Intuitively, the mass fraction of each equilibrium phase could be determined by the volume ratio of the related tetrahedrons. The physical meaning of this equivalence process can be the theoretical Spatial Lever Rule.

We will now derive the Spatial Lever Rule, Figure 8, as a spatial tetrahedron representing a quaternary system. A component point, as O, in A–B–C–D quaternary system is taken for an example to deduce the expression of the Spatial Lever’s Rule under the condition of multi-phase equilibrium. First, connects DO and extends it, crosses the plane A–B–C at point M. Second, connects AO, BO, CO, AM, BM, and CM, respectively. So DP and ON are perpendicular to plane A–B–C.

Fig. 8

Schematic diagram for deduction of Spatial Lever Rule in quaternary system

According to the application of the Lever’s Rule when two phase equilibrium appears, the composition of point O can be expressed as Formula (4):

$$ O = \frac{\text{DO}}{\text{DM}}\,*\,100\,{\text{pct}}\,*\,M + \frac{\text{OM}}{\text{DM}} \,*\,100\,{\text{pct}}\,*\,D. $$

(4)

For component point O, it can be found that the mass fraction of component M is $\frac{\text{DO}}{\text{DM}}\,*\,100\,{\text{pct}}$ and the mass fraction of phase D is $\frac{\text{OM}}{\text{DM}}\,*\,100\,{\text{pct}}.$ Due to the line segment ON and DP are perpendicular to plane A–B–C at same time, Formulae (5) and (6) can be deduce as follow:

$$ \frac{\text{OM}}{\text{DM}} = \frac{\text{ON}}{\text{DP}} = \frac{{h_{{{\text{tetrahedron}}\;{\text{A}} {-} {\text{B}} {-} {\text{C}} {-} {\text{O}}}} }}{{h_{{{\text{tetrahedron}}\;{\text{A}} {-} {\text{B}} {-} {\text{C}} {-} {\text{D}}}} }}, $$

(5)

$$ \frac{\text{MO}}{\text{DM}} = \frac{{S_{{\Updelta {\text{ABC}}}} \,*\,h_{{{\text{tetrahedron}}\;{\text{A}} {-} {\text{B}} {-} {\text{C}} {-} {\text{O}}}} }}{{S_{{\Updelta {\text{ABC}}}} \,*\,h_{{{\text{tetrahedron}}\;{\text{A}} {-} {\text{B}} {-} {\text{C}} {-} {\text{D}}}} }} = \frac{{V_{{{\text{tetrahedron}}\;{\text{A}} {-} {\text{B}} {-} {\text{C}} {-} {\text{O}}}} }}{{V_{{{\text{tetrahedron}}\;{\text{A}} {-} {\text{B}} {-} {\text{C}} {-} {\text{D}}}} }}. $$

(6)

From the Formula (3), it can be found that the mass fraction of phase D can be represented by $\frac{{V_{{{\text{tetrahedron}}\;{\text{A}} {-} {\text{B}} {-} {\text{C}} {-} {\text{O}}}} }}{{V_{{{\text{tetrahedron}}\;{\text{A}} {-} {\text{B}} {-} {\text{C}} {-} {\text{D}}}} }}\,*\,100\,{\text{pct}},$ the mass fraction of other equilibrium phase can be deduced similarly.

In addition to the solid phase, the equilibrium liquid phase could also participate in the calculation process to form the apex of related tetrahedron field. In other words, it is the numerical expression of the Spatial Lever Rule. This method has been used with four-phase equilibrium, but also been used with three-phase (or less than three) equilibrium. The numbers of component in relevant formula need to be reduced and related volume ratio need to be changed to area ratio (or length ratio, corresponding to the traditional Lever’s Rule) in space. In multi-component system (more than four) phase diagram, the physical meaning of the mass fraction of equilibrium phase cannot be intuitively expressed by geometric relation, but the determinant calculation method can still be used.

The results of the equilibrium experiment at 1273 K (1000 °C) of #1 slag in the CaO-SiO₂-La₂O₃-Nb₂O₅ system were taken as examples, the proportion relations of the equilibrium phases in the sample were calculated by the related determinant. The composition of La₂O₃·6Nb₂O₅, Nb₂O₅, SiO₂, and CaO·Nb₂O₅ and the initial composition of #1 slag are shown in Table VI.

Table VI The Theoretical Composition of La₂O₃·6Nb₂O₅, Nb₂O₅, SiO₂, and CaO·Nb₂O₅ and Initial Composition of slag #1

Substituting the data into Formula (1) to get Formulae (7) through (9) can be obtained simultaneously. And then, the equilibrium mass fraction of La₂O₃·6Nb₂O₅ can be calculated, the calculation of other equilibrium phases can be carried out in the same way, the results are given in Table VII.

$$ V = \left| {\begin{array}{ccccc} 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ {1.48\,{\text{pct}}} \hfill & 0 \hfill & 0 \hfill & {10.90\,{\text{pct}}} \hfill & {4.23\,{\text{pct}}} \hfill \\ 0 \hfill & 0 \hfill & {100.00\,{\text{pct}}} \hfill & 0 \hfill & {3.42\,{\text{pct}}} \hfill \\ {14.49\,{\text{pct}}} \hfill & 0 \hfill & 0 \hfill & {6.33\,{\text{pct}}} \hfill & {11.29\,{\text{pct}}} \hfill \\ {84.03\,{\text{pct}}} \hfill & {100.00\,{\text{pct}}} \hfill & 0 \hfill & {82.77\,{\text{pct}}} \hfill & {81.06\,{\text{pct}}} \hfill \\ \end{array} } \right|, $$

(7)

$$ V_{{{\text{La}}_{2} {\text{O}}_{3} \cdot 6{\text{Nb}}_{2} {\text{O}}_{5} }} = \left| {A_{11} } \right| = \left\| {\begin{array}{cccc} 0 \hfill & 0 \hfill & {10.90\,{\text{pct}}} \hfill & {4.23\,{\text{pct}}} \hfill \\ 0 \hfill & {100.00\,{\text{pct}}} \hfill & 0 \hfill & {3.42\,{\text{pct}}} \hfill \\ 0 \hfill & 0 \hfill & {6.33\,{\text{pct}}} \hfill & {11.29\,{\text{pct}}} \hfill \\ {100.00\,{\text{pct}}} \hfill & 0 \hfill & {82.77\,{\text{pct}}} \hfill & {81.06\,{\text{pct}}} \hfill \\ \end{array} } \right\| = 0.00962851, $$

(8)

$$ V_{\# 1} = \left| {V_{15} } \right| = \left\| {\begin{array}{cccc} {1.48\,{\text{pct}}} \hfill & 0 \hfill & 0 \hfill & {10.90\,{\text{pct}}} \hfill \\ 0 \hfill & 0 \hfill & {100\,{\text{pct}}} \hfill & 0 \hfill \\ {14.49\,{\text{pct}}} \hfill & 0 \hfill & 0 \hfill & {6.33\,{\text{pct}}} \hfill \\ {84.03\,{\text{pct}}} \hfill & {100\,{\text{pct}}} \hfill & 0 \hfill & {82.77\,{\text{pct}}} \hfill \\ \end{array} } \right\| = 0.01485726. $$

(9)

Table VII Mass Fraction of Each Equilibrium Phase of Slag #1 at 1273 K (1000 °C)

The mass fraction of La₂O₃·6Nb₂O₅ can obtained by $V_{{{\text{La}}_{2} {\text{O}}_{3} \cdot 6{\text{Nb}}_{2} {\text{O}}_{5} }} /V_{\# 1} .$ Similarly, we can get $V_{{{\text{Nb}}_{2} {\text{O}}_{5} }} = |A_{12} | = 0.00026228,\;V_{{{\text{SiO}}_{2} }} = |A_{13} | = 0.000508118,\;V_{{{\text{CaO}} \cdot {\text{Nb}}_{2} {\text{O}}_{5} }} = |A_{14} | = 0.00445835.$ The value of the determinants is numerically satisfied with $V_{{{\text{La}}_{2} {\text{O}}_{3} \cdot 6{\text{Nb}}_{2} {\text{O}}_{5} }} + V_{{{\text{Nb}}_{2} {\text{O}}_{5} }} + V_{{{\text{SiO}}_{2} }} + V_{{{\text{CaO}} \cdot {\text{Nb}}_{2} {\text{O}}_{5} }} = V_{\# 1} .$ Further calculation results are given in Table VII. The mass fraction of equilibrium phases of sample #1 at 1273 K were calculated by this method.

The mass fraction of equilibrium phases of samples #2, #3, and #4 at 1273 K were calculated respectively at same time, the results were given in Table VIII. All equilibrium phases were conversion to initial composition according to their mass fraction and composition, the comparison between initial composition measured by EDS and calculated by conversion were given in Table IX. It was found that the results showed good consistency.

Table VIII Mass Fraction of Each Equilibrium Phase of Slags #2 Through #4 at 1273 K (1000 °C)

Table IX The Comparison Between Composition of Slags #1 Through #4 by Measured and by Calculated (Mass Percent)

Conclusion

High-temperature equilibrium experiment has been applied to investigate the equilibrium phase relations and the corresponding proportion relations in the CaO-SiO₂-Nb₂O₅-La₂O₃ system at 1273 K (1000 °C). According to the Gibbs Phase Rule, six independent tetrahedron fields in the CaO-SiO₂-Nb₂O₅-La₂O₃ system were determined. A numerical method for quantitatively analyzing the proportion relation of equilibrium phases in multi-component system was deduced. The mass fraction of each equilibrium phase in each experimental slag in the CaO-SiO₂-Nb₂O₅-La₂O₃ system at 1273 K was calculated, respectively.