Introduction

The CAS-OB process (composition adjustment by sealed argon bubbling–oxygen blowing) was developed by Nippon Steel.[1] It is a ladle treatment process that is designed for heating and alloying molten steel. The CAS-OB process has many advantages, including high and predictable yield of alloying materials, low aluminum consumption, more consistent attainment of the target temperature for casting, and low total oxygen content after treatment.[1] There are also some disadvantages related to CAS-OB process. Investment costs for setting up a CAS-OB station are higher compared to some other heating processes (e.g., IR-UT and REHeating), although the heating rates are higher in CAS-OB process.[2,3] Furthermore, slag often sticks to bell structure which causes increase in weight and volume of the bell. This may have undesirable effects on the CAS-OB operation.[4–6]

The main stages of the process are heating, reduction of slag, and (possible) alloying. The purpose of the heating stage is to increase the steel temperature to its target value before continuous casting. Before the actual heating begins, the steel is stirred by bottom blowing to form a slag-free open-eye area on the surface of the steel bath. Consequently, a refractory bell is partly submerged within the steel (see Figure 1). During the heating stage, solid aluminum particles are fed onto the free steel surface inside the bell. The aluminum is oxidized under the refractory bell by blowing oxygen with a supersonic lance and the exothermic reaction causes an increase in the steel temperature.[7] Heating rates of up to 10 K/min (10 °C/min) can be obtained without excessive equipment wear.[2]

Fig. 1
figure 1

Schematic of the CAS-OB process

Full size image

In addition to increasing the Al2O3 content in the slag phase, the oxygen blowing leads to an increase in the amount of FeO, SiO2 and MnO in the slag.[8] In order to avoid excessive losses of the metal components, the reduction of slag is performed after heating. During the reduction stage, the bell structure is lifted and the steel is stirred using argon-blowing from the porous plugs at the bottom of the ladle. Vigorous argon-stirring results in a circulating motion of the steel in the ladle. As a consequence of shear stresses that the turning flow of steel imposes on the top slag, small droplets disengage from the slag layer, leading to an immense increase in the interfacial area between slag and steel. This large interfacial area provides favorable conditions for a high reduction rate.

As far as the authors are aware, only a few studies have been published in relation to CAS-OB process modeling. Computational fluid dynamics has been employed to study the main fluid flows[9,10] as well as emulsification of the top slag[11,12] during bottom blowing; these studies provide valuable information on the fluid flow conditions in the CAS-OB process. In our previous work,[13] a phenomena-based model for the heating stage of the CAS-OB process was proposed. The principle of the model is to solve transient differential equations for mass fractions of species and for temperatures.

In this work, similar approach is applied for the reduction stage. The main objective is to construct a computational model that, for given initial compositions, temperatures, and operating conditions, numerically solves the compositions of the slag and steel phases as well as the temperatures. The model was programmed using C/C++.

Derivation of the Model

Reaction System and Determination of Reaction Rates

The liquid steel phase is considered to be a Fe-Ni-Al-Si-C-Mn alloy in the present model. The slag phase contains Al2O3, SiO2, MnO, CaO, and FeO. In the CAS-OB process, the reduction of slag takes place through aluminum dissolved in the steel during the heating stage. In the reduction stage model, the following system of reactions is considered:

$$ ({\text{FeO}}) + \frac{2}{3}\underline{\text{Al}}\rightleftharpoons {\text{Fe}} + \frac{1}{3}\left( {{\text{Al}}_{2} {\text{O}}_{3} } \right) $$
(R1)
$$ \left( {\text{FeO}} \right) + \frac{1}{2}\underline{\text{Si}} \rightleftharpoons {\text{Fe}} + \frac{1}{2}\left( {{\text{SiO}}_{2} } \right) $$
(R2)
$$ ({\text{FeO}}) + \underline{\text{Mn}} \rightleftharpoons {\text{Fe}} + ({\text{MnO}}) $$
(R3)
$$ ({\text{FeO}}) + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\text{C}} \rightleftharpoons {\text{Fe}} + {\text{CO}}({\text{g}}). $$
(R4)

The corresponding reaction rates for the foregoing Reactions [R1] through [R4] are defined according to modified law of mass action in a similar manner as in our previous work[13] and also in other publications.[14,15]

$$ R_{1} = k_{{f_{1} }} \left( {a_{\text{FeO}} a_{{\underline{\text{Al}} }}^{2/3} - \frac{{a_{\text{Fe}} a_{{{\text{Al}}_{2} {\text{O}}_{3} }}^{1/3} }}{{K_{1} }}} \right) $$
(1)
$$ R_{2} = k_{{f_{2} }} \left( {a_{\text{FeO}} a_{{\underline{\text{Si}} }}^{1/2} - \frac{{a_{\text{Fe}} a_{{{\text{SiO}}_{2} }}^{1/2} }}{{K_{2} }}} \right) $$
(2)
$$ R_{3} = k_{{f_{3} }} \left( {a_{\text{FeO}} a_{{\underline{\text{Mn}} }} - \frac{{a_{\text{Fe}} a_{\text{MnO}} }}{{K_{3} }}} \right) $$
(3)
$$ R_{4} = k_{{f_{4} }} \left( {a_{\text{FeO}} a_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\text{C}}}} - \frac{{a_{\text{Fe}} a_{\text{CO}} }}{{K_{4} }}} \right). $$
(4)

In Eqs. [1] through [4], \( a_{{{\text{Al}}_{2} {\text{O}}_{3} }} \), \( a_{{{\text{SiO}}_{2} }} \), a MnO, and a FeO are the activities of respective slag species, a Fe, a Si, a Mn, and a C are the activities of iron and respective dissolved species, and p CO is the partial pressure of CO. The terms K1 to K4 are the equilibrium constants of Reactions [R1] through [R4], respectively, and \( k_{{f_{1} }} \) to \( k_{{f_{4} }} \) are the reaction rate coefficients of the respective reactions.

The forward reaction rate coefficients \( k_{{f_{i} }} \) are unknown in Eqs. [1] through [4]. The assumption in our approach is that the reactions are mass transfer controlled. This assumption is supported by the fact that at high temperatures, reactions are extremely fast. It should be noted that the rate controlling mass transfer mechanism is not predefined. Instead, the total mass transfer resistance is calculated implicitly by accounting for the mass transfer resistance in each phase. It has been proven that if forward reaction rate coefficients, \( k_{{f_{i} }} \), approach infinity, a mass transfer limited equilibrium is obtained at the reaction interface.[16] Computationally, it is not possible to set infinite values for the forward reaction rate coefficients. Instead, sufficiently high values are set for every \( k_{{f_{i} }} \) such that the solution at interface is arbitrarily close to equilibrium condition. Here, a dimensionless property called the equilibrium number is employed similar to Visuri et al.[17] to provide a quantitative assessment for the fulfillment of this condition. The equilibrium number was employed in the model to ensure that every reaction approaches equilibrium at the reaction interface by allowing a small deviation of E from zero (<0.1 pct):

$$ E = \left| {1 - \frac{Q}{K}} \right| < 0.001, $$
(5)

where Q is the reaction quotient. In equilibrium, the reaction quotient Q is, by definition, equal to the equilibrium constant K. The reaction quotient Q is defined as the quotient of product of reaction product activities, a p, raised to the power of stoichiometric coefficient v p and similar product of reactant activities.

$$ Q = \frac{{\mathop \prod \nolimits_{\text{p}} a_{\text{p}}^{{\nu_{\text{p}} }} }}{{\mathop \prod \nolimits_{\text{r}} a_{\text{r}}^{{\nu_{\text{r}} }} }}. $$
(6)

The equilibrium number is a dimensionless property, which is a measure of the relative deviation of the interfacial composition from the equilibrium composition. It can be interpreted as follows:

$$ \begin{aligned} E = \left| {1 - \frac{Q}{K}} \right| = \frac{{\left| {K - Q} \right|}}{K} & \, = \frac{{{\text{Absolute}}\;{\text{deviation}}\;{\text{from}}\;{\text{equilibrium}}}}{\text{Equilibrium}} \\ & \, = {\text{Relative}}\;{\text{deviation}}\;{\text{from}}\;{\text{equilibrium}} \\ \end{aligned}. $$
(7)

Conservation Equations of the Species

The equations are written in terms of mass fractions, y P,i , of species i in phase P. In general, the mass conservation for the species i in a bulk phase P can be written in the following form:

$$ \rho_{P} \frac{{{\text{d}}y_{P,i} }}{{{\text{d}}t}} + j_{P,i}^{\varepsilon } A_{\varepsilon } = 0. $$
(8)

In this and the following section, by ε-notation we refer to the reaction surface. Conservation of species at the reaction surface is satisfied by

$$ j_{P,i}^{\varepsilon } + S_{i} = 0. $$
(9)

The mass flux, \( j_{P,i}^{\varepsilon } \), through the surface element of the ith species in phase P is described as the mass flux of individual species. Consequently, the equation is

$$ j_{P,i}^{\varepsilon } = h_{P} \rho_{P} \left( {y_{P,i} - y_{\varepsilon ,i} } \right). $$
(10)

The reaction source term, S i , in Eq. [9] is defined as

$$ S_{i} = \mathop \sum \limits_{k = 1}^{{N_{r} }} \tilde{v}_{i,k} R_{k} , $$
(11)

where N r refers to number of reactions and \( \tilde{v}_{i,k} \) is the mass-based stoichiometric coefficient, which can be evaluated as follows:

$$ \tilde{v}_{i,k} = \nu_{i,k} \frac{{M_{i} }}{{M_{k}^{K} }}. $$
(12)

In Eq. [12], M i is the molar mass of species i, v i,k is the stoichiometric coefficient of species j in reaction k, and \( M_{k}^{K} \) is the molar mass of the key component of reaction k. In our case, the key component for all reactions is FeO.

Algebraic form of the conservation equations

Since the conservation equations in the question cannot be solved analytically, a numerical method is needed to find approximate solution for PDEs of the form in Eq. [8]. For this, Eq. [8] must be discretized to obtain a set of algebraic equations that can be solved using a suitable method.

As for discretization of the temporal term, the first-order Euler method was applied. It follows that for species i, the discretized equations for the conservation of mass in bulk steel, bulk slag, and bulk gas, respectively, are

$$ \frac{{m^{t} y_{{{\text{L}},i}}^{t} - m^{t - 1} y_{{{\text{L}},i}}^{t - 1} }}{\Delta t} = - A_{\varepsilon } h_{\text{L}} \rho_{\text{L}} \left( {y_{{{\text{L}},i}} - y_{\varepsilon ,i} } \right) $$
(13)
$$ \frac{{m^{t} y_{{{\text{S}},i}}^{t} - m^{t - 1} y_{{{\text{S}},i}}^{t - 1} }}{\Delta t} = - A_{\varepsilon } h_{\text{S}} \rho_{\text{S}} \left( {y_{{{\text{S}},i}} - y_{\varepsilon ,i} } \right) $$
(14)
$$ \frac{{m^{t} y_{{{\text{G}},i}}^{t} - m^{t - 1} y_{{{\text{G}},i}}^{t - 1} }}{\Delta t} = - A_{\varepsilon } h_{\text{G}} \rho_{\text{G}} \left( {y_{{{\text{G}},i}} - y_{\varepsilon ,i} } \right), $$
(15)

where Δt is the time step. Here, A ε refers to the interfacial area between slag droplets and liquid steel. Conservation of total mass in each phase is obtained by simply summing Eqs. [16] through [18] over all species:

$$ \frac{{m_{\text{L}}^{t} - m_{\text{L}}^{t - 1} }}{\Delta t} = - A_{\varepsilon } \mathop \sum \limits_{i = 1}^{{N_{\text{s}} }} \varGamma_{{{\text{L}},i}} h_{\text{L}} \rho_{\text{L}} \left( {y_{{{\text{L}},i}} - y_{\varepsilon ,i} } \right) $$
(16)
$$ \frac{{m_{\text{S}}^{t} - m_{\text{S}}^{t - 1} }}{\Delta t} = - A_{\varepsilon } \mathop \sum \limits_{i = 1}^{{N_{\text{s}} }} \varGamma_{{{\text{S}},i}} h_{\text{S}} \rho_{\text{S}} \left( {y_{{{\text{S}},i}} - y_{\varepsilon ,i} } \right) $$
(17)
$$ \frac{{m_{\text{G}}^{t} - m_{\text{G}}^{t - 1} }}{\Delta t} = - A_{\varepsilon } \mathop \sum \limits_{i = 1}^{{N_{\text{s}} }} \varGamma_{{{\text{G}},i}} h_{\text{G}} \rho_{\text{G}} \left( {y_{{{\text{G}},i}} - y_{\varepsilon ,i} } \right). $$
(18)

In Eqs. [16] through [18], \( \varGamma_{P,i} \) is a binary operator that equals 1 if species i is contained in phase P, and 0 otherwise. At the reaction interface, the following equations hold for the conservation of species i in steel, slag, and gas phases:

$$ h_{\text{L}} \rho_{\text{L}} \left( {y_{{{\text{L}},i}} - y_{\varepsilon ,i} } \right) + \mathop \sum \limits_{k = 1}^{{N_{\text{r}} }} \tilde{v}_{i,k} R_{k} = 0 $$
(19)
$$ h_{\text{S}} \rho_{\text{S}} \left( {y_{{{\text{S}},i}} - y_{\varepsilon ,i} } \right) + \mathop \sum \limits_{k = 1}^{{N_{\text{r}} }} \tilde{v}_{i,k} R_{k} = 0 $$
(20)
$$ h_{\text{G}} \rho_{\text{G}} \left( {y_{{{\text{G}},i}} - y_{\varepsilon ,i} } \right) + \mathop \sum \limits_{k = 1}^{{N_{\text{r}} }} \tilde{v}_{i,k} R_{k} = 0 $$
(21)

Conservation of Heat

Since one of the main tasks of the CAS-OB process is to ensure sufficient temperature of the steel in the next process step, it is very important that the heat transfer is considered properly in the model. Temperatures in the bulk phases and at the reaction interface are considered. In addition, the temperature of the ladle wall is calculated. The ladle wall consists of a refractory lining and a steel mantle covering the outermost part.

The conservation of heat in the system is described by eight conservation equations. Heat transfer between bulk phases, heat from the reactions, as well as heat losses through ladle was considered. Eqs. [22] through [24] represent the conservation of heat in bulk metal, bulk slag, and bulk gas, respectively.

$$ \begin{aligned} c_{{p,{\text{L}}}} m_{\text{L}} \frac{{T_{\text{L}}^{n} - T_{\text{L}}^{n - 1} }}{\Delta t} = \, & - \dot{m}c_{{p,{\text{Ar}}}} \left( {T_{\text{L}} - T_{{{\text{Ar}},in}} } \right) - \alpha_{\text{L}} A_{\varepsilon } \left( {T_{\text{L}} - T_{\varepsilon } } \right) \\ \, & - \alpha_{{{\text{L}}_{in} }} A_{{{\text{L}}_{in} }} \left( {T_{\text{L}} - T_{{{\text{L}}_{1} }} } \right) - \in_{\text{L}} \sigma A_{\text{O}} \left( {T_{\text{L}}^{4} - T_{\text{Atm}}^{4} } \right) \\ \, & - A_{\varepsilon } \left( {T_{\text{L}} - T_{\varepsilon } } \right)\mathop \sum \limits_{i = 1}^{{N_{\text{s}} }} \mathop \sum \limits_{k = 1}^{{N_{\text{r}} }} \varGamma_{{{\text{L}},i}} R_{k} \nu_{i,k} c_{p,i} \\ \end{aligned} $$
(22)
$$ c_{{p,{\text{S}}}} m_{\text{S}} \frac{{T_{\text{S}}^{n} - T_{\text{S}}^{n - 1} }}{\Delta t} = - \alpha_{\text{S}} A_{\varepsilon } \left( {T_{\text{S}} - T_{\varepsilon } } \right) - A_{\varepsilon } \left( {T_{\text{S}} - T_{\varepsilon } } \right)\mathop \sum \limits_{i = 1}^{{N_{\text{s}} }} \mathop \sum \limits_{k = 1}^{{N_{\text{r}} }} \varGamma_{{{\text{S}},i}} R_{k} \nu_{i,k} c_{p,i} $$
(23)
$$ c_{{p,{\text{G}}}} m_{\text{G}} \frac{{T_{\text{G}}^{n} - T_{\text{G}}^{n - 1} }}{\Delta t} = - \alpha_{\text{G}} A_{\varepsilon } \left( {T_{\text{G}} - T_{\varepsilon } } \right) - A_{\varepsilon } \left( {T_{\text{G}} - T_{\varepsilon } } \right)\mathop \sum \limits_{i = 1}^{{N_{\text{s}} }} \mathop \sum \limits_{k = 1}^{{N_{\text{r}} }} \varGamma_{{{\text{G}},i}} R_{k} \nu_{i,k} c_{p,i} . $$
(24)

In Eq. [22], the first term on the right-hand side is the heating up of argon to the temperature of the steel, and the second and third terms are the convective heat transfer to the reaction surface and ladle wall, respectively. The fourth term is the heat loss by radiation from the surface of the liquid steel. The last term represents the heat from the reactions of the metal species. In the equations above, α p is the heat transfer coefficient for phase P, c p,L , c p,S , and c p,G are the heat capacities of metal, slag and gas, respectively, and c p,i is the heat capacity of species i.

Conservation of heat at the reaction surface is described as follows:

$$ \alpha_{\text{L}} A_{\varepsilon } \left( {T_{\text{L}} - T_{\varepsilon } } \right) + \alpha_{\text{S}} \left( {T_{\text{S}} - T_{\varepsilon } } \right) + \alpha_{\text{G}} \left( {T_{\text{G}} - T_{\varepsilon } } \right) = \mathop \sum \limits_{k = 1}^{{N_{\text{r}} }} R_{k} \Delta h_{k} . $$
(25)

The term on the right-hand side in Eq. [25] is the heat from all the reactions occurring at the surface.

Finally, heat transfer through the ladle wall is considered. The ladle wall consists of an interior layer of refractory lining and an exterior steel mantle. Temperatures are solved at four points: (1) the inner surface of the refractory lining, (2) in the middle of the refractory lining, (3) at the inner surface of the steel mantle, and (4) on the outer surface of the ladle. The temperatures at these points are denoted by \( T_{{{\text{L}}_{1} }} \), \( T_{{{\text{L}}_{2} }} \), \( T_{{{\text{L}}_{3} }} \) and \( T_{{{\text{L}}_{4} }} \), respectively. The heat transfer consists of convection to the inner surface, conduction through the refractory lining and steel mantle, accumulation of heat within the refractory and mantle, as well as convection and radiation at the outer surface. To take these into account, three additional equations are needed:

$$ \alpha_{{{\text{L}}_{\text{in}} }} \left( {T_{\text{L}} - T_{{{\text{L}}_{1} }} } \right) = \frac{{k_{\text{R}} \left( {T_{{{\text{L}}_{1} }} - T_{{L_{2} }} } \right)}}{{0.5\Delta x_{\text{R}} }} $$
(26)
$$ \frac{{k_{\text{R}} A_{{{\text{L}}_{in} }} \left( {T_{{{\text{L}}_{1} }} - T_{{{\text{L}}_{2} }} } \right)}}{{0.5\Delta x_{\text{R}} }} = \frac{{k_{\text{R}} A_{\text{M}} \left( {T_{{{\text{L}}_{2} }} - T_{{{\text{L}}_{3} }} } \right)}}{{0.5\Delta x_{\text{R}} }} + c_{{p_{\text{R}} }} m_{\text{R}} \frac{{T_{{{\text{L}}_{2} }}^{n} - T_{{{\text{L}}_{2} }}^{n - 1} }}{\Delta t} $$
(27)
$$ \frac{{k_{\text{R}} \left( {T_{{{\text{L}}_{2} }} - T_{{{\text{L}}_{3} }} } \right)}}{{0.5\Delta x_{\text{R}} }} = \frac{{k_{\text{M}} \left( {T_{{{\text{L}}_{3} }} - T_{{{\text{L}}_{4} }} } \right)}}{{\Delta x_{\text{M}} }}. $$
(28)

Heat capacities of steel, slag, and gas phases were calculated as weighted average of heat capacities of individual species in the phase:

$$ c_{p,P} = \mathop \sum \nolimits {\varGamma}_{P,i} y_{i} c_{p,i} . $$
(29)

Heat capacities of each species, c p,i, were constant. Heat capacities of the species for the relevant temperature range were calculated using HSC Chemistry 6. Values of the heat capacities are given in Table I.

Table I Specific Heat Capacities of the Species
Full size table

Formation of Slag Droplets

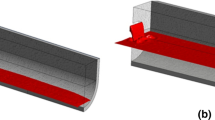
In order to model reactions during the reduction stage, it is essential to determine the interfacial area—or the reaction area—available to steel-slag reactions. In this study, the main assumption is that the reactions take place on the surface of the slag droplets only and the contribution to the total reaction rates of the reactions occurring on the top slag-steel interface is negligible, see Figure 2. This presumption is justified by the fact that the mixing within the top slag layer is fairly weak and, thus, mass transfer through the interface is not very effective. Then again, the relatively small droplet size and powerful argon-stirring intensify the contribution of the interface between the steel and slag droplets. Furthermore, the surface area of the droplets is considerably larger than the surface area between the top slag layer and steel bath. This assumption has been successfully applied by Visuri et al.[18] in their reduction model for the AOD process.

Fig. 2
figure 2

In slag reduction, reactions may occur at two different interfaces: at interface (a), i.e., between the slag droplets and the steel, or at interface (b), i.e., between the top slag layer and the steel. Reactions at interface (b) are omitted from this model

Full size image

Another mechanism affecting reduction reactions is the entrainment of steel droplets into the slag. Due to bottom blowing, gas bubbles that rise within the steel phase are formed. When the bubbles rise, thin steel film is formed around them. The gas bubbles burst when they surpass the steel surface and small steel droplets are formed into the slag. Unfortunately, present knowledge on the issue is not very thorough, and lacking any quantitative model for metal droplet generation it is impossible to include metal droplets in the model. Thus, the approach adopted in the model describes the slag reduction in effective manner. The slag droplets that entrain into the steel form an effective interfacial area through which the reduction reactions take place. Hence, a functional model for the generation of the slag droplet area is indispensable.

In the present model, the slag droplet-steel interface is a multiphase surface element with zero thickness. Species react per this massless surface and, by reason of the assumption above, it is the only interface involved in reactions that is considered in the model.

Average droplet size

In our previous studies,[12,13,19] we examined slag emulsification by means of computational fluid dynamics (CFD). The droplet formation was studied as a function with various physical properties of steel and slag, e.g., density difference, interfacial tension, and steel flow velocity. In the slag reduction model, the effect of steel flow velocity on droplet generation is particularly important. In our recent research,[13] generation of slag droplets was modeled with various steel flow velocities and a Rosin–Rammler–Sperling (RRS) distribution function was fitted to the droplet data. The RRS distribution function has the following form:

$$ {\text{RF}} = \left( {0.001} \right)^{{\left( {\frac{d}{{d_{\text{limit}} }}} \right)^{n} }} . $$
(30)

Parameter d limit was determined from the CFD simulations, after which parameter n, which determines the spread of the distribution, was obtained with the least squares method. It was concluded that n = 2.06 to 2.46.

The reduction model considers only one average droplet size at a given time. The average size may vary as function of time, though, depending on the stirring conditions. The average droplet size was calculated from the droplet size distribution function. With the applied model, the average droplet size varied between 2.5 and 3.4 mm.

Generation rate of droplets

In order to define the conservation of the species and heat properly, the total area between the slag droplets and steel phase must be defined. As we have a description for the average slag droplet size, a model for the birth rate of droplets is needed to calculate the total area formed by the slag droplets. In this work, a model from Oeters[20] was adopted to describe the volumetric generation rate. The model defines the following expression for the generation rate of slag droplets:

$$ b = \frac{{0.4153D\rho_{\text{S}}^{1/2} \mu_{\text{S}}^{1/2} l^{1/2} u_{i}^{5/2} }}{{d_{\text{avg}}^{2} \sigma + \frac{1}{6}d_{\text{avg}}^{4} g\left( {\rho_{\text{M}} - \rho_{\text{S}} } \right)\cos \alpha }}, $$
(31)

where u i , l, and D are the interfacial velocity at the slag-steel interface, slag layer thickness, and diameter of the open-eye area, respectively. The interfacial velocity and open-eye diameter needed to be evaluated along with the dynamic viscosity of the slag, μ S. Oeters[20] also provides a formula for calculating u i . To evaluate D, the model introduced by Krishnapisharody et al.[21] was employed. The same model was also applied to determine the area of the open-eye region, A O, in Eq. [22]. By combining the models for average droplet size and birth rate, an estimation for the reaction area can be obtained. As for the interfacial tension, σ, between slag and steel, the value σ = 0.5 N/m was applied which is in accordance with the value used in our previous study.[13]

Residence time of droplets

The accumulated area formed by slag droplets at a given time is dictated by the residence time, t r, of the droplets. In reality, the residence time of the droplets is not uniform, as the droplet size as well as mixing conditions varies during the reduction stage. The residence time of the slag droplets has not been studied very widely. Oeters[20] points out that, generally, the residence time of droplets in metallurgical systems is less than one minute. Since lacking any quantitative description for residence time, it was considered as an adjustment parameter, bearing in mind the coarse upper limit given by Oeters.[20] Also, only one average residence time, \( \bar{t}_{\text{r}} \), for all droplet sizes was applied.

Physical Properties

The physical properties needed of the phase were determined using equations and models from the literature. The modified Urbain model[22] for modeling dynamic viscosity of slag, μ S , was chosen. According to the slag viscosity model report of Kekkonen et al.[23] the modified Urbain model and Iida model are more reliable in predicting the viscosity of BOF slags. The BOF slag is not exactly similar to the slag in CAS-OB process as the aluminum oxide content of the latter slag is far higher. However, the CAS-OB slag in Raahe steel plant consists of BOF slag and slag formers added after tapping. In the CAS-OB Process, aluminum additions increase the aluminum oxide content of the slag. The modified Urbain model is developed for aluminum containing slags which favors the choice. Density of slag was calculated according to the molar volume method[24] defined as follows:

$$ \rho_{\text{S}} = \frac{{\mathop \sum \nolimits x_{i} M_{i} }}{{\mathop \sum \nolimits x_{i} V_{i} }}, $$
(32)

where xi, M, i and V i are the mole fraction, molar mass, and molar volume of species i (in slag phase), respectively. The molar volumes for the observed slag system were obtained from Slag Atlas.[24]

Viscosity of steel as a function of temperature is calculated with the following equation:

$$ \mu_{\text{L}} = \mu_{0} \exp \left( {\frac{E}{\text{RT}}} \right), $$
(33)

where μ 0 and E are parameters determined experimentally for pure iron. Density of liquid steel was determined by using the model reported by Brandes and Brook.[25] The model gives the density as a function of temperature:

$$ \rho_{\text{L}} = 7015 - 0.883\left( {T_{\text{L}} - 1809} \right). $$
(34)

Thermodynamics of the Model

The reaction rates in Eqs. [1] through [4] are defined in terms of equilibrium constants and activities of the species. By definition, the equilibrium constant can be written as follows:

$$ K_{i} = \exp \left( { - \frac{{\Delta G_{i} }}{\text{RT}}} \right). $$
(35)

That is, the equilibrium constant is related to the standard change of Gibbs free energy which, in turn, is defined as

$$ \Delta G_{i} = \Delta H_{i} + T\Delta S_{i}. $$
(36)

The values that were used for reaction enthalpy ∆H i , reaction entropy ∆S i , and reaction heat ∆h i are listed in Table II. The surface energy has been omitted in determining Gibbs free energy since it has very small effect in comparison to volumetric free energy, the ratio of surface energy and volumetric free energy being approximately ~10−3.

Table II Values of the Reaction Enthalpy, Reaction Entropy, and Specific Reaction Heat
Full size table

Activities were determined according to the composition and temperature at the reaction interface. Composition at the interface corresponds to the dynamic equilibrium limited by the mass transfer. It should be noted that the dynamic equilibrium differs from the equilibrium at the bulk phases.

The Raoultian activity a i of species i in phase P is, by definition,

$$ a_{i} = \gamma_{i} x_{i} $$
(37)

or, as required in our case, expressed in terms of mass fractions

$$ a_{i} = \gamma_{i} \frac{{M_{P} }}{{M_{i} }}y_{i} , $$
(38)

where γ i , x i , y i , and M i are the Raoultian activity coefficient, mole fraction, mass fraction, and molar mass of species i, respectively, and M P is the molar mass of phase P.

To determine the activity coefficients of the species in the steel phase, Unified Interaction Parameter (UIP) formalism was applied.[26] The Raoultian activity coefficient of species i, in terms of mass fractions, is formulated as follows in the UIP formalism:

$$ \ln \gamma_{i} = \ln \gamma_{\text{Fe}} + \ln \gamma_{i}^{\text{o}} + \mathop \sum \limits_{j = 1}^{N} \frac{{\varepsilon_{i}^{j} M_{\text{L}} }}{{M_{j} }}, \quad {\text{where}}\quad \ln \gamma_{\text{Fe}} = - 0.5\mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{k = }^{N} \frac{{\varepsilon_{j}^{k} M_{\text{L}}^{2} }}{{M_{j} M_{k} }}. $$
(39)

In Eq. [39], \( \gamma_{\text{Fe}} \) is the Raoultian activity coefficient of the solvent, \( \gamma_{i}^{\text{o}} \) is the activity coefficient of species i at infinite dilution, and \( \varepsilon_{i}^{j} \) is the molar first-order interaction parameter between species i and j. Interaction parameters as well as activity coefficients of a solute at infinite dilution applied in the UIP formalism were taken from the literature,[27,28] and values are collected in Table III.

Table III UIP Model Parameters Applied in this Work[27,28]
Full size table

The regular solution model by Ban-Ya[29] was chosen to describe the activities of the species in the slag phase. The Raoultian activity coefficient of species i is described as

$$ {\text{RT}}\ln \gamma_{i} = \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{N} \alpha_{ij} X_{j}^{2} + \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne i} \\ \end{array} }}^{N} \mathop \sum \limits_{{\begin{array}{*{20}c} {k = j + 1} \\ {k \ne i} \\ \end{array} }}^{N} \times \left( {\alpha_{ij} + \alpha_{ik} - \alpha_{jk} } \right)X_{j} X_{k} + \Delta G_{\text{conv}} . $$
(40)

In Eq. [40], \( \alpha_{ij} \) is the interaction energy between cations, X i is the cation fraction of species i in slag, and ∆G conv is the conversion factor between regular solution and real solution. The cation fraction, in terms of mass fractions, is given by the following formula[30]:

$$ X_{i} = \frac{{y_{i} N_{{{\text{O}},i}} }}{{M_{i} }}\left( {\mathop \sum \limits_{j = 1}^{N} \frac{{y_{j} N_{{{\text{O}},j}} }}{{M_{j} }}} \right)^{ - 1} . $$
(41)

In Eq. [41], N O,i is the number of O-atoms in species i. The conversion energies between the regular solution state and the Raoultian reference state, as well as the values for the interaction energies applied in this work, are presented in Table IV.[29,31,32]

Table IV Interaction Energies and Conversion Energies for Ban-Ya’s Activity Model[29,31,32]
Full size table

Mass and Heat Transfer Coefficients

In addition to activity models, the mass and heat transfer coefficients have a great impact on the modeling results. In this work, only one mass transfer coefficient for each phase was determined.

The mass transfer coefficient h L of the steel phase can be expressed in the following manner:

$$ h_{\text{L}} = \frac{{{\text{Sh}}L}}{{D_{\text{L}} }}, $$
(42)

where Sh is the Sherwood number, L is the characteristic length, and D L is the mass diffusivity of the steel. An apparent choice for the characteristic length L in Eq. [42] was the average droplet diameter d Aver. Many options for defining the Sherwood number are available in the literature. In order to provide a description for Sh, the flow circumstances and phase characteristics taking place in the CAS-OB process must be considered. According to Oeters,[20] if the viscosity of the emulsified phase is much greater than that of the surrounding phase (i.e., μ S ≫ μ L), the external mass transfer is dictated, as in the case of mass transfer at solid particles. The condition is satisfied in our case, as the viscosity of slag is two orders of magnitude greater than the viscosity of steel. Owing to this fact, a formalism from Ihme et al.[33] to determine the Sherwood number for the steel phase, was chosen which is given by

$$ {\text{Sh}} = 2 + z_{k} \frac{{\text{Re}^{1.7} {\text{Sc}}^{1.7} }}{{1 + \text{Re}^{1.2} {\text{Sc}}^{1.2} }}, $$
(43)
$$ z_{k} = \frac{0.66}{{1 + {\text{Sc}}}} + \frac{{0.79{\text{Sc}}}}{{\left( {2.4 + {\text{Sc}}} \right){\text{Sc}}^{1.6} }}, $$
(44)

where Re and Sc are the Reynolds number and the Schmidt number, respectively. In addition, we chose Eq. [44] because it was reported as applying to the entire range of Reynolds numbers.[20]

Within the slag droplets, the mass transfer is assumed to take place by diffusion only. Here, a spherical droplet geometry was assumed. We applied the expression in accordance with Eq. [45] for the mass transfer coefficient on the slag side. The equation can be derived from the known solutions to Fick’s second law for spherical geometry:[20]

$$ h_{\text{S}} = \frac{{2\pi^{2} D_{\text{S}} }}{{3d_{\text{avg}} }}\left( {\frac{{\mathop \sum \nolimits_{i = 1}^{\infty } \exp \left( { - i^{2} \pi^{2} \frac{{4D_{\text{S}} t}}{{d_{\text{avg}}^{2} }}} \right)}}{{\mathop \sum \nolimits_{i = 1}^{\infty } \frac{1}{{i^{2} }}\exp \left( { - i^{2} \pi^{2} \frac{{4D_{\text{S}} t}}{{d_{\text{avg}}^{2} }}} \right)}}} \right). $$
(45)

It can be seen that Eq. [40] presents a time-dependent mass transfer coefficient. In this case, the maximum value for t is the residence time of the slag droplets. The right-hand side of Eq. [45] approaches \( \frac{{2\pi^{2} D_{\text{S}} }}{{3d_{\text{avg}} }} \) as t approaches infinity. When time exceeds the residence time, h S was taken as a constant, i.e., having the mentioned limit value.

The gas phase has quite a small effect on the results in this model, as the conditions for generation of CO are quite unfavorable. In this work, the mass transfer coefficient on the gas side was calculated according to the surface renewal model,[34] which defines h G as follows:

$$ h_{\text{G}} = \frac{2}{\sqrt \pi }\sqrt {\frac{{D_{\text{G}} u_{\text{b}} }}{{d_{\text{b}} }}} , $$
(46)

where D G, u b, and d b are the mass diffusivity of the gas phase, the rising velocity of the gas bubbles, and the gas bubble diameter, respectively. The rising velocity of the bubbles and the bubble diameter were calculated according to Eqs. [47] and [48], respectively.[20]

$$ d_{\text{b}} = \left( {\frac{3\sigma d}{{g\rho_{\text{L}} }} + \left( {\frac{{9\sigma^{2} d^{2} }}{{g^{2} \rho_{\text{L}}^{2} }} + K\frac{{\dot{V}_{\text{G}}^{2} d}}{g}} \right)^{1/2} } \right)^{1/3} $$
(47)
$$ u_{\text{b}} = \left( {\frac{2\sigma }{{\rho_{\text{L}} d_{\text{b}} }} + \frac{{gd_{\text{b}} }}{2}} \right)^{1/2} , $$
(48)

where d is the nozzle diameter, \( \dot{V}_{\text{G}} \) is the volumetric gas flow rate, and K = 10 is an experimentally determined constant.

As for the heat transfer coefficients, the analogue of mass and heat transfer is applied. That is, in the expressions for the Sherwood number, Sh is replaced by the Nusselt number, Nu, and Sc is replaced by the Prandtl number, Pr. The heat transfer coefficient, α P , for phase P is obtained by replacing the diffusivity D P with the thermal conductivity k P .

For the diffusivities, it was chosen to apply one effective mass diffusivity for each phase: D L = 4 × 10−9 m2/s,[35] D S = 5 × 10−10 m2/s,[35] and \( D_{\text{G}} = 2.1 \times 10^{ - 5} \left( {\frac{T}{{T_{\text{N}} }}} \right)^{1.5} \left( {\frac{{p_{\text{N}} }}{p}} \right){\text{m}}^{2} / {\text{s}} \).[36]

Results and Discussion

The model was validated against temperature and composition measurements obtained from the CAS-OB station in the SSAB Raahe steel plant. The validation campaign consisted of measurements from eight heats. From each heat, steel and slag samples as well as temperature measurement were taken at three stages: (1) before the heating stage, (2) between the heating stage and the reduction stage, and (3) after the reduction stage. For the purposes of this work, samples and temperature measurements from stages (2) and (3) were used. Typical practice for CAS-OB process with sampling and measurements is presented in Figure 3. All measurements were taken with the help of a particular automatic sampling lance. Other data required for the model, such as exact sampling times and bottom blowing data, was also gathered during the campaign.

Fig. 3
figure 3

Typical CAS-OB process practice with sampling and measurements

Full size image

In earlier work, an average slag composition was calculated for Al-killed steel. Calculation was based on samples taken before and after the heat-up stage from 18 CAS-OB heats. Average composition is presented in Table V. The only available data regarding the slag composition after slag reduction in CAS-OB process is presented later together with other validation data. Alloying materials that are used in CAS-OB process can divided into three groups: main alloying materials (FeTi, FeCr, FeSi etc.), microalloying materials (FeNb, Cu, Ni, etc.), and wire alloying materials (CaSi, C, etc.). Other materials include Al for heating and scrap.

Table V Typical Slag Composition Before and After the Heating Stage for Al-Killed Steels
Full size table

The validation heats were of low-alloyed, low-carbon steel. The weight percentage range for dissolved species is presented in Table VI. No additions were used in any of the observed treatments, with the exception of the heating aluminum. In the validation campaign, the reduction stage duration varied between three and seven minutes. The timeline of a usual CAS-OB treatment with typical blowing rates is presented in Figure 3. The sampling and measurement times are marked to the Figure 3 as well. The volumetric gas flow rate varies during the CAS-OB heats; in validation heats the flow rate was 200 to 1500 L/min.

Table VI Weight Percentage Range of the Dissolved Species Within the Steel in Validation Heats
Full size table

Steel and Slag Compositions

In general, the model results regarding the compositions showed good agreement with the measurement data. The initial and final steel sample compositions, along with the predicted final steel compositions, are collected in Table VII. The absolute mean errors for Al, Si, Mn, and C were 0.004, 0.01, 0.03, and 0.001 wt pct, respectively.

Table VII Initial and Final Steel Composition According to Measurements and Final Composition Predicted by the Model
Full size table

The final content of Al, Si, Mn, and C is presented in a graph of measured vs predicted content (Figure 4).

Fig. 4
figure 4

Comparison of measured and predicted dimensionless final content of the steel species

Full size image

The slag compositions in different heats before and after the slag reduction, as well as the final composition predicted by the model, are presented in Table VIII. The mean absolute errors for the slag species were 1.2, 0.7, 1.5, 1.7, and 0.7 wt pct for Al2O3, SiO2, CaO, MnO, and FeO, respectively. The model’s predictions are in reasonably good agreement with the measurements, although some deviation can be seen regarding the MnO and FeO content in a couple of heats.

Table VIII Initial and Final Slag Composition According to Measurements and Final Composition Predicted by the Model
Full size table

Comparison with the measured and predicted final concentrations of the slag species are presented in Figure 5.

Fig. 5
figure 5

Comparison of measured and predicted dimensionless final content of the slag species

Full size image

One reason for the deviation is the uncertainty regarding the initial mass of the slag, which is calculated based on the CaO content of the slag. The total amount of CaO consists of the CaO content of the converter slag that gets poured into the ladle along with the steel in tapping, and the CaO content of the slag formers (bauxite, dolomite, etc.) that are added before the ladle arrives at the CAS-OB station. In this work, the estimation of the mass of the converter slag made at the meltshop was used and, lacking more detailed information on possible variations, it was assumed to be constant. The information on the amount of additions was more precise, and the CaO content of the additions was also available.

Another issue worth considering is the residence time of the slag droplets, as it has a significant effect on the interfacial area. Substantially, the residence time defines the accumulative area formed by the droplets. In the absence of a suitable expression for the residence time, it was treated as an adjustment parameter in the model. As mentioned earlier, an average residence time, \( \bar{t}_{\text{r}} \), was employed. In order to assess the magnitude of \( \bar{t}_{\text{r}} \), the emulsification fraction generated with different residence times by using the models employed described earlier was compared to the studies available in the literature. It was found that employing \( \bar{t}_{\text{r}} \) = 45 seconds produced a reasonable degree of emulsification (approximately 45 to 100 pct), which appeared to be in accordance with comparable studies.[37,38] Given the fact that the applied value for the average residence time is in the reported range[20] (\( \bar{t}_{\text{r}} \le 1\,{ \hbox{min} } \)) and the results are satisfactory, the choice can be considered justified.

Temperature Predictions

Evidently, the bottom blowing during the reduction stage has a cooling effect on the molten steel. In addition, the reduction reactions are endothermic reactions, which for their part expedite the cooling. However, the foremost factor in cooling during vigorous bottom blowing is the radiative heat loss from the surface of the steel, since the stirring breaks the surface slag layer, which also acts as thermal insulation in a nonagitated situation.[39] As pointed out earlier, all of these factors were taken into account in the formulation of the conservation equations for heat.

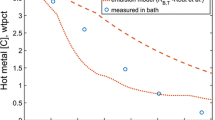
The results of the simulations are collected in Table IX. The absolute mean error in the simulated results was 4 K (4 °C). A comparison between the measured and simulated temperatures is presented in Figure 6. The agreement with the measurements can be considered satisfactory.

Table IX Measured and Predicted Temperatures
Full size table
Fig. 6
figure 6

Comparison of measured and predicted temperatures

Full size image

Heat loss and generation in Heat 3 are illustrated in Figure 7, while the cooling rate of steel in the same heat is shown in Figure 8. Figure 7 shows that heat is lost through radiation through the surface and ladle wall, but reduction reactions also absorb heat. Heat that is lost or absorbed originates from the steel phase. The heat absorption by the reactions is slightly faster at the beginning of the reduction, resulting in a higher cooling rate of the steel. The cooling rate of the steel is consistent with the values reported by Ghosh and Szekely et al.[40,41] According to these studies, the temperature loss is, depending on the size of the ladle, 1 to 2 K/min (1 to 2 °C/min).

Fig. 7
figure 7

Heat consumption from the steel phase in Heat 3

Full size image
Fig. 8
figure 8

Cooling rate of steel in Heat 3

Full size image

As for the heat loss via ladle walls, during the validation campaign for the heating stage model[13] the temperature of outer surface of the ladle was measured from several heats and it was noticed that the temperature is nearly constant, being approximately 673 K (400 °C). Before the ladle arrives to the CAS-OB station from the converter, the steel has been in the ladle for some time and the heat-up precedes the reduction stage. Thus, by the time the slag reduction takes place, heat transfer through the ladle has presumably stabilized. Under normal operating conditions the temperature of the outer surface of the steel mantle is expected to be virtually constant, as indicated also by our measurements. Furthermore, the cooling rate of an empty ladle is relatively slow, and during transferring/casting lid is used to cover the ladle in order to avoid excessive heat loss.

Using a desktop PC (3.4 Ghz), typical calculation times of the studied heats were in the order of 7 seconds using a time step of 1 second. Due to its relatively low running time, the model is, in principle, suitable even for on-line use.

Conclusions

In this work, a new mathematical model for describing transient chemical reactions and heat transfer during the reduction stage of the CAS-OB process was derived and validated. We assumed that the reduction reactions occur at the steel-slag droplet interface alone and that reactions between steel and nonemulsified top slag layer can be omitted. To describe the area formed by the droplets, the results of our previous studies concerning droplet size was employed along with other models, including sub-models for viscosity of top slag, birth rate of metal droplets, and diameter of the open-eye.

The CAS-OB process is used for chemical heating and alloying of steel before casting. Thus, accurate modeling of heat transfer is an important feature of the present model. As for the heat transfer during the reduction stage, the cooling of the steel due to endothermic reactions, radiative heat loss from the steel surface under agitated conditions, and heat loss through the ladle walls was considered.

The results of validation with industrial heats showed that the model is able to predict steel and slag compositions as well as the temperatures accurately for given initial and stirring conditions with good accuracy. The following conclusion could be drawn from the modeling results:

  • Composition predictions were in good agreement with the experimental data.

  • Model is able to predict steel temperature well; the mean absolute error for steel temperature predictions was 4 K (4 °C).

  • The results of the simulations suggest that cooling of the steel is mainly caused by the radiation through the open-eye caused by bottom stirring. Heat losses caused by endothermic reactions and heat losses through the ladle wall were found to be of lesser importance.