Phase Field Simulation of Binary Alloy Dendrite Growth Under Thermal- and Forced-Flow Fields: An Implementation of the Parallel–Multigrid Approach

Abstract

Dendrite growth and morphology evolution during solidification have been studied using a phase field model incorporating melt convection effects, which was solved using a robust and efficient parallel, multigrid computing approach. Single dendrite growth against the flow of the melt was studied under a wide range of growth parameters, including the Lewis number (Le) and the Prandtl number (Pr) that express the relative strengths of thermal diffusivity to solute diffusivity and kinematic viscosity to thermal diffusivity. Multidendrite growths for both columnar and equiaxed cases were investigated, and important physical aspects including solute recirculation, tip splitting, and dendrite tilting against convection have been captured and discussed. The robustness of the parallel–multigrid approach enabled the simulation of dendrite growth for metallic alloys with Le ~ 10⁴ and Pr ~ 10⁻², and the interplay between crystallographic anisotropy and local solid/liquid interfacial conditions due to convection on the tendency for tip splitting was revealed.

Introduction

The commonly observed dendritic microstructure formed in metallic alloys following casting and solidification is one of the main factors that determine the mechanical properties of the final product.[1–6] Consequently, considerable effort has been expended in trying to understand and control solidification conditions to manipulate final microstructure. In practice, the use of grain refiners to promote nucleation and finer, more equiaxed (as opposed to columnar) grains is very effective, while in the laboratory, considerable progress has been made analytically and by simulation in understanding the columnar dendrite growth. Although the growth of dendrites in real castings is always accompanied by convection of the melt,[7–10] which may be relatively quiescent or highly turbulent and prolonged, it is often ignored in analytic or theoretical treatment of dendrite growth to simplify these treatments. Fuller understanding of the coupled thermal–solutal–convective transport on dendrite growth might allow us develop new strategies and casting designs that control better the final microstructure and properties.

Modeling and simulation are potentially powerful tools for investigating solidification phenomena. And by making use of increasingly powerful computing systems, appropriate mathematical formulation of the interlinked heat, momentum, and species conservation equations can be achieved. The phase field method is becoming a standard tool for simulating dendritic microstructural evolution because of its implementation advantages, including removing the need for complex, explicit tracking of the solid–liquid interface.[11–13] Instead, in the phase field approach, an extra equation (the phase field equation) is introduced into the mathematical formulation to characterize the transition between the solid phase and the liquid phase through tracking the variable $\phi$, termed the phase field, which is constant in bulk phases (−1 in liquid and 1 in solid) but changes steeply across the solid–liquid interface.

Many studies have now been performed to simulate the evolution of the dendritic microstructure by employing the phase field method. One of the most influential studies was performed by Beckermann et al.[14] who developed a phase field solidification model coupled with convection by applying the so-called average volume technique. A pure material was considered, and therefore, there was no coupling of temperature and solute fields. For a single dendrite, they showed that an “upstream” primary arm grew faster than both the side and the “downstream” primary arms. Similar phenomena were reported in Reference 15 which employed a multigrid approach to solve the Navier–Stokes equations for the melt flow and where side-branching of primary dendrite arms was manifest as a “stretching” of secondary dendrite arms. The faster growth of upstream primary dendrite arms was suggested to be caused by an increase of the effective undercooling at the dendrite tip.[9,10,16–18]

Efforts have also been made to simulate alloy dendrite growth during convection. Lan et al.[10,19] studied the influence of convection on thermal–solute distributions and morphologic changes in a freely growing dendrite. Siquieri and Emmerich[20] investigated the effect of convection on the morphology of an isothermal, free dendrite growth scenario, and again showed that an upstream dendrite arm grew fastest, but ignored any effects of the release of the latent heat. Despite these advances, the interplay between multiple dendrites and convection in a coupled thermal and solute environment for a realistic metallurgical alloy has yet to be progressed significantly.

The principal difficulties in simulating the coupled thermal–solutal–convective case are[21] (1) simulations of multiple dendrite growth require a relatively large domain, which in turn usually requires enormous computing effort, especially where the phase field method is adopted; and (2) the multiscale complexity of coupling temperature, solute, and convection fields that operate over different length and time scales. Despite the evergrowing power of computation, significant progress can only be made for the fully coupled case by developing new robust and efficient numerical algorithms and their implementation.

In the current article, a parallel–multigrid approach is used to solve the coupled phase field equations. We show that simulation of multiple dendrite growth in a fully coupled thermal–solutal–convective arrangement can be solved efficiently and accurately. The simulations reveal basic behavior of dendrite growth including side-branching, tip splitting, and various morphologic transitions due—in particular—to convection. Different aspects of solidification physics then become tractable for simulation, including competing growth between dendrites with different orientations, self-adjusting spacing of dendrites due to temperature and solute transportation in the case of directional solidification (DS), and equiaxed dendrite tilting, and arm splitting due to external convection. Importantly, these simulations can be performed at different scales, including pushing the Lewis number Le = α/D (ratio between thermal diffusivity and solute diffusivity) to ~10⁴ and Prandtl number Pr = υ/α (ratio between kinematic viscosity and thermal diffusivity) to ~10⁻², which both approach those for realistic metallic alloys in actual solidification condition and which have generally not been studied before by less efficient and capable approaches.

The Phase Field Model and Numerical Approach

To simplify the derivation of the phase field model, the following assumptions are made:

• (1). All physical properties of materials are constants unless stated otherwise. These properties include thermal diffusivity α, liquid solute diffusivity D, latent heat of melting L, alloy specific heat C _p, density ρ, and kinematic viscosity $\upsilon$.

• (2). Solute diffusion in the solid phase is neglected.

• (3). Only forced convection is considered, i.e., the effect of gravity force is neglected.

The Phase Field Model Coupled with Convection

By employing the Ginzburg–Landau free energy functional,[11,13]

$$ F = \int {dV\left( {\frac{\sigma }{2}\left| {\nabla \phi } \right|^{2} + f_{\text{AB}} \left( {\phi ,c,T} \right)} \right)} $$

(1)

where F is the free energy of the system, and $\sigma$ is a gradient energy coefficient. f _AB is a free energy density function for a binary mixture of A and B and is a sum of the free energy of the pure material (double well) and the contribution due to solute addition, details of which are found in Reference 13. $\phi$, c ,and T are phase field, solute concentration, and temperature, respectively; according to References 13, 21 and References 14, 15, the governing equations of the phase field model including convection are

$$ \tau_{0} \frac{\partial \phi }{\partial t} = - K_{\phi } \frac{\delta F}{\delta \phi } $$

(2)

$$ \frac{\partial c}{\partial t} + \varvec{\upnu }\nabla c = \nabla \left( {K_{\text{c}} \nabla \frac{\delta F}{\delta c} - {\bf{j}}_{\text{at}} } \right) $$

(3)

$$ \frac{\partial T}{\partial t} + \varvec{\upnu }\nabla T = \alpha \nabla^{2} T + \frac{L}{{2C_{\text{p}} }}\;\frac{\partial \phi }{\partial t} $$

(4)

$$ \frac{{\partial \varvec{\upnu }}}{\partial t} + \varvec{\upnu }\nabla \left( {\frac{{\varvec{\upnu }}}{{f_{\text{l}} }}} \right) = - f_{\text{l}} \nabla P + \upsilon \nabla^{2} \varvec{\upnu } + {\bf{M}}_{1}^{\text{d}} $$

(5)

$$ \nabla \varvec{\upnu } = 0 $$

(6)

where τ ₀ is the relaxation time, $\varvec{\upnu }$ is the “superficial” velocity equivalent to the product of the local liquid fraction (f _l = (1 − $\phi$)/2) and the actual velocity. $K_{\phi }$ and $K_{\text{c}}$ are constants. ${\bf{j}}_{\text{a}}$ is the so-called anti-trapping current developed by Karma and co-workers[11]

$$ {\bf{j}}_{\text{a}} = - \frac{{W_{0} }}{\sqrt 2 }\;\frac{{c/c_{\infty } }}{{\left[ {1 + k - (1 - k)\phi } \right]}}\;\frac{\partial \phi }{\partial t}\;\frac{\nabla \phi }{{\left| {\nabla \phi } \right|}} $$

(7)

where W ₀ is the width of the diffuse interface, k is the partition coefficient of solute, and c _∞ is the initial solute concentration in the liquid. The anti-trapping current is used to counterbalance spurious effects at the diffusion interface arising in phase field modeling, details of which can be found in Reference 11. α is the thermal diffusivity, L is the latent heat of fusion, C _p is the specific heat of alloy, P is pressure, and $\upsilon$ is the kinematic viscosity. ${\bf{M}}_{1}^{\text{d}}$ is a dissipative interfacial force per unit volume as developed by Beckerman et al.:[14]

$$ {\bf{M}}_{1}^{\text{d}} = - 2\upsilon h_{\text{c}} \left( {1 - f_{\text{l}} } \right)^{2} \varvec{\upnu } $$

(8)

where h _c is 2.757 according to an asymptotic analysis of a plane flow past the diffuse interface. This term serves as a distributed momentum sink in the diffuse interface region, which forces the liquid velocity to zero approaching the solid and vanishes in the bulk liquid.

Applying the dimensionless forms of solute and temperature

$$ U = \frac{{\frac{{2c/c_{\infty } }}{1 + k - (1 - k)\phi } - 1}}{1 - k} $$

(9)

$$ \theta = \frac{{T - T_{\text{M}} - {\text{mc}}_{\infty } }}{{L/C_{\text{p}} }} $$

(10)

and by scaling length and time to the interfacial width W ₀ and relaxation time τ ₀, the final governing equations are

$$ A\left( \psi \right)^{2} \left[ {\frac{1}{Le} + {\text{Mc}}_{\infty } \left( {1 + (1 - k)U} \right)} \right]\frac{\partial \phi }{\partial t} = \nabla \left( {A\left( \psi \right)^{2} \nabla \phi } \right) - \frac{\partial }{\partial x}\left( {A\left( \psi \right)A\left( \psi \right)^{\prime } \frac{\partial \phi }{\partial y}} \right) + \frac{\partial }{\partial y}\left( {A\left( \psi \right)A\left( \psi \right)^{\prime } \frac{\partial \phi }{\partial x}} \right) + \phi \left( {1 - \phi^{2} } \right) - \lambda \left( {1 - \phi^{2} } \right)^{2} \left( {\theta + {\text{Mc}}_{\infty } U} \right)\left( {1 + \dot{\xi }} \right) $$

(11)

$$ \left( {\frac{1 + k}{2} - \frac{1 - k}{2}\phi } \right)\frac{\partial U}{\partial t} = \nabla \left( {\tilde{D}\frac{1 - \phi }{2}\nabla U + \frac{1}{2\sqrt 2 }\left[ {1 + \left( {1 - k} \right)U} \right]\frac{\partial \phi }{\partial t}\;\frac{\nabla \phi }{{\left| {\nabla \phi } \right|}}} \right) + \frac{1}{2}\left[ {1 + \left( {1 - k} \right)U} \right]\frac{\partial \phi }{\partial t} - \frac{1}{2}\tilde{\nu } \left\{ {\left[ {1 + k - (1 - k)\phi } \right]\nabla U - \left[ {1 + (1 - k)U} \right]\nabla \phi } \right\} $$

(12)

$$ \frac{\partial \theta }{\partial t} = \tilde{\alpha }\nabla^{2} \theta + \frac{1}{2}\;\frac{\partial \phi }{\partial t} - \tilde{\nu }\nabla \theta - \dot{q} $$

(13)

$$ \frac{{\partial \tilde{\nu }}}{\partial t} + \tilde{\nu }\nabla \left( {\frac{{\tilde{\nu }}}{{f_{\text{l}} }}} \right) = - f_{\text{l}} \nabla \tilde{P} + \tilde{\upsilon }\nabla^{2} \tilde{\nu } - 2\tilde{\upsilon }h_{\text{c}} \left( {1 - f_{\text{l}} } \right)^{2} \tilde{\nu } $$

(14)

$$ \nabla \tilde{\nu } = 0 $$

(15)

where λ = 15L ²/(16HC _p T _M) is a scaling parameter with its reciprocal measuring the energy barrier height H. T _M is the melting temperature of the pure solvent.

$$ {\text{Mc}}_{\infty } = \frac{{\left| m \right|\left( {1 - k} \right)c_{\infty } }}{{L/C_{\text{p}} }} $$

(16)

is a scaled solute concentration factor where m is the actual liquidus slope of the phase diagram. The anisotropic effect can be characterized by function:

$$ A\left( \psi \right) = 1 + \varepsilon \cos \left( {\omega \psi } \right) $$

(17)

where $\psi$ is the angle between the interface norm ${\bf{n}}$ and the axis x, $\varepsilon$ weights the magnitude of the anisotropy strength, and $\omega$ (4 or 6) is the symmetry or harmonic factor. To mimic the thermal fluctuations in the system, a single noise term $\dot{\xi }$ was introduced in Eq. [11] on the source term and realized using a Gaussian distributed random number (mean = 0 and variance = 1), i.e., GRN(0,1) with specific amplitude N _amp as

$$ \dot{\xi } = N_{\text{amp}} \times {\text{GRN}}\left( {0,1} \right). $$

(18)

In Eq. [13], $\dot{q}$ is either a heat sink ($\dot{q}$ > 0) or heat source ($\dot{q}$ < 0) to characterize the external cooling or melting of the entire system. In Eqs. [11] through [15], variables with tilde are dimensionless.

The Orientation Field

In the case of multidendrite growth with randomly oriented crystals, the orientation of the dendrite is another important factor that needs to be taken into account. Because the focus of the current study is on the dendrite growth and morphologic evolution under forced convection, a simpler approach for dendrite orientation is employed comprising two steps. First, the orientation of each of the dendrites is randomly specified with a pre-existing solid seed introduced in the computational domain. Second, as the dendrite grows, very small volumes of liquid are added/transformed to solid; the crystal orientation for this new increment in solid is assumed to be the same as that of the local crystal orientation of the dendrite. In other words, the dendrite grows by transformation of nearby liquid into solid of the same orientation, which is physically similar to the real case and consistent with numerical approaches used in these sharp interface methods.[22,23]

The Parallel–Multigrid Approach

Equations [11] through [15] were discretized using the finite difference method onto a square computing domain with equal grid spacing of Δx = Δy. Equations [11] through [13] were then solved by employing a parallel–multigrid approach, details which have been given elsewhere.[21] A staggered grid was employed for the solution of the Navier–Stokes equations. The structure of an unit grid (or cell) is then composed of phase field, temperature, and solute field occupying the four corners, pressure at the center, and velocities at the middle of each wall of the grid. Solving efficiently the Navier–Stokes equation is not a trivial problem. In the current study, asymmetric coupled Gauss–Seidel (SCGS) smoothing technique[24] was employed. This approach was then parallelized by using a line smoother scheme.[25] According to the structure of the staggered grid, the parallelization of the SCGS scheme requires that during each relaxation step, at least two block (cell) lines of data be skipped, resulting in a three-step parallel block line-smoothing scheme called the parallel-SCGS.

Single Dendrite Growth with Convection

Description of the Computing Domain

Simulation was performed using a rectangular domain of size #Ω = M × N where M and N are the numbers of cells in a row and a column, respectively. For the rectangular domain, the bottom left corner is regarded as the origin point, i.e., x = 0, and y = 0. In this respect, the left boundary will be located as x = 0, right boundary x = M, top boundary y = N and the bottom boundary y = 0. Convection of the liquid alloy melt was assumed from the top of domain flowing toward the bottom. The boundary conditions were set as follows. For the phase field, solute, and temperature distributions, all sides of the computing domain were set to a Neumann condition (gradient flux zero). For convection, the horizontal velocity u was set to be zero at all boundaries; the vertical velocity at the top side of the domain was v = v ₀, while at the bottom side of the domain ∂v/∂y = 0. For left and right sides, ∂v/∂x = 0. A no-slip boundary condition was applied at the solid surface of the dendrite. The important calculation parameters used in the simulation were k = 0.15, crystallographic anisotropy strength ε = 0.02 and Mc_∞ = 0.035, which corresponded to an Al-4 pct Cu alloy as described in Reference 21. A relatively large scaling parameter, i.e., λ = 15 was used in the calculation to facilitate the growth of the dendrite while keeping the external undercooling Δθ ₀ relatively small to insure that W ₀ v _tip/D was smaller than the unity, as required for accurate phase field simulation. Dendrite growth was initiated by placing a solid seed with radius R ₀ = 30d ₀ (d ₀ is the thermal capillary length) at the center of the left side of the domain with temperature θ = 0, i.e., the nucleation step of solidification was not simulated.

A fixed spatial step of Δx = 0.8 was used for all simulations unless stated otherwise. The time step was set as Δt = 0.8 × Δx ²/(4D), which was 0.8 × Le times larger than the time step constrain for an explicit method. The accuracy and implementation considerations of selecting Δx and Δt and various other simulation parameters were discussed in a previous study.[21] The computing domain had a relatively large size of M = 4096 and N = 2048 to insure that there was enough space for both temperature and flow to develop fully around the dendrite as it grew.

The Use of Noise in Simulations

Side-branching of higher-order dendrite arms is often observed in dendrite growth. To achieve this behavior in the simulations, random numerical noise is usually applied, perhaps mimicking the “natural” oscillations and perturbations of the experimental environment. This noise can be introduced into all equations, including the phase field, temperature, and solute (if considered) conservation equations.[4,26] However, thermal perturbation, i.e., noise in the temperature equation, has been suggested to provide the most significant effect on side-branching of higher-order arms; however, other studies indicate that this might not be always the case.[21] In the current study as shown in Eq. [11], numerical random noise was only applied in the phase field equation on the source term, acting as an fluctuation of the driving force that consequently leads to the stretching and growth of the secondary dendrite arms.

Figure 1 shows the calculated dendrite morphology and solute iso-concentrates in the liquid at t = 3000Δt, for three different noise amplitudes of N _amp = 0, 10⁻⁶ and 10⁻³, a Lewis number Le = 100 and an external imposed undercooling of Δθ ₀ = 0.4. Without the application of noise, the dendrite was branchless, as shown in Figure 1(a). With the application of noise, side-branching (as typically seen in experiment) developed. However, as shown in Figures 1(b) and (c), the amplitude of the noise N _amp had surprisingly little effect on the detailed morphology of side-branching. Further numerical tests revealed that side branching occurred no matter how small the value of N _amp. This behavior was quite different from findings in literature, which suggested that the higher the magnitude of the noise then the more intense (size and frequency) the side-branching. In the experiment, it is well known that except under highly contrived conditions, there is always side-branching, and this is consistent with our numerical results. The comparative sensitivity of other models to the noise amplitude is not readily explained, but may be resolved by additional simulations under different conditions, e.g., Lewis number, which lies outside the scope of this article.

Fig. 1

Comparison of dendrite morphology at t = 3000Δt with different noise amplitude (a) N _amp = 0, (b) N _amp = 10⁻⁶, and (c) N _amp = 10⁻³. The noise is a product of a Gaussian distributed random number with mean of zero and standard deviation of unity and N _amp

Mathematically speaking, the implicit multigrid algorithm employed here treats the noise as the residual error in the various conservation equations and the solving process for these equations will seek to eliminate (at least as fully as possible) such influence on the final solution. This is quite different from the mechanism when an explicit algorithm is employed, which tends to accumulate “error” induced by noise, ultimately rendering it on the calculated dendrite morphology. In this sense, there is a danger that explicit algorithms will significantly amplify the influence of noise on side-branching, beyond the sensitivity seen in practice. Nonetheless, the sensitivity of side-branching requires further study to insure that such side branching arises from correct formulation of the physics, rather than from a coincidence of numerical error or instability.

Dendrite Morphology Changes During Convection

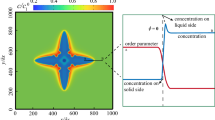
Using the same computing parameters applied in Figure 1 and with Pr = 0.23 and v ₀ = 30 W ₀/τ ₀, Figures 2(a) and (b) show dendrite morphology and the corresponding contour maps of solute and temperature without and with convection. The contour map of the solute concentration was flipped horizontally to achieve a better comparison with the contour map of the temperature. The outline profiles at three different times with an interval of 1000Δt are superimposed to show the evolution of the dendrite morphology in Figures 2(c) (without convection) and (d) (with convection), respectively. The corresponding changes of phase field ($\phi$), solute concentration (c/c _∞) and temperature (θ) along the line where x = 0 (as indicated in Figure 2(c)) at the three time intervals are shown in Figures 2(e) and (f), respectively.

Fig. 2

Contour maps of solute and temperature of dendrite (a) without and (b) with convection. The outlines of the dendrite corresponding to $\phi$ = 0 at three different times are superimposed and shown in (c) without and (d) with convection. Accordingly, the change of phase field, solute transition, and temperature along the line where x = 0 as indicated in (c) are shown in (e) without and (f) with convection, respectively. Distance from seed center in (e) and (f) will be positive on the upstream side while negative on the downstream side

Without convection and as expected, the dendrite grew symmetrically with equal lengths of primary arms. Secondary arms stretched out and grew approximately orthogonal to primary arms, although slightly tilted toward the primary arm's growth direction, especially those near the dendrite center (seed) where interdendrite space became more crowded, the liquid fraction was comparatively low and interdendritic solute concentrations were comparatively high. In these regions, and as seen in Figure 2(c), the dendrite released latent heat as it grew, so that the temperature was comparatively high nearer the dendrite center. Taking the upper primary arm for instance, because the temperature was relatively low toward the tip, the secondary arms tended to grow slightly tilted toward this region. As shown in Figure 2(e) without convection, the solute concentration and temperature profiles around the upstream and downstream primary arms were identical. Beyond the initial transient when the seed first developed a dendritic morphology, these profiles were essentially the same at all times, indicating that the dendrite grew in an approximate steady state.

As convection was applied in Figures 2(b) and (d), the growth of the primary side arm was significantly inhibited. As the melt flow propagated from top to bottom, solute rejected into the liquid during solidification was swept away from around the upstream dendrite tip and carried (convected) downward, along the outside profile of the protruding secondary arms until the side arm tip was reached, where the flow then swept around the side arm tip into the downstream region. Solute then accumulated at the side arm tip, as indicated in Figure 2(d) by the arrowed number “1”. According to the phase diagram, a higher solute concentration leads to a lower solidification liquidus temperature so that the solute pile-up inhibits the growth of the side arm relative to the upstream side which was comparatively depleted of solute. Faster dendrite growth on the upstream side has been reported in the literature for a pure material dendrite,[14–18] but the presence of solute build up in an alloy, which diffuses much slower than heat, exacerbates this upstream–downstream difference. From Figures 2(e) and (f), the temperature at the upstream arm tip was θ = −0.16, which was slightly lower than that at the downstream primary arm tip of θ = −0.156, and both these temperatures were higher than when convection was absent and θ = −0.168. Although a higher temperature should tend to decelerate the growth of the upstream primary arm, it is the solute effect that is dominant and leads to the faster growth. From Figures 2(e) and (f), the solute concentration at the upstream primary arm tip was ~1.95c _∞, lower than that at the downstream primary arm tip of ~2.06c _∞, and significantly lower than without convection of ~2.15c _∞.

As in the case of the upstream primary arm, the growth of the secondary arms in the upstream region was also strongly promoted while growth of secondary arms on the downstream side was inhibited by solute recirculation eddies, as shown in Figure 2(d).

Overall, Figure 2 shows how dendrite growth was influenced by the interplay between solute and temperature distribution, and the effect of convection. For Le = 100 and Pr = 0.23, solute gradients and locally depleted or concentration regions in the liquid were more pronounced than variations in temperature: heat flowed relatively fast with respect to convection/diffusion under these conditions.

Influence of Dendrite Growth Parameters

Figures 3(a) through (g) again show a series of dendrite morphologies and contour line maps of solute concentration (left) and temperature (right) for different combinations of the four major parameters related to dendrite growth: inlet flow velocity v ₀, Prandtl number Pr, anisotropic strength ε, and Lewis number Le. Only one parameter was varied in each figure, and dendrites were allowed to grow to reach similar sizes (longer simulation times were required for a lower level of anisotropy).

Fig. 3

Comparison of dendrite morphology under different situations, using the contour line maps of solute concentration and temperature. Parameters used for simulation are shown in each figure with one parameter varied

Figures 3(a) through (c) show that an increase of the inlet velocity (from 0 to 10 and then 30 with units of W ₀/τ ₀) promoted strongly the growth of the upstream primary arm while decelerating the growth of the side primary arm, as previously explained. However, the length of the downstream primary arm was slightly shorter at v ₀ = 10 than at v ₀ = 30, as shown by comparing Figures 3(b) and (c). The particular way the downstream solute eddy recirculated was responsible for these differences. As seen in Figure 3(c), when the flow velocity was comparatively high at v ₀ = 30, the eddy pattern occupied more area than that when flow velocity was at v ₀ = 10 lower (Figure 3(b)), and the flow direction of the eddy at v ₀ = 30 circulating against the lower primary dendrite arm was upstream, whereas at v ₀ = 10, the eddy flow against the dendrite tip was downstream. The net effect was that the solute swept from the upper regions of the dendrite and recirculating “behind” the side arms was dispersed over a greater eddy area in Figure 3(c) than in Figure 3(b) so that the solute concentration at the downstream primary arm was comparatively low for v ₀ = 30, undercooling the liquid relative to the v ₀ = 10 case, and encouraging dendrite growth.

The increase of the Prandtl number from Pr = 0.23 to 23 in Figure 3(d) reversed this behavior with recirculation against the downstream dendrite arm tip now primarily downstream, and the primary side arm also became significantly longer. This can be understood by comparing the tip solute concentration and temperature as shown in Figure 4. The solute concentrations at the upstream and downstream primary tips wer 2.09c _∞ and 2.27c _∞, respectively, when Pr = 23, compared with 1.95c _∞ and 2.06c _∞ when Pr = 0.23. As expected, a higher solute concentration led to a lower growth velocity and thus a shorter arm. A further increase of the velocity from v ₀ = 30 to v ₀ = 50 did not produce a significant change in dendrite morphology for Pr = 23, and as shown in Figures 3(e) and 4, these increases in velocity only brought in about a 1.6 pct elongation of the upstream primary arm. Conversely, for the equivalent case but with Pr = 0.23, as shown in Figures 3(b), (c) and 4, an equivalent increase in velocity led to a lengthening of the upstream primary arm by 18 pct. The downstream primary arms all shortened as velocity increased for Pr = 23, as shown in Figures 3(d) and (e). No large eddies were created, similar to the case of Figure 3(b).

Fig. 4

The corresponding phase field ($\phi$), solute concentration (c/c _∞), and temperature (θ) along the line x = 0 as shown in Fig. 3, wherein cases (a) to (e) are indicated by the numbers 1 through 5, respectively. Distance from seed center will be positive on the upstream side, while it is negative on the downstream side

A comparison of Figures 3(d) and (f) shows the effect of a decrease in the strength of anisotropy ε, which enhanced the tendency for side branching and side branch growth. The secondary arms on the upstream side developed a pronounced upward tilt following a 50 pct reduction in the anisotropy.

Figure 3(g) shows the dendrite morphology using a fixed temperature, and because the release of the heat of fusion was not considered in this isothermal case, the case is equivalent to using Le = ∞, and produced a generally “fatter” dendrite.

A Sixfold Dendrite

Figures 5(a) and (b) show a similar comparison of dendrite morphology evolution without and with convection, but in the case of a sixfold dendrite. The simulation parameters were the same as those in Figure 3(a) and the superimposed dendrite outlines are at time intervals of 1000Δt. The insert figure of Figure 5(b) shows the flow streamlines. In contrast to the fourfold dendrites, the secondary dendrite arms without convection did not grow approximately normal to the primary dendrite trunk. Taking the upper primary arm for instance, nearly all the secondary arms were tilted at ~30 deg to the normal. The primary arms growing along the y axis were slightly longer (~8 pct) than the other primary arms (shown by the circles touching the dendrite tips in Figures 5(a) and (b)) and indicated that “grid anisotropy” was introduced during the simulations. Numerical tests subsequently showed that this artificial anisotropy could be significantly reduced by decreasing the size of the grid, i.e., a halving of Δx = Δy reduced the difference in length by 80 pct.

Fig. 5

Comparison of sixfold dendrite morphology: (a) without and (b) with convection. The outlines of the dendrite corresponding to $\phi$ = 0 at different time scales at intervals of 1000Δt are superimposed

The presence of convection in Figure 5(b) again enhanced the growth of the upstream primary arm, and side-branch growth was promoted strongly on both sides of the upstream dendrite, and on the upstream side of primary side arms. The downstream primary arm did not change the length appreciably but the primary side arms, and all downstream side arms were much reduced because of the trapping of solute in the eddies shown in the insert of Figure 5(b).

Figures 3 and 5 show that convection-enhanced upstream primary arm growth and eddy behavior strongly influenced downstream growth. The strength of the convection in terms of a recirculating eddy is largely determined by the Prandtl number Pr and when Pr < 1, the recirculation behavior will be pronounced. In this case, solute is distributed, or dispersed, over a relatively large eddy and effects on growth in the downstream region are relatively weak. When Pr > 1, eddies tend to be smaller, any solute swept from upstream regions is comparatively concentrated into these eddies and the growth of the downstream primary or secondary dendrite arm is inhibited. Similar concentration effects develop if the eddies are constrained by geometry, such as in the downstream region of the sixfold dendrite, so that again the solute concentration per unit area (or per unit volume in 3D) is relatively concentrated. When Pr < 1, the convection patterns have greater influence on growth than temperature, and the scenario becomes similar to that of dendritic growth of a pure material.

Multidendrite Growth

Domain Description and Computing Considerations

Two situations are considered concerning multidendrite growth with convection. In the first case, the flow was introduced along the top of the domain at a constant velocity from left to right (an x velocity component only), which induced a recirculating flow inside the computational domain. No slip boundary condition was applied for the domain sides, other than the top. The second case was similar to that applied for the single dendrite in Section III, i.e., the liquid melt flowed through the domain from top to bottom, entering with a constant velocity in the y direction only.

To insure that all dendrites were fully developed, a relatively large domain size of #Ω = 8192 × 8192 was used. For the first case, 15 dendrites were seeded with random orientation at the bottom of the domain while for the second case, 9 dendrites were seeded randomly in the domain. The magnitude of the applied velocity for both cases was fixed at v ₀ = 30 W ₀/τ ₀. For the calculation, 192 cores were used (16 nodes and 12 cores), with most simulations being completed in less than 10 hours.

The first case approximated to that of DS, commonly applied in both experiment and industry. However, in experiment, a finite temperature gradient is imposed from top to bottom, whereas here the top and bottom of the computational domain were maintained at the same constant undercooling temperature, i.e., zero temperature gradient. Because no nucleation events were simulated and the seeds were constrained to remain at the bottom of the domain, their subsequent growth qualitatively mimicked the microstructures developed during DS. While it is possible to impose a finite gradient in the simulations, this was not pursued for the following reason, common to all current phase field approaches. Although the applied domain size M = N = 8192 was relatively large for this type of simulation, the physical domain size recovered by transforming the nondimensional units used in calculation to real lengths was ~100 × 100 μm for the case of a metallic alloy such as Al-Cu, or ~500 × 500 μm for an organic/transparent alloy. In such a “small” domain, the applied temperature gradient for typical DS conditions would be negligible. For example, for an Al-Cu alloy and assuming the temperature gradient as ~100 K/mm, the temperature difference (between the top and bottom sides of domain) would be Δθ ~ 0.0275, which yielded no significant difference in simulation results of microstructure to that produced in the isothermal case. Nonetheless, this observation highlights the restriction of most phase field simulations of dendrite growth, which is not always appreciated, and that the real time and length scales are usually far from realistic, while the robustness and efficiency of the current model begins to allow more realistic solidification conditions to be explored.

Furthermore, it is worth highlighting that the simulations for both columnar and equiaxed cases are quite different from phase field simulations in the literature where the release of latent heat is usually ignored. The growth of dendrites in the current study, including key characteristics such as the tip velocity, morphology evolution and adjustment of the primary and secondary arm spacing are determined by the full coupling of thermo-solutal fields for the first time. The focus of the multiple dendrite growth simulations is the interplay of multidendrites on the growth transients and any effects of the forced convection on morphology change. Dendrite growth under somewhat extreme conditions, i.e., against a large magnitude flows, is also discussed.

Columnar Dendrite Growth with Convection

Figure 6 shows the simulation results for columnar dendrite growth corresponding to the pseudo-DS case, with the uppermost and lowermost temperatures fixed at θ = −0.4, as previously described. Other simulation parameters were the same as those in Figure 3(c). Totally, 15 dendrites were initially seeded at the bottom of the domain, with different growth orientations. The outlines of the dendrite at different times (from t = 1000Δt to t = 20,000Δt with a time interval of 1000Δt) corresponding to $\phi$ = 0 are superimposed and shown in Figure 6(a). Convection was then applied by imposing a constant left-to-right velocity along the top of the domain with a horizontal velocity of v ₀ = 30 W ₀/τ ₀. Simulation was then continued for 5000Δt and the results shown in Figure 6(b). The contour maps of solute concentration (in terms of c/c _∞) and temperature at t = 25,000Δt are shown in Figures 6(c) and (d), respectively.

Fig. 6

Evolution of a columnar dendrite front and the influence of a re-circulating flow. Totally 15 dendrites were initially seeded at the bottom side of domain with different growth orientation. The convection was then introduced by imposing a constant velocity flow at the top side of the domain at the time of 20,000Δt

The seeds with different orientations at the base of the domain began to grow into the undercooled liquid. After a comparatively short interval, eight well-developed primary dendrite arms dominated the growth, reaching approximately similar lengths after 20,000Δt. These were the fastest growing primary arms, most favorably oriented and spaced. As seen from Figure 6(a), as a direct result of growth competition, these “selected” dendrites mostly grew with the primary dendrite arm parallel to the y axis, i.e., the fastest growing direction. The behavior is in qualitative agreement with solidification theory and experimental results obtained by imaging of organic alloy analogs at room temperature and metallurgical alloys using synchrotron X-ray imaging.[27,28]

As seen from the inset figure of Figure 6(a), as the dendrite grows, secondary arms can remelt at their roots and detach from the primary trunk. If buoyancy forces were included in the simulation, then it can be conjectured that for the binary Al-Cu alloy, where the solid has lower density than the liquid, these detached secondary arms would move upward into the unsolidified melt. This behavior is known to lead to “freckling” in Ni superalloys produced by DS, and can also be readily observed in synchrotron X-ray imaging experiments, which leads to a columnar-to-equiaxed transition.[28] The remelting at the base of secondary dendrite arms arose from local solute enrichment in the interdendritic region as growth proceeded, latent heat was evolved, and the comparatively sharp local curvature of the solid–liquid interface that increased its relative solubility. To the best knowledge of the authors, this is the first time these features are revealed in such detail by phase field simulations, which can only be achieved if the release of the latent heat is considered.

The introduction of convection in Figure 6(b) did not have a strong influence on dendrite growth compared with its generally pronounced effect on equiaxed dendrite growth. Although, ahead of the primary dendrite tips, the induced recirculation was comparatively strong, the perpendicular velocity across the dendrite front was close to zero. For this particular combination of flow condition and thermophysical parameters, the spacing of the dendrites was too close for interdendritic flow to be induced, and the solute distribution (Figure 6(c)) and temperature (Figure 6(d)) in these regions were largely insensitive to bulk movement of the liquid ahead of the front.

Equiaxed Dendrite Growth with Convection

Figure 7 shows similar results to Figure 6 (with same simulation parameters) but for the case of equiaxed dendrites. Figure 7(a) is without convection while Figure 7(b) includes convection under the same conditions as those considered in Figure 3(c). The outline profiles for $\phi$ = 0 from 1000Δt to 8000Δt (with intervals of 1000Δt) are superimposed and shown in Figures 7(a) and (b), while the contour maps of solute concentration and temperature at 7000Δt of Figure 7(b) are shown in Figures 7(c) and (d), respectively.

Fig. 7

Superimposed dendrite outlines at $\phi$ = 0 under the case of Le = 100 and Pr = 0.23 showing the comparison of equiaxed multidendrite growth (a) without and (b) with forced convection (v ₀ = 30) applied from top to bottom of the domain. The corresponding contour maps of solute concentration and temperature at 7000Δt for (b) are shown in (c) and (d), respectively

The presence of the convection changed the morphology of all the dendrites with a promotion of growth in the upstream direction, most notably for secondary dendrite arms; correspondingly, the growth of the side and downstream primary arms was significantly inhibited. In the early stages, there was little interaction of dendrites in terms of their surrounding solute, temperature or local flow fields. However, as more solid was developed, the gaps between dendrites reduced and the flow pattern changed: local velocities through narrowing gaps increased with a commensurate increase in recirculation beyond the constrictions. For example, adjacent to some of the dendrites, the local liquid velocity increased five times over the period of the calculation as liquid flowed through the progressively narrowing gap between dendrites.

Figure 7(b) shows further intriguing behavior. The dendrite on the extreme right of the domain labeled “B” was initialized so that primary arms were 45 deg to the top to bottom flow direction. As it grew, the primary dendrite arm first split and then continued to grow, gradually tilting toward the incoming flow. Other simulations emphasized that convection tended to encourage tip splitting, resulting in unusual dendrite morphologies. Further discussion is given in the next section.

Unlike the columnar case, there was no remelting of primary arms in Figure 7(a) under broadly simulation conditions, even though the local solute concentration in between the dendrite arms, either primary or secondary, was more or less the same (as specified by the phase diagram). The way in which the temperature evolved around the different dendrite morphologies may play a role.

Figure 8 shows similar calculations to those presented in Figure 7 but for Le = 10⁴. To achieve similar growth velocities to those in Figure 7 a lower temperature of θ = −0.17 was employed at both the top and bottom sides of domain because otherwise the faster heat transfer associated with a larger Lewis number would produce a much larger effective undercooling. The outline profiles for $\phi$ = 0 from 1000Δt to 9000Δt (with intervals of 1000Δt) are superimposed and shown in Figures 8(a) and (b) and the corresponding contour maps of solute concentration and temperature at 9000Δt for Figure 8(b) are shown in Figures 8(c) and (d), respectively. Further, Pr = 0.023 which was approximately that of an Al-Cu alloy was assumed. This more realistic combination of Le and Pr highlighted multiscale aspects that are usually problematic for these types of calculation: thermal transport is much faster than solute and fluid transport, and depending on flow conditions, there is a similar mismatch between solute and fluid (convection) length-scales. Nevertheless, the current multigrid algorithm worked perfectly well under these traditionally “extreme” conditions, and the simulation time was more or less the same as for the conventional, generally considered more tractable conditions of Figure 7.

Fig. 8

Superimposed dendrite outlines at $\phi$ = 0 under the case of Le = 10⁴ and Pr = 0.02 showing the comparison of equiaxed multidendrite growth (a) without and (b) with convection (v ₀ = 30) applied from top to bottom of domain. The corresponding contour maps of solute concentration and temperature at 9000Δt for (b) are shown in (c) and (d), respectively

When Le increased from 10² to 10⁴, the temperature distribution shown in Figure 8(d) became much more uniform. Consequently, the dendrite morphology was also different with much less side-branching, although again there was marked difference in upstream and downstream behaviors. Figure 8(c) shows that under these conditions, the solute distributions around dendrites extended over shorter distances. For example, the solute “tail” under the tip of the side primary arm of dendrite “A” was significantly reduced when the Lewis number was increased.

Returning to Figure 8(a), the tip splitting of dendrite “B” previously described for Figure 7(a) no longer occurred when Le = 10⁴. To consider this behavior further, the morphology of dendrite “B” under different conditions is shown in more detail in Figure 9. With Le = 10⁴ in Figure 9(a), there was no tip splitting, whereas with Le = 10² in Figure 9(b), the splitting occurred very early in the growth for all primary dendrites, but only for this dendrite orientation. At low Lewis number, heat transport was comparatively slow, and therefore the implication was that, under these conditions, there was a sensitive interplay between the crystal anisotropy and the local temperature gradients. When the Lewis number is increased toward those of metallic alloys, heat flowed faster, local temperatures became more isotropic, and there was no driving force to split the tip; indeed, no tip splitting was contrived for any combination of parameters, flow conditions, or dendrite orientation in the simulations when Le = 10⁴. However, when Le = 10² in Figures 9(c) and (d), convection did have a strong influence on tip behavior. In Figure 9(c), all dendrite arms had a single split, while one arm on the upstream right-hand side underwent multiple tip splittings and gave a morphology similar to the growth structure developed when a dendrite grows along the [111] crystal plane.[29] The inference therefore is that convection had an influence on the local solid–liquid interfacial conditions analogous to the effect to crystallographic anisotropy: under strong convection, the controlling effect of crystallographic anisotropy on growth morphology was weakened, which in turn led to multiple tip splittings as the dendrite sought to accommodate local thermodynamic conditions dominated by flow effects. Figure 9(d) shows how this effect can be exacerbated further by increasing the effective convection strength via a decrease in the Prandtl number from 23 to 0.23, with extensive tip splitting and arm tilting toward the incoming flow. This change of the local growth conditions could be termed “convection-induced anisotropy,” and can dominate over inherent crystal anisotropy under certain conditions.

Fig. 9

Splitting and tilting of an equiaxed dendrite, extracted from Figs. 7 and 8 with (a) Le = 10⁴, no convection applied, (b) Le = 10², no convection applied, (c) Le = 10², v ₀ = 30, Pr = 23 and (d) Le = 10², v ₀ = 30 and Pr = 0

Conclusions

Dendrite growth against forced convection in a coupled thermosolutal situation has been studied using simulations based on the phase field method. The various coupled equations have been solved by employing an efficient parallel, multigrid numerical approach. Dendrite side branching or stretching of secondary arms was achieved by introducing random noise to the simulations, where the noise magnitude was responsible only for the initiation of side branching with no subsequent effect on growth morphology. Dendrite morphology evolution under different combinations of growth-related parameters including the magnitude of flow velocity, Prandtl number, Lewis number, and the crystallographic anisotropy strength has been studied. Under predominantly one-dimensional flow, convection of the melt enhanced the growth of upstream primary arms and inhibited the growth of both side and downstream primary arms. The flow-related solute and temperature distributions controlled upstream–downstream growth differences, the relative strengths of which were determined by the magnitude of the Lewis and Prandtl number. The role of solute-rich recirculating eddies has been simulated in detail, and the sensitivity in particular to the Prandtl number revealed.

Multidendrite growth under convection was also studied for both columnar and equiaxed dendrite growth. Primary and secondary arm dendrite remelting was predicted in later stages of solidification as interdendritic solute concentrations increased. Under realistic metallic alloy conditions of Le ~ 10⁴ and Pr ~ 0.023 corresponding to an Al-Cu alloy, multidendrite growth both with and without convection was successfully simulated in sensible times, emphasizing the robustness of the algorithm and numerical approach. By exploiting this stability, the detailed influence of flow on growth was studied, and the promotion of tip splitting and dendrite tilting was rationalized by the progressive suppression of crystallographic anisotropy effects by local flow-induced conditions that forced significant local departures from equilibrium. These effects were most predominantly manifest when thermal conductivity was comparatively low; otherwise, the comparatively faster transport of heat was the dominant factor in microstructural evolution.