Introduction

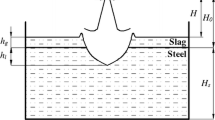
Supersonic gas jets are used widely in basic oxygen furnace (BOF) and electric arc furnace (EAF) steelmaking for refining the liquid iron inside the furnace. Supersonic gas jets are preferred to the subsonic jets because of the high dynamic pressure associated with it, which results in a greater depth of penetration and in better mixing. Laval nozzles are used to accelerate gas jets to supersonic velocities of around 2.0 Mach number in steelmaking.[1] The supersonic gas jets generate droplets upon impingement on the liquid melt, which is known as splashing. Droplet generation has both beneficial and detrimental effects. The droplet increases the interfacial area, which in turn, increases the refining rate.[2] On the other hand, it may cause a wearing of refractories or a skulling on the mouth of the vessels and lances, which can result in a loss of production.[3–5] Therefore, it is necessary to understand the behavior of the supersonic gas jets in a high temperature environment to determine the optimum processing conditions.

Various experimental and numerical investigations of the behavior of the supersonic oxygen jet after emerging from the Laval nozzle have been reported in the literature.[6–12] But only Sumi et al.[8] experimentally studied the behavior of the supersonic oxygen jet at three different ambient temperatures—285 K, 772 K, and 1002 K. The results showed that velocity attenuation of the jet was restrained, and the potential flow core length was extended under high temperature conditions. The potential flow core length was defined as the distance from the nozzle tip to the point where the magnitude of the nozzle exit velocity remains unchanged. Numerical simulations of the supersonic oxygen jet behavior at a high ambient temperature carried out by Allemend et al.,[6] Tago and Higuchi,[9] and Katanoda et al.[12] also showed an increase in the potential flow core length, but their results were not validated against experimental data.

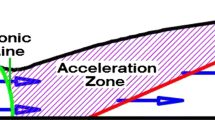
When a supersonic jet exits from a Laval nozzle, it interacts with the surrounding gas to produce a region of turbulent mixing as shown in Figure 1. This process results in an increase in jet diameter and a decrease in jet velocity with an increasing distance from the nozzle exit. However, in a high-speed jet, the mixing of the jet with its surroundings is suppressed, and the growth rate of the turbulent mixing region is reduced.[13] It became known in the late seventies that the standard k−ε model[14] gives a poor prediction of the mean velocity profiles of the high-speed turbulent axisymmetric jets.[15] This result occurs because the standard k−ε model lacks the ability to reproduce the observed reduction in the growth rate of the turbulent mixing region. However, some modifications of the k−ε model have been proposed[16,17] to take into account the effect of compressibility in reducing the growth rate of the turbulent mixing region.

Fig. 1
figure 1

Regions of a supersonic jet exiting from a Laval nozzle

Full size image

In the present study, a numerical simulation of the supersonic oxygen jet showed that the k−ε turbulence model, including the compressibility correction proposed by Heinz,[17] underpredicts the potential flow core length at high ambient temperatures. Abdol-Hamid et al.[18] proposed a temperature corrected turbulence model to take into account the effect of a large temperature gradient when a hot supersonic jet exits into a cold atmosphere. But their[18] model did not give reasonable results when used for simulating a room temperature supersonic jet exiting into a hot atmosphere as described in subsequent sections of the article. Hence, a simple modification to the k−ε turbulence model was proposed in this article based on the temperature-corrected turbulence model developed by Abdol-Hamid et al.[18] As previously mentioned, the corrected turbulence model[18] can address only the hot jet coming into a cold atmosphere. The present proposed modification can address a cold jet coming into the hot environment encountered in steelmaking. The supersonic jet behavior at three different ambient temperatures of 285 K, 772 K, and 1002 K were simulated numerically and validated against experimental data[8] as well as a jet model proposed by previous researchers.[19] This computational fluid dynamics (CFD) model then was used to investigate the supersonic jet behavior and the droplet generation rate at a steelmaking temperature of 1800 K.

Numerical Analysis

Governing Equations

The numerical simulations were carried out by integrating the unsteady Reynolds-averaged Navier–Stokes (RANS) equations. The averaged mass, momentum and the energy equations can be written in a conservative form as shown in the following mass conservation equation:

$$ {\frac{\partial \rho }{\partial t}} + {\frac{{\partial \rho U_{i} }}{{\partial X_{i} }}} = 0 $$
(1)

where ρ is the density of the fluid and U i is the mean velocity component in the ith direction.

The momentum conservation equation is as follows:

$$ {\frac{{\partial \rho U_{i} }}{\partial t}} + {\frac{{\partial \left( {\rho U_{i} U_{j} } \right)}}{{\partial X_{j} }}} = - {\frac{\partial P}{{\partial X_{i} }}} + {\frac{{\partial \left( {\tau_{ij} - \rho \overline{{u_{i} u_{j} }} } \right)}}{{\partial X_{j} }}} $$
(2)
$$ \tau_{ij} = \mu \left( {{\frac{{\partial U_{i} }}{{\partial X_{j} }}} + {\frac{{\partial U_{j} }}{{\partial X_{i} }}} - {\frac{2}{3}}{\frac{{\partial U_{k} }}{{\partial X_{k} }}}\delta_{ij} } \right) $$
(3)

where P is the pressure of fluid, \( \tau_{ij} \) is the viscous stress, u i and u j are the fluctuating velocity components in the ith and jth directions, respectively, and μ is the molecular viscosity.

\( - \rho \overline{{u_{i} u_{j} }} \) is known as “Reynold stresses” and is used to represent the effect of turbulence. The Reynold stresses are modeled according to the Boussinesq approximation, which is expressed as follows:

$$ - \rho \overline{{u_{i} u_{j} }} = \mu_{t} \left( {{\frac{{\partial U_{i} }}{{\partial X_{j} }}} + {\frac{{\partial U_{j} }}{{\partial X_{i} }}}} \right) - {\frac{2}{3}}\left( {\rho k + \mu_{t} {\frac{{\partial U_{k} }}{{\partial X_{k} }}}} \right)\delta_{ij} $$
(4)

where μ t is the turbulent viscosity and k is the turbulent kinetic energy. The modeling of turbulent viscosity and of turbulent kinetic energy is described in following sections.

The energy conservation equation is expressed as follows:

$$ {\frac{\partial \rho E}{\partial t}} + {\frac{{\partial \left( {\rho EU_{i} + PU_{i} } \right)}}{{\partial X_{i} }}} = - {\frac{\partial }{{\partial X_{i} }}}\left( {q_{i} + C_{p} \rho \overline{{u_{i} t^\prime}} } \right) + {\frac{\partial }{{\partial X_{i} }}}\left( {\tau_{ij} U_{j} - \rho \overline{{u_{i} u_{j} }} U_{j} } \right) $$
(5)

where E is the total energy, C p is the specific heat at constant pressure, and t′ is the fluctuating component of temperature. Heat transferred by conduction, q i is expressed as follows:

$$ q_{i} = K{\frac{\partial T}{{\partial X_{i} }}} $$
(6)

where K is the thermal conductivity of fluid. The term \( \rho \overline{{u_{i} t^\prime}} \) is known as the turbulent heat flux and is modeled as follows:

$$ \rho \overline{{u_{i} t^\prime}} = {\frac{{\mu_{t} }}{{Pr_{t} }}}{\frac{\partial T}{{\partial X_{i} }}} $$
(7)

where Pr t is the turbulent Prandtl number. Most common values of the turbulent Prandtl number are 0.9, and it is satisfactory for shock-free flows up to low supersonic speeds and a low heat transfer rate.[20] When a cold supersonic jet (300 K) is introduced inside a steelmaking furnace of around 1800 K ambient temperature, the heat transfer rate from the hot environment to the cold jet will be very high because of the large temperature gradient. Wilcox[20] recommended to use Pr t  = 0.5 for free shear flow and high heat transfer problems. Hence, Pr t  = 0.5 was used in this simulation.

Turbulence Modeling

To close the RANS equations, the two equation k−ε turbulence model[14] was used. In this model, the turbulent kinetic energy k and the dissipation rate ε were obtained from the following transport equations:

$$ {\frac{\partial \rho k}{\partial t}} + {\frac{{\partial \rho U_{j} k}}{{\partial X_{j} }}} = - \rho \overline{{u_{j} u_{i} }} {\frac{{\partial U_{i} }}{{\partial X_{j} }}} + {\frac{\partial }{{\partial X_{j} }}}\left( {\mu + {\frac{{\mu_{t} }}{{\sigma_{k} }}}{\frac{\partial k}{{\partial X_{j} }}}} \right) - \rho \varepsilon $$
(8)
$$ {\frac{\partial \rho \varepsilon }{\partial t}} + {\frac{{\partial \rho U_{j} \varepsilon }}{{\partial X_{j} }}} = - C_{\varepsilon 1} \rho \overline{{u_{j} u_{i} }} {\frac{{\partial U_{i} }}{{\partial X_{j} }}}{\frac{\varepsilon }{k}} + {\frac{\partial }{{\partial X_{j} }}}\left( {\mu + {\frac{{\mu_{t} }}{{\sigma_{\varepsilon } }}}{\frac{\partial k}{{\partial X_{j} }}}} \right) - C_{\varepsilon 2} \rho {\frac{{\varepsilon^{2} }}{k}} $$
(9)

where C ε 1, C ε 2, σ k, and σ ε were the constants for the k−ε model, and their values are 1.44, 1.92, 1.0, and 1.3, respectively.

The turbulent viscosity μ t is defined as follows:

$$ \mu_{t} = C_{\mu } \rho {\frac{{k^{2} }}{\varepsilon }} $$
(10)

In the standard k−ε turbulence model, C μ  = 0.09 is used. Heinze[17] modified the value of C μ to account for the effect of compressibility, which is defined by the following equation:

$$ C_{\mu } = 0.07\exp\,( - 0.4M_{g} ) $$
(11)
$$ M_{g} = {\frac{\left| S \right|l}{a}} $$

where \( \left| S \right| \) is the mean shear rate, l is the turbulence length scale, and a is the speed of sound. This modification of C μ accurately predicts the axial velocity distribution of the gas jet at room ambient temperature but still underpredicts the axial velocity distribution at high ambient temperatures.

In order to take into account the effect of a large temperature gradient, Abdol-Hamid et al.[18] modified the constant C μ according to the following equations:

$$ C_{\mu } = 0.09C_{T} $$
(12)
$$ C_{T} = \left[ {1 + {\frac{{C_{1} T_{g}^{m} }}{{1 + C_{2} f(M_{\tau } )}}}} \right] $$
(13)

where T g is the function of the local total temperature gradient normalized by the local turbulence length scale as follows:

$$ T_{g} = {\frac{{\left| {\nabla T_{t} } \right|\left( {{{k^{3/2} } \mathord{\left/ {\vphantom {{k^{3/2} } \varepsilon }} \right. \kern-\nulldelimiterspace} \varepsilon }} \right)}}{{T_{t} }}} $$
(14)

The reason for using the local total temperature gradient in their model is that the total temperature is not Mach number dependent. Hence, this model will not be influenced by internal shocks and flow expansion.

In order to model high-speed flow, turbulence Mach number M τ was included in their modification. The turbulence Mach number and the function of turbulence Mach number was defined as follows:

$$ M_{\tau } = \sqrt {{\frac{2k}{a}}} $$
(15)
$$ f(M_{\tau } ) = (M_{\tau }^{2} - M_{\tau 0}^{2} )H(M_{\tau } - M_{\tau 0} ) $$
(16)

where a is the speed of sound, H(x) is the Heaviside function, and M τ0 = 0.1. For no compressibility correction, f(M τ ) = 0. The constants and the coefficients of Eq. [13] are listed in Table I.

Table I Coefficients and Constants of Eq. [13]
Full size table

The authors[18] did not derive the functional relationship, constants, and coefficients of Eq. [13] analytically. Instead, it was determined by trial and error to fit the total temperature experimental data of Seinor et al.[21] for the supersonic flow. This modification was proposed for a high temperature supersonic jet flowing into a low ambient temperature. In that case, the potential core length of the jet becomes shorter because of the increment in the growth rate of the turbulent mixing layer.[21] Nonomura and Fujji[22] also reported that the potential core length of the supersonic jet decreased with an increasing supersonic jet temperature. The standard k−ε turbulence model fails to predict the observed increase in the growth rate of the turbulent mixing. This modification[18] of the k−ε model was made to increase the turbulent eddy viscosity in the shear layer by increasing the value of C μ as a function of the total temperature gradient. However, this modification of C μ underpredicts the potential core length of the supersonic jet when used for a cold supersonic jet exiting into a hot atmosphere. This result occurs because the modified model[18] only can increase the growth rate of mixing by increasing the value of C μ , which in turn, makes the potential core length shorter. But when a cold supersonic jet enters into a hot atmosphere, the potential core length increases. Hence, a different model is required to simulate accurately the cold supersonic jet emitting into a high ambient temperature.

In this study, the previous model[18] was modified to simulate accurately the cold supersonic jet exiting into a hot atmosphere. Unlike the previous model,[18] the value of C μ was modified by dividing its standard value (0.09) by the variable C T to achieve the desired decrease in turbulent viscosity at the shear layer, which in turn, reduced the growth rate of mixing. The variable C T was determined by using the similar functional relationship of Eq. [13], which was used by the previous authors.[18] Following their[18] approach, the coefficients and the constants in Eq. [13] were determined by trial and error for the present study to match accurately the experimental velocity distribution of Sumi et al.[8] on the center axis of the supersonic jet at different ambient temperatures. The constants and coefficients for the present study are listed in Table I. Hence, for the present study, Eqs. [12] and [13] become:

$$ C_{\mu } = {\frac{0.09}{{C_{T} }}} $$
(17)
$$ C_{T} = \left[ {1 + {\frac{{1.2T_{g}^{0.6} }}{{1 + f(M_{\tau } )}}}} \right] $$
(18)

According to Eqs. [17] and [18], the value of C μ becomes small in the region of a high total temperature gradient, which in turn, reduces the turbulent viscosity. A lower turbulent viscosity leads to a lower turbulent shear stress (Eq. [4]) and, hence, a lower turbulent mixing, which leads to an increased potential core length. The first term on the right side of Eq. [8] is the turbulence production term, where \( \overline{{u_{j} u_{i} }} \) is the turbulent stress. The decrease in turbulent viscosity results in a reduction of the turbulence production rate and, hence, lowers the turbulent kinetic energy, which further reduces the turbulent viscosity through Eq. [10]. As a result, the growth rate of the turbulent mixing region decreases.

The reason for using the ad-hoc modification of the k−ε turbulence model rather than using the other turbulence model is that it is robust, and the implementation of the modified term into the solution is very easy. This ad-hoc modification approach also was used by the previous researchers[18] at NASA Langley Research Center (Hampton, VA). Our objective was to investigate the supersonic jet behavior at a high ambient temperature in order to simulate the supersonic oxygen jet impinging on the liquid iron inside the steelmaking furnace. The results obtained with this ad-hoc modification are in good agreement with the experimental data and the jet model as shown in Section III.

Computational Domain

The computational grid used for the CFD simulations in the present study is shown in Figure 2. The computational grid is an axisymmetric wedge-shaped grid with only one cell in circumferential direction. In order to reduce the computational time, the flow inside the Laval nozzle was not included in the simulation. Flow conditions at the nozzle exit were calculated by using the isentropic theory.[23] The exit diameter of the nozzle was 9.2 mm and was considered as the inlet to the computational domain. The size of the computational domain was 100 nozzle exit diameters downstream from the nozzle exit and 30 nozzle exit diameters normal to the jet centerline. The mesh had a total of 7760 cells. The grid independency tests are presented in Section II–F. The grid density was very high at the exit of the nozzle and at the shear layer.

Fig. 2
figure 2

The computational domain with boundary conditions

Full size image

Boundary Conditions

All boundary conditions were chosen to match with the experimental study of Sumi et al.[8] A stagnation pressure boundary condition was used at the inlet of the computational domain (the exit of the nozzle). The value of the Mach number and the temperature were defined at the inlet. At the outlet, static pressure boundary condition was used. For the symmetry plane, the symmetry boundary condition was used. At the wall, zero heat flux was used as the wall boundary condition. The values of the boundary conditions are listed in Table II.

Table II Boundary Conditions
Full size table

Computational Procedure

The unsteady, compressible continuity, momentum, and energy equations were solved using a segregated solver with an implicit approach to calculate the pressure, velocity, temperature, and density. For momentum and continuity equations, the values of the variables at cell faces were calculated using the AVL SMART scheme[24]—this manual cites the original SMART scheme proposed by Gaskell and Lau, 1988—which is a second-order accurate total variation diminishing (TVD) scheme. For energy and turbulence equations, the first-order upwind scheme was used. The pressure-velocity correction was done by using the SIMPLE algorithm.[25] In order to advance the solution in time, the first-order Euler scheme[24] was used. Because the velocity of the flow was very high, the time step used in the unsteady calculation was 1 × 10−5 seconds. The simulations were carried out for a sufficient length of time until no further change was observed in the flow field. The simulations were carried out using the commercial CFD software, AVL FIRE 2008.2, which is based on control volume approach.

Grid Independency Test

In order to study the grid sensitivity of the solution, calculations for the 772 K ambient temperature were done using four different grid levels—coarse grid (4716 cells), medium grid (7760 cells), fine grid (10,116 cells), and very fine grid (19,660). The axial velocity profiles for all grid levels are shown in Figure 3. The variation in the axial velocity profiles calculated with medium grid, fine grid, and very fine grid is within 5 pct. Hence, it can be said that the solution is not sensitive to the grid. The solution with the very fine grid takes a longer time than the solution with the medium grid. Therefore, the results obtained with the medium grid were used for analysis and discussion in this study.

Fig. 3
figure 3

The axial velocity distribution of a supersonic oxygen jet at 772 K ambient temperature for coarse, medium, fine, and very fine grid level

Full size image

Results and Discussion

Velocity Distribution

The computed velocity using the standard k− ε model with the compressibility correction of Heinz[17] along the axis of the jet is plotted with experimental data in Figure 4. The graph shows that the potential core length of the jet increased at a high ambient temperature. The agreement between CFD and the experimental results was very good when the ambient temperature was 285 K. But at a higher ambient temperature, it failed to predict accurately the velocity distribution. This model underpredicted the potential core length of the jet at high ambient temperatures. The percentage of deviation increased for higher ambient temperatures. The average percentage of deviation of the computed velocity from the experimental data was about 13 pct and 22 pct for 772 K and 1002 K ambient temperatures, respectively. The ambient temperature inside the steelmaking furnace is about 1800 K, and the deviation would be much larger at such high temperatures. This high deviation would occur because this turbulence model does not take into account the effect of large temperature gradients. Figure 5 shows that the temperature-corrected turbulence model of Abdol-Hamid et al.[18] also underpredicted the potential core length when used for simulating a room temperature supersonic jet entering into a 1002 K ambient temperature. The reason for the discrepancy was explained in Section II–B.

Fig. 4
figure 4

The velocity distribution on the center axis with k−ε turbulence model, including compressibility correction.[17]

Full size image
Fig. 5
figure 5

The velocity distribution on the center axis with the temperature corrected k−ε turbulence model of Abdol-Hamid et al.[18]

Full size image

Figure 6 shows the velocity distribution on the center axis with the modified k− ε model proposed in this study, including the effect of a high temperature gradient. The modified model more accurately predicted the velocity distribution on the center axis at both high and low ambient temperatures. When the ambient temperature was 772 K, the computed value deviated from the experimental value by an average of less than 7 pct. In case of a 1002 K ambient temperature, the average percentage of deviation of the computed velocity from the experimental result was less than 9 pct. Only a CFD result is shown for the 1800 K ambient temperature because there was no experimental data available at the 1800 K ambient temperature. Figure 6 also shows that, although the potential core length of the supersonic jet is longer at higher ambient temperatures, the relative difference in the velocity magnitude at different ambient temperatures reduces beyond \( {\frac{x}{{d_{e} }}} = 30 \).

Fig. 6
figure 6

The velocity distribution on the center axis with the proposed modified k−ε model

Full size image

Figure 7 shows the dynamic pressure distribution on the center axis of the jet obtained with the proposed model. As expected, the dynamic pressure of the jet is higher at high ambient temperatures, which is in contrast with the CFD results of Tago and Higuchi,[9] who reported that the dynamic pressure of the jet is affected very little by the ambient temperature. The reason for this difference is that they did not use any temperature correction term in their modeling. The dynamic pressure of the jet is a very important characteristic because the higher the dynamic pressure, the bigger the momentum transfers to the liquid bath, which results in a higher depth of penetration in the liquid bath. This high penetration, in turn, enhances the mixing of the oxygen and the liquid melt and, therefore, improves the decarburization rate. The CFD results of the present study underpredicted the experimental dynamic pressure distribution[8] as the distance from the nozzle exit increased. The average percentage of deviation of the CFD results from the experimental data was about 20 pct, 17 pct, and 20 pct for 285 K, 772 K, and 1002 K ambient temperatures, respectively. This is because the dynamic pressure is proportional to the square of velocity. As a result, the errors in the velocity magnitude increased by the same proportion. Also, the dynamic pressure is proportional to the density of the gas. The experimental study[8] was performed in an air-tight container, which may have resulted in an increase in pressure, as well as in density, inside the furnace during the experiment. This increase in density may have resulted in a higher dynamic pressure in the experimental study.

Fig. 7
figure 7

The dynamic pressure distribution on the center axis of the jet with the proposed model

Full size image

The data presented in Figure 7 also show that the relative difference in the dynamic pressure of supersonic jets at different ambient temperatures decreased with an increasing distance from the nozzle exit. If the distance between the liquid bath and the nozzle exit is more than 60 nozzle exit diameter, then the effect of the high ambient temperatures is negligible because the dynamic pressure of the impinging jet on the liquid bath would be almost the same as for all ambient temperatures.

The radial velocity distributions of the supersonic jet at different ambient temperatures at \( {\frac{x}{{d_{e} }}} = 5 \), 22.5, and 50 are shown in Figure 8. With an increasing distance from the nozzle exit, the jet spreads, and its axial velocity decreases. But at high ambient temperatures, the axial velocity of the jet decreases at a slower rate compared with lower ambient temperature. This difference occurs because the mass of the entrained fluid from the surrounding medium is low because of the low ambient density. Figure 8(b) shows that at \( {\frac{x}{{d_{e} }}} = 22.5 \), the supersonic jet at 1800 K ambient temperature still maintains a potential core length in which the axial velocity of the jet at room ambient temperature becomes less than half of the jet exit velocity. Figures 8(a)–(c) show that, although the high ambient temperature increases the potential core length of the jet, the width of the jet is affected little by the ambient temperature. Figure 9 shows the spreading rate of the supersonic jet at different ambient temperatures. The spreading rate is defined as follows[26]:

$$ S_{p} = {\frac{{r_{1/2} }}{{x - x_{0} }}} $$

where S p is the spreading rate, \( r_{1/2} \) is the width of the half value of the axial velocity, and x 0 is the potential core length of the jet. Figure 9 shows that near the nozzle exit, the spreading rate of the jet is only 0.025 (1.54 deg spreading angle) at all ambient temperatures. Then, after a certain distance from the nozzle exit, the spreading rate of the jet becomes around 0.1 (6.2 deg spreading angle) and is affected very little by the ambient temperature. This distance is the potential core length of the jet and is longer at a high ambient temperature, as shown in Figure 9. This value of spreading rate after the potential core length of the jet is in close agreement with the experimental study[8] in which spreading angle of 6 deg was obtained .

Fig. 8
figure 8

(a) The radial distribution of a supersonic jet at different ambient temperatures at \( {\frac{x}{{d_{e} }}} = 5. \) (b) The radial distribution of a supersonic jet at different ambient temperatures at \( {\frac{x}{{d_{e} }}} = 22.5. \) (c) The radial distribution of a supersonic jet at different ambient temperatures at \( {\frac{x}{{d_{e} }}} = 50\)

Full size image
Fig. 9
figure 9

The spreading rate of a supersonic jet at different ambient temperatures

Full size image

Temperature Distribution

The calculated temperature distribution on the center axis of the jet is shown in Figure 10 for 285 K, 772 K, 1002 K, and 1800 K ambient temperatures. The figure shows that the temperature of the gas jet increases gradually after the discharge from the nozzle exit and tends to reach the ambient temperature. The computed jet temperature is in very good agreement with the experimental data for the 285 K and 772 K ambient temperatures and is in reasonable agreement for the 1002 K ambient temperature. The computed values differ from the experimental results by less than 2 pct for the 285 K and 772 K ambient temperatures. For the 1002 K ambient temperature, the average percentage of deviation was about 7 pct, except at the point \( {\frac{x}{{d_{e} }}} = 21 \). The reason for this difference is that the numerical model slightly underpredicted the heat transfer through the turbulent shear layer from the ambient to the jet for the 1002 K ambient temperature. In the present model, the turbulent transport of heat was calculated by Eq. [7] in which a constant value of Pr t  = 0.5[20] was used in all cases. But the value of Pr t should be different for a different temperature gradient. If the temperature gradient is large, then the turbulent heat transfer rate will be high. Decreasing the Pr t , enhances the heat-diffusion capacity in the flow. The manner in which Pr t varies with different temperature gradients is the subject of further research.

Fig. 10
figure 10

The temperature distribution on the centre axis with the proposed model

Full size image

Comparison with the Jet Model

The numerical results obtained with the present model were compared with the empirical jet model of Ito and Muchi[19] given in Eq. [19] as follows:

$$ - {\frac{1}{{2ln(1 - U_{m} )}}} = \alpha \sqrt {{\frac{{\rho_{a} }}{{\rho_{e} }}}} {\frac{x}{{d_{e} }}} - \beta $$
(19)
$$U_{m} = {\frac{U}{{U_{e} }}} $$

where U e is the velocity at the nozzle exit, ρ e is the density at the nozzle exit, and ρ a is the ambient density. Sumi et al.[8] calculated the values of constants α = 0.0841 and β = 0.06035 from their experimental study. Figure 11 shows the velocity ratio obtained from the present CFD model as a function of \( \sqrt {{\frac{{\rho_{a} }}{{\rho_{e} }}}} {\frac{x}{{d_{e} }}} \) for different ambient temperatures. The velocity ratio obtained from Eq. [19] and from the experimental study also is shown in Figure 11. The CFD model agrees well with the empirical jet model at both high and low ambient temperatures with a maximum of 10 pct deviation. No experimental data was available for the jet behavior at 1800 K ambient temperature. But the velocity ratio at 1800 K ambient temperature was also in good agreement with the empirical jet model. This finding shows that the present CFD model should be useful in predicting the jet behavior at high ambient temperatures.

Fig. 11
figure 11

A comparison of the velocity ratio with Eq. [19] as a function of \( \sqrt {{\frac{{\rho_{a} }}{{\rho_{e} }}}} {\frac{x}{{d_{e} }}} \)

Full size image

Potential Core Length

From the preceding sections, it already is known that the potential core length of the supersonic jet increases at high ambient temperatures. Sumi et al.[8] calculated the potential core length of the jet at different ambient temperatures from Eq. [19] by taking U m  = 1. If U m  = 1, then the left side of Eq. [19] becomes zero, and after some manipulation, Eq. [19] becomes the following:

$$ {\frac{x}{{d_{e} }}} = {\frac{\beta }{{\alpha \sqrt {{\frac{\rho_a}{\rho_e}}} }}} $$
(20)

Using the earlier values of the constants and the appropriate density, the potential core length of the jet was determined for different ambient temperatures. Allemand et al.[6] also proposed an empirical equation for calculating the potential core length of the jet at different ambient temperatures, which is expressed as follows:

$$ {\frac{x}{{d_{e} }}} = \sqrt {{\frac{\rho_a}{\rho_e}}} \left( {4.2 + 1.1\left( {M_{e}^{2} + 1 - {\frac{{T_{e} }}{{T_{a} }}}} \right)} \right) $$
(21)

Equation [21] is a modification of the original equation proposed by Lau et al.,[10] which is suitable for calculating the potential core length only at room ambient temperature. Figure 12 shows the potential core length of the jet at different ambient temperatures calculated by Eqs. [20] and [21] as well as from the present CFD model. There is a high correlation between the potential core length calculated by Eq. [20] and the results obtained by the present CFD model. At steelmaking temperature (1800 K), the potential core length of the supersonic jet becomes 2.5 times the potential core length at room temperature (285 K). The potential core length calculated by Eq. [21] is higher than those obtained by Eq. [20] and the present CFD model at all ambient temperatures. No experimental data of the potential core length at a high ambient temperature is available in the literature. Hence, it is unknown which empirical equation is correct.

Fig. 12
figure 12

The coherent length of the supersonic jet at different ambient temperatures

Full size image

Droplet Generation

In order to quantify the influence of a high ambient temperature on the droplet generation rate, the blowing number (N B) was calculated for the supersonic jet at different ambient temperatures. The blowing number is a dimensionless number proposed by Subagyo et al.[2] and is expressed as follows:

$$ N_{B} = {\frac{{\rho_{G} U_{G} }^2}{{2\sqrt {\sigma g\rho_{L}} }}} $$
(22)

where ρ G is the gas density, U G is the gas velocity on the bath surface, σ is the surface tension of liquid metal, and ρ L is the density of liquid metal. Using the blowing number, the droplet generation rate per unit volume of blown gas can be calculated as follows[2]:

$$ {\frac{R}{F}} = {\frac{{\left( {N_{B} } \right)^{3.2} }}{{\left[ {2.6 \times 10^{6} + 2.0 \times 10^{ - 4} \left( {N_{B} } \right)^{12} } \right]^{0.2} }}} $$
(23)

where R is the droplet generation in kilograms per second and F is the volumetric flow of blown gas in normal cubic meters. Figure 13 shows the variation of the blowing number with distance from the nozzle exit (it can be assumed as the distance between the nozzle exit and the liquid bath) at different ambient temperatures. The surface tension of the liquid melt was taken as 1.9 N/m, assuming that the liquid melt was Fe.[27] The variation of the surface tension with the temperature and the composition was not considered because the transfer of jet momentum onto the liquid surface is the dominant factor for droplet generation compared with the changes in the liquid properties.[28] The density of the liquid melt was taken as 7030 Kgm−3. It is seen from Figure 13 that the blowing number is higher for the gas jet at a high ambient temperature. When the distance between the nozzle exit and the liquid bath is around 50 d e , N B = 15, for 1800 K ambient temperature compared with N B = 8 for 285 K ambient temperature. Figure 14 shows the droplet generation rate at a different blowing number. The figure shows that the droplet generation rate at N B = 15 is almost double compared with the rate at N B = 8. So the affect of ambient temperature on the generation of droplets needs special consideration to optimize the process.

Fig. 13
figure 13

A variation of the blowing number with the nozzle bath distance at different ambient temperatures

Full size image
Fig. 14
figure 14

The effect of the blowing number on the droplet generation rate

Full size image

Conclusion

The behavior of the supersonic oxygen jet in a high temperature field was investigated by CFD simulation. The results obtained from this study are as follows:

  1. 1.

    The standard k–ε turbulence model with compressibility correction underpredicts the potential core length of the supersonic jet at high ambient temperatures.

  2. 2.

    A modification of the standard k− ε turbulence model has been proposed. The validity of this model has been confirmed by comparing the velocity and the temperature profile obtained by the CFD model with the available experimental data.

  3. 3.

    The potential core length of the supersonic oxygen jet at steelmaking temperature (1800 K) is 2.5 times than that of room ambient temperature. The dynamic pressure of the jet, which characterizes the momentum transfer, is higher at a high ambient temperature but with an increasing distance from the nozzle exit, the relative difference between the dynamic pressure value at a different ambient temperature decreases, and the effect of the ambient temperature becomes less.

  4. 4.

    The spreading rate of the jet is not affected by the ambient temperature after the potential core length of the supersonic jet.

  5. 5.

    The ambient temperature has an influence on the droplet generation rate. The blowing number of the supersonic jet at a high ambient temperature is higher than the room ambient temperature. As a result, the droplet generation rate is higher.

However, this model is not suitable for the simulation of a high temperature supersonic jet flowing into low ambient temperature. Although the trial and error approach has been used in the present study to modify the turbulence model and a more rigorous approach is desirable, the present study will give useful information for developing theoretical turbulence model including the effect of temperature gradient and contribute to the understanding of jet behavior at high ambient temperatures.