Introduction

Flotation is a process widely used in industry to separate a particulate phase from a continuous one. Originally developed and used in the mineral industry, this process has been extended to a wide range of processes such as paper deinking, water treatment, and liquid metals refining. Basically, flotation consists of injecting bubbles into the phase to be purified. During their ascension through the bulk, the bubbles collect the dispersed particles and release them at the surface, where they accumulate and form a dross layer, which is mechanically removed. In mineral flotation, surfactants are frequently added to the liquid phase, in order to enhance the attachment of the particles to the bubbles.

Three factors are considered when assessing the quality of an aluminum alloy: concentrations of dissolved hydrogen, alkali, and inclusions.[1] Removal of these impurities is achieved by bubbling a mixture of argon and chlorine into the melt. Mechanisms of hydrogen and alkali removal (degassing) by diffusion into the bubbles have already been investigated many times (for example, in References 2 through 5) and are not further developed here. The focus of this article is set on the removal, by flotation, of unwanted inclusions from molten alloys prior to casting. The inclusions most frequently found in molten aluminum are oxide films (generated mainly during melting and alloying), refractory particles, and aluminum carbide (originating from refractory degradation or refractory metal reactions). The size of these inclusions may vary from one micrometer to a few hundred micrometers for the coarsest ones.[6]

In an aluminum casthouse, the flotation process is performed either inline (e.g., ALCAN COMPACT DEGASSERFootnote 1) or in semibatch reactors (e.g., SNiFFootnote 2 and ALPURFootnote 3). Prior to the flotation tank (often known as a degasser), a degassing pretreatment and sedimentation operation is performed in a holding furnace. The filtration technique following the flotation operation is the ultimate purification stage and was thoroughly investigated in recent studies.[7–9] In the flotation tank, the gas (a mixture of chlorine and argon) is injected into the melt through a rotating impeller. This impeller generates a turbulent fluid flow in the reactor, enhancing the probability of collisions between the bubbles and unwanted inclusions, and leading to a global improvement in the efficiency of the process.[10] In this turbulent fluid flow, inclusions are also likely to collide with each other; and the agglomeration mechanism leads to a change in the inclusion size distribution.

Finally, sedimentation occurs for the coarser inclusions, which deposit at the bottom of the reactor. While many mathematical studies have been conducted on flotation for mineral applications (for example, References 11 through 13), few studies have been conducted on liquid aluminum. Johansen and Taniguchi[14] studied agglomeration phenomena during aluminum melt treatment using a population balance approach applied to a homogenous reactor. Nevertheless, the agglomeration kernel used by the authors seeks to account for the turbulence inhomogeneity in the reactor. In another study, Johansen[15] investigated the flotation of inclusions in molten aluminum, applying a global approach and an exponential law to describe the time evolution of the inclusion concentration. Agglomeration is not considered in this study. More recently, a Worcester Polytechnic Institute (Worcester, MA) crew[5,16–18] investigated aluminum purification treatment; both agglomeration and flotation were considered through a population balance approach. Their approach is based on the assumption of a perfectly stirred reactor. In a previous attempt at developing a numerical simulation of the flotation tank, we used a similar approach.[19]

However, the assumption of a perfectly stirred reactor must be considered with care; the turbulence properties and local gas holdup in the reactor may differ by more than one order of magnitude, depending on the location considered. Disregarding these heterogeneities may lead to misevaluation of the agglomeration and flotation frequencies and to an inaccurate prediction of the reactor efficiency.

We propose here a two-dimensional (2-D) numerical model to describe the flotation vessel. Such an approach allows consideration of the convective transport of the inclusions into the melt and the calculation of the population balance locally, using flotation and agglomeration kernels evaluated from local fluid flow and turbulence properties.

The model developed is applied to a cylindrical laboratory-scale flotation vessel.

Mathematical Modeling

Global Overview

We consider here a three-phase system, namely, liquid aluminum, bubbles, and inclusions. In a turbulent system, the nonequilibrium between the continuous and discrete phases originates mainly from rapid variations in fluid flow properties in time and space. In such conditions, the influence of the discrete phases on the continuous phase may be assessed by considering the volume fraction α v of the discrete phase, for particles lighter than the continuous phase, and the mass faction α m of the discrete phase, for particles denser than the fluid.[20] Thus, we can assume that the influence of bubbles on the liquid aluminum fluid flow is negligible, if α v  ≪ 1. The same conclusion can be made for inclusions, if α m  ≪ 1. Typically, in industrial conditions, α v is of the order of a few percent for the gas phase,[21] while α m does not exceed 10−6 for the inclusions. It is then obvious that a two-way coupling must be employed between the liquid aluminum and the bubbles, while a one-way coupling may describe the aluminum-inclusions interactions with acceptable accuracy. Moreover, because the inclusion size is small (less than 100 μm, for the most part) and the inclusion density is close to the density of liquid aluminum (a ratio less than 2), the inertial effects are limited. Thus, in a first approximation, we will assume that, regarding the macroscopic convective transport of inclusions into the melt, the inclusion velocities are equal to the local velocity of the fluid to which a settling term is added, to account for the gravitational effect.

With this assumption, an Eulerian approach associated with a finite volume scheme is adopted, to calculate the convective transport of the inclusions. The inclusions are characterized by their number concentration N (number of inclusions per unit volume), and the equation governing their transport through the vessel is reduced to a scalar transport equation. This approach can then be coupled with a local calculation of agglomeration and flotation phenomena via a population balance approach in each cell of the finite volume discretization.

Our approach, summarized in Figure 1, can read as follows.

Fig. 1
figure 1

Schematic chart of the model

Full size image
  1. (a)

    A three-dimensional (3-D) simulation of the steady state of the biphasic (liquid aluminum-bubbles) turbulent fluid flow is performed, using a two-way coupling approach between the two phases. This calculation is done with the commercial computational fluid dynamic (CFD) code FIDAP (ANSYS Inc., Canonsburg, PA).

  2. (b)

    Noticing a good axisymmetry of the fluid flow, the 3-D vessel is turned into a 2-D axisymmetric vessel. In each cell of the new 2-D mesh, a mean value for all physical properties is stored.

  3. (c)

    Local agglomeration and flotation frequencies are calculated in each cell using local fluid flow properties.

  4. (d)

    The convective transport of the inclusions in the vessel is calculated by an Eulerian approach using a finite volume scheme; and the population balance equation (PBE) is resolved in each cell of the domain.

CFD Simulation of Liquid and Gas Flow

A 3-D simulation of the liquid metal/bubbles biphasic fluid flow was carried out with commercial CFD software FIDAP, using an Euler–Lagrange approach. In the first step, molten metal is considered as a continuous phase and a monophasic calculation of the flow is made by resolution of the Navier–Stokes equations with a k-ε turbulence model. Virtual surfaces are built around the impeller; the flow conditions at these boundaries are obtained from correlations formerly validated by laser velocity measurements on a laboratory-scale apparatus designed by Waz.[22] On the walls and bottom of the tank, no slip condition is set. In the second step, the turbulent monophasic flow is used as the initial condition for the steady-state calculation of the biphasic molten metal/bubbles flow. Bubbles are considered to be solid spheres with a constant and unique diameter that depends on the rotor speed and gas flow rate without any interaction between them. For each simulation bubble, the diameter is calculated from a correlation formerly developed by Waz.[21] Bubbles are injected from the tip of the impeller following a common Lagrangian method.

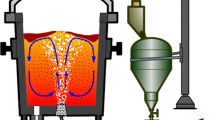
A specular reflexion was first set up as a boundary condition for the bubbles at the crucible wall and on the virtual surfaces surrounding the rotor.[23] Nevertheless, experimental observations performed on a water apparatus tend to show that, when the rotor and the shaft are not wetted by the fluid, which is precisely the case with a graphite impeller and liquid aluminium, bubbles that collide with the top surface of the impeller do not rebound upon it. Bubbles are more likely to coalesce and reach the surface of the reactor through a continuous gas film surrounding the shaft. Mathematical modeling of the formation and behavior of this film is somewhat cumbersome and far beyond the scope of the present work. However, ignoring this gaseous film and considering specular reflexion on the rotor automatically leads to an overestimation of the number of bubbles in the bulk and would, therefore, entail a misevaluation of flotation frequency. Because the trapped bubbles do not play any role in the flotation process, it was decided to remove them from the system: The specular reflexion is, therefore, replaced by an escape condition on the top surface of the rotor and on the shaft surface (Figure 2) so that, if a bubble hit one of these surfaces, it is removed from the melt.

Fig. 2
figure 2

Boundary conditions for the bubbles: specular reflexion on surfaces 1, 2, 3, and 4 and escape condition on surfaces 5 and 6

Full size image

The liquid surface is assumed to be flat and no re-entrainment of removed inclusions at the surface of the bulk is considered. Entrainment from the dross has recently been investigated by Johansen et al.,[24] who emphasize that large and strongly buoyant particles are eligible for entrainment into the melt. However, many questions, such as the role of wetting effects on this mechanism, await further investigation. For these reasons, entrainment from the dross is not taken into account in the present work. The numerical simulation of the liquid/bubbles biphasic fluid flow was validated using the water model apparatus set up by Waz and then transposed to aluminum.[21] Because the 3-D calculations showed that the fluid flow is well axisymmetric, a 2-D fluid flow was extracted and used in a homemade code to solve the 2-D convective transport and PBEs (Section C).

Extracting a 2-D flow field from the 3-D flow field with a change of mesh entails a loss of the conservative property of the flow field. The deviation from the conservation rule is not admissible for the 2-D finite volume method. To restore the conservative property of the flow field, its stream function Ψ was calculated on the 2-D mesh. The flow field was then recalculated from this stream function using the well-known expression

$$ \left\{ \begin{gathered} U_{z} = \frac{1}{\rho r}\frac{\partial \Uppsi }{\partial r} \hfill \\ U_{r} = - \frac{1}{\rho r}\frac{\partial \Uppsi }{\partial z} \hfill \\ \end{gathered} \right. $$
(1)

where ρ accounts for the local gas holdup φ:

$$ \rho = \varphi \rho_{g} + \rho_{f} \left( {1 - \varphi } \right) $$
(2)

By mathematical construction, this new flow field is fully conservative and exhibits a perfect similarity with the original nonconservative fluid flow.[25]

CFD Population Balance

Theory

As presented by Ramkrishna,[26] population balance is a powerful way of synthesizing the behavior of a population of discrete particles from the behavior of single particles in their local environment.

The population of inclusions is characterized by its number density n v (v,r,t) (m−6), which is a function of the internal coordinate v (volume of inclusions) and external coordinates through the space location vector r. The average number of inclusions about the particulate state (v,r) in the infinitesimal volume dvdV r of the inclusion state space is thus given by

$$ n_{v} (v,{\mathbf{r}},t)dvdV_{r} $$
(3)

where dv and dV r are infinitesimal volume measures in the space of internal and external coordinates, respectively.

The number density may evolve with time because of the agglomeration and fragmentation phenomena, the flotation, and, possibly, the growth and entrainment from the dross at the surface of the melt. The present study deals only with agglomeration and flotation, because inclusions are not affected by the growth mechanism.

The time evolution of the number density is given by the following conservation equation, a so-called PBE:[27]

$$ \frac{{\partial n_{v} }}{\partial t} + {\text{div}}_{\text{rz}} \left( {U_{t} n_{v} } \right) = G $$
(4)

where U t is the transport velocity of inclusions and G the net birth rate of inclusions per unit of volume of inclusion state space, which accounts for the agglomeration and flotation phenomena.

To numerically solve this equation, a class method was used.[26] The size distribution of the inclusions is thus split into M different classes. In each class i of inclusions, representative of all the inclusions within the volume interval [v i ; v i+1], the concentration number N i (r,t) is calculated as

$$ N_{i} ({\mathbf{r}},t) = \int\limits_{{v_{i} }}^{{^{{v}_{i + 1}}}} {n_{v} } \left( {{\mathbf{r}},v,t} \right)dv $$
(5)

Thus, for each considered class i, the PBE is

$$ \frac{{\partial N_{i} }}{\partial t} + {\text{div}}_{rz} \left( {N_{i} U_{t} } \right) = G_{i} $$
(6)

As previously mentioned, we assume here that the transport velocity of inclusion is, in first approximation, equal to the sum of the local velocity of the fluid U and a settling velocity V set.

Thus, Eq. [6] can be rewritten as

$$ \frac{{\partial N_{i} }}{\partial t} + {\text{div}}_{rz} \left( {N_{i} \left( {U + V_{\text{set}} } \right)} \right) = G_{i} $$
(7)
$$ \frac{{\partial N_{i} }}{\partial t} + {\text{div}}_{rz} \left( {N_{i} U} \right) + {\text{div}}_{rz}\left( {N_{i} V_{\text{set}} } \right) = G_{i} $$
(8)

where V set is assessed with Stokes’ equation:

$$ V_{\text{set}} = \frac{{2r_{pi}^{2} \left( {\rho_{p} - \rho_{f} } \right)g}}{9\mu } $$
(9)

For a given class of inclusions, V set is constant in the tank, which leads to

$$ \begin{aligned} {\text{div}}_{rz} \left( {N_{i} V_{\text{set}} } \right) & = N_{i} {\text{div}}_{rz} \left( {V_{\text{set}} } \right) + V_{\text{set}} {\cdot} {\text{grad}}\left( {N_{i} } \right) \\ & = V_{\text{set}} {\cdot} {\text{grad}}\left( {N_{i} } \right) \\ & = - V_{\text{set}} \frac{{\partial N_{i} }}{\partial z} \\ \end{aligned} $$
(10)

In the finite volume approach adopted, this last term can be easily split into a birth term, corresponding to the inclusion flux coming from the cell above, and a death term, corresponding to the inclusion flux leaving the given cell.

The same splitting can be performed for agglomeration and flotation phenomena: Birth occurs in the class i when a new inclusion of size v ∈ [v i ; v i+1] is generated by the agglomeration of two inclusions of smaller size; the death of a class i inclusion occurs either by agglomeration with any other particle or by an efficient collision with a bubble (flotation).

We can then define \( G_{i}^{\prime } \) as

$$ G_{i}^{\prime } = G_{i} + V_{\text{set}} \frac{{\partial N_{i} }}{\partial z} = B_{i} - D_{i} $$
(11)

where B i and D i are birth and death terms, respectively, accounting for the agglomeration, flotation, and decantation phenomena.

Considering M different classes of inclusions, we obtain a system of M nonordinary hyperbolic equations coupled within the agglomeration term. Among different numerical methods available to solve such systems, the splitting technique proposed by Toro[28] was applied. This technique separates the former system into two subsystems in the same time-step. The first one deals with the convective transport of inclusions, whereas the second is reduced to agglomeration/flotation phenomena. Both of these systems can easily be solved. The resulting system reads as

$$ \left. \begin{gathered} \frac{{\partial N_{i}^{*} }}{\partial t} = {\text{div}}_{rz} (N_{i} U) = 0 \hfill \\ t = t^{n} ,\quad N_{i}^{*} = N_{i} (t^{n} ,r,z) \hfill \\ \end{gathered} \right\} \Rightarrow N_{i}^{*} \left( {t^{n + 1} ,r,z} \right)\quad i = 1,2, \ldots ,M $$
(12)
$$ \left. \begin{gathered} \frac{{\partial N_{i} }}{\partial t} = G_{i}^{\prime } \hfill \\ t = t^{n} ,\quad N_{i} = N_{i}^{*} (t^{n + 1} ,r,z) \hfill \\ \end{gathered} \right\} \Rightarrow N_{i} (t^{n + 1} ,r,z)\quad i = 1,2, \ldots ,M $$
(13)

A dimensional separation was then operated on the convective part of this system:

$$ \begin{gathered} \left. \begin{gathered} \frac{{\partial N_{i}^{*} }}{\partial t} + U_{r} \frac{{\partial N_{i}^{*} }}{\partial r} = 0 \hfill \\ t = t^{n} ,\quad N_{i}^{*} = N_{i} (t^{n} ,r,z) \hfill \\ \end{gathered} \right\}\mathop \Rightarrow \limits^{\Updelta t} N_{i}^{*} \left( {t^{n + 1/2} ,r,z} \right) \hfill \\ \left. \begin{gathered} \frac{{\partial N_{i}^{*} }}{\partial t} + U_{z} \frac{{\partial N_{i}^{*} }}{\partial z} = 0 \hfill \\ t = t^{n + 1/2} ,\quad N_{i}^{*} = N_{i}^{*} \left( {t^{n + 1/2} ,r,z} \right) \hfill \\ \end{gathered} \right\}\mathop \Rightarrow \limits^{\Updelta t} N_{i}^{*} \left( {t^{n + 1} ,r,z} \right) \hfill \\ \end{gathered} $$
(14)

Numerical simulation

Those transport equations are solved using the finite volume method with an explicit temporal scheme and third-order total variation diminishing fluxes to reduce numerical diffusion.[29]

The fixed pivot technique developed by Kumar and Ramkrishna[30] was applied to solve the PBE. Good implementation and accuracy of this method were checked and validated (details can be found in Reference 25) with the classic analytical function proposed by Scott,[31] which was used many times within the framework of population balance.

For a mesh of 2040 cells, the transient simulation of the evolution of a population of inclusions split into 23 classes undergoing agglomeration, flotation settling, and convective phenomena, the computing time required was about 3 days on a 2.8-GHz AMD OpteronFootnote 4 SE2220 computer with 8 GB of memory.

Agglomeration

In an agitated vessel, turbulence is the main source of agglomeration: Turbulent motion causes collisions of inclusions and agglomeration takes place when the contact established is sufficiently strong.

Two mechanisms may lead to collision in a turbulent flow: the shear mechanism, in which inclusions follow the streamlines into a turbulent structure, and the accelerative mechanism, in which inclusions are projected toward each other from independently moving large-scale eddies. Those mechanisms were described into details by Saffman and Turner[32] and Abrahamson,[33] respectively. Their applicability is, therefore, limited to extreme cases (References 32 and 33), and none of them can be rigorously employed in intermediate cases. More recently, Kruis and Kusters[34] developed a complete model that handles both shear and accelerative mechanisms.

They obtained the following expression for the collision rate:

$$ Z_{12}^{K} = N_{1} N_{2} \sqrt {\frac{8\pi }{3}} d_{12}^{2}\sqrt{\overline{ {w_{\text{accel}}^{\prime 2}}}+\overline{{w_{\text{shear}}^{\prime 2}}}}$$
(15)

The expressions of the mean squared relative velocities induced by accelerative \(\overline{ {w_{\text{accel}}^{\prime 2}}} \) and shear \( \overline{{w_{\text{shear}}^{\prime 2}}} \) mechanisms can be found in References 34 and 35.

A comparison of these three models is presented in Reference 19. This comparison clearly shows the universality of the model developed by Kruis and Kusters, valid both in strong and weak turbulence conditions and for all inclusion sizes found in liquid aluminum. The Kruis and Kusters approach was thus adopted to model the agglomeration phenomenon.

The present study deals with alumina inclusions that are weakly wetted by the liquid aluminum (contact angle of approximately 90 deg). It was shown by Cournil[36] that, under such conditions, sticking forces are strong and the attachment efficiency is high. Thus, we suppose in the following (in the rest of the text) that, once contact between two inclusions is established, the sticking forces are strong enough to form a stable cluster: A collision always results in the formation of a cluster and no breakage of clusters is expected. In addition, inclusions are assumed to be spherical; the agglomeration of two inclusions produces a spherical daughter inclusion the volume of which is equal to the sum of the volumes of the parents. A fractal description of the cluster will be considered in a future work.

Flotation

Bubbles-inclusions collision rate

The elimination of inclusions by flotation originates from the attachment of inclusions to the surface of the bubbles. The flotation rate is usually described through either a deterministic or a stochastic approach.

The stochastic approach is mainly based on the adaptation of the agglomeration model to flotation systems. The applicability of such models relies on many restrictions, principally on particle and bubble sizes and on turbulence intensity, which are not fulfilled here. In liquid aluminum, the bubble diameter is approximately 1 cm for the Alpur rotor, and inclusions may be hundreds to thousands of times less. In such a configuration, inertial effects such as buoyancy cannot be neglected.

The determinist approach relies on the assumption that the bubble and particle velocities are perfectly known and that the flotation rate is directly correlated to the volume of fluid swept by the bubble.

Both stochastic and determinist mechanisms are likely to occur in a flotation cell; thus, we decided to take both of them into account (Figure 3). This was achieved using the universal model recently developed by Kostoglou.[37] Based on an approach similar to the kinetic theory of gas, the author derived a unified and consistent expression that covers all possible sets of the problem parameters. The details of this model, including the numerical method employed, can be found in Reference 37.

Fig. 3
figure 3

Schematic representation of stochastic, determinist, and coupled approach

Full size image

Flotation efficiency

Flotation efficiency may be split in three terms: a collision efficiency E c , based on hydrodynamic considerations; an attachment efficiency E a , predicting the ability of the inclusion to rupture the liquid film at the surface of the bubble; and a stability efficiency E s , based on the force balance on the attached inclusion.

The Reynolds numbers for bubbles (denoted as Re b ) typically range from 103 to 104 in the aluminum flotation tank. We previously used in Reference 38 the Nguyen model[39] (developed for intermediate Reynolds numbers), to calculate the collision and attachment efficiency (E c and E a , respectively). This model is based on a derivation of the streamlined equations for Reynolds numbers up to 500, which is not appropriate for the large bubbles encountered in aluminum (a diameter of approximately 1 cm). To correct this, we decided to use a balance between the Stokes (Re b  = 0) and potential (good approximation for large values of Re b ) flow regimes, as proposed by Yoon and Luttrell.[40] Thus, the expressions used for E c and E a are

$$ E_{c - YL} = \left( {{{d_{p} } \mathord{\left/ {\vphantom {{d_{p} } {d_{b} }}} \right. \kern-\nulldelimiterspace} {d_{b} }}} \right)^{2} \left( {\frac{3}{2} + \frac{{4{\text{Re}}_{b}^{0.72} }}{15}} \right) $$
(16)
$$ E_{A - YL} = \left[ {\cosh^{2} \left( {\frac{{t_{I} U_{b} (45 + 8{\text{Re}}_{b}^{0.72} }}{{30r_{b} (r_{b} /r_{p} + 1)}}} \right)} \right]^{ - 1} $$
(17)

These expressions were derived from laminar flows with deterministic velocities but, as shown by Kostoglou,[37] the kinetic theory approach allows us to use such expressions with combined deterministic and turbulent velocities.

The attachment efficiency expression E A–YL is based on a comparison between the sliding time of the inclusion along the bubble surface and the induction time t I , which is the time required for the inclusion to drain the liquid film to a critical thickness h cr , at which point the film ruptures. The expression for t I was obtained by Schulze:[41]

$$ t_{I} = \frac{3}{64}\mu \frac{{\alpha_{d}^{2} }}{{4\sigma h_{cr}^{2} }}d_{p}^{3} $$
(18)

where α d is the angle for the transition of the spherically deformed part of the bubble to the nonspherically deformed part. The expressions for α d and h cr were proposed by Zhang and Taniguchi:[42]

$$ \alpha_{d} = {\text{arcos}}\left( {1 - 1.02\left( {\frac{{\pi d_{p} \rho_{p} U_{b}^{2} }}{12\sigma }} \right)^{1/2} } \right) $$
(19)
$$ h_{cr} = 2.33 \times 10^{ - 8} \left[ {1000\sigma \left( {1 - \cos \theta_{\text{contact}} } \right)} \right]^{0.16} $$
(20)

For aluminum at 1000 K, the values of the contact angle θ contact and surface tension σ are approximately 90 deg and 0.86 N·m−1, respectively.[43]

Before starting to slide at the bubble surface, inclusions collide with the bubble, resulting in a deformation of the surface. The time required for the bubble to restore its initial shape is usually called the contact time t c and is evaluated as follows:[44]

$$ t_{c} = \pi \left( {\frac{{d_{p}^{3} \rho_{p} }}{12\sigma }} \right)^{1/2} $$
(21)

If the time t c is greater than the induction time t I , the liquid film ruptures before the inclusion starts to slide. As shown in Figure 4, inclusions smaller than 20·10−6 m in diameter always attach themselves to the bubble during the collision step. For the lowest Re b (103) inclusions up to 7·10−5 m in diameter may attach themselves during the collision step; this size limit, however, decreases to 2·10−5 m for the highest Re b (104). When this situation is fulfilled, the attachment efficiency does not need to be evaluated, and can be set to 100 pct.

Fig. 4
figure 4

Comparison between contact time t c (dotted) and induction time t I (plain)

Full size image

Most of the inclusions found in aluminum are less than 2·10−5 m in diameter and, therefore, attach themselves to the bubble during the collision step. Coarser inclusions will slide at the bubble surface and are likely to attach to the bubble because of their weak wettability. Thus, we set the attachment efficiency E a to unity for our calculation.

In addition, the stability of the attachment has not been investigated in the present study; therefore, breakage of the bubble-inclusion cluster is not considered (stability efficiency set to unity).

Results and Discussion

Operating Conditions and Initial Inclusion Size Distribution

A cylindrical laboratory-scale apparatus with an inner diameter of 3.3·10−1 m and containing 70 kg of molten aluminum at 1000 K was modeled (Figure 5). The molten metal is stirred by an Alpur rotor the diameter and height of which are 1.55·10−1 m and 7.5·10−2 m, respectively; the shaft diameter is 8·10−2 m. At the tip of each blade, a gas injector blows a mixture of argon and chlorine into the melt.

Fig. 5
figure 5

Schematic representation of the laboratory-scale apparatus modeled

Full size image

In an industrial casthouse, tuning of the flotation process is achieved with three parameters: the gas flow rate, rotor speed, and location of the rotor in the tank. Because the dimensions of the pilot tank are relatively small, the rotor is positioned close to the bottom, in order to allow a significant residence time of the bubbles into the melt. The influence of the gas flow rate and rotor speed on the efficiency of the process is studied through three different cases, which are referenced in Table I. Under such conditions, bubble diameters, calculated with correlations established from water experiments and transposed to liquid aluminum by Waz,[21] range from 7 to 11 mm. In a former study, the same cases were simulated under the assumption of a perfectly stirred reactor.[19] A valuable comparison between this previous model and the present 2-D model will be set up.

Table I Operating Conditions and Main Characteristics of Predicted Turbulent Fluid Flow; N Refers to Rotor Speed, Q g to Gas Flow Rate, φ m to Mean Gas Holdup, ε m to Mean Turbulence Dissipation Rate, and k tm to Mean Turbulent Kinetic Energy (Mean Refers to Volume Average)
Full size table

The gas usually blown into the melt is a mixture of argon and chlorine. Indeed, according to References 45 and 46, bubbling pure argon results in inefficient flotation. In the same studies, the influence of the chlorine concentration in the gas on the flotation efficiency was experimentally studied by bubbling chlorine mixtures into the melt under various conditions. It was clearly shown that the flotation process can be split into two steps. During the first step, usually termed the incubation period, the gas is blown into the melt and the flotation appears to be inefficient: The global number of inclusions into the melt remains constant. In a second step, at the end of the incubation period, the flotation becomes efficient and the concentration of inclusions decreases exponentially. It was also shown in References 45 and 46 that the stronger the chlorine flow rate, the shorter the incubation period. Once flotation starts, the concentration of chlorine ceases to play an important role and, consequently, pure argon can be blown into the melt during the second step of the process. However, the origin and comprehension of this incubation period are still in progress.[25] For this reason, mathematical modeling of the flotation process always focuses on the efficient part of the flotation. In this way, all the following calculations (concerns all the results presented) assume that enough chlorine has previously been injected into the melt to reach the end of the incubation period.

In the following calculations (concerns all the results presented), we consider alumina inclusions with a density of 3900 kg·m−3. The initial size distribution of the inclusions was established using the mean of several measurements performed with a liquid metal cleanliness analyzer (LIMCAFootnote 5). Twenty-three classes of inclusions were considered, with representative diameters spanning from 2.5·10−6 to 2.05·10−4 m. Because the resolution of the LIMCA does not go below 2·10−5 m, the measured distribution was extrapolated (the four smallest classes), in order to obtain a more realistic distribution. The complete distribution is reported in Figure 6 and is used as the initial particle size distribution (PSD).

Fig. 6
figure 6

Initial inclusion size distribution. In gray, the extrapolated part of the distribution

Full size image

At the initial time, the spatial distribution of the inclusions is supposed to be homogeneous in the melt.

Fluid Flow and Bubbles Repartition

The CFD calculations show a relatively weak influence of the dispersed gas phase on the liquid metal flow pattern in the bulk of the reactor. Figure 7 gives the calculated time-averaged streamlines in the steady state for case B. A weak swirl is noticed near the shaft, close to the surface of the bath; it becomes more pronounced at a higher rotation speed.

Fig. 7
figure 7

Computed streamlines for case B

Full size image

Turbulence properties (ε and k t ) reach their maximum value around the blades of the rotor where the shear is strong. This is clearly observed in Figure 8.

Fig. 8
figure 8

Kinetic energy k t and its dissipation rate ε for (a) case A and (b) case C

Full size image

As shown in Figure 9, an increasing rotor speed with a constant gas flow rate improves the dispersion of bubbles in the reactor, leading to an upward trend in the mean gas holdup. No significant difference between the dispersion of the bubbles in cases A and B (same rotor speed and higher flow rate) is noticed.

Fig. 9
figure 9

Computed local gas holdup φ (volume fraction in percent) and bubbles Reynolds number for cases A, B, and C

Full size image

On the other hand, the highest mean gas holdup is predicted for case B, which has a gas flow rate 3 times higher than cases A and C. The average residence time of the bubble into the melt ranges from 0.6 to 0.86 seconds, depending on the case considered.

Local Flotation Frequency

Local flotation frequencies depend on the turbulence properties, relative bubble/inclusion velocities, inclusions and bubble size, and local gas holdup (i.e., number density of bubbles).

For a given class of inclusions i, the rate of flotation Z fi (m−3·s−1) is given locally by an expression of the form

$$ Z_{fi} = N_{i} N_{b} \beta $$
(22)

where β is the flotation kernel (m3·s−1), including efficiency, and N b the local number of bubbles per unit of volume.

The contours of the local values of β and of the flotation frequency N b β (s−1) are presented in Figure 10 for case A and for inclusions 2.5·10−6 m in diameter. If we refer to Figure 8, we see clearly that the flotation kernel reaches its maximum in the zones in which the turbulence properties are highest. On the other hand, the flotation frequency is strongly correlated to the local gas holdup; its maximum value is reached in the zones in which the local gas holdup is maximal (Figure 9). The same observations were made for cases B and C, for the whole range of inclusions studied.

Fig. 10
figure 10

Computed local flotation kernel and frequency for 2.5-μm-diameter alumina inclusions (case A)

Full size image

This remark is quite important, because it clearly shows that the process would be optimized if the region of maximum gas holdup and the region of maximum turbulence intensity coincide.

Evaluation of Flotation Model

As stated earlier, the flotation model chosen combines stochastic and determinist approaches. To assess this model, we propose here a comparison with purely determinist and stochastic models. Calculation of the local flotation kernel was performed with the three different approaches; the results are reported in Figure 11. In this figure, each marker represents a cell of the mesh.

Fig. 11
figure 11

Computed local flotation kernel for the three different approaches

Full size image

For zones of very low turbulence intensity, the turbulence effects are negligible and the determinist effects are dominant. This can be clearly seen in Figure 11: For the lowest values of ε, the combined model predicts flotation kernel values quite similar to those calculated with the determinist model. Note that the determinist model does not account for turbulence at all, which explains the quasiconstant values of the flotation kernel in Figure 11; the scattering is due only to the corresponding local mean relative bubble/fluid velocity.

On the other hand, in the highly turbulent zones, the stochastic effects should prevail over the determinist effects. Once again, the combined model reflects this behavior, predicting flotation kernel values very close to the stochastic model.

Those observations clearly show the universality of the combined model developed by Kostoglou.[37]

Agglomeration

For comparison purposes, we have plotted in Figure 12 the flotation removal rate (the negative sign of the rate is not mentioned in the figure) and the evolution rate due to agglomeration for the same class of inclusions. Inclusions considered in this plot have a representative diameter of 4.75·10−5 m; the operating conditions correspond to case A. The plotted values are computed at the beginning of the treatment (initial time).

Fig. 12
figure 12

Computed flotation removal rate (left) and agglomeration feed rate (right) (m−3.s−1)

Full size image

Under these conditions, the computed evolution rate due to agglomeration is positive in the entire tank, which means that the birth rate is greater than the death rate. Thus, the plotted values at the right in Figure 12 correspond to a positive balance between the birth and death rates. As expected agglomeration phenomena take place mainly near the rotor, where turbulence is maximal.

A comparison between the left and right sides of Figure 12 reveals that, in a large part of the tank, removal by flotation is in the same order of magnitude as birth by agglomeration. This means that an equilibrium between agglomeration and flotation may be reached locally for certain classes of inclusions, which results in very low evolution rates. For the smallest classes, the evolution rate due to agglomeration is negative (no birth term at all for the first class) and such an equilibrium cannot be reached.

Time Evolution of Population of Inclusions

Global evolution

A 10 minutes treatment was simulated for the three cases studied. The time evolution of the total number of inclusions into the melt is reported in Figure 13. After a strong decrease in the total number of inclusions at the beginning of the treatment, the rate of removal slowly softens. This change is due only to the depletion of the number of inclusions in the melt (the driving force of the agglomeration and flotation phenomena). At the end of the treatment, the global number of inclusions removed from the melt ranges from 36 to 67 pct, depending on the case.

Fig. 13
figure 13

Computed evolution of the total number of inclusions into the melt

Full size image

Cases A and B have the same rotor speed, but the gas flow rate of case B is 3 times higher than that of case A. It appears that cases A and B are relatively close to each other, with case B slightly more efficient: After 10 minutes of treatment, 44 pct of the inclusions are removed from the melt, compared to 36 pct in case A. At the very beginning of the treatment, the removal rate is higher in case B than in case A, due to the greater number of bubbles blown into the melt. Nevertheless, as the number of inclusions decreases more quickly, the removal rate softens more quickly at the same time, which results in a relatively low improvement in the process efficiency in the long run.

On the other hand, case C is much more efficient than cases A and B since, after 10 minutes of treatment, approximately 65 pct of the inclusions are removed from the melt. Case C has a low gas flow rate (equivalent to case A) but a high rotor speed. As previously seen, these operating parameters allow a good dispersion of the bubbles into the liquid bath, especially in the zones of high turbulence intensity, which is the best situation for promoting flotation. Despite a global gas holdup twice that of case C, case B is less efficient. Accordingly, in the range of variation in the process parameters, the stirring conditions have a more sensible effect on inclusion removal than the gas flow rate. Complementary calculations should be performed to confirm this trend and to establish optimal process parameters.

Particle size distribution

The PSDs after 5 and 10 minutes of treatment are shown for case B in Figure 14. No significant difference between these two PSDs can be observed, except for the smallest classes, which keep on losing inclusions.

Fig. 14
figure 14

PSD after 300 s (black) and 600 s (gray), for case B

Full size image

At the beginning of the treatment, coarser inclusions (d p  > 7·10−5 m) are quickly removed from the melt, because they are more likely to collide with bubbles and because of their high settling rate. Evolution rates (agglomeration, flotation, and settling) of the smallest classes remain quasiconstant with respect to time, because the probability of collision and flotation is very low. Intermediate classes (40 < d p  < 70 μm) reach a balance between removal by flotation and feed by agglomeration, as explained in Section III–E.

Settling of inclusions

The settling of inclusions may play an important role, especially for coarse inclusions, and mathematical modeling can assess the contribution of settling to the inclusion removal. The fraction of inclusions removed by settling at the bottom of the tank at different times is shown for case A in Figure 15. We can see that, after 50 seconds, the fraction of settled inclusions hardly evolves with time for coarser inclusions; this is due to the fact that almost all those inclusions have already been removed from the melt either by flotation or by settling. This can easily be explained not only by the high settling velocity of the inclusions and the high probability they will collide with the bubbles, but also by their low initial concentration.

Fig. 15
figure 15

Cumulative fraction of inclusions removed by settling at different times, for case A

Full size image

The removal of inclusions by settling competes with flotation. Therefore, if the flotation rate increases, the fraction of inclusions removed by settling decreases. This can be clearly seen in Figure 16, in which a comparison between cases A and C is established. In addition, in Figure 17, the total fraction of inclusions removed from the melt is compared to the fraction of inclusions removed by settling in case A after 600 seconds of treatment. It is clearly shown that flotation prevails on settling.

Fig. 16
figure 16

Cumulative fraction of inclusions removed by settling after 600 s of treatment (cases A and C)

Full size image
Fig. 17
figure 17

Comparison between total percentage of inclusions removed and percentage of inclusions removed by settling, after 600 s (case A)

Full size image

Comparison with zero-dimensional model

As previously mentioned, we formerly developed a zero-dimensional (0-D) mathematical model[19] based on the assumption of a perfectly stirred reactor. We propose here to compare the present 2-D model to this simplified approach, since the same assumptions related to flotation, agglomeration, and settling were adopted in both models. The mean values of gas holdup and the turbulence properties used by the perfectly stirred model are reported in Table I. These values were calculated from the 3-D biphasic fluid flow simulation presented in Section II–B.

Figure 18 indicates that the time evolutions of the inclusions remaining in the melt predicted by the two models (case A) match well. Cases B and C are not reported on the graph, but the same observation can be made. Although such close results between the two approaches were not expected, they can easily be explained.

Fig. 18
figure 18

Comparison between the perfectly stirred reactor approach and the 2-D approach

Full size image

If we draw the spatial distribution of the inclusions predicted by the 2-D model, it appears that the inclusions concentration number is almost homogeneous in the tank, regardless of the time and case considered. This clearly emphasizes that the mixing in the tank is excellent and that the homogeneous distribution assumption is validated.

Concerning the agglomeration and flotation frequencies, it should be concluded that, despite the apparent heterogeneity revealed in Figures 8 and 9, the average calculations performed by the 0-D model gives a satisfactory description of what actually occurs in the tank.

It should be kept in mind, however, that the modeled tank is relatively small and that the rotor is positioned very low in the melt, resulting in good dispersion of the bubbles. Therefore, the conclusions drawn here may apply only to a confined system and cannot be directly transposed to an industrial configuration in which the tank may contain 10 tons of metal and the rotor may be located higher in the melt, resulting in very strong heterogeneities.

Further calculations should be made, especially on larger systems, to clearly establish the domain of validity of the simplified model.

Conclusions

A mathematical model of the flotation process in a batch reactor for aluminum purification is proposed. The model handles both agglomeration and flotation mechanisms and also the convective transport of inclusions into the melt. The agglomeration process is described by the Kruis and Kusters model, while Kostoglou’s approach is used for the flotation process. The coupling of the convective transport equation and the PBE was achieved using a splitting technique proposed by Toro.

Numerical simulations were performed for three different operating conditions. Increasing the gas flow rate (with a constant rotor speed) gives rise to a significant increase in the global gas holdup without significantly changing the turbulence properties. On the other hand, increasing the rotor speed (with a constant gas flow rate) results in a significant increase in the turbulence properties and in bubble dispersion, with a weak influence on the global gas holdup. It was shown that, in this range of process variations, the removal of inclusions from the melt was found to be far better with a low gas flow rate and high rotor speed than with a low rotor speed and high gas flow rate. As a consequence of numerical simulations, the efficiency of the flotation process can be improved if we manage to get the zones of high turbulence intensity and the zones of high gas holdup to coincide.

It was also shown that, in this range of process variations and for the confined system considered, a 0-D simplified approach based on a perfectly stirred assumption can provide a very good prediction.

More precise descriptions of the agglomeration phenomena, including a fractal approach and an accurate description of the attachment efficiency, should be performed in future work.

The re-entrainment of inclusions at the surface of the melt is also an important issue that should be included in the model. At the same time, in order to validate the present study, experiments are planned for the laboratory-scale apparatus presented; the results will be published later.