Introduction

In modern pyrometallurgical reactors, the overall reaction rate is generally accelerated through either stirring of the bath to promote mass transfer or increasing the interfacial area between phases, normally through gas injection.[1] At low levels of stirring, the interfacial area between slag and metal phases is unchanged and relatively simple equations can be used to model the overall kinetics of a particular reaction system. For example, in the case of mass-transfer control in one of the phases, a first-order ordinary differential equation can be employed:[2]

$$ \frac{{dC_{B} }} {{dt}} = \frac{{{\left( {\frac{A} {V}} \right)}{\left( {C_{B} - C_{I} } \right)}}} {{{\left( {\frac{1} {k}} \right)}}} = \frac{{{\text{area}}}} {{{\text{volume}}}} {\cdot} \frac{{{\text{drive}}}} {{{\text{resistance}}}} $$
(1)

where C I is the concentration of reacting species at interface (mol/m3), C B is the concentration of reacting species in the bulk (mol/m3), A is the interfacial area (m2), V is the volume of the phase (m3), k is the interfacial mass-transfer coefficient (m/s), and t is time (s). Normally, C I is set by an equilibrium relationship between the slag and metal and k is calculated using a semiempirical relationship.[2]

This type of equation is valid when there is little variation in mass-transfer conditions, interfacial area, and equilibrium drive with time. However, it is common in industrial operations for slag chemistry to change with time, as flux additions are carried out and refractories dissolve into the slag, though there is little theoretical treatment of this type of problem in the literature. Desulfurization in ladle metallurgy is an example of this type of transient problem, where the equilibrium drive is changing with time and mixing is nonuniform. A summary of the Subagyo et al. treatment of this problem is provided in this article.[3]

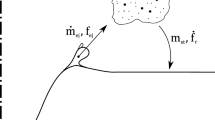
In the case of processes with high-speed gas injection, such as oxygen steelmaking, a large volume of droplets is generated, resulting in complex multiphase regions within the reactor. The regions in top blown oxygen steelmaking are shown schematically in Figure 1. In these processes, the relationships between gas dynamics, fluid properties, mass transfer, and overall kinetics are complex, and simple uniform steady-state equations do not accurately describe the kinetics of the process. The overall kinetics for a particular reaction in such a system can be represented by the equation

$$ J_{\text{overall}} = {\sum\limits_{i{\text{ = }}1}^{i{\text{ = }}m} J _i} $$
(2)

where J is the flux (mol/m2 s) of a particular species and m is the number of distinct interfaces in the system. This relationship can be expanded into the partial differential form:

$$ J_{\text{overall}} = {\sum\limits_{i = 1}^{i = m} {\frac{{\partial C_{i} }} {{\partial t}}\frac{{V_{i} }} {{A_{i} }}} } $$
(3)

where C i is the overall concentration of a particular species (mol/m3) associated with distinct volume V i (m3), which in turn has a particular interfacial area A i (m2) in contact with a reacting phase. In this formulation, m, C i , V i , and A i all vary in time (i.e., droplets may change shape or coalesce), meaning that general analytical solutions to Eq. [2] are unlikely and various numerical approaches will be required. For example, one could integrate the equation over small enough time periods such that assuming constant A i , V i , and m is valid, then step change these variables from known relationships before integrating the next time-step. Of course, establishing how these terms vary with time is both experimentally and theoretically challenging.

Fig. 1
figure 1

Representation of regions within top blown oxygen steelmaking

Full size image

In this article, we summarize some recent work studying how droplets behave in steelmaking reactions, including “bloating” phenomena and spontaneous emulsification, and demonstrate how transient kinetic equations can successfully describe the complex conditions associated with these systems.[4]

Desulfurization

The removal of sulfur at a ladle metallurgy station is a common process requirement in many steel plants and is particularly important for special low sulfur grades of steel. It is well known that low sulfur can be achieved through tight control of the slag chemistry and stirring in the ladle. The model developed deals with the common scenario of the slag chemistry changing significantly during the process, which, in turn, means that the equilibrium drive for sulfur removal is dynamic in this model. In this study, the goal was to develop an online model that could assist operators in making decisions as the process proceeded.[3]

The desulfurization process in the ladle operation can be expressed by the following reaction:

$$ {\left[ {\text{S}} \right]} + {\left( {{\text{O}}^{{2 - }} } \right)} = {\left[ {\text{O}} \right]} + {\left( {{\text{S}}^{{2 - }} } \right)} $$
(4)

By assuming the desulfurization reaction is controlled by mass transport in the metal phase to the slag-metal interface, as commonly accepted by previous researchers, the reaction rate can be written as

$$ \ln {\left( {\frac{{[{\text{pct S}}]_{{j + 1}} - [{\text{pct S}}]_{e} }} {{[{\text{pct S}}]_{j} - [{\text{pct S}}]_{e} }}} \right)} = - k^{1}_{S} \Delta t $$
(5)

where \( k^{1}_{S} \) is a rate constant and [pct S] e , [pct S] j , and [pct S] j + 1 are the concentration of sulfur at equilibrium, at time j, and at time j + 1, respectively (wt pct). From the definition of sulfur partition, L S, and the material balance of sulfur in the ladle, the following equation can be derived:

$$ [{\text{pct S}}]_{e} = \frac{{100{\text{S}}_{T} }} {{L_{{\text{S}}} W_{{\text{S}}} + W_{M} }} $$
(6)

where S T is total weight of sulfur in the ladle (kg), W S is weight of slag (kg), and W M is weight of metal (kg). The value of sulfur partition can be predicted by

$$ L_{{\text{S}}} = \frac{{C_{S} K_{{os}} f_{{\text{s}}} }} {{[{\text{pct O}}]_{i} }} $$
(7)

where K os is the equilibrium constant of Reaction [4], f s is the activity coefficient of sulfur in the metal, C S is the sulfide capacity of slag, and [pct O] i is the oxygen concentration at the slag-metal interface. The values of K os and C S can be predicted using established relationships.[2,6,7] This model aims to deal with the situation of changing slag chemistry on the rate of desulfurization, in particular, with the case of FeO reducing as Al is added to the metal. Changes in composition of FeO and Al in an industrial system used in this calculation are detailed in the Appendix.

The model does not deal with the contribution of SiO2 and MnO to the oxygen potential of the metal, though the approach taken subsequently could be extended to include this contribution. Thus, the value of oxygen concentration at interface, [pct O] i , is assumed as the oxygen concentration in equilibrium with (FeO); that is,

$$ {\left( {{\text{FeO}}} \right)} = {\text{Fe}} + [{\text{O}}]_{i} $$
(8)

and

$$ [{\text{pct O}}]_{i} = \gamma K_{{{\text{FeO}}}} X_{{{\text{FeO}}}} $$
(9)

where X FeO is the mol fraction of FeO in slag, K FeO is the equilibrium constant of Reaction [8], and γ is the activity coefficient FeO in slag. The value of K FeO can be predicted by[5]

$$ \log {\text{ }}(K_{{{\text{FeO}}}} ) = - \frac{{6372}} {T} + 2.73 $$
(10)

The issue of the rate of FeO reduction in slag by Al is complex, and there is limited experimental and plant data to deduce rate mechanisms and the controlling step. In this model, we assume that mass transfer of oxygen from the slag metal interface into the metal phase controls the overall rate of FeO reduction in the slag. By assuming that oxygen transfer from the interface into the metal determines the rate of Reaction [8], the value of [pct O] i can be predicted by the following equation:

$$ \ln {\left( {\frac{{[{\text{pct O}}]_{{i,{\text{ }}(j + 1)}} - [{\text{pct O}}]{}_{b}}} {{[{\text{pct O}}]_{{i,{\text{ }}j}} - [{\text{pct O}}]_{b} }}} \right)} = - k^{1}_{O} \Delta t $$
(11)

where \( k^{1}_{O} \) is a rate constant; [pct O] b is the concentration of oxygen in the bulk metal; and [pct O] i,j and [pct O] i,(j + 1) are the oxygen concentration at interface at time j and at time j + 1, respectively. The value of [pct O] b is controlled by oxygen reaction with aluminum in metal; i.e.,

$$ 2{\left[ {{\text{Al}}} \right]} + 3{\left[ {\text{O}} \right]}_{b} = {\left( {{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} } \right)}_{{{\text{inclusion}}}} $$
(12)

By assuming that Reaction [12] is mass transport control, its rate of reactions can be written as

$$ \ln {\left( {\frac{{{\text{[pct O}}]_{{b,{\text{ }}(j + 1)}} - [{\text{pct O}}]{}_{{b,e}}}} {{[{\text{pct O}}]_{{b,{\text{ }}j}} - {\text{[pct O}}]_{{b,e}} }}} \right)} = - k^{1}_{O} \Delta t $$
(13)

where [pct O] b,e is the equilibrium concentration of oxygen in the bulk metal. The value of [pct O] b,e , in weight percent, can be predicted by[9]

$$ [{\text{pct O}}]_{{b,e}} = 10^{{ - 4}} {\left( {\frac{{a_{{{\text{Al}}_{{\text{2}}} {\text{O}}_{3} }} K_{{{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} }} }} {{[{\text{pct Al}}]^{2} }}} \right)}^{{1/3}} $$
(14)

where

$$ \log {\text{ }}(K_{{{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} }} ) = - \frac{{62,680}} {T} + 31.85 $$
(15)

and

$$ a_{{{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} }} {\text{ = }}\left\{ {\begin{array}{*{20}c} {{\text{1}}} & {{}} & {{{\text{Al}}}} & {{{\text{killed}}}} & {{{\text{no}}}} & {{{\text{Ca}}}} \\ {{{\text{0}}{\text{.064}}}} & {{}} & {{{\text{Al}}}} & {{{\text{killed}}}} & {{{\text{with}}}} & {{{\text{Ca}}}} \\ \end{array} } \right. $$
(16)

Up to this point of discussion, the system has been considered as a perfectly mixed system; however, as reported in the literature,[5,8] the system is not always perfectly mixed over the entire processing time. Consequently, it is appropriate to add a correction factor, α, to account for nonuniform conditions in the system. This correction factor, α, is introduced into the rate constant as follows:

$$ k^{1}_{{\text{O}}} = \alpha k^{m}_{{\text{O}}} $$
(17)

where

$$ \alpha = \frac{1} {{B\ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon }_{{{\text{avg}}}} \tau }}{\int\limits_{t = 0}^t {\ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon }{\text{ }}dt} } \le 1.0 $$
(18)

where \( \ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon } \) is the stirring energy (W/tonne) and τ is the mixing time (s). Equation [17] predicts the correction factor by taking the ratio of the total stirring going into the bath over the total required energy for perfectly mixing. Because the total energy required for perfectly mixing is usually estimated based on single disturbance into the system, which is not true in ladle operation, a correction factor B is introduced in Eq. [18] to account for this behavior. The value of rate constants for sulfur, \( k^{m}_{{\text{S}}} \), and oxygen, \( k^{m}_{{\text{O}}} \), at perfectly mixed condition, are calculated by[2]

$$ k^{m}_{{\text{O}}} = \left\{ {\begin{array}{*{20}c} {{E\ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon }^{{0.25}} }} & {{\ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon } < 50}} \\ {{\frac{E} {{1390.255}}\ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon }^{{2.10}} }} & {{\ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon } > 50}} \\ \end{array} } \right. $$
(19)

and

$$ k^{m}_{{\text{S}}} = \left\{ {\begin{array}{*{20}c} {{E'\ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon }^{{0.25}} }} & {{\ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon } < 50}} \\ {{\frac{{E'}} {{1390.255}}\ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon }^{{2.10}} }} & {{\ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon } > 50}} \\ \end{array} } \right. $$
(20)

where E and E′ are constants. The numeric value of 1390.255 is introduced into Eqs. [19] and [20] to bridge the values of rate constants at \( \ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon }\, = \,50\,{\text{W/tonne}} \).

The mixing time, τ, is predicted by[10]

$$ \tau = 116\ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon }^{{ - 1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}} D^{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-\nulldelimiterspace} 3}} H^{{ - 1}} $$
(21)

where D is the ladle diameter (m) and H is the depth of injection (m). The stirring energy can be evaluated by[10]

$$ \ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon } = 14.23\frac{{QT}} {{M_{B} }}\log {\left( {\frac{{1 + H}} {{1.48P_{o} }}} \right)} $$
(22)

where Q is the flow rate of gas (Nm3/min), M B is the bath weight (tonne), P o is the pressure of gas at the bath surface (atm), and H is the depth of gas injection (m). The constant values in equations, i.e. E, E′, and B, are optimized by minimizing

$$ \beta _{1} {\sum\limits_i {([{\text{pct S}}]_{{m,i}} - [{\text{pct S}}]_{{c,i}} )^{2} } } + (1 - \beta _{1} ){\sum\limits_i {(({\text{pct FeO}})_{{m,i}} - ({\text{pct FeO}})_{{c,i}} )^{2} } } $$
(23)

where [pct S] is the sulfur concentration in steel; (pct FeO) is the FeO concentration in slag; β 1 is the weighted factor; and subscripts m and c represent the measured and computed values, respectively. In effect, the model developed relies on using plant data, with multiple slag, and metal chemistry analysis as a function of time, to determine three semiempirical constants. For online application of the model, generally, several measurements of metal and slag chemistry are carried out during ladle operation. These data could be used to optimize the values of constants in the model, namely, E, E′, and B, in an online basis so the predictability of the inferential model can be improved. The results from the implementation of this strategy are illustrated in Figure 2. The initial values of the constants E, E′, and B are developed using past data. These values are used to construct the initial prediction line (showed as a dashed line in Figure 2). When measured data of process parameters are available, these values are used to optimize the value of the constants. The improved prediction line is shown in Figure 2 as a dash-dot line (corrected with first measurement) and solid line (corrected with first and second measured data). It is important to note that there is a delay between sampling time and the improved prediction line; the reason for this delay is the time taken for analysis of the sample. The details of the results of the validation of the model against plant data are presented in the Appendix.

Fig. 2
figure 2

Illustration of using measurement data to improve a model’s predictability[3]

Full size image

One of the most impressive results of this model is that the general trends observed at the industrial level follow the trends predicted by the model, whereas the opposite is true for predictions based on constant equilibrium conditions. While the model does rely on various assumptions and semiempirical constants, it does provide a framework by which to deal with the case of changing equilibrium conditions and nonuniform mixing.

Bloated Droplet Theory In Steelmaking

In oxygen steelmaking processes, the carbon-containing iron droplets, when ejected into oxidizing slags, often get “bloated” due to internal decarburization. Min and Fruehan[11] and Molloseau and Fruehan,[12] using an X-ray fluoroscopy technique, estimated that the diameter of the droplet was increased more than twice of its original diameter or the volume over 10 times of its original volume. These findings demonstrate that during rapid decarburization, the droplet becomes effectively less dense due to the internal generation of CO gas. Therefore, one would expect a relationship between decarburization rate and the droplet’s apparent density. This, in turn, would make the motion of the bloated droplet in a slag quite different from that of a dense droplet, which should influence the overall kinetics of the process. The authors have developed a model that incorporates the bloating phenomena into both the motion of the droplets and the individual kinetics of decarburization of each droplet.[4]

Based on the data of Fruehan and co-workers,[11,12] we assume that the droplet apparent density is influenced by the decarburization rate via the following relationships:

$$ \rho_{d} = \rho_{d0} \frac{r_{c}*}{r_{c}}\quad {\left( {{\text{if }}r_{c} > r_{c}{*}} \right)} $$
(24)
$$ \rho_{d} = \rho_{{d0}} \quad {\left( {{\text{if }}r_{c} \, \le \,r_{c} {*}} \right)} $$
(25)

where ρ d0 is the initial droplet density (kg/m3); r c is the decarburization rate (wt pct/s); and r c * is the threshold decarburization rate (wt pct/s), above which the droplet starts bloating. It would be expected that the threshold decarburization rate, r c *, is a complex function of interfacial properties of droplet and slag. In this work, the threshold decarburization rate, r c *, was evaluated from the experimental data of Molloseau and Fruehan,[12] as a function of FeO content in slag:

$$ r_{c} {*} = 2.86 \times 10^{{ - 4}} ({\text{pct FeO}}) $$
(26)

We assumed that the overall decarburization rate for a droplet could be effectively represented with a first-order rate equation in the following form:

$$ r_{c} = - \frac{{d[{\text{pct C}}]}} {{dt}} = k_{{{\text{eff}}}} \frac{{A_{{{\text{app}}}} }} {{V_{{{\text{app}}}} }}{\left( {[{\text{pct C}}] - [{\text{pct C}}]_{e} } \right)} $$
(27)

where [pct C] is the carbon content in the droplet (wt pct); [pct C] e is the equilibrium carbon content (wt pct); k eff is the effective rate constant (m/s); A app is the apparent surface area of the droplet (m2); and V app is the apparent volume of the droplet (m3). Further, k eff was calculated by using the following equation derived from Higbie’s penetration theory:[13]

$$ k_{{{\text{eff}}}} = 2{\sqrt {D_{c} u_{d} /(\pi D_{{d,{\text{app}}}} )} } $$
(28)

where D c is the effective diffusivity of carbon in liquid iron (m2/s), u d is the overall velocity of the droplet (m/s), and D d,app is the apparent diameter of the droplet (m).

These kinetic equations can be coupled with equations of motion to unify the reaction kinetics of individual droplets with their motion in the slag.[4] We assume that the generated metal droplets are ejected, in a certain angle θ, into a quiescent slag in which the droplets travel along ballistic trajectories in a two-dimensional (r, z) coordinate system, as schematically illustrated in Figure 3. The mathematical equations describing the balance of various forces acting on a metal droplet can be written as follows:

$$ z{\text{-direction:}}\quad \rho {}_{d}V_{d} \frac{{du_{z} }} {{dt}} = F_{B} - F_{G} - F{}_{{D,z}} - F_{{A,z}} $$
(29)
$$ r{\text{-direction:}}\quad \rho {}_{d}V_{d} \frac{{du_{r} }} {{dt}} = - F{}_{{D,r}} - F_{{A,r}} $$
(30)

where the subscript d stands for droplet; the subscripts z and r stand for vertical and horizontal directions, respectively; F B , F G , F D and F A are buoyancy, gravitation, drag, and “added mass” forces (N), respectively; ρ d is the droplet density (kg/m3); V d is the droplet volume (m3); u is the droplet velocity (m/s); and t is time (s).

Fig. 3
figure 3

Force balance on droplet traveling in slag

Full size image

Further assuming the droplet is spherical in shape with diameter D d and introducing definitions of the relevant forces in terms of density, velocity, and diameter of the droplet, by mathematical derivation, we can obtain the following differential equations that govern the motion of the metal droplet in the slag:

$$ \frac{{du_{z} }} {{dt}} = \frac{{2{\left( {\rho _{s} - \rho _{d} } \right)}g}} {{\rho _{s} + 2\rho _{d} }} - \frac{{3\rho _{s} C_{{D,z}} }} {{2{\left( {\rho _{s} + 2\rho _{d} } \right)}D_{d} }}u^{2}_{z} $$
(31)
$$ \frac{{du_{r} }} {{dt}} = - \frac{{3\rho _{s} C_{{D,r}} }} {{2{\left( {\rho _{s} + 2\rho _{d} } \right)}D_{d} }}u^{2}_{r} $$
(32)

where the subscript s denotes the slag phase and C D is the drag coefficient. Equations [31] and [32] are the major differential equations to be solved, based on which a mathematical model for predicting the trajectory and residence time of a metal droplet moving in slag is developed. The details of the model development can be found in an earlier article by the authors.[4]

A combination of Eqs. [24] through [27] with Eqs. [31] and [32] enables us to predict the trajectory and residence time of bloated metal droplets in slags under the influence of decarburization. This model is termed by the authors as the “bloated droplet motion model,” which accounts for the effects of both fluid mechanics and overall rate of decarburization reactions on the motion of metal droplets in oxidizing slag. In the present modeling work, the following values of physical properties were adopted:[4] ρ d  = 7000 kg/m3, ρ s  = 2991.4 kg/m3, and μ s  = 0.0709 Pa·s.

The trajectory and residence time predicted by the droplet motion model for dense metal droplets ejected in a 30-deg angle and at different ejection velocities are shown in Figure 4. Dense droplets mean that the droplets maintain their size while traveling in slag. The droplet ejection velocity was determined by regression analysis on the data calculated by Subagyo et al.[14] based on the experimental data of Koria and Lange.[15–17]

Fig. 4
figure 4

(a) Trajectory of dense metal droplets and (b) ejection velocity and residence time of dense metal droplets in the slag[4]

Full size image

From the modeling results presented in Figure 4, it can be concluded that the residence times of all dense droplets are very short, less than one-third of a second. Modeling of “bloated droplets,” using the same initial conditions as the dense droplet calculations (2-m slag depth) but incorporating the calculation procedure described previously, results in the prediction of much longer residence times. The calculated trajectory and residence times are shown in Figure 5. The residence time calculations are consistent with the experimental results of Fruehan and co-workers[11,12] and estimates from industrial studies.[4] The results suggest the following:

Fig. 5
figure 5

(a) Trajectory of bloated metal droplets and (b) ejection velocity and residence time of bloated metal droplets[4]

Full size image
  1. (1)

    the residence time of droplets in oxygen steelmaking is dominated by the buoyancy induced through rapid decarburization, and

  2. (2)

    toward the end of decarburization, the residence time of droplets is very short.[4]

The repercussions of this finding on the overall kinetics of steelmaking are the subject of a current study at the Swinburne University of Technology.

Reactions With Spontaneous Emulsification

In the previous examples, the generation of the interfacial area is due to the application of external forces (such as gas blowing) and the internal formation of a gas phase. In the third example, a kinetic analysis of a case where the interfacial area generation is due to a spontaneous emulsification is described.

A spontaneous emulsification has been observed in reactions between liquid slags and liquid iron droplets that contain oxidizable elements, namely, Fe-Al, Fe-Ti, Fe-P, Fe-B, Fe-Cr, and Fe-Si alloys.[18–21] The increase of interfacial area in the event of spontaneous emulsification is very large, i.e., 300 to 500 pct of the original interfacial area.[22] An example, for the case of an oxidation reaction of Al in a Fe-4 wt pct Al droplet by CaO-SiO2-Al2O3 slag at 1650 °C,[23] is shown in Figure 6. Figure 6(a) shows the instantaneous interfacial area during the reaction, while Figure 6(b) shows the associated change in the Al concentration in the metal droplets.

Fig. 6
figure 6

The change in (a) the instantaneous interfacial area and (b) the Al content in the metal droplets in the case of reaction between a 2.35 g Fe-4 wt pct Al droplet and CaO-SiO2-Al2O3 slag at 1650 °C[23]

Full size image

At the beginning, there was a single droplet. As the reaction proceeded, the droplet flattened and at 10 minutes (where the reaction was at its most intense) the droplet broke into numerous droplets, millimeter and micrometer in size. At this point, the instantaneous interfacial area was at maximum. The droplets then recoalesced toward the end of the reactions.

The overall reaction of the preceding process was as follow:

$$ {\left[ {{\text{Al}}} \right]}\, + \,{\text{3/4}}{\left( {{\text{SiO}}_{{\text{2}}} } \right)}\, = \,{\text{3/4}}{\left[ {{\text{Si}}} \right]}\, + \,{\text{1/2}}{\left( {{\text{Al}}_{{\text{2}}} {\text{O}}_{{\text{3}}} } \right)} $$
(33)

In a traditional approach, the kinetics of such a process are evaluated through kinetic equations that assume constant interfacial area. For example, in the process controlled by chemical reaction and following a first order with respect to aluminum in the metal droplets, the change in the Al concentration in the metal can be represented by the following equation:

$$ \frac{1} {{A_{c} }}\ln \frac{{[{\text{pct Al}}]}} {{[{\text{pct Al}}]_{{\text{0}}} }} = - \frac{{k_{1} }} {{V_{m} }} $$
(34)

where [pct Al] and [pct Al]0 are the aluminum contents in the metal at time t and at initial, A c is the constant interfacial area (m2), V m is the volume of the metal droplet (m3), and k 1 is the forward rate constant (m/s).

As can be seen from Figure 6(a), the change in the interfacial area is so large that the preceding approach cannot be used for evaluating the kinetics of this process. Also, the instantaneous interfacial area values shown in Figure 6(a) at any time are affected by the reaction rate in the period immediately before that moment; thus, they cannot be used in an integrated form of kinetic equations such as Eq. [34]. Rhamdhani et al.[24] proposed the use of a time-averaged interfacial area in analyzing the kinetics in the presence of spontaneous emulsification. A first-order chemical reaction controlled kinetics equation is written as

$$ \ln \frac{{{\text{[pct Al]}}}} {{[{\text{pct Al}}]_{0} }} = - \frac{{k_{1} }} {{V_{m} }}{\int\limits_0^t {A(t)dt} } $$
(35)

where A(t) is the instantaneous interfacial area, i.e., interfacial area in Figure 6(a). A factor of t/t is introduced to the right-hand side of Eq. [35], and upon rearranging the equation, the following is obtained:

$$ \frac{1} {{A^{*}(t)}}\ln\ \frac{{[{\text{pct Al}}]}} {{[{\text{pct Al}}]_{{\text{0}}} }} = - \frac{{k_{1} }} {{V_{m} }}t $$
(36)

where A*(t) is the time-averaged interfacial area, calculated using the following equation:

$$ A^{*}(t) = \frac{1} {t} {\cdot} {\int\limits_0^t {A(t)dt} } $$
(37)

In a chaotic process such as in the event of spontaneous emulsification, the change in interfacial area is complicated and cannot easily be represented by a simple function. Numerical calculation of time-averaged interfacial area is required.

Let us consider the case of the reaction between the 2.35 g Fe-4 wt pct Al droplet and CaO-SiO2-Al2O3 slag at 1650 °C, i.e., Figure 6. The kinetics can be evaluated by plotting the left-hand side of Eqs. [34] and [36] against time, which is shown in Figure 7. Lines (A) and (B) in Figure 7 were constructed using the time-averaged interfacial areas and a constant interfacial area, respectively. It can be seen from Figure 7 that in the case of constant interfacial area, there is a change in the slope by a factor of approximately 2 at 10 minutes of reaction, which is associated with the increase of interfacial area due to spontaneous emulsification. On the contrary, all the experimental data closely follow a straight line when the time-averaged interfacial area is incorporated. The slope of this line represents the value of –k 1 /V m . In this case, the rate constant k 1 is calculated to be 1.9 × 10−6 m/s.

Fig. 7
figure 7

Kinetics data plot of 2.35 g Fe-4 wt pct Al reacting in CaO-SiO2-Al2O3 at 1650 °C: Line (A) using the time-averaged interfacial area, A*(t), and Line (B) using a constant interfacial area, A c

Full size image

This approach has been shown to be applicable for the experimental data and to satisfactorily describe the kinetics of reaction between Fe-Al alloy droplets and CaO-SiO2-Al2O3 slag.[24] It has been shown that, in this particular case, the reaction is controlled by mass transfer of aluminum in the metal droplets, and the kinetics can be described by the following equation:[24]

$$ \frac{{V_{m} }} {{A^*(t)}} {\cdot} \frac{{{\text{[pct Al]}}_{{\text{0}}} - {\text{[pct Al]}}_{e} }} {{{\text{[pct Al]}}_{{\text{0}}} }} {\cdot} \ln\ \frac{{[{\text{pct Al}}] - [{\text{pct Al}}]_{e} }} {{[{\text{pct Al}}]_{0} - [{\text{pct Al}}]_{e} }} = - k_{m} {\cdot} t $$
(38)

where [pct Al] e is the aluminum content in the metal droplet at equilibrium and k m is the mass-transfer coefficient in metal phase. The preceding equation can be represented by the following equation:

$$ Y_{m}\ln {\text{ }}Z\, = \, - k_{m} t $$
(39)

where Z is ([pct Al] − [pct Al] e )/([pct Al]0 − [pct Al] e ) and Y m is (V m /A*(t)) . ([pct Al]0 − [pct Al] e )/[pct Al]0.

An example of plots between the left-hand-side term of Eq. [39] and time for various experimental conditions (2.35 g of alloy droplets with different initial Al concentration reacting at 1650 °C) is shown in Figure 8. All these data can be fitted into a single straight line with slope of −0.11074 mm/min (equivalent to k m  = 1.8 × 10−6 m/s).

Fig. 8
figure 8

Kinetics data plot of 2.35 g Fe-Al droplets (with different initial Al concentration) reacting with CaO-SiO2-Al2O3 at 1650 °C. The calculated mass-transfer coefficient in metal phase, k m , is 1.8 × 10−6 m/s

Full size image

The activation energy of the process was found to be 127 kJ/mol (30 kcal/mol), which is slightly higher than the activation energy for a diffusion-controlled reaction, i.e., 20 to 80 kJ/mol. The mass-transfer coefficient obtained using the approach represents an average value, because in the calculation, it was assumed that when the emulsification occurs, the droplet breaks into numerous smaller droplets of similar size. This implies that the mass-transfer coefficient inside each droplet is the same. In actuality, the droplet breaks into smaller droplets of different sizes. The value of the “true” mass-transfer coefficient, interfacial area, and driving force for mass transfer will be different from droplet to droplet depending on the droplet’s diameter and shape and the flow condition of the system. Theoretically, Eq. [3] and the approach outlined in Section I could be applied to this system with this information available. The time-averaging approach taken in this study represents a practical means of solving transient kinetic equations, but more rigorous treatments of these problems should be possible.

Conclusions

The studies summarized in this article illustrate different approaches of dealing with transient kinetic behavior in slag-metal reactions. The model developed for desulfurization in a steel ladle incorporates changing slag conditions and nonhomogeneous mixing and allows useful online predictions.

The “bloated droplet” model for oxygen steelmaking attempts to unite reaction kinetics and fluid mechanics. The calculations from the model provide a fresh insight into the overall kinetics of oxygen steelmaking, suggesting that the motion of iron droplets in the early part of the “blow” is dominated by gas evolution from the decarburization reaction. This result raises many questions about the connection between process dynamics (e.g., gas injection) and the overall chemical kinetics of the process.

The use of the time-averaged interfacial area for evaluating the kinetics in the presence of spontaneous emulsification can accommodate the interfacial area changes, enable the linear plotting of the kinetics data against time, and ascribe a reaction rate constant to the given system under a given set of conditions.

These attempts to model the complex behavior found in slag-metal reactions involve making various assumptions and simplifications. The authors are well aware that many steps of these models can be challenged on both theoretical and experimental grounds. However, these models do provide an intellectual framework to analyze the transient nature of these systems, and the authors hope that various assumptions and simplifications made in the models form the basis of new inquiry.