1 Introduction

Duplex stainless steels (DSS) basically show a dual-phase microstructure consisting of approximately equal volume fractions of BCC ferrite (α) and FCC austenite (γ). For the industries, the duplex steels have attracted great attention due to their lower price, higher strength as well as better corrosion resistance than the traditional AISI 304 austenitic stainless steel. Recently, these steel grades are being increasingly employed in chemical, petro-chemical, nuclear, and energy application fields.[1–3] These stainless steel grades can be processed by different routes, i.e., casting, forging, extrusion, or rolling. Such forming operations are usually performed at high temperature, at least in the earlier manufacturing stages. However, different mechanical responses of the austenitic and ferritic phases under hot working conditions could lead to defects in microstructure and deteriorated properties after hot deformation.[4] Thus, well-developed microstructures and satisfied product performances are strongly controlled by hot forming process parameters.

To investigate hot deformation behavior of these steel grades, two approaches for establishing constitutive relationships have been usually applied. The first one is physical models. Principally, the physically based model is related to various basic physical parameters like grain size and dislocation density. Thus, such model can more reliably describe material strain hardening with regard to microstructure evolution, deformation mechanisms, softening mechanisms (recovery and recrystallization), or grain boundary mobility. Therefore, this model can be used to predict material behavior under different conditions. However, for the physical models large amounts of extensive and costly experiments are required in order to identify their material parameters. For example, a composite model was proposed,[3] in which austenite and ferrite were considered as hard and soft phases. At an early stage of deformation, strain distribution was inhomogeneous, because strain accumulated in ferritic regions, while austenite was not yet deformed. In Reference 5, the flow curves of the ferritic steels exhibited typical dynamic recovery and thus were modeled by a dislocation density evolution. In case of the second approach, namely phenomenological model, empirical models as a mathematical representation were used to describe the correlation between flow stresses of materials and strain, strain rate, and deformation temperature under a wide range of working conditions.[6,7] Generally, material parameters for such models can be just determined from experimental flow stress curves.[4] The advantages of this model are their simplicity and acceptable reliability for engineering applications. Nevertheless, their predictability strongly depends on the experimental results and the models can accurately predict only flow stress behavior of materials under specific boundary conditions.[8] Most parameters in this model have no physical meaning except, for example, the n and Q values. Especially, the Q value represents the activation energy for plastic deformation, which is significant for this investigation. Farnoush et al.[9] studied high-temperature behavior of the DSS grade 2205 by hot compression tests under consideration of each constituent phase. The effects of temperature and strain rate on deformation behaviors were represented by the Zener–Hollomon parameter with a hyperbolic sine-type equation. It was found that empirical material constants for hot working were different at low and high temperatures. Zou et al.[4] developed a constitutive model with compensation of strain based on a hyperbolic sine equation for predicting flow stresses of an as-cast 21Cr economical duplex stainless steel (EDSS). The results showed that the introduced constitutive model exhibited excellent predictability of flow stress under experimental deformation conditions for the investigated alloy. Moreover, hot deformation behavior of X20Cr13 martensitic stainless steel was developed on the basis of the Arrhenius equation by Ren et al.[10] It was reported that the predictable efficiency of the developed constitutive models of the martensitic steel was evaluated by correlation coefficient and average absolute relative error (AARE), which were 0.996 and 3.22 pct, respectively. Han et al.[7] analyzed the hot deformation behavior of a 00Cr23Ni4N DSS under medium to high strain rates (5-50 s−1) using the Zener–Hollomon parameter and processing maps. Significant influences of high strain rates and high temperatures on hot deformation behavior of the duplex steel were observed. Momeni et al.[11] investigated the hot working behavior of 2205 austenite–ferrite DSS, by which constitutive equations based on a hyperbolic sine function were applied. It was recognized that strain at the peak point of flow curve increased with the Zener–Hollomon parameter (Z) during low-temperature deformation, while during high-temperature deformation it actually decreased with Z. Furthermore, Yang et al.[12] examined the microstructure and flow behavior of 2205 DSSs. It was found that by a low strain rate of 0.005 s−1, flow curves exhibited dynamic recrystallization (DRX) at the deformation temperatures of 1223 K and 1323 K (950 °C and 1050 °C), which led to deformed microstructures with more work hardening. Otherwise, the softening effect of flow curves was characterized by dynamic recovery (DRV) at the higher deformation temperatures of 1423 K and 1523 K (1150 °C and 1250 °C), and ferrite grains undergoing DRV became coarser simultaneously. However, the mechanical properties of the DSSs were affected not only by the deformation modes of constituent phases, i.e., ferrite and austenite, but also by the volume fraction of constituent phases.[1] Tehovnik et al.[13] examined the microstructural changes of DSS grade 2507 during hot rolling. It was concluded that this steel grade was very sensitive to phase formation, which was the main reason for the increase in hardness independent of annealing time and temperature, especially in the temperature range between 1073 K and 1173 K (800 °C and 900 °C). It can be seen that the Zener–Hollomon parameter with a hyperbolic sine-type equation has been successfully applied to describe the hot deformation behavior of the stainless steel series and other metals. The as-cast Mg-9Li-3Al-2Sr-2Y alloy investigated by Wei et al.[8] was quite complex and consisted of both the BCC β-Li matrix phase and HCP α-Mg phase. In general, the Zener–Hollomon model could well describe the softening stage, but for high-strain rate (1 and 0.1 s−1) and low-temperature (423 K and 473 K (150 °C and 200 °C) conditions, the predicted flow curves somewhat deviated from the experimental curves. Porntadawit et al.[15] examined hot deformation behavior of the Ti-6Al-4V alloy by dividing into two temperature ranges. In the first temperature range, the α + β two phases were concerned. Another temperature range was for the β single phase. It was found that the empirical material constants were different for both regions. Additionally, the calculated flow stress curves at low temperatures and high strain rates exhibited the highest discrepancies, because here different recrystallization and recovery mechanisms are also incorporated. Han et al. assumed that the Q value of the as-cast 904L austenitic stainless steel was independent of temperature.[17] A duplex brass consisting of α and β phases was studied by Farabi et al.[14] Hereby, it was presented that the activation energies at high and low temperature ranges were different. This was due to the fact that the increasing temperature led to the increased amount of the β phase but the decreased amount of the α phase. In contrast, for the DSS grade 2205, as reported in Reference 9, the Q value decreased at higher temperatures, by which the amount of ferritic phase increased and the amount of austenitic phase decreased. Moreover, Mohamadizadeh et al.[18] modified the Zener–Hollomon model and applied it to predict the flow behavior of a Fe-18Mn-8Al-0.8C low-density steel. It was assumed here that the parameter n was a function of temperature and strain, while the parameters Q and A were dependent on temperature, strain rate, and the amount of deformation. Nevertheless, few works have been carried out to characterize and predict the flow stress behavior of the 2507 DSS under hot working condition.

The aim of the present work was to investigate the flow behavior and microstructure evolution of the DSS grade 2507 using hot compression tests at the temperature range between 1173 K and 1473 K (900 °C to 1200 °C) and strain rates ranging between 0.1 and 10 s−1. For the flow stress modeling, the Zener–Hollomon parameter with a hyperbolic sine-type equation was applied to determine material parameters for the constitutive model. The prediction results were compared with the experimental ones. Additionally, metallographic examinations of the compressed samples were performed by optical microscope (OM) using color tint etching. The area based phase fractions of the existing phases were then determined for each forming condition. Hardness measurement of the specimens was also carried out and discussed with the results of microstructure observations.

2 Experimental Procedures

In this work, hot-rolled cylindrical bars of DSS grade 2507 with a diameter of 50 mm were used. The chemical composition of the investigated DSS was determined by optical emission spectrometer, which is given in Table I. In comparison to the conventional stainless steel grade 304, the 2507 DSS has somewhat lower Ni content, but higher Cr, N, and Mo contents. These higher alloy contents improve the corrosion resistance, whereas the higher N content additionally provides substantial strength of the DSS.

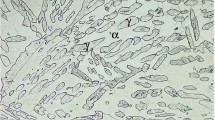
Table I Chemical Composition of the Investigated DSS (in Weight Percent)
Full size table

Metallographic examinations of DSS samples before and after hot compression were done by OM using color tint etching. The observed microstructure of the as-received DSS showed a mixture of approximately 57 pct austenite and 43 pct ferrite, as shown in Figure 1. Severely elongated structures of the as-received DSS could be observed. The light colored areas indicate the austenitic phase, whereas the dark colored areas represent the ferritic phase. Cylindrical specimens with a diameter of 5 mm and a height of 10 mm were prepared for the investigation. Each specimen contained a groove with a diameter of 4 mm and a height of 0.3 mm on the top and bottom surfaces to keep lubricant during compression so that the friction between specimen surfaces and push rods could be reduced. A thermocouple was attached in the middle of the samples for measuring the actual temperature during the whole test. A deformation dilatometer including inductive heating, compression, and cooling modules, as illustrated in Figure 2(a), was used for the hot compression test. All cylindrical specimens were upset at the temperatures of 1173 K, 1273 K, 1373 K, and 1473 K (900 °C, 1000 °C, 1100 °C, and 1200 °C), which were within the hot deformation temperature range of this steel grade by the production. Note that the melting point (T m) of the DSS grade 2507 is 1623 K (1350 °C) and the hot deformation temperatures should be well above 2/3 T m, which is 1173 K (900 °C).[13] Additionally, for the tests the strain rates were varied to be 0.1, 1, and 10 s−1 and the height reduction of 60 pct at the end of the compression was employed. Firstly, the specimens were heated up to the forming temperature and held for 60 seconds in order to obtain a homogeneous temperature distribution throughout the specimen. Then, the specimens were upset and directly cooled down to room temperature at the cooling rate of 40 °C/s. The applied thermo-mechanical process is summarized in the temperature–time schedule shown in Figure 2(b). Subsequently, for characterizing the resulted microstructure, the deformed specimens were sectioned parallel to the longitudinal compression axis. The prepared specimens were then ground and mechanically polished. Hereby, a solution of 122 ml HCl, 6 ml HNO3, and 122 ml H2O with the addition of 1 g K2S2O5 as an etchant. Micrographs of the specimens under each condition were taken by OM. The area fractions of the observed phases were determined by means of the MSQ image analysis. Furthermore, Brinell hardnesses of the compressed specimens under all the testing conditions were measured, in which a ball diameter of 1.588 mm and a load of 100 kg were used.

Fig. 1
figure 1

Microstructure of the as-received duplex stainless steel grade 2507

Full size image
Fig. 2
figure 2

(a) Schematic of deformation dilatometer and (b) temperature–time schedule for the hot compression test

Full size image

3 Stress–Strain Relationships at High Temperatures

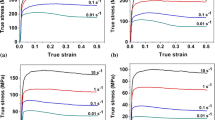
True stress–strain curves determined from the hot compression tests at different temperatures and strain rates are presented in Figure 3. It was found that under all the conditions the peak stresses increased with the increasing strain rate and decreasing temperature, as shown in Figures 4(a) and (b), respectively. The increases of peak stresses with strain rate indicated that the relief mechanism of work hardening factors, e.g., dislocation storage, was more pronounced during slower deformation processes.[12] However, by comparing the results in Figures 4(a) and (b), it was clearly observed that the effects of temperature on the flow stress were more significant than those of the strain rate. Similar results were also observed by Farabi et al.[14]

Fig. 3
figure 3

True stress–strain curves determined from hot compression tests at different temperatures and strain rates for the 2507 DSS

Full size image
Fig. 4
figure 4

Effects of (a) deformation temperature and (b) strain rate on the peak stress for the investigated 2507 DSS

Full size image

Furthermore, at the beginning of hot deformation, flow stresses rapidly increased due to strain hardening mechanism that took place with regard to the increase of dislocation density. Then, strain hardening rate gradually decreased until the flow stresses reached a maximum value. After that, flow stresses slightly decreased due to the occurrence of DRV and DRX depending on the deformation temperatures. It was reported in Reference 19 that a Fe-Cr-Ni-W-Cu-Co alloy exhibited quite low thermal diffusion rate so that dislocation movements became more difficult. Furthermore, the DRX restoration process strongly depended on the diffusion of atoms, grain or subgrain boundary migration, and dislocation density. Therefore, under such condition flow stress curves gradually achieved a balanced stress state without noticeable peak stresses and flow softening.[19] Additionally, the decrease of flow stresses with the increasing temperature was due to the easier movement of dislocations. Therefore, high-temperature deformation behavior of the DSS strongly depended on the deformation temperature and strain rate. Note that the hot deformation behavior with regard to DRV and DRX of each phase should be also investigated for such dual-phase microstructures that will be done in further works.

4 Flow Stress Modeling and Results

4.1 Constitutive Equation

Initially, the constitutive model according to the Zener–Hollomon equation was applied to describe the relationships between flow stresses, strain rate, and temperature on the basis of the experimental results from the hot compression tests. This model in fact describes the strain hardening behavior of the material on the macro-scale. The plastic compatibility between both phases of the DSS could actually lead to locally varying deformations on the micro-scale and consequently caused different softening mechanisms. Such microscopic mechanisms directly affected the overall strain hardening curves of the material. However, the effects of the plastic compatibility were already taken into account in the experimentally obtained compressive stress–strain curves in an indirect manner. And the resulted curves were afterwards used to identify the model parameters. To implement the effects of plastic compatibility between phases into constitutive models for high-temperature deformation is a complex work. On the one hand, for example, high-temperature compression tests of single-phase ferritic and austenitic steels with chemical compositions similar to those constituents in the investigated DSS must be first performed. Then, a law of mixture is applied to the results under the assumption that the total strain imposed on DSS is equal to strain accommodated by ferrite in combination with strain accommodated by austenite with consideration of the phase fractions. Strain interaction coefficients of ferrite and austenite obtained by the law of mixture are used to describe the dominant phase in terms of strain accommodation. Finally, the corresponding microstructure evolution and/or softening mechanism can be predicted for different temperatures. These predicted softening mechanisms could be afterwards incorporated in constitutive models such as Arrhenius-type model. On the other hand, the effects of plastic compatibility can be probably considered on the macro-scale in the Zener–Hollomon model by modifying the parameter n. As seen, the predicted flow curves are strongly governed by this parameter. If the plastic deformation incompatibilities between both phases and their effects on the softening mechanisms during different testing conditions are known, then a correlation between the parameter n and such actually occurred softening could be done. Nevertheless, the results of flow stress predictions by the proposed approach reported in other works[4,7,11,12] were acceptable. Hereby, the material constants and material flow stress could be described by the following equation:[4,7,9,11]

$$ z = \dot{\varepsilon }\exp \left( {\frac{Q}{RT}} \right) $$
(1)
$$ \dot{\varepsilon } = AF\left( \sigma \right)\left( { - \frac{Q}{RT}} \right), $$
(2)

where F(\( \sigma \)) is the stress function, which could be expressed by any of the following equations:

$$ F\left( \sigma \right) = \left\{ {\begin{array}{*{20}c} {\sigma^{{n^{\prime}}} } & {:\sigma < 0.8} & {} \\ {\exp \left( {\beta \sigma } \right)} & {:\sigma > 1.2} & {} \\ {\left[ {\sinh \left( {\alpha \sigma } \right)} \right]^{{n_{1} }} } & {:\begin{array}{*{20}c} {for} & {all} \\ \end{array} } & {} \\ \end{array} }. \right. $$
(3)

Substituting Eq. [3] into Eq. [2], the following equations were obtained:

$$ \dot{\varepsilon } = A\sigma^{n'} \exp \left( { - \frac{Q}{RT}} \right) $$
(4)
$$ \dot{\varepsilon } = Aexp\left( {\beta \sigma } \right)\exp \left( { - \frac{Q}{RT}} \right) $$
(5)
$$ \dot{\varepsilon } = A[\sinh (\alpha \sigma )^{{n_{1} }} ]\exp \left( { - \frac{Q}{RT}} \right), $$
(6)

where \( \dot{\varepsilon } \) is the strain rate (s−1), R is the universal gas constant (8.31 J mol−1 K−1), T is the absolute temperature (K), Q is the activation energy for hot deformation (kJ mol−1), σ is the flow stress (MPa) for a given strain, and A, α, n are the material constants, in which α ≈ β/n. At low stress levels (σ < 0.8), stress function could be approximated by the power law equation, while at high stress levels (σ > 1.2) it approached the exponential law. For a wider stress range, the hyperbolic sine law was considered more representative and was commonly used.[16] In this work, the hyperbolic sine law equation was thus applied and stresses at the strain of 0.05 were taken, for example, to show the solution procedure for determining the material constants. For the constitutive model, there were totally 4 material constants, which were A, n, α, and Q.

4.2 Determination of α

The value of α could be approximated by the relationship\( \alpha \approx \beta /n ' \). \( n^{\prime} \) and β in this equation were calculated by taking the natural logarithm on both sides of Eqs. [4] and [5]. They became Eqs. [7] and [8], respectively:

$$ \ln \dot{\varepsilon } = n^{\prime}\ln \sigma + \ln A - \frac{Q}{RT} $$
(7)
$$ \ln \dot{\varepsilon } = \beta \sigma + \ln A - \frac{Q}{RT}. $$
(8)

At a constant temperature during hot deformation process, the partial differentiation of Eqs. [7] and [8] could be expressed as follows:

$$ \left[ {\frac{\partial \ln \sigma }{{\partial \ln \dot{\varepsilon }}}} \right]_{\text{T}} = \frac{1}{{n^{\prime}}} $$
(9)
$$ \left[ {\frac{\partial \sigma }{{\partial \ln \dot{\varepsilon }}}} \right]_{\text{T}} = \frac{1}{\beta }. $$
(10)

Therefore, the values of \( n^{\prime} \) and β were calculated by a linear regression of the relationship between ln σ vs ln \( \dot{\varepsilon } \) and σ vs ln \( \dot{\varepsilon } \), respectively, as depicted in Figure 5. The average values of \( n^{\prime} \) of 9.68 and \( \beta \) of 0.07 were obtained. Thus, the value of α could be approximated to be 0.008.

Fig. 5
figure 5

Relationships between (a) ln \( \sigma \) vs ln \( \dot{\varepsilon } \) and (b) \( \sigma \) vs ln \( \dot{\varepsilon } \). (Symbols show the experimental data and solid lines represent the linear best fit.)

Full size image

4.3 Determination of n 1

The value of n 1 could be calculated by taking the natural logarithm on both sides of Eq. [6]. Then, it became Eq. [11]:

$$ \ln \dot{\varepsilon } = n_{1} \ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right] + \ln A - \frac{Q}{RT}. $$
(11)

In the same manner, at a constant temperature during hot deformation process, the partial differentiation of Eq. [11] gave the following equation:

$$ \left[ {\frac{{\partial \ln [\sinh \left( {\alpha \sigma } \right)]}}{{\partial \ln \dot{\varepsilon }}}} \right]_{\text{T}} = \frac{1}{{n_{1} }}. $$
(12)

Therefore, the value of \( n_{1} \) was calculated by a linear regression of the plot between \( \ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right] \) and \( \ln \dot{\varepsilon } \) at different temperatures, as shown in Figure 6(a). In this work, the average value of \( n_{1} \) of 5.97 was obtained for the investigated DSS.

Fig. 6
figure 6

Relationships between (a) \( \ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right] \) vs \( \ln \dot{\varepsilon } \) and (b) \( \ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right] \) vs 1/T/10−3. (Symbols show the experimental data and solid lines represent the linear best fit.)

Full size image

4.4 Determination of Activation Energy (Q)

The activation energy (Q) for high-temperature deformation could be calculated by rearranging Eq. [11] as follows:

$$ \ln [\sinh \left( {\alpha \sigma } \right)] = \frac{Q}{{n_{1} R}}\frac{1}{T} + \frac{1}{{n_{1} }}\ln \dot{\varepsilon } - \frac{1}{{n_{1} }}\ln A. $$
(13)

At a constant strain rate during hot deformation process, the partial differentiation of Eq. [13] at different temperatures gave the following equation:

$$ \left[ {\frac{{\partial \ln [\sinh \left( {\alpha \sigma } \right)]}}{{\partial \left( {\frac{1}{T}} \right)}}} \right]_{\text{T}} = \frac{Q}{{n_{1} R}}. $$
(14)

Thus, the activation energy was directly calculated by the following equation:

$$ Q = Rn_{1} \left[ {\frac{{\partial \ln [\sinh \left( {\alpha \sigma } \right)]}}{{\partial \left( {\frac{1}{T}} \right)}}} \right]. $$
(15)

The relationship \( [\partial \ln \{ \sinh (\alpha \sigma )/\partial (1/T)] \) was calculated by a linear regression of the plot between \( \ln [\sinh (\alpha \sigma_{\text{p}} )] \) vs \( \left( {1000/T} \right) \) at different strain rates, as illustrated in Figure 6(b). Therefore, for the investigated DSS the obtained activation energy was 689.50 kJ mol−1. The activation energy (Q value) is the sum of energies required for overcoming the Peierls stress, climbing of edge dislocations, cutting of forest dislocations, cross-slipping of screw dislocations, interactions between mobile dislocations, and tetragonal lattice distortions, which are caused by interstitially dissolved atoms.[20,21] At high temperatures, diffusion rate was increased so that the Q value became lower. Note that the activation energy of the DSS (689.50 kJ mol−1) was higher than those of the duplex steel grade 2205 (432 kJ mol−1),[9] 21CrEDSS (401.59 kJ mol−1)[4], and the as-cast 904L austenitic stainless steel (459.12 kJ mol−1).[17] It was presumed that the activation energy of the two-phase FCC–BCC steel should be approximately the average value of the activation energies of FCC and BCC metals and significantly lower than the activation energies of single FCC metals. In this work, the two-phase steel showed the higher activation energy than the FCC metals. The activation energy is usually influenced by the dissolved alloys and emerged precipitates, which in turn affected dislocation mobility and activated deformation mechanisms. Also, the value of activation energy for hot deformation is a function of alloying composition. The investigated DSS contained about 32 wt pct. solute atoms of Cr and Ni, which likely exhibited a strong effect on solid solution and precipitation strengthening and thus resulted in a relatively higher Q value.

4.5 Determination of A

The value of A could be calculated by substituting Eq. [6] into Eq. [1], from which the following equation was obtained:

$$ Z = A[{ \sinh }(\beta \sigma )^{n} ]. $$
(16)

Then, taking the natural logarithm on both sides of Eq. [16] gave the following equation:

$$ \ln Z = n\ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right] + \ln A. $$
(17)

The relationships between \( \ln Z \) and \( \ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right] \) are plotted in Figure 7. The values of ln A and n were calculated from the intercept and slope of this plot, respectively. Thus, the values of A of 1.51 × 1026 and n of 5.92 were obtained for the investigated DSS.

Fig. 7
figure 7

Relationship between \( \ln Z \) and \( \ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right] \). (Symbols show the experimental data and solid lines represent the linear best fit.)

Full size image

Subsequently, the values of all material constants in the used constitutive equations were calculated for different strains in the range between 0.05 and 0.8 with the strain interval of 0.05 by the similar solution procedure as introduced. The calculated material parameters n, β, ln A, and Q were plotted with increasing strain values, as depicted in Figure 8. It was obvious that the applied polynomial functions could fairly represent the relationships between these parameters and the plastic strain.

Fig. 8
figure 8

Variation of \( n^{\prime},\beta ,\alpha ,\ln A, \)and \( Q \) with strain. (Solid lines represent the polynomial best fit.)

Full size image

From Eq. [16], the plastic flow stress could be now expressed as follows:[4,7,9,11]

$$ \sigma = \frac{1}{\alpha }\sin^{ - 1} \left[ {\frac{Z}{A}} \right]^{{\frac{1}{n}}}. $$
(18)

An inverse sine function can be expressed as

$$ \arcsin hx = \ln \left( {x + \left( {x^{2} + 1} \right)^{{\frac{1}{2}}} } \right). $$
(19)

Then, substitute \( x = \left( {{Z \mathord{\left/ {\vphantom {Z A}} \right. \kern-0pt} A}} \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} \) into Eq. [18]. Finally, the constitutive equation that related flow stress and Zener–Hollomon parameters could be expressed using the hyperbolic sine function in Eq. [20]:

$$ \sigma = \frac{1}{\alpha } + \left\{ {\left( {\frac{Z}{A}} \right)^{1/2} + \left[ {\left( {\frac{Z}{A}} \right)^{2/n} + 1} \right]^{1/2} } \right\}. $$
(20)

Figure 9 shows the calculated flow curves for the deformation temperatures of 1173 K, 1273 K, 1373 K, and 1473 K (900 °C, 1000 °C, 1100 °C, and 1200 °C) under different strain rates using the introduced Zener–Hollomon equation in comparison with the experimental stress–strain curves. It was found that the calculated flow curve for the temperature of 1473 K (1200 °C) and the strain rate of 1 s−1 somewhat deviated from the experimental curves. However, for other combinations of temperature and strain rate the calculated flow curves agreed well with the experimental results.

Fig. 9
figure 9

Comparison between flow stresses determined experimentally and calculated by the Zener–Hollomon equation for different deformation temperatures and strain rates. (Solid line—experiments, symbol—calculations)

Full size image

To verify the predictability of the proposed constitutive model, the predicted flow stresses were taken to quantitatively analyze by standard statistical parameter, namely the correlation coefficient (R). The accuracy of the constitutive model was evaluated by the AARE for the flow stress data at various strains between 0.05 and 0.8 at the strain interval of 0.05 according to Eqs. [21] and [22], respectively[4,16].

$$ R = \frac{{\sum\nolimits_{i = 1}^{i = N} {\left( {\sigma_{\exp }^{i} - \bar{\sigma }_{\exp } } \right)\left( {\sigma_{\text{p}}^{i} - \bar{\sigma }_{\text{p}} } \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^{i = N} {\left( {\sigma_{\exp }^{i} - \bar{\sigma }_{\exp } } \right)^{2} \sum\nolimits_{i = 1}^{i = N} {\left( {\sigma_{\text{p}}^{i} - \bar{\sigma }_{\text{p}} } \right)^{2} } } } }} $$
(21)
$$ {\text{AARE}} = \frac{1}{N}\sum\limits_{i = 1}^{i = N} {\left| {\frac{{\sigma_{\exp }^{i} - \sigma_{\text{p}}^{i} }}{{\sigma_{\exp }^{i} }}} \right|} \times 100\;{\text{pct}}, $$
(22)

where \( \sigma_{\exp } \) is the experimental flow stress, \( \sigma_{\text{p}} \) is the predicted flow stress, \( \bar{\sigma }_{\exp } \)and \( \bar{\sigma }_{\text{p}} \) are the mean values of \( \sigma_{\exp } \) and \( \sigma_{\text{p}} \), respectively, and N is the total number of data points. The comparison between the experimental and calculated flow stresses is shown in Figure 10. It could be seen that most of the data points completely lay close to the best linear regression, and a good correlation (R = 0.995) between the predicted and experimental data was obtained. Moreover, the AARE value of 5.7 pct was determined, which showed that the constitutive model could accurately predict the high-temperature deformation behavior of the investigated DSS grade 2507.

Fig. 10
figure 10

Comparison between the predicted and experimental flow stresses using the hyperbolic sine model

Full size image

5 Flow Stability

During hot deformation, the material typically becomes more sensitive to strain rate and temperature. At higher deformation rate, plastic work was converted into heat and consequently softened the material. Significant amounts of thermal softening could cause material instability.[22] In order to optimize hot forming condition for obtaining a stable material flow, dynamic material modeling (DMM) has been used. By this model, applied temperatures and strain rates were evaluated by two material parameters that are strain rate sensitivity m and temperature sensitivity s. The DMM model described the dynamic path in response to an instantaneous change in strain rate at given temperature and strain. The strain rate sensitivity m and temperature sensitivity s of the flow stress were related to the manner in which the specimen instantly dissipated energy during hot deformation.[23] The values of the strain rate sensitivity m could be calculated by a linear regression of the plot between \( \log \sigma_{\text{P}} \) and \( \log \dot{\varepsilon } \) at different temperatures with regard to Eq. [23], as shown in Figure 11(a). On the other hand, the values of the temperature sensitivity s could also be computed by a linear regression of the plot between \( \log \sigma_{\text{P}} \) and 1/T at different strain rates with respect to Eq. [24], as shown in Figure 11(b).

$$ m = \left\{ {\frac{{\partial \left( {\log \sigma_{P} } \right)}}{{\partial (\log \dot{\varepsilon })}}} \right\}_{\text{T}} $$
(23)
$$ s = \frac{1}{T}\left\{ {\frac{{\partial \left( {\log \sigma_{P} } \right)}}{\partial (1/T)}} \right\}_{{\dot{\varepsilon }}} $$
(24)
Fig. 11
figure 11

Relationships between (a) \( \log \sigma_{P} \) vs \( \log \dot{\varepsilon } \)and (b) \( \log \sigma_{P} \) vs 1/T/10−3

Full size image

Based on the DMM approach, the plastic deformation during hot forming was stable, when the energy dispersion processes of material were in a steady state. The DMM stability criteria were then expressed as follows:[23,24]

$$ 0 \, < m < \, 1 $$
(25)
$$ \frac{\partial m}{{\partial (\log \dot{\varepsilon })}} \le 0 $$
(26)
$$ s > \, 1 $$
(27)
$$ \frac{\partial s}{{\partial (\log \dot{\varepsilon })}} \le 0. $$
(28)

These four stability criteria of the DMM approach could be explained as follows. In the first criterion, it was stated that the value of strain rate sensitivity m for stable material flow (Eq. [25]) should not be negative or equal to zero, which would lead to fracture. On the other hand, under the conditions with high m values, the tendency for localized deformation decreased. Thus, the occurrence of shear band formation could be inhibited. Moreover, the condition with m = 1 represented an ideal superplastic behavior.[23] The second criterion related to the variation of m with \( \log \dot{\varepsilon } \) (Eq. [26]). The positive \( m(\dot{\varepsilon }) \) value led to failure at high strain rates. In contrast, if the \( m(\dot{\varepsilon }) \) value became negative, the probability of inducing fracture in specimen was low. This condition provided more uniform stress fields, by which strain localization was avoided. Figure 12(a) shows the relationships between the m value and \( \log \dot{\varepsilon } \) at different temperatures. It was found that the determined m values of the investigated duplex steel were in the range between 0 and 1 according to the first criterion so that satisfied states were indicated for all the considered temperatures and strain rates. Furthermore, the \( m(\dot{\varepsilon }) \) values were negative for the most tested temperatures except for the temperature of 1173 K (900 °C). Therefore, the second criterion of the DMM model was satisfied for most temperatures and strain rates aside from the temperature of 1173 K (900 °C).

Fig. 12
figure 12

Relationships between (a) m vs \( \log \dot{\varepsilon } \) and (b) s vs \( \log \dot{\varepsilon } \)

Full size image

By the third criterion, the temperature sensitivity s needed to be positive for achieving a stable condition. Besides, low s values were indicative of the DRV process, while the conditions with high s values were usually associated with the DRX process. The last stability criterion concerned with the variation of s value with \( \log \dot{\varepsilon } \) (Eq. [28]). If \( s(\dot{\varepsilon }) \) value increased with \( \dot{\varepsilon } \), significant thermal softening would be encountered in the regime of high strain rates, which could cause severe strain localization and adiabatic shear band.[23] Figure 12(b) illustrates the relationships between the s values and \( \log \dot{\varepsilon } \) at different temperatures. Obviously, the determined s values of the investigated steel were above 1, which meant that all the considered temperatures and strain rates are satisfied according to the third criterion. However, the \( s(\dot{\varepsilon }) \)values were negative for most temperatures except for the strain rate range of 0.1 to 1 s−1 and the temperature range of 1373 K to 1473 K (1100 °C to 1200 °C). Thus, the last criterion was not satisfied for these deformation conditions. The states for satisfaction of each criterion at different temperatures and strain rates are summarized in Table II. It could be concluded that the plastic flow of the examined DSS grade 2507 would be stable under the following hot deformation conditions: the strain rate range of 0.1-1 s−1 in the temperature range of 1273 K to 1373 K (1000 °C to 1100 °C) and the strain rate range of 1-10 s−1 in the temperature range of 1273 K to 1473 K (1000 °C to 1200 °C). These working ranges were recommended for the DSS grade 2507 in order to avoid shear band-induced cracks during forming.

Table II States of Satisfaction for Each Criterion According to DMM Approach for the DSS 2507
Full size table

6 Microstructure Analyses

Generally, it has been known that microstructure evolution during hot compression influenced the flow characteristics of material. Hence, the effects of deformation temperature and strain rate on the microstructure development were investigated by means of OM images, as shown in Figure 13. It could be observed that the microstructures of all deformed 2507 DSS samples consisted of austenite with some deformation twins appearing in light colored area, for example, as shown in Figure 13(g) and ferrite in dark colored area. After the hot compression tests, microstructures became more equiaxed and distributions of the ferritic and austenitic phases were uniform. At the temperature of 1173 K (900 °C), the microstructures of the specimens formed at different strain rates were slightly different. Microhardness measurement of ferrite and austenite in compressed specimens from all the testing conditions was done. A Vickers hardness test with a load of 5 g and a dwell time of 10 seconds was used. The resulted hardness values were used to approximately characterize the occurred recovery and recrystallization phenomena of the investigated DSS. It was found that the hardness values of ferrite for the strain rate of 1 s−1 and the temperature of 1373 K (1100 °C) significantly decreased in comparison to the values for other conditions, as shown in Figure 14(a). This was likely due to the DRX occurrence. However, for other conditions a slight fluctuation in the hardness values of ferrite was observed. As a result, it can be stated that ferrite was less dominant for hot working behavior of the DSS. On the other hand, the hardness values of the austenite showed noticeable differences, as shown in Figure 14(b). It was attempted to classify the determined hardness values into two groups, namely high and low hardness ranges. Decreased hardness values could be attributed to the DRX occurrence. It was found that the conditions, which led to the lower hardness range, were the strain rate of 1 s−1 at the temperatures of 1273 K and 1373 K (1000 °C and 1100 °C) and all the strain rates at the temperature of 1473 K (1200 °C). During compression under these conditions, DRX in austenite likely occurred and was the dominant microstructure evolution, which affected the flow behavior of the material. Note that these results agreed well with the experimentally obtained flow stress curves. However, the occurrences of DRV and DRX of ferrite should be more precisely examined by other advanced methods like TEM.

Fig. 13
figure 13

Observed microstructures of DSS specimens after hot compression tests at different temperatures and strain rates

Full size image
Fig. 14
figure 14

Microhardness of (a) ferrite and (b) austenite in the DSS specimens compressed at different temperatures and strain rates

Full size image

As the DSS consisted of two phases, different mechanical responses of austenite and ferrite occurred during deformation. Hot workability of ferrite was better than that of austenite, because ferrite exhibited high stacking fault energy (SFE) and rather tended to undergo DRV. The rate of strain accumulation in the microstructure depends on local strain rate and temperature, microstructural characteristics, and SFE. As the SFE increases, deformation can be more readily accommodated by the formation of low-energy dislocation substructures that form by dislocation cross-slip and climb. These mechanisms of dislocation movement are favored, when stacking faults are not prevalent. On the other hand, in alloys with relatively low SFE like Cu, CuAl, CuZn, Ag, Ni-Fe, Co, Ni-based superalloys, tool steels, and austenitic stainless steels, cross-slip is limited and recrystallization is consequently favored during conventional hot working processes. The DRX was observed in low-SFE materials (e.g., 304L) during the application of large, continuous strain at low-strain rate and high-temperature conditions. There are several empirical equations for calculating the SFE. The approach introduced by Schramn et al.[25] is one of the most frequently used for stainless steels, which can be expressed as follows:

$$ {\text{SFE }}\left( {{\text{mJ}}/{\text{m}}^{2} } \right) \, = \, - 53 \, + \, 6.2\;{\text{pctNi }} + \, 0.7\;{\text{pctCr }} + \, 3.2\;{\text{pctMn }} + \, 9.3\;{\text{pctMo}}. $$
(29)

Since the investigated DSS consists of two phases, the chemical composition of each phase was firstly analyzed by energy-dispersive spectrometry (EDS), taking into account the mixture law. Note that the chemical compositions obtained from EDS, as shown in Table III, could be used to represent the chemical composition of each phase at high temperature because the compressed specimens were rapidly cooled down to room temperature. Therefore, in this work, the values of SFE of 37 and 42 mJ/m2 were approximately calculated for austenite and ferrite in the examined DSS, respectively.

Table III Determined Chemical Composition of Each Phase at High Temperature for the Investigated DSS Grade 2507
Full size table

However, when dislocation density reached a critical value, DRX would take place.[9] Hereby, DRX mechanism of austenite in the DSS was slower than that in the single-phase austenitic steel. First, it was due to strain partitioning at early stages of deformation. The plastic strain was almost accommodated at the softer ferritic phase. At higher strains, load was transferred from ferrite to austenite, thus leading to DRX. Second, the occurrence of DRX was usually observed at austenite/austenite grain boundaries. In DSS structure, there were a less number of such boundaries.[13] Moreover, Tehovnik et al.[13] distinctly found the occurrences of DRX at the temperature of 1523 K (1250 °C), which was beyond the investigated deformation temperature reported in this work. The effects of deformation temperature on the microstructural morphology were rarely observed at the temperatures of 1173 K, 1273 K, and 1373 K (900 °C, 1000 °C, and 1100 °C) for all strain rates. Nevertheless, at the temperature of 1473 K (1200 °C), austenite grains were definitely more elongated, as shown in Figures 13(j) through (l). Furthermore, area fractions of each occurred phase were determined for the specimens from all the testing conditions, as presented in Figures 15(a) and (b). It was shown that the amount of ferrite gradually increased with the increasing temperature, while the amount of austenite decreased, which corresponded to the ternary Fe-Cr-Ni phase diagram. As the temperature increased, the material came closer to the border line between the single-phase (δ) and two-phase (δ + γ) regions, then it resulted in higher ferritic phase fraction. Moreover, these results were also in accordance with the literature.[4,13,14] Additionally, it was reported in Reference 26 that the ferrite content of superduplex steel slightly increased with the increasing temperature and exhibited similar amount to those found in this work, as depicted in Figure 15(a) for comparison. No distinct influences of strain rate on the developed phase fraction could be observed. Subsequently, macro-hardness measurement of the compressed specimens from all the testing conditions was done and the results are depicted in Figure 16. It was found that the hardness values decreased with the increasing temperature, because at higher temperatures the softer ferritic phase increased, but the harder austenitic phase decreased. No significant effect of strain rate on the hardness value of the DSS specimens was observed. It can be stated that the final mechanical properties of a DSS product manufactured by hot forming process strongly depended on applied deformation temperature.

Fig. 15
figure 15

Determined area fractions of (a) ferrite and (b) austenite in specimens compressed at different temperatures and strain rates

Full size image
Fig. 16
figure 16

Effects of temperature on hardness of the DSS specimens compressed at different temperatures and strain rates

Full size image

7 Conclusion

In this work, the flow behavior and microstructure evolution of the DSS grade 2507 were investigated by the compression test at different temperatures and strain rates. Stress–strain responses of the examined steel were determined. Then, the constitutive model according to the Zener–Hollomon equation was applied for predicting the flow stress curves, by which all the involved material parameters were initially calculated. The calculated flow curves were subsequently compared with the experimental curves. Additionally, metallographic examinations of the compressed samples were performed. The results of this investigation can be given as follows:

  1. 1.

    High-temperature deformation behavior of DSS strongly depended on deformation temperature and strain rate. Flow curves obtained under all the testing conditions showed that the peak stress increased with the increasing strain rate and decreasing temperature.

  2. 2.

    The material constants of the examined 2507 DSS were calculated from the experimental flow curves using the hyperbolic sine law with the Zener–Hollomon equation. The determined averaged values of the parameters \( n^{\prime} \), β, α, Q, A, and n were 10.72, 0.07, 0.0079, 800.37, 5.28 × 1032, and 6.40, respectively.

  3. 3.

    The predicted flow stresses at different temperatures and strain rates were compared with the experimental results. The values of R and AARE of 0.995 and 5.7 pct, respectively, were obtained, which showed acceptable accuracy of the used constitutive equation.

  4. 4.

    According to the resulted microhardness values, DRX in austenite could likely occur at the temperatures of 1273 K and 1373 K (1000 °C and 1100 °C) under the strain rate of 1 s−1 and at the temperature of 1473 K (1200 °C) under all strain rates. The DRX of the austenite was dominant for softening mechanism of the examined DSS.

  5. 5.

    At higher temperature, ferritic phase fraction increased, while austenitic phase fraction decreased. Higher deformation temperature also resulted in decreased hardness value of hot compressed samples.

  6. 6.

    According to the DMM model, the strain rate range of 0.1-1 s−1 within the temperature range of 1273 K to 1373 K (1000 °C to 1100 °C) and the strain rate range of 1-10 s−1 within the temperature range of 1273 K to 1473 K (1000 °C to 1200 °C) were the recommended working ranges for the DSS grade 2507.

  7. 7.

    The proposed flow stress model can be further used to design and optimize a manufacturing process at elevated temperatures for the DSS.