1 Introduction

The present review follows on from participation in the Symposium “Dynamic Behavior of Materials – VI,” in honor of Professor Marc Meyers and sponsored by the Structural Materials Division (SMD) of the TMS-AIME in San Diego, CA, over 16 to 20 February, 2014.[1] In one of the symposium presentations, attention was focused on four topics among the greater number researched over the years by Meyers with colleagues and students, as follow: (1) thermally activated dislocation dynamics;[2] (2) measurements of adiabatic shear banding behaviors;[3] (3) strength level measurements made in shock or shock-less loading experiments;[4] and (4) strain rate sensitivity measurements made for nanopolycrystalline materials.[5]

An interconnection between the listed topics begins with a description of several constitutive equation developments in Section II. Particular attention is given to useful application coming from polycrystal deformation measurements based on the thermal activation strain rate analysis (TASRA), especially relating to the importance of the activation volume parameter,

$$ v* = A*b = k_{\text{B}} T\left\{ {\partial \left[ {\ln \left( {{\text{d}}\gamma /{\text{d}}t} \right)} \right]/\partial \tau_{\text{Th}} } \right\}_{\text{T}} . $$
(1)

In Eq. [1], v* is the activation volume parameter relating to A* as the activation area, b is dislocation Burgers vector, k B is Boltzmann’s constant, T is absolute temperature, (dγ/dt) is the applied shear strain rate, and τ Th is the thermal component of the applied shear stress.[6] Also, attention is paid in Section III to the role of dislocation pile-ups and the Hall–Petch (H–P) relationship in providing a fundamental explanation for the occurrence of adiabatic shear banding.[7] An important extension of an inverse dependence of v* on τ Th, already demonstrated in Section II, is established for shock-induced deformation results in Section IV. And the physically different situation of shock-induced dislocation generation is compared with dislocation drag-controlled measurements obtained in isentropic compression experiments (ICEs). Lastly in Section V, an analogous dependence for v*−1 to the H–P flow stress dependence provides a basis for understanding the enhancement of nanopolycrystal strain rate sensitivity measurements at nanopolycrystalline grain sizes.[8]

2 Dislocation Dynamics

As will be seen in subsequent development, control at an increasing loading rate (or lower temperature) of the plastic flow behavior of metals transitions from dislocation motion for conventional loading behavior to dislocation generation for shock wave loading, in line with an original description given by Orowan[9] as

$$ \left( {{\text{d}}\varepsilon /{\text{d}}t} \right) = \left( { 1/m} \right)\rho b\upsilon \to \left( { 1/m} \right)\left( {{\text{d}}\rho /{\text{d}}t} \right)b\Delta x_{\text{d}} . $$
(2)

In Eq. [2], (dε/dt) is the unidirectional compressive or tensile strain rate, m is a Taylor-type orientation factor, ρ is the mobile dislocation density, υ is the dislocation velocity, and ∆x d is a separation distance for dislocation generation. The dislocation generation relationship is proposed to apply at the highest conceivable rate of loading. Armstrong and Zerilli[10] have discussed the situation of strain rate contributions coming both from migration of the resident dislocation density and from shock-front-induced dislocation generations. A different complication occurs for shock-less ICEs in which comparable-to-shock loading rates are achieved but the load must be carried (in the absence of a shock front) by the originally resident dislocation density now required to move with such high speed as to be retarded only by a crystal lattice-based drag resistance.[11]

2.1 Thermal Activation Strain Rate Analysis (TASRA)

For conventional high-rate loading, the plastic shear strain rate, (dγ/dt), is taken to be a function of temperature, T, and thermal component of shear stress, τ Th, in the functional relationship[6]

$$ ({\text{d}}\gamma /{\text{d}}t) = ({\text{d}}\gamma /{\text{d}}t)_{0} \exp \{ - (G_{0} - \smallint v*{\text{d}}\tau_{\text{Th}} )/k_{\text{B}} T\} . $$
(3)

In Eq. [3], (dγ/dt)0 is the reference shear strain rate and G 0 is the Gibbs free energy. The thermal shear stress, τ Th, is obtained as

$$ \tau_{\text{Th}} = \tau - \, (\tau_{\text{G}} + k_{{{\text{S}}\varepsilon }} \ell^{ - 1/2} ) = \sigma_{\text{Th}} /m. $$
(4)

In Eq. [4], τ is the applied shear stress, τ G is an athermal shear stress determined by the dislocation density and impurities, k Sε is the Hall–Petch (H–P) microstructural shear stress intensity for slip penetration of the polycrystal grain boundary, ℓ is the average polycrystal grain diameter determined most often by the line intercept method, and σ Th is the counterpart thermal compressive or tensile stress. Thus, the shear strain rate is taken to be a function of T and τ Th in the relationship (dγ/dt) = (dγ/dt){T, τ Th}, so that[6]

$$ [\partial \tau_{\text{th}} /\partial T]_{{\ln [{\text{d}}\varepsilon /{\text{d}}t]}} [\partial T/\partial \ln ({\text{d}}\varepsilon /{\text{d}}t)]_{{\tau {\text{Th}}}} [\partial \ln ({\text{d}}\varepsilon /{\text{d}}t)/\partial \tau_{\text{Th}} ]_{\text{T}} = - 1.0. $$
(5)

The first factor on the left side of Eq. [5] is negative for so-called thermal softening. The second factor relates to greater strain rate being measured at higher temperature while the third factor connects with the activation volume parameter defined in Eq. [1]. The current TASRA description relates to the presentation given by Meyers in Reference 2 and carries over to description of the Zerilli–Armstrong (Z–A) relations that are to follow.

2.2 The Zerilli–Armstrong Relations

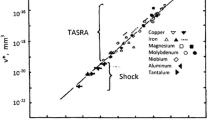
An explicit evaluation of the shear or unidirectional strain rate in Eq. [3] requires knowledge of v* that is taken in the TASRA to be a function only of τ Th, that is v* = v*{τ Th}. An early compilation of v* measurements reported for body-centered cubic (bcc) niobium single crystal and polycrystalline materials tested at different temperatures is shown in Figure 1.[12]

Fig. 1
figure 1

Activation volume measurements, v = v*, for niobium;[12] 1.0 kg/mm2 = 9.81 MPa

Full size image

An inverse dependence of v* on τ Th is shown to be obtained in Figure 1. The v* result led to another compilation of the same type results shown in Figure 2 now including a wider number of bcc, face-centered cubic (fcc), and hexagonal close-packed (hcp) materials.[6] The compilation was described by a same type single dependence for the different metal structures of

$$ v* = W_{0} /\tau_{\text{Th}} . $$
(6)
Fig. 2
figure 2

The v* dependence for a number of metals;[6] 1.0 kg/mm2 = 9.81 MPa

Full size image

A value of W 0 = 3.1 × 10−20 J was determined from Figure 2, just less than the value of W 0 for Figure 1.

A more recent compilation of v* measurements made for a number of hcp metals is shown in Figure 3.[13,14] As will be seen in later development in the present report, the v*–τ Th relationship will carry over to very high stress measurements obtained in shock-induced metal deformations.

Fig. 3
figure 3

v* measurements for hcp crystals and polycrystals;[13,14] 1.0 kg/mm2 = 9.81 MPa

Full size image

Zerilli and Armstrong made use of the τ Th dependence in Eq. [6] and, with consideration of the thermal stress dependence being in the yield stress for bcc metals and in the strain hardening behavior for fcc metals, obtained the following relations for flow stress, σ ε , levels achieved in hydrocode computations of impacted material deformations.[15,16]

$$ \sigma_{\varepsilon } = \sigma_{\text{G}} + B\exp [ - \beta {\text{T]}} + \, B_{0} [\varepsilon_{\text{r}} ( 1{-}\exp \{ - \varepsilon /\varepsilon_{\text{r}} \} )]^{ 1/ 2} \exp [ - \alpha {\text{T}}] \, + k_{\varepsilon } \ell^{ - 1/ 2} $$
(7a)

and

$$ (\beta ,\alpha ) = (\beta_{0} ,\alpha_{0} ) - (\beta_{ 1} ,\alpha_{ 1} )\ln ({\text{d}}\varepsilon /{\text{d}}t). $$
(7b)

In Eq. [7a], σ G and k ε are counterpart parameters to τ G and k Sε in Eq. [4] and B, β, ε r, and α are experimental constants; (β 0,α 0) and (β 1,α 1) in Eq. [7b] are constants relating to the strain rate dependence. For bcc metals, as indicated above, α = α 0 = α 1 = 0, to reflect the temperature and strain rate dependence being in the yield stress, while for fcc metals, B = 0; β = β 0 = β 1 = 0, because the same parametric influences are essentially only in the strain hardening behavior. The constant, ε r, takes into account the influence of dynamic recovery at larger strains, otherwise at smaller strains, the third factor on the right-side of Eq. [7a] is well approximated as a parabolic dependence on ε.[16,17] The athermal strain hardening of tantalum material will be demonstrated, and thus v* is independent of strain for bcc metals. During fcc metal straining, that is associated with thermal overcoming of an increased density of dislocation intersections, v* is found to decrease while both τ G and τ Th are found to increase.[15,18]

At lower temperatures or at very high rates of loading, deformation twinning occurs and the twinning stress, σ T, follows its own H–P-type behavior as

$$ \sigma_{\text{T}} = \sigma_{{0{\text{T}}}} + \, k_{\text{T}} \ell^{ - 1/2} . $$
(8)

The H–P twinning stress, with parameters σ 0T and k T, is essentially athermal although a model constitutive equation description has been given in which there is a weak strain rate dependence of k T.[19] Otherwise, k T > k ε . The consideration of deformation twinning relates to a microstructural assessment of a longitudinal section of an original solid cylinder impact test result that is shown in Figure 4, as obtained by Carrington and Gaylor.[20] The local state of strengthening produced by the impact deformation was probed by determining Vickers Hardness Numbers (VHNs in kg/mm2). A role for strengthening the material was shown to be provided by the impact-induced twinning, described at the time as Neumann bands after their original observation in meteorites.

Fig. 4
figure 4

Longitudinal section of a solid cylinder impact specimen of mild steel[20]

Full size image

2.3 The Johnson–Cook Relation and Z–A Comparison

Johnson and Cook[21] developed numerical relations for the separation of strain hardening, strain rate hardening, and influence of temperature on the deformation behavior of a number of metals so as to employ the dependencies in their own hydrocode, Elastic Plastic Impact Calculation (EPIC), description of the materials subjected to complex deformations:

$$ \sigma_{\varepsilon } = \left( {A + B\varepsilon^{\text{n}} } \right)\left( { 1+ C\ln \left[ {{\text{d}}\varepsilon /{\text{d}}t} \right]} \right)\left( { 1{-}T^{m*} } \right);\;\;T* = \left( {T - T_{\text{A}} } \right)/\left( {T{-}T_{\text{M}} } \right). $$
(9)

In Eq. [9], A, B, n, C, and m* are experimental constants, and T A and T M are the absolute ambient and melting temperatures, respectively. The combination of Eq. [9] and EPIC hydrocode are widely used. A comparison was made by Zerilli and Armstrong with the so-called Z–A equations employing the same test materials for which Johnson and Cook had determined their own material constants.[15] Armstrong and Walley have provided a review on the topic.[22]

More recently, Li[14] employed the Johnson–Cook Eq. [9] to assess the ambient temperature, high rate, deformation behavior in compression of a magnesium single crystal tested with its rod axis along the [0001] direction. The following relationship was obtained:

$$ \sigma_{\varepsilon } = \, \left( { - 7 8. 4+ 1 50 9\varepsilon^{0. 4 1 3} } \right)\left( { 1+ 0.00 9 7 7 8\ln \left[ {\left( {{\text{d}}\varepsilon /{\text{d}}t} \right)/\left( {{\text{d}}\varepsilon /{\text{d}}t} \right)_{0} } \right]} \right). $$
(10)

Because of the restricted crystal orientation for basal slip, the deformation was observed to occur by slip on the pyramidal slip plane with an m-factor of 2.27. The solid diamond point in Figure 3 was determined from Eq. [10] in accordance with Eq. [1] and is shown correspondingly to have a high value of τ taken equal to τ Th.

Figure 5 shows an additional interesting comparison of the stress–strain behaviors measured for Li’s single crystal and polycrystalline material tested under similar conditions of high-rate loading.[14,23] Note the reasonably similar higher rate polycrystal strain hardening at larger strains in comparison with the single crystal value. The comparative strain hardening behavior of the polycrystalline material at larger strain gives credence to the importance of pyramidal (and prism) slip[24] in effecting strain accommodation at grain boundaries, as will be reviewed later with respect to H–P application to hcp materials. The initial smaller polycrystal strain hardening shown in Figure 5 has been attributed recently by Sun and Chang[25] to strain localization in Lueders-type shear banding caused by compressive deformation twinning; see also Tsai and Chang[26] for relation to H–P measurements for the grain size dependence of deformation twinning. Even more recently, the twin-effected polycrystal deformation behavior occurring in compression has been compared with absent twinning in tension for AZ31b and ZEK100 alloy sheet materials, including texture-based anisotropy measurements and use of Z–A description for the rate-dependent tensile stress–strain behavior.[27,28]

Fig. 5
figure 5

Comparison of [0001]-oriented magnesium crystal and polycrystal results[14,23]

Full size image

2.4 TASRA Applications for α-Iron, Copper, Tantalum, and α-Titanium

Johnson and Cook (J–C) had provided their experimental test results to Zerilli and Armstrong for comparison with development of the physically based Z–A constitutive relations.[15,21] Figure 6 shows a comparison of the J–C longitudinal deformation shape of an Armco iron specimen and the Z–A physically based bcc model description employing Eqs. [7a], [7b], and [8] in the EPIC hydrocode.[29]

Fig. 6
figure 6

Experimental and modeled Armco iron solid cylinder impact deformation[29]

Full size image

Note the positive comparison of deformation shapes in Figures 4 and 6. Later computations were made by McKirgan of the sequential time development of the deformation shape, beginning at 1.0 μs and extending to the final shape of Figure 6 after 50 μs;[30] see Figure 31 in Reference 22. As might be imagined, an initial convex interface shape of deformation-twinned material occurred near to the impact face to be followed by time-dependent plastic deformation by slip that inverted the interface for twinning to the concave one that is finally observed.

In Figure 7, the deformation shape measured by Johnson and Cook for impact of an oxygen-free high-conductivity (OFHC) copper material is shown in comparison with the shape obtained by employing the fcc-type Z–A Eqs. [7a], [7b] and [8]. The iso-strain contour lines given in the figure legend, for example for the highest true strain of 1.5 near to the impact face, can be compared with a highest strain rate of ~105 s−1 and highest temperature of 600 K (327 °C) reached from the conversion of plastic work to heat.[15]

Fig. 7
figure 7

Comparative (solid) experimental and (dashed) model shape for copper impact[15]

Full size image

Hoge and Mukherjee are shown in Figure 8 to have provided excellent measurements of the (dashed) stress–strain behavior of tantalum material tested in tension over a wide range of temperatures and strain rates.[31] As indicated in the figure, individual test temperatures from 22 to 790 K (−251 to 517 °C) were employed at a fixed strain rate of 10−4 s−1, and in complementary tests performed at T = 300 K, strain rates in the range from 10−4 to 2 × 104 s−1 were employed. The solid curves matched with the dashed ones in Figure 8 are those fitted with the bcc Z–A equation whose constants are listed in the figure legend and for which c 0 = σ G + k ε ℓ −1/2 in Figures 7(a) and (b) and the athermal strain hardening term was expressed as Kε n, not very different from the model description of the strain hardening term given in Eq. [7a].[32] In addition in Figure 8, the limiting uniform strain locus defined for onset of plastic instability was determined from the Z–A model equation description in accordance with the Consider relationship

$$ \sigma = \left( {{\text{d}}\sigma /{\text{d}}\varepsilon } \right). $$
(11)
Fig. 8
figure 8

Tantalum stress–strain results over a range of temperatures and strain rates[31,32]

Full size image

The computed locus shown in each figure is seen to be in reasonable agreement with the experimental measurements. The total results may be compared with a recent model description of other tantalum material results reported by Barton, Bernier, Becker, Arsenlis, Marian, Rhee, Park, Remington, and Olsen.[33]

Among the hcp metals, cadmium, magnesium, and zinc, follow an fcc-like behavior while α-titanium, zirconium, and hafnium follow bcc-like behavior in that the temperature and strain rate dependence is principally in the yield stress, σ Y. Figure 9 shows a comparison of α-titanium results made on the basis of combining the temperature and strain rate test parameters in Eqs. [7a] and [7b] into a single functional dependence, T ln[(dε 0β /dt)/(dε/dt)].[34] Note might be taken of the “bump” in σ that occurs at higher effective temperature because of a solute strain-ageing effect. Other α-titanium results have been reported by Chichili, Ramesh, and Hemker in which an expected reduction in v* was achieved for tests made at greater strain rates, thus relating in part also to fcc-like behavior.[35]

Fig. 9
figure 9

Z–A description of σ Y for α-titanium on a combined T and (dε/dt) basis[34]

Full size image

It should be mentioned that, following after the review by Armstrong and Walley,[22] there are other more recent models of dislocation dynamics behavior particularly relating to metal deformations subjected to shock loading and in ICEs. As will be seen in Section IV, the two methods of testing bring out fundamental differences in controlling dislocation mechanisms. With regard to the testing of different materials, Comely et al.[36] have made connection of dynamic X-ray diffraction measurements with the multiscale strength model described by Barton et al.[33] for tantalum and vanadium materials. Austin and McDowell[37] have given parameters for a rate-dependent model of shock-induced plasticity in copper, nickel, and aluminum materials. Lloyd, Clayton, Austin, and McDowell[38] have provided a plane wave simulation of the elastic-viscoplastic response of aluminum single crystals over the full range of crystal orientations. Eswar Prasad et al.[39] have provided an important review of the dynamic deformation behavior of magnesium alloys including a description of their own experimental results. Relating to the issue of dislocation generation or migration in Eq. [2], Kattoura and Shehadeh[40] have reported multiscale dislocation dynamics plasticity calculations for copper involving both activation of pre-existing dislocation sources and homogeneous dislocation nucleation at strain rates up to ~1010 s−1.

3 Shear Banding

A review of the origins and consequences of plastic strain localization, such as occurs in shear banding of one sort or another, has been presented recently by Antolovich and Armstrong.[41] Attention to the topic was tracked to the pioneering nineteenth century work of Tresca[42] but is often referenced to the twentieth century article done on steel by Zener and Hollomon,[43] who gave emphasis also to plasticity being thermally activated and drew comparison between lower T and higher (dε/dt) results as shown above to be combined in Figure 9. Translation of a Russian contribution to the topic is found at the website: http://arxiv.org/abs/1410.1353. Localization in the form of Lueders band behavior in magnesium alloy material has been mentioned above (in Section II–C) with regard to a zone of heavily twinned grains being responsible for the observed behavior as shown in Figure 10.[26]

Fig. 10
figure 10

Twin-associated Lueders band in polycrystalline Mg[26]

Full size image

3.1 Adiabatic Shear Banding

Adiabatic shear banding behavior is well known for various steel materials.[22,41] Figure 11 illustrates the same type behavior for ballistic impact of a steel projectile onto a magnesium AM60B alloy material at an impact velocity of 500 m/s;[44] compare with the 190 to 338 m/s impact velocities mentioned for Figures 4, 6, and 7. Note the “curved” distortion of the deformation twin “bands” produced by subsequent heavy slip in the matrix material and then leading to severe localization in the 10 μm or so width of the shear band. Other excellent metallographic examples of damage produced by impact and ballistic penetrations have been described by Murr for steel, copper, aluminum, and other target materials, again, with employment of hardness testing to monitor the local material deformation behavior.[45]

Fig. 11
figure 11

Adiabatic shear band in magnesium alloy AM60B subject to ballistic impact[44]

Full size image

3.2 Dislocation Pile-Up Avalanche Model

Armstrong, Coffey, and Elban attributed the occurrence of adiabatic shear banding behavior to be initiated at dislocation pile-up avalanches.[7] The model, that builds onto the dislocation pile-up model explanation for the H–P relation, is shown schematically in Figure 12. In the sequential images of the figure, a progressive build-up of local shear stress occurs in the sequence from (a) to (b) for piled-up dislocations at a blocking obstacle, at which time a critical concentrated stress is reached and the obstacle collapses at (c). The closely spaced dislocations at the tip of the pile-up speed away from the collapsed obstacle under the action not of the applied stress but of the concentrated stress, thus being associated with a sudden drop in stress at (d), and producing essentially adiabatic heating only limited by the thermal conductivity of the material. Armstrong and Elban further investigated the model as it would apply to metals.[46] Figure 13 provides a comparison of different material results in the limit of pile-up release occurring at a speed equal to the upper-limiting elastic shear wave velocity.

Fig. 12
figure 12

Successive stages of dislocation pile-up and collapse[7]

Full size image
Fig. 13
figure 13

Shear banding susceptibility as a ratio of (k S/K*)[46]

Full size image

The inset equation in Figure 13 gives the temperature rise, ∆T, for modeled pile-up collapse in terms of the following parameters: a limiting H–P shear stress intensity, k S; grain diameter, ℓ; dislocation velocity, υ; thermal conductivity, K*; and specific heat at constant volume, c*.[7] The value of k S on the ordinate axis, with G equal to the shear modulus and α ≈ 0.8 in this case for an average dislocation character, is an upper-limiting stress intensity for separation by a Burgers vector distance of the leading pair of dislocations at the tip of the pile-up. With υ further taken as the upper-limiting shear wave speed, the only parameters showing significant variation among different metals are in the ratio of (k S/K*). On such basis, the slope of the lines drawn to the various plotted open-circle points may be taken as a model estimate of the metal susceptibility to shear banding behavior, thus favoring a larger ∆T for the collapse of a pile-up. The right-hand ordinate scale is expressed in terms of K*∆T and so the slope values for the filled circle points are seen to exhibit reasonably comparable shear banding susceptibilities to that given by the (k S/K*) ratio.

The plotted results in Figure 13 appear to be in line with the known susceptibilities of the shear banding tendencies of the plotted metals. Thus, Ti6Al4V alloy material is indicated to exhibit the greatest shear banding susceptibility, then to be followed by α-titanium. In fact, Z–A computations showed an appreciable self-heating effect for Ti6Al4V material even when undergoing uniform stress–strain behavior albeit under circumstance of high-rate loading.[34] And Figure 14 shows a more definite example of molten metal spray produced on the surface of Ti6Al4V material when subjected to penetration in a ballistic shear plugging experiment.[47]

Fig. 14
figure 14

Molten spray produced in shear plugging of Ti6Al4V material[47]

Full size image

The pile-up avalanche model and other aspects of shear banding were the subject of a co-edited Symposium on “Shear Instabilities and Viscoplasticity Theories,” sponsored by the Society of Engineering Science and published in a special focus issue of Mech. Mater.[48] In agreement also with prediction from Figure 13, additional important results on shear banding in α-titanium materials were presented by Meyers, Subhash, Kad, and Prasad involving “hat-shaped” test specimens.[3] Metallographic observations were reported by these investigators of similar shear band localization to that shown here for magnesium alloy AM60B material in Figure 11; see for example Figure 5 of Reference 3.

4 Shock vs Shock-Less Loading

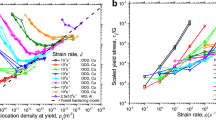
Pioneering split-Hopkinson pressure bar (SHPB) measurements of an increased flow stress for OFHC copper material loaded at increased strain rates were reported by Follansbee, Regazzoni, and Kocks, as shown in Figure 15.[49] The measurements have recently been reviewed in an article commemorating the centenary publication of Bertram Hopkinson’s seminal article on high-rate deformations.[50] And connection of the measurements with more recent test results reported by Jordan et al.[51] is in chart 10 of the ‘Power Point Presentations’ listing “Bertram Hopkinson Centenary Conference” under the ‘Publications’ icon at the University of Maryland website: http://www.cecd.umd.edu.

Fig. 15
figure 15

Split–Hopkinson pressure bar measurements for copper[49]

Full size image

Armstrong, Ramachandran, and Zerilli found that the activation areas, A* = (v*/b) shown in Figure 15, had increased for the measurements from the lowest value of ~1000b 2 at the slowest strain rates to a theoretical limiting value of ~b 2 at the highest strain rates.[52] That observation plus the report of an increased ductility that had occurred also for the material at the highest strain rates led to the consideration that the stress increase was more likely produced by an enhanced rate of dislocation generation. Additional support was provided by the finding that extrapolation of the higher sloped straight line in Figure 15 passed through experimental measurements reported by Swegle and Grady for shock-induced deformation of other copper material.[53] On such basis, it was suggested that the changeover from a lower logarithmic dependence on strain rate to a much steeper dependence occurred because of the transition indicated in Eq. [2] of control by dislocation motion changing to control by dislocation generation. Armstrong, Arnold, and Zerilli[54] reported on the finding in connection with important shock results obtained by Arnold[55] on Armco iron material. As mentioned in the Introduction, Meyers, Jarmakani, Bringa, and Remington have presented an excellent review on the topic of dislocation model considerations in shock compression and release.[4] In agreement with earlier presumptions, Meyers et al. concluded that, under shock wave loading, plastic flow was primarily confined within the nano-scale dimensions of the propagating shock front. And while added dislocation generation seemed to occur from within the resident dislocation density at low shock pressures, homogeneous dislocation generation occurred at higher pressures.

4.1 Shock-Induced Dislocation Generations

The determination of v* = ~b 3 for the steep rise of the plastic flow stress dependence on strain rate for the Follansbee et al. and Swegle and Grady copper results, led to the consideration that v* should reach a constant lower limiting value for shock-induced dislocation generation.[54] The condition leads in Eq. [7a], with neglect of strain hardening and influence of material grain size, to the rather simple equation for the one-dimensional compressive stress

$$ \sigma_{Th} = \, \left( {2G_{0G} /v*} \right) \, {-} \, \left( {2k_{B} T/v*} \right) \, [\ln \{ (d\varepsilon /dt)_{0} /(d\varepsilon /dt)\} ]. $$
(12)

In Eq. [12], G0G is a reference Gibbs free energy for dislocation generation, (dε/dt)0 is the limiting dislocation strain rate, and m has been taken equal to 2.0. Figure 16 shows application of Eq. [12] to important measurements reported by Arnold who had tested material having different average grain sizes.[55] Arnold’s measurements are shown to be in agreement with the higher shock pressure measurements reported by Swegle and Grady for their own Armco iron material.[53] As predicted in the model consideration, the steeper strain rate dependence for the plastic flow stress is independent of grain size. Alternatively, Arnold’s Hugoniot elastic yield stress measurements are shown to be accounted for by deformation twinning, σ T, as compared with the more narrowly confined σ ε curves shown for slip deformation, reflecting the inequality of k T > k ε as mentioned above in the comparison of Eqs. [7a] and [8].[56] More recent results reported for SHPB measurements on tantalum material by Rittel, Silva, Poon, and Ravichandran[57] were shown by Armstrong and Zerilli[10] to follow the same type steeper line established for separate shock measurements reported by Meyers.[58]

Fig. 16
figure 16

Hugoniot elastic limit and plastic flow stresses for Armco iron[55,56]

Full size image

Of particular note in both the referenced copper SHPB and shock results carrying on from Figure 15 and the Armco iron measurements shown in Figure 16 is the abrupt transition from a conventional Z–A type dependence to the much stronger strain rate dependence for the shock-induced deformation plastic flow stress. A very different situation is shown in Figure 17 for deformation measurements made over a wide range in strain rates for a number of aluminum materials.[59] At the lowest range of strain rates shown near to the origin of the figure, relatively low stresses are indicated just above the abscissa scale for ~50 to ~52 MPa strength measurements described by Carreker and Hibbard[60] for commercially pure material. The conventional strain rate measurements are followed by a higher pair of points plotted for the highest SHPB ∆σ measurement reported by Mocko, Rodriguez-Martinez, Kowalewski, and Rusinek for commercial AA 7075-T6 alloy material.[61] The even higher intermediate open square measurements were obtained from the shock measurements reported by Swegle and Grady.[53] And the highest strain rate measurements that are shown in the figure were obtained by Crowhurst, Armstrong, Knight, Zaug, and Behymer.[62] A much more gradual change of the rate dependence is indicated. The heavy-line linear dependence plotted at the top end of Figure 17 was obtained for actual measurements provided by Crowhurst and M.R. Armstrong.

Fig. 17
figure 17

The strain rate dependence of shock measurements for aluminum

Full size image

The curve shown in Figure 17 has been drawn in accordance with a fourth power dependence of stress on strain rate that was proposed by Swegle and Grady[53] and has recently been further analyzed by Grady,[63] that is

$$ P \, = \, K'\left( {d\varepsilon /dt} \right)^{1/4} . $$
(13)

With P = [(1 − ν)/(1 − 2ν)]σ = ~2σ, for a one-dimensional strain representation of the shock, then a dependence on σ, or τ, can be obtained for v* in accordance with Eq. [1]. From the indicated relationship of P and σ, and with employment of Eq. [13],

$$ v* = \sim 8k_{\text{B}} T/\sigma = \sim 4k_{\text{B}} T/\tau . $$
(14)

The indicated reciprocal dependence on v* of τ is in line with the relationship in Eq. [6] and consequently Figure 18 was constructed for comparison of the Figure 2 and shock-based v*–τ measurements that have been mentioned for copper, Armco iron, tantalum, and aluminum materials. Rather good agreement is shown in the increased coverage of the figure. In the shock region of Figure 18, the highest and lowest left-pointed triangle measurements are for the Swegle and Grady[53] and Crowhurst et al.[62] aluminum points shown in Figure 17. Malygin, Ogarkov, and Andriyash have recently given a dislocation model explanation of the fourth power law in which dislocation generation accounts for a large part of the pressure dependence but dislocation drag resistance to dislocation motion is also involved.[64]

Fig. 18
figure 18

Compilation of TASRA and shock determined v* measurements

Full size image

4.2 Control by Dislocation Drag in ICEs

An influence of dislocation drag on the Z–A relations was investigated by Zerilli and Armstrong.[11] A modified equation implicitly containing the thermal stress was obtained from Eq. [7a] with neglect of strain hardening as

$$ \sigma_{\text{Th}} = \{ 1- [c({\text{d}}\varepsilon /{\text{d}}t)/\beta_{ 1} \sigma_{\text{Th}} ]^{ - \beta 1T} \} [B\exp ( - \beta T)]. $$
(15)

In Eq. [15], an effective drag coefficient, c = c 0m2 β 1/ρb 2, for which bτ Th = c 0 υ. At a high value of (dε/dt), the result obtains

$$ \sigma_{\text{Th}} = (c_{0} m^{2} /\rho b^{2} )({\text{d}}\varepsilon /{\text{d}}t). $$
(16)

In Eq. [16], c 0 is the drag coefficient and thus, σ Th depends linearly on the strain rate and the inverse of the mobile dislocation density.

The importance of dislocation drag comes to the fore in shock-less ICEs for which comparable-to-shock strain rates are achieved and the resident (mobile) dislocation density is required to “carry the load” in the absence of a dislocation-generating shock front. Armstrong et al. have pointed to υ being large because ρ is small.[54]

Figure 19 shows such predicted linear behavior for important quasi-ICE results reported by Jarmakani, McNaney, Schneider, Orlikowski et al. as achieved in gas gun experiments.[65] In the figure there is near coincidence of the Eqs. [15] and [16] relations. One might note that the highest stress of 20 GPa in Figure 19 compares with a conventional flow stress of ~40 MPa for copper[13] thus giving an increase of ~500 times in plastic flow stress for the influence of the ICE-imposed strain rate.

Fig. 19
figure 19

Quasi-ICE measurements on copper[54,65]

Full size image

Smith, Eggert, Rudd, Swift, Bolme, and Collins have reported more recently on laser-induced ICE results obtained for the Hugoniot elastic limit stress, σ E, for Armco iron material also having different grain sizes as shown in Figure 20.[66] An H–P grain size, kℓ −12, term has been subtracted for the different grain sizes of the various materials. Smith et al. had included the dashed curve of Barton et al. for model comparison with the results.[33] Two lines have been added to the figure for comparison with the results currently being reported. The single-dot-dash line on the left (central) side of the figure, with AAZ designation, is the shock result shown for Armco iron in Figure 16. The double-dot-dash line on the right-side of the figure is an arbitrarily positioned line for consideration of a drag-based linear dependence of the higher stress results. Comparison with the higher experimental measurements indicates that a drag explanation is a more likely fit to the measurements.

Fig. 20
figure 20

Isentropic compression experiment on Armco iron[11,33,66]

Full size image

5 Hall–Petch for Nanopolycrystals

The first three terms in Eq. [7a] are normally combined into a single “friction” stress, σ 0ε , in the Hall–Petch relation that is widely employed, after the report by Petch and colleagues, in the better-known form of Eq. [17] to describe the dependence of σ ε on grain size for the full stress–strain behavior of bcc, fcc, and hcp metals and alloys.[67]

$$ \sigma_{\varepsilon } = \sigma_{0\varepsilon } + \, k_{\varepsilon } \ell^{ - 1/2} . $$
(17)

As indicated above, the strain rate (and temperature) dependence is in σ 0ε for bcc metals but fcc and certain hcp metals have a significant TASRA-type dependence in k ε . Recently, Armstrong has provided a review of broader applications of the relationship to other material properties.[68] Of particular interest to our present purpose is the model evaluation given for k ε :

$$ k_{\varepsilon } = \, m[\pi m*Gb\tau_{C} /2\alpha ]^{1/2} . $$
(18)

In Eq. [18], m* is a Sachs orientation factor for selection of slip systems at the tip of a pile-up and τ C is taken as the local shear stress needed for transmission of plastic flow across a grain boundary. As will be seen, the presence of τ C provides for the possibility of k ε exhibiting a thermal dependence. Among the common metals, the following inequalities hold: k Al < k Cu < k Mg ≪ k α-Fe with k ε  < k l.y.p. ≪ k T ~ k C ≪ K IC = σ(πc)1/2. The value of k C is for cleavage and K IC is the fracture mechanics stress intensity parameter that has an analogous theoretical basis, as will be demonstrated, for its dependence on pre-crack length, c, shown to have the same role as ℓ.[68,69] As noted in the comparison of ki inequalities, the smallest values are determined for fcc metals in which at conventional grain sizes, often the value of k ε ℓ −1/2 < σ 0ε .[70]

Continuing research results are being reported on all aspects of the H–P relation that was originally proposed to apply only for the observation of lower yield point and cleavage behavior in iron and steel materials, with values of k l.y.p and k C. Takeda, Nakada, Tsuchiyama, and Takaki have presented excellent H–P results on the effect of interstitial carbon on the H–P relationship.[71] Massart and Pardoen have assessed the H–P dependence for steel on the basis of a strain gradient plasticity model description.[72] A comparison of k ε values for the different bcc, fcc, and hcp metals also has been given recently by Wu, Zhang, Huang, Bei, and Nieh.[73] Comparison of the H–P dependence for polycrystals with subgrain influence within the grains and with particle size strengthening has been made by Lesuer, Syn, and Sherby.[74] The linking of such different sizes, even including inhomogeneity within amorphous materials, to macroscale functional behavior has been proposed in a commentary provided by Yip and Short to be at the frontiers of mesoscale science.[75] Greater strengthening effects occur at the nano-scale, as documented by Meyers, Mishra, and Benson in an extensive review of the mechanical properties of nanocrystalline materials including 374 references.[5]

5.1 H–P at Small Dislocation Numbers

Early consideration of the H–P effect at effective small grain sizes began in response to understanding the exceptional strength levels achieved in cold-drawn steel wires of eutectoid composition.[76,77] Figure 21 illustrates prediction of strength levels approaching the theoretical limit when only a few dislocations are in a pile-up, whether modeled in a single-ended, double-ended, or circular geometry.[78] The slope evaluations shown outside of the figure match the fracture mechanics descriptions of an edge crack, internal two-dimensional crack, and circular crack geometry. In Figure 21, r 0 is the dislocation core radius and if taken as ~0.2 nm, the right-hand value of ℓ would be ~5 nm.

Fig. 21
figure 21

Dislocation pile-up geometries at ultrafine grain sizes[78]

Full size image

Figure 21 demonstrates the important effect at small grain size of each added dislocation in the pile-up lowering the required stress to overcome the blocking obstacle, for example, as described in (b) of Figure 12. For each added dislocation, the stress drop, ∆τ, is obtained as

$$ \Delta \tau = \left( { - 1/n} \right)\tau . $$
(19)

At large n, as for the continuum description of dislocation pile-up characteristics, an apparently continuous H–P dependence is obtained. At small dislocation numbers, for example, for the single-ended dislocation pile-up in Figure 21, one can readily determine that the stress drop at n = 3 is (1/3) of the τ value at n = 2; for n = 4, (1/4) of τ, and so on. The figure gives reason for expectation of a scatter in experimental results at small grain size and provides a theoretical basis for expectation of a more pronounced yield point behavior at smaller grain size. Meyers et al. have given emphasis to the increased tendency toward shear banding in nanocrystalline metals.[5] Lee, Ding, Sun, Hsaio et al. have reported on ASB formation in conventional compression tests at ambient temperature of ultrafine grained magnesium AZ31 material.[79] Recently, comparison of the stress concentration ahead of a discrete dislocation pile-up for small n and that of a Griffith crack was proposed to provide a basis for observations of an absence of cleavage in nanopolycrystal iron material.[80,81] The issue was discussed in Reference 13. Other interesting evaluation of H–P prediction of stress concentration at the tip of a dislocation pile-up, this time for a particular grain boundary obstacle in copper, has been given by Britton and Wilkinson.[82]

5.2 H–P Transition to Single Loop Dependence

At the smallest dislocation number, n = 1.0, for a single loop expanding against the grain boundary resistance, the H–P reciprocal square root of grain size dependence changes over to a modified reciprocal length dependence.[83] Figure 22 shows application[70] of the predicted changeover in H–P dependence as it relates to nano-scale growth twinning results obtained by Lu, Chen, Huang, and Lu on copper material.[84] Armstrong and Smith had obtained the increased single loop stress, transitioning at n = 1.0 from the extrapolated Hansen and Ralph[85] result by employing previous calculations reported by Li and Liu[77]. A reversed H–P dependence was observed at the smallest twin spacings that were taken by Lu et al. to act in the same manner as the polycrystal grain size.[84] And the somewhat lower H–P dependence of the Lu et al. twinned material result, even compared to the extrapolated Hansen and Ralph result, is very probably explained by the weaker character of the twin boundaries.[67] Recently, Jian, Cheng, Xu, Yuan et al. have reported similar strengthening of magnesium material and attributed to nano-spaced twin stacking faults.[86]

Fig. 22
figure 22

Comparison on a log/log scale of H–P measurements and model predictions for copper[70]

Full size image

A very interesting case of the same type single loop consideration is shown in Figure 23 for a variety of iron and steel results beginning with the H–P dependence described for conventional steel results by Armstrong et al.[67] Embury and Fisher had reported the open square measurements plotted at somewhat lower H–P k ε for effective nano-scale grain sizes achieved in cold-drawn steel wire of eutectoid carbon concentration.[87] Jang and Koch had reported the plotted open-circle points for ball-milled α-iron.[88] The highest stresses shown for two open diamond points were obtained from hardness measurements, H, reported by Jang and Atzmon[89], and taken to be transformed by the relationship, σ ε  ≈ H/3. In each case, a displacement to the right-side for a parallel unit slope dependence marks a reduction in k ε . For example, the open triangle measurements were reported more recently for carbon-free iron[90] and are shown to exhibit a lower σ 0ε  ≈ 43 MPa and k ε  ≈ 11 MPa mm1/2 as compared with σ 0y = 71 MPa and k l.y.p. = 24 MPa mm1/2, respectively, for the Armstrong et al. steel results.[67]

Fig. 23
figure 23

Compiled H–P results for α-iron and steel materials on a log/log scale

Full size image

The shift in the H–P dependence for the filled inverted triangle results of Zhang, Godfrey, Huang, Hansen, and Liu[91] are of special interest because the measurements apply for cold-drawn eutectoid steel material of the same type measured by Embury and Fisher[87]. In this case, however, the results appear to follow a reciprocal length dependence that brings to mind the single loop behavior just described for copper. The predicted transition to single loop behavior occurs at larger grain size for smaller k ε . Zhang et al. had employed a relatively low value of k ε  = 12.7 MPa mm1/2 for their measurements and on that basis attributed different σ 0ε values to the different material points. In Figure 23, an alternative possibility is indicated for the upper-dashed single loop equation that, at n = 1.0, is shown to transition to the solid curve at an effective grain size of ~0.5 μm corresponding to a modified reciprocal length dependence. The lower k ε value cannot be explained on the basis of a lack of carbon content. Armstrong has suggested that low k ε values might apply for ultrafine grain size material because of the grain boundaries being disordered as a result of the material processing history or from alloying effect.[92] Such result could easily apply for the ball-milled Jang and Koch[88] measurements that show the greatest shift toward lower k ε and steeper grain size dependence in Figure 23. Hansen has reported on comparing the H–P relation for the lower yield point stress, k l.y.p., and modification of k ε for the flow stress of deformed metals.[93]

5.3 H–P Strain Rate Sensitivity

Figure 24 provides an H–P assessment of the strain rate dependence measured by Okitsu, Takata, and Tsuji[94] for ultrafine grain size α-iron material at different grain sizes. Estimated values of the H–P parameters have been added to the figure for (dε/dt) values of 10−2, 10, and 103 s−1. The thermal dependence is seen to be in the friction stress, σ 0ε , even for the relatively low values determined for k ε . As mentioned in connection with Eqs. [7a] and [7b], the behavior is typical of bcc metals. In contrast, the thermal dependence for relatively pure fcc metals, and for certain hcp ones, is principally in the local stress τ C contained within k ε , in accordance with Eq. [18].[95] On such basis, determination of the activation volume dependence in accordance with Eq. [1] is expressed in Reference 8 as

Fig. 24
figure 24

The flow of α-iron at ε = 0.05 with strain rate dependence in σ 0ε [94]

Full size image
$$ v*^{ - 1} = \, v_{0} *^{ - 1} + \, (k_{\varepsilon } /2m\tau_{C\varepsilon } v_{C} *)\ell^{ - 1/2} . $$
(20)

In Eq. [20], v 0* is the activation volume stemming from σ 0ε and v C* is from the τ C dependence that also contains an athermal shear stress component, τ CG, that can be neglected at small strains. Under such condition, τ CTh v C*Th is constant, as shown in Figure 3, and so an H–P dependence is obtained for v*−1. Prasad and Armstrong first showed that conventional grain size measurements reported on cadmium material by Risebrough and Teghtsoonian[96] followed Eq. [20], and the result was followed soon after with the same type measurements made on zinc material.[97] Rodriguez, Armstrong, and Mannan followed up with H–P-type v*−1 results reported on both the strain and temperature dependence measured for cadmium material.[98]

Figure 25 shows a compilation of v*−1 measurements for polycrystalline magnesium materials in comparison with an experimental range in single crystal measurements indicated on the right-hand ordinate axis.[13,23,99–103] One might note the added complication of deformation twinning at conventional grain sizes and which is avoided for ℓ ≤ ~10 μm. At smaller grain sizes, v*−1 is shown to be controlled by prism slip, or as indicated in the [0001]-oriented single crystal measurement reported by Li,[24] by pyramidal slip. Chun and Davies have presented a comparison of the prism and pyramidal slip stresses measured in single crystal experiments.[104] Very recently, Gzyl, Rosochowski, Pesci, Olejnik et al. have commented on the suppression of deformation twinning in severe plastically deformed AZ31B material having a grain size of ~5 μm.[105] Excellent photomicrographs were presented of deformation twinning occurring only in ~100 μm size grains of as-received material exhibiting a heterogeneous distribution of grain sizes, not unlike that shown in Figure 10. Comparable compression test results were obtained at a slower strain rate to those shown here in Figure 5 for polycrystalline material. Similar to the results described above in References 24 and 25, apparent Lueders-type deformation bands, associated both with twinning and slip, were found to occur on metallographic examination of tensile test specimens.

Fig. 25
figure 25

An H–P dependence of v*−1 for magnesium relating to single crystal values[13,24]

Full size image

The H–P dependence for v*−1 was shown also to provide a ready explanation[101] of increased strain rate sensitivity measurements compiled for nano-scale grain size measurements by Asaro and Suresh.[106] Armstrong has provided a review of the topic.[107] Figure 26 provides an update[70] of results that are extended to include a reverse dependence of v*−1 for the smallest twin-determined grain size results reported by Lu et al. for the same type material.[84,108] Weng[109] had obtained the important crossed points shown in Figure 26 from measurements reported by Schwaiger, Moser, Dao, Chollacoop, and Suresh[110]. An interesting aspect of Figure 26 concerns the essentially coincident dependence observed for the combination of copper and nickel measurements and which coincidence has been explained on the basis of Eq. [18].[101] Whereas nickel has an elastic shear modulus that is two times higher than that of copper, the value of τ C is controlled for fcc metals by the cross-slip shear stress that for nickel is one-half that of copper. Wang and Ma[111] have reported strain rate sensitivity measurements for nanostructured copper having grain sizes as small as 80 nm and from which measurements of (v*/b 3)−1 = ~0.03 are obtained and may be seen in Figure 26 to be in the range of v*−1 values that are controlled by cross-slip in the grain boundary regions. Note the comparison with the very much larger v* measurements indicated in Figure 15 for conventional strain rate tests on copper at ε = 0.15.[52]

Fig. 26
figure 26

An H–P dependence of v* values for copper and nickel[70]

Full size image

Figure 26 includes calculated values of v*−1 corresponding to the reversed H–P flow stress measurements obtained by Lu et al.[84,108] as shown in Figure 22. For these particular results, the softening from the highest H–P peak stress has been attributed to the availability of pre-existing mobile partial dislocations[84] or to easier nucleation of dislocations at the grain boundaries.[112] The reverse, or as commonly designated, ‘inverse’ H–P dependence has been reviewed more generally on a physical mechanism basis by Pande and Cooper.[113] In this regime, the grain boundaries are taken to produce for one reason or another weakening that begins from the peak stress values reached on an H–P basis and occurs over a range of a few tens of nm grain sizes. The weakening is generally accounted for on an analogous constitutive equation basis to that described for grain boundary weakening at higher temperatures.[114] The behavior is described with a general equation of the form[5,115]

$$ \left( {{\text{d}}\varepsilon /{\text{d}}t} \right) = \left( {AD_{\text{L}} Gb/k_{\text{B}} T} \right)\left( {b/\ell } \right)^{p} \left( {\sigma /G} \right)^{q} . $$
(21)

In Eq. [21], A, p, and q are experimental constants and D L is a diffusivity for mass transport. The indicated v*−1 in Figure 26 for grain boundary weakening was obtained from Eq. [19] by employing Eq. [1] with assumption of p = q = 1.0. Very importantly, larger v*−1 are to be expected for viscous-like displacements associated with deformation mechanisms within a grain boundary. Similar values of v*−1 and a reversed dependence on grain size had been computed[116] for nanopolycrystal zinc material from results reported by Conrad and Narayan.[117] Most recently, Song and Lu have provided atomic simulation results of the reverse grain size dependence exhibited by magnesium material when tested at temperatures of 10 and 300 K (−263 and 27 °C).[118] Such weakening was shown to occur for material with a modeled GPa peak strength level at a grain size of ~25 nm and proceeding downward.

6 Summary

A number of topics associated with the strain rate dependence of plastic deformation in metals have been reviewed in connection with research activities undertaken also by Professor Marc Meyers with colleagues and students. The general observation of greater plastic strength levels being exhibited at higher loading rates in conventional tests is attributed to the requirement of stress-assisted enhancement of thermal activation for either dislocation movements or dislocation generations or their combination. The dislocation activation volume parameter, v* = A*b, is shown to be a key element in characterizing such high-rate deformation behavior. Larger scale inhomogeneous plastic flow, such as occurs in Lueders-type yielding mainly of bcc metals or more broadly in adiabatic shear banding of bcc and hcp metals, is associated with the build-up and collapse of dislocation pile-ups and/or the occurrence of deformation twinning. The inverse relationship between v* and the thermal component of shear stress, τ Th, carries over to the characterization of shock-induced plasticity measurements. Comparable plastic strain rates imposed in shock-less ICEs require even higher stresses because of the different consideration of drag resistance experienced by the initially present mobile dislocation density. The plastic flow stress and reciprocal activation volume, v*−1, dependencies follow a Hall–Petch dependence that is predictably magnified at smaller nanopolycrystal grain sizes until reversal or changeover, respectively, at an effectively smaller limiting tens of nanometers scale.