Effect of Tungsten on Primary Creep Deformation and Minimum Creep Rate of Reduced Activation Ferritic-Martensitic Steel

Abstract

Effect of tungsten on transient creep deformation and minimum creep rate of reduced activation ferritic-martensitic (RAFM) steel has been assessed. Tungsten content in the 9Cr-RAFM steel has been varied between 1 and 2 wt pct, and creep tests were carried out over the stress range of 180 and 260 MPa at 823 K (550 °C). The tempered martensitic steel exhibited primary creep followed by tertiary stage of creep deformation with a minimum in creep deformation rate. The primary creep behavior has been assessed based on the Garofalo relationship, $\varepsilon = \varepsilon_{\text{o}} + \varepsilon_{\text{T}} [1-\exp (-r^{\prime} \cdot t)] + \dot{\varepsilon }_{\text{m}} \cdot t$, considering minimum creep rate $\dot{\varepsilon }_{\text{m}}$ instead of steady-state creep rate $\dot{\varepsilon }_{\text{s}}$. The relationships between (i) rate of exhaustion of transient creep r′ with minimum creep rate, (ii) rate of exhaustion of transient creep r′ with time to reach minimum creep rate, and (iii) initial creep rate $\dot{\varepsilon }_{\text{i}}$ with minimum creep rate revealed that the first-order reaction-rate theory has prevailed throughout the transient region of the RAFM steel having different tungsten contents. The rate of exhaustion of transient creep r′ and minimum creep rate $\dot{\varepsilon }_{\text{m}}$ decreased, whereas the transient strain ɛ _T increased with increase in tungsten content. A master transient creep curve of the steels has been developed considering the variation of $\frac{{\left( {\varepsilon - \varepsilon_{\text{o}} } \right)}}{{\varepsilon_{\text{T}} }}$ with $\frac{{\dot{\varepsilon }_{\text{m}} \cdot t}}{{\varepsilon_{\text{T}} }}$. The effect of tungsten on the variation of minimum creep rate with applied stress has been rationalized by invoking the back-stress concept.

1 Introduction

Creep resistant ferritic-martensitic steels have been developed and used successfully for the applications in different sectors like fossil-fired power plants, petrochemical industries, and steam generators of fast nuclear reactors. These ferritic-martensitic steels are now under consideration for clad and wrapper applications in the core of fast fission reactor and for blanket module (TBM) in fusion reactor.[1] For TBM application, the chemical composition of conventional grade 91 steel (9Cr-1Mo-0.06Nb-0.2V-0.05N) has been modified with the substitution of elements producing high residual radioactive elements in a fusion reaction environment with the elements having low radioactivity such as Mo by W and Nb by Ta. Strict controls over long half-life residual radioactive and embrittling elements have been exercised to facilitate easy handling and disposal of blanket module at the end of service life.[2–4] These steels containing 9 to 12 wt pct chromium, tungsten, and tantalum are commonly classified as the reduced activation ferritic-martensitic (RAFM) steels.[5–9] These steels have tempered martensitic structure and gain their strength from the presence of phase transformation-induced high dislocation density, dispersion of intragranular fine MX type of precipitates, and M₂₃C₆ precipitates arranged in the lath and grain boundaries. Such complex microstructure resists recovery during creep deformation and exerts high creep deformation resistance and creep rupture strength to the RAFM steel.[10]

Design of nuclear reactor components including TBM of fusion reactor is based on accumulation of creep strain over the stipulated time period. The creep curve is described into three distinct regions namely primary, secondary, and tertiary stages. Recovery, recrystallization, and strain-hardening characteristics affect the creep behavior. Alloying the steel significantly affects these factors which in turn govern the creep curve. The mechanisms of strain-hardening and recovery prevail in all the regions of creep deformation except the dominance of one over the other in each region. In many cases, the resistance to recovery and strain hardening cannot be separated since recovery and strain hardening can occur simultaneously. Once a dislocation distribution is established by strain hardening, recovery tends to change the dislocation distribution through rearrangements into a stable structure. So the role of interaction between solute atom, precipitates, and dislocation is to resist the rearrangement of dislocation structure and, hence, the recovery.

Bailey–Orowan equation relating the steady-state creep rate with recovery rate r (=δσ/δt) and strain-hardening rate h (=δσ/δε) is expressed as

$$ \dot{\varepsilon }_{\text{s}} = \frac{r}{h}. $$

(1)

From the experimental measurements of recovery rate r and strain-hardening rate h, Sidey and Wilshire[11] concluded that in precipitation-strengthened creep-resistant alloys, steady-state creep rate is mainly governed by recovery rate.

The primary regime creep deformation of materials especially at higher temperatures (T/T _m > 0.4, T _m melting point in Kelvin) has been represented by empirical relationship proposed by Garofalo[12] as

$$ \varepsilon = \varepsilon_{\text{o}} + \varepsilon_{\text{T}} \left[ {1 - \exp ( - r^{\prime}.t)} \right] + \dot{\varepsilon }_{\text{s}} .t, $$

(2)

where ɛ _o is the instantaneous strain on loading, ɛ _T is the transient creep strain, r′ is the rate of exhaustion of transient creep, and $\dot{\varepsilon }_{\text{s}}$ is the steady-state creep rate. The gap between the quantitative assessment of creep curve and the physical understanding of rate controlling mechanisms has been attempted to close by Webster et al.[13] by invoking the concept of first-order reaction-rate kinetics during creep deformation as $\frac{{{\text{d}}\dot{\varepsilon }}}{{{\text{d}}t}} = \frac{{ - (\dot{\varepsilon } - \dot{\varepsilon }_{\text{s}} )}}{\tau }$, where τ is the relaxation time for rearrangement of dislocation into stable configuration, and the $\frac{1}{\tau } = r^{\prime}$ has the same dependence on stress and temperature as in $\dot{\varepsilon }_{\text{s}}$ ($\frac{1}{\tau } = r^{\prime} = K \cdot \dot{\varepsilon }_{\text{s}}$, K = constant). Integration twice of the above first-order rate equation for creep deformation has led to the Garofalo Eq. [2]. On differentiating Garofalo Eq. [2] and at t = 0, one can obtain the relation between the initial creep rate $\dot{\varepsilon }_{\text{i}}$ and the steady-state creep rate $\dot{\varepsilon }_{\text{s}}$ as $\dot{\varepsilon }_{\text{i}}$ = ($\dot{\varepsilon }_{\text{s}}$ + r′·ε _T). Another important relationship for consideration is that between the initial creep rate $\dot{\varepsilon }_{\text{i}}$ and the steady-state creep rate $\dot{\varepsilon }_{\text{s}}$ as $\dot{\varepsilon }_{\text{i}} = \beta \cdot \dot{\varepsilon }_{\text{s}}$, where β is a constant. These lead to the concept of universal creep curve of the form

$$ \varepsilon - \varepsilon_{\text{o}} = \frac{{\left( {\beta - 1} \right)}}{K}\left[ {1 - \exp ( - K\cdot \dot{\varepsilon }_{\text{s}} \cdot t)} \right] + \dot{\varepsilon }_{\text{s}} \cdot t , $$

(3)

where $\frac{{\left( {\beta - 1} \right)}}{K} = \varepsilon_{\text{T}}$ is constant since both β and K are constants. For such materials having constant ɛ _T, a single master curve is expected for the plot between (ε−ε _o) and $\dot{\varepsilon }_{\text{s}}$. The constancy of ɛ _T has been reported for many materials,[13] and Eq. [3] could generate the master curve for the prediction of creep strain at a particular stress, temperature, and time.

For many materials[11–14] including tempered martensitic steel,[15] the constancy of ɛ _T has not been obtained. To deal with such situation involving first-order kinetics, Phaniraj et al.[16] has introduced an alternate equation for constructing master creep curve for such materials. The equation is arrived in the following way.

From Eq. [2], it can be understood that transient creep ends when $\varepsilon_{\text{T}} \left[ {1 - \exp ( - r^{\prime}\cdot t)} \right]$ becomes equal to ɛ _T. It has been observed that for many materials, the rate of exhaustion of transient creep r′ can be correlated with time to onset of secondary i.e., t _os in the form r′·t _os = constant.[11,14,16] Substituting r′ from relations r′·t _os = constant in the relation $r^{\prime} = K \cdot \dot{\varepsilon }_{\text{s}}$ leads to $\dot{\varepsilon }_{\text{s}} \cdot t_{\text{os}}$ = $\frac{\text{constant}}{K}$. Since {$\varepsilon_{\text{T}} = \frac{{\left( {\beta - 1} \right)}}{K}$} as described earlier, $\dot{\varepsilon }_{\text{s}} \cdot t_{\text{os}}$ = $\frac{{{\text{constant }} . { }\varepsilon_{\text{T}} }}{{\left( {\beta - 1} \right)}}$. On rearranging this leads to

$$ \frac{{\dot{\varepsilon }_{\text{s}} \cdot t_{\text{os}} }}{{ \, \varepsilon_{\text{T}} }} = \frac{\text{constant }}{{\left( {\beta - 1} \right)}} = {\text{ constant}}. $$

(4)

Based on this, Eq. [2] in terms of a parameter P = $\frac{{\left( {\dot{\varepsilon }_{\text{s}} \cdot t_{\text{os}} } \right)}}{{\varepsilon_{\text{T}} }}$ ≥ 0 is rewritten as

$$ \varepsilon - \varepsilon_{\text{o}} = \varepsilon_{\text{T}} [ 1 { }{-}{ \exp }\{ - P \, (\beta - { 1})\} \, + \, P] . $$

(5)

An important implication of Eq. [5] is that when ε _T varies with stress for condition obeying first-order kinetic, plot of (ε − ε _o)/ε _T with respect to P would result in a master curve only if β is constant.

In tempered martensitic steels, many investigators have reported the absence of secondary stage of creep deformation.[17,18] The primary stage leads to the tertiary stage of creep deformation with a minimum in the variation of creep deformation rate with creep strain or creep exposure. In such steels, the t _os in Eq. [4] can be replaced by t _m, time to reach minimum creep rate and $\dot{\varepsilon }_{\text{s}}$ as $\dot{\varepsilon }_{\text{m}}$, minimum creep rate.

In this investigation, the transient and minimum creep rate behavior for three heats of RAFM steel having different tungsten contents have been investigated, and attempt has been made to construct a master curve for the transient creep deformation. The effect of tungsten in the variation of minimum creep rate with applied stress has been assessed considering the back-stress concept.

2 Experimental Procedure

Three heats of 9-CrWVTa RAFM steel with different contents of tungsten in the range 1 to 2 wt pct were procured. Chemical compositions of the steels are given in Table I. The steels are designated as 9Cr-1W, 9Cr-1.4W, and 9Cr-2W according to their tungsten content. The steels were produced by the selection of proper raw materials and employing vacuum induction melting and vacuum arc refining routes with stringent control over the thermo-mechanical processing parameters during forging, rolling, and heat treatments. The final heat treatment given to the material was normalization at 1253  K (980 °C) for 30 minutes and tempering at 1033  K (760 °C) for 90 minutes.

Table I Chemical Composition (Weight Percent) of the Three Heats of RAFM Steels

Constant load creep tests were carried out on the steels in air at 823 K (550 °C) over a stress range of 180 to 260 MPa. Cylindrical creep specimens of 5 mm diameter and 50 mm gage length were used. The temperature across gage length of the specimen was maintained within ±2  K (±2 °C) during the creep tests. The creep elongation was recorded continuously by an extensometer with digimatic dial indicator and data logger system.

3 Results

Typical effects of tungsten on creep strain accumulation and creep rate with creep exposure are shown in Figures 1(a) and (b), respectively. The creep deformation of the steels showed the characteristic behavior of ferritic-martensitic steels[17,18] with (i) a small instantaneous strain on loading, (ii) decrease of creep rate to a minimum value instead of steady state as in the case of austenitic stainless steels, and (iii) extended tertiary stage of creep deformation. The variation of minimum creep rate with applied stress (Figure 2) for the steels displayed power law relationship as $\dot{\varepsilon }_{\text{m}}$ = A·σ ⁿ. Minimum creep rate decreased significantly with increase in tungsten content as shown in Figure 2.

Fig. 1

Effect of tungsten in variations in (a) creep strain and (b) creep strain rate of the RAFM steels with creep exposure

Fig. 2

Variation of minimum creep rate of the steel with applied stress of the RAFM steels, tested at 823 K (550 °C)

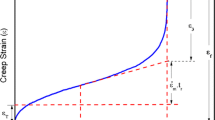
The primary creep curve has been analysed in the frame work of Garofalo Eq. [2]. The primary creep is considered to have contribution from transient creep and minimum creep deformation, which are shown schematically in Figure 3. The transient creep parameters r′ rate of exhaustion of transient creep and ε _T transient creep strain are evaluated from experimental creep curves of the steels. The r′ value was evaluated graphically as the slope of ln(1−Δ/ε _T) vs t plots, where Δ is the transient creep component (Δ = ε − ε _o − $\dot{\varepsilon }_{\text{m}} \cdot t$), become 0 at t = 0 and approaches to ε _T at t = t _m, i.e., the time to reach minimum creep rate. The stress dependence of r′ display power law relationship (r′ = K$\cdot \dot{\varepsilon }_{\text{m}}$) with applied stress (Figure 4). The r′ value decreases, whereas the stress index increases with increase in tungsten content. The variation of r′ with stress has also been observed for 70 to 30 α-brass[14] with a power of 3.5 at higher temperature. For Ni-20 wt pct Cr alloy, r α σ ^4.8 and for Nimonic 80A, r′ α σ ^6.4 have been reported.[11]

Fig. 3

Schematic illustration of analysis of transient creep behavior of the steels

Fig. 4

Variation of rate of exhaustion of transient creep r′ with applied stress of the RAFM steels, creep tested at 823 K (550 °C)

From Eq. [2], the transient stage ends after time t _m i.e., time to reach minimum creep rate such that the contribution from the transient term [r′·ε _T·exp(−r′·t _m)] becomes negligible compared to that from $\dot{\varepsilon }_{\text{m}}$. The variations of r′ with t _m of the steels are shown in Figure 5 in log–log scale. The variation follows as

$$ r^{\prime} \cdot t_{\text{m}}^{ 1.0 1} = {\text{ constant }}( \simeq6.3), $$

(6)

and is independent of tungsten constant of the RAFM steels. Similar observation with a constant value of ~4 was observed for different materials viz copper, α-iron, zinc, 70 to 30 α-brass,[19] Ni-20 wt pct Cr alloy, and Nimonic 80A.[11]

Fig. 5

Variation of rate of exhaustion of transient creep r′ with time to reach minimum creep rate of the RAFM steels, creep tested at 823 K (550 °C)

The relationships between the rate of exhaustion of transient creep r′ and the minimum creep rate $\dot{\varepsilon }_{\text{m}}$ of the steels are illustrated in Figure 6 in log–log scale. The relationship follows a power law as

$$ r^{\prime} \cdot \dot{\varepsilon }_{\text{m}}^{ - 1.02} = {\text{ constant }}( \simeq638) $$

(7)

and independent of tungsten constant of the RAFM steels with K in the relationship 1/τ = r′ = $K \cdot \dot{\varepsilon }_{\text{m}}$ as 638. This relationship has been studied for a wide range of metals and alloys like iron, nickel, zinc, austenitic iron base alloy, type 316 stainless steel, Nimonic 80A, and Ni-20 wt pct Cr alloy.[11,13] The proportionality constant varies with the material and with the stress regime.

Fig. 6

Variation of rate of exhaustion of transient creep r′ with minimum creep rate of the RAFM steels, creep tested at 823 K (550 °C)

The initial creep rate $\dot{\varepsilon }_{\text{i}}$ is given by (r′·ε _T + $\dot{\varepsilon }_{\text{m}}$). Figure 7 shows the logarithmic plot of initial creep rate $\dot{\varepsilon }_{\text{i}}$ and the minimum creep rate $\dot{\varepsilon }_{\text{m}}$. The relation follows a power law as

$$ \dot{\varepsilon }_{\text{i}} \cdot \dot{\varepsilon }_{\text{m}}^{ - 0.9} = {\text{ constant }}( \simeq1.9) $$

(8)

and independent of tungsten constant of the RAFM steels, with constant of proportionality β in equation $\dot{\varepsilon }_{\text{i}} = \beta \cdot \dot{\varepsilon }_{\text{m}}$ is around 1.9. The relation $\dot{\varepsilon }_{\text{i}} = \beta \cdot \dot{\varepsilon }_{\text{m}}$ has been found valid for a wide range of materials viz iron, nickel, zinc, austenitic iron base alloy, type 316 stainless steel, AISI 304 stainless steel, Al, Ag, Cu, Pt, Mo, W, 9Cr-1Mo ferritic steel, etc.[15,16,19–21]

Fig. 7

Variation of initial creep rate with minimum creep rate of the RAFM steels, creep tested at 823 K (550 °C)

Transient strain ε _T was evaluated for all the steels from the creep curves and plotted in Figure 8 against applied stress in log–log scale. The transient creep strain of the steels had tendency of constant values at lower applied stresses and subsequently decreased with increasing stress, and was high for steel with higher tungsten content. However, in literature for pure metals and simple alloys, the strain values were observed to be constant.[13,20,21] Few exceptional results in case of 70–30 α-brass[14] and Ni-20 wt pct Cr alloy[11] were observed in which transient strain value decreases with decreasing stress. In the case of 9Cr-1Mo ferritic steel,[15] the variation observed is similar to the present work. The variation in transient strain with respect to tungsten content could be understood when the role of effective stress instead of applied stress is considered. The role of effective stress is described in the later part of the manuscript.

Fig. 8

Variation of transient creep strain with applied stress of the RAFM steels, creep tested at 823 K (550 °C)

4 Discussion

4.1 Transient Creep Behavior

The steady-state creep rate $\dot{\varepsilon }_{\text{s}}$ or the minimum creep rate $\dot{\varepsilon }_{\text{m}}$ as expressed by Bailey–Orowan equation [1] is directly proportional to rate of recovery and inversely proportional to rate of hardening. From their detailed study on recovery, hardening and transient creep behavior of Nimonic 80A superalloy, Sidey and Wilshire[11] have concluded that the creep rate is controlled by rate of recovery, and the rate of exhaustion of transient creep (r′) in the Garofalo equation [2] has direct relationship with rate of recovery. In this investigation, the rate of exhaustion of transient creep (r′) of the RAFM steels decreased with increase in tungsten content (Figure 4) over the stress range studied. The strain-hardening behavior of the RAFM steels having different tungsten contents under tensile deformation is shown in Figure 9. The work-hardening behavior of the RAFM steel is found not to depend appreciably on the tungsten content. In 9Cr steel, Park et al.[22] have investigated the effect of tungsten (0 to 2.7 wt pct) on strain-hardening exponent in monotonic tensile test and cyclic stress–strain curve. They have observed insignificant variation of the strain-hardening exponent in monotonic tensile test which varies in the range of 0.042 to 0.059, and in cyclic stress–strain curve, it varies in the range of 0.059 to 0.070 at 873  K (600 °C). It is expected that under creep condition also the strain-hardening behavior is not dependent on the tungsten content appreciably. The near-linear relationship between rate of exhaustion of transient creep r′ and minimum creep rate $\dot{\varepsilon }_{\text{m}}$ (Figure 6) clearly establishes that recovery is the dominant process governing the creep deformation of the RAFM steels. The increase in tungsten content reduces the rate of exhaustion of transient creep r′ (Figure 4), and hence the recovery rate to decrease the minimum creep rate (Figure 2).

Fig. 9

Variation of work-hardening rate with true stress of the RAFM steels from tensile test results at 773  K (500 °C)

The complex microstructure of the ferritic-martensitic RAFM steel resists the recovery rate to decrease the creep deformation rate. The ferritic-martensitic RAFM steels derive creep strength from the complex microstructure consisting of (i) phase transformation-induced high dislocation density and dislocation cell, (ii) martensitic lath/subgrain with boundaries decorated with chromium- and tungsten-rich M₂₃C₆ type of carbide, and (iii) very fine intragranular V-Ta carbonitride precipitates of the MX type.[17,23] SEM micrographs of the as-received normalized and tempered RAFM steels are shown in Figure 10. Microstructural evolution during creep deformation in ferritic-martensitic steels has been studied extensively by many investigators.[17,24,25] The M₂₃C₆ type of carbides on subgrain boundaries plays an important role in stabilizing the dislocation substructure to increase creep deformation resistance. Effect of tungsten on the stability of the M₂₃C₆ and dislocation substructure has been studied by Abe.[26] The refinement of martensitic lath size and the sluggish coarsening of the lath with creep exposure in 9Cr-steel with increase in tungsten content have been reported by Abe[17] and Hong et al[27] Tungsten dissolves in chromium-rich M₂₃C₆ carbides and reduces the coarsening kinetics due to retardation of iron self-diffusion in the presence of tungsten.[28] Fine and high density of the M₂₃C₆ carbides for higher tungsten ferritic-martensitic steels[10,17] are more effective in stabilizing the martensitic substructure during creep exposure and delay the onset of microstructural instability to longer creep exposure. The increase in creep rupture strength of grade 92 steel having 1.8 wt pct tungsten over grade 91 steel is understood as higher resistance of grade 92 steel to recovery in the presence of tungsten.[29] Sluggish microstructural recovery in the RAFM steel having higher tungsten content is reflected into the recovery-related parameter of rate of exhaustion of transient creep r′ (Figure 4), and thus decrease the creep rate (Figure 2).

Fig. 10

SEM micrographs of the normalised and tempered steels showing the tempered martensitic structure (a) 9Cr-1W-0.06Ta, (b) 9Cr-1.4W-0.06Ta, and (c) 9Cr-2W-0.06Ta

The variations of (i) rate of exhaustion of transient creep r′ with minimum creep $\dot{\varepsilon }_{\text{m}}$ and time to reach minimum creep rate t _m and (ii) initial creep rate $\dot{\varepsilon }_{\text{i}}$ with minimum creep rate $\dot{\varepsilon }_{\text{m}}$ of the RAFM steels are displayed by Eqs. [6] through [8], respectively. These relationships have been derived based on the concept that the transient creep deformation obeys first-order kinetics. Near-linear dependencies of the parameters relating the transient creep deformation and minimum creep rate behavior, which are independent of steels concerned, proved quite conclusively that the creep deformation of the microstructurally complex-tempered martensitic RAFM steel is governed by the first-order kinetics of dislocation annihilation and multiplication. Physical understanding of Garofalo equation [2] has been provided by Webster et al.[13] considering details of dislocation multiplication and annihilation.

Implication of applicability of first-order kinetics to transient creep behavior in the complex RAFM steel is that Eq. [3] can be adopted to construct transient master creep curve when plotted between (ε − ε _o) and $\dot{\varepsilon }_{\text{m}} \cdot t$. Figure 11 shows such plot of the RAFM steels, depicting that unique master curve could not be achieved. Derivation of Eq. [3] is based on the assumption that the transient strain ε _T = ((β − 1)/K) is constant. On the contrary, in this investigation, the strain ε _T varies with applied stress and is also different for different RAFM steels (Figure 8). The failure to achieve a unique creep curve might be due to non-constancy of ε _T. The approach suggested by Phaniraj et al.[16] has been adopted to construct master curve for transient creep of the RAFM steel based on Eq. [5]. Figure 12 illustrates the plot between (ε − ε _o)/ε _T and $\dot{\varepsilon }_{\text{m}} \cdot t$/ε _T derived from Eq. [5] for all the three steels showing single master curve. Slight scattering in master curve is observed in the initial part. The scattering is mainly caused by relatively short-term test (9Cr-1W, 260 MPa, t _r = 26 hours) and long-term test (9Cr-1W, 180 MPa and 9Cr-2W, 200 Mpa) which might be resulted from microstructural changes. Such deviation was also observed more evidently in ferritic and austenitic steels when creep test was carried out in two different stress regimes.[15,16]

Fig. 11

Plot of (ε − ε _o) vs έ_s·t for RAFM steels at 823 K (550 °C)

Fig. 12

Single master creep curve according to Eq. [5] for all the three steels at 823 K (550 °C)

4.2 Minimum Creep Rate Behavior

The stress dependence of the minimum creep rate is described by a power law as

$$ \dot{\varepsilon }_{\text{m}} = \, AD\mu b/\left( {kT} \right) \, (\sigma_{\text{a}} /\mu )^{\text{n}} , $$

(9)

where D = D _o exp (−Q _c/RT), where D is the self-diffusion coefficient, D _o is the frequency factor, Q _c is the activation energy for creep deformation, R is the gas constant (8.314 J mol⁻¹ K⁻¹), T is the temperature in Kelvin, µ is the shear modulus, b is the Burgers vector, k is a Boltzmann’s constant, n is the stress exponent, and A is a dimensionless constant. The value of n is an index of creep deformation mechanism. The value of stress exponent in the range of 4 to 5 has been observed at low stress but increases above 8 at high stress. Figure 2 shows the double logarithmic plot of minimum creep rate vs stress. The stress exponent n varies as 19 for 9Cr-1W and 9Cr-1.4W steels and 23 for 9Cr-2W steel. Such higher values of stress exponent have also been reported for other ferritic-martensitic steels[18,30,31] and have been attributed to complex alloy structure.

Many attempts have been made to clarify such high-stress exponents based on the concept that creep deformation occurs not under the fully applied stress but under the effective stress. It has been proposed that the creep deformation of precipitation hardened alloys can be rationalized by conventional dislocation creep theories by expressing creep rate in terms of the effective stress i.e., difference of the applied stress and the resisting stress σ _R, (σ _a − σ _R), instead of applied stress alone, where the resisting stress is associated with the operating particle-by-pass mechanism of dislocation.[32] The total resisting stress has been expressed as a superposition of individual contributions from dislocations, precipitates, and the contribution from subgrain boundaries.

On this basis, the dependence of creep rate with stress and temperature takes the form of

$$ \dot{\varepsilon }_{\text{m}} = \, A_{\text{o}} D\mu b/\left( {kT} \right) \, [(\sigma_{\text{a}} - \sigma_{\text{R}} )/\mu ]^{\text{p}} , $$

(10)

with p having a constant value of around four over the entire stress and temperature regime, where dislocation creep is the rate controlling creep deformation mechanism. This approach has been widely applied to study the creep deformation behavior of particle-hardened materials. However, in view of the experimental difficulties for evaluation of σ _R values, Lagneborg and Bergman[33] proposed a graphical method to estimate the resisting stress σ _R by plotting ($\dot{\varepsilon }_{\text{m}}$ kT/Dµb)^1/4 against applied stress σ _a. The resisting stress σ _R was obtained as the stress intercept by extrapolating the plotted straight line to zero-creep rate. A plot of ($\dot{\varepsilon }_{\text{m}}$ kT/Dµb)^1/4 against σ _a/µ has been shown in Figure 13, where the reported values of D, µ, and b of α-iron[34] were used. The σ _R values were determined from the plot as the stress intercepts at $\dot{\varepsilon }_{\text{m}}$ = 0 and found to be 167, 178, and 198 MPa at 823 K (550 °C), respectively, for 9Cr-1W, 9Cr-1.4W, and 9Cr-2W steels. The values of resisting stress were used to calculate the effective stress. The rationalization of $\dot{\varepsilon }_{\text{m}}$ in terms of effective stress for all the steels is shown in Figure 14 revealing a single slope. Similarly, the role of effective stress in governing the transient creep strain behavior of all the tungsten varying steels is revealed from the convergence of transient creep strain of the steels when plotted against effective stress (Figures 8 and 15). The above observation suggests that tungsten addition increases the resisting stress by enriching the microstructure. Abe et al.[17] have reported that with increase in tungsten content, stability of M₂₃C₆ carbides increases and inhibits its coarsening. This in turn restricts the lath and subgrain width coarsening, and hence stabilizes the martensitic structure resistant to recovery. The improvement in creep rupture strength of RAFM steels is understood as the increase in resistance to recovery with increasing tungsten content.

Fig. 13

The variation of (έ _m KT/Dµb)^1/4 with σ _a/µ for RAFM steels on linear scale to determine resisting stress following method suggested by Lagneborg and Bergman

Fig. 14

A plot of diffusivity compensated creep rate vs normalized effective stress on log scale of the steels creep tested at 823 K (550 °C)

Fig. 15

Variation of transient creep strain with effective stress of the RAFM steels, creep tested at 823 K (550 °C)

5 Conclusions

Based on the study of effect of tungsten on primary creep regime of RAFM steels having different tungsten contents, the following conclusions have been drawn:

• 1. The transient creep behavior of RAFM steels having varying tungsten content at 823 K (550 °C) obeys first-order reaction-rate theory.

• 2. Increase in tungsten content in the RAFM steels reduce the recovery rate leading to decrease in minimum creep rate $\dot{\varepsilon }_{\text{m}}$ and increase in transient strain ε _T.

• 3. Transient master creep curve of all the steels has been established from the plot between (ε − ε _o)/ε _T and $\dot{\varepsilon }_{\text{m}} \cdot t$/ε _T.

• 4. The stress dependency of minimum creep rate of all the tungsten varying steels has been rationalized on invoking the concept of resisting stress.