Model for Strain-Induced Precipitation Kinetics in Microalloyed Steels

Abstract

Based on Dutta and Sellars’s expression for the start of strain-induced precipitation in microalloyed steels, a new model has been constructed which takes into account the influence of variables such as microalloying element percentages, strain, temperature, strain rate, and grain size. Although the equation given by these authors reproduces the typical “C” shape of the precipitation start time (P _s) curve well, the expression is not reliable for all cases. Recrystallization–precipitation–time–temperature diagrams have been plotted thanks to a new experimental study carried out by means of hot torsion tests on approximately twenty microalloyed steels with different Nb, V, and Ti contents. Mathematical analysis of the results recommends the modification of some parameters such as the supersaturation ratio (K _s) and constant B, which is no longer a constant, but a function of K _s when the latter is calculated at the nose temperature (T _N) of the P _s curve. The value of parameter B is deduced from the minimum point or nose of the P _s curve, where ∂t _0.05/∂T is equal to zero, and it can be demonstrated that B cannot be a constant. The new expressions for these parameters are derived from the latest studies undertaken by the authors and this work represents an attempt to improve the model. The expressions are now more consistent and predict the precipitation–time–temperature curves with remarkable accuracy. The model for strain-induced precipitation kinetics is completed by means of Avrami’s equation.

1 Introduction

When strain-induced precipitation starts in microalloyed steels, static recrystallization is inhibited for a certain time, normally until the end of precipitation, before proceeding until recrystallization is complete. It is well known that the static recrystallization of microalloyed steels is different before and after strain-induced precipitation. Before the precipitation, all the elements are in solution and recrystallization kinetics occurs in the same way as in low alloy steels, whereby the various alloying elements contribute to delaying recrystallization to a greater or lesser degree.[1–3] As the temperature drops, a critical temperature is reached, after which static recrystallization is momentarily inhibited by the effect of strain-induced precipitates. This momentary inhibition of recrystallization appears as a plateau on the recrystallized fraction vs time curves.[4] When the end of the plateau is reached, recrystallization recommences as the coarsening of precipitates consequently reduces the pinning forces against driving forces. After the plateau, the superiority of driving forces for recrystallization over pinning forces is about two orders of magnitude.[5] Good definition of the plateau allows the plotting of recrystallization–precipitation–time–temperature (RPTT) diagrams.[6]

The most important reference to predict strain-induced precipitation nucleation as a function of hot deformation variables (strain, strain rate, and temperature) is perhaps the expression given by Dutta and Sellars[7] for a time corresponding to 5 pct of the precipitated volume t _0.05, which in practical terms can be taken as the nucleation time for precipitation. These authors state that the density of preferential nucleation sites in deformed austenite is expected to be sensitive to the density and arrangement of dislocations and therefore to the conditions of the prior deformation expressed in terms of the aforementioned variables. Dutta and Sellars’s model was applied to Nb-microalloyed steels and takes into account the Nb content, strain, strain rate, and temperature, and its expression is as follows:

$$ t_{0.05} = A({\text{Nb}})^{ - 1} \varepsilon^{ - 1} Z^{ - 0.5} \exp \left( {\frac{270,000}{\text{RT}}} \right)\exp \left[ {\frac{B}{{T^{3} \left( {\ln k_{\text{s}} } \right)^{2} }}} \right]. $$

(1)

In the present work, a precipitation model based on the above is proposed, taking into account the influence of variables such as microalloying element percentages, strain, temperature, strain rate, and grain size, and new parameters and relationships are established. Several years ago, Medina et al.[8] published a model which was a preliminary approach to that described herewith. New adjustments have been made and in particular the influence of the temperature has been reassessed thanks to the performance of new calculations based on experimental results and new thermodynamic considerations.

Given the complexity of the model’s construction, it has been partly published in various papers, each of which has discussed the influence of one of the many variables that intervene in strain-induced precipitation kinetics. Previous publications have considered variables such as the strain,[9] strain rate,[10] and austenite grain size[11] and their influence on the nucleation time for precipitation. The influence of the temperature, the single most important parameter, has been reserved for the present paper. Therefore, although the model will be presented in its entirety, the quantitative influence of the aforementioned variables will simply be summarized, and only in the case of the temperature will the expression found be developed in greater detail.

2 Materials and Experimental Procedure

Nineteen steels were manufactured by Electroslag Remelting (ESR) in a laboratory unit capable of producing 30-kg ingots. The steels contained various combinations of carbon, nitrogen, and precipitate-forming elements such as V, Nb, and Ti. Their compositions are listed in Table I. Given that niobium nitrides, carbides, and carbonitrides are less soluble in austenite than those of vanadium, the limit imposed on carbon and nitrogen contents was that the solubility temperature should not exceed 1573 K (1300 °C). In this sense, some compositions, such as steel N9, with a very low niobium content and high carbon content, are not currently standard compositions, but the interest in studying them lies in ascertaining the influence of low niobium contents on recrystallization.

Table I Chemical Composition (Mass Pct), Transformation Critical Temperature (A _r3, at 0.2 K/s), and Austenite Grain Size (D _γ ) at Reheating Temperature (R.T.), with X _i = V, Nb, Ti pct

Torsions specimens were prepared with a gage length of 50 mm and a diameter of 6 mm. The reheating temperature before torsion deformation varied according to whether the steel was microalloyed with V or Nb, as the solubility temperature of the precipitates depends on their nature and on the precipitate-forming element content.

The parameters of torsion (torque, number of revolutions) and the equivalent parameters of tension (stress, strain) were related according to the Von Mises criterion.[12]

For steels containing vanadium, designated by the letter V, the reheating temperature was 1503 K (1230 °C) for steels V1, V2, and V3 and 1473 K (1200 °C) for the rest, which is sufficient to dissolve vanadium nitrides and carbides. In the case of niobium steels, designated by the letter N, the reheating temperature depended on the carbon, niobium, and nitrogen contents, but was always above the solubility temperature of niobium carbonitrides.[13] To insure that the testing temperatures corresponded to the austenitic phase, critical transformation temperatures (A _r3) were measured by dilatometry at a cooling rate of 0.2 K/s (Table I). Once the specimens had been reheated, the temperature was rapidly lowered to the testing temperature to prevent precipitation from taking place before the strain was applied.

Three of the steels contained Ti, and it is well known that titanium nitrides do not completely dissolve at the reheating temperatures used.[13,14] The austenite grain size at the reheating temperature was determined by quenching of the specimens applying standard ASTM E-112 (Table II).

Table II Test Conditions: Strain (ε), Strain Rate ($\dot{\varepsilon }$), Reheating Temperature (R.T.), and Austenite Grain Size (D) of Steels Used

The testing temperatures varied between 1373 K and 1073 K (1100 °C and 800 °C) for vanadium steels and between 1423 K and 1123 K (1150 °C and 850 °C) for niobium steels. In all cases, the testing temperatures were set as the recrystallized fraction was determined and the recrystallized fraction curves drawn, so that the curves finally obtained would include curves where strain-induced precipitation had taken place and curves where it had not, as is discussed below.

The recrystallized fraction (X _a) was determined using the “back extrapolation” method.[1,15] The study of precipitates was carried out using transmission electron microscopy (TEM).

3 Model of Strain-Induced Precipitation Kinetics

In order to find the influence of every deformation variable, namely, the strain (ε), strain rate ($\dot{\varepsilon }$, in s⁻¹), austenite grain size (D, in μm), and the temperature (T, in K), a new equation based on Dutta and Sellars’s expression[7] has been proposed:

$$ t_{0.05} = A\varepsilon^{ - \beta } D^{\text{s}} Z^{\text{r}} \exp \left( {\frac{{Q_{\text{diff}} }}{\text{RT}}} \right)\exp \left[ {\frac{B}{{T^{3} \left( {\ln k_{\text{s}} } \right)^{2} }}} \right]. $$

(2)

Equation [2] has been proposed because the results showed that the exponent of the strain (β) is not a constant and is not equal to 1, but is dependent on the chemical composition, particularly on the microalloying element content. It was also seen that the austenite grain size (D) influences the parameter t _0.05. Furthermore, as will be seen below, the determination of the supersaturation ratio parameter (k _s) was not a constant, and the mathematical expression found shows that it depends on the chemical composition of the steel, in particular the microalloying type and content. The use of nineteen steels with different Nb, V, and Ti contents allowed values and expressions to be found for the different parameters in Eq. [2], making it possible to predict with good approximation the experimental values found for t _0.05.

Equation [2] also differs from the equation proposed by Sellars in the exponent r of the Zener–Hollomon parameter $\left( {Z = \dot{\varepsilon }\exp \frac{{Q_{\text{def}} }}{\text{RT}}} \right)$ which will be newly determined. The good approximation of the activation energy (Q _d) to the energy for self-diffusion in Fe _γ indicates that the mechanism which governs the plastic flow of austenite is principally the climb of edge dislocations, which depends in turn on the diffusion of vacancies.[16] The activation energy for the self-diffusion of iron in austenite varied with the presence of solutes, and the value of this variation depends on the atomic fraction of each solute, on its atomic volume, and on its heat sublimation.[17] Therefore, it seems logical to imagine that an increase in Q _d would also raise the value of t _0.05.

On the other hand, a drop in the temperature leads to a rise in the value of the term $\left( {\exp \frac{{Q_{\text{def}} }}{\text{RT}}} \right)$, which in turn causes an increase in t _0.05, as is to be expected, given that decreases in the temperature are accompanied by decreases in the value of the diffusivity coefficient of precipitate-forming elements such as V, Nb, and Ti.[18–21]

Another difference to Sellars’s expression is the influence of the microalloying element content, which is not directly reflected in expression [2], since, as will be seen below, the exponent of the strain (β) is not a constant and depends on the percentage of the microalloying element.

As occurs in other physical phenomena, where a nucleation time is necessary for the phenomenon to start, precipitation obeys Avrami’s law and the precipitated fraction can be expressed in the following way[22]:

$$ X_{\text{p}} = 1 - \exp \left[ {\ln 0.95\left( {\frac{t}{{t_{0.05} }}} \right)^{n} } \right], $$

(3)

where n is a constant and t _0.05 is given by Eq. [2].

Equation [3] complies with the limit conditions of Avrami’s equation:

$$ t = 0 \to X_{\text{p}} = 0 $$

$$ t = \infty \to X_{\text{p}} = 1. $$

If in Eq. [3] X _p = 0.95, the following expression is found:

$$ t_{0.95} = \left( {\frac{\ln 0.05}{\ln 0.95}} \right)^{1/n} \quad t_{0.05} = \left( {58.4} \right)^{1/n} t_{0.05} . $$

(4)

Expression [4] can be used to determine the value of n, since the times t _0.05 and t _0.95 are determined experimentally.

4 Experimental Results

4.1 Static Recrystallization Curves

The recrystallized fraction, determined by applying the back extrapolation method, was drawn against time for each testing temperature. The shape of the recrystallized fraction vs time curves was similar for all the V-microalloyed steels, with it being observed that some curves display a plateau caused by the formation of precipitates which momentarily inhibit the progress of recrystallization (Figure 1). The plateau is caused by strain-induced precipitation, as occurs in all microalloyed steels, and the start and end of the plateau are identified approximately with the start and end of strain-induced precipitation, respectively.

Fig. 1

Variation of recrystallized fraction (X _a) with time (t) for steel V4

However, while the start of the plateau seems to coincide with exactness with the start of strain-induced precipitation, the end of the plateau may coincide with important growth in the average size of precipitates, which become incapable of inhibiting recrystallization,[23] or where, despite the fact that the average size has grown, there is still a certain volume of small size precipitates uniformly distributed in the austenite matrix.[24] Though the two definitions may at first sight seem different, in fact they mean practically the same thing.

The curves corresponding to higher temperatures than those mentioned have the sigmoidal shape of Avrami’s law. Furthermore, the plateau is not unlimited, i.e., precipitation does not permanently inhibit recrystallization, and recrystallization again progresses until it is complete, following a graphic plot similar to that recorded before the formation of the plateau.

With regard to the steels containing titanium (TV1, TV2), their behavior was like that of the vanadium steels. Figure 2 shows recrystallized fraction curves for steel TV2, with it being seen that the plateau starts to appear after the curve corresponding to 1173 K (900 °C).

Fig. 2

Variation of recrystallized fraction (X _a) with time (t) for steel TV2

The Nb-microalloyed steels showed varying behavior. Some presented a similar plateau to the V-steels,[25] as in the case of steels N1, N2, N3, N8, and N9, an example of which is shown for steel N3 in Figure 3. However, other steels, such as N4, N5, and N7, presented a double plateau. Figure 4 refers to steel N7 and shows that the double plateau was formed when the deformation temperature was equal to or less than 1223 K (950 °C). This phenomenon is due to the formation of two types of carbonitrides which start to form at practically the same temperature,[6] but the second precipitation is promoted by the first when the nitrogen or carbon content is reduced.

Fig. 3

Variation of recrystallized fraction (X _a) with time (t) for steel N3

Fig. 4

Variation of recrystallized fraction (X _a) with time (t) for steel N7

To date, it has not been possible to establish what the chemical composition of the steel needs to be, with regard to C, N, and Nb contents, in order to exactly predict the occurrence of the second precipitation. Until now, it has only been shown that when the C and N contents are such that the calculated solubility temperatures of Nb nitrides and carbides are similar, then the probability of induced double precipitation occurring is relatively high.[6]

Once the kinetics of the first precipitation (first plateau) ends and recrystallization continues, the second precipitation starts to take place. When this ends, recrystallization continues until it is complete. This means that before and after the plateau, i.e., before and after precipitation, the static recrystallization kinetics (SRX) obeys Avrami’s law.[26–28]

The steel containing niobium and titanium (NT1) displayed the double precipitation found for other niobium steels with similar C and Nb contents.

4.2 RPTT Diagrams

The recrystallized fraction vs time curves were used to plot RPTT diagrams. The points defining the start and the end of the plateau were taken to plot the curves for the start (P _s) and the end (P _f) of precipitation, respectively. On the other hand, the lines corresponding to the different recrystallized fractions were determined by regression of the points resulting from the intersection of the horizontal lines corresponding to different X _a values with the recrystallized fraction curves. In this way, RPTT diagrams were obtained for the two strains of 0.20 and 0.35. The recrystallized fraction does not change between P _s and P _f, and for times in excess of P _f, the slope of the line for any X _a value is lower, which means that recrystallization is more difficult after precipitation.

Figures 5 through 7 are three examples corresponding to steels V4, N7, and N8, respectively. In the case of steel N7, the RPTT diagram shows two P _s curves and two P _f curves as a consequence of the double plateau obtained in the recrystallized fraction vs time curves. With regard to the recrystallization–precipitation interaction, it is seen that at the nose of the P _s curve, where the incubation time of the precipitates (t _N) is minimal, the recrystallized volume fraction is approximately 50 pct. When the recrystallized volume fraction (X _a) is less than 20 pct, the nucleation of the precipitates is very difficult, even though the dislocation density increases with the decrease in X _a. This is due to the drop in diffusivity with the temperature of the precipitate-forming substitutional elements (V, Nb).

Fig. 5

RPTT diagram for steel V5

Fig. 6

RPTT diagram for steel N7

Fig. 7

RPTT diagram for steel N8

The most important magnitudes that can be deduced from an RPTT diagram, and which are also indispensable for the perfect configuration of the diagram, are the aforementioned minimum incubation time (t _N), minimum precipitation end time ($t_{N}^{\prime}$), curve nose temperature (T _N), and finally the precipitation duration time ($t_{N}^{\prime} - t_{N}$) (Table III).

Table III Solubility Temperature (T _s) According to Turkdogan,[13] Experimental and Predicted Nose Temperature (T _N), Minimum Incubation Time t _N, and Minimum Time of the End of Precipitation $t_{N}^{\prime}$ for V-Steels. $\dot{\varepsilon }$ = 3.63/s

At the moment when precipitation starts, whatever the temperature (P _s curve), it is assumed that the precipitated fraction corresponds to a value of 5 pct. In the same way, when the P _f curve is reached, the precipitated volume is close to 95 pct. Once the P _f curve has been reached, recrystallization starts to progress again due to fact that the pinning forces exerted by the precipitates are lower than the driving forces for recrystallization.

The RPTT diagrams, and especially the P _s and P _f curves, define a time interval, whatever the temperature, during which the precipitation state (size and precipitated volume) is changing. For times after P _f, the precipitated fraction does not vary, but a coarsening of the precipitates occurs due to the effect of Ostwald ripening.[6]

However, while the start of the plateau seems to coincide with exactness with the start of strain-induced precipitation,[29,30] recent studies have demonstrated that at the end of the plateau a small fraction of precipitates conserves the same size as the precipitates formed at the start of precipitation. Therefore, this suggests that the end of the plateau, or the P _f curve, coincides approximately with the end of precipitation.[6]

RPTT diagrams were drawn for the steels used, in the conditions indicated in Table II. For most of the steels, the diagrams were determined for strains of 0.20 and 0.35, as the strain is the most important variable for promoting strain-induced precipitation. The reheating temperature was normally 1473 K (1200 °C) for V-microalloyed steels and somewhat higher for Nb-microalloyed steels. In the former case, it was seen that VN-type particles were precipitated, and therefore the temperature of 1473 K (1200 °C) was sufficient to place them in solution. In the case of steels containing Nb, the precipitated particles were carbonitride types, and for this reason one of the prototypes with the highest probability of formation, NbC_0.7N_0.2, was chosen, in agreement with Turkdogan.[13]

Solubility temperatures (T _s) were calculated for the aforementioned precipitates, bearing in mind that in the case of the steels containing Ti, the N content combining with Ti at the reheating temperatures was first deduced, since these particles are also present. The values of T _N were measured from the RPTT diagrams and are set out in Tables III and IV. The increase in the strain and the strain rate raises the dislocation density and thus lowers the value of the parameter t _0.05. This also accelerates recrystallization and leads to a lower nose temperature (T _N) on the P _s curve (Tables III, IV).

Table IV Solubility Temperature (T _s) According to Turkdogan,[13] Experimental and Predicted Nose Temperature (T _N), Minimum Incubation Time t _N, and Minimum Time of the End of Precipitation $t_{N}^{\prime}$ for Nb-Steels

4.3 Precipitate Analysis

The start of the plateau is identified with the start of precipitation and its duration is related with two phenomena that take place simultaneously, namely, increases in the precipitated volume and in the size of precipitates. The latter effect is due to the heterogeneous nucleation of new precipitates. In this sense, several studies carried out with the assistance of TEM have shown the speed with which the coarsening of precipitates occurs, while at the same time indicating how the size distribution changes from a lognormal distribution at the start of the plateau to a frequently bimodal distribution at its end.[31–33]

The coarsening of precipitates by coalescence occurs once the precipitation is complete, i.e., when the plateau has ended and recrystallization progresses again. Coalescence can be explained by the modified Lifshitz–Slyozov–Wagner theory (MLSW).[34] This theory predicts that while the basic t ^1/3 kinetics of the LSW theory is maintained, the coarsening rate increases with an increase in the volume fraction, even at very small precipitated volume fraction values. According to the MLSW theory, the theoretical distribution of particle sizes broadens rapidly at small volume fraction values.

The TEM resolution of vanadium nitrides corresponding to steel V4 was obtained on strained and quenched specimens at a time close to the start of the plateau. The carbon extraction replica technique was used. The spectrum showed the presence of V and electron diffraction revealed a f.c.c. cubic lattice with a value of a = 4.156 Å, in accordance with the reference value found in the literature,[35,36] which is identified as vanadium nitride VN,[11] coinciding with other reported results.[37]

The evolution of the precipitate size was studied from the start of the plateau until after its end. Samples of steel V4 were austenitized at 1373 K (1100 °C), rapidly cooled to 1123 K (850 °C), strained applying a strain of 0.35, and held at the same temperature for 25, 190, and 300 seconds before subsequently being quenched. The holding times correspond to a time after the start of precipitation, after its end, and after the plateau, respectively.

Figure 8(a), corresponding to a holding time of 25 seconds, shows a lognormal distribution of the precipitate sizes with a weighted mean size of 5.12 nm, with the greatest frequency corresponding to an average size of 2 nm. In contrast, Figure 8(b), corresponding to a holding time of 190 seconds, shows a weak bimodal distribution with a weighted mean size of 13.83 nm and two relative maximum frequencies of 2 and 34 nm. Figure 8(c), corresponding to a holding time of 300 seconds, displays a distribution with a mean size of 19.91 nm. The three distributions serve to confirm that the end of the plateau is due to the growth of precipitates and consequently to a decrease in inhibition forces.

Fig. 8

Relative frequency of precipitate size for steel tested at 1123 K (850 °C); D = 95 μm; ε = 0.35; $\dot{\varepsilon }$ = 3.63/s. Holding time (Δt), (a) Δt = 25 s; (b) Δt = 190 s; (c)Δt = 300 s. Steel V4

Other studies carried out with Nb-microalloyed steels have shown similar results with regard to precipitate coarsening and also in relation with the two types of size distribution. By means of differential thermal analysis (DTA), the presence of two exothermic reactions, corresponding to the dissolution of the precipitates, was seen. The dissolution of two types of precipitates, corresponding to the formation of two peaks, was verified for steel N4.[6]

Gómez et al.[38] reported the formation of only one kind of precipitate on the first plateau and two different precipitate groups on the second plateau. In the specimen corresponding to the first plateau, the electron energy dispersive X-ray spectrum showed the presence of Nb and the lattice parameter determined from the electron diffraction image revealed a f.c.c. cubic lattice with a value of a = 4.39 to 4.44 Å, which is identified, in accordance with the reference value found in the literature, as a niobium carbonitride, carbide, or nitride. On the second plateau, two series of different lattice parameters were observed in the finer precipitates. The first series presented a lattice parameter of 4.41 to 4.44 Å, similar to the above precipitates, while the second series presented a lattice parameter of 4.46 to 4.58 Å. In accordance with the above, the former should correspond to carbonitrides or nitrides and the latter to carbides. Nevertheless, the coarser precipitates presented a lattice parameter of close to 4.46 Å.

5 Model of Strain-Induced Precipitation Kinetics

5.1 Influence of Strain

P _s and P _f values corresponding to the nose of the curves were determined from the RPTT diagrams, and both were seen to decrease as the microalloying element content or the strain increased. According to expression [2], the time (t _0.05) is related with the strain (ε) in accordance with the following expression:

$$ \ln t_{0.05} \propto - \beta \ln \varepsilon . $$

(5)

According to expression [5], and accepting that t _0.05 and P _s may be assumed to be approximately equal, the values of β were determined. The value taken for t _0.05 corresponding to each strain has been the minimum nucleation time (t _N) corresponding to the nose of the P _s curve.

The graphic representation of β against the microalloying element content in solution clearly shows that this parameter depends on the microalloy content and the influence of its nature can be practically disregarded (Figure 9). The strong influence of the microalloy content is probably due to the fact that the influence of the strain gradually diminishes as the chemical driving force increases,[39] this in turn being proportional to the content in solution. The shape of the regression curve suggests a hyperbolic secant or Avrami-type expression for β. The latter was chosen as it presents a better correlation coefficient and allows for possible physical interpretation. The resulting expression for β was as follows:

$$ \beta = 1.96\left[ {1 - \exp \left( { - 3.994 \times 10^{ - 2} \left( \frac{1}{w} \right)^{0.813} } \right)} \right], $$

(6)

where w is the microalloying element content (wt. pct).

Fig. 9

Plot of β against the total microalloying element content (wt. pct) (V, Nb)

Equation [6] means that the strain starts to influence the precipitation kinetics when the microalloying element content is less than a certain amount, which in practical terms could be approximately 0.5 (wt. pct). At the same time, the maximum value of β should be 1.96 (wt. pct). This maximum value has been set by introducing a new steel with Ti (0.021 wt. pct) as the only microalloying element (Ti = 0.021, N = 0.0105, wt. pct), which, at the reheating temperature 1503 K (1230 °C), had a Ti percentage of 0.004 wt. pct in solution,[13] sufficient to produce a deformation-induced precipitation plateau.[9] The point corresponding to this steel has also been drawn in Figure 9.

According to Eq. [6], the effect of the microalloying element content is included in parameter β. Moreover, the value of β will indicate what type of nucleation will be preponderant. For high β values, it is obvious that the preponderant nucleation will be heterogeneous nucleation on dislocations produced by the deformation. At low β values, the nucleation could also be heterogeneous on other defects like grain boundaries or homogeneous due to the relatively high percentage of microalloys.

5.2 Influence of Zener–Hollomon Parameter

Dutta and Sellars stated that the density of preferential nucleation sites in deformed austenite is expected to be sensitive to the density and arrangement of dislocations and therefore to the conditions of the prior deformation expressed in terms of strain, strain rate, and absolute temperature of deformation. However, they also note that the effect of the strain rate has not been separately investigated and it has been combined with the effect of the deformation temperature in terms of the Zener–Hollomon parameter Z.[7]

Two V-microalloyed steels, V7 and TV2, and the Nb-microalloyed steel N5 were tested at different strain rates, whose t _N values are shown in Table III and Table IV.

In the case of steel N5, which presents two precipitations or plateaus, minimum incubation time t _N and minimum precipitation end time $t_{N}^{\prime}$ values have been noted for the two precipitations, referred to as 1 and 2, and the second precipitation is seen to have a relatively long incubation time and very slow recrystallization kinetics, expressed by the difference $t_{N2}^{\prime}-t_{N2},$ compared to the first precipitation.

The value of t _N decreases as the strain rate increases. This occurs in all three steels. Furthermore, in the case of steel N5, it also occurs with the second precipitation, where the minimum nucleation times t _N2 corresponding to strain rates of 1.09 and 3.63/s were 50 and 40 seconds, respectively. According to expression [2], the time (t _0.05) is related with the Zener–Hollomon parameter (Z) in accordance with the following expression:

$$ \ln t_{0.05} \propto - r\ln Z. $$

(7)

Applying Eq. [7] to the t _N1 values from Tables III and IV, we obtain values of 0.18, 0.19, and 0.21 for the exponent (r) of Z for steels V7, TV2, and N5, respectively (Figure 10). These values may be considered by fair approximation to be similar, and therefore the average value, i.e., 0.20, may be taken as the most appropriate. This value could be generalized for all microalloyed steels, as the three steels used can be considered to be of different natures within the family of microalloyed steels.[10]

Fig. 10

Parameter t _0.05 (s) vs Zener–Hollomon parameter Z (s⁻¹)

The graphic representation of ln(t _0.05) against ln$(\dot{\varepsilon })$ shows that the strain rate has a separate influence similar to Z, i.e., regression of the results yields an average hypothetical strain exponent value also of −0.20 (Figure 11).

Fig. 11

Parameter t _0.05 vs strain rate for steels V7, N5, and TV2

The duration of precipitation ($t_{N}^{\prime}-t_{N}$) is also affected by the strain rate. The values deduced clearly indicate that the time ($t_{N1}^{\prime}-t_{N1}$) decreases as the strain rate increases, which is translated into more rapid precipitation kinetics. Therefore, it may be stated that an increase in the strain rate, causing an increase in the dislocation density and thus in internal defects, reduces the nucleation time for precipitates and accelerates the precipitation kinetics. It is observed, however, that the t _N1 values for the same strain rate are different for each steel, having been seen above that the chemical composition of a given steel has a notable influence on the corresponding nucleation time.

5.3 Influence of Austenite Grain Size

According to Dutta and Sellars,[7] the density of preferential nucleation sites for precipitation in deformed austenite is expected to be sensitive to the density and arrangement of dislocations and therefore to the conditions of the prior deformation expressed in terms of the aforementioned variables. These authors did not take into account the influence of the size of austenite grains and the expression given for t _0.05 does not include the grain size as a variable to bear in mind.

In addition to the dislocations, grain boundaries are sites known as classic sources of the heterogeneous nucleation of precipitation.[40] The lattice parameter of the precipitate is 20 to 25 pct greater than that of the matrix, and a flux of vacancies to the precipitated particles is required in order to accommodate the internal stresses arising from the growth of these particles. Such vacancy fluxes are provided by hot deformation processes, and the dislocation density is also increased, thereby providing an increased number of nucleation sites.[34] Bhadeshia and Honeycombe[41] have also pointed out that the grain boundaries and dislocations are highly preferred nucleation sites.

Steels V3 and V4 were used to determine the influence of the austenite grain size on the t _0.05 parameter in expression [2]. Two RPTT diagrams were determined for each steel at two different austenitization temperatures, 1373 K and 1503 K (1100 °C and 1230 °C) for steel V3 and 1373 K and 1473 K (1100 °C and 1200 °C) for steel V4, and the same strain of 0.35. V and N are in solution at all the stated austenitization temperatures, as the solubility temperature for VN particles is 1343 K (1070 °C) in steel V3 and 1296 K (1023 °C) in steel V4 (Table III). At the mentioned temperatures of 1373 K and 1473 K (1100 °C and 1200 °C), the austenite grain sizes were 95 and 180 μm, respectively (Table II).

The aforementioned minimum incubation time (t _N) and minimum precipitation end time ($t_{N}^{\prime}$) are shown in Table III. With regard to the value of the grain size exponent s, this was determined by representing lnt _0.05 against lnD (Figure 12), finding a value of 0.48, close to 0.5. Thus, it is deduced that a reduction in the grain size shortens the nucleation time of the precipitates and accelerates the recrystallization kinetics.

Fig. 12

Parameter t _0.05 vs austenite grain size for steels V3 and V4

5.4 Influence of Temperature

The temperature appears to be the most important magnitude influencing the parameter t _0.05. Therefore, in order to study the influence of the temperature, expression [2] can be simplified as follows:

$$ t_{0.05} \propto \exp \left( {\frac{{ - 0.2Q_{\text{def}} + Q_{\text{diff}} }}{\text{RT}}} \right)\exp \left[ {\frac{B}{{T^{3} \left( {\ln K_{\text{s}} } \right)^{2} }}} \right], $$

(8)

where K _s is the supersaturation ratio.

The activation energy (Q _def) for hot deformation is expressed as a function of the chemical composition of the steel and is as follows[17]:

$$ Q_{\text{def}} ({\text{J}}\,{\text{mol}}^{ - 1} ) = 267,000 - 2535.52\left[ {\text{C}} \right] + 1010\left[ {\text{Mn}} \right] + 33,620.76\left[ {\text{Si}} \right] + 70,729.85\left[ {\text{Nb}} \right]^{0.565} + 31,673.46\left[ {\text{V}} \right] + 93,680.52\left[ {\text{Ti}} \right]^{0.5919} . $$

(9)

The activation energy for bulk diffusivity of Nb and V atoms in Fe _γ is given by[7,42,43]

Nb-steels: Q _diff = 270,000 J/mol

V-steels: Q _diff = 264,000 J/mol

The solubility product is given by a general expression:

$$ \log \left[ {\text{M}} \right]\left[ {\text{I}} \right] = H - \frac{P}{T}, $$

(10)

where H and P are constants; M represents V, Nb, or Ti; and I represents N, C, or [C]^x[N]^y.

According to Turkdogan, the supersaturation ratio defined by K _s will be as follows[13]:

Nb-Steels:

$$ K_{\text{s}} = \frac{{\left[ {\text{Nb}} \right]\left[ {\text{C}} \right]^{0.7} \left[ {\text{N}} \right]^{0.2} }}{{\left[ {10^{{4.12 - \frac{9450}{T}}} } \right]}}. $$

(11)

V-Steels:

$$ K_{\text{s}} = \frac{{\left[ {\text{V}} \right]\left[ {\text{N}} \right]}}{{\left[ {10^{{2.86 - \frac{7700}{T}}} } \right]}}. $$

(12)

Figure 13 displays a scheme of an RPTT diagram, where the lines corresponding to the recrystallized fractions and the precipitation start and end curves have been plotted. From the plot, the next expression is deduced:

$$ T_{\text{N}} = T_{\text{S}} - \Updelta T_{\text{N}} $$

(13)

where T _s is the solubility temperature and T _N is the nose temperature of the precipitation start curve (P _s). The experimental data obtained are displayed in Tables III and IV.

Fig. 13

General scheme of RPTT diagram

The expressions for T _s are as follows[13]:

V-Steels:

$$ T_{\text{s}} = \frac{7700}{{2.86 - \log \left( {{\text{V}}\,{\text{pct}}} \right)\left( {{\text{N}}\,{\text{pct}}} \right)}} $$

(14)

Nb-Steels:

$$ T_{\text{s}} = \frac{9450}{{4.12 - \log \left( {{\text{Nb}}\,{\text{pct}}} \right)\left( {{\text{C}}\,{\text{pct}}} \right)^{0.7} \left( {{\text{N}}\,{\text{pct}}} \right)^{0.2} }}. $$

(15)

Figure 14 shows the values obtained for ∆T _N vs the solubility product, which has been represented by X _i. In the case of V-steels, X _i is (V pct)(N pct) and in the case of Nb-steels it should be (pct Nb)(pctC)^0.7(pctN)^0.2. The next expressions were found:

Fig. 14

Parameter ΔT _N vs solubility product

V-Steels:

$$ \Updelta T_{\text{N}} = 176.1\left[ {X_{\text{i}} } \right]^{0.382}. $$

(16)

Nb-Steels:

$$ \Updelta T_{\text{N}} = 139\left[ {X_{\text{i}} } \right]^{0.283} . $$

(17)

V-Ti and Nb-Ti Steels:

$$ \Updelta T_{\text{N}} = 118\left[ {X_{\text{i}} } \right]^{0.293} . $$

(18)

In the case of the steels containing Ti, the value of X _i has been calculated by subtracting the percentage of N combined with Ti at the austenitization temperatures forming non-dissolved TiN particles.

In accordance with the Eqs. [13] through [18], the parameter T _N was calculated and a graphic representation between experimental and predicted values has been made in Figure 15. It is possible to see the good fit of the regression line between the experimental and calculated values and this shows the high prediction power of the equations.

Fig. 15

Experimental vs calculated nose temperature (T _N)

The parameter B was determined by taking into account the derivative of the parameter t _0.05 in Eq. [2] on the temperature. Writing Eq. [2] as lnt _0.05 and determining the partial derivative, the next expression is obtained in the nose temperature of the curve P _s:

$$ \left( {\frac{{\partial \ln t_{0.05} }}{\partial T}} \right)_{{T = T_{\text{N}} }} = 0. $$

(19)

From the above equations, an expression for the parameter B was deduced:

$$ B_{{T = T_{\text{N}} }} = \left[ {\frac{{T^{2} \Updelta Q\left( {\ln K_{\text{s}} } \right)^{2} }}{3R}} \right] \cdot \left[ { - \frac{{\ln K_{\text{s}} }}{{\ln K_{s} - \frac{2}{3}\frac{P}{T}\ln 10}}} \right], $$

(20)

where

$$ \Updelta Q = - 0.2Q_{\text{def}} + Q_{\text{diff}} . $$

(21)

Therefore, B depends on the supersaturation ratio K _s calculated for the nose temperature (T _N) and taking into account the chemical composition of each steel. In this way, B was represented against lnK _s (Figure 16), obtaining the following expression with a high correlation index of 0.99:

$$ B\left( {K^{3} } \right) = 4.238 \times 10^{8} \exp \left( {1.689\ln K_{\text{s}} } \right). $$

(22)

Fig. 16

Parameter B against supersaturation ratio K _s

Equation [22] is valid for all the microalloyed steels with V or Nb including the steels that contain Ti in addition to these elements. In the latter case, K _s would be calculated by reducing the nitrogen percentage that has combined with Ti. In agreement with Eq. [22] and Figure 16, the B values calculated for the studied steels are approximately between 2·10⁹ and 7·10¹⁰ K³.

5.5 Determination of Coefficient A

Coefficient A values were determined by replacing in Eq. [2] the t _0.05 values determined experimentally for each steel and dividing these values by the expression of the second member determined in the corresponding strain, strain rate, austenitic grain size, and P _s curve nose temperature conditions. Coefficient A was seen to be a function of the saturation ratio defined by expressions [11] and [12], as shown in Figure 17. The following relationships were deduced from the graph in which three tendencies can be seen:

Fig. 17

Coefficient A vs supersaturation ratio K _s

V-Steels:

$$ A({\text{s}}^{ - 1} ) = 3.142 \times 10^{ - 10} \exp \left( { - 1.20\ln K_{\text{s}} } \right). $$

(23)

Nb-Steels:

$$ A({\text{s}}^{ - 1} ) = 4.766 \times 10^{ - 11} \exp \left( { - 0.07\ln K_{\text{s}} } \right). $$

(24)

V-Ti and Nb-Ti Steels:

$$ A({\text{s}}^{ - 1} ) = 4.13 \times 10^{ - 10} \exp \left( { - 0.47\ln K_{\text{s}} } \right). $$

(25)

6 Verification of the Model

The t _0.05 times calculated according to expression [2] and all the corresponding parameters were compared with the experimental t _0.05 times, finding a good correlation between both sets of values (Figure 18). Some relevant dispersion is observed in some Nb-steels, which is probably due to the formation of Nb(C,N) precipitates with a different stoichiometric ratio between C and N.[10]

Fig. 18

Experimental vs calculated parameter t _0.05

Nevertheless, this comparison refers only to the curve nose temperature, and thus it is more interesting to compare the experimental P _s and P _f curves with those predicted by expression [2]. Given that each parameter in the model has been calculated separately, it is very useful from the point of view of its application to reunite expression [2] with all the parameters determined as shown in the Appendix.

If we consider that t _N, the time corresponding to the nose of the P _s curve, and $t_{N}^{\prime}$, the time corresponding to the nose of the P _f curve, coincide approximately with t _0.05 and t _0.95, respectively, then Eq. [4] may be used to determine the value of n. When the steel presents two plateaus (e.g., Nb-steels), t _0.95 will coincide with the end of the second plateau. In this way, it is intended to simplify the precipitation kinetics when there are two precipitations or two plateaus, since, as has previously been mentioned, the formation of the two plateaus cannot be exactly predicted.

The regression of the values of t _0.95 to t _0.05 gave the following equations (Figures 19 and 20):

Fig. 19

Experimental parameter t _0.95 vs t _0.05 for V-steels

Fig. 20

Experimental parameter t _0.95 vs t _0.05 for Nb-steels

V and V-Ti Steels:

$$ t_{0.95} = 7.26\left( {t_{0.05} } \right)^{0.999} . $$

(26)

Nb and Nb-Ti Steels:

$$ t_{0.95} = 14.15\left( {t_{0.05} } \right)^{1.001} . $$

(27)

Expressions [26] and [27] indicate that strain-induced precipitation obeys Avrami’s law, as in both cases the exponent of parameter t _0.05 is close to 1, according to expression [4].

By comparing Eqs. [4], [26], and [27], the following values for n were obtained:

V and V-Ti Steels:

$$ n = 2.05. $$

Nb and Nb-Ti Steels:

$$ n = 1.54. $$

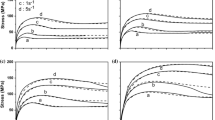
By replacing t _0.05 from Eq. [2] and the values of 2.05 and 1.54 for n in Eq. [3], two models of strain-induced precipitation kinetics were finally obtained for V-steels and Nb-steels, respectively, in isothermal conditions. Figures 21 and 22 show the prediction of the model in two random examples, showing the good concordance between the experimental and calculated P _s and P _f curves, respectively.

Fig. 21

Experimental and calculated P _s and P _f curves for steel V8

Fig. 22

Experimental and calculated P _s and P _f curves for steel N3

7 Precipitation Kinetics in Cooling Conditions

From Eq. [3], the resulting expression for cooling conditions, applying the method known as “compensated times,” is as follows:

$$ X_{\text{p}} = 1 - \exp \left[ {\ln 0.95\left( {\int\limits_{0}^{t} {\frac{{{\text{d}}t}}{{t_{0.05}^{*} }}} } \right)^{n} } \right]. $$

(28)

t _0.05 is given by Eq. [2], where T should be replaced by (T _D-νt), being T _D = deformation temperature (pass temperature, K); ν = cooling rate (K/s); and t = time (s).

Some examples of the precipitated fraction vs time for isothermal conditions and cooling conditions are shown in Figures 23 and 24, respectively. It is seen that if steel V4 is deformed applying a strain of 0.35 at 1127 K (854 °C), which coincides with the calculated curve nose temperature (T _N), precipitation is approximately finished in 120 seconds for isothermal conditions, but for cooling conditions at a cooling rate of 1 K/s, precipitation is never completed (Figure 23), and in this case the maximum precipitated fraction is 80 pct. At higher cooling rates, the precipitated fraction is lower; thus, for instance at a cooling rate of 2 K/s, the maximum fraction is 30 pct and for a rate of 4 K/s the precipitated fraction is only 10 pct.

Fig. 23

Precipitated fraction (X _p) vs time. Isothermal and cooling conditions. Steel V4

Fig. 24

Precipitated fraction (X _p) vs time. Isothermal and cooling conditions. Steel N3

The second example refers to a Nb-microalloyed steel (Figure 24). In this case, steel N3 shows that when a strain of 0.35 is applied at a temperature of 1227 K (954 °C), precipitation takes place after a holding time of approximately 240 seconds. When applying a cooling rate of 1 K/s, a maximum precipitated fraction of approximately 90 pct is reached. At cooling rates of 2 and 4 K/s, the precipitated fractions are 45 and 15 pct, respectively.

These results are very important as they show that the cooling conditions can prevent the precipitation from being completed. However, in hot rolling, the successive passes guarantee complete precipitation at temperatures below the no-recrystallization temperature.[44–46]

8 Conclusions

• 1. A new model for strain-induced precipitation in microalloyed steels has been constructed.

• 2. The incubation time (t _0.05) for precipitation decreases as the microalloying element content increases, but does not depend on the nature of the precipitates.

• 3. At greater strains, the times for incubation of the precipitates and for complete precipitation are shorter.

• 4. The strain rate would be affected by an exponent equal to −0.19, somewhat different from the value of −0.5 supposed by others authors. As the strain rate increases, the duration of precipitation decreases.

• 5. For larger austenite grain sizes, the times for incubation of the precipitates and complete precipitation are also longer.

• 6. B depends on the supersaturation ratio K _s calculated for the nose temperature (T _N). The B values calculated for the studied steels are approximately between 2·10⁹ and 7·10¹⁰ K³.

• 7. Strain-induced precipitation kinetics obeys Avrami’s law, where the time necessary for precipitation to finalize (t _0.95) is linearly related to the incubation time (t _0.05).

• 8. The strain-induced precipitation kinetics model was constructed in isothermal conditions and converted to cooling rate conditions by applying the “compensated times” method.

• 9. The cooling conditions could prevent precipitation from being completed.

Appendix: Model Expressions for the Start of Precipitation

$$ t_{0.05} = A\varepsilon^{ - \beta } D^{\text{s}} Z^{\text{r}} \exp \left( {\frac{{Q_{\text{diff}} }}{\text{RT}}} \right)\exp \left[ {\frac{B}{{T^{3} \left( {\ln k_{\text{s}} } \right)^{2} }}} \right] $$

$$ T_{\text{N}} = T_{\text{s}} - T_{\text{N}} . $$

The expressions for T _s are as follows:

V-Steels: $T_{\text{s}} = \frac{7700}{{2.86 - \log \left( {{\text{V}}\,{\text{pct}}} \right)\left( {{\text{N}}\,{\text{pct}}} \right)}}.$

Nb-Steels: $T_{\text{s}} = \frac{9450}{{4.12 - \log \left( {{\text{Nb}}\,{\text{pct}}} \right)\left( {{\text{C}}\,{\text{pct}}} \right)^{0.7} \left( {{\text{N}}\,{\text{pct}}} \right)^{0.2} .}}$

V-Steels: $\Updelta T_{\text{N}} = 176.1\left[ {X_{\text{i}} } \right]^{0.382}.$

Nb-Steels: $\Updelta T_{\text{N}} = 139\left[ {X_{\text{i}} } \right]^{0.283} .$

V-Ti and Nb-Ti Steels: $\Updelta T_{\text{N}} = 118\left[ {X_{\text{i}} } \right]^{0.293} .$

V-Steels: $A({\text{s}}^{ - 1} ) = 3.142 \times 10^{ - 10} \exp \left( { - 1.20\ln K_{\text{s}} } \right).$

Nb-Steels: $A({\text{s}}^{ - 1} ) = 4.766 \times 10^{ - 11} \exp \left( { - 0.07\ln K_{\text{s}} } \right).$

V-Ti and Nb-Ti Steels: $A({\text{s}}^{ - 1} ) = 4.13 \times 10^{ - 10} \exp \left( { - 0.47\ln K_{\text{s}} } \right).$

$$ \beta = 1.96\left[ {1 - \exp \left( { - 3.994 \times 10^{ - 2} \left( \frac{1}{w} \right)^{0.813} } \right)} \right] $$

w is the microalloying element content (Nb, V) (wt. pct).

$$ r = - 0.20 $$

$$ s = 0.5 $$

$$ Z({\text{s}}^{ - 1} ) = \dot{\varepsilon }\exp \left( {\frac{{Q_{\text{def}} }}{\text{RT}}} \right) $$

$$ Q_{\text{def}} ({\text{J}}\,{\text{mol}}^{ - 1} ) = 267,000 - 2535.52\left[ {\text{C}} \right] + 1010\left[ {\text{Mn}} \right] + 33,620.76\left[ {\text{Si}} \right] + 70,729.85\left[ {\text{Nb}} \right]^{0.565} + 31,673.46\left[ {\text{V}} \right] + 93,680.52\left[ {\text{Ti}} \right]^{0.5919} . $$

Nb-Steels:$K_{\text{s}} = \frac{{\left[ {\text{Nb}} \right]\left[ {\text{C}} \right]^{0.7} \left[ N \right]^{0.2} }}{{\left[ {10^{{4.12 - \frac{9450}{T}}} } \right]}}.$

V-Steels:$K_{\text{s}} = \frac{{\left[ {\text{V}} \right]\left[ {\text{N}} \right]}}{{\left[ {10^{{2.86 - \frac{7700}{T}}} } \right]}}.$

$$ B = 4.238 \times 10^{8} \exp \left( {1.689\ln K_{\text{s}} } \right). $$

To draw curve P _s for any steel, the parameter t _0.05 is calculated as a function of the temperature, with fixed A and B values, calculated as a function of K _s (for the corresponding T _N temperature), ε ^−β, and D ^0.5. The other terms Z ^−0.2, exp(Q _diff/RT), and exp(B/T ³(lnK _s)²) will be calculated as a function of the temperature including K _s.