1 Introduction

The Larson–Miller (LM) parameter was developed to estimate the long-term creep strength of heat-resistant materials using results obtained over a short period.[1] Similar time–temperature parameters have been developed for the same purpose. Among these, the LM parameter is the most commonly used around the world. It has been well established that the LM constant is approximately 20 for carbon steel, low-alloy steel, and austenitic stainless steel when the time and temperature are measured in units of hours and Kelvin, respectively. However, a large value of approximately 30 has been used to fit the times to stress rupture of high-Cr martensitic steel in a regression equation; a typical steel is modified 9 pct Cr-1 pct Mo steel (T91). Rules for Design and Construction for Nuclear Reactors published in France[2] recommends C = 20 for austenitic steel and C = 27 for high-Cr ferritic steel. The long-term rupture strength of a high-Cr martensitic steel decreases occasionally, and the long-term strength can be overestimated using short-term rupture data. Therefore, a suitable value of the LM constant needs to be selected for estimating the long-term creep rupture strength of high-Cr martensitic steels. However, there is little literature discussing in detail on the LM constant. Therefore, the current study investigates the LM constants for heat-resistant steels and explains the large values of the LM constant for high-Cr martensitic steel.

2 Materials

The development of numerous heat-resistant steels and alloys since the Second World War has contributed to the progress of supercritical boiler and turbine systems for power generation. During this long period, innumerable creep rupture tests have been performed at public institutes and within industry. Data were collected by, for example, the American Society of Mechanical Engineering (ASME) and European Creep Collaborative Committee and used to determine and revise the allowable stresses of heat-resistant steels and alloys. Nowadays, powerful data base systems such as Key to Metals are also available. However, these creep rupture data are not provided with related data such as data relating to the manufacturing procedures of the material. Heat-resistant steels and alloys are extensively used in industry such as in the power generation, chemical, nuclear, and aircraft industries, and the heat-resistant materials used in these industries are categorized by the type of steel, form of product, and so on. There are several hundred heat-resistant steels and alloys for which allowable stresses have been determined by creep tests. Analyzing all these materials is time consuming; fortunately, however, we can use a compact and integrated database produced by the National Institute for Materials Science (NIMS) (Tsukuba, Japan). Since 1972, the NIMS has issued 61 booklets of creep data sheets for almost all heat-resistant steels and alloys in practical applications in Japan.[3–62] Some manufacturers supplied a few heats for each type of material to the NIMS, and the NIMS has performed creep tests. The NIMS data sheets contain not only creep data but also tensile properties at ambient and elevated temperatures, chemical composition, manufacturing procedures, and microstructure. The purpose of this study is to investigate the LM constant of typical heat-resistant steels and the reasons for the large values of the LM constant of high-Cr martensitic steels; for this purpose, analysis of NIMS data sheets is sufficient.

The NIMS provides in the booklets the rupture life data for far longer than 100,000 hours for 19 types of carbon steels and low-alloy steels (total alloying element: below 5 pct), nine types of high-alloy steels (total alloying element: above 5 pct), 10 types of austenitic stainless steels, and 13 types of Fe-, Ni-, and Co-based superalloys (total alloying element: above 50 pct). Most of these steels and alloys are specified in Japanese Industrial Standards (JIS), but some are specified by ASTM International, the ASME, and in the Technical Regulation of Equipment for Thermal Power Plant published by the Ministry of Economy, Trade and Industry (Japan). In addition, commercially available alloys that have been used in engineering plants for a long time are included. Most specimens in creep rupture tests were machined from tubing, piping, plates, forged rings, bars, bolting materials, turbine blades, disks, rotors, and related components that were manufactured as a product of rolling, forging, or casting. In a few cases, specimens were machined from blocks in simulation of an actual manufacturing process. The data sheets have been occasionally revised, and each booklet contains rupture life data for several heats, and so, as a rule, one heat was selected at random from the latest booklet. The standard and code number, the nominal composition in units of percent, and the product form of each material are presented in the literature, and the details are omitted here for brevity. Additional heats were selected from creep data sheets for the cases of different forms (e.g., tubing and piping) and different manufacturing processes (i.e., castings and forgings of alloys equivalent to N 155[35] and U 500,[36] and a ring forged of low-alloy steel[55] that has a quench-and-tempered state and a stress-relieved state). In addition, to verify the effects of heat-to-heat variation, two heats were selected for 2.25Cr-1Mo steel, 9Cr-1Mo steel, and 9Cr-1Mo-VNb steel.

Moreover, rupture data of 8Cr-2W-VTa steel (F-82H) developed for fusion reactors,[63,64] Fe-23Cr-44Ni-7W steel developed for power boilers (HR6W),[65,66] and Ni-23Cr-18W-TiZr alloy (SSS113MA)[67,68] and Ni-18Cr-10Co-4Mo-6W-2Al-2Ti-ZrB alloy (R4286)[67,69] developed for high-temperature heat exchangers are referred to. For these steels and alloys, the creep rupture tests were performed for a long period and the mechanical properties and microstructures were well investigated.

In addition, rupture data for experimental steels of a plain 9 pct Cr steel and a 9 pct Cr-4 pct W steel[70] (9Cr-0W and 9Cr-4W, respectively) and a 9Cr-1Mo-VNb steel that was tempered at 1073 K (800 °C), 1013 K (740 °C), and 773 K (500 °C)[71] (Gr.91-B, Gr.91-C, Gr.91-D, respectively) were also used. The initial microstructure of each of these steels is full martensite, except the steel of 9Cr-4W, which contains 10 pct δ-ferrite.

Altogether, time-to-creep-rupture data were analyzed for 79 types of steel.

The LM parameter was initially proposed referring to Hollomon and Yaffe’s tempering parameter.[72] Therefore, the variations in mechanical properties due to tempering for selected steels, namely, carbon steel with 0.31 pct carbon from the original article of Hollomon and Yaffe, 2.25Cr-1Mo steel,[73] 9Cr-1Mo-VNb steel (Grade T91) from Sikka’s original article[74] and F-82H steel,[64] were also analyzed.

3 Analysis Method

Larson and Miller proposed the LM parameter, \( P_{\text{LM}} \):

$$ P_{\text{LM}} = T(\log t_{\text{r}} + C_{\text{LM}} ) , $$
(1)

where T is the absolute temperature, \( t_{\text{r}} \) is the time to creep rupture, and C LM is the LM constant. The relation between the LM parameter and the applied stress, σ, forms a master curve for a steel. In the current study, to fit a single regression equation to all data of a specified type of material, representing P LM by a cubic equation of the logarithm of σ, regression analysis was performed on the variable \( T\log t_{\text{r}} \) on the right side of Eq. [1], and consequently, the LM constant C LM was obtained as a regression coefficient of the variable T. The apparent activation energy, \( Q' \), was calculated using Eq. [24], which will be detailed later.

Hollomon and Yaffe[72] first introduced the concept of the temperature-compensated time to investigate the tempering behavior of steel. A quenched steel is assumed to be softened by a diffusion process during tempering, and the hardness is expressed by a function of the parameter \( t_{0} = t\exp ( - Q^{\prime\prime}/RT) \), where \( t,\,Q^{\prime\prime} \), and \( R \) are the tempering time, apparent activation energy for tempering, and gas constant, respectively. Rewriting this parameter as \( Q^{\prime\prime} = 2.3RT\left( {\log t - \log t_{0} } \right) \), the hardness, H, is considered to be a function of the apparent activation energy, \( Q^{\prime\prime} \), or

$$ H = f\left( {P_{\text{HY}} } \right) , $$
(2)

where the Hollomon–Yaffe (HY) parameter, \( P_{\text{HY}} \), and the HY constant, C HY, are defined as

$$ P_{\text{HY}} = T\left( {\log t + C_{\text{HY}} } \right) , $$
(3)
$$ C_{\text{HY}} = - \log t_{0} . $$
(4)

Hollomon and Yaffe[72] confirmed that when plotting the hardness against the HY parameter, almost all data points for six types of carbon steels fall on a single line, for each steel with narrow scatter and that \( C_{\text{HY}} \approx 20 \) for time given in units of hours and temperature given in units of Kelvin. This achievement was referred to in Larson and Miller’s study.[1] Here, we assume that hardness, H, is a linear function of the HY parameter. The regression equation

$$ H = X_{0} + X_{1} T\log t + X_{2} T $$
(5)

is analyzed, where \( X_{\text{i}} \) are the regression coefficients. We obtain the HY constant as

$$ C_{\text{HY}} = - \log t_{0} = X_{2} /X_{1} . $$
(6)

The apparent activation energy for tempering, \( Q^{\prime\prime} \), is given by

$$ Q^{\prime\prime} = 2.3R\bar{P}_{\text{HY}} , $$
(7)

where \( \bar{P}_{\text{HY}} \) is the average of the HY parameters.

4 Results of Regression Analysis

4.1 LM Parameter and HY Parameter for Selected Steels

Figure 1 shows the relation between the applied stress and LM parameter (LM plot) for 0.2C steel.[9] We obtained C LM = 18.56 and \( Q^{\prime} = 303.3 \) kJ/mol. Figure 2 shows the relation between the Rockwell hardness value, HRC, and the HY parameter (HY plot) for 0.31C steel.[72] We obtained C HY = 16.41 and \( Q^{\prime\prime} = 248.9 \) kJ/mol for the steel tempered at temperatures higher than 673 K (400 °C), which correspond to the creep temperatures shown in Figure 1 (in the figures, both C LM and C HY are expressed simply as C unless otherwise noted). Figures 1 and 2 show that both the HY parameter and LM parameter are useful as widely accepted and that both the parameter constants, C LM and C HY, are approximately 20 and both the apparent activation energies, \( Q^{\prime} \) and \( Q^{\prime\prime} \), are close to the activation energy for the self-diffusion of α-iron. The LM and HY plots for 2.25Cr-1Mo steel[5,73] are shown in Figures 3 and 4, respectively. In both cases (i.e., creep rupture and recovery due to tempering), the values of the parameter constant and apparent activation energy for the 2.25Cr-1Mo steel are a little larger than those for the carbon steel shown in Figures 1 and 2, respectively. However, it is reconfirmed that \( C \approx 20 \) and that the apparent activation energy is approximately the same as that of self-diffusion.

Fig. 1
figure 1

A plot of stress vs LM parameter for the time to creep rupture of 0.2 pct carbon steel[9]

Full size image
Fig. 2
figure 2

Plot of Rockwell hardness (HRC) vs. HY parameter for the tempering time of steel with 0.31 pct carbon.[72] A straight regression line is drawn for the data above 400 °C, and a horizontal line denotes the initial hardness

Full size image
Fig. 3
figure 3

LM plot for 2.25Cr-1Mo steel[5]

Full size image
Fig. 4
figure 4

HY plot for 2.25Cr-1Mo steel.[73] A straight regression line is drawn for the data above 500 °C, and a horizontal line denotes the initial Vickers hardness

Full size image

The LM and HY plots for 8Cr-2W-VTa steel[64] with tempered martensite are shown in Figures 5 and 6, respectively. While the parameter constant and apparent activation energy for creep rupture data are relatively high, C LM = 26.81 and \( Q^{\prime\prime} = 483.2 \) kJ/mol, respectively, the parameter constant and apparent activation energy obtained using proof stress (PS) at room temperature are relatively low, C HY = 21.08 and \( Q'' = 408.3 \) kJ/mol, respectively. Figure 7 shows the LM plot for 9Cr-1Mo-VNb steel (T91)[45] with tempered martensite. Considerably large values of \( C_{\text{LM}} = 31.85 \) and \( Q^{\prime} = 601.3 \) kJ/mol were obtained, in agreement with previous studies. In addition, large values of \( C_{\text{HY}} = 25.74 \) and \( Q^{\prime\prime} = 515.7 \) kJ/mole were obtained from the HY plot for the PS of the T91[74] as shown in Figure 8. Although the results are obtained by linear analysis, the slope in the high-PS region appears steeper than that in the low-PS region. After grouping the data as shown in Figure 8, it was found that both values of the HY constant and apparent activation energy for the low-PS group were lower than those for the high-PS group. Even the lower values of C HY and \( Q^{\prime\prime} \) in the low-PS region are larger than the values for both carbon steel and low-alloy steel as shown in Figures 2 and 4. These results of regression analyses for the selected ferritic/martensitic heat-resistant steels are listed in Tables I and II with the related metallurgical information.

Fig. 5
figure 5

LM plot for 8Cr-2W-VTa steel.[64]

Full size image
Fig. 6
figure 6

HY plot for 8Cr-2W-VTa steel[64]

Full size image
Fig. 7
figure 7

LM plot for 9Cr-1Mo-VNb steel[45]

Full size image
Fig. 8
figure 8

HY plot for 9Cr-1Mo-VNb steel.[74] Values of C HY and \( Q^{\prime\prime} \) indicated by arrows were calculated using data in high and low ranges of the HY parameter as indicated

Full size image
Table I Microstructure, Initial Hardness, Ranges of Creep Temperature and Time to Rupture, LM Constant, and Apparent Activation Energy for Selected Heat-resistant Steels
Full size table
Table II Initial Hardness, Ranges of Tempering Temperature and Time, HY Constant, and Apparent Activation Energy for Steels Corresponding to Table I. Initial Microstructures for these Steels were Full Martensite
Full size table

4.2 Correlation Between the Parameter Constant and the Apparent Activation Energy

Figure 9 is a diagram of the correlation between the parameter constants, C LM and C HY, and the apparent activation energies, \( Q^{\prime} \) and \( Q^{\prime\prime} \), of the selected steels shown in Figures 1 through 8. A straight regression line for all data is presented in the figure and very strong correlation (\( r = \, 97 \).9 pct) is confirmed regardless of creeping or tempering. The figure shows two other findings.

Fig. 9
figure 9

Correlation diagram for the parameter constants, C LM and C HY, and the apparent activation energy, \( Q^{\prime} \) and \( Q^{\prime\prime} \) of carbon steel,[9,72] 2.25C-1Mo steel,[5,73] 8Cr-2W-VTa steel,[64] and 9Cr-1Mo-VNb steel.[45,74] A straight regression line is drawn using all data

Full size image
  1. (1)

    Concerning the microstructural effect, both the parameter constant and activation energy of the martensitic steels are larger than those of carbon and low-alloy steels with ferrite and pearlite (ferrite/pearlite) structure irrespective of creeping or tempering.

  2. (2)

    Concerning the stress effect, the constants for creep rupture, C LM and \( \;Q^{\prime} \), are on average 17 pct larger than those for tempering, C HY and \( Q^{\prime\prime} \).

The correlation between C LM and \( \;Q^{\prime} \) in creep data is very close to the correlation between C HY and \( Q^{\prime\prime} \) in tempering data. Therefore, in Figure 9, a single straight regression line is drawn, and a high correlation coefficient was confirmed for all data. However, this could be a casual coincidence because there are several differences between a creep test and tempering test: (a) the initial microstructure is martensite in the tempering test, but tempered martensite or ferrite/pearlite in the creep test; (b) the test temperatures are very different; and (c) the analysis method for creep is different from that for tempering owing to the applied stress in the creep test. In contrast, the apparent activation energy of creep, \( Q^{\prime} \), for carbon steel and low-alloy steel is approximately the same as that of tempering, \( Q^{\prime\prime} \), and these values are close to the activation energy of self-diffusion of α-iron, which means that the elementary activation process of either creep rupture or tempering is mainly controlled by self-diffusion in the matrix. Based on this metallurgical consideration, it is meaningful to compare the values of not only the apparent activation energies, but C LM and C HY, and it is thus concluded that the difference between C LM for creep and C HY for tempering implies the intrinsic qualities of creep deformation that proceeds with applied stress. In particular, the findings obtained from Figures 1 through 9 that the values of the LM constant of martensitic steel are considerably larger than the values of the parameter constant of tempering and much larger than the values of the LM constant of carbon steel and low-alloy steel suggest that creep deformation of the martensitic structure should be realized under special circumstances.

4.3 Relation Between the LM Constant and the Apparent Activation Energy for General Heat-Resistant Steels

Figure 9 shows that the LM constant is strongly correlated with the apparent activation energy and that the values of the LM constant for the martensitic steels are much larger than those for the carbon steel and low-alloy steel with ferrite/pearlite structure. To examine carefully these findings, it is desirable to investigate the LM constant for many types of heat-resistant steels and alloys having practical uses.

The steels listed in the NIMS data sheets were creep-tested under a wide range of conditions to estimate the long-term strength using short-term data. In the regression analyses for the times to rupture of the steels, the parameter constant, C, is obtained by minimizing the sum of squared residuals of a regression model. This means that the LM constant, C, is not a unique material constant but should depend on temperature and stress. Therefore, when we compare the values of C, we need to prepare an equivalent dataset as much as possible.

Creep tests were sometimes performed at higher stresses than the PS at a test temperature. However, such stresses are hardly applied in engineering plants. Therefore, to obtain an equivalent dataset excluding data obtained at stresses higher than the PS is an idea. Figures 10 and 11 show the LM plots for 0.3C steel[19] and 18Cr-8Ni steel[34], respectively, where the data were grouped according to whether the stresses were higher than the PS at each test temperature. Both figures show that when the stress is higher than the PS, the LM constant is larger than the LM constant for all data, and in contrast, when the stress is lower than the PS, the LM constant is lower than the LM constant for all data. However, the variation in the apparent activation energy does not agree with that in the LM constant. Although the apparent activation energy for 0.3C steel is higher than that for all data when the stress is higher than the PS and the apparent activation energy is lower than that for all data when the stress is lower than the PS, the variation in the apparent activation energy for 18Cr-8Ni steel is simply the opposite of that for carbon steel. In the NIMS creep data sheets, creep rupture data obtained in tests at stresses higher than PS at each test temperature are given for some carbon steels, low-alloy steels, high-alloy steels, and austenitic stainless steels with relatively low PS at room temperature.

Fig. 10
figure 10

LM plots for all rupture data and the rupture data obtained at stresses higher and lower than the PS at a given temperature for 0.3 carbon steel plate[19]

Full size image
Fig. 11
figure 11

LM plots for all rupture data and the rupture data obtained at stresses higher and lower than the PS at a given temperature for 18Cr-8Ni austenitic stainless steel plate[34]

Full size image

Some creep rupture data have been obtained at high temperatures far beyond those of practical circumstances. The ASME defines the allowable stresses at temperatures below 1098 K (825 °C) for many heat-resistant steels and alloys. In this sense, the LM plot for Fe-21Cr-32Ni AlTi alloy[28] is shown in Figure 12, where the data were grouped according to whether the temperature was higher than 1098 K (825 °C). Although the apparent activation energy is higher than that for all data in the high-temperature range, the LM constant decreases in the high-temperature range. In contrast, in the low-temperature range, although the apparent activation energy decreases, the LM constant increases.

Fig. 12
figure 12

LM plots for all rupture data and the rupture data obtained above 900 °C and below 800 °C for Fe-21Cr-32Ni-AlTi alloy.[28] The LM plot for the rupture data that satisfy Eq. [11], X < 1, is also shown

Full size image

An idea for calculating the LM constant is to exclude data obtained at temperatures higher than 1098 K (825 °C). However, data for temperatures higher than 1098 K (825 °C) are also needed for estimating the long-term creep strength at high temperatures. Moreover, superalloys used for turbines are subjected to temperatures around 1273 K (1000 °C). Therefore, another criterion is necessary for excluding “high-temperature” data.

The following equation for the creep rate, \( \dot{\varepsilon } \), is generally accepted:

$$ \dot{\varepsilon } = A_{0} \sinh \left( {\alpha \sigma /RT} \right) , $$
(8)

where \( A_{0} \) and \( \alpha \) are material constants.[75] The usefulness of this equation has been validated not only for pure metals but also for several steels.[76] Instead of Eq. [8], the creep rate or time to rupture is usually expressed by a power law of the stress. However, since the stress exponent, \( n \), in the power law depends on both temperature and stress, the relation between \( \log t_{r} \) and \( \log \sigma \) becomes complicated even for a constant temperature. Therefore, it is generally difficult to extrapolate short-time data to a longer time. Contrary to the power law for creep, Tamura et al.[77] reported that the time to rupture for many heat-resistant steels and alloys is reasonably expressed by

$$ t_{r} = B_{0} \cdot \exp ( - \sigma V/RT) , $$
(9)

where B 0 is a constant, and V is the activation volume. Monkman and Grant[78] showed that the product of the creep rate and time to rupture is roughly constant, and \( \sinh (x) \approx 0.5\exp (x) \)when x > 1 therefore, Eq. [9] is an approximate equation of Eq. [8] at high stress. When \( x < 1,\,\sinh (x) \approx x \), and \( \dot{\varepsilon } \propto \sigma \) is thus another approximate form of Eq. [8]. Although the relation of \( \dot{\varepsilon } \propto \sigma \) is confirmed even for high-strength steels such as 9Cr-1Mo-VNb steel in a low-stress region at high temperatures,[79] the deformation mechanism in the low-stress region may differ from that in the higher-stress region of engineering circumstances. Therefore, it is reasonable to exclude the data from the analyses when

$$ X = \sigma V/RT < 1 . $$
(10)

In the current study, the activation volume is not obtained using Eq. [9]. Instead, the LM constant is directly calculated using the conventional method mentioned above. However, the values of the activation volume in units of cubic centimeters per mole are approximately the same as the values of the activation energy in units of kJ/mol.[77] That is, the apparent activation energy calculated using all data is considered to be an approximate value of the activation volume, \( V_{\text{Q'}} \). Therefore, the data that satisfied the following equation instead of Eq. [10] were excluded from the analyses:

$$ X = \sigma V/RT \approx \sigma V_{\text{Q'}} /RT < 1 . $$
(11)

Figure 12 for Fe-21Cr-32Ni-AlTi alloy shows that the range for the data excluded according to X < 1 is roughly the same as the range for the data above 1173 K (900 °C). In the NIMS creep data sheets, there are no rupture data for ferritic/martensitic steels or austenitic stainless steels that satisfy the condition of Eq. [11], and there are no rupture data that satisfy Eq. [10] when the rupture data for several selected heat-resistant steels were analyzed according to Eq. [9].[80] However, there were rupture data for some superalloys that satisfy Eq. [11].

Based on the above considerations, the rupture data in the NIMS data sheets and the quoted literature were selected with exclusion of data obtained at stresses higher than the PS and lower stresses corresponding to Eq. [11]. The selected data were then defined as a standard dataset. The standard dataset was used for the calculation of the LM constant hereinafter, unless otherwise noted.

First, to check the heat-to-heat variation, the LM constant and the apparent activation energy were calculated for 2.25Cr-1Mo steel (tube and plate),[5,13] 9Cr-1Mo steel (tube),[21] and 9Cr-1Mo-VNb steel (tube and plate)[45,62]. Correlation between C and \( Q^{\prime} \) is shown in Figure 13, which indicates clearly that the heat-to-heat variation in C and \( Q^{\prime} \) is much smaller than the differences among the different types of steel. A linear regression line passing through the origin for all data presented in the figure has a slope and high correlation coefficient similar to those for Figure 9, where the regression line does not pass through the origin to be exact.

Fig. 13
figure 13

Correlation diagram for the LM constant and apparent activation energy for 2.25Cr-1Mo steel,[5,13] 9Cr-1Mo steel,[21] and 9Cr-1Mo-VNb steel,[45,62] indicating that the heat-to-heat variation of the material constants is small

Full size image

The correlations between the LM constant and the apparent activation energy for all standard rupture datasets are shown in Figure 14, where the data for the carbon/low-alloy steels, high-alloy steels, austenitic stainless steels, and superalloys are plotted separately. The figure shows that the apparent activation energy increases proportionally with an increase in the LM constant, similar to the case in Figure 9. In addition, it is found that the correlation can be clearly stratified according to the crystal structure; i.e., FCC or BCC structure. In the figure, straight lines passing through the origin are drawn for the BCC and FCC structures. The slope for the FCC structure is 27 pct greater than that for the BCC structure. The apparent activation energy for the FCC structure is greater than that of the BCC structure for the same LM constant, and in contrast, the LM constant for the BCC structure is larger than that of the FCC structure for the same apparent activation energy.

Fig. 14
figure 14

Correlation diagram for the LM constant and the apparent activation energy for the standard datasets of all steels and alloys studied in the current report. The data were categorized into four groups: carbon steel/low-alloy steel, high-alloy steel, austenitic stainless steel, and superalloy. Straight regression lines passing through the origin are presented for BCC and FCC structures

Full size image

The values of the LM constant for almost all austenitic stainless steels are distributed loosely from 13 to 19 and the average was 15.1, although the LM constant for 25Cr-20Ni-0.4C steel[18] used for reformer tubes made by centrifugal casting is the lowest, C = 6.22. The highest value of the LM constant is C = 19.32, for 18Cr-8Ni steel plates.[34]

Among the superalloys, the LM constant is lowest (C = 12.36) for Ni-15.5Cr-8Fe alloy[43] used for heat- and corrosion-resistant bars, and highest (C = 23.67) for Co-25Cr-10Ni-7.5W-B alloy[32] used for gas turbine blades made by casting. \( C \approx 19 \) for the remaining superalloys, and the average was 18.3. For the superalloys equivalent to N155 and U500, creep rupture data were obtained for both castings and forgings. The LM constant for Fe-21Cr-20Ni-20Co-3Mo-2.5W-NbN alloy (N155)[35] was 21.02 and 15.85 for castings and forgings, respectively, while that for Ni-19Cr-18Co-4Mo-3Ti-3Al-B alloy (U500)[36] was 17.17 and 21.37 for castings and forgings, respectively. The rupture strengths of both alloys in the case of casting are higher than those in the case of forging, and therefore, the LM constant is not always correlated with the rupture strength. However, the strong correlation between C and Q is established, as seen in Figure 14. Some of the superalloys are considerably hardened by a large amount of \( \gamma^{\prime} \) phase, and the LM constants for these alloys are larger than those for the Fe-21Cr-32Ni-TiAl alloy[27,28]; however, the constants are still small compared with those of T91 (Figure 7), and range approximately from 19 to 24.

Among the carbon steels and low-alloy steels, the LM constant is lowest (C = 17.46) for 2.25Cr-1Mo steel[13] used for pressure-vessel plates, and largest (C = 23.96) for 2.25Cr-1.6W steel[56] used for boiler tubing. \( C \approx 20 \) for most of the remaining carbon steels and low-alloy steels, and the average was 20.4. There is a clear effect of stress relief (SR) on the LM constant for 2.25Cr-1Mo-0.3V steel forgings[55] used for pressure vessels. Although the SR treatment reduces the rupture strength, the LM constant is increased by the SR treatment; i.e., C = 20.42 after SR treatment and C = 17.58 for the quenched and tempered state. The microstructures of most carbon and low-alloy steels are ferrite/pearlite and the microstructures of some tempered steels harder than approximately HRC13 are bainite or tempered martensite. However, the LM constants for the carbon and low-alloy steels are still rather low, approximately 20 regardless of microstructure and chemical composition. Among these steels, 2.25Cr-1.6W steel (ASTM A213 Gr. 23) is considerably strengthened by both the bainitic structure and the addition of V, Nb, and B. The rupture strength of this steel is comparable to that of T91 below approximately 873 K (600 °C). However, the LM constant of 2.25Cr-1.6W steel is not as large as that of T91, C = 31.85, although it is the highest C = 23.96, among the carbon and low-alloy steels.

Among the high-alloy steels, the lowest LM constant is C = 16.45 for 12Cr-1Mo-1W-0.3V steel[12] used in heat-resistant bars of turbine blades, the high values are C = 34.10 for 9Cr-1Mo-VNb steel[62] used for boiler and pressure vessel plates and C = 33.83 for 9Cr-0.5Mo-1.8W-VNb steel[50] used for piping. Most LM constants for high-alloy steel are distributed widely around \( C \approx 30 \), and the average was 27.3.

Summarizing Figure 14, it was found that the average LM constant for the superalloys is a little larger than that for stainless steel, and the average LM constant for high-alloy steels is much larger than that for carbon steel and low-alloy steels. It is generally accepted that the creep rupture strength of a superalloy is higher than that of austenitic stainless steel and that the creep rupture strength of high-alloy steel is higher than that of carbon and low-alloy steel. Therefore, the LM constant for high-strength steel and alloy is generally higher than that for low-strength steel in the same crystal system. However, the value of the LM constant for an individual material is not always correlated with the rupture strength as mentioned above for N155 and U500. The LM constant is certainly affected by many factors, such as the test conditions, alloy system, and creep strength; however, Figure 14 clearly shows the LM constants of some high-alloy steels are outstanding among many heat-resistant steels and alloys.

Figure 14 also shows that there is strong correlation between C and Q, although it depends on crystal structure. It is well known that the apparent activation energies of pure metals are close to the activation energies for self-diffusion,[81] and the activation energy of heat-resistant alloys for practical use is far higher than that of self-diffusion because of the increase in internal energy.[82–84] That is, the physical meaning of the apparent activation energy for creep has been clarified to some extent. In contrast, the LM constant has been used as an adjustable parameter to find a regression equation for the time to creep rupture. The correlation in Figure 14 does not indicate the existence of a causal relation between C and Q. However, the strong correlation suggests the LM constant itself should have physical meaning like the apparent activation energy, \( Q^{\prime} \). Therefore, the physical meaning of the LM constant should be studied further. Such investigation may explain the large LM constant observed only for martensitic steels with high strength.

4.4 Requirements for a Large LM Constant

The LM constant for some high-alloy steels represented by the modified 9Cr-1Mo steel are concentrated around \( C \approx 30 \) as shown in Figure 14. These steels are easily hardened and the initial microstructures are tempered martensite, which is an essential difference from the carbon steel and low-alloy steels with microstructure of ferrite/pearlite. Therefore, tempered martensite as an initial microstructure is the first requirement for a large value of the LM constant.

Figure 15 shows the LM plot for creep rupture data of 9Cr-0W and 9Cr-4W steel.[70] The initial microstructure of both steels is tempered martensite. 9Cr-0W steel is a plain 9 pct Cr steel and strengthened by martensite structure and the M23C6 carbide particles precipitated on the boundaries and within lath martensite. 9Cr-4W steel is strengthened not only by the martensite structure and M23C6 carbide particles but also by finely dispersed Laves phase. Although the LM constant for 9Cr-4W steel is rather large, C = 28.11, the LM constant for 9Cr-0W steel is comparable to the values for steels with ferrite/pearlite. Therefore, tempered martensite may be necessary, but not sufficient, for a large LM constant, and sufficient strengthening factors such as the presence of fine Laves phase is the second requirement for large values of the LM constant. Incidentally, 9Cr-4W steel contains 10 to 20 pct δ-ferrite, but the effect of the existence of δ-ferrite on the LM constant is yet unknown. The LM constant is low when the creep temperature is high as shown in Figure 12. Therefore, selecting adequate test conditions (not only temperature but stress) is the third requirement for large values of the LM constant.

Fig. 15
figure 15

LM plots for 9Cr-0W steel and 9Cr-4W steel[70]

Full size image

Figure 16 shows an example of the large variation in the LM constant of modified 9Cr-1Mo steel, although the martensitic steel tested contains a proper amount of strengthening elements. The notations Gr.91-B, -C, and -D indicate that the modified 9Cr-1Mo steel is tempered at 1073 K, 1013 K, and 773 K (800 °C, 740 °C and 500 °C), respectively.[71] The LM constant for each is C = 32.86, 28.99, and 21.07, respectively. Within the test results, the order of rupture strength is sequentially Gr.91-D > Gr.91-C > Gr.91-B.[71] This indicates that the martensite structure of Gr.91-D with the highest rupture strength is hardly tempered within the test conditions, but the LM constant for Gr.91-D is the lowest, C = 21.07. A general tendency that the LM constant of high-strength material is large is confirmed in Figures 9, 13, and 14, but Figure 16 clearly shows the inverse result. Kabadwal et al.[71] reported that although Gr.91-D has high hardness and high-creep resistance due to excess dislocations, transient and accelerating creep deformation could be continued with very low activation energy as compared with Gr.91-B and Gr.91-C. In Figure 16, the low apparent activation energy for Gr.91-D is reconfirmed using the rupture data. This indicates that recovery is easily accelerated in Gr.91-D, and in contrast to this, the high-temperature tempering could stabilize the martensitic microstructure for a long time, resulting in an increase in the LM constant, although Gr.91-B is weak in the short-term. It is well known that the rupture strength of martensitic steel tempered at rather low temperatures tends to decrease after a long time, even though the short-term strength is high. In contrast, less degradation of long-term strength in high-temperature services is confirmed when martensite is stabilized by high-temperature tempering.[85,86] Reflecting these circumstances, the tempering temperature of 9Cr-1Mo-VNb steel is chosen to be rather high, specifically 1033 K to 1053 K (760 °C to 780 °C),[45] compared with the original temperature of 1033 K (760 °C).[87] Therefore, stabilizing martensite by high-temperature tempering is the fourth requirement for a large LM constant.

Fig. 16
figure 16

LM plots for Gr.91-B, Gr.91-C, and Gr.91-C steels[71]

Full size image

The requirements for a large LM constant are summarized as (1) an initial microstructure of tempered martensite, (2) the steel having sufficient strengthening factors, (3) the steel being tested under adequate conditions where martensite is not recovered too easily, and (4) martensite being sufficiently stabilized by high-temperature tempering. However, these four requirements are neither mutually independent nor sufficient for a large LM constant. The LM constant for high-strength steel and alloy is generally high than that for low-strength steel. However, the value of the LM constant for an individual material is not always correlated with the rupture strength as mentioned above for N155, U500, Gr.91-B, -C, and -D. Therefore, high-strength material is not the requirement for a large LM constant.

To verify the above four requirements, the details of practical high-alloy steels shown in Figure 14 are re-plotted in Figure 17. In the figure, data are classified into three groups: steel containing V and Nb (Ta), Cr–Mo steel tubing, and high-Cr steel bars and bolts. Among the steels containing V and Nb (Ta), 12Cr-2W-0.4Mo-1Cu-NbV[54] has approximately 10 pct δ-ferrite and strength rather lower than that of similar 11Cr-2W-0.4Mo-1Cu-NbV steel[53] with full martensitic structure, and 8Cr-2W-VTa steel[64] for fusion reactors contains little nitrogen compared with the steels for general uses, which results in rather low strength. The other V- and Nb-containing steels,[45,50,53,62] the so-called Grade T91, T92, T122 steels, are martensitic steels with high-creep strength developed since the 1980s. The LM constants of these steels are extremely large, exceeding 30. An evaluation test after very-long-term creep tests indicates that martensite of the high-alloy steels with high strength is stabilized by finely dispersed particles and the decomposition is considerably slow.[88] Certainly, degradation is accelerated by the formation of Z phase,[89] local recovery accompanying the dissolution of finely dispersed carbo-nitride particles;[90,91] however, the microstructure of the high-alloy steels is generally stable for a long time.[92,93]

Fig. 17
figure 17

Details of martensitic steels shown in Fig. 14. Numbers in parentheses are the reference number for each material

Full size image

Martensite of 12Cr steel[15], 12Cr-1Mo-1W-0.3V steel[12], and 12Cr-1Mo-1W-0.25V steel[46] used for bars and bolts is tempered at rather high tensile strength levels of 600 or 900 MPa, depending on the practical use. The LM constants of these steels are rather small, \( C \approx 20 \). The test temperatures for 12Cr steel[15] and 12Cr-1Mo-1W-0.25V steel[46] range from 723 K to 600 K (450 °C to 600 °C) and from 773 K to 873 K (500 °C to 600 °C), respectively. The test temperature for 12Cr-1Mo-1W-0.3V steel ranges from 773 K to 823 K (500 °C to 650 °C). Referring to Figure 12, rather high test temperatures for 12Cr-1Mo-1W-0.3V steel are considered to account for the lowest LM constant, C = 16.45.

Boiler tubing of 5Cr-0.5Mo steel[14], 9Cr-1Mo steel,[21] and 9Cr-2Mo steel[48] is tempered at rather high temperatures, and the tensile strengths are a relatively low, ~500 MPa. The microstructure of 5Cr-0.5Mo steel and 9Cr-1Mo steel is a mixed structure of ferrite/pearlite and bainite. The LM constant of 5Cr-0.5Mo steel is a rather low 18.92. The LM constant of 9Cr-1Mo steel is \( C \approx 27 \), which is rather high compared with 5Cr-0.5Mo steel and the bars and bolts with 12 pct Cr, which may result from the stability of microstructure due to high-temperature tempering. In contrast, although 9Cr-2Mo steel does not contain strengthening elements such as V and Nb, C = 32.91 for 9Cr-2Mo steel is comparable to the LM constants of Nb-doped martensitic steels with high strength. This may be due to the precipitation of Laves phase.[94] 9Cr-2Mo steel contains 10 to 20 pct δ-ferrite in the tempered martensite matrix, which could affect the LM constant, but the effect of δ-ferrite on the LM constant is not clear.

In summary, the four requirements for large values of the LM constant mentioned above are suitably verified, excepting the effect of δ-ferrite.

4.5 LM Constant for Low-Stress Data of High-Alloy Steels

Kimura et al.[95] recommended \( C = 20 \) for selected rupture data below 50 pct of the PS at a given temperature to estimate appropriately the long-term strength of martensitic steel. The reason for this recommendation is that although \( C \approx 32 \) is deduced from all data of 9Cr-1Mo-VNb steel, such a large LM constant results in the overestimation of long-term rupture strength. Figure 18 shows the LM plot for creep rupture time of the 9Cr-1Mo-VNb steel tube;[45] data are grouped above and below 50 pct of the PS at each temperature. It is found that although high values of C = 31.85 for all rupture data and C = 38.35 for data satisfying σ > 0.5PS are obtained, a relatively low value of the LM constant, C = 27.55, is obtained for data satisfying σ < 0.5PS. However, it does not seem necessary to reduce the LM constant as low as C = 20 as Kimura and colleagues proposed. They also reported that 0.5PS is an engineering measure near the elastic limit for high-Cr martensitic steel, since the deformation mechanism differs above and below the elastic limit and the operating stresses are roughly lower than 0.5PS. However, similar discussions on carbon steel and/or low-alloy steel have not yet been published.

Fig. 18
figure 18

LM plots for all data, the rupture data obtained at stresses higher and lower than 0.5PS at a given temperature for 9Cr-1Mo-VNb steel[45]

Full size image

Incidentally, there is a clear difference in the structure of data among the high-alloy steels, carbon steels, and low-alloy steels. There are many data obtained at high stresses, σ > PS, for the carbon steels and the low-alloy steels owing to their low yield ratios. In contrast, data satisfying σ > PS are rare for high-alloy steels owing to their high yield ratios. Figure 19 shows the LM constant using the data of σ > PS for carbon steels and low-alloy steels plotted against the LM constant obtained using the standard datasets. In the figure, the LM constants for austenitic stainless steels are also plotted. A straight regression line passing through the origin for the data of the carbon steels, low-alloy steels, and austenitic stainless steels is drawn in the figure. It is found that the LM constant for σ > PS is 25 pct larger than the standard LM constant on average. In the figure, the LM constant using data of σ > 0.5PS for high-alloy steels is also plotted. The regression line for the high-alloy steels agrees with that shown in the figure and is omitted for simplicity. The agreement in the correlation shown in Figure 19 does not logically have any physical meaning. However, Figure 19 implies that excess dislocations in the high-alloy steels behave during creep deformation equivalently to the retained dislocations in the carbon steel, low-alloy steel, and austenitic stainless steel when stress higher than the PS is applied. Since high stresses approximately σ > 0.5PS are seldom applied in practice, even for high-alloy steels, to estimate appropriately the long-term creep strength, it is reasonable to put restrictions on the data as Kimura et al. proposed. However, it is necessary to further investigate the adequacy of different criteria; e.g., whether a limit of 50 pct PS or 67 pct PS, that is one of the criteria to determine the allowable stresses in ASME, is used.

Fig. 19
figure 19

Correlation diagram for the LM constant using a standard dataset and the LM constant using high-stress data of carbon steel, low-alloy steel (LAS), austenitic stainless steel (ASS), and high-alloy steel (HAS). High stress refers to stress higher than the PS for LAS and ASS, and higher than 0.5PS for HAS. Carbon steel is indicated as LAS in this figure

Full size image

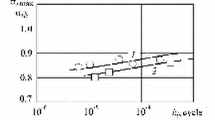
In any event, that the LM constant using the data for σ > 0.5PS is smaller than that for the standard data has already been shown in Figure 18 for 9Cr-1Mo-VNb steel. To generalize this finding, Figure 20 shows the correlation between the LM constant for σ < 0.5PS and the LM constant obtained using a standard dataset for high-alloy steels in practical use. The regression line indicates that the LM constant for σ < 0.5PS is 15 pct smaller than the LM constant for the standard data. The average LM constant obtained using the standard data for recently developed Gr.T91, T92, and T122 is approximately 32, and it decreases to approximately 27 for σ < 0.5PS. However, \( C \approx 27 \) for the high-strength martensitic steels is still considerably larger than the universally accepted value of \( C \approx 20. \)

It is concluded that although the LM constant for high-strength martensitic steels could be reduced to some extent by the instability of the microstructure, the LM constant is essentially still high compared with LM constants for other carbon steels, low-alloy steels, austenitic stainless steels, and superalloys.

Fig. 20
figure 20

Correlation diagram for the LM constant using a standard dataset and the LM constant using data corresponding to stresses lower than 50 pct of the PS of the high-alloy steels. The data were categorized into three groups: Nb (Ta)-containing steel, Cr-Mo steel tube, and a bar and bolt with 12 pct Cr. Numbers in parentheses are the reference number of each material

Full size image

5 Discussion

5.1 Theoretical Derivation of the LM Constant

It is well understand that both C LM and C HY depend on not only the material itself but test conditions. However, it should be reasonably explained that the LM constant is considerably large, approximately 30, only for high-Cr tempered martensitic steels with high creep strength, while \( C_{\text{LM}} \approx 20 \) is widely accepted for many heat-resistant steels and alloys. For this reason, the LM constant should be derived theoretically.

The steady state creep rate is given by

$$ \dot{\varepsilon } = 0.5\rho bv , $$
(12)

where the factor 0.5 is the factor of conversion from shear strain to nominal strain, ρ is the dislocation density, b is the length of the Burgers vector, and v is the average velocity of gliding dislocations. For the case of thermally activated movement of dislocations over localized obstacles, the creep rate is given by

$$ \dot{\varepsilon } = \dot{\varepsilon }_{0} \exp \left( {\frac{ - \Updelta G}{RT}} \right) , $$
(13)

where ΔG is the change in Gibbs free energy of a system and \( \dot{\varepsilon }_{0} \) is a constant.[96–98] Combining Eqs. [12] and [13], we obtain the dislocation velocity, v, of Eq. [12] as

$$ v = v_{0} \exp \left( {\frac{ - \Updelta G}{RT}} \right) , $$
(14)
$$ \dot{\varepsilon }_{0} = 0.5\rho bv_{0} . $$
(15)

A pre-factor, v 0, denotes the maximum velocity of a dislocation in crystal (i.e., the velocity of sound) and is defined as

$$ v_{0} = \lambda \nu_{\text{eff}} , $$
(16)

where λ is the maximum distance that a dislocation can move from a start point to the next stable position through the activation process, and v eff is the effective attempt frequency per unit time to overcome the obstacles. The effective frequency, v eff, depends on the interaction between the dislocation and the obstacle. If the dislocation is strongly pinned by the obstacles, the effective frequency is nearly equal to the Debye frequency, \( \nu_{\text{eff}} \approx \nu_{\text{D}} \), and it is estimated to be smaller than the Debye frequency by 2 to 3 orders of magnitude for intermediate pinning strengths.[99]

\( \Updelta G \) is defined as

$$ \Updelta G = Q - \sigma V - \Updelta ST , $$
(17)

where Q and ΔS are the increases in internal energy and entropy in the activation process, respectively.

The Monkman–Grant relation[82] has been established empirically for many heat-resistant steels and alloys:

$$ \dot{\varepsilon } \cdot t_{r} = C_{\text{MG}} . $$
(18)

From Eqs. [12] through [18] we deduce that

$$ t_{r} = \frac{{C_{\text{MG}} }}{{0.5\rho b\lambda \nu_{\text{eff}} \exp \left( {\Updelta S/R} \right)}} \cdot \exp \left( {\frac{Q - \sigma V}{RT}} \right) . $$
(19)

Rewriting Eq. [19], we obtain

$$ T\left[ {\log (t_{r} ) + C_{\text{LM}} } \right] = \frac{Q - \sigma V}{2.3R} $$
(20)

and

$$ C = \log \left[ {\frac{{0.5\rho b\lambda \nu_{\text{eff}} \exp \left( {\Updelta S/R} \right)}}{{C_{\text{MG}} }}} \right] = \log \left( {\frac{{0.5\rho b\lambda \nu_{\text{eff}} }}{{C_{\text{MG}} }}} \right) + {{\Updelta S} \mathord{\left/ {\vphantom {{\Updelta S} {2.3R}}} \right. \kern-0pt} {2.3R}} . $$
(21)

The left side of Eq. [20] is the LM parameter, and therefore, the LM constant has the physical meaning given by Eq. [21].

The so-called experimental activation energy, Q exp, is determined by incremental tests assuming that the strain rate obeys Eq. [13] and the increment, δT, is small enough to be treated as a differential:[97]

$$ Q_{\exp } \equiv RT^{2} \left( {\frac{{\delta \ln \dot{\varepsilon }}}{\delta T}} \right)_{\sigma } = \Updelta G - T\left( {\frac{\partial \Updelta G}{\partial T}} \right)_{\sigma } + RT^{2} \left( {\frac{{\partial \ln \dot{\varepsilon }_{0} }}{\partial T}} \right)_{\sigma } . $$
(22)

The last term on the right side of Eq. [22] is usually neglected, because the explicit dependence of \( \dot{\varepsilon }_{0} \) on the temperature is generally considered to be weak.[97] Therefore, we obtain from Eqs. [17] and [22]

$$ Q_{\exp } \approx \Updelta G - T\left( {\frac{\partial \Updelta G}{\partial T}} \right)_{\sigma } = Q - \sigma V = \Updelta H . $$
(23)

That is, the activation energy experimentally obtained by the Arrhenius plot indicates the change in the enthalpy, ΔH, for creep.[97] However, in many articles on creep, Q in Eq. [19] is called the activation energy for creep. For convenience, the current study uses the same notation, Q, but the original meaning of Q is the increase in the internal energy for creep.

When the creep rate is controlled by a single activation process (i.e., Eq. [13] is effective), C LM, Q, and V are determined definitely by the regression analysis of Eq. [20]. However, the LM constant was calculated by regression analysis using the rupture data for a wide range of conditions, and therefore, the LM constant obtained is a middle or average value, but the values of Q and V were not calculated directly. However, the activation energy, Q exp, defined by Eqs. [22] and [23], is proportional to the LM parameter as shown by Eq. [20]. Therefore, the current study defines the apparent activation energy, \( Q^{\prime} \), as the average of the true activation energy, Q exp:

$$ Q' = \overline{{Q_{\exp } }} = \overline{Q - \sigma V} = 2.3R\bar{P}_{\text{LM}} . $$
(24)

In creep study, rupture data are usually formulated by a power law, instead of Eqs. [13] and [19]. Equation [1] is also valid for the power law creep, and the LM constant is thus the same for both the exponential law and power law of Eqs. [13] and [19]. However, in the case of the power law, the apparent activation energy should contain the variable of the stress exponent, n, and therefore, the meaning of the apparent activation energy is unclear. Fortunately, the value of the stress-dependent term, σV in the case of the exponential law, is not large compared with the value of Q for both the power law and exponential law, and therefore, \( Q' \approx Q \) for both methods.

5.2 Interpretation of the LM Constant for Martensitic Steel

When the creep rate obeys Eq. [13], the LM constant itself possesses the physical meaning indicated by Eq. [21], in the same way that the parameters ΔH, Q, and V in Eq. [17] have physical meaning. Substituting C = 20 and

$$ \begin{gathered} \rho = 4 \times 10^{13} {\text{m}}^{ - 2} ,\,\lambda = 8\,\mu {\text{m}},\,b = 2.5 \times 10^{ - 10} \,{\text{m}} \hfill \\ C_{\text{MG}} = 0.1,{\text{ and}},\,\nu_{\text{eff}} = 3600 \times 10^{13} {\text{h}}^{ - 1} \hfill \\ \end{gathered} $$
(25)

into Eq. [21] for steel with ferrite/pearlite structure, we obtain

$$ (\Updelta S/R)_{\text{FP}} = 8.8. $$
(26)

The values for ρ and λ are the total dislocation density[100] and the sub-grain size[101] for carbon steel, respectively. The Debye frequency is used for v eff. Equation [26] indicates that the relative contribution of the entropy change to the LM constant is \( (\Updelta S/2.3R)_{\text{FP}} /C = 8.8/20/2.3 = 19 \) pct and is not so small.

The pre-factor of self-diffusion is given by[102]

$$ D_{0} = \frac{Z}{6}a^{2} \nu \exp \left( {\frac{\Updelta S}{R}} \right) , $$
(27)

where Z, a, and v are the coordinate number, inter-planer spacing, and thermal frequency, respectively. Substituting a = 2.5 × 10−10 m, Z = 8, and v = 1013 s−1 into Eq. [27], the entropy change for self-diffusion of α-iron is given by

$$ \left( {\Updelta S/R} \right)_{\text{D}}^{\alpha } = 6.0 . $$
(28)

In the calculation of Eq. [28] D 0 = 0.0003 m2/s[103] for the paramagnetic region was used, because there are limited reliable data for the ferromagnetic region, while most creep tests are performed in the ferromagnetic region of the steels with ferrite/pearlite structure. Oikawa[103] proposed D 0 = 0.0002 m2/s in the ferromagnetic region, and in the calculation the correlation factor (0.72 for BCC) was omitted for simplicity. Even in this case, the value obtained from Eq. [28] is larger than 5.5 at least. In any event, it is concluded that a major portion of the entropy change in Eq. [26] is explained by the increase in entropy due to self-diffusion in the matrix in Eq. [28]. Considering factors other than the diffusion effect (i.e., the ambiguous variations in ρ, λ and C MG), \( C_{\text{LM}} \approx 20 \) for ferritic steels is a rational and explainable statement. The HY parameter is deduced experientially and so the physical meaning of the HY constant is not so clear. However, recovery is controlled by self-diffusion, and therefore, \( C_{\text{HY}} \approx 20 \) for ferritic steels is also understandable.

In the case of austenitic stainless steel, the LM constant is slightly smaller than that of ferritic steel; therefore, assuming C = 18 and the same values as Eq. [25] except for λ = 2.5 × 1013 m−2[104,105] and λ = 5 μm as a subgrain size[105], we obtain a value slightly smaller than that for ferritic steels,

$$ (\Updelta S/R)_{\gamma } = 5.2. $$
(29)

The entropy change in the self-diffusion of austenitic steel is obtained as

$$ \left( {\Updelta S/R} \right)_{\text{D}}^{\gamma } = 4.3 $$
(30)

by substituting a = 2.5 × 10−10 m, Z = 12, v = 1013 s−1, and D 0 = 0.000089 m2/s[103] into Eq. [27]. That is, \( C \approx 18 \) for austenitic steels is also rationally explained.

Conversely, by substituting C = 30 for the martensitic steels and simply using the values for the ferrite/pearlite steels in Eq. [25], we obtain \( \Updelta S/R = 31.8 \), a considerably large value. C MG = 0.1 as the first term of Eq. [21] may not depend on the microstructure; i.e., ferrite/pearlite or martensite. However, the dislocation density is possibly greater in martensitic steel. We therefore assume ρ = 1015 m−2, and the maximum distance of dislocation movement can be approximated as a prior austenitic grain size, λ = 100 μm. Substituting these values instead, the entropy change decreases to

$$ (\Updelta S/R)_{\text{M}} = 26.1 . $$
(31)

Equation [31] indicates that the relative contribution of the entropy change to the LM constant is \( (\Updelta S/2.3R)_{\text{M}} /C = 26.1/30/2.3 = 38\;\;{\text{pct}} \) for creep in martensite matrix, and this value is twice that for ferrite matrix, namely 19 pct as mentioned above.

The difference between the values obtained using Eqs. [26] and [31] is

$$ \delta (\Updelta S/R)_{\text{M} - \text{FP}} \, = \, \left({\Updelta S/R} \right)_{\text{M}} - \left( {\Updelta S/R}\right)_{\text{FP}} \, = \, 26.1 - 8.8 = 17.3 . $$
(32)

This indicates the excess entropy for creeping of the high-strength martensitic steel as compared with the steel with ferrite/pearlite structure.

In the calculations, we use the Debye frequency as the effective frequency. Assuming that the effective frequency is lower than the Debye frequency by two orders of magnitude,[99] the entropy term for creep, ΔS/R, increases by 2.3 × 2 = 4.6. Therefore, the value of 17.3 given by Eq. [32] could decrease approximately by this value of 4.6, if the pinning force in ferrite/pearlite structure was weaker than that in martensite. Nevertheless, the difference in the entropy change between martensite and ferrite/pearlite matrix \( \delta \left( {\Updelta S/R} \right)_{{{\text{M}} - {\text{FP}}}} \) is still large. However, the relation between the effective frequency and microstructure, that is, martensite or ferrite/pearlite, is unknown.

In the calculation of the entropy change for the high-strength martensitic steels using Eq. [21], the value obtained from Eq. [31], \( (\Updelta S/R)_{\text{M}} = 26.1 \), could be reduced further if dislocation density higher than ρ = 1015 m−2 is substituted. However, the dislocation density should not increase indefinitely. Equations [13] and [15] do not explicitly contain the vibration entropy term of the dislocation core. Cottrell[106] showed that the excess entropy change per unit length of the inter-atom spacing along the dislocation line of the dislocation core can be approximated as 3k, where k is the Boltzmann constant.

This statement can be restated as the excess entropy due to the vibration of dislocation core being equivalent to the value of Eq. [31]:

$$ \Updelta S_{\text{disl}} = 3k \cdot \rho v_{\text{m}} /b = 3k \cdot \rho Nb^{3} /b = 3R\rho b^{2} , $$
(33)

where N and v m denote the Avogadro number and molar volume, respectively.From Eqs. [21] and [33], we obtain

$$ \Updelta S/R + \Updelta S_{\text{disl}} /R = - \ln \left( {\frac{{\rho b\lambda \nu_ {\text{eff}}}}{{C_{\text{MG}} }}} \right) + 3\rho b^{2} + C. $$
(34)

The value on the right side of Eq. [34] becomes a minimum for \( \rho \approx 10^{19} \) m−2, independently of the value of the LM constant, C; i.e.,

$$ (\Updelta S/R)_{\text{M}} \Rightarrow \left( {\Updelta S/R + \Updelta S_{\text{disl}} /R} \right)_{\text{M}} \ge 19.2. $$
(35)

Therefore, it is concluded from Eqs. [26] and [35] that the relation

$$ \delta (\Updelta S/R)_{{{\text{M}} - {\text{FP}}}} \succ \succ 19.2 - 8.8 \approx 10 $$
(36)

should be established as the excess entropy besides the entropy change due to self-diffusion and creep deformation, when the thermal activation process expressed by Eq. [13] is valid in martensitic steels. In other words, the deformation mechanism for martensitic steels with very high creep resistance accompanies very large entropy change, that is, 10 times the gas constant at least, besides the entropy change due to self-diffusion.

Incidentally, the entropy changes for melting and evaporation are calculated as 0.9R and 16.1R using the latent heats of iron, 13.81 and 415.5 kJ/mol, respectively.[107] These values appear to indicate that several errors could occur in the calculation of the abovementioned excess entropy for creep of the martensitic steels (i.e., ranging from 19.2 to 26.1R), because we know by intuition that the entropy changes in solid should not exceed the entropy changes in either a liquid state or a gas state. However, it is also a fact that the entropy changes for self-diffusion in α- and γ-iron with the help of a single vacancy range from 4.3 to 6.0R. These values are greater than the entropy change for melting of iron. If the intuition that the entropy changes in solid should not exceed the entropy changes in either a liquid state or a gas state is correct, we could observe neither diffusion phenomena in a solid state nor creeping. These apparently conflicting conclusions cannot be compatible, if we understand that plastic deformation in solid is an inhomogeneous phenomenon and is controlled by atomistic phenomena balancing thermodynamic variables such as Q, V, and ΔS, while melting and evaporation are truly macroscopic phenomena in a homogeneous system.

5.3 Estimation of Long-term Rupture Strength Using the LM Parameter

The ASME estimates creep rupture strengths at 100,000 h and specified temperatures using both the LM parameter and logarithm of stress, and determines the allowable tensile stresses combining with tensile properties and using specified safety factors. This decision method has been established for a long time and is well accepted. However, how to estimate the long-term rupture strength more accurately and quickly is still an issue in developing new materials and estimating residual lives. To address this problem, temperature-compensated time parameters such as the LM parameter were proposed and have helped in the development of heat-resistant materials. However, overestimation of the long-term rupture strength using the LM parameter has been pointed out for high-Cr martensitic steels.[95] Therefore, rather low values of LM constants, C = 27 for high-Cr martensitic steel[2] and C = 20 for selected data below proof stresses of 50 pct for high-Cr martensitic steel,[95] have been recommended. These statements are consistent with the results shown in Figures 18 and 19. Therefore, it is reasonable to lower the value of C to prevent overestimation. However, whether the long-term strength is higher or lower than the value estimated using short-term data depends on not only test conditions but also the intrinsic characters of the material itself. If some heats of a specified type of steel show strength lower than the values expected from short-term data, it is suggested that there is still a chance to improve the creep properties of those heats. In other words, the use of the LM parameter is not responsible for the overestimation of long-term creep strength. In the first place, the relationship between the logarithm of rupture life and the logarithm of stress could follow Norton’s law, which is not based on metallurgical considerations. Therefore, overestimation cannot be prevented by only selecting an adequate LM constant.

As shown in Eq. [20], the LM parameter is formulated as a function of linear stress and not the logarithm of stress, when a single deformation mechanism is predominant under some test conditions. This reads that accurate estimation of long-term strength is possible when data points on a plot of linear stress vs logarithm of time to rupture are separated into certain groups. Figure 21 shows a conventional relation of the logarithm of stress vs logarithm of rupture life for 2.25Cr-1Mo steel. Fitting curves were calculated using the master curve shown in Figure 3. Underestimation at 823 K (550 °C) and overestimation at 873 K (600 °C) are confirmed near 100,000 hours. There is inevitable unreliability in the estimated strengths far beyond 100,000 hours at temperatures from 823 K to 873 K (550 °C to 600 °C), which corresponds to the upper service conditions for 2.25Cr-1Mo steel.

Fig. 21
figure 21

A conventional plot for stress vs time to rupture of 2.25Cr-1Mo steel. Fitting curves were calculated using a master curve shown in Fig. 3

Full size image

Contrary to this conventional plotting, Eq. [20] indicates that the logarithm of rupture life should be plotted as a linear function of stress as shown in Figure 22. Data were divided into four groups, Gr.I through Gr.IV, and regression analysis for each data group gives linear fitting lines. Numbers beside the name of each group denote the LM constant and apparent activation energy in units of kJ/mol. The LM constant tends to decrease as the test temperature increases and stress decreases. Using these material constants, the estimated lines for Gr.III and Gr.IV, at 823 K (550 °C) are easily drawn, as shown in the figure. According to these prediction lines, the estimated rupture strength at 823 K (550 °C) and after several hundreds of hours may be lower than the extrapolation line for Gr.II, and follows the line for Gr.III or Gr.IV. Although metallurgical observation such as precipitation behavior should be necessary for determining in which group the actual rupture data fall, Gr.III or Gr.IV, the extrapolation method based on Eq.[20] should provide a more accurate estimation than the conventional logarithmic stress method. Previous study[80] confirmed the usefulness of the estimation method, as shown in Figure 22, by applying the method to several heat-resistant steels.

Fig. 22
figure 22

Relation between time to rupture and linear stress of 2.25Cr-1Mo steel. Rupture data were grouped by four and regression analysis for each group was performed using Eq. [20] and regression lines were drawn for each temperature. Numbers beside the name of each group denote the LM constant and apparent activation energy in kJ/mol

Full size image

6 Conclusions

  1. 1.

    The LM constant for creep rupture is larger than the HY constant for tempering.

  2. 2.

    The LM constant for carbon steel, low-alloy steel, austenitic stainless steel, and superalloy is approximately 20. In contrast, the LM constant for creep rupture of the martensitic steels with high creep strength is approximately 30.

  3. 3.

    Even the high value of the LM constant for martensitic steel with high strength approaches the values for general heat-resistant steels, when the steel loses strengthening factors owing to service at high temperatures in actual plants.

  4. 4.

    The LM constant is positively proportional to the apparent activation energy for creep with a strong correlation coefficient. The correlation can be clearly stratified according to crystal structure. The LM constant for BCC structure is larger than that for FCC structure when the apparent activation energy is the same.

  5. 5.

    The LM constant can be expressed by a formula with an intrinsic meaning, and the contribution of the entropy change to the LM constant, especially for martensitic steel with high creep strength, is not negligible.

  6. 6.

    The deformation mechanism for martensitic steel with very high creep resistance accompanies a very large entropy change, that is, 10 times the gas constant at least, besides the entropy change due to self-diffusion.