1 Introduction

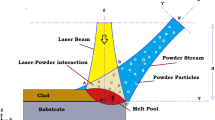
Laser engineered net shaping (LENS) process, developed by Sandia National Laboratory and commercialized by Optomec Inc., (Albuquerque, NM) facilitates building of metallic parts layer by layer by melting and deposition of metal powders using a focused, high-powered laser beam.[1–3] Powders are carried through an inert gas and delivered concentrically to the laser spot through suitably angled four nozzles placed in the deposition head. After deposition of each layer, the laser head and the powder delivery nozzles are moved upward to deposit the subsequent layers from bottom to top. LENS process is widely used in manufacturing complex parts of titanium alloy,[4,5] stainless steel,[6,7] and H13 tool steel.[8,9]

The deposited layers in LENS experience high peak temperature with repeated and steep thermal cycles, which influence the microstructural features and mechanical properties of the final part. The real-time monitoring of the temperature fields and the layer dimensions during LENS process is difficult due to small melt pool size and steep gradient in the temperature field.[10–12] Attempts are made to numerically predict the thermal cycles[13] and to establish the influence of process parameters on thermal cycles, residual stress levels,[14] microstructure,[15] and microhardness[6,7,16] in deposits of SS304, SS316, and various tool steels. Zheng et al.[16] found the solidification structure of SS316 deposits to be primarily cellular without prominent secondary branching and attributed it to the high cooling rate during solidification. Smugeresky et al.[17] reported that secondary dendrite arm spacing (DAS) and cell spacing in LENS deposited structures would be the same, and in the range of 7 to 10 μm. Zheng et al.[16] used the measured DAS (i.e., cell spacing) to estimate the corresponding cooling rate using an empirical relation

$$ \lambda_{2} = A\left( {C_{R} } \right)^{ - n} $$
(1)

where C R refers to the cooling rate, λ 2 the DAS, and A and n the materials constants. They found these estimates to be comparable to the corresponding numerically computed values.[16]

There is no unique approach to correlate solidification structure of the deposited layers to their final hardness distributions. In multiphase materials such as martensitic steels, volume fractions of the analytically estimated phases and their corresponding hardness values are used to compute the overall hardness following rules of mixture.[6,7,18,19] In single-phase materials, on the other hand, grain size is used to estimate hardness.[14] To estimate yield strength in the deposited layers of stainless steel (as multiple, and not absolute values, of the yield strength of conventional wrought material), Zheng et al. used a Hall–Petch like relation:[16]

$$ \sigma_{y} = \sigma_{0} + k_{y} \left( {d_{g} } \right)^{ - 0.5} $$
(2)

where σ y and d g refer to yield strength and grain size, respectively, and, σ 0 and k y are, respectively, the lattice resistance and the grain boundary resistance to dislocation motion. It is, however, evident from the microstructures presented in Reference 16 that the authors have used cell spacing (~3 μm) and not the grain size for their strength calculations. The fact that the predicted values of hardness are much greater than the corresponding measured values indicates that d g in Eq. [2] corresponds to cell spacing and not grain size.[16] In the recent past, Allison et al. proposed an integrated approach, referred to as integrated computational materials engineering, to relate the computed temperature field to the final mechanical properties for a given set of process variables and powder materials in metal casting.[20,21] Attempts toward the development of a similar approach in LENS processing are rare in the open literature.

In summary, it is widely recognized that LENS process needs an integrated predictive model that can compute temperature field and also provide an estimate of basic microstructural features and mechanical properties. The present work includes a three-dimensional (3-D) heat transfer model based on the finite element method to predict the peak temperature, melt pool dimensions, and cooling rate in the deposited layers of SS316. The computed values of cooling rates during solidification are used to estimate the layerwise variation in cell spacing. The layerwise cell spacing is used to estimate the corresponding microhardness following a Hall–Petch like relation. The computed results are validated with the corresponding measured results in actual multilayer deposits of SS316.

2 Experimental Investigation

Single-line wall structures of 1, 3, 5, 7, and 9 layers are built using SS316 powders with particle sizes of 150 to 200 μm and a feed rate of 25 g/min on separate SS316 substrates, each of size 10 mm × 25 mm × 2 mm (length × width × height). The deposition direction alternates during building of successive layers with the target length and height of each layer as 8 and 0.38 mm, respectively. A LENS750 machine (OPTOMEC made, Optomec Inc., Albuquerque, NM) fitted with a diode pumped ytterbium fiber laser and an inert atmosphere of Ar with less than 20 ppm O2 are used for all the experiments. The laser power and the scanning velocity are kept constant at 210 W and 12.5 mm/s, respectively, for all the layers. An idle time of 0.05 seconds is used for the laser head to move up (z-increment) 0.38 mm and start the deposition of the next layer. The initial working distance between the laser head and the incident surface plays a key role in determining the deposition layer thickness and is optimized in the present work through experience so that the deposition layer thickness equals the z-increment, implying a steady-state deposition.

A set of trial experiments at several combinations of laser power and scanning speed have indicated a powder transfer efficiency of around 15 pct, and the same is presumed to be constant in model calculations. All the deposited structures are sectioned at the midlength and subjected to metallographic polishing and etching to view the layer dimensions and the net build height. Cell spacing was measured by the line intercept method. Within the limited thickness of each layer, three randomly oriented lines of 1-mm length were superimposed on the microstructures and the corresponding cell boundary intercepts were measured. In the first two layers with fine cells, the measurements were made at 500 times, while in the remaining layers, the magnification was reduced to 200 times due to the presence of coarser cells. The Vickers microhardness is measured in each layer of all the single layered and multilayered builds by applying a load of 300 g for 30 seconds using a diamond indenter. The measurement is carried out randomly at five points in each layer to realize the extent of variation in the measured values.

3 Numerical Model

A 3-D heat transfer model based on the finite element method is developed using a commercial software ABAQUS (version 6.8EF1).[22] The deposition of the powder materials is modeled using activation of discrete elements in the solution domain. The transient heat conduction equation in the 3-D Cartesian coordinate system can be given as

$$ \frac{\partial }{\partial x}\left( {k\frac{\partial T}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {k\frac{\partial T}{\partial y}} \right) + \frac{\partial }{\partial y}\left( {k\frac{\partial T}{\partial z}} \right) = \rho C\frac{\partial T}{\partial t} $$
(3)

where ρ, C, k, T, and t refer, respectively, to density, specific heat, thermal conductivity, temperature, and time variables. The typical boundary conditions are represented as

$$ k_{n} \frac{\partial T}{\partial n} - q_{s} + h_{c} \left( {T - T_{a} } \right) + \sigma \varepsilon \left( {T^{4} - T_{a}^{4} } \right) = 0 $$
(4)

where n refers to the direction normal to the surface; and k n , h c , ε, σ, and T a refer to thermal conductivity, the surface heat transfer coefficient, the emissivity, the Stefan–Boltzmann constant, and the ambient temperature, respectively. The first term in Eq. [4] represents heat loss due to conduction from the surface whose unit normal is n. The third and fourth terms on the left-hand side refer to convection and radiation from the surface open to air. The second term, q s , considers the heat flux input from the laser beam following a Gaussian distribution as

$$ q_{s} = \frac{\eta Pd}{{\pi \cdot r_{\text{eff}}^{2} }}\exp \left( { - \frac{{d\left( {x^{2} + y^{2} } \right)}}{{r_{\text{eff}}^{2} }}} \right) $$
(5)

where P, η, r eff, and d refer to the laser power, the absorption coefficient of the laser beam, the effective radius of the laser beam, and the beam distribution parameter, respectively. The values of d, r eff, and η are considered as 3.0, 0.5 mm, and 0.28, respectively. The high value of d (>2.0) allows the distribution of the applied heat flux to follow a high peak with a steep descent within a small focused area, which is typical for the type of laser used in the LENS750 machine. The effective beam radius of 0.5 mm is obtained by measuring several melt pool radii that are produced by the LENS750 laser on a SS316 substrate without any powder material. The absorption coefficient, η, of the laser beam is a complex function of substrate temperature, incident surface quality, and shielding atmosphere. To avoid complexity, an average value of η is estimated following Bramson’s equation as

$$ \eta = 0.365\left( {\frac{R}{\lambda }} \right)^{1/2} - 0.067\left( {\frac{R}{\lambda }} \right) + 0.006\left( {\frac{R}{\lambda }} \right)^{3/2} $$
(6)

where R is the temperature-dependent electrical resistivity of the material and λ is the wavelength of the laser beam, the latter being equal to 1.067 μm in the present case. Based on the available values of electrical resistivity of SS316 such as 74 μΩ cm at 300 K (27 °C) and 108 μΩ cm at 900 K (627 °C) and the corresponding computed values of as 0.262 to 0.307, an average value of equal to 0.28 is used. To avoid nonlinearity arising out of the radiation heat loss term, the fourth term in Eq. [4] is omitted and an equivalent surface heat transfer coefficient (h c ) is taken as 0.0024εT 1.16 with the emissivity (ε) as 0.35 and T as the temperature variable.[22,23]

During the LENS process, the powder particles travel through the laser beam until they fall into the melt pool. It is difficult to estimate the real-time temperature of the powder particles, and most of the previous models have considered that these particles would join the melt pool either at ambient[17] or at melting temperature.[7,12] A different approach is considered in the present work. It is presumed that the deposited powder particles are getting heated also in the defocused region of the beam, which is represented by a cylindrical heat source as[24]

$$ q_{v} = \frac{\eta Pd}{{\pi \left( {r_{\text{eff}}^{z} } \right)^{2} h}}\exp \left[ { - d\left( {\frac{{x^{2} }}{{\left( {r_{\text{eff}}^{z} } \right)^{2} }} + \frac{{y^{2} }}{{\left( {r_{\text{eff}}^{z} } \right)^{2} }} + \frac{{z^{2} }}{{h^{2} }}} \right)} \right]\quad {\text{with}}\quad x, \, y \, \le r_{\text{eff}}^{z} ; \, z \le h $$
(7)

away from the substrate. In Eq. [7], q v is the volumetric heat input to a newly activated element representing powder particle, h the deposited layer height, (x, y, z) the coordinate of integration points in any newly activated element with respect to the center of the focused laser beam, and \( r_{\text{eff}}^{z} \) the defocused radius of the laser beam at any height z, which is computed as[25]

$$ r_{\text{eff}}^{z} = r_{\text{eff}} \sqrt {1 + \left( {\frac{\lambda z}{{\pi r_{\text{eff}}^{2} }}} \right)^{2} } $$
(8)

where λ is the wavelength of the laser beam and r eff is the focused beam radius at z = 0.

Three-dimensional 20-node quadratic brick element (DC3D20 in ABAQUS) with temperature as the nodal degree of freedom is used for model calculations.[26] The transient heat transfer calculations are performed using a uniform time-step of 0.08 seconds and a number of very small time increments (~8.0 × 10−7 s) within each time-step. For a constant powder feed rate of 25 g/min (~4.167 × 10−4 kg/s) and powder transfer efficiency of 15 pct, the actual powder mass reaching the substrate in each time-step of 0.08 seconds is estimated as 5.0 × 10−6 kg. The corresponding volume of deposited powder particles is 0.62505 mm3 with the density of SS316 as 8000 kg/m3. This is simulated by activating a set of 160 numbers of discrete elements each of size 0.20 mm × 0.20 mm × 0.095 mm (length × width × height) and arranging them in the form of a 3-D deposit of size 1.0 mm × 1.6 mm × 0.38 mm (length × width × height) in each time-step. The length (1.0 mm) of the block corresponds to the distance traveled by the laser head in 0.08 seconds with a scanning speed of 12.5 mm/s. The height (0.38 mm) of the block corresponds to the target height of each deposited layer. The width of the block equals 1.6 mm to correspond to the net powder volume of 0.62505 mm3. Thus, each layer is simulated through the sequential activation of eight such blocks of new elements. The sequential activation of elements and the application of the heat input to these elements following Eqs. [5] and [7] are realized through a special user subroutine within ABAQUS. All materials properties of SS316 are considered temperature dependent.[22] The liquidus and solidus temperatures of SS316 are taken as 1733 K and 1693 K (1460 °C and 1420 °C), respectively. The layer width at any time instant is estimated by the maximum width of the region that is heated above the liquidus temperature [1733 K (1460 °C)] of the powder material. The estimated build height is the accumulated height of the molten regions of all the layers simulated up to a certain time instant.

4 Estimation Of Cooling Rate, Cell Spacing, and Hardness

The computed transient temperature field is first used to calculate the cooling rate in the freezing range in each deposited layer considering remelting of the same, if any, during deposition of upper layers. Equation [1] is used next to estimate the corresponding layerwise variation in cell spacing. For the estimation of yield strength, it is hypothesized that in a cellular structure, cell spacing, which is much finer than grain size, would correlate well with the material yield strength (or hardness). This is because, though part of the same grain, small misorientation between the neighboring cells, and, more importantly, microsegregation within the cell core and at the boundaries, would further impede the dislocation motion.[27–30] A Hall–Petch like relation (Eq. [2]) is used next to estimate the yield strength (σ y ) with d g as the cell spacing and k y interpreted as a measure of cell boundary resistance to the dislocation motion.

An artifact of applying Eqs. [1] and [2], however, is the absence of reliable values of A and n to predict cell size (as opposed to secondary dendrite arm spacing) and of σ0 and k y to predict yield strength for cellular solidification structure (as opposed to grain structure). In the absence of values applicable to cell structure, we have taken A and n (Eq. [1]) as 80 and 0.33, respectively,[16] strictly applicable to secondary dendrite arm spacing. The coefficients, σ0 and k y , in the Hall–Petch relation are sensitive to the initial condition of the alloy, especially the dislocation structure. The available literature suggests a wide range of possible values of σ0 and k y for SS316, and selection of the most suitable values of σ0 and k y applicable to the multilayer deposits of SS316 has remained a puzzle. In a recent experimental study, Singh et al.[30] reported the values of σ0 and k y as 150.8 and 575 MPa (μm)0.5, respectively, for well-annealed cold-rolled SS316 and the same are followed in the present work. The layerwise hardness (H v ) is calculated as[27,28,30–32]

$$ H_{V} = 3\sigma_{y} \left( {0.1} \right)^{2 - m} $$
(9)

where H V and σ y are in kg/mm2 and m is the Meyer exponent, which is taken as 2.25 based on the range given for steels.[31,32]

5 Results and Discussion

Figure 1 shows a schematic presentation of how the actual deposition is simulated. A set of transparent (deactivated) elements in each layer are continually activated (solid elements) as the laser beam reaches above it to correspond to the addition of powder materials. Figure 2(a) shows a comparison between the simulated (right) and the corresponding actual deposited (left) profiles of a 7-layer build. The colors in the simulated profile indicate several ranges of computed temperature. The red color, in particular, indicates the region that has experienced melting temperature [1733 K (1460 °C)] or above. The thick black line in the simulated structure corresponds to the 1733 K (1460 °C) isotherm and outlines the simulated 7-layer build profile. A slight change in the cross section each time a new layer is deposited is distinct in both the simulated and the actual build profiles. Figure 2(a) indicates a fair agreement between the actual and the corresponding simulated overall profiles of the 7-layer deposit. Figure 2(b) further shows the simulated melt pool profile of each layer that is enclosed by the black curved line [~1733 K (1460 °C) isotherm] and its natural extension to two white dashed lines at the top and bottom. These white lines also correspond to the 1733 K (1460 °C) isotherm and are shown as dashed, since they are inside the total simulated deposit structure.

Fig. 1
figure 1

Schematic outline of powder deposition

Full size image
Fig. 2
figure 2

Comparison of actually deposited 7-layer build profile of austenitic stainless steel with the corresponding (a) simulated build profile and (b) simulated build and layerwise melt pool profiles

Full size image

The actual build profile of a deposited layer tends to confirm to a freeform shape with an irregular convex top, as is evident in the case of the topmost layer shown in Figure 2. However, similar convex top profiles are not visible in the intermediate layers of a multilayer build due to remelting during deposition of the upper layers. The simulated layerwise melt pools in Figure 2(b) also indicate typical convex profiles, however, with flat top surface. This is attributed to the fact that the numerical model represents the powder particles through an ordered geometry of 3-D discrete elements with rectangular cross section, which cannot take a freeform shape. Figure 2(b) depicts an increase in both melt pool size and the extent of remelting of the previously deposited layer as the deposition moves upward. This can be attributed to the reduced heat loss through the substrate and increase in resident temperature of the build structure as the laser beam moves up.

Figure 2 also indicates the difficulty in recognizing the layerwise melt pool depth (or height) of the intermediate layers in the actual build structure. In particular, the extent of remelting into an existing layer during the deposition of the preceding upper layer erases the trace of the fusion zone formed during the deposition of the former. As a result, the reliable estimate of the actual melt pool height or depth in any intermediate layer in a multilayered structure is difficult. A comparison of the computed and the corresponding measured maximum melt pool widths of the topmost layer and the total build height in separately built 1-, 3-, 5-, 7-, and 9- layer structures, therefore, is considered for the primary validation of the computed results. Figure 3 depicts a reasonable agreement between the computed and the corresponding measured melt pool widths and total build heights, although the computed values indicate slight underprediction. This can be attributed to the calculated heat loss into the unmelted elements surrounding the molten region (e.g., green-colored elements in Figure 2). In reality, these unmelted powders hardly remain in contact with the build structure, while these model elements remain ever present in the solution domain of the model and act as a heat sink since deactivation of activated elements is not possible in the commercial software used here.

Fig. 3
figure 3

Comparison of computed and corresponding measured layer width of topmost layer and net build height in separately built 1-, 3-, 5-, 7-, and 9-layer structures

Full size image

Figure 4 shows the computed thermal cycles at the midlength of the 1-, 3-, 5-, 7-, and 9- layer structures. The peak temperatures in each case indicate the time instant when the laser beam passes over the selected location in the respective layer. The computed values of the maximum peak temperatures increase from 1865 K (1592 °C) in the first layer to 2135 K, 2325 K, 2490 K, and 2620 K (1862 °C, 2052 °C, 2217 °C, and 2347 °C) corresponding to the third, fifth, seventh, and ninth layers. The peak temperatures experienced in a specific layer diminish in a characteristic manner as the laser beam moves upward to deposit upper layers. With the increase in the deposit height, the influence of the original substrate in conducting away heat reduces, resulting in greater peak temperature, reduced cooling rate, and enlarged melt pool widths (Figures 2 and 3).

Fig. 4
figure 4

Computed thermal cycles in alternate layers on a 9-layer deposit

Full size image

Figure 5(a) shows the average and the extent of variations in the computed values of layerwise cooling rates during solidification in a 9-layer deposit. The cooling rate reduces markedly from the first to the fifth layer and gently in the upper layers. The high cooling rates in the bottom layers are due to high peak temperature and the possibility of rapid heat loss through the original substrate. The steep reduction in the cooling rate in the upper layers can be attributed to the increase in the resident temperature of the build, as can be observed in Figure 4, which slows the rate of conduction heat loss. The average cell spacing, irrespective of their orientations, is measured by the line intercept method in different layers. Figure 5(b) shows a fair agreement between the measured and the corresponding estimate values of average cell spacing (following Eq. [1]). The cell spacing increases with the build height due to the decrease in the cooling rate. For example, the estimated cell spacing in the first layer is 3.0 μm, which increases to nearly 8.0 μm in the ninth layer. The extent of scatter in the computed and corresponding measured values of cell spacing in the layerwise solidified structures are also indicated in Figure 5(b). The slight underestimation of the cell spacing in comparison to the corresponding measured values can obviously be attributed to the overprediction of computed cooling rates, as explained earlier. In reality, the unmelted powder particles can hardly contribute to heat loss, and thus, the actual cooling rates during solidification would possibly be slightly lower. The fact that the convective transport of heat in the melt pool is neglected here is also possibly a factor to compute slightly higher peak temperatures and cooling rates.

Fig. 5
figure 5

(a) Computed values of layerwise variation in cooling rates and (b) comparison between the estimated and the corresponding measured layerwise values of cell spacing in a 9-layer deposit

Full size image

Figures 6(a) through (c) show the typical microstructure at different locations of the 9-layer deposit. The solidified structures primarily depict cells with no appreciable dendritic growth (except in the top layer where the cooling rates are lower), as reported earlier in independent literature.[16] Solidification is predominantly columnar in all the layers. The orientation of the cells is not the same in all the grains, though, and follows the changing direction of the prevailing maximum thermal gradient. Since a thin hatch of liquid metal solidifies progressively in successive layers, true equiaxed grains are not likely to form. Figure 7(a) shows the BSE image of the cell structure from the first layer of a 9-layer build. The BSE image of the cell structure from the ninth layer is qualitatively similar to the first layer (and, hence, is not shown), but shows wider cell spacing. The black line in the middle of Figure 7(a) indicates that Figures 7(b) and (c) depict the corresponding line scans (along the black line shown in the middle of Figure 7(a)) of Cr and Mo across the cells. Microsegregation in the form of Cr and Mo enrichment toward the cell boundaries is clearly seen. This is the result of incomplete solute diffusion in the solid phase due to the high cooling rates prevailing during the overall deposition process. Nickel was found to be more uniformly distributed across the cells, possibly due to its high partition ratio k during solidification. While the primary phase to solidify is known to be austenite in these steels, it is not clear at this point if any new phase forms at the cell boundaries due to microsegregation. Similar evidence of Cr and Mo segregation was found in the top layer of the deposits in spite of the comparatively lower, but otherwise high, cooling rates.

Fig. 6
figure 6

Solidified microstructures at the (a) lower, (b) middle, and (c) top layer for a 9-layer structure

Full size image
Fig. 7
figure 7

(a) EPMA BSE image of the cell structure from the first layer of the 9-layer deposit. (b) and (c) Line scans of Cr and Mo, in the first and ninth layers, respectively

Full size image

Figure 8 shows a comparison between the estimated and the corresponding measured values of layerwise microhardness in a 9-layer build structure. The extent of variation in the estimated value of hardness in a specific layer corresponds to the variations in the layerwise cell spacing. The hardness decreases with the increase in build height due to the reduction in the cooling rate and resulting increase in the cell spacing. The discrepancy between the estimated and the corresponding measured hardness values can possibly be attributed to the value used for σ0 and k y in Eq. [2], which are extracted from the statistically fitted results reported in independent literature for well-annealed SS316.[29] Furthermore, it can be pointed out that the Hall–Petch like relation and the corresponding coefficients, σ0 and k y , are originally conceived for typical grain boundaries and used here for the cell boundaries that have much smaller misorientations across them. A more reliable set of values of these coefficients would possibly be able to provide more realistic estimation of layerwise hardness distribution.

Fig. 8
figure 8

Comparison between estimated and measured microhardness in deposited layers

Full size image

The computed values of cooling rate, computed and measured values of cell spacing, and the measured values of microhardness reported in the present work are in line with the similar values reported earlier for LENS-deposited layers of austenitic stainless steels. Zheng et al. reported the cooling rates, DAS, and layer hardness values in the ranges of 103 to 104 K/s (103 to 104 °C/s), 1 to 5 μm, and 200 to 300 Hv, respectively.[16] Smugeresky reported the cell spacing and layer hardness values in the ranges of 2 to 10 μm and 180 to 230 (Knoop hardness), respectively.[17] The ranges of the estimated values of cooling rates, cell spacing, and hardness distributions in the present work confirm, respectively, to 103 to 104 K/s (103 to 104 °C/s), 3 to 8 μm, and 190 to 245 Hv. Moreover, the values of deposit dimensions, cell spacing, and hardness distributions in the solidified layers are estimated fairly using a numerical heat transfer analysis and an organized set of analytical relations. It is thus hoped that a similar integrated approach can be used as a tool to optimize parameters in the LENS process to achieve the desired mechanical properties in deposited layers.

6 Conclusions

A 3-D heat transfer analysis followed by an organized set of constitutive relations is used to compute layerwise variation in the peak temperatures, deposit dimensions, cooling rates, cell spacing, and hardness distributions in the LENS-deposited multilayered build structure of SS316. For a constant laser power and scanning velocity, the layer width and peak temperature increase while the cooling rate decreases toward the top layers. The solidified deposit has confirmed primarily to a cellular structure with an increase in the cell spacing as the cooling rate reduces toward the top layers. Correspondingly, the yield strength and hardness also reduce from the bottom toward the top layers. The computed values of the deposit dimensions and cell spacing are in fair agreement with the corresponding experimentally measured values. The computed values of layerwise hardness are slightly overpredicted in comparison to the actual measured values. Further investigation is needed to acquire more reliable values of cell boundary strengthening parameter for more accurate prediction of layerwise hardness distribution.