Introduction

High-end instrument plays an important role in key departments of national economy. And, their malfunction and lose efficacy may cause very serious economic losses and social impacts. As advanced equipment for petroleum exploration and development, electromagnetic wave logging-while-drilling (LWD) tools are not only conducive to the description of drilling reservoirs and geo-steering, but also for timely identification of “sweets point” in front of the bit and reservoir boundaries (Li et al. 2019; Bittar et al. 2009). What’s more, real-time adjustment of borehole trajectory and drilling engineering parameters are of great significance to improve reservoir drilling rate as well as single-well production. However, current research directions about advanced azimuthal electromagnetic wave LWD tool mainly focused on numerical modeling, logging response analysis, logging multi-parameter inversion models, and resistivity imaging simulations (Wu et al. 2020; Yan et al. 2020). At the same time, due to the actual working conditions and extreme environmental stresses, the compensation-type electromagnetic wave LWD tools have many deficiencies such as large measurement errors, high-maintenance costs, uncontrollable working time, and hard to interpret logging data. During the process of drilling construction, the tool may break down by many faults such as antenna breakage, negative electrode shedding of high-voltage rod, wet connector damage, capacitor failure, lithium battery explosion of power supply, receiving board damage, core female connector fracture, and microprocessor burnout frequently. These above-mentioned tool failures would not only affect measurement accuracy and real-time geology steering capability of logging instruments but also affect the normal construction of the drilling team, which may consume a lot of manpower and material resources. How to ensure stable and safe operation of the electromagnetic wave LWD tool is the main research content of technologies of reliability improvement and instrument health management. Therefore, in this paper, the electromagnetic wave LWD tool can be taken as an example. The failure data and the failure time of antenna system have been counted, thus failure mode and failure mechanism can be analyzed. Based on statistical data of the failure time of each component of antenna system, a failure model based on Weibull distribution has been established and the remaining service life also can be evaluated. Combine the reliability failure model and working conditions with the first-line spare parts management conditions, as a result of studying the assessment of the instrument health status as well as operation and maintenance decision-making.

Principle and method

Weibull distribution

The failure process of electromagnetic wave LWD tool could be divided into early failure period, accidental failure period, and loss validity period. As a failure distribution model of Weibull distribution, it has a wide range of applications (Kam et al. 2021; Wang et al. 2021). It contains three parameters. Different parameter can degenerate the failure distribution into an exponential distribution or a normal distribution. Therefore, the Weibull distribution can be described to various stages of instrument failure. If T obeys the Weibull distribution with three parameters m, η, and σ. Thus it can be expressed as T ~ W(m, η, σ). And then, the failure probability density function f(t) of Weibull distribution can be expressed as:

$$f(t) = \frac{m}{\eta }\left(\frac{t - \sigma }{\eta }\right)^{m - 1} \cdot e^{{ - \left(\frac{t - \sigma }{\eta }\right)^{m} }},$$
(1)

where m represents the shape parameter. η represents the scale parameter. σ represents the position parameter. The probability density distribution function F(t) of Weibull distribution can be expressed as:

$$F(t) = {1 - }e^{{ - \left(\frac{t - \sigma }{\eta }\right)^{m} }}.$$
(2)

According to the f(t) and F(t) of the three-parameters Weibull distribution, the failure rate function, reliable life, median life, characteristic life, average life and replacement life could be obtained (Dey et al. 2020; Strzelecki 2021).

$$\lambda (t) = \frac{m}{\eta }\left(\frac{t - \sigma }{\eta }\right)^{m - 1} ,\left(\sigma \le t\right)$$
(3)
$$T_{R} = \delta + \eta \left(\ln \frac{1}{R}\right)^{\frac{1}{m}}$$
(4)
$$T_{0.5} = \delta + \eta \left(\ln \frac{1}{0.5}\right)^{\frac{1}{m}}$$
(5)
$$T_{{e^{ - 1} }} = \delta + \eta \left(\ln \frac{1}{{e^{ - 1} }}\right)^{\frac{1}{m}}$$
(6)
$$E(T) = \int_{0}^{R} {R(t)dt} = \delta + \eta \Gamma \left(1 + \frac{1}{m}\right)$$
(7)
$$T_{\lambda } = \delta + \eta \left(\frac{\lambda \eta }{m}\right)^{{\frac{1}{m - 1}}},$$
(8)

where, R represents the reliability. λ represents the failure rate. t represents the time. λ(t) represents failure rate function. TR represents reliable life. T0.5 represents median life. Te-1 represents characteristic life. E(T) represents average life. Tλ represents replacement life.

Model parameters

Weibull function can be solved by many statistical methods and mathematical methods such as graphical method, least square method, genetic algorithm, maximum likelihood estimation, and so on (Zhou et al. 2019; Jalobeanu et al. 2002). This paper used maximum likelihood estimation method to solve parameters of the Weibull function failure model. The fault data of a certain type of electromagnetic wave LWD tool has been used as timing censored data, and by using these fault data the reliability of each component’s of antenna system can be computed. The reliability of each component could be used to analyzed the influence between units and system of the tool. Assuming that f(t) represents the failure probability density function, according to the observation data of random variable t and then the likelihood function L(θ) can be obtained and which is shown in Eq. (9).

$$\begin{aligned} L(\theta ) &= L\left(t_{1} ,t_{2} , \ldots ,t_{n} ;\theta \right) \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} &= \coprod\limits_{i = 1}^{n} {f\left(t_{i} ;\theta \right)}, \hfill \\ \end{aligned}$$
(9)

where, t1, t2, …, tn represent sampled values. f(t, θ) represents the overall probability density function. θ represents pending parameters in the probability density function, and where θ = (θ1, θ2,…, θn). Deriving the two ends of Eq. (9), then estimated values of θ1, θ2,…, θncan be obtained.

$$\frac{\partial \ln L(\theta )}{{\partial \theta_{i} }} = 0,\begin{array}{*{20}c} {} & {i = 1,2, \ldots ,n} \\ \end{array}$$
(10)

Assuming that fails are broken down at t = 0, then three-parameter Weibull distribution could be simplified to two-parameter Weibull distribution. When σ is equal to 0, the two-parameter Weibull distribution can be briefly expressed as T ~ W(m, η).

$$f(t) = \frac{m}{\eta }\left(\frac{t}{\eta }\right)^{m - 1} \cdot e^{{ - \left(\frac{t}{\eta }\right)^{m} }} ,\left(m,\eta > 0;\quad t \ge 0\right)$$
(11)
$$F(t) = 1 - e^{{ - \left(\frac{t}{\eta }\right)^{m} }} ,\left(m,\eta > 0;\quad t \ge 0\right)$$
(12)

And then, the log-likelihood function of the shape function m and the scale function η can be shown as follows:

$$\ln L(\theta ) = n\ln \left( {\frac{m}{\eta }} \right) + \mathop{\sum}\limits_{i = 1}^{n} \left[ - \left(\frac{x}{\eta }\right)^{m} + (m - 1)\ln \left(\frac{x}{\eta }\right)\right]$$
(13)
$$\left\{ \begin{gathered} \frac{\partial \ln L(m,\eta )}{{\partial m}} = 0 \hfill \\ \frac{\partial \ln L(m,\eta )}{{\partial \eta }} = 0 \hfill \\ \end{gathered} \right. .$$
(14)

Calculating the extreme value of likelihood function and solving Eq. (14), the solution of shape function m and the scale function η can be calculated.

Modeling process

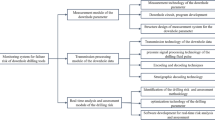
The map of technical route can be shown in Fig. 1. Firstly, faults data of antenna system such as coil, circuit board, lithium battery, etc. have been collected. Thus, faults statistics and classifications can be implemented by using those faults data. Secondly, exponential distribution, Weibull distribution, lognormal distribution can be used to build up failure models. And by using goodness-of-fit method we can test and obtain the optimal failure model. At last, based on Weibull distribution failure model, reliability quantitative analysis results of the antenna system can be obtained. That is to say, fault prediction and health management of the tool could be carried out based on instrument characteristics, reliability, failure mode.

Fig. 1
figure 1

The map of technical route

Full size image

Failure analysis and failure model screening

Failure mode and failure statistics

Main components of the antenna system can be divided into a lot of units such as coil system, data acquisition and processing system, power supply, antenna protection system, etc. In actual using of the tool, because of the existence of environmental stresses such as underground high-temperature, high-pressure, strong vibration, high torque, mud erosion, etc. It could be leaded to many faults such as receiving and transmitting antennas breaking, circuit board burnout, protective sleeve deformation, and window colloid sealing breakdown, power supply explosion, etc. High-frequency faults are happened to antenna system are fracture of receiving, transmitting antennas, circuit board transmitting burning, circuit board reception, power drive board, data acquisition board, data storage board, and power supply explosion. A fault example is shown in Fig. 2. And failure time of subsystem of the antenna system is shown in Fig. 3.

Fig. 2
figure 2

Faults in antenna system

Full size image
Fig. 3
figure 3

Failure time of subsystem

Full size image

According to statistical data of failure time samples shown in Fig. 3. And combine the Eq. (13) to solve the Eq. (14), the parameter m1 and η1 of the two-parameter Weibull distribution corresponding to the coil failure model are obtained (where, m1 = 1.74 and η1 = 5789.7). The parameter m2 and η2 of the two-parameter Weibull distribution corresponding to the circuit board failure model also can be obtained (where, m2 = 2.19 and η2 = 161.5). The parameter m3 and η3 of the two-parameter Weibull distribution corresponding to the lithium battery failure model are obtained (where, m3 = 1.78 and η3 = 2136.4). Because the antenna, circuit boards, and power supply components in the antenna system are independent of each other, thus according to the principles of reliability prediction and distribution, we can acquire the failure probability density function and the failure probability distribution function. The failure probability density function of each subsystem is shown as follows:

$$\begin{gathered} f_{1} (t) = 0.4\frac{{m_{1} }}{{\eta _{1} }}\left( {\frac{t}{{\eta _{1} }}} \right)^{{m_{1} - 1}} \cdot e^{{ - \left( {\frac{t}{{\eta _{1} }}} \right)^{{m1}} }} = 1.2 \times 10^{{ - 4}} \left( {\frac{t}{{5789.7}}} \right)^{{0.74}} \cdot e^{{ - \left( {\frac{t}{{5789.7}}} \right)^{{1.74}} }} \hfill \\ f_{2} (t) = 0.4\frac{{m_{2} }}{{\eta _{2} }}\left( {\frac{t}{{\eta _{2} }}} \right)^{{m_{2} - 1}} \cdot e^{{ - \left( {\frac{t}{{\eta _{2} }}} \right)^{{m_{2} }} }} = 5.4 \times 10^{{ - 3}} \left( {\frac{t}{{161.5}}} \right)^{{1.19}} \cdot e^{{ - \left( {\frac{t}{{161.5}}} \right)^{{2.19}} }} \hfill \\ f_{3} (t) = 0.2\frac{{m_{3} }}{{\eta _{3} }}\left( {\frac{t}{{\eta _{3} }}} \right)^{{m_{3} - 1}} \cdot e^{{ - \left( {\frac{t}{{\eta _{3} }}} \right)^{{m3}} }} \begin{array}{*{20}c} = \\ \end{array} 2.6 \times 10^{{ - 4}} \left( {\frac{t}{{2136.4}}} \right)^{{1.78}} \cdot e^{{ - \left( {\frac{t}{{2136.4}}} \right)^{{2.78}}, }} \hfill \\ \end{gathered}$$

where f1(t) represents failure probability density function of coil failure model. f2(t) represents failure probability density function of circuit board failure model. f3(t) represents failure probability density function of lithium battery failure model. The failure probability distribution function of each subsystem can be shown as:

$$F_{1} (t) = 0.4\left[1 - e^{{ - \left(\frac{t}{{\eta_{1} }}\right)^{{m_{1} }} }} \right]\begin{array}{*{20}c} {\begin{array}{*{20}c} { = 0.4[1 - } \\ \end{array} } \\ \end{array} e^{{ - \left(\frac{t}{5789.7}\right)^{1.74} }} ]$$
$$F_{2} (t) = 0.4\left[1 - e^{{^{{ - \left(\frac{t}{{\eta_{{_{2} }} }}\right)^{{m_{2} }} }} }} \right]\begin{array}{*{20}c} {\begin{array}{*{20}c} { = 0.4[1 - } \\ \end{array} } \\ \end{array} e^{{ - \left(\frac{t}{161.5}\right)^{2.19} }} ]$$
$$F_{3} (t) = 0.2\left[1 - e^{{^{{ - \left(\frac{t}{{\eta_{3} }}\right)^{{m_{3} }} }} }} \right]\begin{array}{*{20}c} {\begin{array}{*{20}c} { = 0.2[1 - } \\ \end{array} } \\ \end{array} e^{{ - \left(\frac{t}{2136.4}\right)^{1.78} }} ],$$

where, F1(t) represents probability density distribution function of coil failure model. F2(t) represents probability density distribution function of circuit board failure model. F3(t) represents probability density distribution function of lithium battery failure model. Therefore, the mixed failure probability density function fi(t) and the mixed failure probability distribution function Fi(t) of the antenna system are shown as:

$$\begin{aligned} f_{i} (t) &= f_{1} (t) + f_{2} (t) + f_{3} (t) \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \\&= 1.2 \times 10^{ - 4} \left(\frac{t}{5789.7}\right)^{0.74} \cdot e^{{ - \left(\frac{t}{5789.7}\right)^{1.74} }} + 5.4 \times 10^{ - 3} \left(\frac{t}{161.5}\right)^{1.19} \cdot e^{{ - \left(\frac{t}{161.5}\right)^{2.19} }} + 2.6 \times 10^{ - 4} \left(\frac{t}{2136.4}\right)^{1.78} \cdot e^{{ - \left(\frac{t}{2136.4}\right)^{2.78} }} \hfill \\ \end{aligned}$$
$$\begin{gathered} F_{i} (t) = F_{1} (t) + F_{2} (t) + F_{3} (t) \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} = \begin{array}{*{20}c} {\begin{array}{*{20}c} {0.4[1 - } \\ \end{array} } \\ \end{array} e^{{ - \left(\frac{t}{5789.7}\right)^{1.74} }} ] + \begin{array}{*{20}c} {\begin{array}{*{20}c} {0.4[1 - } \\ \end{array} } \\ \end{array} e^{{ - \left(\frac{t}{161.5}\right)^{2.19} }} ] + \begin{array}{*{20}c} {\begin{array}{*{20}c} {0.2[1 - } \\ \end{array} } \\ \end{array} e^{{ - \left(\frac{t}{2136.4}\right)^{1.78} }} ] \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} = 1 - 0.4e^{{ - \left(\frac{t}{5789.7}\right)^{1.74} }} - 0.4e^{{ - \left(\frac{t}{161.5}\right)^{2.19} }} - 0.2e^{{ - \left(\frac{t}{2136.4}\right)^{1.78} }} \hfill \\ \end{gathered}.$$

Failure model inspection

Assuming that the failure of each component in the antenna system is independent of each other. We can select the exponential distribution model and the logarithmic distribution model to compare with the Weibull distribution model to acquire the result of goodness-of-fit test (Kim 2020; He et al. 2020). According to fn(t) and Fn(t), and by using Matlab software to build up the failure modeling, curves of antenna system failure probability density function and failure probability distribution function can be obtained which are shown in Figs. 4 and 5.

Fig. 4
figure 4

Failure probability density function curve

Full size image
Fig. 5
figure 5

Failure probability distribution function curve

Full size image

Combining the statistical data of the failure time of each component and failure probability distribution function, values of parameter estimation of each failure model could be calculated and shown in Table 1.

Table 1 Parameters estimation results
Full size table

Assuming that t1, t2, …, tn are independently distributed samples, the common distribution of them is denoted as F, and the goodness-of-fit test is used to test the hypothesis:

$$H_{0} :F \in P_{0},$$
(15)

where P0 represents the distribution family, which consists of distributions of specific properties. H0 means that the distribution of the sample population obeys the theoretical distribution. Assuming that F represents a continuous distribution, t1, t2, …, tn represent independent random samples which are extracted from F. And we consider the null hypothesis:

$$H_{0} :F \in F_{0},$$
(16)

where, F0 represents the continuous distribution function of the known distribution. In order to test the above hypothesis, the empirical cumulative distribution function Fn of T1, T2, …, Tn are used to calculate a variety of different cumulants. Because the Kolmogorov–Smirnov (K-S) test method is suitable for small sample test (Kovalev and Utkin 2020), thus the following can use the K-S test method to testing the failure model. Assuming that samples distribution of H1 is not obey the theoretical distribution. Then compare the empirical distribution function Fn(t) with the hypothetical theoretical distribution function F(t) to establish the statistic Dn.

$$\begin{aligned} D_{n} &= \mathop {{\text{sup}}}\limits_{ - \infty \le x \le \infty } \left| {F_{n} (t) - F(t)} \right| \hfill \\ \begin{array}{*{20}c} {} & = \\ \end{array} {\text{max}}\{ d_{i} \} \hfill \\ \end{aligned}$$
(17)
$$d_{i} = \max \left[\left| {F(t) - \frac{i - 0.3}{{n + 0.4}}} \right|\right],$$
(18)

where, i = 1, 2, …50. n represents the sample size. The sample size n of invalid samples in Fig. 3 is all equal to 50. And the significance level α is equal to 0.05. According to the K-S test critical value table, the rejection critical value Dn, α is equal to 0.192. When Dn<Dn, α the test passes, otherwise the null hypothesis is rejected. According to the F(t), assuming that the failure time obeys the two-parameter Weibull distribution, then:

$$F(t) = 1 - 0.4e^{{ - \left(\frac{t}{5789.7}\right)^{1.74} }} - 0.4e^{{ - \left(\frac{t}{161.5}\right)^{2.19} }} - 0.2e^{{ - \left(\frac{t}{2136.4}\right)^{1.78} }}.$$

According to the F(t) of the above-mentioned antenna system, Dn could be calculated and here Dn is equal to 0.187. Therefore, Dn < Dn, α the test passes. The three failure models have been tested according to the K-S test method, and test results are shown in Table 2. In Table 2 we can see that the Weibull distribution model is passed and the data model is correct.

Table 2 Test results of failure model
Full size table

Instrument reliability analysis and health management

Reliability analysis

According to the Weibull distribution failure model, the mean time between failures (MTBF), characteristic life (Te-1), reliable life (TR), median life (T0.5), the system reliability function R(t) and the system failure rate function λ(t) can be calculated.

$$\begin{aligned}MTBF &=\,0.4\left[\delta_{1} + \eta_{1} \Gamma \left(1 + \frac{1}{{m_{1} }}\right)\right]\\& + 0.4\left[\delta_{2} + \eta_{2} \Gamma \left(1 + \frac{1}{{m_{2} }}\right)\right]\begin{array}{*{20}c} \\& +{ 0.2\left[\delta_{3} + \eta_{3} \Gamma \left(1 + \frac{1}{{m_{3} }}\right)\right]} \\ \end{array} = 3502(h)\end{aligned}$$
$$\begin{aligned} T_{{e^{ - 1} }}& = 0.4[\delta {}_{1} + \eta {}_{1}\left(\ln \frac{1}{{e^{ - 1} }}\right)^{{\frac{1}{{m_{1} }}}} ] \\&+ 0.4[\delta_{2} + \eta_{2} \left(\ln \frac{1}{{e^{ - 1} }}\right)^{{\frac{1}{{m_{2} }}}} ]\\& + 0.2[\delta_{3} + \eta_{3} \left(\ln \frac{1}{{e^{ - 1} }}\right)^{{\frac{1}{{m_{3} }}}} ] = 1749(h) \end{aligned}$$
$$\begin{aligned}{T_R}& = 0.4\left[ {{\delta _1} + {\eta _1}{{\left( {\ln \frac{1}{R}} \right)}^{\frac{1}{{m1}}}}} \right] \\&+ 0.4\left[ {{\delta _2} + {\eta _2}{{\left( {\ln \frac{1}{R}} \right)}^{\frac{1}{{{m_2}}}}}} \right] \\&+ 0.2\left[ {{\delta _3} + {\eta _3}{{\left( {\ln \frac{1}{R}} \right)}^{\frac{1}{{{m_3}}}}}} \right] = 454(h)\end{aligned}$$
$$\begin{aligned}T_{0.5} &= 0.4\left[\delta_{1} + \eta_{1} \left(\ln \frac{1}{0.5}\right)^{{\frac{1}{{m_{1} }}}} \right] \\&+ 0.4\left[\delta_{2} + \eta_{2} \left(\ln \frac{1}{0.5}\right)^{{\frac{1}{{m_{2} }}}} \right]\\& + 0.2\left[\delta_{3} + \eta_{3} \left(\ln \frac{1}{0.5}\right)^{{\frac{1}{{m_{3} }}}} \right] = 1409(h)\end{aligned}$$
$$R(t) = 1 - F(t)\begin{array}{*{20}c} = \\ \end{array} 1 - [1 - 0.4e^{{ - \left(\frac{t}{5789.7}\right)^{1.74} }} - 0.4e^{{ - \left(\frac{t}{161.5}\right)^{2.19} }} - 0.2e^{{ - \left(\frac{t}{2136.4}\right)^{1.78} }}] \begin{array}{*{20}c} { = 0.4e^{{ - \left(\frac{t}{5789.7}\right)^{1.74} }} } + \\ \end{array} 0.4e^{{ - \left(\frac{t}{161.5}\right)^{2.19} }} + 0.2e^{{ - \left(\frac{t}{2136.4}\right)^{1.78} }}$$
$$\begin{aligned} \lambda (t) &= \frac{{1.2 \times 10^{ - 4} (\frac{t}{5789.7})^{0.74} \cdot e^{{ - (\frac{t}{5789.7})^{1.74} }} }}{{\begin{array}{*{20}c} {0.4e^{{ - (\frac{t}{5789.7})^{1.74} }} + } \\ \end{array} 0.4e^{{ - (\frac{t}{161.5})^{2.19} }} + 0.2e^{{ - (\frac{t}{2136.4})^{1.78} }} }}\\ &+ \frac{{5.4 \times 10^{ - 3} (\frac{t}{161.5})^{1.19} \cdot e^{{ - (\frac{t}{161.5})^{2.19} }} }}{{\begin{array}{*{20}c} {0.4e^{{ - (\frac{t}{5789.7})^{1.74} }} + } \\ \end{array} 0.4e^{{ - (\frac{t}{161.5})^{2.19} }} + 0.2e^{{ - (\frac{t}{2136.4})^{1.78} }} }} \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array}\\& + \frac{{2.6 \times 10^{ - 4} (\frac{t}{2136.4})^{1.78} \cdot e^{{ - (\frac{t}{2136.4})^{2.78} }} }}{{\begin{array}{*{20}c} {0.4e^{{ - (\frac{t}{5789.7})^{1.74} }} + } \\ \end{array} 0.4e^{{ - (\frac{t}{161.5})^{2.19} }} + 0.2e^{{ - (\frac{t}{2136.4})^{1.78} }} }} \hfill \\ \end{aligned}$$

According to quantitative analysis of the reliability of antenna system, the MTBF of the antenna system can be acquired, where the MTBF is equal to 3502 h. In order to increase the MTBF, the method to improve the top value of the probability density can be used. It can let the confidence interval of MTBF contain the true value of the unknown parameter. The two-sided confidence interval for estimating the MTBF with 90% confidence level can be expressed as:

$${\hat \theta _L} = \frac{{2T}}{{\chi _{0.05}^2(2r + 2)}} < MTBF < {\hat \theta _U} = \frac{{2T}}{{\chi _{0.95}^2(2r)}},$$
(19)

where r represents the number of failure of each unit in antenna system. T represents the total reliability test time. After calculation, when the confidence level is equal to 90%, the estimated value of the two-sided confidence interval of MTBF is between 1853.04.81 h and 5432.37 h. According to the reliability function, failure probability density function, and probability density distribution function, we can compute the reliable life, median life, characteristic life, average life, and replacement life of the antenna system. Combined with the 90% confidence level to estimate the MTBF of the tool, then the remaining service life of instrument can be estimated.

Health management of instrument

Based on the remaining service life estimation model, the failure rate and failure time of the electromagnetic wave LWD tool could be evaluated and predicted in a certain period. The prediction scale of remaining service life can determine the maintenance management of the tool. It also decides maintenance management from preventive maintenance to condition-based on maintenance, or from preventive maintenance to forecasting maintenance (Tsui et al. 2019). Because the actual working conditions and working environments have a lot of uncertain situations, thus based on the failure model and comprehensively considering the maintenance cost of the tool, then the tool’s operation and maintenance decision can be proposed. Meanwhile, considering the interference of the different operating conditions and the uncertain factors in the working environment, the input information of the instrument system should be cleaned and summarized. After that, we should report fault diagnosis results and compute the probability of the fault which may occur within a certain period. And the optimization strategy of system operation and maintenance can be proposed. That means, it can maximum manufacturing the reliability of the instrument and reducing operation and maintenance costs. The relationship between instrument reliability and maintenance costs is shown in Fig. 6.

Fig. 6
figure 6

Reliability and instrument maintenance cost

Full size image

In the process of drilling operations, usually, the drilling team equips with two electromagnetic wave LWD tools within the same operating model and testing standard. Because different types of tool requirements may occur in different regions and different time periods. Therefore it is necessary to establish a joint scheduling model for maintenance and spare parts management. According to this model, the optimal spare parts order cycle and the maximum production value of the instrument could be evaluated. When the supply side encounters a sudden changing, the optimal scheduling model can be given within the shortest time and the emergency plan also could be quickly reconstructed. The operation and maintenance joint optimization program is shown in Fig. 7.

Fig. 7
figure 7

Operation and maintenance joint optimization program

Full size image

During the working process, by using portable sensors the electromagnetic wave LWD tool can measure engineering parameters and geological parameters. Meanwhile, the optimized instrument system can also measure the performance parameters of the instrument's own components and system performance parameters itself. Through the processing of noise reduction, dimension reduction, feature extraction, and fusion of multi-dimensional input parameters, we can achieve state monitoring, extreme value judgment, and deviation calculation of the electromagnetic wave LWD tool system. When the instrument system judges that the system may be malfunctioning through the comparison of key parameters, the instrument state assessment, and abnormality detection will be launched. Then, failure mode, failure mechanism, and fault location detection for the failure of key units will be detected by instrument system. Meanwhile, fault prediction and health management of the instrument could be carried out based on signal, characteristics, reliability, failure mode, etc. Because system fault characteristics are closely connected with the multi-dimensional digital model, therefore the inversion of fault evolution mechanism can be acquired.

Conclusions

The failure mode and the failure mechanism of the electromagnetic wave LWD tool have been studied according to statistics of faults and failure time during the drilling process. Based on the big data of failure time and by using the reliability failure model, the mixed failure probability density function and failure probability distribution function of the instrument system could be acquired. Combined with the goodness-of-fit test method, the validity of the failure model in the reliability analysis of the antenna system can be verified.

According to the instrument reliability failure model, the reliability, failure rate, reliability life, characteristic life, and median life of each component or subsystem of the electromagnetic wave LWD tool could be calculated, so as to evaluate using time and endurance capability of the tool when it working underground. Meanwhile, according to antenna system failure model, the quality control and optimization of the antenna components during the production process and maintenance process can be guided. It means that antenna system failure model can reduce failure cost and control maintenance cost of the tool. And it also can improve the instrument reliability largely. The study of the failure probability density function and failure probability distribution function of the instrument system is of practical significance for exploring laws of failure and defect occurrence of the same type of electromagnetic wave LWD tool. It has great importance to the development of new type high-reliability azimuth electromagnetic wave LWD tool.