Noise reduction for desert seismic data using spectral kurtosis adaptive bandpass filter

Abstract

In view of the heterogeneity and week similarity of random noise in the desert seismic exploration, and lots of random noise focused on low frequency, the traditional bandpass filter and wavelet transform are used to separate the signal and noise. Although there are some denoising effects, the noise cannot be suppressed well, and effective signal is damaged to some extent. Because of the above shortcomings, we propose a bandpass filter denoising method based on spectral kurtosis in this paper. This method is based on the signal and the random noise’s energy distribution characteristics in the frequency domain. First, through short-time Fourier transform (STFT), the spectral kurtosis of noisy signals is obtained. Second, we design a new threshold by the obtained spectral kurtosis, the value of spectral kurtosis greater than the threshold is preserved, and the spectral kurtosis less than the threshold is set to 0. So, the method realises the adaptive choice of the filter passband, getting an adaptive bandpass filter. At the same time, the noise can be suppressed to a greater extent while the effective signal is retained very well. The noise removal results of synthetic data and actual data show that the proposed method has very good denoising performance and amplitude preserving capability.

Introduction

In recent years, many signal processing experts all over the world have been constantly researching to improve the signal-to-noise ratio. At present, many methods from different fields have been proposed and applied effectively to signal extraction and noise suppression of seismic data. The representative of these methods is multi-scale analysis denoising method and time–frequency analysis denoising method. Wavelet transform (WT) is a typical multi-scale analysis method. It has a better time–frequency local analyzing ability, so it is more effective than Fourier transform on the signal representation. Since the 90s of the last century, a lot of researches on the combination of wavelet and other technologies have been achieved (Johnstone and Silverman 1997; Chang et al. 2002; Liu et al. 2015). At present, the wavelet domain denoising technology is preferably applied in the field of seismic exploration. However, the transformation is not directional. When dealing with complicated desert noisy signal, it has limitations in preservation of effective signal in different directions. Moreover, because of the similarity between the desert noise and the effective signal, the setting of threshold cannot separate signals and noises very well.

Time–frequency peak filtering (TFPF) method is a typical time–frequency analysis method. It can construct locally parallel radial trajectories, hyperbolic trajectory, parabolic trajectory and the Radon domain of TFPF complex nonlinear random noise denoising model (Xiong et al. 2014; Wu et al. 2016; Zhuang et al. 2014; Tian et al. 2014), respectively, from the aspects of window function, joint time–frequency distribution and PWVD weights reset to increase the accuracy of the algorithm and realize the optimization of parameter (Zhang et al. 2015; Lin et al. 2013). This method can handle non-stationary signals, and the processing type of the signal is characterized by wide aperture. The method deals with weak signals in seismic exploration records with unbiased estimation of the time–frequency peak filtering. In this process, random noise suppression can be realized without the design of the time–frequency filter. However, the results of random noise reduction in desert areas are not satisfactory. TFPF requires that the signal recovered from the noisy signal must be an unbiased estimation. For a nonlinear signal, its smoothness depends on the length of the window, and the characteristics of desert signal including the low frequency and non-uniform consistency make the TFPF extract some noises as signals in time and frequency domain.

Current noise suppression technology can extract the traditional seismic signal very well and suppress the random noise. However, in the face of the complicated geological conditions and exploration environment in the desert area, some seismic signal extraction algorithms have shown great inadaptability. Due to the bad environment for seismic acquisition, the final collected seismic data have a large amount of complicated and strong random noise. The noise whose intensity is large can damage characteristics of effective signal events in the time and frequency domain. As the difference in characteristics weakens between the effective signal and random noise in spatial domain and various transform domains, the signal–noise separation algorithm based on the difference of signal and noise characteristics is not accurate to extract effective signal. When there is a lot of low-frequency noise which has irregular distribution in the data, the continuity of the phase axis becomes worse and the spatial correlation is reduced. In view of the limitations of the above two methods, through the analysis of the energy characteristics of the noisy signal of the desert in frequency domain, we found that we can use the traditional bandpass filter which separates the signal and noise from the noisy signals (Kar and Maity 2016; Sinno et al. 2018). It is found that the bandpass filter can roughly remove the random low-frequency noise of the desert and retain the signal. But the signal-to-noise ratio is not high, the amplitude preservation is not satisfactory, and it is difficult to set the passband accurately without a priori knowledge of the desert noise.

Spectral kurtosis adaptive bandpass filter

The definition of spectral kurtosis

A non-stationary random signal $X(t)$ is decomposed by Wold–Cramer (Antoni and Randall 2006; Cramér 1971), which means that any time series can be decomposed into deterministic trend components and stable zero mean error components. And its frequency domain expression is:

$${\text{Y}}(t) = \int_{ - \infty }^{ + \infty } {e^{j2\pi ft} H(t,f){\text{d}}X(f)}$$

(1)

${\text{d}}X(f)$ is the spectral process of $X(t)$, which can be expressed as:

$$X(t) = \int_{ - \infty }^{ + \infty } {e^{j2\pi ft} } {\text{d}}X(f)$$

(2)

$H(t,f)$ is the value of the Fourier transform of the time-varying pulse response $H(t,s)$ (Cramér 1971, 2010) at the frequency $f$, where $s$ is a dummy variable for time, $t$ represents a specific time variable, and $H(t,f)$ can also be understood as the complex envelope of the signal at the frequency $f$.

$S_{2nY} (t,f)$ is defined as $2n$-order instantaneous moment, it can be expressed as the strength of the energy of the complex envelope at time $t$ and frequency $f$, and its expression is:

$$S_{2nY} (f) = E\left\{ {\left| {H(t,f)dX(f)} \right|^{2n} } \right\}/df = E\left\{ {\left| {H(t,f)^{2n} } \right|} \right\} \cdot S_{2nX}$$

(3)

among them, $n = 0,1,2 \cdots$ By combining the instantaneous moments of $2n$-order spectra at different orders, the four-order spectral cumulants $C_{4Y} (f)$ are obtained. The expression is as follows:

$$C_{4Y} (f) = S_{4Y} (f) - 2S^{2}_{2Y} (f),\quad f \ne 0$$

(4)

The upper formula can represent the non-Gaussianity of the signal. The closer to the Gaussianity, the closer to 0 of the value; the greater the deviation of a process from Gaussianity, the greater its value. Its physical meaning is the measurement of the kurtosis of the probability density distribution function at the frequency $f$. $S_{2Y} (f)$ represents the power spectral density of the signal, which can be understood as the time averaged energy of the envelope of the noisy signal at the frequency $f$.

Through the explanation of the above physical quantities, the expression of the spectral kurtosis (SK) can be defined as:

$$K_{Y} (f) = \frac{{C_{4Y} (f)}}{{S^{2}_{2Y} (f)}} = \frac{{S_{4Y} (f)}}{{S^{2}_{2Y} (f)}} - 2,\quad f \ne 0$$

(5)

From the physical point of energy (Dwyer 1983; Lei et al. 1994; Antoni 2006), it can be understood as the measuring for the peakedness of the squared envelope at the frequency of $f$. It is to measure the energy characteristic of the different frequency of the noisy signal. Therefore, spectral kurtosis has a strong recognition ability for non-stationary signals (energy transient), and the frequency of energy transients can be obtained from spectral kurtosis.

A non-stationary stochastic process is $Z(t) = Y(t) + N(t)$, where $Y(t)$ is the pure signal to be detected, $N(t)$ is additive Gauss stationary random noise, and $N(t)$ is independent of signal $Y(t)$. The expression of the spectral kurtosis of $Z(t)$ is obtained as follows:

$$K_{Z} (f) = \frac{{K_{Y} (f)}}{{(1 + \rho (f))^{2} }},\quad f \ne 0$$

(6)

$\rho (f) = S_{2N} (f)/S_{2Y} (f)$ is noise-to-signal ratio, $S_{2N} (f)$ is the power spectral density of the noise, and $S_{2Y} (f)$ is the power spectral density of the signal. When the ratio $\rho (f)$ of the noise to the signal is very small, $K_{Z} (f) \approx K_{Y} (f)$. When the ratio of the noise to the signal is very large, it can be approximately considered to contain only the noise, $K_{Z} (f)$ reaching to 0. Therefore, the spectral kurtosis can be used to find the range of the frequency band of the signal. The expression of Wiener filter is:

$$W(f) = \frac{1}{1 + \rho (f)}$$

(7)

For formula (6), we can use spectral kurtosis to blindly estimate the noise-to-signal ratio of noisy signals. Therefore, an adaptive bandpass filter based on spectral kurtosis can be designed based on the relationship among $\rho (f)$, spectral kurtosis and Wiener filter (Combet and Gelman 2009).

Spectral kurtosis based on short-time Fourier transform

Based on the connection between theoretical framework above and the actual noisy signal of the desert, STFT is selected as a method to estimate the spectral kurtosis in this paper. This method transforms the signal into frequency domain, and it is closely related with the Wold–Cramer decomposition which is mentioned above. Because of the characteristics of the window function, when choosing the appropriate window length, the noise can be approximately considered as a stationary Gaussian noise which is easy to handle.

A random signal $X(T)$ is used for discrete random sampling to get the discrete random signal $X(n)$, and the discrete random expression is obtained as follows:

$$Y_{w} (kP,f) = \sum\limits_{ - \infty }^{\infty } {x(n)w(n - kP)e^{ - j2\pi f} }$$

(8)

where $w(n)$ is window function, $p$ is the each moving step of time window, and $k$ is the times of the window moves.

The $2n$-order spectral moment estimation of the above sampled signal $Y_{w} (kP,f)$ can be expressed as follows:

$$\hat{S}_{2nY} (f) = \left\langle {\left| {Y_{w} (kP,f)} \right|^{2n} } \right\rangle_{k}$$

(9)

where $\left\langle \ldots \right\rangle_{k}$ is the k-order time average operator, according to the above definition of the spectral kurtosis, $n = 1$ and $n = 2$ are substituted into the upper form, respectively. The formula of spectral kurtosis based on STFT is obtained as follows:

$$\hat{K}_{Y} (f) = \frac{{\hat{S}_{4Y} (f)}}{{\hat{S}^{2}_{2Y} (f)}} - 2,\quad \left| {f - \bmod (1/2)} \right| > \frac{1}{{N_{w} }}$$

(10)

$Y_{w} (kP,f)$ is the complex envelop of the signal $Y(n)$ filtered by a narrow band filter at the frequency $f$, so the upper $\hat{K}_{Y} (f)$ can be used to measure the envelope energy deviation of $Y_{w} (kP,f)$.

It is worth mentioned that the window length $N_{w}$ is a very important parameter; the smaller the value of $N_{w}$ is, the greater the peak of SK is, but a too small $N_{w}$ will lead the condition that the SK cannot reflect the details of the signal. So, not only the length of window is as small as possible, but it is necessary to ensure to reserve the signal details as far as possible.

The design of adaptive spectral kurtosis bandpass filter

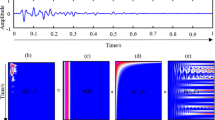
The selection of spectral kurtosis diagram has a significant impact on the final filtering function and further plays a decisive role in denoising and amplitude preservation. So we need to select the appropriate window length. In order to better explain the effect of different window lengths on spectral kurtosis. First, we take the simulated desert seismic signal as a signal source. Second, we use Hanning window for STFT to obtain the SK. Third, the overlap is set to 75%. In the end, we successively select the window length is 30, 45, 60, 75, the spectral kurtosis chart is shown in Fig. 1.

Fig. 1

Spectral kurtosis based on STFT

From the above diagram, we can see that when selecting the right window length, the spectral kurtosis starts with a transient phenomenon from the value 0.04 of the abscissa, until 0.2 tends to be gentle, and the rest is basically floating up and down at 0. So we can infer that the frequency band of the transient is a frequency band with a signal and the rest of the frequency band floating up and down at 0 can be considered the frequency band of noise. Because the value of the spectral kurtosis’s noise is close to 0, according to the nature of SK, when choosing the appropriate window length, noise can be considered as stationary Gauss noise. Therefore, we can get the filter function expression based on the 2.1 property formulas (6) and (7):

$$W(f) = \sqrt {\frac{{K_{Z} (f)}}{k}}$$

(11)

where $K_{Z} (f)$ is the spectral kurtosis of the noisy signal, and K is an unknown adjustable parameter, which can set a range of around the maximum spectral kurtosis, through the substitution of the minimum of the range, getting an initial filtering function, then calculate the kurtosis after filtering, and gradually increase the K. After several iterations, the filter function is required when the maximum kurtosis of the filtered signal is found by multiple iterations. From the above analysis of spectral kurtosis chart, the conclusion can be drawn that spectral kurtosis can automatically and accurately identify the frequency bands of the signal and the noise. The threshold function is proposed through the spectral kurtosis’s difference between the signal and the noise (the spectral kurtosis of signal is larger and the spectral kurtosis of noise is floating up and down in 0); the expression is:

$$\sigma = 0. 1\times \hat{K}_{Y} (f)_{\rm{max} }$$

(12)

where $\hat{K}_{Y} (f)_{\rm{max} }$ is the maximum of spectral kurtosis of noisy signal, the spectral kurtosis which is less than threshold can be considered as the noise part, this part is set to 0, and the final spectral kurtosis $K_{Z} (f)$ is obtained; then we can get the filtering function $W(f)$.

Finally, the expression is obtained:

$$y(t) = FT^{ - 1} \left\{ {W(f) \cdot Y(f)} \right\}$$

(13)

$Y(f)$ is the frequency domain representation of the original noisy signal after Fourier transform; $y(t)$ is the time-domain signal after filtering.

Experimental results

Synthetic seismic record

In order to verify the effectiveness of the proposed algorithm for denoising, we apply it to a 24 traces synthetic desert seismic signal record. Each trace has 400 sampling points, the sampling frequency is 400 Hz, the amplitude is 1, the signal’s main frequency is 30 Hz, the path spacing is 8 m, and the velocities are 900 m/s and 950 m/s, respectively, as shown in Fig. 2a. Then, the synthetic desert noise is added in the synthetic desert seismic signal record, and we get the desert noisy simulative record whose signal-to-noise ratio is − 12.37 dB, as shown in Fig. 2b. A large amount of desert random noises exist in the record of the desert, and the phase axis is submerged in random noise. Figure 2c–f is the pictures of simulation effect under TFPF, wavelet threshold denoising, ordinary bandpass filter denoising and spectral kurtosis bandpass filter denoising, respectively. Through the comparison of these graphs, we can find that, in Fig. 2c, although the noise is suppressed, the effective signal’s loss is very serious. The wavelet threshold denoising of Fig. 2d cannot suppress the noise while retaining the valid signal; the distortion of peaks and valleys is very serious. Obviously, Fig. 2f shows spectral kurtosis bandpass filter recovers the events with small distortion under strong noise, the removal of background noise is more thorough, and its effect is better than that in Fig. 2d. In Fig. 2e, f, most random noise can be effectively suppressed after denoising for the two methods, events become clear and coherent, but in contrast, the rest noise of Fig. 2f (spectrum kurtosis bandpass filter) is significantly lower than that in Fig. 2e (traditional bandpass filter), and at the same time, the retention of peaks and valleys in Fig. 2f is better than that in Fig. 2e.

Fig. 2

Analysis of different denoising algorithms on the example of synthetic seismic record. a synthetic record without noise; b result of denoising with TFPF; c synthetic record with noise; d result of denoising with wavelet threshold; e result of denoising with bandpass filter; f result of denoising with spectral kurtosis filter

In order to make a clearer comparison of the differences among these methods, we extract 5th trace from Fig. 2 for comparison, as shown in Fig. 3. Figure 3a is the 5th trace of the upper event. As we can see from the graph, TFPF does not suppress the noise well, and the amplitude’s attenuation and distortion are more serious. The preservation for the amplitude of wave peak of this method is better than the wavelet threshold denoising result, and it is also better than the bandpass filter denoising result; the method of preserving amplitude at the trough is also better than the bandpass filter, and the wavelet threshold denoising has been seriously distorted at the trough. Figure 3b is the 5th trace of the underneath event; from the diagram, we can see that TFPF does not suppress the noise effectively, and the distortion at the trough is very serious. The preservation for the amplitude of the wave peak of this method is better than the bandpass filter, and the wavelet threshold denoising has signal distortion at the wave peak. At the trough, this method is better and the bandpass filter deviates from the original signal, and the wavelet threshold denoising also has serious distortion. In terms of spectrum, we can conclude that the result of the proposed algorithm is closer to the noise-free data both on middle and low-frequency components. The frequency range and direction of the amplitude-frequency characteristics are the same as that of noise-free data in general; the results have recovered the characteristics of the signals both in time domain and frequency domain after the method of this paper.

Fig. 3

Single trace comparison, a the above signal of 5th trace, b the underneath signal of 5th trace, c spectrum of the trace

In order to make a quantitative comparison among the three methods, a contrast diagram of the SNR of Table 1 is given as follows. It can be seen from the table that the signal-to-noise ratio of this method is better than the other two methods.

Table 1 SNRs of different methods under different noise levels

Processing of actual desert seismic data

Finally, in order to further illustrate the effectiveness of the method, we apply this method to the actual desert seismic data. Figure 4a is a certain actual desert record with 101 seismic channels, and in each channels, there are 3202 sampling points. The sampling frequency is 500 Hz. There are various complex desert random noises in the sample, and the SNR is low. The noise is suppressed by TFPF, wavelet transform, bandpass filter and the method of this paper; the results are, respectively, shown in Fig. 4b–e.

Fig. 4

Analysis of different denoising algorithms on the actual seismic record. a actual desert record, b result of denoising with TFPF; c result of denoising with wavelet threshold; d result of denoising with bandpass filter; e result of denoising with spectral kurtosis filter

Compared with the experimental results, in the red region, we can see that Fig. 4b (TFPF) and Fig. 4c (wavelet transform) have a little suppression on the noise, but the overall effect is not significant, and the events is not more clear. Figure 4d (bandpass filter) has a certain effect of suppressing the actual noise, but in Fig. 4e, the proposed method is better than that in Fig. 4d for noise suppression, and the events of Fig. 4e are more clear and coherent than the other two methods.

Discussions and conclusions

In this paper, in order to solve the disadvantages of traditional methods which have bad performance in noise suppression and signals’ retainment in the desert seismic data, we combined the traditional bandpass filter with the spectral kurtosis which is often used in the diagnosis of mechanical signals. In this method, the spectral kurtosis is used to characterize the energy characteristics in the frequency domain of the noisy signal in the desert data. By setting the threshold, the larger spectral kurtosis (signal’s part) is retained and the filter function is obtained, and an adaptive spectral kurtosis bandpass filter can be designed for denoising. Compared with the traditional bandpass filter, this method does not require a priori knowledge of the desert seismic signal and the frequency range of noise to adjust the passband range repeatedly. It can automatically find the signal frequency range, retain the signal and suppress the noise. The simulation results and actual data processing results show that the proposed method can achieve further noise reduction better than the traditional bandpass filter and has a significant advantage over the bandpass filter in amplitude preservation.