New stepsizes for the gradient method

Abstract

Gradient methods are famous for their simplicity and low complexity, which attract more and more attention for large scale optimization problems. A good stepsize plays an important role to construct an efficient gradient method. This paper proposes a new framework to generate stepsizes for gradient methods applied to convex quadratic function minimization problems. By adopting different criterions, we propose four new gradient methods. For 2-dimensional unconstrained problems with convex quadratic objective functions, we prove that the new methods either terminate in finite iterations or converge R-superlinearly; for n-dimensional problems, we prove that all the new methods converge R-linearly. Numerical experiments show that the new methods enjoy lower complexity and outperform the existing gradient methods.

1 Introduction

The gradient method plays an important role in solving large scale optimization problems. It is widely used in many applications, e.g., machine learning and inverse problems [24]. Thus it is necessary to exploit efficient stepsizes for gradient methods and their theoretical analysis.

Consider the unconstrained convex quadratic optimization problem:

$$\begin{aligned} \min _{x\in \mathbf {R}^n}f(x)=b^Tx+\frac{1}{2}x^THx, \end{aligned}$$

(1)

where $b\in \mathbb {R}^n$, and $H\in \mathbb {R}^{n\times n}$ is symmetric positive definite. We want to find the minimal value of f(x) by means of gradient methods. Let $x_k$ be the iterate point achieved from the kth iteration, and $g_k=\nabla f(x_k)=Hx_k+b$ be the gradient vector at $x_k$. The iteration formulation of the gradient method is:

$$\begin{aligned} x_{k+1}=x_k-\alpha _k g_k. \end{aligned}$$

(2)

Different choices of the stepsize $\alpha _k$ lead to various performances. One particular choice is the exact linesearch, which is also called Cauchy stepsize [2, 3]:

$$\begin{aligned} \alpha _k^{*}={\text {argmin}}_{\alpha >0} f(x_k-\alpha g_k). \end{aligned}$$

It has the closed form as:

$$\begin{aligned} \alpha _k^{*}=\frac{\Vert g_k\Vert _2^2}{g_k^THg_k}. \end{aligned}$$

By using exact linesearch steps, the gradient method becomes the steepest descent method. It has linear convergence rate [23], but suffers from the zigzag phenomenon.

Another choice of stepsize was proposed by Barzilai and Borwein [1]. The BB stepsizes are designed as the approximation of the inverse of the Hessian matrix, and have certain quasi-Newton property. This provides two BB stepsizes as:

$$\begin{aligned}&\alpha _k^{BB1}=\frac{s_k^Ts_k}{s_k^Ty_k}={\text {argmin}}_{\alpha }\Vert y_k-\alpha ^{-1}s_k\Vert ^2,\\&\alpha _k^{BB2}=\frac{s_k^Ty_k}{y_k^Ty_k}={\text {argmin}}_{\alpha }\Vert s_k-\alpha y_k\Vert ^2, \end{aligned}$$

where $s_k=x_k-x_{k-1}$, $y_k=g_k-g_{k-1}$. For 2-dimensional convex quadratic objective functions, Barzilai and Borwein [1] showed that the gradient method (2) with the BB stepsize $\alpha _k^{BB1}$ converges R-superlinearly and the R-order is $\sqrt{2}$. Its R-linear convergence rate for general n-dimensional problems is proved in [8].

This result has inspired many studies on the gradient method [4,5,6, 8, 11, 15, 17,18,19,20, 25]. For example, Dai [4] suggested to use an alternate step (AS) method, which combines the Cauchy stepsize with the BB stepsize:

$$\begin{aligned} \alpha _k^{AS}=\left\{ \begin{array}{ll} \alpha _k^{*},&{}\quad \mod (k,2)=1; \\ \alpha _k^{BB},&{}\quad \mod (k,2)=0. \end{array} \right. \end{aligned}$$

Yuan [21] proposed a new kind of stepsize (Yuan stepsize) which ensures 3-step termination for minimizing 2-dimensional convex quadratic objective functions:

$$\begin{aligned} \alpha _k=\left\{ \begin{array}{ll} \alpha _k^{Y}=2\left( \sqrt{\left( \frac{1}{\alpha _{k-1}^{*}}-\frac{1}{\alpha _k^{*}}\right) ^2+\frac{4\Vert g_k\Vert _2^2}{ (\Vert s_{k-1}\Vert _2)^2}}+\frac{1}{\alpha _{k-1}^{*}}+\frac{1}{\alpha _k^{*}}\right) ^{-1},&{}\quad \mod (k,t)=0;\\ \alpha _k^{*},&{}\quad {\text {otherwise}}. \end{array} \right. \end{aligned}$$

(3)

Later on, Dai and Yuan [7] proposed a variant strategy of Yuan stepsize, which improves the aforementioned method and keeps the finite termination property for 2-dimensional convex quadratic function minimization:

$$\begin{aligned} \alpha _k^{DY}=\left\{ \begin{aligned}&\alpha _k^{*},&\mod (k,4)=1,2;\\&\alpha _k^{YV}=2\left( \sqrt{\left( \frac{1}{\alpha _{k-1}^{*}}-\frac{1}{\alpha _k^{*}}\right) ^2+\frac{4\Vert g_k\Vert _2^2}{ (\alpha _{k-1}^{*}\Vert g_{k-1}\Vert _2)^2}}+\frac{1}{\alpha _{k-1}^{*}}+\frac{1}{\alpha _k^{*}}\right) ^{-1},&\mod (k,4)=0,3. \end{aligned} \right. \end{aligned}$$

(4)

In the framework of (3), $\alpha _k^{Y}$ is equivalent to $\alpha _k^{YV}$. But $\alpha _k^{YV}$ in (4) is different from $\alpha _k^{Y}$. The new method (4), short as DY method, performs very competitive with the BB method for large scale problems. Due to the numerical experiences, Yuan [22] believed that “a good gradient method would use at least one exact linesearch in every few iterations”. Based on this idea, a number of gradient methods have been discussed. Recent work by De Asmundis et al. [10] modified the DY method and proposed the SDC gradient method. In one loop, it consists of $h+l$ inner iterations, where the first h iterations ($h\ge 2$) apply the Cauchy stepsizes, and the rest l iterations ($l\ge 1$) use the fixed steplengths generated from Yuan step. The detailed stepsize is updated as follows:

$$\begin{aligned} \alpha _k^{SDC }=\left\{ \begin{array}{ll} \alpha _k^{*},&{} \quad \mod (k,h+l)<h;\\ \alpha _k^{YV},&{}\quad \mod (k,h+l)=h; \\ \alpha _{k-1},&{} \quad {\text {otherwise.}} \end{array} \right. \end{aligned}$$

(5)

The work [10] also exploited the asymptotic spectral behaviour of the DY method, and proved that the SDC algorithm has R-linear convergence rate for minimizing convex quadratic functions. The SDC method outperforms the DY method with proper parameters h and l.

In [12], di Serafino et al. analyzed several gradient methods, including the SDC method, Adaptive BB method [14], Limited Memory Steepest Descent (LMSD) method [13] and so on. The methods were also extended to general unconstrained problems. It showed that the gradient methods with groups of short steps followed by several long steps are efficient for strongly convex quadratic problems. Similar analysis for the SD method was presented in [16].

Inspired by the SDC method, we propose new gradient methods by modifying (5). The modification mainly include two aspects. On one hand, the basic framework is improved, and only two exact linesearch steps are required in a loop. On the other hand, several new stepsizes are plugged in the new framework. For 2-dimensional problems, we prove that the corresponding gradient methods either terminate in finite iterations or converge R-superlinearly. For general n-dimensional problems ($n>2$), we prove that all the proposed gradient methods converge R-linearly. The rest of the paper is organized as follows. The new methods are introduced in Sect. 2. The convergence analysis is shown in Sect. 3. In Sect. 4, numerical results show that our new gradient algorithms outperform the state of the art.

2 New gradient methods

In this section, new gradient methods are proposed.

2.1 New framework

Consider problem (1). We construct new gradient methods by proposing new stepsizes $\alpha _k$. First, a cyclic framework that combines Cauchy steps with fixed steplengthes is proposed as follows:

$$\begin{aligned} \alpha _k=\left\{ \begin{array}{ll} \alpha _k^{*}, &{}\quad {\text {if}}\,\mod (k,m)<2; \\ \alpha _{k-1}^{F}, &{}\quad {\text {if}}\, \mod (k,m)=2; \\ \alpha _{k-1}, &{}\quad {\text {otherwise}}. \end{array} \right. \end{aligned}$$

(6)

Here the stepsize $\alpha _{k}^{F}$ has different choices, which is analyzed in the next subsection. In each loop, we take 2 Cauchy steps followed by $m-2$ gradient steps with fixed stepsizes, where the fixed stepsize is computed according to the 2 Cauchy steps.

Such framework is different from the SDC method [10], in the following two aspects. First, the new framework only requires 2 exact linesearch steps, while (5) requires $h+1$. Thus the computational cost is reduced compared to SDC. Second, the key stepsize $\alpha _{k-1}^{F}$ is constructed by the information of the last ($(k-1)$th) iteration rather than the current (kth) iteration, which makes the generated iterate points completely different from SDC.

2.2 New stepsizes

In the new framework, we apply various types of stepsizes. Here we consider four different choices of $\alpha _k^F$ as follows:

$$\begin{aligned}&\alpha _k^{F(1)} = \alpha _k^{YV} \,\end{aligned}$$

(7)

$$\begin{aligned}&\alpha _k^{F(2)} =\tilde{\alpha }_k=\left( \frac{1}{\alpha _{k-1}^{*}}+\frac{1}{\alpha _k^{*}}\right) ^{-1}\, ,\end{aligned}$$

(8)

$$\begin{aligned}&\alpha _k^{F(3)} =\alpha _{k}^{Fmin}=\min \{\alpha _{k-1}^{*},\alpha _{k}^{*}\} \, ,\end{aligned}$$

(9)

$$\begin{aligned}&\alpha _k^{F(4)} =\alpha _{k}^{Fmax}=\max \{\alpha _{k-1}^{*},\alpha _{k}^{*}\} \, . \end{aligned}$$

(10)

The stepsizes (7) and (8) were proposed in [7, 9], respectively. As analyzed in [10], the stepsizes (7) and (8) approximate the inverse of the largest eigenvalue and that of the sum of the largest and smallest eigenvalues of the Hessian matrix, respectively. If the approximation is sufficiently accurate, we can reduce the gradient component corresponding to the largest eigenvalue significantly. In this case the problem is reduced into a lower dimensional problem. Hopefully the dimension reduction happens frequently. The stepsizes (9) and (10) are proposed in this paper, with the purpose to approximate the inverse eigenvalues of the Hessian matrix H on the 2-dimensional subspace spanned by $g_k$ and $g_{k-1}$. Let $v_k=\frac{g_k}{\Vert g_k\Vert }$ and $v_{k-1}=\frac{g_{k-1}}{\Vert g_{k-1}\Vert }$. Then the Hessian matrix H on the subspace $\mathcal {S}={\text {Span}}\{g_k,g_{k-1}\}$ is expressed as

$$\begin{aligned} H_{\mathcal {S}}=\left( \begin{array}{cc} v_k^THv_k, &{} v_k^THv_{k-1} \\ v_{k-1}^THv_k, &{} v_{k-1}^THv_{k-1} \end{array} \right) = \left( \begin{array}{cc} \frac{1}{\alpha _k^{*}} &{} v_k^THv_{k-1} \\ v_{k-1}^THv_k &{} \frac{1}{\alpha _{k-1}^{*}} \end{array} \right) . \end{aligned}$$

The eigenvalues of $H_{\mathcal {S}}$ can be approximated by the diagonal elements (9) and (10). Compared to the stepsizes (7) and (8), the computational cost of (9) and (10) are lower. In summary, all these four stepsizes are designed to approximate the inverse of the eigenvalues of the Hessian matrix H; the new framework uses the fewest Cauchy steps to generate the aforementioned four stepsizes, and combines them to reduce the problem into lower and lower dimensional subspaces.

It is easy to show the following relations among the four stepsizes:

$$\begin{aligned} \tilde{\alpha }_k\le \alpha _{k}^{YV}\le \alpha _k^{Fmin} \le \alpha _k^{Fmax} \, . \end{aligned}$$

(11)

Let $\lambda _1\ge \ldots \lambda _n>0$ be the eigenvalues of the Hessian matrix H. Then the stepsizes $\alpha _{k}^{YV}$, $\alpha _k^{Fmin}$ and $\alpha _k^{Fmax}$ are bounded by the inverse of the eigenvalues:

$$\begin{aligned} {\lambda _1}^{-1}\le \alpha _{k}^{YV}\le \alpha _k^{Fmin} \le \alpha _k^{Fmax}\le {\lambda _n}^{-1}. \end{aligned}$$

(12)

This can be verified by the fact that ${\lambda _1}^{-1} \le \alpha _k^* \le {\lambda _n}^{-1}$ holds for all k. Yet $\tilde{\alpha }_k$ is possibly smaller than ${\lambda _1}^{-1}$.

By using (7)–(10), the gradient method with stepsizes (6) gives four different algorithms. We call the new gradient methods as Alg. 1 to Alg. 4 corresponding to (7)-(10), respectively. The detailed framework of Alg. 1 is shown in Algorithm 1, and the frameworks for the other three algorithms are similar.

The proposed algorithms make full use of the computed Cauchy steps. In one loop of each proposed algorithm, we only compute two Cauchy steps in the first two iterations, and then easily construct the fixed step length $\alpha _{k-1}^F$ with simple calculation by using the two Cauchy steps. In this way, the computational cost is reduced compared to the state of the art such as SDC.

3 Theoretical analysis

In this section we analyze the convergence properties of the new gradient algorithms proposed in Sect. 2. The analysis for 2-dimensional cases and general n $(n>2)$ dimensional cases are considered individually.

3.1 Convergence analysis for 2-dimensional problems

Assume that the four proposed gradient algorithms are applied to problem (1) with $n=2$. We consider the special 2-dimensional case to show that the proposed algorithms are able to avoid the zigzag phenomenon caused by Cauchy steps.

First, we show that Alg. 1 has finite termination property.

Theorem 1

Apply the gradient method Alg. 1 to problem (1) with $n=2$. $x_0$ is any initial point. Suppose that $\lambda _{1}=\lambda>\lambda _{2}>0$ are the two eigenvalues of the Hessian matrix H of the objective function, and $d_1$ and $d_2$ are the corresponding orthonormal eigenvectors. The gradient vector $g_{k}=Hx_k+b$ can be represented as

$$\begin{aligned} g_k = \mu _1^{k} d_1 + \mu _2^{k} d_2 \end{aligned}$$

with $\mu _i^{k}= d_i^T g_k \, (i=1,2)$. If the initial point $x_0$ satisfies that $\mu _1^{0}\ne 0$ and $\mu _2^{0}\ne 0$, the method terminates in finite iterations.

Proof

Without loss of generality we assume that $d_1= (1,0 )^T$, $d_2= (0,1)^T$ and $\lambda _2 = 1$. In this case, $g_k = (\mu _1^{k}, \mu _2^{k})^T$ and

$$\begin{aligned} H=\left( \begin{array}{cc} \lambda &{} \quad 0 \\ 0 &{}\quad 1 \end{array} \right) . \end{aligned}$$

Suppose that $\mu _1^{k}\ne 0$. Otherwise the problem degenerates into one-dimensional subspace, and the algorithm will terminate after the next Cauchy step. Define

$$\begin{aligned} q_{k}=\frac{(\mu _2^{k})^2}{(\mu _1^{k})^2}. \end{aligned}$$

(13)

Since $g_{k+1}=(I-\alpha _kH)g_{k}$, we can establish that

$$\begin{aligned} \mu _1^{k+1}=(1-\lambda \alpha _k)\mu _1^{k},\mu _2^{k+1}=(1-\alpha _k)\mu _2^{k} \end{aligned}$$

(14)

and

$$\begin{aligned} \Vert g_{k+1}\Vert _2^2=\frac{1+q_{k+1}}{1+q_{k}}(1-\lambda \alpha _k)^2\Vert g_{k}\Vert _2^2. \end{aligned}$$

(15)

For Cauchy steps, we have

$$\begin{aligned} \alpha _{k}^{*}=\frac{\Vert g_{k}\Vert _2^2}{g_{k}^THg_{k}}=\frac{1+q_{k}}{\lambda +q_{k}} \end{aligned}$$

and

$$\begin{aligned} q_{k+1}=\frac{1}{q_{k}}. \end{aligned}$$

(16)

From the update strategy (6), we have $\alpha _0=\alpha _0^{*}=\frac{1+q_{0}}{\lambda +q_{0}}$ and $\alpha _1=\alpha _1^{*}=\frac{1+q_{1}}{\lambda +q_{1}}=\frac{1+q_{0}}{\lambda q_{0}+1}$. Introducing

$$\begin{aligned}&\tilde{\alpha }_1=\left( \frac{1}{\alpha _{0}^{*}}+\frac{1}{\alpha _1^{*}}\right) ^{-1}=\left( \frac{\lambda +q_{0}}{1+q_{0}}+\frac{\lambda q_{0}+1}{1+q_{0}}\right) ^{-1}=\frac{1}{\lambda +1},\\&\rho _1=\frac{1}{\alpha _{0}^{*}\alpha _1^{*}}-\frac{\Vert g_1\Vert _2^2}{(\alpha _{0}^{*}\Vert g_{0}\Vert _2)^2}=\frac{(\lambda +q_{0})(\lambda q_{0}+1)}{(1+q_{0})^2}-\frac{q_0(\lambda -1)^2}{(1+q_{0})^2}=\lambda , \end{aligned}$$

we can deduce that

$$\begin{aligned} \alpha _{2} =\alpha _{1}^{YV}=2(\sqrt{(\lambda +1)^2-4\lambda }+\lambda +1)^{-1}=\frac{1}{\lambda } \, . \end{aligned}$$

Then (14) implies that $\mu _{1}^3=0$. Consequently $\mu _{1}^k$ keeps 0 for $k\ge 3$. The gradient residue $\mu _{2}^k$ can be further eliminated by the exact linesearch in the $(m+1)$th iteration. Thus Alg. 1 terminates in at most $m+1$ iterations. $\square$

Next the other three proposed gradient algorithms are analyzed.

Theorem 2

Apply Alg. 2, Alg. 3 and Alg. 4 to problem (1) with $n=2$. Under the assumptions in Theorem 1, the three methods converges R-superlinearly.

Proof

In all the three methods, $\alpha _{mk}=\alpha _{mk}^{*}$, $\alpha _{mk+1}=\alpha _{mk+1}^{*}$ and $q_{mk+1}=q_{mk}^{-1}$.

For Alg. 2, due to (16), we have

$$\begin{aligned} \alpha _{mk+i}=\tilde{\alpha }_{mk+1}=\left( \frac{1}{\alpha _{mk}^{*}}+\frac{1}{\alpha _{mk+1}^{*}}\right) ^{-1}=\frac{1}{\lambda +1}, i=2,\ldots ,m-1. \end{aligned}$$

From (13) and (14), we can deduce that

$$\begin{aligned} q_{mk+i}=\left\{ \begin{array}{ll} \frac{1}{q_{mk+i-1}}, &{}\quad {\text {if}}\, i=1,2;\\ \lambda ^{2}q_{mk+i-1}, &{}\quad {\text {if}}\, 2< i\le m \end{array} \right. \end{aligned}$$

(17)

and thus conclude that

$$\begin{aligned} q_{mk}=\lambda ^{(2m-4)k}q_0. \end{aligned}$$

(18)

Taking (17) into (15), we have

$$\begin{aligned} \Vert g_{mk+m}\Vert _2^2=\frac{1+\lambda ^{2m-4}q_{mk}}{1+q_{mk}}\frac{(\lambda -1)^4}{(\lambda +1)^{2m-4}(\lambda +q_{mk}^{-1})^2(\lambda +q_{mk})^2}\Vert g_{mk}\Vert _2^2. \end{aligned}$$

For simplicity, define $q=q_{mk}$. From (18) we have $q>q_0$, with $\lambda >1$ and $m>2$. From $q_{mk+1}=\lambda ^{2m-4}q=\frac{q^2}{q_0}$, we have

$$\begin{aligned}&\frac{1+\lambda ^{2m-4}q}{1+q}\cdot \frac{1}{(\lambda +q^{-1})^2(\lambda +q)^2}\\&\quad =\frac{q_0+q^2}{q_0(1+q)}\cdot \frac{1}{[\lambda ^2+\lambda (q^{-1}+q)+1]^2}\\&\quad \le \frac{q_0+q^2}{q_0(1+q)}\cdot \frac{1}{\lambda ^2(q_0+q^2)}\le \lambda ^{-2}q_{0}^{-1}q^{-1}. \end{aligned}$$

Thus

$$\begin{aligned} \Vert g_{mk+m}\Vert _2^2\le C_1q_0^{-2}\lambda ^{-(2m-4)k}\Vert g_{mk}\Vert _2^2\le C_{1}^{k}q_0^{-2k}\lambda ^{-(m-2)(k^2+k)}\Vert g_{0}\Vert _2^2, \end{aligned}$$

where $C_1(\lambda ,m)=\frac{(\lambda -1)^4}{\lambda ^2(\lambda +1)^{2m-4}}$ is a constant. When k goes to infinity,

$$\begin{aligned} \root k \of {\Vert g_{mk+m}\Vert _2}\le \sqrt{C_1}\root k \of {\Vert g_{0}\Vert _2}q_{0}^{-1}\lambda ^{-\frac{m-2}{2}(k+1)}\rightarrow 0. \end{aligned}$$

The above analysis implies that Alg. 2 converges R-superlinearly.

Similarly, we can prove that Alg. 3 and Alg. 4 converges R-superlinearly.$\square$

3.2 Convergence analysis for n-dimensional problems

Besides the convergence results for 2-dimensional problems, we also analyze the convergence property of the proposed gradient algorithms for general n-dimensional problems.

Lemma 1

Suppose $d_1,\ldots ,d_n$ are the orthonormal eigenvectors corresponding to $\lambda _1,\ldots ,\lambda _n$. The proposed gradient methods are applied to problem (1). Suppose that the initial point $x_0$ satisfies $g_0^{T}d_1\ne 0$ and $g_0^{T}d_n\ne 0$. Let $g_k=\sum _{i=1}^{n}\mu _{i}^{k}d_i$ and define $h(k,l)=\sum _{i=l}^{n}(\mu _{i}^{k})^2$. Then all the proposed gradient methods satisfy the following two properties:

• (i) there exists a constant $M_1\ge \lambda _n$, such that $\lambda _n\le \alpha _{k}^{-1}\le M_1$ holds for all $k\ge 0$;

• (ii) if there exists a positive integer $k_0$ and a positive constant $M_2$, such that $h(k-j,l)<\epsilon$ and $(\mu _{l-1}^{k-j})^2<M_2\epsilon$ holds for any $j\in \{0,\ldots ,\min \{k,k_0\}\}$, then $\alpha _{k}^{-1}\ge \frac{2}{3}\lambda _{l-1}$.

Proof

First, we prove that all the four proposed algorithms satisfy property (i). By the framework (6), we only need to prove that both the Cauchy steps and $\alpha _k^{F}$ in each method satisfy property (i).

Since $\alpha _{k}^{*}=\frac{g_k^{T}g_k}{g_k^{T}Hg_k}$, it is trivial to show that

$$\begin{aligned} \lambda _n\le (\alpha _{k}^{*})^{-1}\le \lambda _1. \end{aligned}$$

(19)

For Alg. 1 and Alg. 2, we have from (11) that

$$\begin{aligned} \lambda _1\le \min \{(\alpha _{k}^{*})^{-1},(\alpha _{k-1}^{*})^{-1}\} \le (\alpha _{k}^{YV})^{-1}\le (\widetilde{\alpha }_k)^{-1}=\alpha _{k}^{-1}+\alpha _{k-1}^{-1}\le 2\lambda _n. \end{aligned}$$

Let $M_1=2\lambda _n$. We conclude that both algorithms satisfy property (i).

For Alg. 3 and Alg. 4, (19) holds, thus

$$\begin{aligned} \lambda _n\le \alpha _{k}^{Fmin}=\min \{(\alpha _{k}^{*})^{-1},(\alpha _{k-1}^{*})^{-1}\}\le \alpha _{k}^{Fmax}=\max \{(\alpha _{k}^{*})^{-1},(\alpha _{k-1}^{*})^{-1}\}\le \lambda _1. \end{aligned}$$

Let $M_1=\lambda _1$, and property (i) holds for both methods.

Next, we prove that property (ii) holds for all the four proposed algorithms.

For Alg. 1, Alg. 2, and Alg. 3, from (11), we have that

$$\begin{aligned} \widetilde{\alpha }_k\le \alpha _{k}^{YV}\le \alpha _{k}^{Fmin}\le \alpha _{k}^{*}. \end{aligned}$$

For the considered three algorithms, given k, if $\mod (k,m)\ge 2$, then $\alpha _{k}=\alpha _{r+1}=\alpha _{r}^{F}\le \alpha _{r}^{*}$ holds, where $r={\text {argmax}}\{i\le k|\alpha _{i}=\alpha _{i}^{*}\}$ is the iteration number of the last Cauchy step during all the k iterations. Thus $\alpha _{k}^{-1}\ge (\alpha _{r}^{*})^{-1}$. Let $k_0=m-2$ and $M_2=2$. Then $\max \{k-k_0,0\}\le r\le k$. We can deduce that

$$\begin{aligned} (\alpha _{r}^{*})^{-1}= & {} \frac{g_r^THg_r}{g_r^Tg_r}=\frac{\sum _{i=1}^{n}(\mu _{i}^{r})^2\lambda _{i}}{\sum _{i=1}^{n}(\mu _{i}^{r})^2} \ge \frac{\sum _{i=1}^{l-1}(\mu _{i}^{r})^2\lambda _{i}}{\sum _{i=1}^{l-1}(\mu _{i}^{r})^2+h(r,l)}\nonumber \\\ge & {} \frac{\lambda _{l-1}\sum _{i=1}^{l-1}(\mu _{i}^{r})^2}{\sum _{i=1}^{l-1}(\mu _{i}^{r})^2+\epsilon } =\frac{\lambda _{l-1}}{1+\frac{\epsilon }{\sum _{i=1}^{l-1}(\mu _{i}^{r})^2}}\nonumber \\\ge & {} \frac{\lambda _{l-1}}{1+\frac{\epsilon }{(\mu _{l-1}^{r})^2}}\ge \frac{\lambda _{l-1}}{1+\frac{\epsilon }{2\epsilon }}=\frac{2}{3}\lambda _{l-1}. \end{aligned}$$

(20)

Thus $\alpha _{k}^{-1}\ge (\alpha _{r}^{*})^{-1}\ge \frac{2}{3}\lambda _{l-1}$. The considered three algorithms satisfy property (ii).

For Alg. 4, we have

$$\begin{aligned} (\alpha _{k}^{Fmax})^{-1}\ge \min \{(\alpha _{k}^{*})^{-1},(\alpha _{k-1}^{*})^{-1}\}. \end{aligned}$$

Given k, $\alpha _{k}^{-1}\ge (\alpha _{r_{0}}^{*})^{-1}$ holds, where

$$\begin{aligned} r_{0}=\left\{ \begin{array}{ll} r, &{}\quad {\text {if}}\, (\alpha _{r}^{*})^{-1}\le (\alpha _{r-1}^{*})^{-1};\\ r-1, &{}\quad {\text {otherwise}} \end{array} \right. \end{aligned}$$

and $r={\text {argmax}}\{i\le k|\alpha _{i}=\alpha _{i}^{*}\}$. Let $k_0=m-1$ and $M_2=2$. Then $\max \{k-k_0,0\}\le r_{0}\le k$. Similar to (20) we can deduce that $\alpha _{k}^{-1}\ge (\alpha _{r_{0}}^{*})^{-1}\ge \frac{2}{3}\lambda _{l-1}$. Thus we conclude that property (ii) also holds for this algorithm.$\square$

Theorem 3

[4, Theorem 4.1] Consider the same assumptions in Lemma 1. As long as the stepsizes satisfy property (i) and (ii), the gradient method either terminates in finite iterations or converges R-linearly.

From the above theorem, we conclude that all the four proposed gradient algorithms converge R-linearly when they are applied to n-dimensional convex quadratic functions.

4 Numerical Results

In this section, we show the performances of the proposed algorithms. The algorithms are compared with several gradient methods mentioned in Sect. 1. For all the generated test problems, the Hessian matrix is set as a diagonal matrix, where $H=Diag(\lambda _1,\ldots ,\lambda _n)$. For each setting, we generate 10 examples, and show the average iteration numbers as well as the computational time. All the tests are done on Matlab R2014a, Intel core i7-6700HQ.

For Alg. 1, two different versions are implemented. In version A, we use $\alpha _k^{YV}$ computed by (4); while in version B, we replace $\alpha _k^{YV}$ by

$$\begin{aligned} \alpha _k^{New} = \tilde{\alpha }_k [ 1 + \rho _k (\alpha _k^{YV} )^2 ] \, , \end{aligned}$$

where $\rho _k=\frac{1}{\alpha _{k-1}^{*}\alpha _k^{*}}-\frac{\Vert g_k\Vert _2^2}{(\alpha _{k-1}^{*}\Vert g_{k-1}\Vert _2)^2}$. Theoretically $\alpha _k^{New} = \alpha _k^{YV}$, but computationally they give slightly different numerical performances. Here we report the better results between the two versions.

We consider four kinds of test problems. Given dimension n and condition number $\kappa$, their detailed settings are as follows:

• Test 1. [10] In the Hessian matrix, we set $\lambda _1=\kappa$, $\lambda _n=1$; $\lambda _j$ are randomly generated in $[1,\kappa ]$, for $j=2,\ldots ,n-1$; b is randomly generated in $[-5,5]^n$. The stopping parameter $\epsilon =10^{-8}\Vert g_0\Vert$.

• Test 2. [10, 12] Let $\lambda _j=\kappa ^{\frac{n-j}{n-1}}$, for $j=1,\ldots ,n$, and b be a zero vector. The initial point $x_0$ is randomly generated in $[-5,5]^n$.

• Test 3. [12] Let $\lambda _j=1+(\kappa -1)s_j$ and b be a zero vector. $s_j$ is randomly generated from [0.8, 1] for $j=1,\ldots ,\frac{n}{2}$, and randomly generated from [0, 0.2] for $j=\frac{n}{2}+1,\ldots ,n$. The stopping parameter $\epsilon =10^{-6}$. The initial point $x_0$ is randomly generated on a unit sphere.

• Test 4. [16] Let $\lambda _j=\frac{\kappa }{2}(\cos \frac{n-j}{n-1}\pi +1)$ and b be a zero vector. The stopping parameter $\epsilon =10^{-6}$. The initial point $x_0$ is randomly generated on a unit sphere.

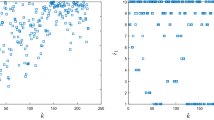
First, the property of the proposed algorithms are explored. Fig. 1 depicts the average iteration numbers of the considered four algorithms with respect to different values of the parameter m, where “Test 2” is solved. Here $n=10^3$, $\kappa =10^4$ and the stopping parameter $\epsilon =10^{-6}$. It shows that Alg. 1 and Alg. 3 with $m=10$ outperform the other settings. We also plot the iteration curves representing function values of the four algorithms in Fig. 2. “Test 1” is considered, with $n=10^3$, $\kappa =10^4$, $m=10$ and $x_0$ randomly generated in $[-5,5]^n$. It indicates that all the four algorithms are nonmonotonic. The good performances of Alg. 1 and Alg. 3 are observed again.

Fig. 1

Iteration number with respect to different m for “Test 2”

Fig. 2

Iteration curves for “Test 1”

Table 1 Comparison with the existing methods for different test problems

Next, we test some problems with various dimensions and condition numbers. Here we compare the proposed algorithms with the effective gradient methods analyzed in [12], such as SDC, ${\text {ABB}}_{\min }$ and LMSD. Let $m=10$. The parameters in SDC, ${\text {ABB}}_{\min }$ and LMSD are the same as in [12]. In “Test 1”, $n=10^4$, $\kappa =10^4$ and $x_0$ is randomly generated in $[-5,5]^n$; in “Test 2”, $n=10^4$, $\kappa =10^6$ and $\epsilon =10^{-8}\Vert g_0\Vert$; in “Test 3”, $n=10^3$ and $\kappa =10^3$; in “Test 4”, $n=10^3$ and $\kappa =10^5$. Table 1 shows the iteration numbers as well as the computational time of the compared methods for the four kinds of test problems. The best results are marked in boldface type. It turns out that Alg. 1 and Alg. 3 outperform the compared algorithms generally, in terms of computational time. Due to the fixed step lengths in each loop, the proposed algorithms have lower per iteration computational cost¹. Consequently they require lower total computational cost compared to the state of the art. But Alg. 2 and Alg. 4 are overperformed by the compared algorithms. The reason may be that the stepsize (8) in Alg. 2 is sometimes too short, and that (10) in Alg. 4 is sometimes too long. From the four tests, we can also observe that the computational complexity of all the considered gradient methods increases with the increment of the dimension and the condition number.

With various types of problems and different settings, the above numerical tests indicate the superior performances of the proposed algorithms Alg. 1 and Alg. 3.

5 Conclusion

In this paper, we proposed four gradient methods for convex quadratic programming. First, a new framework to update the stepsizes was proposed. In each outer loop, only 2 exact linesearch steps are calculated and the other $m-2$ iterations use the fixed steplengths. Four different stepsizes were applied in the new framework, and thus four new gradient algorithms were proposed. Theoretically, for 2-dimensional convex quadratic function minimization problems, we proved that the proposed algorithms have either finite terminations or R-superlinear convergence rate. For general n-dimensional problems, we proved that all new algorithms converge R-linearly. Numerical results indicate the effectiveness and the robustness of the proposed Alg. 1 and Alg. 3.