Cross validation of discontinuous Galerkin method and Monte Carlo simulations of charge transport in graphene on substrate

Abstract

The aim of this work is to simulate the charge transport in a monolayer graphene on a substrate. This requires the inclusion of the scatterings of the charge carriers with the impurities and the phonons of the substrate, besides the interaction mechanisms already present in the graphene layer. As physical model, the semiclassical Boltzmann equation will be assumed. Two approaches will be used for the simulations: a numerical scheme based on the Discontinuous Galerkin method for finding deterministic (non stochastic) solutions and a new Direct Monte Carlo Simulation formulated in Romano et al. (J Comput Phys 302:267–284, 2015) in order to deal in the appropriate way with the Pauli exclusion principle for degenerate Fermi gases. A cross validation of the deterministic and stochastic solutions shows the robustness and accuracy of both the approaches.

1 Introduction

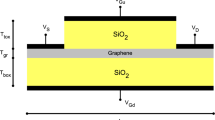
Graphene is a gapless semiconductor made of a single layer of carbon atoms arranged into a honeycomb hexagonal lattice. Around the Dirac points, it has, as first approximation, a conical band structure, so electrons have a zero effective mass and they exhibit a photon-like behavior. A physically accurate model for charge transport is given by a semiclassical Boltzmann equation whose scattering terms have been deeply analyzed in the last decade. Quantum effects has also been included in the literature but for Fermi energies high enough, as those considered in this paper, the interband tunneling effect is practically negligible and the semiclassical approach reveals satisfactory [2]. The aim of this work is to simulate a monolayer graphene on a substrate, as, for instance, considered in [3] (see Fig. 1), at variance with the case of suspended graphene studied in [1].

Fig. 1

The graphene sheet over a substrate

Due to the computational difficulties, usually the available solutions have been obtained with direct Monte Carlo simulations. However, in presence of a high electron density the Pauli exclusion principle must be taken into account and most part of the standard approaches suffer from a violation of the maximum occupation number. This leads, in turn, to a violation of Pauli’s exclusion principle. In [1] a new Direct Simulation Monte Carlo (DSMC) procedure has been devised in order to overcome such a difficulty and successfully applied to charge transport in suspended monolayer graphene. A promising alternative for getting direct solutions of the electron Boltzmann equation is also the use of Discontinuous Galerkin (DG) methods [4] as indicated by the applications to more conventional semiconductors, like silicon [5, 6]. Also hydrodynamical models based on the maximum entropy principle have been formulated, see for example [7–11].

Apart from the scatterings already present in the suspended case, now we need to include also the effects of the remote phonons and the impurities of the substrate. The scattering rate between the electrons and the phonons of the substrate is similar to that of the suspended case but the interaction with the impurities adds noticeable additional difficulties, mainly due to the rather involved expression of the dielectric function which is itself a source of theoretical debates [12, 13].

We will assume the model proposed in [13] for the charge-impurities scattering. However, different models can be easily accounted for with technical changes in the simulation schemes. A crucial parameter is the depth d of the remote impurities. It is of the order of a few angstroms but the exact value can vary from a specimen to another. We will consider several values of d and discuss the influence on the results.

In order to get cross validation of the simulations, both the DG and DSMC methods will be adopted. The good agreement between the results obtained with both methods, of course within the intrinsic statistical noise of the Monte Carlo approach, strongly indicates the validity, robustness and accuracy of the adopted procedures.

The plan of the paper is as follows. In Sect. 2 the semiclassical kinetic model for charge transport in graphene on a substrate is outlined. Section 3 is devoted to the presentation of the DG approach while in Sect. 4 the DSMC is discussed. The numerical results are presented and commented in the last section.

2 Semiclassical charge transport in graphene on a substrate

In a semiclassical kinetic setting, the charge transport in graphene is described by four Boltzmann equations, one for electrons in the valence ($\pi$) band and one for electrons in the conductions ($\pi ^*$) band, that in turn can belong to the K or $K'$ valley,

$$\begin{aligned} \frac{\partial f_{\ell ,s}(\mathrm {t},\mathbf {x},\mathbf {k}) }{\partial \mathrm {t}} + \mathbf{v}_{\ell ,s} \cdot \nabla _{{\mathbf {x}}} f_{\ell ,s}(\mathrm {t},\mathbf {x},\mathbf {k}) - \frac{e}{\hbar } \mathbf{E} \cdot \nabla _{\mathbf {k}} f_{\ell ,s}(\mathrm {t},\mathbf {x},\mathbf {k}) = \left( \dfrac{df_{\ell ,s}}{d \mathrm {t}}(\mathrm {t},\mathbf {x},\mathbf {k}) \right) _{coll},\quad \end{aligned}$$

(1)

where $f_{\ell ,s}(\mathrm {t},\mathbf {x},\mathbf {k})$ represents the distribution function of charge carriers in the valley $\ell$ (K or $K'$), band $\pi$ or $\pi ^*$ ($s = -1$ or $s=1$) at position ${\mathbf {x}}$, time $\mathrm {t}$ and wave-vector ${\mathbf {k}}$. We denote by $\nabla _{\mathbf {x}}$ and $\nabla _{\mathbf {k}}$ the gradients with respect to the position and wave-vector, respectively. The group velocity $\mathbf{v}_{\ell ,s}$ is related to the energy band $\varepsilon _{\ell ,s}$ by

$$\begin{aligned} \mathbf{v}_{\ell ,s} = \dfrac{1}{\hbar } \, \nabla _{\mathbf {k}} \, \varepsilon _{\ell ,s} \, .\end{aligned}$$

With a very good approximation [14] a linear dispersion relation holds for the energy bands $\varepsilon _{\ell ,s}$ around the equivalent Dirac points; so that $\varepsilon _{\ell ,s} = s \, \hbar \, v_F \left| \mathbf {k}-\mathbf {k}_{\ell } \right|$, where $v_F$ is the (constant) Fermi velocity, $\hbar$ is the Planck constant divided by $2 \, \pi$, and $\mathbf {k}_{\ell }$ is the position of the Dirac point $\ell$ in the first Brillouin zone. The elementary (positive) charge is denoted by e, and $\mathbf{E}$ is the electric field, here assumed to be constant. The right hand side of Eq. (1) is the collision term representing the interaction of electrons with impurities and phonons, the latter due to both the graphene crystal and substrate [15]. Acoustic phonon scattering is intra-valley and intra-band. Optical phonon scattering is intra-valley and can be longitudinal optical (LO) and transversal optical (TO); it can be intra-band or inter-band. Scattering with optical phonons of type K pushes electrons from a valley to the other one (inter-valley scattering). In addition to the interactions already present in the suspended case, surface optical phonon scattering and charged impurity (imp) scattering induced by the substrate are also included. Here, the substrate considered is SiO$_{2}$.

We assume that phonons are at thermal equilibrium. The general form of the collision operator can be written as

$$\begin{aligned} \left( \dfrac{d f_{\ell ,s}}{d \mathrm {t}}(\mathrm {t},\mathbf {x},\mathbf {k}) \right) _{coll}= & {} \sum _{\ell ', s'} \left[ \int S_{\ell ', s', \ell , s}(\mathbf {k}', \mathbf {k}) \, f_{\ell ',s'}(\mathrm {t},\mathbf {x},\mathbf {k}') \left( 1 - f_{\ell ,s}(\mathrm {t},\mathbf {x},\mathbf {k}) \right) d \mathbf {k}' \right. \\&\left. - \int S_{\ell , s, \ell ', s'}(\mathbf {k}, \mathbf {k}') \, f_{\ell ,s}(\mathrm {t},\mathbf {x},\mathbf {k}) \left( 1 - f_{\ell ',s'}(\mathrm {t},\mathbf {x},\mathbf {k}') \right) d \mathbf {k}' \right] \end{aligned}$$

where the transition rate $\displaystyle S_{\ell ', s', \ell , s}(\mathbf {k}', \mathbf {k})$ is given by the sum of terms of the kind

(2)

related to electron-phonon scatterings and other terms corresponding to the scatterings with the impurities.

The index $\nu$ labels the $\nu$th phonon mode, $G^{(\nu )}_{\ell ', s', \ell , s}(\mathbf {k}', \mathbf {k})$ is the kernel, which describes the scattering mechanism, due to phonons $\nu$, of electrons belonging to valley $\ell '$ and band $s'$, and electrons belonging to valley $\ell$ and band s. The symbol $\delta$ denotes the Dirac distribution, $\omega ^{(\nu )}_{\mathbf {q}}$ is the $\nu$th phonon frequency, $n^{(\nu )}_{\mathbf {q}}$ is the Bose-Einstein distribution for the phonon of type $\nu$

$$\begin{aligned} n^{(\nu )}_{\mathbf {q}} = \dfrac{1}{e^{\hbar \, \omega ^{(\nu )}_{\mathbf {q}} /k_B T} - 1} \, ,\end{aligned}$$

$k_B$ is the Boltzmann constant and T the constant graphene lattice temperature. When, for a phonon $\nu _{*}$, $\hbar \, \omega ^{(\nu _{*})}_{\mathbf {q}} \ll k_B T$, the scattering with the phonon $\nu _{*}$ can be assumed elastic. In this case, we eliminate in Eq. (2) the term $\hbar \, \omega ^{(\nu _{*})}_{\mathbf {q}}$ inside the delta distribution and we use the approximation $n^{(\nu _{*})}_{\mathbf {q}} \approx k_B T / \hbar \, \omega ^{(\nu )}_{\mathbf {q}} - \frac{1}{2}$.

We will describe the terms of the collision operator concerning the scatterings with the impurities in the next section.

2.1 The model with only one distribution function

By applying a gate voltage transversal with respect to the graphene sheet, it is possible to modify the Fermi energy $\varepsilon _F$ and therefore the charge density. If a high positive value of the Fermi energy is considered, the electrons responsible for the current are those belonging to the conduction band. Therefore, only the transport equation for electrons in the conduction band is considered and interband electron transitions are neglected. Moreover the valleys K and $K'$ are considered as equivalent. A reference frame centered in the K-point will be used. Of course, we simplify the notation, omitting the indexes s and $\ell$ and denoting with f the only relevant distribution function.

The expressions of the electron-phonon scattering matrices used in our simulations are as follows.

For acoustic phonons, usually one considers the elastic approximation, and therefore

$$\begin{aligned} \left( 2 \, n^{(ac)}_{\mathbf {q}} + 1 \right) \left| G^{(ac)}(\mathbf {k}', \mathbf {k}) \right| ^{2} = \dfrac{1}{(2 \, \pi )^{2}} \, \dfrac{\pi \, D_{ac}^{2} \, k_{B} \, T}{2 \hbar \, \sigma _m \, v_{p}^{2}} \left( 1 + \cos \vartheta _{\mathbf {k}\, ,\mathbf {k}'} \right) , \end{aligned}$$

(3)

where $D_{ac}$ is the acoustic phonon coupling constant, $v_{p}$ is the sound speed in graphene, $\sigma _m$ the graphene areal density, and $\vartheta _{\mathbf {k}\, ,\mathbf {k}'}$ is the convex angle between $\mathbf {k}$ and ${\mathbf {k}'}$.

There are three relevant optical phonon scatterings: the longitudinal optical (LO), the transversal optical (TO) and the K phonons. The electron-phonon scattering matrices are

$$\begin{aligned} \left| G^{(LO)}(\mathbf {k}', \mathbf {k}) \right| ^{2}= & {} \dfrac{1}{(2 \, \pi )^{2}} \, \dfrac{\pi \, D_{O}^{2}}{\sigma _m \, \omega _{O}} \left( 1 - \cos ( \vartheta _{\mathbf {k}\, ,\mathbf {k}' - \mathbf {k}} + \vartheta _{\mathbf {k}' \, ,\mathbf {k}' - \mathbf {k}} ) \right) \end{aligned}$$

(4)

$$\begin{aligned} \left| G^{(TO)}(\mathbf {k}', \mathbf {k}) \right| ^{2}= & {} \dfrac{1}{(2 \, \pi )^{2}} \, \dfrac{\pi \, D_{O}^{2}}{ \sigma _m \, \omega _{O}} \left( 1 + \cos ( \vartheta _{\mathbf {k}\, ,\mathbf {k}' - \mathbf {k}} + \vartheta _{\mathbf {k}' \, ,\mathbf {k}' - \mathbf {k}} ) \right) \end{aligned}$$

(5)

$$\begin{aligned} \left| G^{(K)}(\mathbf {k}', \mathbf {k}) \right| ^{2}= & {} \dfrac{1}{(2 \, \pi )^{2}} \, \dfrac{2 \pi \, D_{K}^{2}}{\sigma _m \, \omega _{K}} \left( 1 - \cos \vartheta _{\mathbf {k}\, ,\mathbf {k}'} \right) , \end{aligned}$$

(6)

where $D_{O}$ is the optical phonon coupling constant, $\omega _{O}$ is the optical phonon frequency, $D_{K}$ is the K-phonon coupling constant and $\omega _{K}$ is the K-phonon frequency. The angles $\vartheta _{\mathbf {k}\, ,\mathbf {k}' - \mathbf {k}}$ and $\vartheta _{\mathbf {k}' \, ,\mathbf {k}' - \mathbf {k}}$ denote the convex angles between $\mathbf {k}$ and $\mathbf {k}' - \mathbf {k}$ and between $\mathbf {k}'$ and $\mathbf {k}' - \mathbf {k}$, respectively.

Due to the presence of the SiO$_{2}$ substrate, we must also include the interactions between the electrons of the graphene sheet and the remote phonons and impurities of the substrate. The remote optical phonons are assumed to have an energy equal to 55 meV and a deformation potential $D_{f} = 5.14 \times 10^{7}$ eV/cm. The electron-phonon scattering matrices have the same form of (4) and (5). Regarding the remote impurity scattering, we assume that they stay in a plane at distance $d\, \,$ from the graphene sheet. The definition of the transition rate for electron-impurity scattering is highly complex; so many approximate models are proposed. Following [13], we adopt the transition rate

$$\begin{aligned} S^{(imp)}(\mathbf {k}, \mathbf {k}') = \dfrac{2 \pi }{\hbar } \, \dfrac{n_{i}}{(2 \, \pi )^{2}} \left| \dfrac{V_{i}(|\mathbf {k}- \mathbf {k}'|, d)}{\epsilon (|\mathbf {k}- \mathbf {k}'|)} \right| ^{2} \dfrac{\left( 1 + \cos \vartheta _{\mathbf {k}\, ,\mathbf {k}'} \right) }{2} \delta \left( \varepsilon (\mathbf {k}') - \varepsilon (\mathbf {k}) \right) ,\quad \end{aligned}$$

(7)

where

• (a) $n_{i}$ is the number of impurities per unit area.

• (b) $\displaystyle V_{i}(|\mathbf {k}- \mathbf {k}'|, d) = 2 \, \pi e^{2} \, \dfrac{\exp (- \, d \, |\mathbf {k}- \mathbf {k}'|)}{\tilde{\kappa } \, |\mathbf {k}- \mathbf {k}'|}$

  • d is the location of the charged impurity measured from the graphene sheet

  • $\displaystyle \tilde{\kappa }$ is the effective dielectric constant, defined by $\displaystyle 4 \pi \epsilon _{0} \left( \kappa _{top} + \kappa _{bottom} \right) / 2$, where $\epsilon _{0}$ is the vacuum dielectric constant and $\kappa _{top}$ and $\kappa _{bottom}$ are the relative dielectric constants of the medium above and below the graphene layer. In typical cases, the materials are SiO$_{2}$ and air, implying $\displaystyle \tilde{\kappa } = 4 \pi \epsilon _{0} \left( 1 + \kappa _{SiO_{2}} \right) / 2 \approx 4 \pi \times 2.45 \, \epsilon _{0}$.

• (c)
  $$\begin{aligned} \displaystyle \epsilon (|\mathbf {k}- \mathbf {k}'|) = \left\{ \begin{array}{ll} 1 + \dfrac{q_{s}}{|\mathbf {k}- \mathbf {k}'|} - \dfrac{\pi \, q_{s}}{8 \, k_{F}}\quad \text{ if } |\mathbf {k}- \mathbf {k}'| < 2 \, k_{F} &{} \\ 1 + \dfrac{q_{s}}{|\mathbf {k}- \mathbf {k}'|} - \dfrac{q_{s} \sqrt{|\mathbf {k}- \mathbf {k}'|^{2} - 4 \, k_{F}^{2}}}{2 \, |\mathbf {k}- \mathbf {k}'|^{2}} - \dfrac{q_{s}}{4 \, k_{F}} \quad \text{ as } \text{ in } \left( \dfrac{2 \, k_{F}}{|\mathbf {k}- \mathbf {k}'|} \right) \text{ otherwise }&{} \end{array} \right. \end{aligned}$$

  is the 2D finite temperature static random phase approximation (RPA) dielectric (screening) function appropriate for graphene;

  • $\displaystyle q_{s} = \dfrac{4 \, e^{2} \, k_{F}}{\tilde{\kappa } \, \hbar \, v_{F}}$ is the effective Thomas-Fermi wave-vector for graphene; it can be rewritten in terms of the dimensionless Wigner-Seitz radius as $\displaystyle q_{s} = 4 r_S k_F$;

  • $\displaystyle k_{F} = \dfrac{\varepsilon _F}{\hbar v_F}$ is the Fermi wave-vector.

We close this section evaluating the transition rates (collision frequencies) associated to the scattering mechanisms introduced above. For the Ath type of scattering the transition rate is defined as

$$\begin{aligned} \Gamma _A (\mathbf {k}) = \int S_A (\mathbf {k}, \mathbf {k}') \, d \mathbf {k}' \end{aligned}$$

and depends on $\mathbf {k}$ through the energy, that is indeed $\Gamma _A (\mathbf {k}) = \Gamma _A (\varepsilon )$.

For the acoustic phonon scattering we get

$$\begin{aligned} \Gamma _{ac} (\varepsilon ) = \dfrac{ D_{ac}^{2} \, k_{B} \, T}{4 \hbar ^3 \, v_F^2 \, \sigma _m \, v_{p}^{2}} \,\, \varepsilon \end{aligned}$$

while for the total optical phonon scattering, given by the sum of the longitudinal and transversal contribution, we have

$$\begin{aligned} \Gamma _{op} (\varepsilon ) = \dfrac{D_{O}^{2}}{ \sigma _m \, \omega _{O} \hbar ^2 \, v_F^2} \left[ \left( \varepsilon - \hbar \, \omega _{O} \right) \left( n^{(O)}_{\mathbf {q}} + 1 \right) H (\varepsilon + \hbar \, \omega _{O}) + \left( \varepsilon + \hbar \, \omega _{O} \right) \, n^{(O)}_{\mathbf {q}} \right] , \end{aligned}$$

where the fact that the coupling constants are the same for both the longitudinal and the transversal optical phonons has been used. In Eq. (8) H is the Heaviside function and $n^{(O)}_{\mathbf {q}}$ the equilibrium optical phonon distribution.

The expression of the transition rate for the K phonon scattering is the same as for the optical phonon

$$\begin{aligned} \Gamma _{K} (\varepsilon ) = \dfrac{D_{K}^{2}}{ \sigma _m \, \omega _{K} \hbar ^2 \, v_F^2} \left[ \left( \varepsilon - \hbar \, \omega _{K} \right) \left( n^{(K)}_{\mathbf {q}} + 1 \right) H (\varepsilon - \hbar \, \omega _{K}) + \left( \varepsilon + \hbar \, \omega _{K} \right) \, n^{(K)}_{\mathbf {q}} \right] . \end{aligned}$$

Above $n^{(K)}_{\mathbf {q}}$ is the equilibrium K phonon distribution. At last the transition rate for the impurity scattering, due to the rather involved expression, has to be evaluated numerically. Following a standard procedure, the following correction is adopted [16]

$$\begin{aligned} \Gamma _{imp} (\varepsilon ) = \int S^{(imp)} (\mathbf {k}, \mathbf {k}') \left( 1 - \cos \vartheta _{\mathbf {k}\, ,\mathbf {k}'} \right) \, d \mathbf {k}'. \end{aligned}$$

(8)

The physical parameters for the scattering rates are summarized in Table 1.

Table 1 Physical parameters for the scattering rates

We look for spatially homogeneous solutions to Eq. (1) under a constant applied electric field. In such a case the transport equation reduces to

$$\begin{aligned} \dfrac{\partial f(\mathrm {t},\mathbf {k})}{\partial \mathrm {t}} - \dfrac{e}{\hbar } \, \mathbf {E} \cdot \nabla _{\mathbf {k}} f(\mathrm {t},\mathbf {k})= & {} \int S(\mathbf {k}', \mathbf {k}) \, f(\mathrm {t},\mathbf {k}') \left( 1 - f(\mathrm {t},\mathbf {k}) \right) d \mathbf {k}' \nonumber \\&- \int S(\mathbf {k}, \mathbf {k}') \, f(\mathrm {t},\mathbf {k}) \left( 1 - f(\mathrm {t},\mathbf {k}') \right) d \mathbf {k}' \, .\end{aligned}$$

(9)

As initial condition, we take a Fermi-Dirac distribution,

$$\begin{aligned} f(0, \mathbf {k}) = \dfrac{1}{1 + \exp \left( \dfrac{\varepsilon (\mathbf {k}) - \varepsilon _F}{k_{B} \, T} \right) } , \end{aligned}$$

where $T = 300\, \,$ K is the room lattice temperature which will be kept constant. Two different approaches will be used and then compared: the DG and the DSMC methods.

Remark 1

A review of the properties of the transport equations in semiconductors can found in [17]. Most part of the results are valid only for regularized collision operators. The existence and uniqueness of the solution, without any regularization of the collisional kernels, have been proved for the homogeneous semiconductor Boltzmann equations, in the case of zero electric field, in [18, 19] where it has been also shown that $0 \le f \le 1$ provided that such a condition is satisfied by the initial data. The general situation is still an open problem.

3 The DG method

Since $f(\mathrm {t},\cdot )$ must belong to $L^1 (\mathbb {R}^2)$ for each $\mathrm {t}>0$, firstly the space of the wave-vector is approximated by a bounded domain¹ $\Omega \subset \mathbb {R}^{2}$ such that $f(\mathrm {t},\mathbf {k}) \approx 0$ for every $\mathbf {k}\notin \Omega$ and $\mathrm {t}> 0$. Then we introduce a finite decomposition $\left\{ C_{\alpha } \right\}$ of $\Omega$, with $C_{\alpha }$ appropriate open sets, such that

$$\begin{aligned} C_{\alpha } \cap C_{\beta } = \emptyset \quad \text{ if } \alpha \ne \beta , \text{ and } \quad \bigcup _{\alpha = 1}^{N} \overline{C_{\alpha }} = \Omega \, .\end{aligned}$$

The geometry of $\Omega$ will be specified later and will be chosen in order to exploit the symmetries of the scattering terms.

We approximate the distribution function f with a constant in each cell $C_{\alpha }$. If we denote by $\chi _{\alpha }(\mathbf {k})$ the characteristic function relative to the cell $C_{\alpha }$, then

$$\begin{aligned} f(\mathrm {t},\mathbf {k}) \approx f^{\alpha }(\mathrm {t}) \quad \forall \,\mathbf {k}\in C_{\alpha } \, \Longleftrightarrow \, f(\mathrm {t},\mathbf {k}) \approx \sum _{\alpha = 1}^{N} f^{\alpha }(\mathrm {t}) \, \chi _{\alpha }(\mathbf {k}) \quad \forall \,\mathbf {k}\in \bigcup _{\alpha = 1}^{N} C_{\alpha } \, .\end{aligned}$$

This assumption replaces the unknown f, which depends on the two variables $\mathrm {t}$ and $\mathbf {k}$, with a set of N unknowns $f^{\alpha }$, which depend only on time $\mathrm {t}$. In order to obtain a set of N equations for the new unknowns $f^{\alpha }$, we integrate Eq. (9) with respect to $\mathbf {k}$ over every cell $C_{\alpha }$ and replace f with its approximation. Up the truncation error, one gets

$$\begin{aligned}&M_{\alpha } \, \dfrac{d \, f^{\alpha }(\mathrm {t})}{d \mathrm {t}} - \frac{e}{\hbar } \, \mathbf {E} \cdot \int _{\partial C_{\alpha }} f(\mathrm {t}, \mathbf {k}) \, \mathbf {n} \, d \sigma \nonumber \\&\quad = \sum _{\beta = 1}^{N} \left[ A^{\beta , \alpha } \left( 1 - f^{\alpha }(\mathrm {t}) \right) f^{\beta }(\mathrm {t}) - A^{\alpha , \beta } \, f^{\alpha }(\mathrm {t}) \left( 1 - f^{\beta }(\mathrm {t}) \right) \right] \end{aligned}$$

(10)

where

$$\begin{aligned} A^{\alpha , \beta } = \int _{C_{\alpha }} \left[ \int _{C_{\beta }} S(\mathbf {k}, \mathbf {k}') \, d \mathbf {k}' \right] d \mathbf {k}\, ,\end{aligned}$$

(11)

$M_{\alpha }$ is the measure of the cell $C_{\alpha }$ and $\mathbf {n}$ is the external unit normal to the boundary $\partial C_{\alpha }$ of the cell $C_{\alpha }$. If a suitable discretization of the drift term is performed, it is clear that the numerical method yields a system of ordinary differential equations. This latter can be numerically integrated by using a total variation diminishing (TVD) Runge-Kutta scheme [20] in order to avoid the introduction of spurious oscillations.

3.1 Discretization of the drift term

First we tackle the issue of discretizing the drift term

$$\begin{aligned} \frac{e}{\hbar } \, \mathbf {E} \cdot \int _{\partial C_{\alpha }} f(\mathrm {t}, \mathbf {k}) \, \mathbf {n} \, d \sigma . \end{aligned}$$

Since, due to the Galerkin method, the approximation of f is not defined on the boundary of the cells, we must introduce a numerical flux, that furnishes reasonable values of f on every $\partial C_{\alpha }$, depending on the values of the approximation of f in the nearest neighborhoods of the cell $C_{\alpha }$ and on the sign of $\mathbf {E} \cdot \mathbf {n}$.

We use a zero flux condition at the boundary of $\Omega$ which guarantees the conservation of the total charge. For the interior boundaries, a simple approach is given by upwind rule between the nearest adjacent cells.

On account of the symmetry of the $\mathbf {k}$-domain, we approximate it by the circle $| \mathbf {k} | \le k_{max}$ and introduce the regular decomposition of Fig. 2, where $k_{max}$ is a fixed maximum value such that f is negligible for all $| \mathbf {k} | > k_{max}$.

Fig. 2

Grid in polar coordinates used for the discretization of the $\mathbf{k}$-domain

Since our unknowns are defined only in the open cell $C_{\alpha }$, an approximation of f must be defined on the boundary of the generic cell, which now, see Fig. 3, consists in four simple arcs.

Fig. 3

Numbering of the edges of each cell for the evaluation of the flux across it

Let us fix an arc $\gamma$ of $C_{\alpha }$. If we denote by $C_{\alpha '}$ the cell adiacent to $C_{\alpha }$ along the considered arc, in the simplest version, the upwind scheme leads to the following algorithm

$$\begin{aligned} \forall z \in \gamma : \text{ if } \quad - e \mathbf {E} \cdot \mathbf {n} \ge 0 \quad \text{ then } \quad f (z) = f^{\alpha } \quad \text{ else } \quad f (z) = f^{\alpha '}. \end{aligned}$$

(12)

In other words f on the arc is approximated by the interior value of the adjacent cell according to the component of the drift force along the outer normal $\mathbf {n}$. We remark that if the grid is chosen in such a way that each cell belongs only to a single quadrant, e.g. as in Fig. 2, then in each arc of the cell boundary $\mathbf {E} \cdot \mathbf {n}$ has a sign which is simple to determine.

A more elaborate approach is based on the Min-Mod slope limiter [21]. In order to make clear the algorithm, first we consider the following case. Let $z_1$, $z_2$, $\ldots$, $z_N$ be a set of grid points, which represent a partition of the interval $[z_1, z_N]$, and let $g: [z_1, z_N] \rightarrow \mathbb {R}$ be a smooth function. We look for an approximation of the value $g(z_{n + \frac{1}{2}})$ when the following piecewise approximation of g(z) is known: $g(z) \approx g (z_{k }) : = g_k$ in the open interval $]z_{k - \frac{1}{2}}, z_{k + \frac{1}{2}}[$, $k = n-1, n, n+1, n+2$.

We denote $z_{n + \frac{1}{2}} - z_{n - \frac{1}{2}}$ by $\Delta z_{n}$ for every n.

Taking into account the hyperbolic character of the equations, if we define the wind velocity $a = - e \mathbf {E} \cdot \mathbf {n}$, a simple Taylor expansion gives

$$\begin{aligned} g_{n+\frac{1}{2}} \approx \left\{ \begin{array}{l@{\quad }l} \displaystyle g_{n} + \frac{\Delta z_{n}}{2} \, g_{n}' &{} \text{ if } a>0 \\ \displaystyle g_{n+1} - \frac{\Delta z_{n+1}}{2} \, g_{n+1}' &{} \text{ if } a<0 \end{array} \right. , \end{aligned}$$

(13)

where, only in this section, a prime denotes partial derivatives with respect to z. Of course, the case of vanishing a does not need to be considered. Eq. (13) allows us to replace the function $\displaystyle g_{n+\frac{1}{2}}$ with an approximation containing $\displaystyle g_{n}$ or $\displaystyle g_{n+1}$, but also one derivative. Now, we define for $a>0$

$$\begin{aligned} d_{-} = 2 \, \frac{g_{n} - g_{n-1}}{\Delta z_{n-1} + \Delta z_{n}} \, , \quad d_{+} = 2 \, \frac{g_{n+1} - g_{n}}{\Delta z_{n} + \Delta z_{n+1}} \end{aligned}$$

and approximate the sought derivative according to

$$\begin{aligned} g_{n}' \approx \left\{ \begin{array}{l@{\quad }l} \displaystyle \min \left\{ |d_{-}|, |d_{+}|\right\} \text{ sgn }(d_{-}) &{} \text{ if } d_{-} d_{+}>0 \\ \displaystyle 0 &{} \text{ otherwise } \end{array} \right. . \end{aligned}$$

For $a<0$, a similar formula holds.

On account of the geometry of the decomposition, it is more convenient to employ polar coordinates r and $\vartheta$. Let us denote with $\mathbf {i}$ and $\mathbf {j}$ the unit vectors of the x and y axes. Moreover, for regularity reasons, let us introduce also the variable $s = r^2$. In the coordinates s and $\vartheta$ each cell $C_{\alpha }$ is now expressed as

$$\begin{aligned} C_{\alpha } = \bigg \{(s, \vartheta ) \in [0, s_{max}]\times [0, 2 \pi ]: s_{k - \frac{1}{2}} \le s \le s_{k + \frac{1}{2}}, \vartheta _{n - \frac{1}{2}} \le \vartheta \le \vartheta _{n + \frac{1}{2}} \bigg \} \end{aligned}$$

for suitable index n and k depending on $\alpha$, where $s_{- 1/2} = 0< s_{1/2}< s_{3/2}< \cdots < s_{N + 1/2} = s_{max}$ is a partition of $[0, s_{max}]$ and $0 = \vartheta _{- 1/2}< \vartheta _{1/2}< \cdots < \vartheta _{M + 1/2} = 2 \pi$ is a partition of $[0, 2 \pi ]$.

Since

$$\begin{aligned} \nabla u = \dfrac{\partial u}{\partial r} \, \mathbf {e}_{r} + \dfrac{1}{r} \, \dfrac{\partial u}{\partial \vartheta } \, \mathbf {e}_{\vartheta } = 2 \, \sqrt{s} \, \dfrac{\partial u}{\partial s} \, \mathbf {e}_{r} + \dfrac{1}{\sqrt{s}} \, \dfrac{\partial u}{\partial \vartheta } \, \mathbf {e}_{\vartheta } \, ,\end{aligned}$$

where $\mathbf {e}_{r} = \cos \vartheta \, \mathbf {i} + \sin \vartheta \, \mathbf {j}$ and $\mathbf {e}_{\vartheta } = - \sin \vartheta \, \mathbf {i} + \cos \vartheta \, \mathbf {j}$, set $g (s, \vartheta ) = f (\sqrt{s} \cos \vartheta , \sqrt{s} \sin \vartheta )$, one has

$$\begin{aligned} \mathbf {E} \cdot \int _{C_{\alpha }} \nabla _{\mathbf {k}} \, g \, d \mathbf {k}= & {} \mathbf {E} \cdot \int _{s_{k - \frac{1}{2}}}^{s_{k + \frac{1}{2}}} ds \int _{\vartheta _{n - \frac{1}{2}}}^{\vartheta _{n + \frac{1}{2}}} d \vartheta \left[ \left( \sqrt{s} \, \cos \vartheta \, \dfrac{\partial g}{\partial s} - \dfrac{1}{2 \, \sqrt{s}} \, \sin \vartheta \, \dfrac{\partial g}{\partial \vartheta } \right) \mathbf {i} \right. \\&\left. + \left( \sqrt{s} \, \sin \vartheta \, \dfrac{\partial g}{\partial s} + \dfrac{1}{2 \, \sqrt{s}} \, \cos \vartheta \, \dfrac{\partial g}{\partial \vartheta } \right) \mathbf {j} \right] \\= & {} \left( \mathbf {E} \cdot \mathbf {i} \right) \left\{ \int _{\vartheta _{n - \frac{1}{2}}}^{\vartheta _{n + \frac{1}{2}}} \cos \vartheta \left[ \sqrt{s_{k + \frac{1}{2}}} \, g \left( s_{k + \frac{1}{2}}, \vartheta \right) - \sqrt{s_{k - \frac{1}{2}}} \, g \left( s_{k - \frac{1}{2}}, \vartheta \right) \right] d \vartheta \right. \\&\left. - \int _{s_{k - \frac{1}{2}}}^{s_{k + \frac{1}{2}}} \dfrac{1}{2 \, \sqrt{s}} \left[ \sin \vartheta _{n + \frac{1}{2}} \, g \left( s, \vartheta _{n + \frac{1}{2}}\right) - \sin \vartheta _{n - \frac{1}{2}} \, g \left( s, \vartheta _{n - \frac{1}{2}}\right) \right] ds \right\} \\&+ \left( \mathbf {E} \cdot \mathbf {j} \right) \left\{ \int _{\vartheta _{n - \frac{1}{2}}}^{\vartheta _{n + \frac{1}{2}}} \sin \vartheta \left[ \sqrt{s_{k + \frac{1}{2}}} \, g \left( s_{k + \frac{1}{2}}, \vartheta \right) - \sqrt{s_{k - \frac{1}{2}}} \, g \left( s_{k - \frac{1}{2}}, \vartheta \right) \right] d \vartheta \right. \\&\left. - \int _{s_{k - \frac{1}{2}}}^{s_{k + \frac{1}{2}}} \dfrac{1}{2 \, \sqrt{s}} \left[ \cos \vartheta _{n + \frac{1}{2}} \, g \left( s, \vartheta _{n + \frac{1}{2}}\right) + \cos \vartheta _{n - \frac{1}{2}} \, g \left( s, \vartheta _{n - \frac{1}{2}}\right) \right] ds \right\} \\\approx & {} \left( \mathbf {E} \cdot \mathbf {i} \right) \left\{ \left[ \sqrt{s_{k + \frac{1}{2}}} \, g_{k + \frac{1}{2}, n} - \sqrt{s_{k - \frac{1}{2}}} \, g_{k - \frac{1}{2}, n} \right] \int _{\vartheta _{n - \frac{1}{2}}}^{\vartheta _{n + \frac{1}{2}}} \cos \vartheta \, d \vartheta \right. \\&\left. - \left[ \sin \vartheta _{n + \frac{1}{2}} \, g_{k, n + \frac{1}{2}} - \sin \vartheta _{n - \frac{1}{2}} \, g_{k, n - \frac{1}{2}} \right] \int _{s_{k - \frac{1}{2}}}^{s_{k + \frac{1}{2}}} \dfrac{1}{2 \, \sqrt{s}} \, ds \right\} \\&+ \left( \mathbf {E} \cdot \mathbf {j} \right) \left\{ \left[ \sqrt{s_{k + \frac{1}{2}}} \, g_{k + \frac{1}{2}, n} - \sqrt{s_{k - \frac{1}{2}}} \, g_{k - \frac{1}{2}, n} \right] \int _{\vartheta _{n - \frac{1}{2}}}^{\vartheta _{n + \frac{1}{2}}} \sin \vartheta \,d \vartheta \right. \\&\left. - \left[ \cos \vartheta _{n + \frac{1}{2}} \, g_{k, n + \frac{1}{2}} + \cos \vartheta _{n - \frac{1}{2}} \, g_{k, n - \frac{1}{2}} \right] \int _{s_{k - \frac{1}{2}}}^{s_{k + \frac{1}{2}}} \dfrac{1}{2 \, \sqrt{s}} \, ds \right\} . \end{aligned}$$

The discretization is completed by approximating the terms $g_{k + \frac{1}{2}, n}$ with the Min-Mod slope limiter along $\vartheta =$ constant and and by approximating the terms $g_{k, n + \frac{1}{2}}$ with the Min-Mod slope limiter along $s =$ constant.

3.2 Discretization of the collision term

We need to evaluate the coefficients (11). They are, except for the impurity scattering, a sum of integrals of this kind

$$\begin{aligned}&\int _{\vartheta _{a}'}^{\vartheta _{b}'} d \vartheta ' \int _{\vartheta _{a}}^{\vartheta _{b}} d \vartheta \int _{s_{a}'}^{s_{b}'} d s' \int _{s_{a}}^{s_{b}} d s \, \frac{1}{4} \, \left[ A + B \, \cos ( \vartheta - \vartheta ') \right] \nonumber \\&\quad \times \left[ \delta \left( \varepsilon (\mathbf {k}') - \varepsilon (\mathbf {k}) + \hbar \, \omega ^{(\nu )}_{\mathbf {q}} \right) \left( n^{(\nu )}_{\mathbf {q}} + 1 \right) + \delta \left( \varepsilon (\mathbf {k}') - \varepsilon (\mathbf {k}) - \hbar \, \omega ^{(\nu )}_{\mathbf {q}} \right) n^{(\nu )}_{\mathbf {q}} \right] , \end{aligned}$$

where A and B are constant and the factor $\frac{1}{4}$ is the product of the Jacobian of the transformations $r = \sqrt{s}$ and $r' = \sqrt{s'}$. We have taken into account that the function $\displaystyle \cos ( \vartheta _{\mathbf {k}\, ,\mathbf {k}' - \mathbf {k}} + \vartheta _{\mathbf {k}' \, ,\mathbf {k}' - \mathbf {k}} )$, which appears both in the longitudinal and transversal optical scattering, is canceled when the sum of the scattering terms is performed. The previous integral can be factorized as the product of twofold integrals. If we introduce the paramter $\displaystyle \xi = \left( \hbar \, \omega ^{(\nu )}_{\mathbf {q}} \right) / \left( \hbar \, v_{F} \right)$ and the characteristic function $\chi _{\left[ a, b \right] }(z)$ relative to the interval [a, b], one has

$$\begin{aligned}&\int _{\vartheta _{a}'}^{\vartheta _{b}'} d \vartheta ' \int _{\vartheta _{a}}^{\vartheta _{b}} d \vartheta \left[ A + B \, \cos ( \vartheta - \vartheta ') \right] = \\&A \left( \vartheta _{b}' - \vartheta _{a}' \right) \left( \vartheta _{b} - \vartheta _{a} \right) + 4 \sin \left( \dfrac{\vartheta _{b}' - \vartheta _{a}'}{2} \right) \cos \left( \dfrac{\vartheta _{a} + \vartheta _{b}}{2} - \dfrac{\vartheta _{a}' + \vartheta _{b}'}{2} \right) \sin \left( \dfrac{\vartheta _{b} - \vartheta _{a}}{2} \right) , \\&\frac{1}{4} \int _{s_{a}'}^{s_{b}'} d s' \int _{s_{a}}^{s_{b}} d s \left[ \delta \left( \varepsilon (\mathbf {k}') - \varepsilon (\mathbf {k}) + \hbar \, \omega ^{(\nu )}_{\mathbf {q}} \right) \left( n^{(\nu )}_{\mathbf {q}} + 1 \right) + \delta \left( \varepsilon (\mathbf {k}') - \varepsilon (\mathbf {k}) - \hbar \, \omega ^{(\nu )}_{\mathbf {q}} \right) n^{(\nu )}_{\mathbf {q}} \right] \\&\quad = \frac{1}{4} \,\dfrac{1}{ \hbar \, v_{F} } \int _{s_{a}'}^{s_{b}'} d s' \int _{s_{a}}^{s_{b}} d s \, \left[ \left( n^{(\nu )}_{\mathbf {q}} + 1 \right) \delta \left( |\mathbf {k}'| - |\mathbf {k}| + \xi \right) + n^{(\nu )}_{\mathbf {q}} \, \delta \left( |\mathbf {k}'| - |\mathbf {k}| - \xi \right) \right] \\&\quad = \frac{1}{2} \,\dfrac{1}{ \hbar \, v_{F}} \int _{s_{a}}^{s_{b}} d s \int _{\sqrt{s_{a}'}}^{\sqrt{s_{b}'}} dr' \left[ \left( n^{(\nu )}_{\mathbf {q}} + 1 \right) \delta \left( |\mathbf {k}'| - |\mathbf {k}| + \xi \right) + n^{(\nu )}_{\mathbf {q}} \, \delta \left( |\mathbf {k}'| - |\mathbf {k}| - \xi \right) \right] r' \\&\quad = \frac{1}{2} \,\dfrac{1}{\hbar \, v_{F} } \int _{s_{a}}^{s_{b}} d s \int _{\mathbb {R}} dr' \left[ \left( n^{(\nu )}_{\mathbf {q}} + 1 \right) \delta \left( r' - |\mathbf {k}| \!+\! \xi \right) \!+\! n^{(\nu )}_{\mathbf {q}} \, \delta \left( r' - |\mathbf {k}| - \xi \right) \right] \chi _{\left[ \sqrt{s_{a}'}, \sqrt{s_{b}'} \right] }(r') \, r'\\&\quad = \frac{1}{2} \,\dfrac{1}{\hbar \, v_{F} } \int _{s_{a}}^{s_{b}} d s \left[ \left( n^{(\nu )}_{\mathbf {q}} \!+\! 1 \right) \chi _{\left[ \sqrt{s_{a}'}, \sqrt{s_{b}'} \right] }(|\mathbf {k}| - \xi ) \, (|\mathbf {k}| - \xi ) \!+\! n^{(\nu )}_{\mathbf {q}} \chi _{\left[ \sqrt{s_{a}'}, \sqrt{s_{b}'} \right] }(|\mathbf {k}| + \xi ) \, (|\mathbf {k}| \!+\! \xi ) \right] \\&\quad = \frac{1}{2} \,\dfrac{1}{\hbar \, v_{F}} \int _{s_{a}}^{s_{b}} d s \left[ \left( n^{(\nu )}_{\mathbf {q}} + 1 \right) \chi _{\left[ \sqrt{s_{a}'}, \sqrt{s_{b}'} \right] }(\sqrt{s} - \xi ) \, (\sqrt{s} - \xi ) \right. \\&\qquad + \left. n^{(\nu )}_{\mathbf {q}} \chi _{\left[ \sqrt{s_{a}'}, \sqrt{s_{b}'} \right] }(\sqrt{s} + \xi ) \, (\sqrt{s} + \xi ) \right] \\&\quad = \dfrac{1}{\hbar \, v_{F} } \int _{\sqrt{s_{a}}}^{\sqrt{s_{b}}} dr \left[ \left( n^{(\nu )}_{\mathbf {q}} + 1 \right) \chi _{\left[ \sqrt{s_{a}'}, \sqrt{s_{b}'} \right] }(r - \xi ) \, (r - \xi ) + n^{(\nu )}_{\mathbf {q}} \chi _{\left[ \sqrt{s_{a}'}, \sqrt{s_{b}'} \right] }(r + \xi ) \, (r + \xi ) \right] r \\&\quad = \dfrac{n^{(\nu )}_{\mathbf {q}} + 1}{ \hbar \, v_{F} } \int _{\left[ \sqrt{s_{a}}, \sqrt{s_{b}} \right] \cap \left[ \sqrt{s_{a}'} + \xi , \sqrt{s_{b}'} + \xi \right] } (r - \xi ) \, r \, dr \\&\qquad + \dfrac{n^{(\nu )}_{\mathbf {q}}}{ \hbar \, v_{F} } \int _{\left[ \sqrt{s_{a}}, \sqrt{s_{b}} \right] \cap \left[ \sqrt{s_{a}'} - \xi , \sqrt{s_{b}'} - \xi \right] } (r + \xi ) \, r \, dr \\&\quad = \dfrac{n^{(\nu )}_{\mathbf {q}} + 1}{ \hbar \, v_{F} } \left[ \frac{1}{3} \, r^{3} - \frac{1}{2}\, \xi \, r^{2} \right] _{\left[ \sqrt{s_{a}}, \sqrt{s_{b}} \right] \cap \left[ \sqrt{s_{a}'} + \xi , \sqrt{s_{b}'} + \xi \right] }\\&\qquad + \dfrac{n^{(\nu )}_{\mathbf {q}}}{ \hbar \, v_{F} } \left[ \frac{1}{3} \, r^{3} + \frac{1}{2}\, \xi \, r^{2} \right] _{\left[ \sqrt{s_{a}}, \sqrt{s_{b}} \right] \cap \left[ \sqrt{s_{a}'} - \xi , \sqrt{s_{b}'} - \xi \right] } . \end{aligned}$$

The scattering term for the impurity is rather complex. For this reason only the delta function has been solved analytically while the remaining integrals, over a three-dimensional domain, have been evaluated by using a standard quadrature formula.

Remark 2

As the numerical results confirm, the DG approach guarantees that the distribution function never exceed the unit. To understand such an outcome, we observe that by using the simple splitting the overall DG scheme can be formulated, at first order in the time step, given $\mathrm {t}= \mathrm {t}_n$, as the numerical discretization of

$$\begin{aligned} M_{\alpha } \, \dfrac{d \, f^{\alpha }(\mathrm {t})}{d \mathrm {t}} - \frac{e}{\hbar } \, \mathbf {E} \cdot \int _{\partial C_{\alpha }} f(\mathrm {t}, \mathbf {k}) \, \mathbf {n} \, d \sigma = 0, \quad \mathrm {t}_n \le \mathrm {t}\le \mathrm {t}_{n+1}, \end{aligned}$$

followed by the numerical discretization of

$$\begin{aligned} M_{\alpha } \, \dfrac{d \, f^{\alpha }(\mathrm {t})}{d \mathrm {t}} = \sum _{\beta = 1}^{N} \left[ A^{\beta , \alpha } \left( 1 - f^{\alpha }(\mathrm {t}) \right) f^{\beta }(\mathrm {t}) - A^{\alpha , \beta } \, f^{\alpha }(\mathrm {t}) \left( 1 - f^{\beta }(\mathrm {t}) \right) \right] ,\\ \quad \mathrm {t}_n \le \mathrm {t}\le \mathrm {t}_{n+1}. \end{aligned}$$

The first equation is solved by taking as initial condition the solution at $\mathrm {t}= \mathrm {t}_n$. The second equation is solved by taking as initial condition the solution of the drift equation.

The drift part is an advection equation. The use of the Min-Mod slope limiter prevents the formation of spurious oscillations [22] and does not allow to increase the maximum values of the distribution function or decrease the minimum one. Moreover, the DG scheme preserves the dissipative character of the collision term as well. Therefore, at first order in the time step, the numerical solution remains bounded by the extrema of the initial data.

4 DSMC method

In order to compare the DG method, we have also used, for solving the transport equation (1), the ensemble DSMC method recently proposed in [1].

The $\mathbf {k}$-space is approximated by the set $[-k_{x \, max}, k_{x \, max}] \times [-k_{y \, max}, k_{y \, max}]$ with $k_{x \, max}$ and $k_{y\, max}$ such that the number of electrons with a wave-vector $\mathbf {k}$ outside such a set is practically negligible. The $\mathbf {k}$-space is partitioned into a uniform rectangular grid. We shall denote by $C_{ij}$ the generic cell of the grid centered at the $\mathbf {k}_{ij}$ wave-vector.

The distribution function is approximated with a piecewise constant function in each cell. Initially the $n_P$ particles used for the simulation are distributed in each cell according to the equilibrium Fermi-Dirac distribution.

The motion of each particle alternates free-flight and scattering. The latter is the most involved and delicate part and in graphene it is particularly important to include the Pauli exclusion principle. This implies a heavy computational cost and, more importantly, requires a continuous update of the distribution function.

In the standard approach the free-flight is performed according to the semiclassical equation of motion

$$\begin{aligned} \hbar \dot{\mathbf {k}} = - e \, \mathbf {E}. \end{aligned}$$

(14)

The time interval $\Delta \mathrm {t}$ is chosen for each particle in a random way by

$$\begin{aligned} \Delta \mathrm {t}= - \frac{\ln \xi }{\Gamma _{tot}}, \end{aligned}$$

(15)

$\xi$ being a random number with uniform distribution in the interval [0, 1] and $\Gamma _{tot}$ being the total scattering rate (see for example [23])

$$\begin{aligned} \Gamma _{tot} = \Gamma _{ac} (\varepsilon (\mathrm {t}) ) + \Gamma _{op} (\varepsilon (\mathrm {t}) ) + \Gamma _{K} (\varepsilon (\mathrm {t}) ) + \Gamma _{imp} (\varepsilon (\mathrm {t}) ) + \Gamma _{ss} (\varepsilon (\mathrm {t}) ). \end{aligned}$$

$\Gamma _{ss}$, called self-scattering rate, is the scattering rate associated to a fictitious scattering that does not change the state of the electron. It is introduced so that $\Gamma _{tot}$ is constant leading to the simple relation (15). To fix the value of $\Gamma _{tot}$ one considers the range of the energy involved in the simulation and takes the maximum value $\Gamma _M$ of the sum $\Gamma _{ac} + \Gamma _{op} + \Gamma _{K} + \Gamma _{imp}$. $\Gamma _{tot}$ is then set equal to $\alpha \Gamma _M$ with $\alpha > 1$ a tuning parameter, e.g., $\alpha = 1.1$.

Since the range of $\Gamma _{ac}$, $\Gamma _{op}$, $\Gamma _{K}$, $\Gamma _{imp}$ can be very large, in order to reduce the computational cost, a good variant is to use a variable $\Gamma _{tot}$ which depends on the energy $\varepsilon (\mathrm {t})$ of the considered particle at the current time $\mathrm {t}$

$$\begin{aligned} \Gamma _{tot} = \alpha \left( \Gamma _{ac} (\varepsilon (\mathrm {t}) ) + \Gamma _{op} (\varepsilon (\mathrm {t}) ) + \Gamma _{K} (\varepsilon (\mathrm {t}) ) \right) . \end{aligned}$$

We will use this procedure and set $\alpha = 1.1$ in our simulations.

After the free-flight the scattering is selected randomly according to the values of the transition rates, and the Pauli exclusion principle is taken into account as in [24]. Once the state after the scattering has been determined, let us denote by $\mathbf {k}'$ its wave-vector, the initial state is changed or left the same with a rejection technique: a random number $\xi$ is generated uniformly in [0, 1] and if $\xi < 1 - f(\mathbf {k}')$ the transition is accepted, otherwise it is rejected. Then, according to the angular distribution of the scattering rate, a rejection method allows to select the angular dependence of the wave-vector after the scattering event.

At fixed times the momentum, velocity, energy of each electron are recorded and the mean values are evaluated along with the distribution of electrons among the cells in the $\mathbf {k}$-space in order to follow the time evolution of the system.

The maximum number $n_{ij}^{*}$ of simulated particles accommodated in each cell is easily evaluated (see [24]). Let $N_{ij}$ be the number of real particles in the cell $C_{ij}$ and let $n_{ij}$ be the number of simulated particles in the same cell. Let A be the area of the sample and let N be the number of real particles in the sample, $N = \rho A$. By observing that $N/n_p$ is the statistical weight of each particle entering the simulation and taking into account the condition $0 \le f \le 1$, one has

$$\begin{aligned} n_{ij}= & {} \frac{N_{ij}}{N} n_P = \frac{n_P}{N }\frac{2}{(2 \pi )^2} A \int _{C_{ij}} f \, d\, \mathbf{k} \le \frac{n_P}{N } \frac{2}{(2 \pi )^2} A \int _{C_{ij}} d\, \mathbf{k} \nonumber \\= & {} \frac{2}{(2 \pi )^2} \text{ meas } ({C_{ij}}) \frac{n_P}{N} A = \frac{2}{(2 \pi )^2} \text{ meas } ({C_{ij}}) \frac{n_P}{\rho } = n_{ij}^{*}, \end{aligned}$$

(16)

where $\text{ meas } ({C_{ij}})$ is the measure of the cell $C_{ij}$. Of course $n_{ij}^{*}$ is not in general an integer, therefore rounding errors are introduced. Usually the problem is solved by using a number of simulated particles $n_P$ great enough to make such errors negligible. The convergence of the procedure is often checked just by comparing the results with different $n_P$.

The main concern with the procedure delineated above is that, according to the semiclassical approximation, the compatibility with Pauli’s exclusion principle of the positions occupied during the free flight is not checked. It may occur that the particle at the end of the free-flight reaches a cell in the $\mathbf {k}$ -space already fully occupied making the occupation number greater than one (see [1]).

The fact that, for high values of the Fermi energy, the maximum occupation number can greatly exceed the maximum one is of course unphysical, although the average quantities could be acceptable according to the large number law. Even if the scattering can redistribute the particles among the cells, in general it is not possible to eliminate the presence of anomalous occupation numbers.

For overcoming the problem, in [25] it has been proposed to apply the rejection technique not only to the scattering event but also at the end of each free-flight. However, even implementing this variant, the same drawbacks are still present as shown in [1].

In order to avoid such a difficulty in [1] the following approach has been proposed. The crucial point in the previous procedure is the step concerning the free-flight. If we go back to the original transport equation, we can use a splitting scheme to avoid unphysical results. The basic idea is to reformulate the splitting method in terms of a particle method.

Fig. 4

Comparison of the average velocity (top) and average energy (bottom) versus time for $d =0, 0.5, 1$ nm in the case of an applied electric field of 5 kV/cm and Fermi energy $\varepsilon _F = 0.4$ eV.

Fig. 5

Comparison of the average velocity (top) and average energy (bottom) versus time for $d =0, 0.5, 1$ nm in the case of an applied electric field of 10 kV/cm and Fermi energy $\varepsilon _F = 0.4$ eV.

Fig. 6

Comparison of the average velocity (top) and average energy (bottom) versus time for $d =0, 0.5, 1$ nm in the case of an applied electric field of 5 kV/cm and Fermi energy $\varepsilon _F = 0.6$ eV.

In a time interval $\Delta \mathrm {t}$, first we solve the drift part of the equation corresponding to the free-flight in the analogous DSMC approach,

$$\begin{aligned} \frac{\partial f (\mathrm {t},\mathbf {x},\mathbf {k}) }{\partial \mathrm {t}} - \frac{e}{\hbar } \mathbf{E} \cdot \nabla _{\mathbf {k}} f (\mathrm {t},\mathbf {x},\mathbf {k}) = 0, \end{aligned}$$

(17)

taking as initial condition the distribution at time $\mathrm {t}$, and then the collision part

$$\begin{aligned} \frac{\partial f (\mathrm {t},\mathbf {x},\mathbf {k}) }{\partial \mathrm {t}} = \left. \dfrac{d f}{d \mathrm {t}}(\mathrm {t},\mathbf {x},\mathbf {k}) \right| _{coll} \, ,\end{aligned}$$

(18)

taking as initial condition the solution of Eq. (17). The global procedure gives a numerical approximation of $f (\mathrm {t}+ \Delta \mathrm {t},\mathbf {x},\mathbf {k})$ up to first order in $\Delta \mathrm {t}$. The solution of Eq. (17) is just a rigid translation of the distribution function along the characteristics and can be reformulated from a particle point of view as a free-flight of the same duration for each electron. In this way, the cells in the $\mathbf {k}$-space are moved of the displacement vector $\hbar \Delta \mathbf {k}= - e \, \mathbf {E} \, \Delta \mathrm {t}$ but without changing the occupation number of the cells themselves. To avoid considering a computational domain as too large, we adopt a Lagrangian approach and move the grid by adapting it to the new position of the cells instead of moving the cells.

Eq. (18) is solved by considering a sequence of collision steps for each particle during the time interval $[\mathrm {t}, \mathrm {t}+ \Delta \mathrm {t}]$ in a standard way: choice of the scattering, including also the self one, and selection of the final state. Since the collision mechanisms take into account the Pauli exclusion principle, the occupation number cannot exceed the maximum occupation number in this second step as well. Hence, neither the drift nor the collision step give rise to the possibility of having, in a single cell, more particles than the maximum allowed number.

The overall scheme is a hybrid approach which furnishes a first order in time approximation of the distribution function. Average quantities can be evaluated as well by taking the mean values of the quantities of interest, e.g. velocity and energy.

5 Numerical results

We consider a surface impurity density of $n_{i} = 2.5 \times 10^{11}$ cm$^{-2}$ and several values of the distance d between the graphene sheet and the remote impurities. d should be of the order of few angstroms. In the literature a range from 0 to 1 nm is considered. The simulations are performed at several values of the electric field and Fermi energy. The parameter $r_S$ is set equal to 0.8.

Mass conservation implies that the charge density $\rho$, given by

$$\begin{aligned} \rho = \dfrac{2}{(2 \, \pi )^{2}} \int f(\mathrm {t}, \mathbf {k}) \, \, d \mathbf {k}\, ,\end{aligned}$$

(19)

is constant in time.

We can choose the reference frame in space such that only the $x-$component of the electric field is different from 0; therefore only the $x-$component of the mean velocity is relevant. In the DSMC 10$^{4}$ particles have been used.

In Figs. 4, 5, 6, we show the numerical results of the average velocity $\mathbf {v}$ and the average energy W, defined as

$$\begin{aligned} \mathbf {v}(\mathrm {t}) = \dfrac{2}{(2 \, \pi )^{2} \, \rho } \int f(\mathrm {t}, \mathbf {k}) \dfrac{1}{\hbar } \, \nabla _{\mathbf {k}} \, \varepsilon (\mathbf {k}) \, d \mathbf {k}\, ,\quad W (\mathrm {t}) = \dfrac{2}{(2 \, \pi )^{2} \, \rho } \int f(\mathrm {t}, \mathbf {k}) \, \varepsilon (\mathbf {k}) \, d \mathbf {k}\, .\nonumber \\ \end{aligned}$$

(20)

There is an excellent agreement, of course within the unavoidable stochastic noise of the DCMS data, between the deterministic solutions obtained with the DG method and the stochastic ones in all the considered cases. Since the theoretical basis of the two simulation approaches are radically different, the results represent a strong evidence of the accuracy and validity of the obtained solutions.

We can observe that the values of the average velocity and energy, in the case of graphene on substrate, become lower by reducing the distance d from the impurities in the oxide, confirming the degradation of the mobility due to the substrate as a direct consequence of the additional scatterings with the remote impurities. The simulations are in a qualitative agreement with the theoretical expectations and are crucial for the determination of the characteristic curves in graphene on a substrate.

6 Conclusions

The charge transport in graphene on a substrate has been simulated by using two approaches: a deterministic one based on the DG method and a stochastic one based on DSMC. The very good agreement of the solutions obtained with both the approaches validates the methods and the accuracy of the results.

The differences in the charge transport are in agreement with the expected effects and confirm a degradation of the mobility when the graphene is on a substrate.