AC impedance analysis, equivalent circuit, and modulus behavior of NaFeP₂O₇ ceramic

Abstract

II-NaFeP₂O₇ was prepared by conventional ceramic fabrication technique. Rietveld refinement, impedance properties, conductivity dispersion, electric modulus, and their scaling were carried out as a function of frequency and temperature. Thus, X-ray diffraction analysis indicates that the sample exhibits a single-phase nature with a monoclinic structure. In addition, analysis of Nyquist plots as well as modulus analysis revealed the contribution of two electrically active regions corresponding to bulk mechanism and distribution of grain boundaries. The near values of activation energies, obtained from the impedance and modulus spectra, confirm that the transport happens through an ion hopping mechanism, dominated by the motion of the Na⁺ ions in the framework of the investigated material resulting from intersecting tunnels or voids where Na⁺ is located.

Introduction

The metal diphosphates A^IM^IIIP₂O₇ show a variety of structure types that are controlled by the stereochemical behaviors of the A and M cations. On the one hand, they affect the coordination numbers, the degree of distortion of the coordination polyhedra, and the conformation of the P₂O₇ groups.

Research focus, on the development of such materials, is on the rise. On the other hand, these materials, in particular for M=Fe with all the alkali cations, are fascinating as they comprise electrically and/or magnetically active transition metal ions [1]. Such a significant class of materials is widely used in the making of transformers, chokes, microwave absorbers, and sensors [2–4]. Besides, recently, some of them have been proposed as cathode materials for lithium batteries [5–8] and even as nanoparticles for decontamination and remediation of water [9].

Among these compounds, NaFeP₂O₇ is an interesting candidate, mainly due to its prospective potential technological applications. This latter presents two structures [10]: a low temperature form, called NaFeP₂O₇-I [11, 12], and a high-temperature form, known as NaFeP₂O₇-II [11–13].

Recently, we have reported the electrical properties of the KFeP₂O₇ and AgFeP₂O₇ compounds [14, 15], and as continuity, we have synthesized the II-NaFeP₂O₇. Hence, the purpose of the present work is to determine the equivalent electrical circuit which can model the experimental data and characterize the electrical microstructure via impedance spectroscopy in a wide range of frequencies and temperatures.

Experimental

For the sake of an easy and satisfying understanding of the topic of this paper, an explanation of the characteristics and fabrication of the sample as well as the description of the details related to the way measurements are performed is given here.

The II-NaFeP₂O₇ ceramic sample was prepared by a standard high-temperature solid-state reaction technique using AR grade (purity more than 99.5 %, Hi-Media) oxides and/or carbonates: Na₂CO₃, Fe₂O₃, and NH₄H₂PO₄ in a suitable stoichiometry. The abovementioned ingredients were mixed thoroughly in air using an agate mortar and pestle. This mixture was calcined at an optimized temperature of 573 K for about 8 h in an open silica crucible air using an electrical furnace to eliminate NH₃, CO₂, and H₂O. Then, the calcined powder of circular disc-shaped pellets was fabricated by applying a uniaxial pressure of 3 T/cm². Once again, the pellets were subsequently sintered at an optimized temperature of 1,073 K in air atmosphere for about 8 h.

Characterization of the compound has been carried out by powder X-ray diffraction (XRD). Thereby, the XRD pattern of the material was recorded at room temperature using a Philips powder diffractometer PW 1710 with CuKα radiation (λ = 1.5405 Å) in a wide range of Bragg angles (9° ≤ 2θ ≤ 63°).

The dielectric property and conductivity (AC–DC) measurements of the sample were made by a Tegam 3550 ALF impedance analyzer by sandwiching circular pellets of a diameter 8 mm and a thickness of about 1 mm thickness between platinum electrodes. Measurements were carried out at temperatures from 573 to 700 K (frequency range 209 Hz to 5 MHz). Specifically, the temperature of the sample was measured with the aid of a copper-constantan thermocouple placed near the sample.

Results and discussions

Crystalline parameters

The X-ray diffraction study of the sample was carried out at room temperature and the data were analyzed with the Rietveld refinement technique using the FullProf code. Figure 1 shows the XRD spectrum of II-NaFeP₂O₇ powder at room temperature. The quality factors are R _B = 3.15, R _F = 4.26, and χ ² = 1.29 indicating a good agreement between the observed and calculated profiles and no trace of any extra peaks was found, thereby suggesting the formation of a single-phase compound having the monoclinic P21_/C space group with lattice parameters a = 7.325 (3) Å, b = 7.903 (4) Å, c = 9.574 (4) Å, β = 111.819 (9)°, and V = 514.622 (7) ų. These parameters are very similar to those previously published for the II-NaFeP₂O₇ compound [16].

Fig. 1

Powder X-ray diffraction pattern and Rietveld refinement for the sample II-NaFeP₂O₇

At this point, the structure of the diphosphate II-NaFeP₂O₇ is known and it is isostructural with AgFeP₂O₇ [17]. In fact, it can be described as a cage structure whose host lattice FeP₂O₇ is built up from corner-sharing octahedra and P₂O₇ groups. The pyro group is formed from two slightly distorted PO₄ groups having one common oxygen. Each PO₄ tetrahedron shares its corners with three octahedra and one tetrahedron, while a FeO₆ octahedron shares all its apices with PO₄ tetrahedra. Additionally, all the P₂O₇ groups have a lengthening direction parallel to a. The arrangement of the polyhedral allows us to distinguish two sorts of layers parallel to (001): the octahedral layers with the composition FeO₃ and the tetrahedral layers with the composition P₂O₄. These layers are alternately stacked along c in such a way that every P₂O₇ group shares four corners with one octahedral layer, and the two other corners with the other octahedral layer. Two sorts of tunnels are indeed observed as very wide tunnels running along the [001] direction and distorted hexagonal tunnels running along the [110] direction which could be able to exhibit mobility of the inserted Na⁺ [14].

Impedance analysis

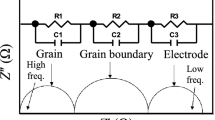
The complex impedance spectroscopy is an important tool to analyze the electrical properties and to get more information about the relaxation process of the investigated device [18]. This technique shows the response of a sample to a sinusoidal perturbation and gives the impedance as a function of frequency. The resultant response (when plotted in a complex plane which is known as Nyquist diagrams) appears in the form of a succession of semicircles representing electrical phenomena inside the material due to the bulk, grain boundary, and interface. In this plot, we expect a separation of the bulk phenomena from the surface (grain boundary) phenomena [19]. In fact, evaluation of the real and imaginary impedance curves is preferred in terms of equivalent circuit representation of the sample and evaluation of any relaxation mechanism, in case of its existence. To study the contribution due to different effects, the impedance plane plots have been performed at different temperatures in the frequency range of 209 Hz–5 MHz.

Characteristically, two semicircular arcs have been observed (Fig. 2a, b). In order to study and understand the impedance spectrum, it is helpful to have an equivalent circuit model that provides a sensible illustration of the electrical properties of the observed regions. As a matter of fact, the high-frequency semicircle is due to the grain and the one at lower frequencies, which exhibits some degree of depression instead of a semicircle centered on the abscissa axis assigned to the grain boundary [18, 20]. Thus, a typical equivalent circuit consisting of a series of combinations of grains and grain boundary elements was thereby used to fit the measured data. The first consists of a parallel combination of resistance (R _g) and capacitance (C _g), whereas the second consists of a parallel combination of resistance (R _gb) and a constant phase element CPE_gb.

Fig. 2

a, b Complex impedance spectrum as a function of temperature with electrical equivalent circuit (inset), accompanied by theoretical data calculated with expressions (2) and (3)

The impedance of CPE_gb is given by:

$$ {Z_{\mathrm{CPE}}}_{{}_{\mathrm{gb}}}=\frac{1}{\left[{Q}_{\mathrm{gb}}{\left( i\omega \right)}^{\alpha}\right]} $$

(1)

where Q _gb indicates the value of the capacitance of the CPE_gb element and α represents the magnitude of the departure of the electrical response from an ideal condition and also indicates the degree of depression of arc below the real axis.

In the present situation, the real and imaginary components of the whole impedance were calculated according to the following expressions:

$$ \mathrm{Z}^{\prime }=\frac{R_{\mathrm{g}}}{1+{\left(\upomega {R}_{\mathrm{g}}{C}_{\mathrm{g}}\right)}^2}+\frac{{R_{\mathrm{g}}}^2{Q}_{\mathrm{g}\mathrm{b}}{\omega}^{\alpha_{\mathrm{g}\mathrm{b}}} \cos \left(\frac{\alpha_{\mathrm{g}\mathrm{b}}\uppi}{2}\right)+{R}_{\mathrm{g}\mathrm{b}}}{{\left(1+{R}_{\mathrm{g}}{Q}_{\mathrm{g}\mathrm{b}}{\omega}^{\alpha_{\mathrm{g}\mathrm{b}}} \cos \left(\frac{\alpha_{\mathrm{g}\mathrm{b}}\uppi}{2}\right)\right)}^2+\left({R}_{\mathrm{g}}{Q}_{\mathrm{g}\mathrm{b}}{\omega}^{\alpha_{\mathrm{g}\mathrm{b}}} \sin \right(\Big(\frac{\alpha_{\mathrm{g}\mathrm{b}}\uppi}{2}{\left)\right)}^2} $$

(2)

$$ Z^{{\prime\prime} }={R}_{\mathrm{g}}\left[\frac{\omega {R}_{\mathrm{g}}{C}_{\mathrm{g}}}{1+{\left(\upomega {R}_{\mathrm{g}}{C}_{\mathrm{g}}\right)}^2}\right]+\frac{{R_{\mathrm{g}}}^2{Q}_{\mathrm{g}\mathrm{b}}{\omega}^{\alpha_{\mathrm{g}\mathrm{b}}} \sin \left(\frac{\alpha_{\mathrm{g}\mathrm{b}}\uppi}{2}\right)}{{\left(1+{R}_{\mathrm{g}}{Q}_{\mathrm{g}\mathrm{b}}{\omega}^{\alpha_{\mathrm{g}\mathrm{b}}} \cos \left(\frac{\alpha_{\mathrm{g}\mathrm{b}}\uppi}{2}\right)\right)}^2+\left({R}_{\mathrm{g}}{Q}_{\mathrm{g}\mathrm{b}}{\omega}^{\alpha_{\mathrm{g}\mathrm{b}}} \sin \right(\Big(\frac{\alpha_{\mathrm{g}\mathrm{b}}\uppi}{2}{\left)\right)}^2} $$

(3)

Figure 3a, b shows the experimental and calculated values of real and imaginary parts of the impedance (Z′ and Z″) as a function of frequency at different temperatures (573–700 K) using the equivalent circuit. Typical curves are observed in the previously mentioned figures. The temperature affects strongly the magnitude of resistance. At lower temperatures, Z′ decreases monotonically with increases in frequency up to a certain frequency and then becomes frequency independent (Fig. 3a). Moreover, the magnitude of Z″ maxima decreases with temperatures showing the thermally activated nature of the relaxation time as well as an increasing loss in resistive property of the sample. This behavior of the impedance pattern arises possibly due to the presence of space charge in the materials [21].

Fig. 3

a, b The real and the imaginary parts of the impedance as a function of angular frequency at several temperatures

Figure 4 shows the frequency dependence of Z′ and Z″ fits to the equivalent circuit and their corresponding Argand diagram [22, 23] (inset figure) drawn at 690 K in II-NaFeP₂O₇. It is clear that Z″ increases, whereas Z′ decreases, and at a particular frequency, Z″ occupies a maximum value and Z′ intersects, and above this frequency, both values merge with the X-axis. Those diagrams clearly show a good agreement between theoretical and experimental data. The extracted parameters, as obtained from the ZView software, are collected in Table 1. The capacitance values of the high- and the low-frequency semicircles are found to be in the range of 10⁻¹² and 10⁻¹⁰ F, respectively, proving that the observed semicircles represent the bulk and grain boundary response of the system, respectively [24, 25].

Fig. 4

Variation of Z′ and Z″ with angular frequency at 690 K; inset is the Cole–Cole plot at the same temperature

Table 1 The equivalent circuit parameters for the NaFeP₂O₇ sample

Thus, the obtained values of bulk resistance (R _g), corresponding to the grain at different temperatures, enable finding the electrical conductivity σ _g defined by the relation as follows:

$$ {\sigma}_{\mathrm{g}}=\frac{e}{R_{\mathrm{g}}*s} $$

(4)

where $\frac{e}{s}$ represents the sample geometrical ratio.

The temperature dependence of the conductivity σ _g,gb of II-NaFeP₂O₇ is represented in Fig. 5 in the form of Ln(σ _g,gb T) vs. 1,000 / T. An Arrhenius type behavior σ _g,gb T = σ ₀ exp (−E _a / k _B T) is shown. While E _a is the activation energy, T is the absolute temperature, k _B is Boltzmann’s constant, and σ ₀ is the pre-exponential factor which includes the charge carrier mobility and density of states.

Fig. 5

σ _g and σ _gb as a function of temperature

Both σ _g (grain) and σ _gb (grain boundary) increase with increasing temperature, indicating that the electrical conduction in the material is a thermally activated process. For the whole studied temperature ranges, the bulk conductivity is higher than the grain boundary one. The value of activation energy estimated from the Arrhenius plot of σ _g and σ _gb with respect to 1,000 / T is 0.85 (2) eV and 0.83 (3) eV, respectively. Thus, we notice that the bulk and the grain boundary activation energy values are very close. This indicates that the conduction of the grain and the grain boundary increases at a similar rate with an increase in temperature.

Electric modulus analysis

Electrical transport process parameters (such as carrier/ion hopping rate, conductivity relaxation time, etc.) in ceramic materials can be analyzed via complex electric modulus formalism. Although the physical meaning of this type of representation is still controversially discussed, the dielectric modulus is frequently used in the analysis of dielectric data of ionic conductors [26].

The electric modulus M*(ω) as expressed in the complex modulus formalism is:

$$ {M}^{*}\left(\omega \right)=M^{\prime }+ iM^{{\prime\prime} } $$

where M′ = ωC ₀ Z″, M″ = ωC ₀ Z′, and C ₀ is the vacuum capacitance of the cell. The graph of the imaginary part of the dielectric modulus, as a function of frequency at different temperatures, is shown in Fig. 6. As a matter of fact, two relaxation peaks are observed in the patterns. Thus, the smaller peak at the lower frequency is associated with the grain boundary effect, and the well-defined one at the higher frequency is correlated with the bulk effects. The positions of these relaxation peaks are found to shift to higher frequencies with the increase of the temperature showing a temperature-dependent relaxation, as well as a correlation between motions of mobile ion charges [27]. From the view of the higher frequency peak of M″ for each temperature, the frequency region below the peak represents the range in which the charge carriers are mobile over long distances [28], whereas the frequency region above the peak determines the range in which the charge carriers are confined to the potential wells being mobile on short distances within the wells [29, 30].

Fig. 6

Frequency dependence of the imaginary part of the electric modulus at several temperatures

A conventional equation to fit the frequency dependence curve of M″, at constant temperature, in a variety of materials, is based on the Havriliak–Negami equation [31]. In this case, the electric modulus is given by:

$$ {M}^{*}={M}_{\infty}\left[1-{\varphi}_{\mathrm{HN}}\left(\omega \right)\right]={M}_{\infty}\left[1-\frac{1}{{\left[1+{\left( i\omega \tau \right)}^{\alpha}\right]}^{\gamma }}\right] $$

(5)

HN is the Havriliak–Negami (HN) function and both HN parameters α and γ define the Kohlrausch parameter β as β = (αγ)^1/1.23. Therefore, in order to simulate the two relaxation peaks, we have modified the above expression as follows:

$$ {M}^{*}={M}_{\infty}\left[1-\frac{1}{{\left[1+{\left( i\omega {\tau}_{\mathrm{g}}\right)}^{\alpha_{\mathrm{g}}}\right]}^{\gamma_{\mathrm{g}}}}\right]+{M}_{\mathrm{S}}\left[1-\frac{1}{{\left[1+{\left( i\omega {\tau}_{\mathrm{g}\mathrm{b}}\right)}^{\alpha_{\mathrm{g}\mathrm{b}}}\right]}^{\gamma_{\mathrm{g}\mathrm{b}}}}\right] $$

(6)

where M _∞ = 1 / ε _∞, M _S = 1 / ε _S, ε _∞, and ε _S being the high- and low-frequency asymptotic values of the real part of the dielectric permittivity, respectively. The parameters α _g and γ _g represent the shape of the high-frequency peak corresponding to the grains, and α _gb and γ _gb are the corresponding quantities for the low-frequency peak [19]. A good fit was performed using this equation as shown in Fig. 6.

The high-frequency peak in the M″ curves is found to be asymmetric, implying a nonexponential behavior of the bulk conductivity relaxation. This type of behavior suggests the possibility that the ion migration takes place via hopping accompanied by a consequential time-dependent mobility of other charge carriers of the same type in their vicinity [32, 33]. The nonexponential conductivity relaxation is well described by a Kohlrausch–Williams–Watts (KWW) function [34]:

$$ \varphi (t)= \exp \left[{\left(\frac{-t}{\tau}\right)}^{\beta}\right]\kern4em 0<\beta \kern0.5em <1 $$

(7)

where φ(t) represents the distribution of relaxation time in ion-conducting materials and τ is the conductivity relaxation time. The value of β determined from the full width at half maximum (FWHM) of the high-frequency peak (β = 1.14/FWHM) and the β obtained by fitting the M″ curve to Eq. 6 are very close. Therefore, the β values obtained lie in the range of 0.72 for the high-frequency peak, whereas for the peak at low frequency, it is found to be between 0.61 and 0.68. Hence, the variations of the relaxation frequency with temperature for the bulk and the grain boundary follow the Arrhenius behavior, as shown in Fig. 5. The activation energy calculation was based on the slopes of the Log (ω _g,_gb) vs. 1,000 / T plot. Consequently, the activation energy values are E _g = 0.84 (3) eV and E _gb = 0.83 (4) eV. In short, the spectra are close enough to suggest that the Na⁺ ion transport is probably due to a hopping mechanism through tunnels presented in the structure of II-NaFeP₂O₇. Otherwise, these values are typical values for ionic conduction mechanism [35, 36].

Figure 7 shows the M″ / M″_max vs. Log (f / f _max) at different temperature (normalized plot), and it shows the scaling behavior in the material. This is called the modulus master curve that enables us to have an insight into the dielectric processes occurring in the material. It is characterized by a broad asymmetric pattern with a crossover from the long range. Moreover, it shows that the shape and FWHM of the asymmetric M″ / M″_max curve remain constant in the temperature range studied, implying a nonexponential behavior of the conductivity relaxation. Indeed, the approximate overlap of the modulus curves for all temperatures indicates the dynamical processes occurring at different frequencies and independence of temperature. This has usually been regarded as an indication of a distribution of relaxation times in the conduction process occurring in the material. Consequently, this might be due to the ion migration that takes place via the hopping mechanism [37].

Fig. 7

Normalized plots of M″ / M″_max vs. Ln(f / f _max) for II-NaFeP₂O₇ at different temperatures

Frequency and temperature dependence of AC conductivity

The conductivity spectra throw light on the hopping motion of the mobile ions. Hence, a typical frequency dependence of AC conductivity within the considered temperature ranges for the sample is shown in Fig. 8. As a matter of fact, the values of the AC conductivity were calculated from the complex impedance data using:

Fig. 8

Variation of AC conductivity of II-NaFeP₂O₇ with frequency and temperature. The solid lines are the best fits to Eq. 8

$$ {\sigma}_{\mathrm{AC}}=\left(\frac{e}{s}\right)\left(\frac{Z^{\prime }}{Z{\prime}^2+Z{{\prime\prime}}^2}\right) $$

(8)

where Z′ and Z″ are the real and the imaginary parts of the complex impedance, and e and s are the thickness and the area, respectively, of the present pellet.

The frequency-dependent conductivity spectrum shows a low-frequency plateau, followed by a region that is sensitive to frequency as well as temperature. The frequency-independent region characterizes the DC conductivity due to the random diffusion of the ionic charge carriers via activated hopping. However, for the region of frequencies where conductivity increases markedly with frequency, the hopping takes place by charge carriers through trap sites separated by energy barriers of varied heights. This typical behavior suggests the presence of a hopping mechanism between the allowed sites [38]. The conductivity results are fitted by the following equation referred to as Jonscher’s law [39]. Taking into account the fitting procedure, A and n values have been varied simultaneously to get the best fits.

$$ {\sigma}_{\mathrm{AC}}\left(\omega \right)={\sigma}_{\mathrm{DC}}+A{\omega}^n $$

(9)

where σ _DC is the DC conductivity, A is a constant temperature-dependent parameter, and n is the power law exponent, where 0 < n < 1. As a matter of fact, n represents the degree of interaction between mobile ions with the environments surrounding them and A determines the strength of polarizability. Added to that, the obtained values of (n) for the sample under investigation are in the range of 0.362–0.476, in which the values decrease with the rise in temperature as shown in Fig. 9.

Fig. 9

The exponent factor, n, as a function of temperature of the II-NaFeP₂O₇ ceramic sample

Following, the hopping rate, ω _h has been obtained by using the equation:

$$ {\omega}_{\mathrm{h}}={\left(\frac{\sigma_{\mathrm{DC}}}{A}\right)}^{1/n} $$

(10)

The DC conductivity represents the random process in which the ion diffuses throughout the network by performing repeated hops between charge-compensating sites [40].

Figure 10 depicts the dependence of the hopping frequency, and it follows the Arrhenius behavior. In the present ceramic sample, the hopping frequency and DC conductivity are thermally activated indicating that both are originating from the sodium ion migration. The activation energy extracted from the slope of the plot is 0.85 (3) eV. The near value of activation energies, obtained from the analyses of impedance and conductivity data suggesting the mobility of the charge carrier, is due to a hopping mechanism in the tunnel-type cavities occurring in the structure of the title compound.

Fig. 10

Temperature dependence of the hopping frequency ω _h

In addition, we consider the scaling of the conductivity spectra at different temperatures. In the past few years, different scaling models have been proposed [41, 42]. We have scaled the conductivity spectra by a scaling process [43] reported recently.

To put it simply, the AC conductivity is scaled by σ _DC, while the frequency axis is scaled by the crossover frequency ω _h, which is expected to be more appropriate for scaling the conductivity spectra of ionic conductors, since it takes into account the dependence of the conductivity spectra on the structure and the possible changes of the hopping distance experienced by the mobile ions [42]. As shown in Fig. 11, the scaled AC conductivity data collapsed into a single curve and it implies that the relaxation dynamics of charge carriers in the present sample is independent of temperature and compositions [43].

Fig. 11

The scaled conductivity Log (σ _AC / σ _DC) vs. Log (ω / ω _h)

The electrical properties of II-NaFeP₂O₇ can be compared with those relative to AgFeP₂O₇. Although they are isostructural, the materials show different features in the conductivity parameters presented in Table 2. In fact, the differences between both compounds are due to the different alkali cation radii: r (Ag⁺) = 1.15 Å and r (Na⁺) = 1.09 Å. As expected, the better activation energy of the title compound can be attributed to a lower Na⁺ radii with regard to Ag⁺ ion. Otherwise, it is also related to the wide bottlenecks of the tunnels in NaFeP₂O₇ (bottlenecks of 4.45 Å). However, the low polarizability of the Na⁺ ion explains the lower conductivity of the investigated compound.

Table 2 Activation energies and conductivities at 573 K for NaFeP₂O7 and AgFeP₂O7 compounds

Conclusions

Overall, this research paper reports the results of a systematic investigation on AC conductivity, AC conductivity scaling, and electrical modulus of II-NaFeP₂O₇ compound synthesized by the classic ceramic method. X-ray structural analysis exhibits the formation of a single-phase monoclinic at room temperature. Two semicircles are observed in an impedance plot indicating the presence of two relaxation processes in the compound associated with grain and grain boundary. Indeed, the dielectric data have also been analyzed in modulus formalism. Similarly, two dielectric relaxation peaks thermally activated in the modulus loss spectra confirmed the grain and grain boundary contribution to electrical response in the title compound. Also, AC conductivity measurements and its scaling analysis are studied on the II-NaFeP₂O₇ in the frequency range from 209 Hz to 5 MHz and in the temperature range from 573 to 700 K. Finally, the activation energies obtained from the impedance and modulus spectra are proven to be close, suggesting that the ionic transport in the investigated material can be described by a hopping mechanism.